TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub এ দেখুন GitHub এ দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
AI অ্যাপ্লিকেশনগুলিতে যেগুলি নিরাপত্তা-সমালোচনামূলক (যেমন, চিকিৎসা সংক্রান্ত সিদ্ধান্ত গ্রহণ এবং স্বায়ত্তশাসিত ড্রাইভিং) বা যেখানে ডেটা সহজাতভাবে কোলাহলপূর্ণ (যেমন, প্রাকৃতিক ভাষা বোঝা), এটি একটি গভীর শ্রেণিবিন্যাসকারীর জন্য তার অনিশ্চয়তাকে নির্ভরযোগ্যভাবে পরিমাপ করা গুরুত্বপূর্ণ। গভীর শ্রেণিবিন্যাসকারীকে তার নিজস্ব সীমাবদ্ধতা সম্পর্কে সচেতন হতে হবে এবং কখন এটি মানব বিশেষজ্ঞদের হাতে নিয়ন্ত্রণ হস্তান্তর করবে। এই টিউটোরিয়ালটি দেখায় কিভাবে স্পেকট্রাল-নর্মালাইজড নিউরাল গাউসিয়ান প্রসেস ( SNGP ) নামক একটি কৌশল ব্যবহার করে অনিশ্চয়তা পরিমাপ করার ক্ষেত্রে গভীর শ্রেণীবদ্ধকারীর ক্ষমতা উন্নত করা যায়।
SNGP-এর মূল ধারণা হল নেটওয়ার্কে সাধারণ পরিবর্তনগুলি প্রয়োগ করে একটি গভীর শ্রেণিবিন্যাসকারীর দূরত্ব সচেতনতা উন্নত করা। একটি মডেলের দূরত্ব সচেতনতা হল তার ভবিষ্যদ্বাণীমূলক সম্ভাব্যতা পরীক্ষার উদাহরণ এবং প্রশিক্ষণ ডেটার মধ্যে দূরত্বকে কীভাবে প্রতিফলিত করে তার একটি পরিমাপ। এটি একটি আকাঙ্খিত সম্পত্তি যা গোল্ড-স্ট্যান্ডার্ড সম্ভাব্য মডেলগুলির জন্য সাধারণ (যেমন, আরবিএফ কার্নেলের সাথে গাউসিয়ান প্রক্রিয়া ) কিন্তু গভীর নিউরাল নেটওয়ার্ক সহ মডেলগুলির অভাব রয়েছে। SNGP তার ভবিষ্যদ্বাণীমূলক নির্ভুলতা বজায় রেখে এই গাউসিয়ান-প্রক্রিয়া আচরণকে গভীর শ্রেণীবিভাগে ইনজেক্ট করার একটি সহজ উপায় প্রদান করে।
এই টিউটোরিয়ালটি দুটি চাঁদের ডেটাসেটে একটি গভীর অবশিষ্ট নেটওয়ার্ক (ResNet)-ভিত্তিক SNGP মডেল প্রয়োগ করে, এবং এর অনিশ্চয়তার পৃষ্ঠকে অন্যান্য দুটি জনপ্রিয় অনিশ্চয়তা পদ্ধতির সাথে তুলনা করে - মন্টে কার্লো ড্রপআউট এবং ডিপ এনসেম্বল )।
এই টিউটোরিয়ালটি একটি খেলনা 2D ডেটাসেটে SNGP মডেলকে চিত্রিত করে। BERT-বেস ব্যবহার করে বাস্তব-বিশ্বের প্রাকৃতিক ভাষা বোঝার কাজে SNGP প্রয়োগ করার উদাহরণের জন্য, অনুগ্রহ করে SNGP-BERT টিউটোরিয়ালটি দেখুন। বিভিন্ন ধরণের বেঞ্চমার্ক ডেটাসেটে (যেমন, CIFAR-100 , ImageNet , Jigsaw বিষাক্ততা সনাক্তকরণ , ইত্যাদি) SNGP মডেলের (এবং অন্যান্য অনেক অনিশ্চয়তা পদ্ধতি) উচ্চ-মানের বাস্তবায়নের জন্য, অনুগ্রহ করে অনিশ্চয়তার বেসলাইন বেঞ্চমার্কটি দেখুন।
এসএনজিপি সম্পর্কে
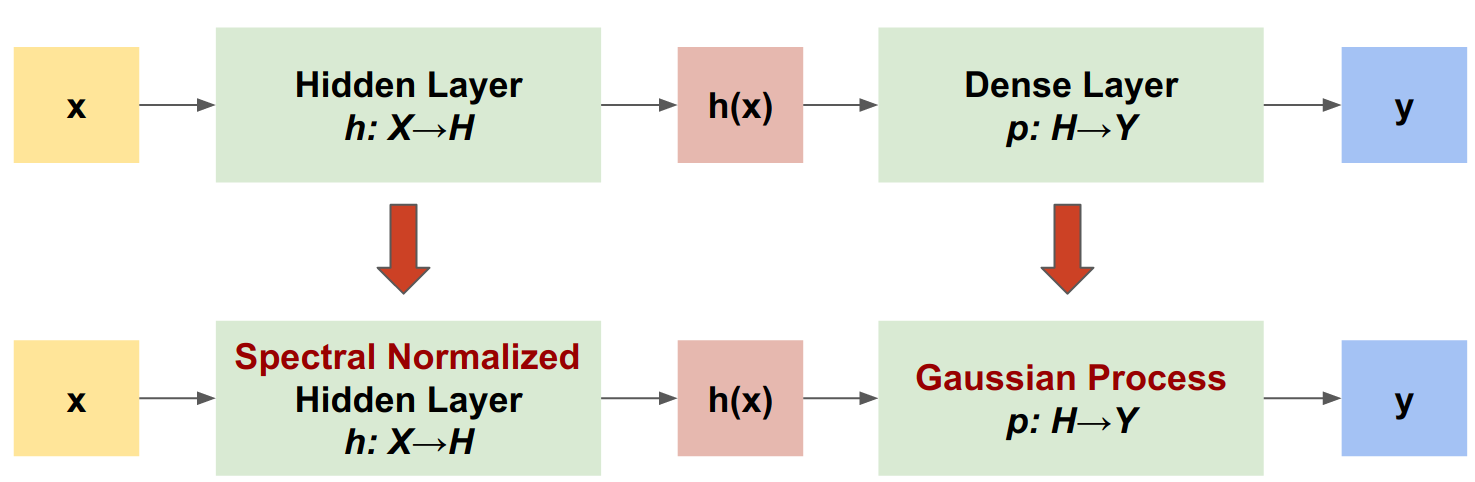
স্পেকট্রাল-নর্মালাইজড নিউরাল গাউসিয়ান প্রসেস (SNGP) হল একটি গভীর শ্রেণীবিভাগের অনিশ্চয়তার গুণমান উন্নত করার জন্য একটি সহজ পদ্ধতি যা একই রকম নির্ভুলতা এবং লেটেন্সি বজায় রেখে। একটি গভীর অবশিষ্ট নেটওয়ার্ক দেওয়া, SNGP মডেলটিতে দুটি সহজ পরিবর্তন করে:
- এটি লুকানো অবশিষ্ট স্তরগুলিতে বর্ণালী স্বাভাবিককরণ প্রয়োগ করে।
- এটি একটি গাউসিয়ান প্রক্রিয়া স্তর দিয়ে ঘন আউটপুট স্তর প্রতিস্থাপন করে।
অন্যান্য অনিশ্চয়তা পদ্ধতির তুলনায় (যেমন, মন্টে কার্লো ড্রপআউট বা ডিপ এনসেম্বল), SNGP-এর বেশ কিছু সুবিধা রয়েছে:
- এটি বিস্তৃত অত্যাধুনিক অবশিষ্ট-ভিত্তিক আর্কিটেকচারের জন্য কাজ করে (যেমন, (প্রশস্ত) ResNet, DenseNet, BERT, ইত্যাদি)।
- এটি একটি একক-মডেল পদ্ধতি (অর্থাৎ, ensemble গড় উপর নির্ভর করে না)। তাই SNGP-এর একক নির্ধারক নেটওয়ার্কের মতো একই স্তরের লেটেন্সি রয়েছে এবং ইমেজনেট এবং জিগস টক্সিক কমেন্ট শ্রেণীবিভাগের মতো বড় ডেটাসেটে সহজেই স্কেল করা যেতে পারে।
- দূরত্ব-সচেতনতা সম্পত্তির কারণে এটির ডোমেনের বাইরের সনাক্তকরণ কার্যক্ষমতা রয়েছে।
এই পদ্ধতির খারাপ দিকগুলি হল:
একটি SNGP-এর ভবিষ্যদ্বাণীমূলক অনিশ্চয়তা ল্যাপ্লেস আনুমানিকতা ব্যবহার করে গণনা করা হয়। তাই তাত্ত্বিকভাবে, SNGP-এর উত্তরীয় অনিশ্চয়তা একটি সঠিক গাউসিয়ান প্রক্রিয়ার থেকে ভিন্ন।
একটি নতুন যুগের সূচনায় SNGP প্রশিক্ষণের জন্য একটি সহভরিতা রিসেট পদক্ষেপ প্রয়োজন। এটি একটি প্রশিক্ষণ পাইপলাইনে অল্প পরিমাণে অতিরিক্ত জটিলতা যোগ করতে পারে। এই টিউটোরিয়ালটি কেরাস কলব্যাক ব্যবহার করে এটি বাস্তবায়ন করার একটি সহজ উপায় দেখায়।
সেটআপ
pip install --use-deprecated=legacy-resolver tf-models-official
# refresh pkg_resources so it takes the changes into account.
import pkg_resources
import importlib
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import sklearn.datasets
import numpy as np
import tensorflow as tf
import official.nlp.modeling.layers as nlp_layers
ভিজ্যুয়ালাইজেশন ম্যাক্রো সংজ্ঞায়িত করুন
plt.rcParams['figure.dpi'] = 140
DEFAULT_X_RANGE = (-3.5, 3.5)
DEFAULT_Y_RANGE = (-2.5, 2.5)
DEFAULT_CMAP = colors.ListedColormap(["#377eb8", "#ff7f00"])
DEFAULT_NORM = colors.Normalize(vmin=0, vmax=1,)
DEFAULT_N_GRID = 100
দুই চাঁদের ডেটাসেট
দুটি চাঁদের ডেটাসেট থেকে প্রশিক্ষণ এবং মূল্যায়ন ডেটাসেট তৈরি করুন।
def make_training_data(sample_size=500):
"""Create two moon training dataset."""
train_examples, train_labels = sklearn.datasets.make_moons(
n_samples=2 * sample_size, noise=0.1)
# Adjust data position slightly.
train_examples[train_labels == 0] += [-0.1, 0.2]
train_examples[train_labels == 1] += [0.1, -0.2]
return train_examples, train_labels
সম্পূর্ণ 2D ইনপুট স্থানের উপর মডেলের ভবিষ্যদ্বাণীমূলক আচরণের মূল্যায়ন করুন।
def make_testing_data(x_range=DEFAULT_X_RANGE, y_range=DEFAULT_Y_RANGE, n_grid=DEFAULT_N_GRID):
"""Create a mesh grid in 2D space."""
# testing data (mesh grid over data space)
x = np.linspace(x_range[0], x_range[1], n_grid)
y = np.linspace(y_range[0], y_range[1], n_grid)
xv, yv = np.meshgrid(x, y)
return np.stack([xv.flatten(), yv.flatten()], axis=-1)
মডেল অনিশ্চয়তা মূল্যায়ন করতে, একটি তৃতীয় শ্রেণীর অন্তর্গত একটি আউট-অফ-ডোমেন (OOD) ডেটাসেট যোগ করুন৷ প্রশিক্ষণের সময় মডেলটি কখনই এই OOD উদাহরণগুলি দেখে না।
def make_ood_data(sample_size=500, means=(2.5, -1.75), vars=(0.01, 0.01)):
return np.random.multivariate_normal(
means, cov=np.diag(vars), size=sample_size)
# Load the train, test and OOD datasets.
train_examples, train_labels = make_training_data(
sample_size=500)
test_examples = make_testing_data()
ood_examples = make_ood_data(sample_size=500)
# Visualize
pos_examples = train_examples[train_labels == 0]
neg_examples = train_examples[train_labels == 1]
plt.figure(figsize=(7, 5.5))
plt.scatter(pos_examples[:, 0], pos_examples[:, 1], c="#377eb8", alpha=0.5)
plt.scatter(neg_examples[:, 0], neg_examples[:, 1], c="#ff7f00", alpha=0.5)
plt.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
plt.legend(["Postive", "Negative", "Out-of-Domain"])
plt.ylim(DEFAULT_Y_RANGE)
plt.xlim(DEFAULT_X_RANGE)
plt.show()

এখানে নীল এবং কমলা ইতিবাচক এবং নেতিবাচক শ্রেণীর প্রতিনিধিত্ব করে, এবং লাল OOD ডেটার প্রতিনিধিত্ব করে। একটি মডেল যা অনিশ্চয়তাকে ভালভাবে পরিমাপ করে তা প্রশিক্ষণের ডেটার কাছাকাছি থাকাকালীন আত্মবিশ্বাসী হতে পারে (যেমন, \(p(x_{test})\) 0 বা 1 এর কাছাকাছি), এবং প্রশিক্ষণ ডেটা অঞ্চল থেকে দূরে থাকলে (যেমন, \(p(x_{test})\) 0.5 এর কাছাকাছি) অনিশ্চিত হবে )
নির্ধারক মডেল
মডেল সংজ্ঞায়িত করুন
(বেসলাইন) ডিটারমিনিস্টিক মডেল থেকে শুরু করুন: ড্রপআউট নিয়মিতকরণ সহ একটি মাল্টি-লেয়ার রেসিডুয়াল নেটওয়ার্ক (ResNet)।
class DeepResNet(tf.keras.Model):
"""Defines a multi-layer residual network."""
def __init__(self, num_classes, num_layers=3, num_hidden=128,
dropout_rate=0.1, **classifier_kwargs):
super().__init__()
# Defines class meta data.
self.num_hidden = num_hidden
self.num_layers = num_layers
self.dropout_rate = dropout_rate
self.classifier_kwargs = classifier_kwargs
# Defines the hidden layers.
self.input_layer = tf.keras.layers.Dense(self.num_hidden, trainable=False)
self.dense_layers = [self.make_dense_layer() for _ in range(num_layers)]
# Defines the output layer.
self.classifier = self.make_output_layer(num_classes)
def call(self, inputs):
# Projects the 2d input data to high dimension.
hidden = self.input_layer(inputs)
# Computes the resnet hidden representations.
for i in range(self.num_layers):
resid = self.dense_layers[i](hidden)
resid = tf.keras.layers.Dropout(self.dropout_rate)(resid)
hidden += resid
return self.classifier(hidden)
def make_dense_layer(self):
"""Uses the Dense layer as the hidden layer."""
return tf.keras.layers.Dense(self.num_hidden, activation="relu")
def make_output_layer(self, num_classes):
"""Uses the Dense layer as the output layer."""
return tf.keras.layers.Dense(
num_classes, **self.classifier_kwargs)
এই টিউটোরিয়ালটি 128টি লুকানো ইউনিট সহ একটি 6-স্তর ResNet ব্যবহার করে।
resnet_config = dict(num_classes=2, num_layers=6, num_hidden=128)
resnet_model = DeepResNet(**resnet_config)
resnet_model.build((None, 2))
resnet_model.summary()
Model: "deep_res_net"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 384
dense_1 (Dense) multiple 16512
dense_2 (Dense) multiple 16512
dense_3 (Dense) multiple 16512
dense_4 (Dense) multiple 16512
dense_5 (Dense) multiple 16512
dense_6 (Dense) multiple 16512
dense_7 (Dense) multiple 258
=================================================================
Total params: 99,714
Trainable params: 99,330
Non-trainable params: 384
_________________________________________________________________
ট্রেন মডেল
লস ফাংশন এবং অ্যাডাম অপ্টিমাইজার হিসাবে SparseCategoricalCrossentropy ব্যবহার করার জন্য প্রশিক্ষণের পরামিতিগুলি কনফিগার করুন।
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.keras.metrics.SparseCategoricalAccuracy(),
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
train_config = dict(loss=loss, metrics=metrics, optimizer=optimizer)
ব্যাচ আকার 128 সহ 100 যুগের জন্য মডেলটিকে প্রশিক্ষণ দিন।
fit_config = dict(batch_size=128, epochs=100)
resnet_model.compile(**train_config)
resnet_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 1s 4ms/step - loss: 1.1251 - sparse_categorical_accuracy: 0.5050 Epoch 2/100 8/8 [==============================] - 0s 3ms/step - loss: 0.5538 - sparse_categorical_accuracy: 0.6920 Epoch 3/100 8/8 [==============================] - 0s 3ms/step - loss: 0.2881 - sparse_categorical_accuracy: 0.9160 Epoch 4/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1923 - sparse_categorical_accuracy: 0.9370 Epoch 5/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1550 - sparse_categorical_accuracy: 0.9420 Epoch 6/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1403 - sparse_categorical_accuracy: 0.9450 Epoch 7/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1269 - sparse_categorical_accuracy: 0.9430 Epoch 8/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1208 - sparse_categorical_accuracy: 0.9460 Epoch 9/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1158 - sparse_categorical_accuracy: 0.9510 Epoch 10/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1103 - sparse_categorical_accuracy: 0.9490 Epoch 11/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1051 - sparse_categorical_accuracy: 0.9510 Epoch 12/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1053 - sparse_categorical_accuracy: 0.9510 Epoch 13/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1013 - sparse_categorical_accuracy: 0.9450 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0967 - sparse_categorical_accuracy: 0.9500 Epoch 15/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9530 Epoch 16/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0984 - sparse_categorical_accuracy: 0.9500 Epoch 17/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0982 - sparse_categorical_accuracy: 0.9480 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0918 - sparse_categorical_accuracy: 0.9510 Epoch 19/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0903 - sparse_categorical_accuracy: 0.9500 Epoch 20/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0883 - sparse_categorical_accuracy: 0.9510 Epoch 21/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0870 - sparse_categorical_accuracy: 0.9530 Epoch 22/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0884 - sparse_categorical_accuracy: 0.9560 Epoch 23/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0850 - sparse_categorical_accuracy: 0.9540 Epoch 24/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0808 - sparse_categorical_accuracy: 0.9580 Epoch 25/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0773 - sparse_categorical_accuracy: 0.9560 Epoch 26/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0801 - sparse_categorical_accuracy: 0.9590 Epoch 27/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0779 - sparse_categorical_accuracy: 0.9580 Epoch 28/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0807 - sparse_categorical_accuracy: 0.9580 Epoch 29/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0820 - sparse_categorical_accuracy: 0.9570 Epoch 30/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0730 - sparse_categorical_accuracy: 0.9600 Epoch 31/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0782 - sparse_categorical_accuracy: 0.9590 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0704 - sparse_categorical_accuracy: 0.9600 Epoch 33/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0709 - sparse_categorical_accuracy: 0.9610 Epoch 34/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0758 - sparse_categorical_accuracy: 0.9580 Epoch 35/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9610 Epoch 36/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0688 - sparse_categorical_accuracy: 0.9600 Epoch 37/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0675 - sparse_categorical_accuracy: 0.9630 Epoch 38/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9690 Epoch 39/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0677 - sparse_categorical_accuracy: 0.9610 Epoch 40/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9650 Epoch 41/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0614 - sparse_categorical_accuracy: 0.9690 Epoch 42/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0663 - sparse_categorical_accuracy: 0.9680 Epoch 43/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0626 - sparse_categorical_accuracy: 0.9740 Epoch 44/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9760 Epoch 45/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0573 - sparse_categorical_accuracy: 0.9780 Epoch 46/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0568 - sparse_categorical_accuracy: 0.9770 Epoch 47/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0595 - sparse_categorical_accuracy: 0.9780 Epoch 48/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0482 - sparse_categorical_accuracy: 0.9840 Epoch 49/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0515 - sparse_categorical_accuracy: 0.9820 Epoch 50/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0525 - sparse_categorical_accuracy: 0.9830 Epoch 51/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0507 - sparse_categorical_accuracy: 0.9790 Epoch 52/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0433 - sparse_categorical_accuracy: 0.9850 Epoch 53/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0511 - sparse_categorical_accuracy: 0.9820 Epoch 54/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0501 - sparse_categorical_accuracy: 0.9820 Epoch 55/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0440 - sparse_categorical_accuracy: 0.9890 Epoch 56/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9850 Epoch 57/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9880 Epoch 58/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0416 - sparse_categorical_accuracy: 0.9860 Epoch 59/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0479 - sparse_categorical_accuracy: 0.9860 Epoch 60/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0434 - sparse_categorical_accuracy: 0.9860 Epoch 61/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0414 - sparse_categorical_accuracy: 0.9880 Epoch 62/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0402 - sparse_categorical_accuracy: 0.9870 Epoch 63/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0376 - sparse_categorical_accuracy: 0.9890 Epoch 64/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0337 - sparse_categorical_accuracy: 0.9900 Epoch 65/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0309 - sparse_categorical_accuracy: 0.9910 Epoch 66/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9910 Epoch 67/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0389 - sparse_categorical_accuracy: 0.9870 Epoch 68/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0333 - sparse_categorical_accuracy: 0.9920 Epoch 69/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0331 - sparse_categorical_accuracy: 0.9890 Epoch 70/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0346 - sparse_categorical_accuracy: 0.9900 Epoch 71/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0367 - sparse_categorical_accuracy: 0.9880 Epoch 72/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0283 - sparse_categorical_accuracy: 0.9920 Epoch 73/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0315 - sparse_categorical_accuracy: 0.9930 Epoch 74/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0271 - sparse_categorical_accuracy: 0.9900 Epoch 75/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0257 - sparse_categorical_accuracy: 0.9920 Epoch 76/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0289 - sparse_categorical_accuracy: 0.9900 Epoch 77/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0264 - sparse_categorical_accuracy: 0.9900 Epoch 78/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0272 - sparse_categorical_accuracy: 0.9910 Epoch 79/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9880 Epoch 80/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0249 - sparse_categorical_accuracy: 0.9900 Epoch 81/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0216 - sparse_categorical_accuracy: 0.9930 Epoch 82/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0279 - sparse_categorical_accuracy: 0.9890 Epoch 83/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0261 - sparse_categorical_accuracy: 0.9920 Epoch 84/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0235 - sparse_categorical_accuracy: 0.9920 Epoch 85/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0236 - sparse_categorical_accuracy: 0.9930 Epoch 86/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0219 - sparse_categorical_accuracy: 0.9920 Epoch 87/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0196 - sparse_categorical_accuracy: 0.9920 Epoch 88/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0215 - sparse_categorical_accuracy: 0.9900 Epoch 89/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0223 - sparse_categorical_accuracy: 0.9900 Epoch 90/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0200 - sparse_categorical_accuracy: 0.9950 Epoch 91/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0250 - sparse_categorical_accuracy: 0.9900 Epoch 92/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0160 - sparse_categorical_accuracy: 0.9940 Epoch 93/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 94/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 95/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0172 - sparse_categorical_accuracy: 0.9960 Epoch 96/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0209 - sparse_categorical_accuracy: 0.9940 Epoch 97/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0179 - sparse_categorical_accuracy: 0.9920 Epoch 98/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0195 - sparse_categorical_accuracy: 0.9940 Epoch 99/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0165 - sparse_categorical_accuracy: 0.9930 Epoch 100/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0170 - sparse_categorical_accuracy: 0.9950 <keras.callbacks.History at 0x7ff7ac5c8fd0>
অনিশ্চয়তা কল্পনা করুন
def plot_uncertainty_surface(test_uncertainty, ax, cmap=None):
"""Visualizes the 2D uncertainty surface.
For simplicity, assume these objects already exist in the memory:
test_examples: Array of test examples, shape (num_test, 2).
train_labels: Array of train labels, shape (num_train, ).
train_examples: Array of train examples, shape (num_train, 2).
Arguments:
test_uncertainty: Array of uncertainty scores, shape (num_test,).
ax: A matplotlib Axes object that specifies a matplotlib figure.
cmap: A matplotlib colormap object specifying the palette of the
predictive surface.
Returns:
pcm: A matplotlib PathCollection object that contains the palette
information of the uncertainty plot.
"""
# Normalize uncertainty for better visualization.
test_uncertainty = test_uncertainty / np.max(test_uncertainty)
# Set view limits.
ax.set_ylim(DEFAULT_Y_RANGE)
ax.set_xlim(DEFAULT_X_RANGE)
# Plot normalized uncertainty surface.
pcm = ax.imshow(
np.reshape(test_uncertainty, [DEFAULT_N_GRID, DEFAULT_N_GRID]),
cmap=cmap,
origin="lower",
extent=DEFAULT_X_RANGE + DEFAULT_Y_RANGE,
vmin=DEFAULT_NORM.vmin,
vmax=DEFAULT_NORM.vmax,
interpolation='bicubic',
aspect='auto')
# Plot training data.
ax.scatter(train_examples[:, 0], train_examples[:, 1],
c=train_labels, cmap=DEFAULT_CMAP, alpha=0.5)
ax.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
return pcm
এখন নির্ধারক মডেলের ভবিষ্যদ্বাণীগুলি কল্পনা করুন। প্রথমে ক্লাসের সম্ভাব্যতা প্লট করুন:
\[p(x) = softmax(logit(x))\]
resnet_logits = resnet_model(test_examples)
resnet_probs = tf.nn.softmax(resnet_logits, axis=-1)[:, 0] # Take the probability for class 0.
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_probs, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Class Probability, Deterministic Model")
plt.show()

এই প্লটে, হলুদ এবং বেগুনি দুটি শ্রেণীর জন্য ভবিষ্যদ্বাণীমূলক সম্ভাব্যতা। একটি অরৈখিক সিদ্ধান্তের সীমানা সহ দুটি পরিচিত শ্রেণী (নীল এবং কমলা) শ্রেণীবদ্ধ করার ক্ষেত্রে নির্ধারণবাদী মডেলটি একটি ভাল কাজ করেছে। যাইহোক, এটি দূরত্ব-সচেতন নয়, এবং কমলা শ্রেণী হিসাবে আত্মবিশ্বাসের সাথে ডোমেন-এর বাইরে কখনো দেখা না যাওয়া লাল (OOD) উদাহরণগুলিকে শ্রেণীবদ্ধ করে৷
ভবিষ্যদ্বাণীমূলক ভিন্নতা গণনা করে মডেল অনিশ্চয়তা কল্পনা করুন:
\[var(x) = p(x) * (1 - p(x))\]
resnet_uncertainty = resnet_probs * (1 - resnet_probs)
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_uncertainty, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Predictive Uncertainty, Deterministic Model")
plt.show()

এই প্লটে, হলুদ উচ্চ অনিশ্চয়তা নির্দেশ করে, এবং বেগুনি কম অনিশ্চয়তা নির্দেশ করে। একটি নির্ধারক ResNet এর অনিশ্চয়তা শুধুমাত্র পরীক্ষার উদাহরণের সিদ্ধান্তের সীমানা থেকে দূরত্বের উপর নির্ভর করে। এটি প্রশিক্ষণের ডোমেনের বাইরে থাকাকালীন মডেলটিকে অতিরিক্ত আত্মবিশ্বাসী হতে পরিচালিত করে। পরবর্তী বিভাগ দেখায় কিভাবে SNGP এই ডেটাসেটে ভিন্নভাবে আচরণ করে।
এসএনজিপি মডেল
SNGP মডেলের সংজ্ঞা দাও
এবার এসএনজিপি মডেল বাস্তবায়ন করা যাক। SNGP কম্পোনেন্ট, SpectralNormalization নরমালাইজেশন এবং র্যান্ডমফিচার গাউসিয়ানপ্রসেস, RandomFeatureGaussianProcess এর অন্তর্নির্মিত স্তরগুলিতে উপলব্ধ।
আসুন আরো বিস্তারিতভাবে এই দুটি উপাদান তাকান. (সম্পূর্ণ মডেলটি কীভাবে বাস্তবায়িত হয় তা দেখতে আপনি SNGP মডেল বিভাগেও যেতে পারেন।)
বর্ণালী স্বাভাবিকীকরণ মোড়ক
SpectralNormalization স্বাভাবিককরণ একটি কেরাস স্তরের মোড়ক। এটি এই মত একটি বিদ্যমান ঘন স্তর প্রয়োগ করা যেতে পারে:
dense = tf.keras.layers.Dense(units=10)
dense = nlp_layers.SpectralNormalization(dense, norm_multiplier=0.9)
বর্ণালী স্বাভাবিকীকরণ লুকানো ওজন \(W\) কে ধীরে ধীরে তার বর্ণালী আদর্শ (অর্থাৎ, \(W\)এর বৃহত্তম eigenvalue) লক্ষ্য মান norm_multiplier এর দিকে পরিচালিত করে নিয়মিত করে।
গাউসিয়ান প্রসেস (GP) স্তর
RandomFeatureGaussianProcess একটি গাউসিয়ান প্রসেস মডেলের একটি র্যান্ডম-ফিচার ভিত্তিক আনুমানিকতা প্রয়োগ করে যা একটি গভীর নিউরাল নেটওয়ার্কের সাথে এন্ড-টু-এন্ড প্রশিক্ষণযোগ্য। হুডের নীচে, গাউসিয়ান প্রক্রিয়া স্তরটি একটি দ্বি-স্তর নেটওয়ার্ক প্রয়োগ করে:
\[logits(x) = \Phi(x) \beta, \quad \Phi(x)=\sqrt{\frac{2}{M} } * cos(Wx + b)\]
এখানে \(x\) হল ইনপুট, এবং \(W\) এবং \(b\) হিমায়িত ওজনগুলি যথাক্রমে গাউসিয়ান এবং অভিন্ন বন্টন থেকে এলোমেলোভাবে শুরু করা হয়েছে। (অতএব \(\Phi(x)\) কে "র্যান্ডম ফিচার" বলা হয়।) \(\beta\) হল একটি ঘন স্তরের মতই শেখার যোগ্য কার্নেলের ওজন।
batch_size = 32
input_dim = 1024
num_classes = 10
gp_layer = nlp_layers.RandomFeatureGaussianProcess(units=num_classes,
num_inducing=1024,
normalize_input=False,
scale_random_features=True,
gp_cov_momentum=-1)
জিপি স্তরগুলির প্রধান পরামিতিগুলি হল:
-
units: আউটপুট লগিটের মাত্রা। -
num_inducing: লুকানো ওজন \(W\) \(M\) -placeholder14। ডিফল্ট 1024. -
normalize_input: ইনপুট \(x\)এ লেয়ার নরমালাইজেশন প্রয়োগ করতে হবে কিনা। -
scale_random_features: লুকানো আউটপুটে স্কেল \(\sqrt{2/M}\) প্রয়োগ করতে হবে কিনা।
-
gp_cov_momentumনিয়ন্ত্রণ করে কিভাবে মডেল কোভেরিয়েন্স গণনা করা হয়। যদি একটি ইতিবাচক মান সেট করা হয় (যেমন, 0.999), কোভেরিয়েন্স ম্যাট্রিক্সটি ভরবেগ-ভিত্তিক চলমান গড় আপডেট (ব্যাচ স্বাভাবিককরণের অনুরূপ) ব্যবহার করে গণনা করা হয়। যদি -1 তে সেট করা হয়, কোভেরিয়েন্স ম্যাট্রিক্স কোনো গতি ছাড়াই আপডেট হয়।
আকৃতি (batch_size, input_dim) সহ একটি ব্যাচ ইনপুট দেওয়া হলে, জিপি লেয়ার ভবিষ্যদ্বাণীর জন্য একটি logits টেনসর (আকৃতি (batch_size, num_classes) ) প্রদান করে এবং এছাড়াও covmat টেনসর (আকৃতি (batch_size, batch_size) ) প্রদান করে যা কোভ্যারিয়েন্সের পোস্টেরিয়র টেন্সর। ব্যাচ লগিট.
embedding = tf.random.normal(shape=(batch_size, input_dim))
logits, covmat = gp_layer(embedding)
তাত্ত্বিকভাবে, বিভিন্ন শ্রেণীর জন্য বিভিন্ন বৈচিত্র্যের মান গণনা করার জন্য অ্যালগরিদম প্রসারিত করা সম্ভব (যেমন মূল SNGP কাগজে প্রবর্তিত হয়েছে)। যাইহোক, বড় আউটপুট স্পেস (যেমন, ইমেজনেট বা ভাষা মডেলিং) এর সমস্যাগুলির স্কেল করা কঠিন।
সম্পূর্ণ SNGP মডেল
বেস ক্লাস DeepResNet দেওয়া, SNGP মডেলটি অবশিষ্ট নেটওয়ার্কের লুকানো এবং আউটপুট স্তরগুলি পরিবর্তন করে সহজেই প্রয়োগ করা যেতে পারে। model.fit() API-এর সাথে সামঞ্জস্যের জন্য, মডেলের call() পদ্ধতিটিও পরিবর্তন করুন যাতে এটি প্রশিক্ষণের সময় শুধুমাত্র logits আউটপুট করে।
class DeepResNetSNGP(DeepResNet):
def __init__(self, spec_norm_bound=0.9, **kwargs):
self.spec_norm_bound = spec_norm_bound
super().__init__(**kwargs)
def make_dense_layer(self):
"""Applies spectral normalization to the hidden layer."""
dense_layer = super().make_dense_layer()
return nlp_layers.SpectralNormalization(
dense_layer, norm_multiplier=self.spec_norm_bound)
def make_output_layer(self, num_classes):
"""Uses Gaussian process as the output layer."""
return nlp_layers.RandomFeatureGaussianProcess(
num_classes,
gp_cov_momentum=-1,
**self.classifier_kwargs)
def call(self, inputs, training=False, return_covmat=False):
# Gets logits and covariance matrix from GP layer.
logits, covmat = super().call(inputs)
# Returns only logits during training.
if not training and return_covmat:
return logits, covmat
return logits
নির্ধারক মডেল হিসাবে একই আর্কিটেকচার ব্যবহার করুন।
resnet_config
{'num_classes': 2, 'num_layers': 6, 'num_hidden': 128}
sngp_model = DeepResNetSNGP(**resnet_config)
sngp_model.build((None, 2))
sngp_model.summary()
Model: "deep_res_net_sngp"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) multiple 384
spectral_normalization_1 (S multiple 16768
pectralNormalization)
spectral_normalization_2 (S multiple 16768
pectralNormalization)
spectral_normalization_3 (S multiple 16768
pectralNormalization)
spectral_normalization_4 (S multiple 16768
pectralNormalization)
spectral_normalization_5 (S multiple 16768
pectralNormalization)
spectral_normalization_6 (S multiple 16768
pectralNormalization)
random_feature_gaussian_pro multiple 1182722
cess (RandomFeatureGaussian
Process)
=================================================================
Total params: 1,283,714
Trainable params: 101,120
Non-trainable params: 1,182,594
_________________________________________________________________
একটি নতুন যুগের শুরুতে কোভেরিয়েন্স ম্যাট্রিক্স রিসেট করতে একটি Keras কলব্যাক প্রয়োগ করুন।
class ResetCovarianceCallback(tf.keras.callbacks.Callback):
def on_epoch_begin(self, epoch, logs=None):
"""Resets covariance matrix at the begining of the epoch."""
if epoch > 0:
self.model.classifier.reset_covariance_matrix()
DeepResNetSNGP মডেল ক্লাসে এই কলব্যাক যোগ করুন।
class DeepResNetSNGPWithCovReset(DeepResNetSNGP):
def fit(self, *args, **kwargs):
"""Adds ResetCovarianceCallback to model callbacks."""
kwargs["callbacks"] = list(kwargs.get("callbacks", []))
kwargs["callbacks"].append(ResetCovarianceCallback())
return super().fit(*args, **kwargs)
ট্রেন মডেল
মডেলকে প্রশিক্ষণ দিতে tf.keras.model.fit ব্যবহার করুন।
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 2s 5ms/step - loss: 0.6223 - sparse_categorical_accuracy: 0.9570 Epoch 2/100 8/8 [==============================] - 0s 4ms/step - loss: 0.5310 - sparse_categorical_accuracy: 0.9980 Epoch 3/100 8/8 [==============================] - 0s 4ms/step - loss: 0.4766 - sparse_categorical_accuracy: 0.9990 Epoch 4/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4346 - sparse_categorical_accuracy: 0.9980 Epoch 5/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4015 - sparse_categorical_accuracy: 0.9980 Epoch 6/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3757 - sparse_categorical_accuracy: 0.9990 Epoch 7/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3525 - sparse_categorical_accuracy: 0.9990 Epoch 8/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3305 - sparse_categorical_accuracy: 0.9990 Epoch 9/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3144 - sparse_categorical_accuracy: 0.9980 Epoch 10/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2975 - sparse_categorical_accuracy: 0.9990 Epoch 11/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2832 - sparse_categorical_accuracy: 0.9990 Epoch 12/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2707 - sparse_categorical_accuracy: 0.9990 Epoch 13/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2568 - sparse_categorical_accuracy: 0.9990 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2470 - sparse_categorical_accuracy: 0.9970 Epoch 15/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2361 - sparse_categorical_accuracy: 0.9990 Epoch 16/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2271 - sparse_categorical_accuracy: 0.9990 Epoch 17/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2182 - sparse_categorical_accuracy: 0.9990 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2097 - sparse_categorical_accuracy: 0.9990 Epoch 19/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2018 - sparse_categorical_accuracy: 0.9990 Epoch 20/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1940 - sparse_categorical_accuracy: 0.9980 Epoch 21/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1892 - sparse_categorical_accuracy: 0.9990 Epoch 22/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1821 - sparse_categorical_accuracy: 0.9980 Epoch 23/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1768 - sparse_categorical_accuracy: 0.9990 Epoch 24/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1702 - sparse_categorical_accuracy: 0.9980 Epoch 25/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1664 - sparse_categorical_accuracy: 0.9990 Epoch 26/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1604 - sparse_categorical_accuracy: 0.9990 Epoch 27/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1565 - sparse_categorical_accuracy: 0.9990 Epoch 28/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1517 - sparse_categorical_accuracy: 0.9990 Epoch 29/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1469 - sparse_categorical_accuracy: 0.9990 Epoch 30/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1431 - sparse_categorical_accuracy: 0.9980 Epoch 31/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1385 - sparse_categorical_accuracy: 0.9980 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1351 - sparse_categorical_accuracy: 0.9990 Epoch 33/100 8/8 [==============================] - 0s 5ms/step - loss: 0.1312 - sparse_categorical_accuracy: 0.9980 Epoch 34/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1289 - sparse_categorical_accuracy: 0.9990 Epoch 35/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1254 - sparse_categorical_accuracy: 0.9980 Epoch 36/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1223 - sparse_categorical_accuracy: 0.9980 Epoch 37/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1180 - sparse_categorical_accuracy: 0.9990 Epoch 38/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1167 - sparse_categorical_accuracy: 0.9990 Epoch 39/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1132 - sparse_categorical_accuracy: 0.9980 Epoch 40/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1110 - sparse_categorical_accuracy: 0.9990 Epoch 41/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1075 - sparse_categorical_accuracy: 0.9990 Epoch 42/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1067 - sparse_categorical_accuracy: 0.9990 Epoch 43/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1034 - sparse_categorical_accuracy: 0.9990 Epoch 44/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1006 - sparse_categorical_accuracy: 0.9990 Epoch 45/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9990 Epoch 46/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0963 - sparse_categorical_accuracy: 0.9990 Epoch 47/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0943 - sparse_categorical_accuracy: 0.9980 Epoch 48/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0925 - sparse_categorical_accuracy: 0.9990 Epoch 49/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0905 - sparse_categorical_accuracy: 0.9990 Epoch 50/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0889 - sparse_categorical_accuracy: 0.9990 Epoch 51/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0863 - sparse_categorical_accuracy: 0.9980 Epoch 52/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0847 - sparse_categorical_accuracy: 0.9990 Epoch 53/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0831 - sparse_categorical_accuracy: 0.9980 Epoch 54/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0818 - sparse_categorical_accuracy: 0.9990 Epoch 55/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0799 - sparse_categorical_accuracy: 0.9990 Epoch 56/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0780 - sparse_categorical_accuracy: 0.9990 Epoch 57/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0768 - sparse_categorical_accuracy: 0.9990 Epoch 58/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0751 - sparse_categorical_accuracy: 0.9990 Epoch 59/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0748 - sparse_categorical_accuracy: 0.9990 Epoch 60/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0723 - sparse_categorical_accuracy: 0.9990 Epoch 61/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0712 - sparse_categorical_accuracy: 0.9990 Epoch 62/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 63/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 64/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0683 - sparse_categorical_accuracy: 0.9990 Epoch 65/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0665 - sparse_categorical_accuracy: 0.9990 Epoch 66/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0661 - sparse_categorical_accuracy: 0.9990 Epoch 67/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9990 Epoch 68/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0631 - sparse_categorical_accuracy: 0.9990 Epoch 69/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0620 - sparse_categorical_accuracy: 0.9990 Epoch 70/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0606 - sparse_categorical_accuracy: 0.9990 Epoch 71/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0601 - sparse_categorical_accuracy: 0.9980 Epoch 72/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9990 Epoch 73/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0586 - sparse_categorical_accuracy: 0.9990 Epoch 74/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0574 - sparse_categorical_accuracy: 0.9990 Epoch 75/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0565 - sparse_categorical_accuracy: 1.0000 Epoch 76/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0559 - sparse_categorical_accuracy: 0.9990 Epoch 77/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0549 - sparse_categorical_accuracy: 0.9990 Epoch 78/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0534 - sparse_categorical_accuracy: 1.0000 Epoch 79/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0532 - sparse_categorical_accuracy: 0.9990 Epoch 80/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0519 - sparse_categorical_accuracy: 1.0000 Epoch 81/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0511 - sparse_categorical_accuracy: 1.0000 Epoch 82/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0508 - sparse_categorical_accuracy: 0.9990 Epoch 83/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0499 - sparse_categorical_accuracy: 1.0000 Epoch 84/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 1.0000 Epoch 85/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 0.9990 Epoch 86/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0470 - sparse_categorical_accuracy: 1.0000 Epoch 87/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 88/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 89/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0453 - sparse_categorical_accuracy: 1.0000 Epoch 90/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0448 - sparse_categorical_accuracy: 1.0000 Epoch 91/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0441 - sparse_categorical_accuracy: 1.0000 Epoch 92/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0434 - sparse_categorical_accuracy: 1.0000 Epoch 93/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0431 - sparse_categorical_accuracy: 1.0000 Epoch 94/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0424 - sparse_categorical_accuracy: 1.0000 Epoch 95/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0420 - sparse_categorical_accuracy: 1.0000 Epoch 96/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0415 - sparse_categorical_accuracy: 1.0000 Epoch 97/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0409 - sparse_categorical_accuracy: 1.0000 Epoch 98/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0401 - sparse_categorical_accuracy: 1.0000 Epoch 99/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0396 - sparse_categorical_accuracy: 1.0000 Epoch 100/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0392 - sparse_categorical_accuracy: 1.0000 <keras.callbacks.History at 0x7ff7ac0f83d0>
অনিশ্চয়তা কল্পনা করুন
প্রথমে ভবিষ্যদ্বাণীমূলক লগিট এবং বৈচিত্রগুলি গণনা করুন।
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_variance = tf.linalg.diag_part(sngp_covmat)[:, None]
এখন পোস্টেরিয়র ভবিষ্যদ্বাণীমূলক সম্ভাব্যতা গণনা করুন। একটি সম্ভাব্য মডেলের ভবিষ্যদ্বাণীমূলক সম্ভাব্যতা গণনার ক্লাসিক পদ্ধতি হল মন্টে কার্লো স্যাম্পলিং ব্যবহার করা, অর্থাৎ,
\[E(p(x)) = \frac{1}{M} \sum_{m=1}^M logit_m(x), \]
যেখানে \(M\) হল নমুনার আকার, এবং \(logit_m(x)\) হল SNGP পোস্টেরিয়র \(MultivariateNormal\)( sngp_logits , sngp_covmat ) থেকে র্যান্ডম নমুনা৷ যাইহোক, স্বায়ত্তশাসিত ড্রাইভিং বা রিয়েল-টাইম বিডিংয়ের মতো লেটেন্সি-সংবেদনশীল অ্যাপ্লিকেশনগুলির জন্য এই পদ্ধতিটি ধীর হতে পারে। পরিবর্তে, গড়-ক্ষেত্র পদ্ধতি ব্যবহার করে \(E(p(x))\) আনুমানিক করতে পারে:
\[E(p(x)) \approx softmax(\frac{logit(x)}{\sqrt{1+ \lambda * \sigma^2(x)} })\]
যেখানে \(\sigma^2(x)\) হল SNGP ভ্যারিয়েন্স, এবং \(\lambda\) প্রায়ই \(\pi/8\) বা \(3/\pi^2\)placeholder29 হিসাবে বেছে নেওয়া হয়।
sngp_logits_adjusted = sngp_logits / tf.sqrt(1. + (np.pi / 8.) * sngp_variance)
sngp_probs = tf.nn.softmax(sngp_logits_adjusted, axis=-1)[:, 0]
এই গড়-ক্ষেত্র পদ্ধতিটি একটি অন্তর্নির্মিত ফাংশন হিসাবে প্রয়োগ করা হয় layers.gaussian_process.mean_field_logits :
def compute_posterior_mean_probability(logits, covmat, lambda_param=np.pi / 8.):
# Computes uncertainty-adjusted logits using the built-in method.
logits_adjusted = nlp_layers.gaussian_process.mean_field_logits(
logits, covmat, mean_field_factor=lambda_param)
return tf.nn.softmax(logits_adjusted, axis=-1)[:, 0]
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
SNGP সারাংশ
def plot_predictions(pred_probs, model_name=""):
"""Plot normalized class probabilities and predictive uncertainties."""
# Compute predictive uncertainty.
uncertainty = pred_probs * (1. - pred_probs)
# Initialize the plot axes.
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# Plots the class probability.
pcm_0 = plot_uncertainty_surface(pred_probs, ax=axs[0])
# Plots the predictive uncertainty.
pcm_1 = plot_uncertainty_surface(uncertainty, ax=axs[1])
# Adds color bars and titles.
fig.colorbar(pcm_0, ax=axs[0])
fig.colorbar(pcm_1, ax=axs[1])
axs[0].set_title(f"Class Probability, {model_name}")
axs[1].set_title(f"(Normalized) Predictive Uncertainty, {model_name}")
plt.show()
সবকিছু একসাথে রাখুন। সম্পূর্ণ পদ্ধতি (প্রশিক্ষণ, মূল্যায়ন এবং অনিশ্চয়তা গণনা) মাত্র পাঁচটি লাইনে করা যেতে পারে:
def train_and_test_sngp(train_examples, test_examples):
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, verbose=0, **fit_config)
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
return sngp_probs
sngp_probs = train_and_test_sngp(train_examples, test_examples)
SNGP মডেলের ক্লাস সম্ভাব্যতা (বাম) এবং ভবিষ্যদ্বাণীমূলক অনিশ্চয়তা (ডান) কল্পনা করুন।
plot_predictions(sngp_probs, model_name="SNGP")

মনে রাখবেন যে ক্লাস সম্ভাব্যতা প্লটে (বাম), হলুদ এবং বেগুনি হল শ্রেণী সম্ভাব্যতা। প্রশিক্ষণ ডেটা ডোমেনের কাছাকাছি থাকাকালীন, SNGP উচ্চ আত্মবিশ্বাসের সাথে উদাহরণগুলিকে সঠিকভাবে শ্রেণীবদ্ধ করে (অর্থাৎ, 0 বা 1 সম্ভাব্যতার কাছাকাছি বরাদ্দ করা)। প্রশিক্ষণের তথ্য থেকে দূরে থাকাকালীন, SNGP ধীরে ধীরে কম আত্মবিশ্বাসী হয়ে ওঠে এবং এর ভবিষ্যদ্বাণীমূলক সম্ভাবনা 0.5 এর কাছাকাছি হয়ে যায় যখন (সাধারণকৃত) মডেলের অনিশ্চয়তা 1-এ উঠে যায়।
এটিকে নির্ধারক মডেলের অনিশ্চয়তা পৃষ্ঠের সাথে তুলনা করুন:
plot_predictions(resnet_probs, model_name="Deterministic")

যেমন আগে উল্লিখিত হয়েছে, একটি নির্ধারক মডেল দূরত্ব-সচেতন নয়। এর অনিশ্চয়তা সিদ্ধান্তের সীমানা থেকে পরীক্ষার উদাহরণের দূরত্ব দ্বারা সংজ্ঞায়িত করা হয়। এটি ডোমেনের বাইরের উদাহরণগুলির (লাল) জন্য অতিরিক্ত আত্মবিশ্বাসী ভবিষ্যদ্বাণী তৈরি করতে মডেলটিকে নেতৃত্ব দেয়।
অন্যান্য অনিশ্চয়তা পদ্ধতির সাথে তুলনা
এই বিভাগটি মন্টে কার্লো ড্রপআউট এবং ডিপ এনসেম্বলের সাথে SNGP-এর অনিশ্চয়তার তুলনা করে।
এই উভয় পদ্ধতিই মন্টে কার্লোর নির্ধারক মডেলের একাধিক ফরোয়ার্ড পাসের গড় উপর ভিত্তি করে। প্রথমে ensemble আকার \(M\)সেট করুন।
num_ensemble = 10
মন্টে কার্লো ড্রপআউট
ড্রপআউট স্তর সহ একটি প্রশিক্ষিত নিউরাল নেটওয়ার্ক দেওয়া, মন্টে কার্লো ড্রপআউট গড় ভবিষ্যদ্বাণীমূলক সম্ভাব্যতা গণনা করে
\[E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\]
একাধিক ড্রপআউট-সক্ষম ফরওয়ার্ড পাস \(\{logit_m(x)\}_{m=1}^M\)এর বেশি গড় করে।
def mc_dropout_sampling(test_examples):
# Enable dropout during inference.
return resnet_model(test_examples, training=True)
# Monte Carlo dropout inference.
dropout_logit_samples = [mc_dropout_sampling(test_examples) for _ in range(num_ensemble)]
dropout_prob_samples = [tf.nn.softmax(dropout_logits, axis=-1)[:, 0] for dropout_logits in dropout_logit_samples]
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
plot_predictions(dropout_probs, model_name="MC Dropout")

গভীর ensemble
ডিপ এনসেম্বল হল গভীর শিক্ষার অনিশ্চয়তার জন্য একটি অত্যাধুনিক (কিন্তু ব্যয়বহুল) পদ্ধতি। একটি ডিপ এনসেম্বল প্রশিক্ষণের জন্য, প্রথমে \(M\) ensemble সদস্যদের প্রশিক্ষণ দিন।
# Deep ensemble training
resnet_ensemble = []
for _ in range(num_ensemble):
resnet_model = DeepResNet(**resnet_config)
resnet_model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
resnet_model.fit(train_examples, train_labels, verbose=0, **fit_config)
resnet_ensemble.append(resnet_model)
লগিট সংগ্রহ করুন এবং গড় ভবিষ্যদ্বাণীমূলক সম্ভাব্যতা \(E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\)গণনা করুন।
# Deep ensemble inference
ensemble_logit_samples = [model(test_examples) for model in resnet_ensemble]
ensemble_prob_samples = [tf.nn.softmax(logits, axis=-1)[:, 0] for logits in ensemble_logit_samples]
ensemble_probs = tf.reduce_mean(ensemble_prob_samples, axis=0)
plot_predictions(ensemble_probs, model_name="Deep ensemble")

এমসি ড্রপআউট এবং ডিপ এনসেম্বল উভয়ই সিদ্ধান্তের সীমানা কম নির্দিষ্ট করে একটি মডেলের অনিশ্চয়তার ক্ষমতাকে উন্নত করে। যাইহোক, তারা উভয়ই দূরত্ব সচেতনতার অভাবের কারণে ডিটারমিনিস্টিক গভীর নেটওয়ার্কের সীমাবদ্ধতার উত্তরাধিকারী।
সারসংক্ষেপ
এই টিউটোরিয়ালে, আপনার আছে:
- এর দূরত্ব সচেতনতা উন্নত করতে একটি গভীর শ্রেণিবিন্যাসকারীতে একটি SNGP মডেল প্রয়োগ করেছে৷
- Keras
model.fit()API ব্যবহার করে SNGP মডেল এন্ড-টু-এন্ড প্রশিক্ষিত। - SNGP-এর অনিশ্চয়তা আচরণকে কল্পনা করা হয়েছে।
- SNGP, মন্টে কার্লো ড্রপআউট এবং ডিপ এনসেম্বল মডেলের মধ্যে অনিশ্চয়তার আচরণের তুলনা।
সম্পদ এবং আরও পড়া
- অনিশ্চয়তা-সচেতন প্রাকৃতিক ভাষা বোঝার জন্য একটি BERT মডেলে SNGP প্রয়োগ করার উদাহরণের জন্য SNGP-BERT টিউটোরিয়াল দেখুন।
- বিভিন্ন ধরণের বেঞ্চমার্ক ডেটাসেটে (যেমন, CIFAR , ImageNet , Jigsaw টক্সিসিটি সনাক্তকরণ ইত্যাদি) SNGP মডেল (এবং অন্যান্য অনেক অনিশ্চয়তা পদ্ধতি) বাস্তবায়নের জন্য অনিশ্চয়তা বেসলাইন দেখুন।
- SNGP পদ্ধতির আরও গভীরভাবে বোঝার জন্য, দূরত্ব সচেতনতার মাধ্যমে ডিটারমিনিস্টিক ডিপ লার্নিং সহ সরল এবং নীতিগত অনিশ্চয়তা অনুমানের কাগজটি দেখুন।