ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูบน GitHub ดูบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
ในแอปพลิเคชัน AI ที่มีความสำคัญต่อความปลอดภัย (เช่น การตัดสินใจทางการแพทย์และการขับขี่อัตโนมัติ) หรือในกรณีที่ข้อมูลมีเสียงดัง (เช่น ความเข้าใจในภาษาธรรมชาติ) สิ่งสำคัญสำหรับตัวแยกประเภทเชิงลึกเพื่อประเมินความไม่แน่นอนของข้อมูลอย่างน่าเชื่อถือ ตัวแยกประเภทลึกควรสามารถรับรู้ถึงข้อจำกัดของตนเองและเมื่อใดควรมอบการควบคุมให้กับผู้เชี่ยวชาญที่เป็นมนุษย์ บทช่วยสอนนี้แสดงวิธีปรับปรุงความสามารถของตัวแยกประเภทเชิงลึกในการหาปริมาณความไม่แน่นอนโดยใช้เทคนิคที่เรียกว่า Spectral-normalized Neural Gaussian Process ( SNGP )
แนวคิดหลักของ SNGP คือการปรับปรุงการ รับรู้ระยะทาง ของตัวแยกประเภทแบบลึกโดยใช้การปรับเปลี่ยนอย่างง่ายกับเครือข่าย การ รับรู้ระยะทาง ของแบบจำลองคือการวัดว่าความน่าจะเป็นในการคาดการณ์สะท้อนระยะห่างระหว่างตัวอย่างการทดสอบและข้อมูลการฝึกอย่างไร นี่เป็นคุณสมบัติที่พึงประสงค์ซึ่งเป็นเรื่องปกติสำหรับแบบจำลองความน่าจะเป็นมาตรฐานทองคำ (เช่น กระบวนการเกาส์เซียน ที่มีเมล็ด RBF) แต่ขาดโมเดลที่มีโครงข่ายประสาทเทียมแบบลึก SNGP ให้วิธีง่ายๆ ในการฉีดพฤติกรรมของกระบวนการเกาส์เซียนนี้ลงในตัวแยกประเภทเชิงลึกในขณะที่ยังคงรักษาความแม่นยำในการทำนายไว้
บทช่วยสอนนี้ใช้โมเดล SNGP แบบ Deep Residual Network (ResNet) ในชุดข้อมูล ดวงจันทร์สองดวง และเปรียบเทียบพื้นผิวความไม่แน่นอนกับแนวทางความไม่แน่นอนที่เป็นที่นิยมอื่นๆ อีก 2 วิธี ได้แก่ Monte Carlo dropout และ Deep ensemble
บทช่วยสอนนี้แสดงตัวอย่างโมเดล SNGP บนชุดข้อมูลของเล่น 2D สำหรับตัวอย่างการใช้ SNGP กับงานทำความเข้าใจภาษาธรรมชาติในโลกแห่งความเป็นจริงโดยใช้ BERT-base โปรดดูที่ บทช่วยสอน SNGP-BERT สำหรับการใช้งานแบบจำลอง SNGP คุณภาพสูง (และวิธีการที่ไม่แน่นอนอื่น ๆ อีกมากมาย) ในชุดข้อมูลเปรียบเทียบที่หลากหลาย (เช่น CIFAR-100 , ImageNet , การตรวจจับความเป็นพิษของจิ๊กซอว์ ฯลฯ ) โปรดดูที่เกณฑ์มาตรฐาน ความไม่แน่นอน
เกี่ยวกับ SNGP
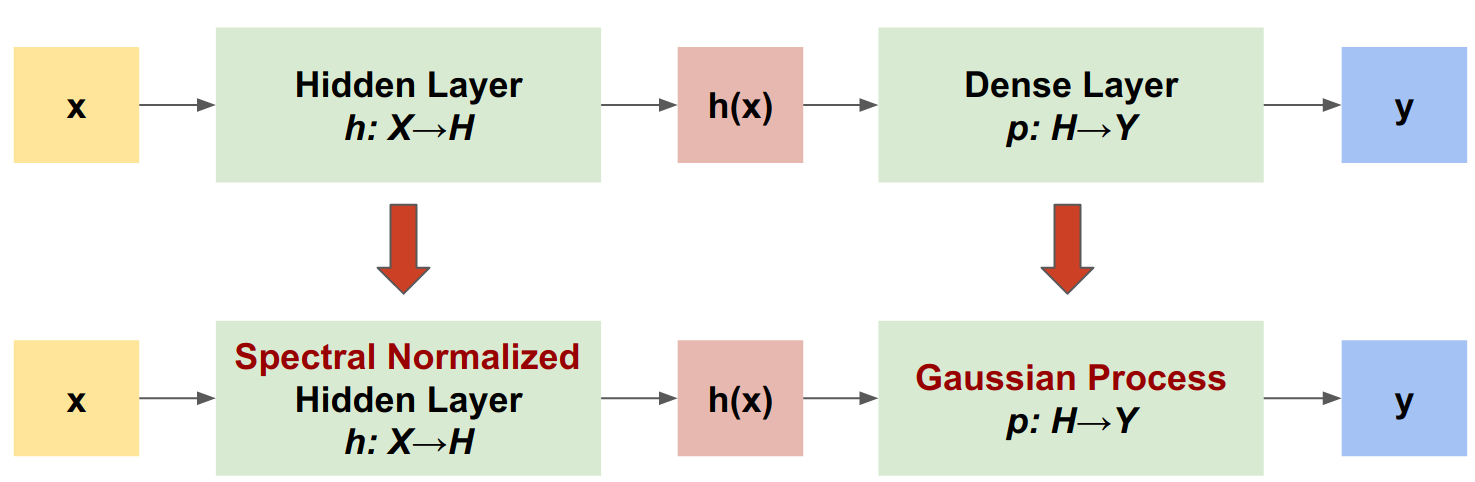
Spectral-normalized Neural Gaussian Process (SNGP) เป็นแนวทางง่ายๆ ในการปรับปรุงคุณภาพความไม่แน่นอนของตัวแยกประเภทในเชิงลึก ในขณะที่ยังคงระดับความแม่นยำและเวลาแฝงที่ใกล้เคียงกัน ด้วยเครือข่ายที่เหลือลึก SNGP ทำการเปลี่ยนแปลงอย่างง่ายสองรูปแบบกับแบบจำลอง:
- มันใช้การทำให้เป็นมาตรฐานของสเปกตรัมกับเลเยอร์ที่เหลือที่ซ่อนอยู่
- มันแทนที่เลเยอร์เอาต์พุตหนาแน่นด้วยเลเยอร์กระบวนการเกาส์เซียน
เมื่อเทียบกับแนวทางความไม่แน่นอนอื่นๆ (เช่น Monte Carlo dropout หรือ Deep ensemble) SNGP มีข้อดีหลายประการ:
- ใช้งานได้กับสถาปัตยกรรมที่ล้ำสมัยมากมาย (เช่น (Wide) ResNet, DenseNet, BERT เป็นต้น)
- เป็นวิธีการแบบโมเดลเดียว (เช่น ไม่ต้องอาศัยการหาค่าเฉลี่ยทั้งมวล) ดังนั้น SNGP จึงมีความหน่วงแฝงในระดับใกล้เคียงกับเครือข่ายที่กำหนดได้เพียงเครือข่ายเดียว และสามารถปรับขนาดได้อย่างง่ายดายเป็นชุดข้อมูลขนาดใหญ่ เช่น การจำแนก ImageNet และ Jigsaw Toxic Comments
- มีประสิทธิภาพการตรวจจับนอกโดเมนที่แข็งแกร่งเนื่องจากคุณสมบัติ การรับรู้ระยะทาง
ข้อเสียของวิธีนี้คือ:
ความไม่แน่นอนเชิงคาดการณ์ของ SNGP คำนวณโดยใช้การ ประมาณ Laplace ดังนั้นในทางทฤษฎี ความไม่แน่นอนภายหลังของ SNGP จึงแตกต่างจากกระบวนการเกาส์เซียนที่แน่นอน
การฝึกอบรม SNGP จำเป็นต้องมีขั้นตอนการรีเซ็ตความแปรปรวนร่วมเมื่อเริ่มต้นยุคใหม่ สิ่งนี้สามารถเพิ่มความซับซ้อนเพิ่มเติมเล็กน้อยให้กับไปป์ไลน์การฝึกอบรม บทช่วยสอนนี้แสดงวิธีง่ายๆ ในการดำเนินการนี้โดยใช้การเรียกกลับของ Keras
ติดตั้ง
pip install --use-deprecated=legacy-resolver tf-models-official
# refresh pkg_resources so it takes the changes into account.
import pkg_resources
import importlib
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import sklearn.datasets
import numpy as np
import tensorflow as tf
import official.nlp.modeling.layers as nlp_layers
กำหนดมาโครการแสดงภาพ
plt.rcParams['figure.dpi'] = 140
DEFAULT_X_RANGE = (-3.5, 3.5)
DEFAULT_Y_RANGE = (-2.5, 2.5)
DEFAULT_CMAP = colors.ListedColormap(["#377eb8", "#ff7f00"])
DEFAULT_NORM = colors.Normalize(vmin=0, vmax=1,)
DEFAULT_N_GRID = 100
ชุดข้อมูลดวงจันทร์สองดวง
สร้างชุดข้อมูลการฝึกอบรมและประเมินผลจากชุดข้อมูล สองดวง
def make_training_data(sample_size=500):
"""Create two moon training dataset."""
train_examples, train_labels = sklearn.datasets.make_moons(
n_samples=2 * sample_size, noise=0.1)
# Adjust data position slightly.
train_examples[train_labels == 0] += [-0.1, 0.2]
train_examples[train_labels == 1] += [0.1, -0.2]
return train_examples, train_labels
ประเมินพฤติกรรมการคาดเดาของโมเดลบนพื้นที่อินพุต 2D ทั้งหมด
def make_testing_data(x_range=DEFAULT_X_RANGE, y_range=DEFAULT_Y_RANGE, n_grid=DEFAULT_N_GRID):
"""Create a mesh grid in 2D space."""
# testing data (mesh grid over data space)
x = np.linspace(x_range[0], x_range[1], n_grid)
y = np.linspace(y_range[0], y_range[1], n_grid)
xv, yv = np.meshgrid(x, y)
return np.stack([xv.flatten(), yv.flatten()], axis=-1)
ในการประเมินความไม่แน่นอนของโมเดล ให้เพิ่มชุดข้อมูลนอกโดเมน (OOD) ที่เป็นของคลาสที่สาม โมเดลไม่เคยเห็นตัวอย่าง OOD เหล่านี้ระหว่างการฝึก
def make_ood_data(sample_size=500, means=(2.5, -1.75), vars=(0.01, 0.01)):
return np.random.multivariate_normal(
means, cov=np.diag(vars), size=sample_size)
# Load the train, test and OOD datasets.
train_examples, train_labels = make_training_data(
sample_size=500)
test_examples = make_testing_data()
ood_examples = make_ood_data(sample_size=500)
# Visualize
pos_examples = train_examples[train_labels == 0]
neg_examples = train_examples[train_labels == 1]
plt.figure(figsize=(7, 5.5))
plt.scatter(pos_examples[:, 0], pos_examples[:, 1], c="#377eb8", alpha=0.5)
plt.scatter(neg_examples[:, 0], neg_examples[:, 1], c="#ff7f00", alpha=0.5)
plt.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
plt.legend(["Postive", "Negative", "Out-of-Domain"])
plt.ylim(DEFAULT_Y_RANGE)
plt.xlim(DEFAULT_X_RANGE)
plt.show()

ในที่นี้สีน้ำเงินและสีส้มแสดงถึงคลาสบวกและลบ และสีแดงแสดงถึงข้อมูล OOD แบบจำลองที่วัดปริมาณความไม่แน่นอนของหลุมคาดว่าจะมีความมั่นใจเมื่ออยู่ใกล้กับข้อมูลการฝึกอบรม (เช่น \(p(x_{test})\) ใกล้ 0 หรือ 1) และไม่แน่ใจเมื่ออยู่ห่างไกลจากขอบเขตข้อมูลการฝึกอบรม (เช่น \(p(x_{test})\) ใกล้ 0.5 ).
แบบจำลองที่กำหนดขึ้นได้
กำหนดรูปแบบ
เริ่มต้นจากโมเดลที่กำหนด (พื้นฐาน): เครือข่ายที่เหลือหลายชั้น (ResNet) พร้อมการทำให้เป็นมาตรฐานกลางคัน
class DeepResNet(tf.keras.Model):
"""Defines a multi-layer residual network."""
def __init__(self, num_classes, num_layers=3, num_hidden=128,
dropout_rate=0.1, **classifier_kwargs):
super().__init__()
# Defines class meta data.
self.num_hidden = num_hidden
self.num_layers = num_layers
self.dropout_rate = dropout_rate
self.classifier_kwargs = classifier_kwargs
# Defines the hidden layers.
self.input_layer = tf.keras.layers.Dense(self.num_hidden, trainable=False)
self.dense_layers = [self.make_dense_layer() for _ in range(num_layers)]
# Defines the output layer.
self.classifier = self.make_output_layer(num_classes)
def call(self, inputs):
# Projects the 2d input data to high dimension.
hidden = self.input_layer(inputs)
# Computes the resnet hidden representations.
for i in range(self.num_layers):
resid = self.dense_layers[i](hidden)
resid = tf.keras.layers.Dropout(self.dropout_rate)(resid)
hidden += resid
return self.classifier(hidden)
def make_dense_layer(self):
"""Uses the Dense layer as the hidden layer."""
return tf.keras.layers.Dense(self.num_hidden, activation="relu")
def make_output_layer(self, num_classes):
"""Uses the Dense layer as the output layer."""
return tf.keras.layers.Dense(
num_classes, **self.classifier_kwargs)
บทช่วยสอนนี้ใช้ ResNet 6 เลเยอร์พร้อม 128 ยูนิตที่ซ่อนอยู่
resnet_config = dict(num_classes=2, num_layers=6, num_hidden=128)
resnet_model = DeepResNet(**resnet_config)
resnet_model.build((None, 2))
resnet_model.summary()
Model: "deep_res_net"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 384
dense_1 (Dense) multiple 16512
dense_2 (Dense) multiple 16512
dense_3 (Dense) multiple 16512
dense_4 (Dense) multiple 16512
dense_5 (Dense) multiple 16512
dense_6 (Dense) multiple 16512
dense_7 (Dense) multiple 258
=================================================================
Total params: 99,714
Trainable params: 99,330
Non-trainable params: 384
_________________________________________________________________
โมเดลรถไฟ
กำหนดค่าพารามิเตอร์การฝึกอบรมเพื่อใช้ SparseCategoricalCrossentropy เป็นฟังก์ชันการสูญเสียและเครื่องมือเพิ่มประสิทธิภาพ Adam
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.keras.metrics.SparseCategoricalAccuracy(),
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
train_config = dict(loss=loss, metrics=metrics, optimizer=optimizer)
ฝึกแบบจำลองสำหรับ 100 ยุคด้วยขนาดแบทช์ 128
fit_config = dict(batch_size=128, epochs=100)
resnet_model.compile(**train_config)
resnet_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 1s 4ms/step - loss: 1.1251 - sparse_categorical_accuracy: 0.5050 Epoch 2/100 8/8 [==============================] - 0s 3ms/step - loss: 0.5538 - sparse_categorical_accuracy: 0.6920 Epoch 3/100 8/8 [==============================] - 0s 3ms/step - loss: 0.2881 - sparse_categorical_accuracy: 0.9160 Epoch 4/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1923 - sparse_categorical_accuracy: 0.9370 Epoch 5/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1550 - sparse_categorical_accuracy: 0.9420 Epoch 6/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1403 - sparse_categorical_accuracy: 0.9450 Epoch 7/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1269 - sparse_categorical_accuracy: 0.9430 Epoch 8/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1208 - sparse_categorical_accuracy: 0.9460 Epoch 9/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1158 - sparse_categorical_accuracy: 0.9510 Epoch 10/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1103 - sparse_categorical_accuracy: 0.9490 Epoch 11/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1051 - sparse_categorical_accuracy: 0.9510 Epoch 12/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1053 - sparse_categorical_accuracy: 0.9510 Epoch 13/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1013 - sparse_categorical_accuracy: 0.9450 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0967 - sparse_categorical_accuracy: 0.9500 Epoch 15/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9530 Epoch 16/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0984 - sparse_categorical_accuracy: 0.9500 Epoch 17/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0982 - sparse_categorical_accuracy: 0.9480 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0918 - sparse_categorical_accuracy: 0.9510 Epoch 19/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0903 - sparse_categorical_accuracy: 0.9500 Epoch 20/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0883 - sparse_categorical_accuracy: 0.9510 Epoch 21/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0870 - sparse_categorical_accuracy: 0.9530 Epoch 22/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0884 - sparse_categorical_accuracy: 0.9560 Epoch 23/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0850 - sparse_categorical_accuracy: 0.9540 Epoch 24/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0808 - sparse_categorical_accuracy: 0.9580 Epoch 25/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0773 - sparse_categorical_accuracy: 0.9560 Epoch 26/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0801 - sparse_categorical_accuracy: 0.9590 Epoch 27/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0779 - sparse_categorical_accuracy: 0.9580 Epoch 28/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0807 - sparse_categorical_accuracy: 0.9580 Epoch 29/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0820 - sparse_categorical_accuracy: 0.9570 Epoch 30/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0730 - sparse_categorical_accuracy: 0.9600 Epoch 31/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0782 - sparse_categorical_accuracy: 0.9590 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0704 - sparse_categorical_accuracy: 0.9600 Epoch 33/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0709 - sparse_categorical_accuracy: 0.9610 Epoch 34/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0758 - sparse_categorical_accuracy: 0.9580 Epoch 35/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9610 Epoch 36/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0688 - sparse_categorical_accuracy: 0.9600 Epoch 37/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0675 - sparse_categorical_accuracy: 0.9630 Epoch 38/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9690 Epoch 39/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0677 - sparse_categorical_accuracy: 0.9610 Epoch 40/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9650 Epoch 41/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0614 - sparse_categorical_accuracy: 0.9690 Epoch 42/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0663 - sparse_categorical_accuracy: 0.9680 Epoch 43/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0626 - sparse_categorical_accuracy: 0.9740 Epoch 44/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9760 Epoch 45/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0573 - sparse_categorical_accuracy: 0.9780 Epoch 46/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0568 - sparse_categorical_accuracy: 0.9770 Epoch 47/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0595 - sparse_categorical_accuracy: 0.9780 Epoch 48/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0482 - sparse_categorical_accuracy: 0.9840 Epoch 49/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0515 - sparse_categorical_accuracy: 0.9820 Epoch 50/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0525 - sparse_categorical_accuracy: 0.9830 Epoch 51/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0507 - sparse_categorical_accuracy: 0.9790 Epoch 52/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0433 - sparse_categorical_accuracy: 0.9850 Epoch 53/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0511 - sparse_categorical_accuracy: 0.9820 Epoch 54/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0501 - sparse_categorical_accuracy: 0.9820 Epoch 55/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0440 - sparse_categorical_accuracy: 0.9890 Epoch 56/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9850 Epoch 57/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9880 Epoch 58/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0416 - sparse_categorical_accuracy: 0.9860 Epoch 59/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0479 - sparse_categorical_accuracy: 0.9860 Epoch 60/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0434 - sparse_categorical_accuracy: 0.9860 Epoch 61/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0414 - sparse_categorical_accuracy: 0.9880 Epoch 62/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0402 - sparse_categorical_accuracy: 0.9870 Epoch 63/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0376 - sparse_categorical_accuracy: 0.9890 Epoch 64/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0337 - sparse_categorical_accuracy: 0.9900 Epoch 65/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0309 - sparse_categorical_accuracy: 0.9910 Epoch 66/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9910 Epoch 67/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0389 - sparse_categorical_accuracy: 0.9870 Epoch 68/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0333 - sparse_categorical_accuracy: 0.9920 Epoch 69/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0331 - sparse_categorical_accuracy: 0.9890 Epoch 70/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0346 - sparse_categorical_accuracy: 0.9900 Epoch 71/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0367 - sparse_categorical_accuracy: 0.9880 Epoch 72/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0283 - sparse_categorical_accuracy: 0.9920 Epoch 73/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0315 - sparse_categorical_accuracy: 0.9930 Epoch 74/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0271 - sparse_categorical_accuracy: 0.9900 Epoch 75/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0257 - sparse_categorical_accuracy: 0.9920 Epoch 76/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0289 - sparse_categorical_accuracy: 0.9900 Epoch 77/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0264 - sparse_categorical_accuracy: 0.9900 Epoch 78/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0272 - sparse_categorical_accuracy: 0.9910 Epoch 79/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9880 Epoch 80/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0249 - sparse_categorical_accuracy: 0.9900 Epoch 81/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0216 - sparse_categorical_accuracy: 0.9930 Epoch 82/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0279 - sparse_categorical_accuracy: 0.9890 Epoch 83/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0261 - sparse_categorical_accuracy: 0.9920 Epoch 84/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0235 - sparse_categorical_accuracy: 0.9920 Epoch 85/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0236 - sparse_categorical_accuracy: 0.9930 Epoch 86/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0219 - sparse_categorical_accuracy: 0.9920 Epoch 87/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0196 - sparse_categorical_accuracy: 0.9920 Epoch 88/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0215 - sparse_categorical_accuracy: 0.9900 Epoch 89/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0223 - sparse_categorical_accuracy: 0.9900 Epoch 90/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0200 - sparse_categorical_accuracy: 0.9950 Epoch 91/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0250 - sparse_categorical_accuracy: 0.9900 Epoch 92/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0160 - sparse_categorical_accuracy: 0.9940 Epoch 93/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 94/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 95/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0172 - sparse_categorical_accuracy: 0.9960 Epoch 96/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0209 - sparse_categorical_accuracy: 0.9940 Epoch 97/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0179 - sparse_categorical_accuracy: 0.9920 Epoch 98/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0195 - sparse_categorical_accuracy: 0.9940 Epoch 99/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0165 - sparse_categorical_accuracy: 0.9930 Epoch 100/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0170 - sparse_categorical_accuracy: 0.9950 <keras.callbacks.History at 0x7ff7ac5c8fd0>
เห็นภาพความไม่แน่นอน
def plot_uncertainty_surface(test_uncertainty, ax, cmap=None):
"""Visualizes the 2D uncertainty surface.
For simplicity, assume these objects already exist in the memory:
test_examples: Array of test examples, shape (num_test, 2).
train_labels: Array of train labels, shape (num_train, ).
train_examples: Array of train examples, shape (num_train, 2).
Arguments:
test_uncertainty: Array of uncertainty scores, shape (num_test,).
ax: A matplotlib Axes object that specifies a matplotlib figure.
cmap: A matplotlib colormap object specifying the palette of the
predictive surface.
Returns:
pcm: A matplotlib PathCollection object that contains the palette
information of the uncertainty plot.
"""
# Normalize uncertainty for better visualization.
test_uncertainty = test_uncertainty / np.max(test_uncertainty)
# Set view limits.
ax.set_ylim(DEFAULT_Y_RANGE)
ax.set_xlim(DEFAULT_X_RANGE)
# Plot normalized uncertainty surface.
pcm = ax.imshow(
np.reshape(test_uncertainty, [DEFAULT_N_GRID, DEFAULT_N_GRID]),
cmap=cmap,
origin="lower",
extent=DEFAULT_X_RANGE + DEFAULT_Y_RANGE,
vmin=DEFAULT_NORM.vmin,
vmax=DEFAULT_NORM.vmax,
interpolation='bicubic',
aspect='auto')
# Plot training data.
ax.scatter(train_examples[:, 0], train_examples[:, 1],
c=train_labels, cmap=DEFAULT_CMAP, alpha=0.5)
ax.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
return pcm
ตอนนี้ให้เห็นภาพการทำนายของแบบจำลองที่กำหนดขึ้นเอง อันดับแรก วางแผนความน่าจะเป็นของคลาส:
\[p(x) = softmax(logit(x))\]
resnet_logits = resnet_model(test_examples)
resnet_probs = tf.nn.softmax(resnet_logits, axis=-1)[:, 0] # Take the probability for class 0.
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_probs, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Class Probability, Deterministic Model")
plt.show()

ในพล็อตนี้ สีเหลืองและสีม่วงคือความน่าจะเป็นในการทำนายสำหรับทั้งสองคลาส แบบจำลองดีเทอร์มินิสติกทำงานได้ดีในการจำแนกคลาสที่รู้จักทั้งสองคลาส (สีน้ำเงินและสีส้ม) ด้วยขอบเขตการตัดสินใจที่ไม่เป็นเชิงเส้น อย่างไรก็ตาม มันไม่ได้ รับรู้ถึงระยะทาง และจัดประเภทตัวอย่างนอกโดเมนสีแดงที่ไม่เคยเห็น (OOD) อย่างมั่นใจเป็นคลาสสีส้ม
เห็นภาพความไม่แน่นอนของแบบจำลองโดยการคำนวณ ความแปรปรวนเชิงพยากรณ์ :
\[var(x) = p(x) * (1 - p(x))\]
resnet_uncertainty = resnet_probs * (1 - resnet_probs)
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_uncertainty, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Predictive Uncertainty, Deterministic Model")
plt.show()

ในพล็อตนี้ สีเหลืองแสดงถึงความไม่แน่นอนสูง และสีม่วงแสดงถึงความไม่แน่นอนต่ำ ความไม่แน่นอนของ ResNet ที่กำหนดขึ้นได้ขึ้นอยู่กับระยะห่างของตัวอย่างทดสอบจากขอบเขตการตัดสินใจเท่านั้น สิ่งนี้ทำให้โมเดลมีความมั่นใจมากเกินไปเมื่ออยู่นอกขอบเขตการฝึกอบรม ส่วนถัดไปจะแสดงให้เห็นว่า SNGP ทำงานแตกต่างกันอย่างไรในชุดข้อมูลนี้
รุ่น SNGP
กำหนดแบบจำลอง SNGP
มาเริ่มใช้งานโมเดล SNGP กัน ทั้งส่วนประกอบ SNGP, SpectralNormalization และ RandomFeatureGaussianProcess มีอยู่ ในเลเยอร์ในตัว ของ tensorflow_model
ลองดูองค์ประกอบทั้งสองนี้โดยละเอียดยิ่งขึ้น (คุณสามารถข้ามไปที่ส่วน โมเดล SNGP เพื่อดูว่ามีการนำโมเดลทั้งหมดไปใช้อย่างไร)
กระดาษห่อหุ้มสเปกตรัม
SpectralNormalization เป็นเครื่องห่อหุ้มเลเยอร์ Keras สามารถใช้กับเลเยอร์หนาแน่นที่มีอยู่ได้ดังนี้:
dense = tf.keras.layers.Dense(units=10)
dense = nlp_layers.SpectralNormalization(dense, norm_multiplier=0.9)
การทำให้เป็นมาตรฐานของสเปกตรัมทำให้น้ำหนักที่ซ่อนอยู่ \(W\) เป็นปกติโดยค่อยๆ นำทางบรรทัดฐานสเปกตรัม (เช่น ค่าลักษณะเฉพาะที่ใหญ่ที่สุดของ \(W\)) ไปสู่ค่าเป้าหมาย norm_multiplier
เลเยอร์กระบวนการ Gaussian Process
RandomFeatureGaussianProcess นำการ ประมาณตามคุณสมบัติสุ่ม ไปใช้กับโมเดลกระบวนการเกาส์เซียนที่ฝึกได้แบบ end-to-end ด้วยโครงข่ายประสาทเทียมระดับลึก ภายใต้ประทุน เลเยอร์กระบวนการเกาส์เซียนใช้เครือข่ายสองชั้น:
\[logits(x) = \Phi(x) \beta, \quad \Phi(x)=\sqrt{\frac{2}{M} } * cos(Wx + b)\]
ที่นี่ \(x\) เป็นอินพุต และ \(W\) และ \(b\) เป็นตุ้มน้ำหนักแช่แข็งที่เริ่มต้นแบบสุ่มจากการแจกแจงแบบเกาส์เซียนและการแจกแจงแบบสม่ำเสมอตามลำดับ (ดังนั้น \(\Phi(x)\) จึงเรียกว่า "คุณสมบัติสุ่ม") \(\beta\) คือน้ำหนักเคอร์เนลที่เรียนรู้ได้ซึ่งคล้ายกับของเลเยอร์หนาแน่น
batch_size = 32
input_dim = 1024
num_classes = 10
gp_layer = nlp_layers.RandomFeatureGaussianProcess(units=num_classes,
num_inducing=1024,
normalize_input=False,
scale_random_features=True,
gp_cov_momentum=-1)
พารามิเตอร์หลักของเลเยอร์ GP คือ:
-
units: ขนาดของล็อกเอาท์พุต -
num_inducing: มิติ \(M\) ของน้ำหนักที่ซ่อนอยู่ \(W\)ค่าเริ่มต้นคือ 1024 -
normalize_input: ว่าจะใช้การทำให้เป็นมาตรฐานของเลเยอร์กับอินพุต \(x\)หรือไม่ -
scale_random_features: จะใช้มาตราส่วน \(\sqrt{2/M}\) กับเอาต์พุตที่ซ่อนอยู่หรือไม่
-
gp_cov_momentumควบคุมวิธีการคำนวณความแปรปรวนร่วมของแบบจำลอง หากตั้งค่าเป็นค่าบวก (เช่น 0.999) เมทริกซ์ความแปรปรวนร่วมจะถูกคำนวณโดยใช้การอัปเดตค่าเฉลี่ยเคลื่อนที่ตามโมเมนตัม (คล้ายกับการทำให้เป็นมาตรฐานแบบกลุ่ม) หากตั้งค่าเป็น -1 เมทริกซ์ความแปรปรวนร่วมจะได้รับการอัปเดตโดยไม่มีโมเมนตัม
รับอินพุตแบบแบตช์ที่มีรูปร่าง (batch_size, input_dim) เลเยอร์ GP จะส่งกลับเทนเซอร์บันทึก (shape (batch_size, num_classes) ) สำหรับการทำนายและ logits covmat (รูปร่าง (batch_size, batch_size) ) ซึ่งเป็นเมทริกซ์ความแปรปรวนร่วมหลังของ ล็อกแบทช์
embedding = tf.random.normal(shape=(batch_size, input_dim))
logits, covmat = gp_layer(embedding)
ในทางทฤษฎี เป็นไปได้ที่จะขยายอัลกอริทึมเพื่อคำนวณค่าความแปรปรวนที่แตกต่างกันสำหรับคลาสต่างๆ (ตามที่แนะนำใน เอกสาร SNGP ดั้งเดิม ) อย่างไรก็ตาม นี่เป็นเรื่องยากที่จะปรับขนาดให้เป็นปัญหากับพื้นที่ส่งออกขนาดใหญ่ (เช่น ImageNet หรือการสร้างแบบจำลองภาษา)
รุ่น SNGP แบบเต็ม
ด้วยคลาสพื้นฐาน DeepResNet โมเดล SNGP สามารถใช้งานได้ง่ายโดยการปรับเปลี่ยนเลเยอร์ที่ซ่อนอยู่และเอาต์พุตของเครือข่ายที่เหลือ เพื่อความเข้ากันได้กับ Keras model.fit() API ให้แก้ไขเมธอด call() ของโมเดลด้วย เพื่อให้ส่งออกเฉพาะ logits ระหว่างการฝึก
class DeepResNetSNGP(DeepResNet):
def __init__(self, spec_norm_bound=0.9, **kwargs):
self.spec_norm_bound = spec_norm_bound
super().__init__(**kwargs)
def make_dense_layer(self):
"""Applies spectral normalization to the hidden layer."""
dense_layer = super().make_dense_layer()
return nlp_layers.SpectralNormalization(
dense_layer, norm_multiplier=self.spec_norm_bound)
def make_output_layer(self, num_classes):
"""Uses Gaussian process as the output layer."""
return nlp_layers.RandomFeatureGaussianProcess(
num_classes,
gp_cov_momentum=-1,
**self.classifier_kwargs)
def call(self, inputs, training=False, return_covmat=False):
# Gets logits and covariance matrix from GP layer.
logits, covmat = super().call(inputs)
# Returns only logits during training.
if not training and return_covmat:
return logits, covmat
return logits
ใช้สถาปัตยกรรมเดียวกันกับตัวแบบที่กำหนด
resnet_config
{'num_classes': 2, 'num_layers': 6, 'num_hidden': 128}
sngp_model = DeepResNetSNGP(**resnet_config)
sngp_model.build((None, 2))
sngp_model.summary()
Model: "deep_res_net_sngp"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) multiple 384
spectral_normalization_1 (S multiple 16768
pectralNormalization)
spectral_normalization_2 (S multiple 16768
pectralNormalization)
spectral_normalization_3 (S multiple 16768
pectralNormalization)
spectral_normalization_4 (S multiple 16768
pectralNormalization)
spectral_normalization_5 (S multiple 16768
pectralNormalization)
spectral_normalization_6 (S multiple 16768
pectralNormalization)
random_feature_gaussian_pro multiple 1182722
cess (RandomFeatureGaussian
Process)
=================================================================
Total params: 1,283,714
Trainable params: 101,120
Non-trainable params: 1,182,594
_________________________________________________________________
ใช้การเรียกกลับของ Keras เพื่อรีเซ็ตเมทริกซ์ความแปรปรวนร่วมเมื่อเริ่มต้นยุคใหม่
class ResetCovarianceCallback(tf.keras.callbacks.Callback):
def on_epoch_begin(self, epoch, logs=None):
"""Resets covariance matrix at the begining of the epoch."""
if epoch > 0:
self.model.classifier.reset_covariance_matrix()
เพิ่มการเรียกกลับนี้ไปยังคลาสโมเดล DeepResNetSNGP
class DeepResNetSNGPWithCovReset(DeepResNetSNGP):
def fit(self, *args, **kwargs):
"""Adds ResetCovarianceCallback to model callbacks."""
kwargs["callbacks"] = list(kwargs.get("callbacks", []))
kwargs["callbacks"].append(ResetCovarianceCallback())
return super().fit(*args, **kwargs)
โมเดลรถไฟ
ใช้ tf.keras.model.fit เพื่อฝึกโมเดล
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 2s 5ms/step - loss: 0.6223 - sparse_categorical_accuracy: 0.9570 Epoch 2/100 8/8 [==============================] - 0s 4ms/step - loss: 0.5310 - sparse_categorical_accuracy: 0.9980 Epoch 3/100 8/8 [==============================] - 0s 4ms/step - loss: 0.4766 - sparse_categorical_accuracy: 0.9990 Epoch 4/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4346 - sparse_categorical_accuracy: 0.9980 Epoch 5/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4015 - sparse_categorical_accuracy: 0.9980 Epoch 6/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3757 - sparse_categorical_accuracy: 0.9990 Epoch 7/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3525 - sparse_categorical_accuracy: 0.9990 Epoch 8/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3305 - sparse_categorical_accuracy: 0.9990 Epoch 9/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3144 - sparse_categorical_accuracy: 0.9980 Epoch 10/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2975 - sparse_categorical_accuracy: 0.9990 Epoch 11/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2832 - sparse_categorical_accuracy: 0.9990 Epoch 12/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2707 - sparse_categorical_accuracy: 0.9990 Epoch 13/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2568 - sparse_categorical_accuracy: 0.9990 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2470 - sparse_categorical_accuracy: 0.9970 Epoch 15/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2361 - sparse_categorical_accuracy: 0.9990 Epoch 16/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2271 - sparse_categorical_accuracy: 0.9990 Epoch 17/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2182 - sparse_categorical_accuracy: 0.9990 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2097 - sparse_categorical_accuracy: 0.9990 Epoch 19/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2018 - sparse_categorical_accuracy: 0.9990 Epoch 20/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1940 - sparse_categorical_accuracy: 0.9980 Epoch 21/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1892 - sparse_categorical_accuracy: 0.9990 Epoch 22/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1821 - sparse_categorical_accuracy: 0.9980 Epoch 23/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1768 - sparse_categorical_accuracy: 0.9990 Epoch 24/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1702 - sparse_categorical_accuracy: 0.9980 Epoch 25/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1664 - sparse_categorical_accuracy: 0.9990 Epoch 26/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1604 - sparse_categorical_accuracy: 0.9990 Epoch 27/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1565 - sparse_categorical_accuracy: 0.9990 Epoch 28/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1517 - sparse_categorical_accuracy: 0.9990 Epoch 29/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1469 - sparse_categorical_accuracy: 0.9990 Epoch 30/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1431 - sparse_categorical_accuracy: 0.9980 Epoch 31/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1385 - sparse_categorical_accuracy: 0.9980 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1351 - sparse_categorical_accuracy: 0.9990 Epoch 33/100 8/8 [==============================] - 0s 5ms/step - loss: 0.1312 - sparse_categorical_accuracy: 0.9980 Epoch 34/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1289 - sparse_categorical_accuracy: 0.9990 Epoch 35/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1254 - sparse_categorical_accuracy: 0.9980 Epoch 36/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1223 - sparse_categorical_accuracy: 0.9980 Epoch 37/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1180 - sparse_categorical_accuracy: 0.9990 Epoch 38/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1167 - sparse_categorical_accuracy: 0.9990 Epoch 39/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1132 - sparse_categorical_accuracy: 0.9980 Epoch 40/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1110 - sparse_categorical_accuracy: 0.9990 Epoch 41/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1075 - sparse_categorical_accuracy: 0.9990 Epoch 42/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1067 - sparse_categorical_accuracy: 0.9990 Epoch 43/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1034 - sparse_categorical_accuracy: 0.9990 Epoch 44/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1006 - sparse_categorical_accuracy: 0.9990 Epoch 45/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9990 Epoch 46/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0963 - sparse_categorical_accuracy: 0.9990 Epoch 47/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0943 - sparse_categorical_accuracy: 0.9980 Epoch 48/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0925 - sparse_categorical_accuracy: 0.9990 Epoch 49/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0905 - sparse_categorical_accuracy: 0.9990 Epoch 50/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0889 - sparse_categorical_accuracy: 0.9990 Epoch 51/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0863 - sparse_categorical_accuracy: 0.9980 Epoch 52/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0847 - sparse_categorical_accuracy: 0.9990 Epoch 53/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0831 - sparse_categorical_accuracy: 0.9980 Epoch 54/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0818 - sparse_categorical_accuracy: 0.9990 Epoch 55/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0799 - sparse_categorical_accuracy: 0.9990 Epoch 56/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0780 - sparse_categorical_accuracy: 0.9990 Epoch 57/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0768 - sparse_categorical_accuracy: 0.9990 Epoch 58/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0751 - sparse_categorical_accuracy: 0.9990 Epoch 59/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0748 - sparse_categorical_accuracy: 0.9990 Epoch 60/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0723 - sparse_categorical_accuracy: 0.9990 Epoch 61/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0712 - sparse_categorical_accuracy: 0.9990 Epoch 62/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 63/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 64/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0683 - sparse_categorical_accuracy: 0.9990 Epoch 65/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0665 - sparse_categorical_accuracy: 0.9990 Epoch 66/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0661 - sparse_categorical_accuracy: 0.9990 Epoch 67/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9990 Epoch 68/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0631 - sparse_categorical_accuracy: 0.9990 Epoch 69/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0620 - sparse_categorical_accuracy: 0.9990 Epoch 70/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0606 - sparse_categorical_accuracy: 0.9990 Epoch 71/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0601 - sparse_categorical_accuracy: 0.9980 Epoch 72/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9990 Epoch 73/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0586 - sparse_categorical_accuracy: 0.9990 Epoch 74/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0574 - sparse_categorical_accuracy: 0.9990 Epoch 75/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0565 - sparse_categorical_accuracy: 1.0000 Epoch 76/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0559 - sparse_categorical_accuracy: 0.9990 Epoch 77/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0549 - sparse_categorical_accuracy: 0.9990 Epoch 78/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0534 - sparse_categorical_accuracy: 1.0000 Epoch 79/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0532 - sparse_categorical_accuracy: 0.9990 Epoch 80/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0519 - sparse_categorical_accuracy: 1.0000 Epoch 81/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0511 - sparse_categorical_accuracy: 1.0000 Epoch 82/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0508 - sparse_categorical_accuracy: 0.9990 Epoch 83/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0499 - sparse_categorical_accuracy: 1.0000 Epoch 84/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 1.0000 Epoch 85/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 0.9990 Epoch 86/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0470 - sparse_categorical_accuracy: 1.0000 Epoch 87/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 88/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 89/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0453 - sparse_categorical_accuracy: 1.0000 Epoch 90/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0448 - sparse_categorical_accuracy: 1.0000 Epoch 91/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0441 - sparse_categorical_accuracy: 1.0000 Epoch 92/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0434 - sparse_categorical_accuracy: 1.0000 Epoch 93/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0431 - sparse_categorical_accuracy: 1.0000 Epoch 94/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0424 - sparse_categorical_accuracy: 1.0000 Epoch 95/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0420 - sparse_categorical_accuracy: 1.0000 Epoch 96/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0415 - sparse_categorical_accuracy: 1.0000 Epoch 97/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0409 - sparse_categorical_accuracy: 1.0000 Epoch 98/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0401 - sparse_categorical_accuracy: 1.0000 Epoch 99/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0396 - sparse_categorical_accuracy: 1.0000 Epoch 100/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0392 - sparse_categorical_accuracy: 1.0000 <keras.callbacks.History at 0x7ff7ac0f83d0>ตัวยึดตำแหน่ง72
เห็นภาพความไม่แน่นอน
ขั้นแรกให้คำนวณบันทึกการทำนายและความแปรปรวน
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_variance = tf.linalg.diag_part(sngp_covmat)[:, None]
ตอนนี้คำนวณความน่าจะเป็นที่คาดการณ์ภายหลัง วิธีคลาสสิกในการคำนวณความน่าจะเป็นเชิงพยากรณ์ของแบบจำลองความน่าจะเป็นคือการใช้การสุ่มตัวอย่างแบบมอนติคาร์โล กล่าวคือ
\[E(p(x)) = \frac{1}{M} \sum_{m=1}^M logit_m(x), \]
โดยที่ \(M\) คือขนาดตัวอย่าง และ \(logit_m(x)\) เป็นตัวอย่างสุ่มจาก SNGP หลัง \(MultivariateNormal\)( sngp_logits , sngp_covmat ) อย่างไรก็ตาม วิธีการนี้อาจช้าสำหรับแอปพลิเคชันที่ไวต่อเวลาแฝง เช่น การขับขี่อัตโนมัติหรือการเสนอราคาแบบเรียลไทม์ \(E(p(x))\) ประมาณได้โดยใช้วิธี mean-field :
\[E(p(x)) \approx softmax(\frac{logit(x)}{\sqrt{1+ \lambda * \sigma^2(x)} })\]
โดยที่ \(\sigma^2(x)\) คือความแปรปรวน SNGP และ \(\lambda\) มักถูกเลือกเป็น \(\pi/8\) หรือ \(3/\pi^2\)
sngp_logits_adjusted = sngp_logits / tf.sqrt(1. + (np.pi / 8.) * sngp_variance)
sngp_probs = tf.nn.softmax(sngp_logits_adjusted, axis=-1)[:, 0]
เมธอดหมายถึงฟิลด์นี้ถูกนำไปใช้เป็นฟังก์ชันที่มีอยู่แล้วภายใน layers.gaussian_process.mean_field_logits :
def compute_posterior_mean_probability(logits, covmat, lambda_param=np.pi / 8.):
# Computes uncertainty-adjusted logits using the built-in method.
logits_adjusted = nlp_layers.gaussian_process.mean_field_logits(
logits, covmat, mean_field_factor=lambda_param)
return tf.nn.softmax(logits_adjusted, axis=-1)[:, 0]
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
สรุป SNGP
def plot_predictions(pred_probs, model_name=""):
"""Plot normalized class probabilities and predictive uncertainties."""
# Compute predictive uncertainty.
uncertainty = pred_probs * (1. - pred_probs)
# Initialize the plot axes.
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# Plots the class probability.
pcm_0 = plot_uncertainty_surface(pred_probs, ax=axs[0])
# Plots the predictive uncertainty.
pcm_1 = plot_uncertainty_surface(uncertainty, ax=axs[1])
# Adds color bars and titles.
fig.colorbar(pcm_0, ax=axs[0])
fig.colorbar(pcm_1, ax=axs[1])
axs[0].set_title(f"Class Probability, {model_name}")
axs[1].set_title(f"(Normalized) Predictive Uncertainty, {model_name}")
plt.show()
ใส่ทุกอย่างเข้าด้วยกัน ขั้นตอนทั้งหมด (การฝึกอบรม การประเมิน และการคำนวณความไม่แน่นอน) สามารถทำได้ในห้าบรรทัด:
def train_and_test_sngp(train_examples, test_examples):
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, verbose=0, **fit_config)
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
return sngp_probs
sngp_probs = train_and_test_sngp(train_examples, test_examples)
เห็นภาพความน่าจะเป็นของชั้นเรียน (ซ้าย) และความไม่แน่นอนเชิงคาดการณ์ (ขวา) ของแบบจำลอง SNGP
plot_predictions(sngp_probs, model_name="SNGP")

จำไว้ว่าในแผนภาพความน่าจะเป็นของคลาส (ซ้าย) สีเหลืองและสีม่วงคือความน่าจะเป็นของคลาส เมื่ออยู่ใกล้กับโดเมนข้อมูลการฝึก SNGP จะจำแนกตัวอย่างอย่างถูกต้องด้วยความมั่นใจสูง (เช่น กำหนดความน่าจะเป็นเกือบ 0 หรือ 1) เมื่อห่างไกลจากข้อมูลการฝึก SNGP จะค่อยๆ เกิดความมั่นใจน้อยลง และความน่าจะเป็นในการคาดการณ์จะเข้าใกล้ 0.5 ในขณะที่ความไม่แน่นอนของแบบจำลอง (การทำให้เป็นมาตรฐาน) เพิ่มขึ้นเป็น 1
เปรียบเทียบสิ่งนี้กับพื้นผิวความไม่แน่นอนของแบบจำลองดีเทอร์มีนิสติก:
plot_predictions(resnet_probs, model_name="Deterministic")

ดังที่กล่าวไว้ก่อนหน้านี้ แบบจำลองที่กำหนดไม่ได้ แบบทราบระยะทาง ความไม่แน่นอนถูกกำหนดโดยระยะห่างของตัวอย่างทดสอบจากขอบเขตการตัดสินใจ สิ่งนี้ทำให้โมเดลสร้างการคาดคะเนที่มั่นใจมากเกินไปสำหรับตัวอย่างที่อยู่นอกโดเมน (สีแดง)
เปรียบเทียบกับแนวทางความไม่แน่นอนอื่นๆ
ส่วนนี้เปรียบเทียบความไม่แน่นอนของ SNGP กับ Monte Carlo dropout และ Deep ensemble
ทั้งสองวิธีนี้ใช้ Monte Carlo ในการหาค่าเฉลี่ยของการส่งต่อหลายตัวของโมเดลที่กำหนดขึ้นเอง อันดับแรก ตั้งค่าขนาดทั้งมวล \(M\)
num_ensemble = 10
มอนติคาร์โลออกกลางคัน
ด้วยโครงข่ายประสาทเทียมที่ผ่านการฝึกอบรมด้วยเลเยอร์ Dropout การดรอปเอาต์ของ Monte Carlo จะคำนวณความน่าจะเป็นเชิงคาดการณ์เฉลี่ย
\[E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\]
โดยหาค่าเฉลี่ยผ่านการส่งไปข้างหน้าที่เปิดใช้งาน Dropout หลาย \(\{logit_m(x)\}_{m=1}^M\)
def mc_dropout_sampling(test_examples):
# Enable dropout during inference.
return resnet_model(test_examples, training=True)
# Monte Carlo dropout inference.
dropout_logit_samples = [mc_dropout_sampling(test_examples) for _ in range(num_ensemble)]
dropout_prob_samples = [tf.nn.softmax(dropout_logits, axis=-1)[:, 0] for dropout_logits in dropout_logit_samples]
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
plot_predictions(dropout_probs, model_name="MC Dropout")

วงลึก
Deep Ensemble เป็นวิธีการที่ทันสมัยที่สุด (แต่มีราคาแพง) สำหรับความไม่แน่นอนของการเรียนรู้เชิงลึก ในการฝึกวง Deep ให้ฝึกสมาชิกกลุ่ม \(M\) ก่อน
# Deep ensemble training
resnet_ensemble = []
for _ in range(num_ensemble):
resnet_model = DeepResNet(**resnet_config)
resnet_model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
resnet_model.fit(train_examples, train_labels, verbose=0, **fit_config)
resnet_ensemble.append(resnet_model)
รวบรวมบันทึกและคำนวณความน่าจะเป็นเชิงคาดการณ์เฉลี่ย \(E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\)
# Deep ensemble inference
ensemble_logit_samples = [model(test_examples) for model in resnet_ensemble]
ensemble_prob_samples = [tf.nn.softmax(logits, axis=-1)[:, 0] for logits in ensemble_logit_samples]
ensemble_probs = tf.reduce_mean(ensemble_prob_samples, axis=0)
plot_predictions(ensemble_probs, model_name="Deep ensemble")

ทั้ง MC Dropout และ Deep ensemble ปรับปรุงความสามารถในการไม่แน่นอนของโมเดลโดยทำให้ขอบเขตการตัดสินใจมีความแน่นอนน้อยลง อย่างไรก็ตาม ทั้งคู่สืบทอดข้อจำกัดของ Deep Network ที่กำหนดโดยขาดการตระหนักรู้ในระยะทาง
สรุป
ในบทช่วยสอนนี้ คุณมี:
- นำโมเดล SNGP ไปใช้กับตัวแยกประเภทลึกเพื่อปรับปรุงการรับรู้ระยะทาง
- ฝึกโมเดล SNGP แบบ end-to-end โดยใช้ Keras
model.fit()API - เห็นภาพพฤติกรรมความไม่แน่นอนของ SNGP
- เปรียบเทียบพฤติกรรมความไม่แน่นอนระหว่าง SNGP, Monte Carlo dropout และ deep ensemble models
แหล่งข้อมูลและการอ่านเพิ่มเติม
- ดู บทช่วยสอน SNGP-BERT สำหรับตัวอย่างการใช้ SNGP กับโมเดล BERT เพื่อความเข้าใจในภาษาธรรมชาติที่รับรู้ถึงความไม่แน่นอน
- ดูข้อมูล พื้นฐานความไม่แน่นอน สำหรับการนำแบบจำลอง SNGP ไปใช้ (และวิธีการที่ไม่แน่นอนอื่นๆ มากมาย) ในชุดข้อมูลเปรียบเทียบที่หลากหลาย (เช่น CIFAR , ImageNet , การตรวจจับความเป็นพิษของจิ๊กซอว์ เป็นต้น)
- เพื่อความเข้าใจที่ลึกซึ้งยิ่งขึ้นเกี่ยวกับวิธี SNGP ให้ดูบทความ การประเมินความไม่แน่นอนแบบง่ายและตามหลักการด้วยการเรียนรู้เชิงลึกเชิงกำหนดผ่านการรับรู้ทางไกล