Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza su GitHub Visualizza su GitHub |  Scarica quaderno Scarica quaderno |
Nelle applicazioni di intelligenza artificiale critiche per la sicurezza (ad esempio, processo decisionale medico e guida autonoma) o in cui i dati sono intrinsecamente rumorosi (ad esempio, comprensione del linguaggio naturale), è importante che un classificatore approfondito quantifichi in modo affidabile la sua incertezza. Il classificatore profondo dovrebbe essere in grado di essere consapevole dei propri limiti e quando dovrebbe cedere il controllo agli esperti umani. Questo tutorial mostra come migliorare l'abilità di un classificatore profondo nella quantificazione dell'incertezza utilizzando una tecnica chiamata Processo gaussiano neurale normalizzato spettrale ( SNGP ) .
L'idea centrale di SNGP è migliorare la consapevolezza della distanza di un classificatore profondo applicando semplici modifiche alla rete. La consapevolezza della distanza di un modello è una misura di come la sua probabilità predittiva riflette la distanza tra l'esempio di test ei dati di addestramento. Questa è una proprietà desiderabile che è comune per i modelli probabilistici gold standard (ad esempio, il processo gaussiano con i kernel RBF), ma è carente nei modelli con reti neurali profonde. SNGP fornisce un modo semplice per iniettare questo comportamento del processo gaussiano in un classificatore profondo mantenendo la sua accuratezza predittiva.
Questo tutorial implementa un modello SNGP basato sulla rete residua profonda (ResNet) sul set di dati delle due lune e confronta la sua superficie di incertezza con quella di altri due approcci di incertezza popolari: Monte Carlo dropout e Deep ensemble ).
Questo tutorial illustra il modello SNGP su un set di dati 2D giocattolo. Per un esempio di applicazione di SNGP a un'attività di comprensione del linguaggio naturale del mondo reale utilizzando BERT-base, vedere il tutorial SNGP-BERT . Per implementazioni di alta qualità del modello SNGP (e di molti altri metodi di incertezza) su un'ampia varietà di set di dati di riferimento (ad es. CIFAR-100 , ImageNet , rilevamento della tossicità Jigsaw , ecc.), consultare il benchmark Uncertainty Baselines .
A proposito di SNGP
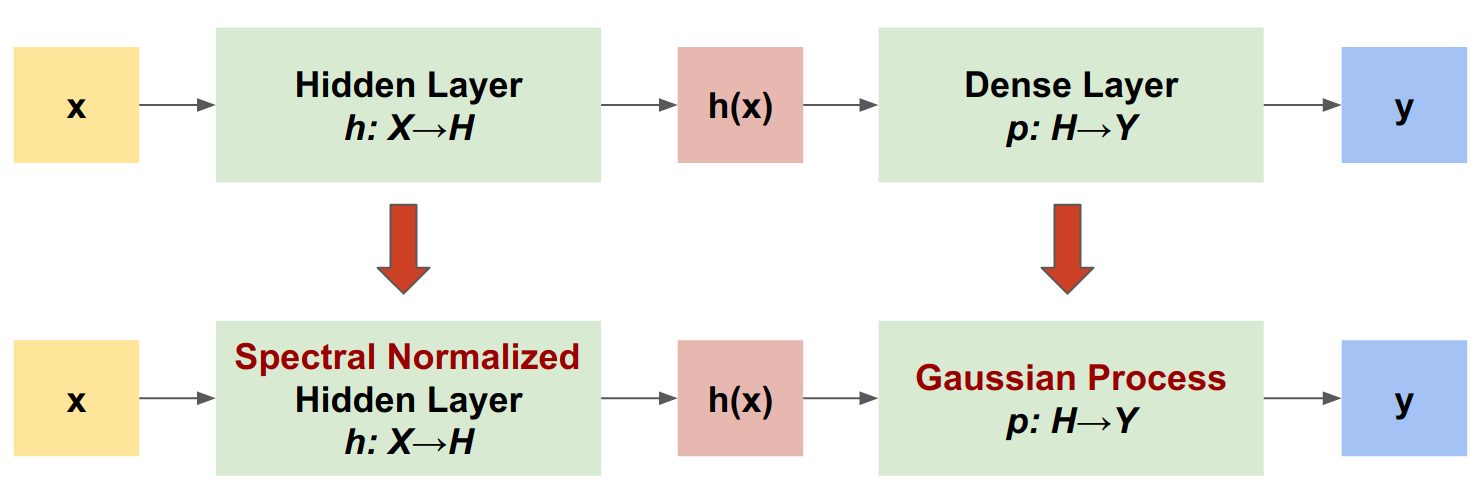
Il processo gaussiano neurale spettrale (SNGP) è un approccio semplice per migliorare la qualità dell'incertezza di un classificatore profondo mantenendo un livello simile di accuratezza e latenza. Data una profonda rete residua, SNGP apporta due semplici modifiche al modello:
- Applica la normalizzazione spettrale agli strati residui nascosti.
- Sostituisce il livello di output Denso con un livello di processo gaussiano.
Rispetto ad altri approcci all'incertezza (ad es. Monte Carlo dropout o Deep ensemble), SNGP presenta diversi vantaggi:
- Funziona per un'ampia gamma di architetture basate sui residui all'avanguardia (ad es. (Wide) ResNet, DenseNet, BERT, ecc.).
- È un metodo a modello singolo (cioè, non si basa sulla media dell'insieme). Pertanto SNGP ha un livello di latenza simile a quello di una singola rete deterministica e può essere facilmente scalato su grandi set di dati come la classificazione ImageNet e Jigsaw Toxic Comments .
- Ha ottime prestazioni di rilevamento fuori dominio grazie alla proprietà di consapevolezza della distanza .
Gli svantaggi di questo metodo sono:
L'incertezza predittiva di un SNGP viene calcolata utilizzando l' approssimazione di Laplace . Pertanto, in teoria, l'incertezza a posteriori di SNGP è diversa da quella di un processo gaussiano esatto.
L'addestramento SNGP necessita di una fase di ripristino della covarianza all'inizio di una nuova epoca. Ciò può aggiungere una piccola quantità di complessità extra a una pipeline di formazione. Questo tutorial mostra un modo semplice per implementarlo usando i callback Keras.
Impostare
pip install --use-deprecated=legacy-resolver tf-models-official
# refresh pkg_resources so it takes the changes into account.
import pkg_resources
import importlib
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import sklearn.datasets
import numpy as np
import tensorflow as tf
import official.nlp.modeling.layers as nlp_layers
Definire le macro di visualizzazione
plt.rcParams['figure.dpi'] = 140
DEFAULT_X_RANGE = (-3.5, 3.5)
DEFAULT_Y_RANGE = (-2.5, 2.5)
DEFAULT_CMAP = colors.ListedColormap(["#377eb8", "#ff7f00"])
DEFAULT_NORM = colors.Normalize(vmin=0, vmax=1,)
DEFAULT_N_GRID = 100
Il set di dati delle due lune
Crea i set di dati di addestramento e valutazione dal set di dati delle due lune .
def make_training_data(sample_size=500):
"""Create two moon training dataset."""
train_examples, train_labels = sklearn.datasets.make_moons(
n_samples=2 * sample_size, noise=0.1)
# Adjust data position slightly.
train_examples[train_labels == 0] += [-0.1, 0.2]
train_examples[train_labels == 1] += [0.1, -0.2]
return train_examples, train_labels
Valuta il comportamento predittivo del modello sull'intero spazio di input 2D.
def make_testing_data(x_range=DEFAULT_X_RANGE, y_range=DEFAULT_Y_RANGE, n_grid=DEFAULT_N_GRID):
"""Create a mesh grid in 2D space."""
# testing data (mesh grid over data space)
x = np.linspace(x_range[0], x_range[1], n_grid)
y = np.linspace(y_range[0], y_range[1], n_grid)
xv, yv = np.meshgrid(x, y)
return np.stack([xv.flatten(), yv.flatten()], axis=-1)
Per valutare l'incertezza del modello, aggiungi un set di dati fuori dominio (OOD) che appartiene a una terza classe. Il modello non vede mai questi esempi OOD durante l'allenamento.
def make_ood_data(sample_size=500, means=(2.5, -1.75), vars=(0.01, 0.01)):
return np.random.multivariate_normal(
means, cov=np.diag(vars), size=sample_size)
# Load the train, test and OOD datasets.
train_examples, train_labels = make_training_data(
sample_size=500)
test_examples = make_testing_data()
ood_examples = make_ood_data(sample_size=500)
# Visualize
pos_examples = train_examples[train_labels == 0]
neg_examples = train_examples[train_labels == 1]
plt.figure(figsize=(7, 5.5))
plt.scatter(pos_examples[:, 0], pos_examples[:, 1], c="#377eb8", alpha=0.5)
plt.scatter(neg_examples[:, 0], neg_examples[:, 1], c="#ff7f00", alpha=0.5)
plt.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
plt.legend(["Postive", "Negative", "Out-of-Domain"])
plt.ylim(DEFAULT_Y_RANGE)
plt.xlim(DEFAULT_X_RANGE)
plt.show()

Qui il blu e l'arancione rappresentano le classi positive e negative e il rosso rappresenta i dati OOD. Un modello che quantifica bene l'incertezza dovrebbe essere sicuro quando è vicino ai dati di addestramento (cioè, \(p(x_{test})\) vicino a 0 o 1) ed essere incerto quando è lontano dalle regioni dei dati di addestramento (cioè, \(p(x_{test})\) vicino a 0,5 ).
Il modello deterministico
Definisci modello
Partiamo dal modello deterministico (di base): una rete residua multistrato (ResNet) con regolarizzazione del dropout.
class DeepResNet(tf.keras.Model):
"""Defines a multi-layer residual network."""
def __init__(self, num_classes, num_layers=3, num_hidden=128,
dropout_rate=0.1, **classifier_kwargs):
super().__init__()
# Defines class meta data.
self.num_hidden = num_hidden
self.num_layers = num_layers
self.dropout_rate = dropout_rate
self.classifier_kwargs = classifier_kwargs
# Defines the hidden layers.
self.input_layer = tf.keras.layers.Dense(self.num_hidden, trainable=False)
self.dense_layers = [self.make_dense_layer() for _ in range(num_layers)]
# Defines the output layer.
self.classifier = self.make_output_layer(num_classes)
def call(self, inputs):
# Projects the 2d input data to high dimension.
hidden = self.input_layer(inputs)
# Computes the resnet hidden representations.
for i in range(self.num_layers):
resid = self.dense_layers[i](hidden)
resid = tf.keras.layers.Dropout(self.dropout_rate)(resid)
hidden += resid
return self.classifier(hidden)
def make_dense_layer(self):
"""Uses the Dense layer as the hidden layer."""
return tf.keras.layers.Dense(self.num_hidden, activation="relu")
def make_output_layer(self, num_classes):
"""Uses the Dense layer as the output layer."""
return tf.keras.layers.Dense(
num_classes, **self.classifier_kwargs)
Questo tutorial utilizza un ResNet a 6 livelli con 128 unità nascoste.
resnet_config = dict(num_classes=2, num_layers=6, num_hidden=128)
resnet_model = DeepResNet(**resnet_config)
resnet_model.build((None, 2))
resnet_model.summary()
Model: "deep_res_net"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 384
dense_1 (Dense) multiple 16512
dense_2 (Dense) multiple 16512
dense_3 (Dense) multiple 16512
dense_4 (Dense) multiple 16512
dense_5 (Dense) multiple 16512
dense_6 (Dense) multiple 16512
dense_7 (Dense) multiple 258
=================================================================
Total params: 99,714
Trainable params: 99,330
Non-trainable params: 384
_________________________________________________________________
Modello di treno
Configura i parametri di addestramento per utilizzare SparseCategoricalCrossentropy come funzione di perdita e l'ottimizzatore Adam.
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.keras.metrics.SparseCategoricalAccuracy(),
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
train_config = dict(loss=loss, metrics=metrics, optimizer=optimizer)
Addestra il modello per 100 epoche con lotto 128.
fit_config = dict(batch_size=128, epochs=100)
resnet_model.compile(**train_config)
resnet_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 1s 4ms/step - loss: 1.1251 - sparse_categorical_accuracy: 0.5050 Epoch 2/100 8/8 [==============================] - 0s 3ms/step - loss: 0.5538 - sparse_categorical_accuracy: 0.6920 Epoch 3/100 8/8 [==============================] - 0s 3ms/step - loss: 0.2881 - sparse_categorical_accuracy: 0.9160 Epoch 4/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1923 - sparse_categorical_accuracy: 0.9370 Epoch 5/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1550 - sparse_categorical_accuracy: 0.9420 Epoch 6/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1403 - sparse_categorical_accuracy: 0.9450 Epoch 7/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1269 - sparse_categorical_accuracy: 0.9430 Epoch 8/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1208 - sparse_categorical_accuracy: 0.9460 Epoch 9/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1158 - sparse_categorical_accuracy: 0.9510 Epoch 10/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1103 - sparse_categorical_accuracy: 0.9490 Epoch 11/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1051 - sparse_categorical_accuracy: 0.9510 Epoch 12/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1053 - sparse_categorical_accuracy: 0.9510 Epoch 13/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1013 - sparse_categorical_accuracy: 0.9450 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0967 - sparse_categorical_accuracy: 0.9500 Epoch 15/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9530 Epoch 16/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0984 - sparse_categorical_accuracy: 0.9500 Epoch 17/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0982 - sparse_categorical_accuracy: 0.9480 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0918 - sparse_categorical_accuracy: 0.9510 Epoch 19/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0903 - sparse_categorical_accuracy: 0.9500 Epoch 20/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0883 - sparse_categorical_accuracy: 0.9510 Epoch 21/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0870 - sparse_categorical_accuracy: 0.9530 Epoch 22/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0884 - sparse_categorical_accuracy: 0.9560 Epoch 23/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0850 - sparse_categorical_accuracy: 0.9540 Epoch 24/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0808 - sparse_categorical_accuracy: 0.9580 Epoch 25/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0773 - sparse_categorical_accuracy: 0.9560 Epoch 26/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0801 - sparse_categorical_accuracy: 0.9590 Epoch 27/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0779 - sparse_categorical_accuracy: 0.9580 Epoch 28/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0807 - sparse_categorical_accuracy: 0.9580 Epoch 29/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0820 - sparse_categorical_accuracy: 0.9570 Epoch 30/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0730 - sparse_categorical_accuracy: 0.9600 Epoch 31/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0782 - sparse_categorical_accuracy: 0.9590 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0704 - sparse_categorical_accuracy: 0.9600 Epoch 33/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0709 - sparse_categorical_accuracy: 0.9610 Epoch 34/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0758 - sparse_categorical_accuracy: 0.9580 Epoch 35/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9610 Epoch 36/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0688 - sparse_categorical_accuracy: 0.9600 Epoch 37/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0675 - sparse_categorical_accuracy: 0.9630 Epoch 38/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9690 Epoch 39/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0677 - sparse_categorical_accuracy: 0.9610 Epoch 40/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9650 Epoch 41/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0614 - sparse_categorical_accuracy: 0.9690 Epoch 42/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0663 - sparse_categorical_accuracy: 0.9680 Epoch 43/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0626 - sparse_categorical_accuracy: 0.9740 Epoch 44/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9760 Epoch 45/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0573 - sparse_categorical_accuracy: 0.9780 Epoch 46/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0568 - sparse_categorical_accuracy: 0.9770 Epoch 47/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0595 - sparse_categorical_accuracy: 0.9780 Epoch 48/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0482 - sparse_categorical_accuracy: 0.9840 Epoch 49/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0515 - sparse_categorical_accuracy: 0.9820 Epoch 50/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0525 - sparse_categorical_accuracy: 0.9830 Epoch 51/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0507 - sparse_categorical_accuracy: 0.9790 Epoch 52/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0433 - sparse_categorical_accuracy: 0.9850 Epoch 53/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0511 - sparse_categorical_accuracy: 0.9820 Epoch 54/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0501 - sparse_categorical_accuracy: 0.9820 Epoch 55/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0440 - sparse_categorical_accuracy: 0.9890 Epoch 56/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9850 Epoch 57/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9880 Epoch 58/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0416 - sparse_categorical_accuracy: 0.9860 Epoch 59/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0479 - sparse_categorical_accuracy: 0.9860 Epoch 60/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0434 - sparse_categorical_accuracy: 0.9860 Epoch 61/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0414 - sparse_categorical_accuracy: 0.9880 Epoch 62/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0402 - sparse_categorical_accuracy: 0.9870 Epoch 63/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0376 - sparse_categorical_accuracy: 0.9890 Epoch 64/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0337 - sparse_categorical_accuracy: 0.9900 Epoch 65/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0309 - sparse_categorical_accuracy: 0.9910 Epoch 66/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9910 Epoch 67/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0389 - sparse_categorical_accuracy: 0.9870 Epoch 68/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0333 - sparse_categorical_accuracy: 0.9920 Epoch 69/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0331 - sparse_categorical_accuracy: 0.9890 Epoch 70/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0346 - sparse_categorical_accuracy: 0.9900 Epoch 71/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0367 - sparse_categorical_accuracy: 0.9880 Epoch 72/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0283 - sparse_categorical_accuracy: 0.9920 Epoch 73/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0315 - sparse_categorical_accuracy: 0.9930 Epoch 74/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0271 - sparse_categorical_accuracy: 0.9900 Epoch 75/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0257 - sparse_categorical_accuracy: 0.9920 Epoch 76/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0289 - sparse_categorical_accuracy: 0.9900 Epoch 77/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0264 - sparse_categorical_accuracy: 0.9900 Epoch 78/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0272 - sparse_categorical_accuracy: 0.9910 Epoch 79/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9880 Epoch 80/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0249 - sparse_categorical_accuracy: 0.9900 Epoch 81/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0216 - sparse_categorical_accuracy: 0.9930 Epoch 82/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0279 - sparse_categorical_accuracy: 0.9890 Epoch 83/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0261 - sparse_categorical_accuracy: 0.9920 Epoch 84/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0235 - sparse_categorical_accuracy: 0.9920 Epoch 85/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0236 - sparse_categorical_accuracy: 0.9930 Epoch 86/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0219 - sparse_categorical_accuracy: 0.9920 Epoch 87/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0196 - sparse_categorical_accuracy: 0.9920 Epoch 88/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0215 - sparse_categorical_accuracy: 0.9900 Epoch 89/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0223 - sparse_categorical_accuracy: 0.9900 Epoch 90/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0200 - sparse_categorical_accuracy: 0.9950 Epoch 91/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0250 - sparse_categorical_accuracy: 0.9900 Epoch 92/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0160 - sparse_categorical_accuracy: 0.9940 Epoch 93/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 94/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 95/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0172 - sparse_categorical_accuracy: 0.9960 Epoch 96/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0209 - sparse_categorical_accuracy: 0.9940 Epoch 97/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0179 - sparse_categorical_accuracy: 0.9920 Epoch 98/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0195 - sparse_categorical_accuracy: 0.9940 Epoch 99/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0165 - sparse_categorical_accuracy: 0.9930 Epoch 100/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0170 - sparse_categorical_accuracy: 0.9950 <keras.callbacks.History at 0x7ff7ac5c8fd0>
Visualizza l'incertezza
def plot_uncertainty_surface(test_uncertainty, ax, cmap=None):
"""Visualizes the 2D uncertainty surface.
For simplicity, assume these objects already exist in the memory:
test_examples: Array of test examples, shape (num_test, 2).
train_labels: Array of train labels, shape (num_train, ).
train_examples: Array of train examples, shape (num_train, 2).
Arguments:
test_uncertainty: Array of uncertainty scores, shape (num_test,).
ax: A matplotlib Axes object that specifies a matplotlib figure.
cmap: A matplotlib colormap object specifying the palette of the
predictive surface.
Returns:
pcm: A matplotlib PathCollection object that contains the palette
information of the uncertainty plot.
"""
# Normalize uncertainty for better visualization.
test_uncertainty = test_uncertainty / np.max(test_uncertainty)
# Set view limits.
ax.set_ylim(DEFAULT_Y_RANGE)
ax.set_xlim(DEFAULT_X_RANGE)
# Plot normalized uncertainty surface.
pcm = ax.imshow(
np.reshape(test_uncertainty, [DEFAULT_N_GRID, DEFAULT_N_GRID]),
cmap=cmap,
origin="lower",
extent=DEFAULT_X_RANGE + DEFAULT_Y_RANGE,
vmin=DEFAULT_NORM.vmin,
vmax=DEFAULT_NORM.vmax,
interpolation='bicubic',
aspect='auto')
# Plot training data.
ax.scatter(train_examples[:, 0], train_examples[:, 1],
c=train_labels, cmap=DEFAULT_CMAP, alpha=0.5)
ax.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
return pcm
Ora visualizza le previsioni del modello deterministico. Per prima cosa traccia la probabilità di classe:
\[p(x) = softmax(logit(x))\]
resnet_logits = resnet_model(test_examples)
resnet_probs = tf.nn.softmax(resnet_logits, axis=-1)[:, 0] # Take the probability for class 0.
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_probs, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Class Probability, Deterministic Model")
plt.show()

In questo grafico, il giallo e il viola sono le probabilità predittive per le due classi. Il modello deterministico ha svolto un buon lavoro nel classificare le due classi note (blu e arancione) con un confine decisionale non lineare. Tuttavia, non è consapevole della distanza e ha classificato con sicurezza gli esempi rossi fuori dominio (OOD) mai visti come classe arancione.
Visualizza l'incertezza del modello calcolando la varianza predittiva :
\[var(x) = p(x) * (1 - p(x))\]
resnet_uncertainty = resnet_probs * (1 - resnet_probs)
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_uncertainty, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Predictive Uncertainty, Deterministic Model")
plt.show()

In questo grafico, il giallo indica un'elevata incertezza e il viola indica una bassa incertezza. L'incertezza di un ResNet deterministico dipende solo dalla distanza degli esempi di test dal confine della decisione. Ciò porta il modello a essere eccessivamente sicuro quando è fuori dal dominio di addestramento. La sezione successiva mostra come SNGP si comporta in modo diverso su questo set di dati.
Il modello SNGP
Definisci il modello SNGP
Ora implementiamo il modello SNGP. Entrambi i componenti SNGP, SpectralNormalization e RandomFeatureGaussianProcess , sono disponibili nei livelli integrati di tensorflow_model .
Diamo un'occhiata a questi due componenti in modo più dettagliato. (Puoi anche passare alla sezione Il modello SNGP per vedere come viene implementato il modello completo.)
Wrapper di normalizzazione spettrale
SpectralNormalization è un wrapper di livello Keras. Può essere applicato a uno strato Denso esistente come questo:
dense = tf.keras.layers.Dense(units=10)
dense = nlp_layers.SpectralNormalization(dense, norm_multiplier=0.9)
La normalizzazione spettrale regolarizza il peso nascosto \(W\) guidando gradualmente la sua norma spettrale (cioè il più grande autovalore di \(W\)) verso il valore target norm_multiplier .
Il livello del processo gaussiano (GP).
RandomFeatureGaussianProcess implementa un'approssimazione basata su funzionalità casuali a un modello di processo gaussiano che può essere addestrato end-to-end con una rete neurale profonda. Sotto il cofano, il livello di processo gaussiano implementa una rete a due livelli:
\[logits(x) = \Phi(x) \beta, \quad \Phi(x)=\sqrt{\frac{2}{M} } * cos(Wx + b)\]
Qui \(x\) è l'input e \(W\) e \(b\) sono pesi congelati inizializzati casualmente rispettivamente da distribuzioni gaussiane e uniformi. (Pertanto \(\Phi(x)\) è chiamato "caratteristiche casuali".) \(\beta\) è il peso del kernel apprendibile simile a quello di un livello Dense.
batch_size = 32
input_dim = 1024
num_classes = 10
gp_layer = nlp_layers.RandomFeatureGaussianProcess(units=num_classes,
num_inducing=1024,
normalize_input=False,
scale_random_features=True,
gp_cov_momentum=-1)
I parametri principali dei livelli GP sono:
-
units: la dimensione dei log di output. -
num_inducing: la dimensione \(M\) del peso nascosto \(W\). Il valore predefinito è 1024. -
normalize_input: se applicare la normalizzazione del livello all'input \(x\). -
scale_random_features: se applicare la scala \(\sqrt{2/M}\) all'output nascosto.
-
gp_cov_momentumcontrolla come viene calcolata la covarianza del modello. Se impostata su un valore positivo (ad es. 0,999), la matrice di covarianza viene calcolata utilizzando l'aggiornamento della media mobile basato sulla quantità di moto (simile alla normalizzazione batch). Se impostato a -1, la matrice di covarianza viene aggiornata senza quantità di moto.
Dato un input batch con shape (batch_size, input_dim) , il livello GP restituisce un tensore logits (shape (batch_size, num_classes) ) per la previsione e anche il tensore covmat (shape (batch_size, batch_size) ) che è la matrice di covarianza posteriore del log in batch.
embedding = tf.random.normal(shape=(batch_size, input_dim))
logits, covmat = gp_layer(embedding)
Teoricamente, è possibile estendere l'algoritmo per calcolare diversi valori di varianza per classi diverse (come introdotto nel documento SNGP originale ). Tuttavia, questo è difficile da adattare a problemi con ampi spazi di output (ad es. ImageNet o modellazione del linguaggio).
Il modello SNGP completo
Data la classe base DeepResNet , il modello SNGP può essere implementato facilmente modificando i livelli nascosti e di output della rete residua. Per compatibilità con l'API Keras model.fit() , modificare anche il metodo call() del modello in modo che restituisca logits solo durante l'addestramento.
class DeepResNetSNGP(DeepResNet):
def __init__(self, spec_norm_bound=0.9, **kwargs):
self.spec_norm_bound = spec_norm_bound
super().__init__(**kwargs)
def make_dense_layer(self):
"""Applies spectral normalization to the hidden layer."""
dense_layer = super().make_dense_layer()
return nlp_layers.SpectralNormalization(
dense_layer, norm_multiplier=self.spec_norm_bound)
def make_output_layer(self, num_classes):
"""Uses Gaussian process as the output layer."""
return nlp_layers.RandomFeatureGaussianProcess(
num_classes,
gp_cov_momentum=-1,
**self.classifier_kwargs)
def call(self, inputs, training=False, return_covmat=False):
# Gets logits and covariance matrix from GP layer.
logits, covmat = super().call(inputs)
# Returns only logits during training.
if not training and return_covmat:
return logits, covmat
return logits
Utilizzare la stessa architettura del modello deterministico.
resnet_config
{'num_classes': 2, 'num_layers': 6, 'num_hidden': 128}
sngp_model = DeepResNetSNGP(**resnet_config)
sngp_model.build((None, 2))
sngp_model.summary()
Model: "deep_res_net_sngp"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) multiple 384
spectral_normalization_1 (S multiple 16768
pectralNormalization)
spectral_normalization_2 (S multiple 16768
pectralNormalization)
spectral_normalization_3 (S multiple 16768
pectralNormalization)
spectral_normalization_4 (S multiple 16768
pectralNormalization)
spectral_normalization_5 (S multiple 16768
pectralNormalization)
spectral_normalization_6 (S multiple 16768
pectralNormalization)
random_feature_gaussian_pro multiple 1182722
cess (RandomFeatureGaussian
Process)
=================================================================
Total params: 1,283,714
Trainable params: 101,120
Non-trainable params: 1,182,594
_________________________________________________________________
Implementare un callback Keras per reimpostare la matrice di covarianza all'inizio di una nuova epoca.
class ResetCovarianceCallback(tf.keras.callbacks.Callback):
def on_epoch_begin(self, epoch, logs=None):
"""Resets covariance matrix at the begining of the epoch."""
if epoch > 0:
self.model.classifier.reset_covariance_matrix()
Aggiungi questo callback alla classe del modello DeepResNetSNGP .
class DeepResNetSNGPWithCovReset(DeepResNetSNGP):
def fit(self, *args, **kwargs):
"""Adds ResetCovarianceCallback to model callbacks."""
kwargs["callbacks"] = list(kwargs.get("callbacks", []))
kwargs["callbacks"].append(ResetCovarianceCallback())
return super().fit(*args, **kwargs)
Modello di treno
Utilizzare tf.keras.model.fit per addestrare il modello.
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 2s 5ms/step - loss: 0.6223 - sparse_categorical_accuracy: 0.9570 Epoch 2/100 8/8 [==============================] - 0s 4ms/step - loss: 0.5310 - sparse_categorical_accuracy: 0.9980 Epoch 3/100 8/8 [==============================] - 0s 4ms/step - loss: 0.4766 - sparse_categorical_accuracy: 0.9990 Epoch 4/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4346 - sparse_categorical_accuracy: 0.9980 Epoch 5/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4015 - sparse_categorical_accuracy: 0.9980 Epoch 6/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3757 - sparse_categorical_accuracy: 0.9990 Epoch 7/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3525 - sparse_categorical_accuracy: 0.9990 Epoch 8/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3305 - sparse_categorical_accuracy: 0.9990 Epoch 9/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3144 - sparse_categorical_accuracy: 0.9980 Epoch 10/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2975 - sparse_categorical_accuracy: 0.9990 Epoch 11/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2832 - sparse_categorical_accuracy: 0.9990 Epoch 12/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2707 - sparse_categorical_accuracy: 0.9990 Epoch 13/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2568 - sparse_categorical_accuracy: 0.9990 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2470 - sparse_categorical_accuracy: 0.9970 Epoch 15/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2361 - sparse_categorical_accuracy: 0.9990 Epoch 16/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2271 - sparse_categorical_accuracy: 0.9990 Epoch 17/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2182 - sparse_categorical_accuracy: 0.9990 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2097 - sparse_categorical_accuracy: 0.9990 Epoch 19/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2018 - sparse_categorical_accuracy: 0.9990 Epoch 20/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1940 - sparse_categorical_accuracy: 0.9980 Epoch 21/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1892 - sparse_categorical_accuracy: 0.9990 Epoch 22/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1821 - sparse_categorical_accuracy: 0.9980 Epoch 23/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1768 - sparse_categorical_accuracy: 0.9990 Epoch 24/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1702 - sparse_categorical_accuracy: 0.9980 Epoch 25/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1664 - sparse_categorical_accuracy: 0.9990 Epoch 26/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1604 - sparse_categorical_accuracy: 0.9990 Epoch 27/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1565 - sparse_categorical_accuracy: 0.9990 Epoch 28/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1517 - sparse_categorical_accuracy: 0.9990 Epoch 29/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1469 - sparse_categorical_accuracy: 0.9990 Epoch 30/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1431 - sparse_categorical_accuracy: 0.9980 Epoch 31/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1385 - sparse_categorical_accuracy: 0.9980 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1351 - sparse_categorical_accuracy: 0.9990 Epoch 33/100 8/8 [==============================] - 0s 5ms/step - loss: 0.1312 - sparse_categorical_accuracy: 0.9980 Epoch 34/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1289 - sparse_categorical_accuracy: 0.9990 Epoch 35/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1254 - sparse_categorical_accuracy: 0.9980 Epoch 36/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1223 - sparse_categorical_accuracy: 0.9980 Epoch 37/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1180 - sparse_categorical_accuracy: 0.9990 Epoch 38/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1167 - sparse_categorical_accuracy: 0.9990 Epoch 39/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1132 - sparse_categorical_accuracy: 0.9980 Epoch 40/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1110 - sparse_categorical_accuracy: 0.9990 Epoch 41/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1075 - sparse_categorical_accuracy: 0.9990 Epoch 42/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1067 - sparse_categorical_accuracy: 0.9990 Epoch 43/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1034 - sparse_categorical_accuracy: 0.9990 Epoch 44/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1006 - sparse_categorical_accuracy: 0.9990 Epoch 45/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9990 Epoch 46/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0963 - sparse_categorical_accuracy: 0.9990 Epoch 47/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0943 - sparse_categorical_accuracy: 0.9980 Epoch 48/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0925 - sparse_categorical_accuracy: 0.9990 Epoch 49/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0905 - sparse_categorical_accuracy: 0.9990 Epoch 50/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0889 - sparse_categorical_accuracy: 0.9990 Epoch 51/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0863 - sparse_categorical_accuracy: 0.9980 Epoch 52/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0847 - sparse_categorical_accuracy: 0.9990 Epoch 53/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0831 - sparse_categorical_accuracy: 0.9980 Epoch 54/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0818 - sparse_categorical_accuracy: 0.9990 Epoch 55/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0799 - sparse_categorical_accuracy: 0.9990 Epoch 56/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0780 - sparse_categorical_accuracy: 0.9990 Epoch 57/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0768 - sparse_categorical_accuracy: 0.9990 Epoch 58/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0751 - sparse_categorical_accuracy: 0.9990 Epoch 59/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0748 - sparse_categorical_accuracy: 0.9990 Epoch 60/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0723 - sparse_categorical_accuracy: 0.9990 Epoch 61/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0712 - sparse_categorical_accuracy: 0.9990 Epoch 62/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 63/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 64/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0683 - sparse_categorical_accuracy: 0.9990 Epoch 65/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0665 - sparse_categorical_accuracy: 0.9990 Epoch 66/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0661 - sparse_categorical_accuracy: 0.9990 Epoch 67/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9990 Epoch 68/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0631 - sparse_categorical_accuracy: 0.9990 Epoch 69/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0620 - sparse_categorical_accuracy: 0.9990 Epoch 70/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0606 - sparse_categorical_accuracy: 0.9990 Epoch 71/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0601 - sparse_categorical_accuracy: 0.9980 Epoch 72/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9990 Epoch 73/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0586 - sparse_categorical_accuracy: 0.9990 Epoch 74/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0574 - sparse_categorical_accuracy: 0.9990 Epoch 75/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0565 - sparse_categorical_accuracy: 1.0000 Epoch 76/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0559 - sparse_categorical_accuracy: 0.9990 Epoch 77/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0549 - sparse_categorical_accuracy: 0.9990 Epoch 78/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0534 - sparse_categorical_accuracy: 1.0000 Epoch 79/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0532 - sparse_categorical_accuracy: 0.9990 Epoch 80/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0519 - sparse_categorical_accuracy: 1.0000 Epoch 81/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0511 - sparse_categorical_accuracy: 1.0000 Epoch 82/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0508 - sparse_categorical_accuracy: 0.9990 Epoch 83/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0499 - sparse_categorical_accuracy: 1.0000 Epoch 84/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 1.0000 Epoch 85/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 0.9990 Epoch 86/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0470 - sparse_categorical_accuracy: 1.0000 Epoch 87/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 88/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 89/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0453 - sparse_categorical_accuracy: 1.0000 Epoch 90/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0448 - sparse_categorical_accuracy: 1.0000 Epoch 91/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0441 - sparse_categorical_accuracy: 1.0000 Epoch 92/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0434 - sparse_categorical_accuracy: 1.0000 Epoch 93/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0431 - sparse_categorical_accuracy: 1.0000 Epoch 94/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0424 - sparse_categorical_accuracy: 1.0000 Epoch 95/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0420 - sparse_categorical_accuracy: 1.0000 Epoch 96/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0415 - sparse_categorical_accuracy: 1.0000 Epoch 97/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0409 - sparse_categorical_accuracy: 1.0000 Epoch 98/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0401 - sparse_categorical_accuracy: 1.0000 Epoch 99/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0396 - sparse_categorical_accuracy: 1.0000 Epoch 100/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0392 - sparse_categorical_accuracy: 1.0000 <keras.callbacks.History at 0x7ff7ac0f83d0>
Visualizza l'incertezza
Per prima cosa calcola i logit predittivi e le varianze.
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_variance = tf.linalg.diag_part(sngp_covmat)[:, None]
Ora calcola la probabilità predittiva a posteriori. Il metodo classico per calcolare la probabilità predittiva di un modello probabilistico consiste nell'utilizzare il campionamento Monte Carlo, ovvero
\[E(p(x)) = \frac{1}{M} \sum_{m=1}^M logit_m(x), \]
dove \(M\) è la dimensione del campione e \(logit_m(x)\) sono campioni casuali dal SNGP posteriore \(MultivariateNormal\)( sngp_logits , sngp_covmat ). Tuttavia, questo approccio può essere lento per le applicazioni sensibili alla latenza come la guida autonoma o le offerte in tempo reale. Invece, può approssimare \(E(p(x))\) usando il metodo del campo medio :
\[E(p(x)) \approx softmax(\frac{logit(x)}{\sqrt{1+ \lambda * \sigma^2(x)} })\]
dove \(\sigma^2(x)\) è la varianza SNGP e \(\lambda\) viene spesso scelto come \(\pi/8\) o \(3/\pi^2\).
sngp_logits_adjusted = sngp_logits / tf.sqrt(1. + (np.pi / 8.) * sngp_variance)
sngp_probs = tf.nn.softmax(sngp_logits_adjusted, axis=-1)[:, 0]
Questo metodo mean-field è implementato come funzione layers.gaussian_process.mean_field_logits :
def compute_posterior_mean_probability(logits, covmat, lambda_param=np.pi / 8.):
# Computes uncertainty-adjusted logits using the built-in method.
logits_adjusted = nlp_layers.gaussian_process.mean_field_logits(
logits, covmat, mean_field_factor=lambda_param)
return tf.nn.softmax(logits_adjusted, axis=-1)[:, 0]
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
Riepilogo SNGP
def plot_predictions(pred_probs, model_name=""):
"""Plot normalized class probabilities and predictive uncertainties."""
# Compute predictive uncertainty.
uncertainty = pred_probs * (1. - pred_probs)
# Initialize the plot axes.
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# Plots the class probability.
pcm_0 = plot_uncertainty_surface(pred_probs, ax=axs[0])
# Plots the predictive uncertainty.
pcm_1 = plot_uncertainty_surface(uncertainty, ax=axs[1])
# Adds color bars and titles.
fig.colorbar(pcm_0, ax=axs[0])
fig.colorbar(pcm_1, ax=axs[1])
axs[0].set_title(f"Class Probability, {model_name}")
axs[1].set_title(f"(Normalized) Predictive Uncertainty, {model_name}")
plt.show()
Metti tutto insieme. L'intera procedura (formazione, valutazione e calcolo dell'incertezza) può essere eseguita in sole cinque righe:
def train_and_test_sngp(train_examples, test_examples):
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, verbose=0, **fit_config)
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
return sngp_probs
sngp_probs = train_and_test_sngp(train_examples, test_examples)
Visualizza la probabilità di classe (a sinistra) e l'incertezza predittiva (a destra) del modello SNGP.
plot_predictions(sngp_probs, model_name="SNGP")

Ricorda che nel diagramma di probabilità di classe (a sinistra), il giallo e il viola sono probabilità di classe. Quando è vicino al dominio dei dati di addestramento, SNGP classifica correttamente gli esempi con alta confidenza (cioè, assegnando una probabilità prossima a 0 o 1). Quando è lontano dai dati di addestramento, SNGP diventa gradualmente meno sicuro e la sua probabilità predittiva si avvicina a 0,5 mentre l'incertezza del modello (normalizzata) sale a 1.
Confronta questo con la superficie di incertezza del modello deterministico:
plot_predictions(resnet_probs, model_name="Deterministic")

Come accennato in precedenza, un modello deterministico non è consapevole della distanza . La sua incertezza è definita dalla distanza dell'esempio di prova dal confine della decisione. Questo porta il modello a produrre previsioni troppo sicure per gli esempi fuori dominio (rosso).
Confronto con altri approcci di incertezza
Questa sezione confronta l'incertezza di SNGP con il dropout Monte Carlo e l' ensemble Deep .
Entrambi questi metodi si basano sulla media Monte Carlo di più passaggi in avanti di modelli deterministici. Impostare prima la dimensione dell'insieme \(M\).
num_ensemble = 10
L'abbandono di Montecarlo
Data una rete neurale addestrata con livelli di dropout, il dropout di Monte Carlo calcola la probabilità predittiva media
\[E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\]
calcolando la media su più passaggi in avanti abilitati per Dropout \(\{logit_m(x)\}_{m=1}^M\).
def mc_dropout_sampling(test_examples):
# Enable dropout during inference.
return resnet_model(test_examples, training=True)
# Monte Carlo dropout inference.
dropout_logit_samples = [mc_dropout_sampling(test_examples) for _ in range(num_ensemble)]
dropout_prob_samples = [tf.nn.softmax(dropout_logits, axis=-1)[:, 0] for dropout_logits in dropout_logit_samples]
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
plot_predictions(dropout_probs, model_name="MC Dropout")

Insieme profondo
Deep ensemble è un metodo all'avanguardia (ma costoso) per l'incertezza del deep learning. Per addestrare un ensemble Deep, addestrare prima i membri dell'ensemble \(M\) .
# Deep ensemble training
resnet_ensemble = []
for _ in range(num_ensemble):
resnet_model = DeepResNet(**resnet_config)
resnet_model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
resnet_model.fit(train_examples, train_labels, verbose=0, **fit_config)
resnet_ensemble.append(resnet_model)
Raccogli i logit e calcola la probabilità predittiva media \(E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\).
# Deep ensemble inference
ensemble_logit_samples = [model(test_examples) for model in resnet_ensemble]
ensemble_prob_samples = [tf.nn.softmax(logits, axis=-1)[:, 0] for logits in ensemble_logit_samples]
ensemble_probs = tf.reduce_mean(ensemble_prob_samples, axis=0)
plot_predictions(ensemble_probs, model_name="Deep ensemble")

Sia MC Dropout che Deep ensemble migliorano la capacità di incertezza di un modello rendendo meno certo il confine decisionale. Tuttavia, entrambi ereditano il limite deterministico della rete profonda nella mancanza di consapevolezza della distanza.
Riepilogo
In questo tutorial, hai:
- Implementato un modello SNGP su un classificatore profondo per migliorarne la consapevolezza della distanza.
- Addestrato end-to-end del modello SNGP utilizzando l'API Keras
model.fit(). - Visualizzato il comportamento di incertezza di SNGP.
- Confrontato il comportamento di incertezza tra i modelli SNGP, Monte Carlo dropout e deep ensemble.
Risorse e ulteriori letture
- Vedere il tutorial SNGP-BERT per un esempio di applicazione di SNGP su un modello BERT per la comprensione del linguaggio naturale consapevole dell'incertezza.
- Vedere le linee di base dell'incertezza per l'implementazione del modello SNGP (e molti altri metodi di incertezza) su un'ampia varietà di set di dati di riferimento (ad es. CIFAR , ImageNet , rilevamento della tossicità Jigsaw , ecc.).
- Per una comprensione più approfondita del metodo SNGP, consulta il documento Stima dell'incertezza semplice e di principio con apprendimento profondo deterministico tramite consapevolezza a distanza .