مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  در GitHub مشاهده کنید در GitHub مشاهده کنید |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
در برنامههای هوش مصنوعی که از نظر ایمنی حیاتی هستند (مثلاً تصمیمگیری پزشکی و رانندگی مستقل) یا در جایی که دادهها ذاتاً پر سر و صدا هستند (مثلاً درک زبان طبیعی)، برای یک طبقهبندی عمیق مهم است که به طور قابل اعتماد عدم قطعیت خود را کمیت کند. طبقهبندیکننده عمیق باید بتواند از محدودیتهای خود آگاه باشد و چه زمانی باید کنترل را به متخصصان انسانی بسپارد. این آموزش نشان میدهد که چگونه میتوان توانایی طبقهبندیکننده عمیق را در کمیسازی عدم قطعیت با استفاده از تکنیکی به نام فرآیند گاوسی عصبی-طبیعی ( SNGP ) بهبود بخشید .
ایده اصلی SNGP بهبود آگاهی از فاصله طبقهبندیکننده عمیق با اعمال تغییرات ساده در شبکه است. آگاهی از فاصله یک مدل معیاری است برای اینکه چگونه احتمال پیشبینی آن فاصله بین نمونه آزمایشی و دادههای آموزشی را منعکس میکند. این ویژگی مطلوبی است که برای مدلهای احتمالی استاندارد طلایی رایج است (مثلاً فرآیند گاوسی با هستههای RBF) اما در مدلهایی با شبکههای عصبی عمیق فاقد آن است. SNGP یک راه ساده برای تزریق این رفتار فرآیند گاوسی به یک طبقهبندی عمیق و در عین حال حفظ دقت پیشبینی آن ارائه میکند.
این آموزش یک مدل SNGP مبتنی بر شبکه باقیمانده عمیق (ResNet) را بر روی مجموعه داده دو قمر پیادهسازی میکند و سطح عدم قطعیت آن را با دو رویکرد رایج عدم قطعیت دیگر - ترک مونت کارلو و گروه عمیق مقایسه میکند.
این آموزش مدل SNGP را بر روی مجموعه داده های دو بعدی اسباب بازی نشان می دهد. برای مثالی از بکارگیری SNGP در یک کار درک زبان طبیعی دنیای واقعی با استفاده از BERT-base، لطفاً به آموزش SNGP-BERT مراجعه کنید. برای اجرای باکیفیت مدل SNGP (و بسیاری از روشهای عدم قطعیت دیگر) در طیف گستردهای از مجموعه دادههای معیار (مانند CIFAR-100 ، ImageNet ، تشخیص سمیت Jigsaw ، و غیره)، لطفاً معیار Uncertainty Baselines را بررسی کنید.
درباره SNGP
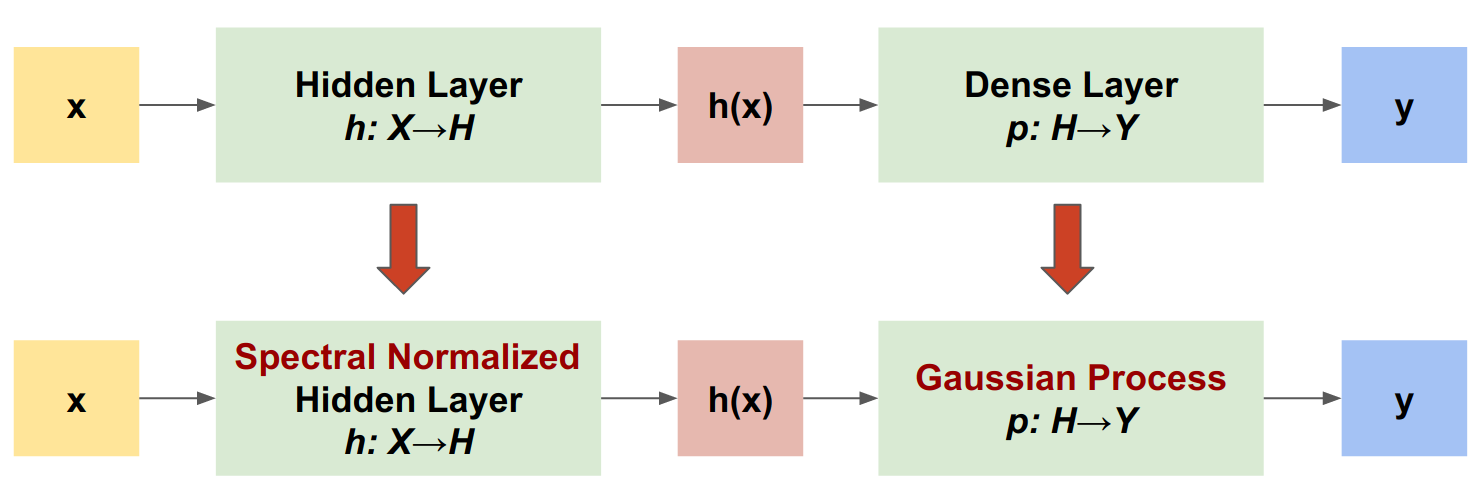
فرآیند گاوسی عصبی با نرمال طیفی (SNGP) یک رویکرد ساده برای بهبود کیفیت عدم قطعیت طبقهبندیکننده عمیق و در عین حال حفظ سطح مشابهی از دقت و تأخیر است. با توجه به شبکه باقیمانده عمیق، SNGP دو تغییر ساده در مدل ایجاد می کند:
- نرمال سازی طیفی را برای لایه های باقیمانده پنهان اعمال می کند.
- لایه خروجی متراکم را با یک لایه فرآیند گاوسی جایگزین می کند.
SNGP در مقایسه با سایر رویکردهای عدم قطعیت (مانند ترک تحصیل در مونت کارلو یا گروه Deep)، چندین مزیت دارد:
- این برای طیف وسیعی از پیشرفته ترین معماری های مبتنی بر باقی مانده (به عنوان مثال، (Wide) ResNet، DenseNet، BERT، و غیره کار می کند.
- این یک روش تک مدلی است (یعنی به میانگین گیری گروهی متکی نیست). بنابراین SNGP دارای یک سطح تاخیر مشابه به عنوان یک شبکه قطعی منفرد است و می تواند به راحتی در مجموعه داده های بزرگ مانند ImageNet و طبقه بندی نظرات سمی Jigsaw مقیاس بندی شود.
- به دلیل ویژگی آگاهی از فاصله، عملکرد تشخیص خارج از دامنه قوی دارد.
معایب این روش عبارتند از:
عدم قطعیت پیشبینی یک SNGP با استفاده از تقریب لاپلاس محاسبه میشود. بنابراین از نظر تئوری، عدم قطعیت پسین SNGP با فرآیند گاوسی دقیق متفاوت است.
آموزش SNGP به یک مرحله تنظیم مجدد کوواریانس در آغاز یک دوره جدید نیاز دارد. این می تواند مقدار کمی از پیچیدگی اضافی را به خط لوله آموزشی اضافه کند. این آموزش یک راه ساده برای پیاده سازی این کار با استفاده از فراخوان Keras را نشان می دهد.
برپایی
pip install --use-deprecated=legacy-resolver tf-models-official
# refresh pkg_resources so it takes the changes into account.
import pkg_resources
import importlib
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import sklearn.datasets
import numpy as np
import tensorflow as tf
import official.nlp.modeling.layers as nlp_layers
ماکروهای تجسم را تعریف کنید
plt.rcParams['figure.dpi'] = 140
DEFAULT_X_RANGE = (-3.5, 3.5)
DEFAULT_Y_RANGE = (-2.5, 2.5)
DEFAULT_CMAP = colors.ListedColormap(["#377eb8", "#ff7f00"])
DEFAULT_NORM = colors.Normalize(vmin=0, vmax=1,)
DEFAULT_N_GRID = 100
مجموعه داده دو ماه
مجموعه داده های آموزشی و ارزیابی را از مجموعه داده های دو ماه ایجاد کنید.
def make_training_data(sample_size=500):
"""Create two moon training dataset."""
train_examples, train_labels = sklearn.datasets.make_moons(
n_samples=2 * sample_size, noise=0.1)
# Adjust data position slightly.
train_examples[train_labels == 0] += [-0.1, 0.2]
train_examples[train_labels == 1] += [0.1, -0.2]
return train_examples, train_labels
رفتار پیشبینیکننده مدل را در کل فضای ورودی دو بعدی ارزیابی کنید.
def make_testing_data(x_range=DEFAULT_X_RANGE, y_range=DEFAULT_Y_RANGE, n_grid=DEFAULT_N_GRID):
"""Create a mesh grid in 2D space."""
# testing data (mesh grid over data space)
x = np.linspace(x_range[0], x_range[1], n_grid)
y = np.linspace(y_range[0], y_range[1], n_grid)
xv, yv = np.meshgrid(x, y)
return np.stack([xv.flatten(), yv.flatten()], axis=-1)
برای ارزیابی عدم قطعیت مدل، یک مجموعه داده خارج از دامنه (OOD) که به کلاس سوم تعلق دارد اضافه کنید. مدل هرگز این نمونه های OOD را در طول آموزش نمی بیند.
def make_ood_data(sample_size=500, means=(2.5, -1.75), vars=(0.01, 0.01)):
return np.random.multivariate_normal(
means, cov=np.diag(vars), size=sample_size)
# Load the train, test and OOD datasets.
train_examples, train_labels = make_training_data(
sample_size=500)
test_examples = make_testing_data()
ood_examples = make_ood_data(sample_size=500)
# Visualize
pos_examples = train_examples[train_labels == 0]
neg_examples = train_examples[train_labels == 1]
plt.figure(figsize=(7, 5.5))
plt.scatter(pos_examples[:, 0], pos_examples[:, 1], c="#377eb8", alpha=0.5)
plt.scatter(neg_examples[:, 0], neg_examples[:, 1], c="#ff7f00", alpha=0.5)
plt.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
plt.legend(["Postive", "Negative", "Out-of-Domain"])
plt.ylim(DEFAULT_Y_RANGE)
plt.xlim(DEFAULT_X_RANGE)
plt.show()

در اینجا آبی و نارنجی نشان دهنده کلاس های مثبت و منفی و قرمز نشان دهنده داده های OOD است. انتظار میرود مدلی که عدم قطعیت را به خوبی کمیت میکند، زمانی که به دادههای آموزشی نزدیک است (یعنی \(p(x_{test})\) نزدیک به 0 یا 1) مطمئن باشد و زمانی که از مناطق داده آموزشی دور است (یعنی \(p(x_{test})\) نزدیک به 0.5) نامشخص باشد. ).
مدل قطعی
مدل را تعریف کنید
از مدل قطعی (خط پایه) شروع کنید: یک شبکه باقیمانده چند لایه (ResNet) با نظم بخشیدن به خروج.
class DeepResNet(tf.keras.Model):
"""Defines a multi-layer residual network."""
def __init__(self, num_classes, num_layers=3, num_hidden=128,
dropout_rate=0.1, **classifier_kwargs):
super().__init__()
# Defines class meta data.
self.num_hidden = num_hidden
self.num_layers = num_layers
self.dropout_rate = dropout_rate
self.classifier_kwargs = classifier_kwargs
# Defines the hidden layers.
self.input_layer = tf.keras.layers.Dense(self.num_hidden, trainable=False)
self.dense_layers = [self.make_dense_layer() for _ in range(num_layers)]
# Defines the output layer.
self.classifier = self.make_output_layer(num_classes)
def call(self, inputs):
# Projects the 2d input data to high dimension.
hidden = self.input_layer(inputs)
# Computes the resnet hidden representations.
for i in range(self.num_layers):
resid = self.dense_layers[i](hidden)
resid = tf.keras.layers.Dropout(self.dropout_rate)(resid)
hidden += resid
return self.classifier(hidden)
def make_dense_layer(self):
"""Uses the Dense layer as the hidden layer."""
return tf.keras.layers.Dense(self.num_hidden, activation="relu")
def make_output_layer(self, num_classes):
"""Uses the Dense layer as the output layer."""
return tf.keras.layers.Dense(
num_classes, **self.classifier_kwargs)
این آموزش از یک ResNet 6 لایه ای با 128 واحد مخفی استفاده می کند.
resnet_config = dict(num_classes=2, num_layers=6, num_hidden=128)
resnet_model = DeepResNet(**resnet_config)
resnet_model.build((None, 2))
resnet_model.summary()
Model: "deep_res_net"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 384
dense_1 (Dense) multiple 16512
dense_2 (Dense) multiple 16512
dense_3 (Dense) multiple 16512
dense_4 (Dense) multiple 16512
dense_5 (Dense) multiple 16512
dense_6 (Dense) multiple 16512
dense_7 (Dense) multiple 258
=================================================================
Total params: 99,714
Trainable params: 99,330
Non-trainable params: 384
_________________________________________________________________
مدل قطار
پارامترهای آموزشی را برای استفاده از SparseCategoricalCrossentropy به عنوان تابع ضرر و بهینه ساز Adam پیکربندی کنید.
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.keras.metrics.SparseCategoricalAccuracy(),
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
train_config = dict(loss=loss, metrics=metrics, optimizer=optimizer)
مدل را برای 100 دوره با سایز دسته ای 128 آموزش دهید.
fit_config = dict(batch_size=128, epochs=100)
resnet_model.compile(**train_config)
resnet_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 1s 4ms/step - loss: 1.1251 - sparse_categorical_accuracy: 0.5050 Epoch 2/100 8/8 [==============================] - 0s 3ms/step - loss: 0.5538 - sparse_categorical_accuracy: 0.6920 Epoch 3/100 8/8 [==============================] - 0s 3ms/step - loss: 0.2881 - sparse_categorical_accuracy: 0.9160 Epoch 4/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1923 - sparse_categorical_accuracy: 0.9370 Epoch 5/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1550 - sparse_categorical_accuracy: 0.9420 Epoch 6/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1403 - sparse_categorical_accuracy: 0.9450 Epoch 7/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1269 - sparse_categorical_accuracy: 0.9430 Epoch 8/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1208 - sparse_categorical_accuracy: 0.9460 Epoch 9/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1158 - sparse_categorical_accuracy: 0.9510 Epoch 10/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1103 - sparse_categorical_accuracy: 0.9490 Epoch 11/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1051 - sparse_categorical_accuracy: 0.9510 Epoch 12/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1053 - sparse_categorical_accuracy: 0.9510 Epoch 13/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1013 - sparse_categorical_accuracy: 0.9450 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0967 - sparse_categorical_accuracy: 0.9500 Epoch 15/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9530 Epoch 16/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0984 - sparse_categorical_accuracy: 0.9500 Epoch 17/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0982 - sparse_categorical_accuracy: 0.9480 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0918 - sparse_categorical_accuracy: 0.9510 Epoch 19/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0903 - sparse_categorical_accuracy: 0.9500 Epoch 20/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0883 - sparse_categorical_accuracy: 0.9510 Epoch 21/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0870 - sparse_categorical_accuracy: 0.9530 Epoch 22/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0884 - sparse_categorical_accuracy: 0.9560 Epoch 23/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0850 - sparse_categorical_accuracy: 0.9540 Epoch 24/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0808 - sparse_categorical_accuracy: 0.9580 Epoch 25/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0773 - sparse_categorical_accuracy: 0.9560 Epoch 26/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0801 - sparse_categorical_accuracy: 0.9590 Epoch 27/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0779 - sparse_categorical_accuracy: 0.9580 Epoch 28/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0807 - sparse_categorical_accuracy: 0.9580 Epoch 29/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0820 - sparse_categorical_accuracy: 0.9570 Epoch 30/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0730 - sparse_categorical_accuracy: 0.9600 Epoch 31/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0782 - sparse_categorical_accuracy: 0.9590 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0704 - sparse_categorical_accuracy: 0.9600 Epoch 33/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0709 - sparse_categorical_accuracy: 0.9610 Epoch 34/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0758 - sparse_categorical_accuracy: 0.9580 Epoch 35/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9610 Epoch 36/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0688 - sparse_categorical_accuracy: 0.9600 Epoch 37/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0675 - sparse_categorical_accuracy: 0.9630 Epoch 38/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9690 Epoch 39/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0677 - sparse_categorical_accuracy: 0.9610 Epoch 40/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0702 - sparse_categorical_accuracy: 0.9650 Epoch 41/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0614 - sparse_categorical_accuracy: 0.9690 Epoch 42/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0663 - sparse_categorical_accuracy: 0.9680 Epoch 43/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0626 - sparse_categorical_accuracy: 0.9740 Epoch 44/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9760 Epoch 45/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0573 - sparse_categorical_accuracy: 0.9780 Epoch 46/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0568 - sparse_categorical_accuracy: 0.9770 Epoch 47/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0595 - sparse_categorical_accuracy: 0.9780 Epoch 48/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0482 - sparse_categorical_accuracy: 0.9840 Epoch 49/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0515 - sparse_categorical_accuracy: 0.9820 Epoch 50/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0525 - sparse_categorical_accuracy: 0.9830 Epoch 51/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0507 - sparse_categorical_accuracy: 0.9790 Epoch 52/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0433 - sparse_categorical_accuracy: 0.9850 Epoch 53/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0511 - sparse_categorical_accuracy: 0.9820 Epoch 54/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0501 - sparse_categorical_accuracy: 0.9820 Epoch 55/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0440 - sparse_categorical_accuracy: 0.9890 Epoch 56/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9850 Epoch 57/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0438 - sparse_categorical_accuracy: 0.9880 Epoch 58/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0416 - sparse_categorical_accuracy: 0.9860 Epoch 59/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0479 - sparse_categorical_accuracy: 0.9860 Epoch 60/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0434 - sparse_categorical_accuracy: 0.9860 Epoch 61/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0414 - sparse_categorical_accuracy: 0.9880 Epoch 62/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0402 - sparse_categorical_accuracy: 0.9870 Epoch 63/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0376 - sparse_categorical_accuracy: 0.9890 Epoch 64/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0337 - sparse_categorical_accuracy: 0.9900 Epoch 65/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0309 - sparse_categorical_accuracy: 0.9910 Epoch 66/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9910 Epoch 67/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0389 - sparse_categorical_accuracy: 0.9870 Epoch 68/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0333 - sparse_categorical_accuracy: 0.9920 Epoch 69/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0331 - sparse_categorical_accuracy: 0.9890 Epoch 70/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0346 - sparse_categorical_accuracy: 0.9900 Epoch 71/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0367 - sparse_categorical_accuracy: 0.9880 Epoch 72/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0283 - sparse_categorical_accuracy: 0.9920 Epoch 73/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0315 - sparse_categorical_accuracy: 0.9930 Epoch 74/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0271 - sparse_categorical_accuracy: 0.9900 Epoch 75/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0257 - sparse_categorical_accuracy: 0.9920 Epoch 76/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0289 - sparse_categorical_accuracy: 0.9900 Epoch 77/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0264 - sparse_categorical_accuracy: 0.9900 Epoch 78/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0272 - sparse_categorical_accuracy: 0.9910 Epoch 79/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0336 - sparse_categorical_accuracy: 0.9880 Epoch 80/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0249 - sparse_categorical_accuracy: 0.9900 Epoch 81/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0216 - sparse_categorical_accuracy: 0.9930 Epoch 82/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0279 - sparse_categorical_accuracy: 0.9890 Epoch 83/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0261 - sparse_categorical_accuracy: 0.9920 Epoch 84/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0235 - sparse_categorical_accuracy: 0.9920 Epoch 85/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0236 - sparse_categorical_accuracy: 0.9930 Epoch 86/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0219 - sparse_categorical_accuracy: 0.9920 Epoch 87/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0196 - sparse_categorical_accuracy: 0.9920 Epoch 88/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0215 - sparse_categorical_accuracy: 0.9900 Epoch 89/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0223 - sparse_categorical_accuracy: 0.9900 Epoch 90/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0200 - sparse_categorical_accuracy: 0.9950 Epoch 91/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0250 - sparse_categorical_accuracy: 0.9900 Epoch 92/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0160 - sparse_categorical_accuracy: 0.9940 Epoch 93/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 94/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0203 - sparse_categorical_accuracy: 0.9930 Epoch 95/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0172 - sparse_categorical_accuracy: 0.9960 Epoch 96/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0209 - sparse_categorical_accuracy: 0.9940 Epoch 97/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0179 - sparse_categorical_accuracy: 0.9920 Epoch 98/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0195 - sparse_categorical_accuracy: 0.9940 Epoch 99/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0165 - sparse_categorical_accuracy: 0.9930 Epoch 100/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0170 - sparse_categorical_accuracy: 0.9950 <keras.callbacks.History at 0x7ff7ac5c8fd0>
عدم قطعیت را تجسم کنید
def plot_uncertainty_surface(test_uncertainty, ax, cmap=None):
"""Visualizes the 2D uncertainty surface.
For simplicity, assume these objects already exist in the memory:
test_examples: Array of test examples, shape (num_test, 2).
train_labels: Array of train labels, shape (num_train, ).
train_examples: Array of train examples, shape (num_train, 2).
Arguments:
test_uncertainty: Array of uncertainty scores, shape (num_test,).
ax: A matplotlib Axes object that specifies a matplotlib figure.
cmap: A matplotlib colormap object specifying the palette of the
predictive surface.
Returns:
pcm: A matplotlib PathCollection object that contains the palette
information of the uncertainty plot.
"""
# Normalize uncertainty for better visualization.
test_uncertainty = test_uncertainty / np.max(test_uncertainty)
# Set view limits.
ax.set_ylim(DEFAULT_Y_RANGE)
ax.set_xlim(DEFAULT_X_RANGE)
# Plot normalized uncertainty surface.
pcm = ax.imshow(
np.reshape(test_uncertainty, [DEFAULT_N_GRID, DEFAULT_N_GRID]),
cmap=cmap,
origin="lower",
extent=DEFAULT_X_RANGE + DEFAULT_Y_RANGE,
vmin=DEFAULT_NORM.vmin,
vmax=DEFAULT_NORM.vmax,
interpolation='bicubic',
aspect='auto')
# Plot training data.
ax.scatter(train_examples[:, 0], train_examples[:, 1],
c=train_labels, cmap=DEFAULT_CMAP, alpha=0.5)
ax.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
return pcm
حال پیشبینیهای مدل قطعی را تجسم کنید. ابتدا احتمال کلاس را رسم کنید:
\[p(x) = softmax(logit(x))\]
resnet_logits = resnet_model(test_examples)
resnet_probs = tf.nn.softmax(resnet_logits, axis=-1)[:, 0] # Take the probability for class 0.
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_probs, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Class Probability, Deterministic Model")
plt.show()

در این نمودار، زرد و بنفش احتمالات پیش بینی کننده برای دو کلاس هستند. مدل قطعی در طبقه بندی دو کلاس شناخته شده (آبی و نارنجی) با یک مرز تصمیم غیرخطی کار خوبی انجام داد. با این حال، از فاصله آگاه نیست، و نمونههای قرمز خارج از دامنه (OOD) را که هرگز دیده نشدهاند، با اطمینان به عنوان کلاس نارنجی طبقهبندی کرد.
عدم قطعیت مدل را با محاسبه واریانس پیش بینی تجسم کنید:
\[var(x) = p(x) * (1 - p(x))\]
resnet_uncertainty = resnet_probs * (1 - resnet_probs)
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_uncertainty, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Predictive Uncertainty, Deterministic Model")
plt.show()

در این نمودار رنگ زرد نشان دهنده عدم قطعیت زیاد و بنفش نشان دهنده عدم قطعیت کم است. عدم قطعیت ResNet قطعی فقط به فاصله نمونه های آزمایشی از مرز تصمیم بستگی دارد. این باعث می شود که مدل در خارج از حوزه آموزشی بیش از حد اعتماد به نفس داشته باشد. بخش بعدی نشان می دهد که چگونه SNGP در این مجموعه داده متفاوت رفتار می کند.
مدل SNGP
مدل SNGP را تعریف کنید
حال بیایید مدل SNGP را پیاده سازی کنیم. هر دو مولفه SNGP، SpectralNormalization و RandomFeatureGaussianProcess ، در لایه های داخلی tensorflow_model موجود هستند.
بیایید این دو جزء را با جزئیات بیشتری بررسی کنیم. (همچنین می توانید به بخش مدل SNGP بروید تا ببینید که چگونه مدل کامل پیاده سازی شده است.)
لفاف نرمال سازی طیفی
SpectralNormalization یک لایه لایه Keras است. می توان آن را به یک لایه متراکم موجود مانند زیر اعمال کرد:
dense = tf.keras.layers.Dense(units=10)
dense = nlp_layers.SpectralNormalization(dense, norm_multiplier=0.9)
نرمال سازی طیفی وزن پنهان \(W\) با هدایت تدریجی هنجار طیفی آن (یعنی بزرگترین مقدار ویژه \(W\)) به سمت مقدار هدف norm_multiplier می کند.
لایه فرآیند گاوسی (GP).
RandomFeatureGaussianProcess یک تقریب مبتنی بر ویژگی تصادفی را برای یک مدل فرآیند گاوسی پیادهسازی میکند که با یک شبکه عصبی عمیق قابل آموزش است. در زیر هود، لایه فرآیند گاوسی یک شبکه دو لایه را پیاده سازی می کند:
\[logits(x) = \Phi(x) \beta, \quad \Phi(x)=\sqrt{\frac{2}{M} } * cos(Wx + b)\]
در اینجا \(x\) ورودی است، و \(W\) و \(b\) وزن های منجمد شده ای هستند که به ترتیب به طور تصادفی از توزیع های گاوسی و یکنواخت مقداردهی اولیه شده اند. (بنابراین \(\Phi(x)\) "ویژگی های تصادفی" نامیده می شود.) \(\beta\) وزن هسته قابل یادگیری است که مشابه وزن یک لایه متراکم است.
batch_size = 32
input_dim = 1024
num_classes = 10
gp_layer = nlp_layers.RandomFeatureGaussianProcess(units=num_classes,
num_inducing=1024,
normalize_input=False,
scale_random_features=True,
gp_cov_momentum=-1)
پارامترهای اصلی لایه های GP عبارتند از:
-
units: بعد لجیت های خروجی. -
num_inducing: بعد \(M\) وزن پنهان \(W\). پیش فرض 1024 است. -
normalize_input: آیا باید نرمال سازی لایه را در ورودی \(x\)اعمال کرد یا خیر. -
scale_random_features: آیا باید مقیاس \(\sqrt{2/M}\) را در خروجی پنهان اعمال کرد یا خیر.
-
gp_cov_momentumنحوه محاسبه کوواریانس مدل را کنترل می کند. اگر روی یک مقدار مثبت تنظیم شود (به عنوان مثال، 0.999)، ماتریس کوواریانس با استفاده از به روز رسانی میانگین متحرک مبتنی بر تکانه محاسبه می شود (شبیه به نرمال سازی دسته ای). اگر روی -1 تنظیم شود، ماتریس کوواریانس بدون تکانه به روز می شود.
با توجه به یک ورودی دسته ای با شکل (batch_size, input_dim) ، لایه GP یک تانسور logits (شکل (batch_size, num_classes) ) برای پیش بینی و همچنین تانسور covmat (شکل (batch_size, batch_size) ) که ماتریس کوواریانس خلفی است برمی گرداند. لاجیت های دسته ای
embedding = tf.random.normal(shape=(batch_size, input_dim))
logits, covmat = gp_layer(embedding)
از نظر تئوری، امکان گسترش الگوریتم برای محاسبه مقادیر مختلف واریانس برای کلاسهای مختلف وجود دارد (همانطور که در مقاله اصلی SNGP معرفی شده است). با این حال، مقیاس کردن آن به مشکلات فضاهای خروجی بزرگ (مثلاً ImageNet یا مدلسازی زبان) دشوار است.
مدل کامل SNGP
با توجه به کلاس پایه DeepResNet ، مدل SNGP را می توان به راحتی با اصلاح لایه های مخفی و خروجی شبکه باقی مانده پیاده سازی کرد. برای سازگاری با Keras model.fit() ، متد call() () مدل را نیز تغییر دهید تا در طول آموزش فقط logits ها را خروجی کند.
class DeepResNetSNGP(DeepResNet):
def __init__(self, spec_norm_bound=0.9, **kwargs):
self.spec_norm_bound = spec_norm_bound
super().__init__(**kwargs)
def make_dense_layer(self):
"""Applies spectral normalization to the hidden layer."""
dense_layer = super().make_dense_layer()
return nlp_layers.SpectralNormalization(
dense_layer, norm_multiplier=self.spec_norm_bound)
def make_output_layer(self, num_classes):
"""Uses Gaussian process as the output layer."""
return nlp_layers.RandomFeatureGaussianProcess(
num_classes,
gp_cov_momentum=-1,
**self.classifier_kwargs)
def call(self, inputs, training=False, return_covmat=False):
# Gets logits and covariance matrix from GP layer.
logits, covmat = super().call(inputs)
# Returns only logits during training.
if not training and return_covmat:
return logits, covmat
return logits
از همان معماری مدل قطعی استفاده کنید.
resnet_config
{'num_classes': 2, 'num_layers': 6, 'num_hidden': 128}
sngp_model = DeepResNetSNGP(**resnet_config)
sngp_model.build((None, 2))
sngp_model.summary()
Model: "deep_res_net_sngp"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) multiple 384
spectral_normalization_1 (S multiple 16768
pectralNormalization)
spectral_normalization_2 (S multiple 16768
pectralNormalization)
spectral_normalization_3 (S multiple 16768
pectralNormalization)
spectral_normalization_4 (S multiple 16768
pectralNormalization)
spectral_normalization_5 (S multiple 16768
pectralNormalization)
spectral_normalization_6 (S multiple 16768
pectralNormalization)
random_feature_gaussian_pro multiple 1182722
cess (RandomFeatureGaussian
Process)
=================================================================
Total params: 1,283,714
Trainable params: 101,120
Non-trainable params: 1,182,594
_________________________________________________________________
برای بازنشانی ماتریس کوواریانس در آغاز یک دوره جدید، یک فراخوان Keras را اجرا کنید.
class ResetCovarianceCallback(tf.keras.callbacks.Callback):
def on_epoch_begin(self, epoch, logs=None):
"""Resets covariance matrix at the begining of the epoch."""
if epoch > 0:
self.model.classifier.reset_covariance_matrix()
این callback را به کلاس مدل DeepResNetSNGP اضافه کنید.
class DeepResNetSNGPWithCovReset(DeepResNetSNGP):
def fit(self, *args, **kwargs):
"""Adds ResetCovarianceCallback to model callbacks."""
kwargs["callbacks"] = list(kwargs.get("callbacks", []))
kwargs["callbacks"].append(ResetCovarianceCallback())
return super().fit(*args, **kwargs)
مدل قطار
برای آموزش مدل از tf.keras.model.fit استفاده کنید.
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 2s 5ms/step - loss: 0.6223 - sparse_categorical_accuracy: 0.9570 Epoch 2/100 8/8 [==============================] - 0s 4ms/step - loss: 0.5310 - sparse_categorical_accuracy: 0.9980 Epoch 3/100 8/8 [==============================] - 0s 4ms/step - loss: 0.4766 - sparse_categorical_accuracy: 0.9990 Epoch 4/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4346 - sparse_categorical_accuracy: 0.9980 Epoch 5/100 8/8 [==============================] - 0s 5ms/step - loss: 0.4015 - sparse_categorical_accuracy: 0.9980 Epoch 6/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3757 - sparse_categorical_accuracy: 0.9990 Epoch 7/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3525 - sparse_categorical_accuracy: 0.9990 Epoch 8/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3305 - sparse_categorical_accuracy: 0.9990 Epoch 9/100 8/8 [==============================] - 0s 5ms/step - loss: 0.3144 - sparse_categorical_accuracy: 0.9980 Epoch 10/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2975 - sparse_categorical_accuracy: 0.9990 Epoch 11/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2832 - sparse_categorical_accuracy: 0.9990 Epoch 12/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2707 - sparse_categorical_accuracy: 0.9990 Epoch 13/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2568 - sparse_categorical_accuracy: 0.9990 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2470 - sparse_categorical_accuracy: 0.9970 Epoch 15/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2361 - sparse_categorical_accuracy: 0.9990 Epoch 16/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2271 - sparse_categorical_accuracy: 0.9990 Epoch 17/100 8/8 [==============================] - 0s 5ms/step - loss: 0.2182 - sparse_categorical_accuracy: 0.9990 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2097 - sparse_categorical_accuracy: 0.9990 Epoch 19/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2018 - sparse_categorical_accuracy: 0.9990 Epoch 20/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1940 - sparse_categorical_accuracy: 0.9980 Epoch 21/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1892 - sparse_categorical_accuracy: 0.9990 Epoch 22/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1821 - sparse_categorical_accuracy: 0.9980 Epoch 23/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1768 - sparse_categorical_accuracy: 0.9990 Epoch 24/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1702 - sparse_categorical_accuracy: 0.9980 Epoch 25/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1664 - sparse_categorical_accuracy: 0.9990 Epoch 26/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1604 - sparse_categorical_accuracy: 0.9990 Epoch 27/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1565 - sparse_categorical_accuracy: 0.9990 Epoch 28/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1517 - sparse_categorical_accuracy: 0.9990 Epoch 29/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1469 - sparse_categorical_accuracy: 0.9990 Epoch 30/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1431 - sparse_categorical_accuracy: 0.9980 Epoch 31/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1385 - sparse_categorical_accuracy: 0.9980 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1351 - sparse_categorical_accuracy: 0.9990 Epoch 33/100 8/8 [==============================] - 0s 5ms/step - loss: 0.1312 - sparse_categorical_accuracy: 0.9980 Epoch 34/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1289 - sparse_categorical_accuracy: 0.9990 Epoch 35/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1254 - sparse_categorical_accuracy: 0.9980 Epoch 36/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1223 - sparse_categorical_accuracy: 0.9980 Epoch 37/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1180 - sparse_categorical_accuracy: 0.9990 Epoch 38/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1167 - sparse_categorical_accuracy: 0.9990 Epoch 39/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1132 - sparse_categorical_accuracy: 0.9980 Epoch 40/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1110 - sparse_categorical_accuracy: 0.9990 Epoch 41/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1075 - sparse_categorical_accuracy: 0.9990 Epoch 42/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1067 - sparse_categorical_accuracy: 0.9990 Epoch 43/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1034 - sparse_categorical_accuracy: 0.9990 Epoch 44/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1006 - sparse_categorical_accuracy: 0.9990 Epoch 45/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9990 Epoch 46/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0963 - sparse_categorical_accuracy: 0.9990 Epoch 47/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0943 - sparse_categorical_accuracy: 0.9980 Epoch 48/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0925 - sparse_categorical_accuracy: 0.9990 Epoch 49/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0905 - sparse_categorical_accuracy: 0.9990 Epoch 50/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0889 - sparse_categorical_accuracy: 0.9990 Epoch 51/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0863 - sparse_categorical_accuracy: 0.9980 Epoch 52/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0847 - sparse_categorical_accuracy: 0.9990 Epoch 53/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0831 - sparse_categorical_accuracy: 0.9980 Epoch 54/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0818 - sparse_categorical_accuracy: 0.9990 Epoch 55/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0799 - sparse_categorical_accuracy: 0.9990 Epoch 56/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0780 - sparse_categorical_accuracy: 0.9990 Epoch 57/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0768 - sparse_categorical_accuracy: 0.9990 Epoch 58/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0751 - sparse_categorical_accuracy: 0.9990 Epoch 59/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0748 - sparse_categorical_accuracy: 0.9990 Epoch 60/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0723 - sparse_categorical_accuracy: 0.9990 Epoch 61/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0712 - sparse_categorical_accuracy: 0.9990 Epoch 62/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 63/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0701 - sparse_categorical_accuracy: 0.9990 Epoch 64/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0683 - sparse_categorical_accuracy: 0.9990 Epoch 65/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0665 - sparse_categorical_accuracy: 0.9990 Epoch 66/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0661 - sparse_categorical_accuracy: 0.9990 Epoch 67/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9990 Epoch 68/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0631 - sparse_categorical_accuracy: 0.9990 Epoch 69/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0620 - sparse_categorical_accuracy: 0.9990 Epoch 70/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0606 - sparse_categorical_accuracy: 0.9990 Epoch 71/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0601 - sparse_categorical_accuracy: 0.9980 Epoch 72/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0590 - sparse_categorical_accuracy: 0.9990 Epoch 73/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0586 - sparse_categorical_accuracy: 0.9990 Epoch 74/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0574 - sparse_categorical_accuracy: 0.9990 Epoch 75/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0565 - sparse_categorical_accuracy: 1.0000 Epoch 76/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0559 - sparse_categorical_accuracy: 0.9990 Epoch 77/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0549 - sparse_categorical_accuracy: 0.9990 Epoch 78/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0534 - sparse_categorical_accuracy: 1.0000 Epoch 79/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0532 - sparse_categorical_accuracy: 0.9990 Epoch 80/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0519 - sparse_categorical_accuracy: 1.0000 Epoch 81/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0511 - sparse_categorical_accuracy: 1.0000 Epoch 82/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0508 - sparse_categorical_accuracy: 0.9990 Epoch 83/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0499 - sparse_categorical_accuracy: 1.0000 Epoch 84/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 1.0000 Epoch 85/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0490 - sparse_categorical_accuracy: 0.9990 Epoch 86/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0470 - sparse_categorical_accuracy: 1.0000 Epoch 87/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 88/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0468 - sparse_categorical_accuracy: 1.0000 Epoch 89/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0453 - sparse_categorical_accuracy: 1.0000 Epoch 90/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0448 - sparse_categorical_accuracy: 1.0000 Epoch 91/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0441 - sparse_categorical_accuracy: 1.0000 Epoch 92/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0434 - sparse_categorical_accuracy: 1.0000 Epoch 93/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0431 - sparse_categorical_accuracy: 1.0000 Epoch 94/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0424 - sparse_categorical_accuracy: 1.0000 Epoch 95/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0420 - sparse_categorical_accuracy: 1.0000 Epoch 96/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0415 - sparse_categorical_accuracy: 1.0000 Epoch 97/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0409 - sparse_categorical_accuracy: 1.0000 Epoch 98/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0401 - sparse_categorical_accuracy: 1.0000 Epoch 99/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0396 - sparse_categorical_accuracy: 1.0000 Epoch 100/100 8/8 [==============================] - 0s 5ms/step - loss: 0.0392 - sparse_categorical_accuracy: 1.0000 <keras.callbacks.History at 0x7ff7ac0f83d0>
عدم قطعیت را تجسم کنید
ابتدا لاجیت ها و واریانس های پیش بینی را محاسبه کنید.
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_variance = tf.linalg.diag_part(sngp_covmat)[:, None]
اکنون احتمال پیش بینی پسین را محاسبه کنید. روش کلاسیک برای محاسبه احتمال پیش بینی یک مدل احتمالی استفاده از نمونه گیری مونت کارلو است، به عنوان مثال،
\[E(p(x)) = \frac{1}{M} \sum_{m=1}^M logit_m(x), \]
که در آن \(M\) اندازه نمونه است، و \(logit_m(x)\) نمونه های تصادفی از \(MultivariateNormal\)پسین SNGP هستند ( sngp_logits ، sngp_covmat ). با این حال، این رویکرد میتواند برای برنامههای حساس به تأخیر مانند رانندگی خودکار یا پیشنهاد قیمت در زمان واقعی کند باشد. در عوض، میتوان \(E(p(x))\) را با استفاده از روش میدان میانگین تقریب زد:
\[E(p(x)) \approx softmax(\frac{logit(x)}{\sqrt{1+ \lambda * \sigma^2(x)} })\]
که در آن \(\sigma^2(x)\) واریانس SNGP است و \(\lambda\) اغلب به عنوان \(\pi/8\) یا \(3/\pi^2\)انتخاب می شود.
sngp_logits_adjusted = sngp_logits / tf.sqrt(1. + (np.pi / 8.) * sngp_variance)
sngp_probs = tf.nn.softmax(sngp_logits_adjusted, axis=-1)[:, 0]
این روش میدان میانگین به عنوان یک تابع layers.gaussian_process.mean_field_logits پیاده سازی می شود:
def compute_posterior_mean_probability(logits, covmat, lambda_param=np.pi / 8.):
# Computes uncertainty-adjusted logits using the built-in method.
logits_adjusted = nlp_layers.gaussian_process.mean_field_logits(
logits, covmat, mean_field_factor=lambda_param)
return tf.nn.softmax(logits_adjusted, axis=-1)[:, 0]
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
خلاصه SNGP
def plot_predictions(pred_probs, model_name=""):
"""Plot normalized class probabilities and predictive uncertainties."""
# Compute predictive uncertainty.
uncertainty = pred_probs * (1. - pred_probs)
# Initialize the plot axes.
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# Plots the class probability.
pcm_0 = plot_uncertainty_surface(pred_probs, ax=axs[0])
# Plots the predictive uncertainty.
pcm_1 = plot_uncertainty_surface(uncertainty, ax=axs[1])
# Adds color bars and titles.
fig.colorbar(pcm_0, ax=axs[0])
fig.colorbar(pcm_1, ax=axs[1])
axs[0].set_title(f"Class Probability, {model_name}")
axs[1].set_title(f"(Normalized) Predictive Uncertainty, {model_name}")
plt.show()
همه چیز را کنار هم بگذارید. کل روش (آموزش، ارزیابی و محاسبه عدم قطعیت) را می توان تنها در پنج خط انجام داد:
def train_and_test_sngp(train_examples, test_examples):
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, verbose=0, **fit_config)
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
return sngp_probs
sngp_probs = train_and_test_sngp(train_examples, test_examples)
احتمال کلاس (چپ) و عدم قطعیت پیشبینی (راست) مدل SNGP را تجسم کنید.
plot_predictions(sngp_probs, model_name="SNGP")

به یاد داشته باشید که در نمودار احتمال کلاس (سمت چپ)، رنگ زرد و بنفش احتمالات کلاس هستند. هنگامی که به دامنه داده های آموزشی نزدیک است، SNGP به درستی نمونه ها را با اطمینان بالا طبقه بندی می کند (یعنی تخصیص نزدیک به 0 یا 1 احتمال). هنگامی که از داده های آموزشی دور می شود، SNGP به تدریج اعتماد به نفس کمتری پیدا می کند و احتمال پیش بینی آن نزدیک به 0.5 می شود در حالی که عدم قطعیت مدل (نرمال شده) به 1 افزایش می یابد.
این را با سطح عدم قطعیت مدل قطعی مقایسه کنید:
plot_predictions(resnet_probs, model_name="Deterministic")

همانطور که قبلا ذکر شد، یک مدل قطعی از فاصله آگاه نیست. عدم قطعیت آن با فاصله مثال تست از مرز تصمیم تعریف می شود. این باعث می شود که مدل پیش بینی های بیش از حد مطمئن برای نمونه های خارج از دامنه (قرمز) تولید کند.
مقایسه با سایر رویکردهای عدم قطعیت
این بخش عدم قطعیت SNGP را با ترک تحصیل مونت کارلو و گروه Deep مقایسه می کند.
هر دوی این روشها مبتنی بر میانگینگیری مونت کارلو از چندین پاس رو به جلو مدلهای قطعی هستند. ابتدا اندازه مجموعه را \(M\)تنظیم کنید.
num_ensemble = 10
ترک تحصیل مونت کارلو
با توجه به یک شبکه عصبی آموزشدیده با لایههای Dropout، مونت کارلو افت خروجی میانگین احتمال پیشبینی را محاسبه میکند.
\[E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\]
با میانگین گیری بیش از چندین پاس رو به جلو فعال شده با Dropout \(\{logit_m(x)\}_{m=1}^M\).
def mc_dropout_sampling(test_examples):
# Enable dropout during inference.
return resnet_model(test_examples, training=True)
# Monte Carlo dropout inference.
dropout_logit_samples = [mc_dropout_sampling(test_examples) for _ in range(num_ensemble)]
dropout_prob_samples = [tf.nn.softmax(dropout_logits, axis=-1)[:, 0] for dropout_logits in dropout_logit_samples]
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
plot_predictions(dropout_probs, model_name="MC Dropout")

گروه عمیق
Deep ensemble یک روش پیشرفته (اما گران قیمت) برای عدم قطعیت یادگیری عمیق است. برای آموزش یک گروه Deep، ابتدا اعضای گروه \(M\) را آموزش دهید.
# Deep ensemble training
resnet_ensemble = []
for _ in range(num_ensemble):
resnet_model = DeepResNet(**resnet_config)
resnet_model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
resnet_model.fit(train_examples, train_labels, verbose=0, **fit_config)
resnet_ensemble.append(resnet_model)
logit ها را جمع آوری کنید و میانگین احتمال پیش بینی \(E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\)را محاسبه کنید.
# Deep ensemble inference
ensemble_logit_samples = [model(test_examples) for model in resnet_ensemble]
ensemble_prob_samples = [tf.nn.softmax(logits, axis=-1)[:, 0] for logits in ensemble_logit_samples]
ensemble_probs = tf.reduce_mean(ensemble_prob_samples, axis=0)
plot_predictions(ensemble_probs, model_name="Deep ensemble")

هر دو گروه MC Dropout و Deep توانایی عدم قطعیت مدل را با قطعی کردن مرز تصمیم بهبود می بخشند. با این حال، هر دوی آنها محدودیت شبکه عمیق قطعی در عدم آگاهی از فاصله را به ارث می برند.
خلاصه
در این آموزش شما دارید:
- یک مدل SNGP را بر روی یک طبقهبندی کننده عمیق برای بهبود آگاهی از فاصله آن پیادهسازی کرد.
- با استفاده از Keras
model.fit()API مدل SNGP را به صورت سرتاسری آموزش داد. - رفتار عدم قطعیت SNGP را تجسم کرد.
- رفتار عدم قطعیت را بین مدلهای SNGP، ترک تحصیل مونت کارلو و گروه عمیق مقایسه کرد.
منابع و مطالعه بیشتر
- برای مثالی از بکارگیری SNGP در مدل BERT برای درک زبان طبیعی آگاه از عدم قطعیت، به آموزش SNGP-BERT مراجعه کنید.
- برای اجرای مدل SNGP (و بسیاری از روشهای عدم قطعیت دیگر) در طیف گستردهای از مجموعه دادههای معیار (مانند CIFAR ، ImageNet ، تشخیص سمیت Jigsaw ، و غیره) به خطوط پایه عدم قطعیت مراجعه کنید.
- برای درک عمیقتر روش SNGP، مقاله برآورد عدم قطعیت ساده و اصولی با یادگیری عمیق قطعی از طریق آگاهی از راه دور را بررسی کنید.