 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu eğitim, TensorFlow kullanılarak zaman serisi tahminine giriş niteliğindedir. Evrişimsel ve Tekrarlayan Sinir Ağları (CNN'ler ve RNN'ler) dahil olmak üzere birkaç farklı model stili oluşturur.
Bu, alt bölümlerle birlikte iki ana bölümde ele alınmaktadır:
- Tek bir zaman adımı için tahmin:
- Tek bir özellik.
- Tüm özellikler.
- Birden çok adımı tahmin edin:
- Tek atış: Tahminleri bir kerede yapın.
- Otoregresif: Her seferinde bir tahmin yapın ve çıktıyı modele geri besleyin.
Kurmak
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
hava durumu veri seti
Bu eğitim, Max Planck Biyojeokimya Enstitüsü tarafından kaydedilen bir hava durumu zaman serisi veri setini kullanır.
Bu veri seti hava sıcaklığı, atmosferik basınç ve nem gibi 14 farklı özelliği içermektedir. Bunlar 2003'ten başlayarak her 10 dakikada bir toplanmıştır. Verimlilik için yalnızca 2009 ve 2016 yılları arasında toplanan verileri kullanacaksınız. Veri kümesinin bu bölümü François Chollet tarafından Deep Learning with Python kitabı için hazırlanmıştır.
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
Bu eğitimde yalnızca saatlik tahminler ele alınacaktır, bu nedenle verileri 10 dakikalık aralıklarla bir saatlik aralıklarla alt örnekleyerek başlayın:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Verilere bir göz atalım. İşte ilk birkaç satır:
df.head()
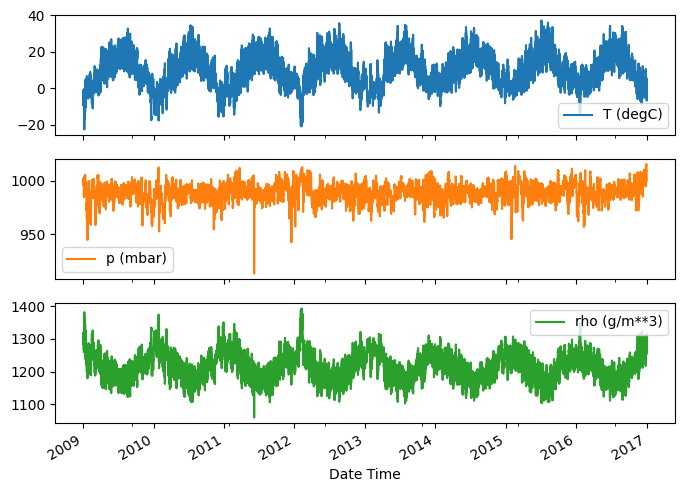
İşte birkaç özelliğin zaman içindeki gelişimi:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
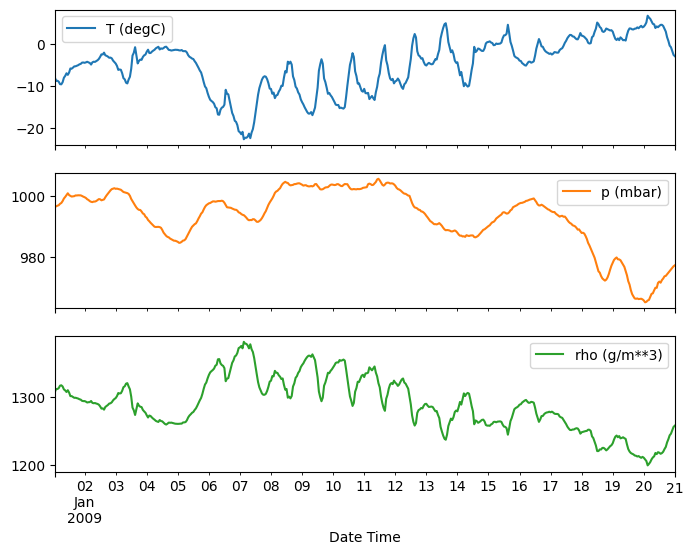
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
İnceleme ve temizleme
Ardından, veri kümesinin istatistiklerine bakın:
df.describe().transpose()
Rüzgar hızı
Öne çıkması gereken bir şey, rüzgar hızının min değeri ( wv (m/s) ) ve maksimum değeri ( max. wv (m/s) ) sütunlarıdır. Bu -9999 muhtemelen hatalıdır.
Ayrı bir rüzgar yönü sütunu vardır, bu nedenle hız sıfırdan büyük olmalıdır ( >=0 ). Sıfırlarla değiştirin:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Özellik mühendisliği
Bir model oluşturmaya başlamadan önce, verilerinizi anlamak ve modeli uygun şekilde biçimlendirilmiş verileri ilettiğinizden emin olmak önemlidir.
Rüzgâr
Verinin son sütunu, wd (deg) — rüzgar yönünü derece cinsinden verir. Açılar iyi model girdileri yapmaz: 360 ° ve 0 ° birbirine yakın olmalı ve düzgün bir şekilde sarılmalıdır. Rüzgar esmiyorsa yön önemli değildir.
Şu anda rüzgar verilerinin dağılımı şöyle görünüyor:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
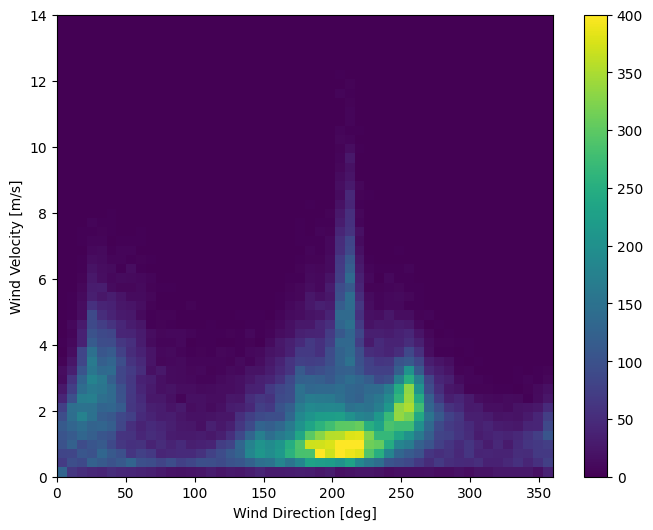
Ancak, rüzgar yönü ve hız sütunlarını bir rüzgar vektörüne dönüştürürseniz, bu modelin yorumlanması daha kolay olacaktır:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
Modelin doğru yorumlaması için rüzgar vektörlerinin dağılımı çok daha basittir:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
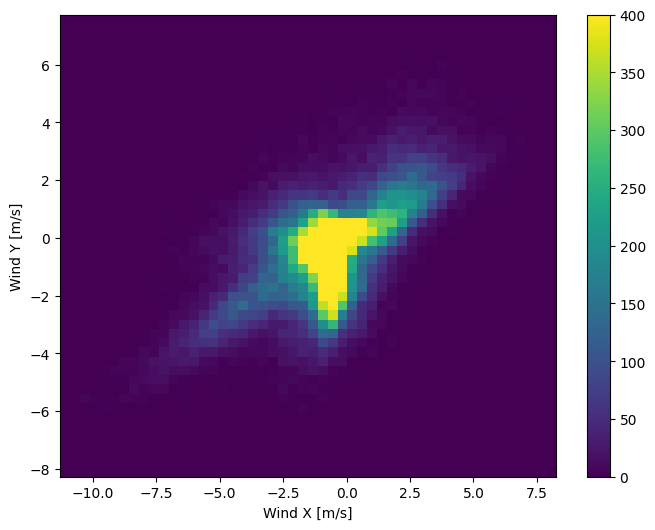
Zaman
Benzer şekilde, Date Time sütunu çok kullanışlıdır, ancak bu dize biçiminde değildir. Saniyeye çevirerek başlayın:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Rüzgar yönüne benzer şekilde, saniye cinsinden süre, kullanışlı bir model girişi değildir. Hava durumu verileri olduğundan, net günlük ve yıllık periyodikliğe sahiptir. Periyodiklikle başa çıkmanın birçok yolu vardır.
"Günün saati" ve "Yılın saati" sinyallerini temizlemek için sinüs ve kosinüs dönüşümlerini kullanarak kullanılabilir sinyaller alabilirsiniz:
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
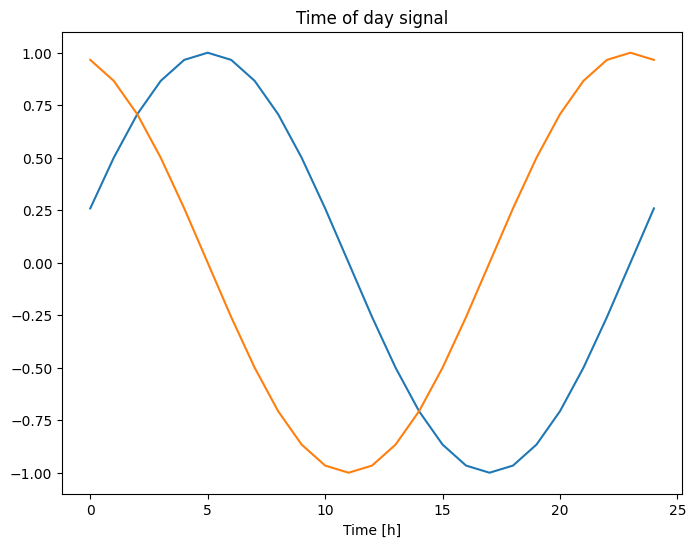
Bu, modele en önemli frekans özelliklerine erişim sağlar. Bu durumda, hangi frekansların önemli olduğunu önceden biliyordunuz.
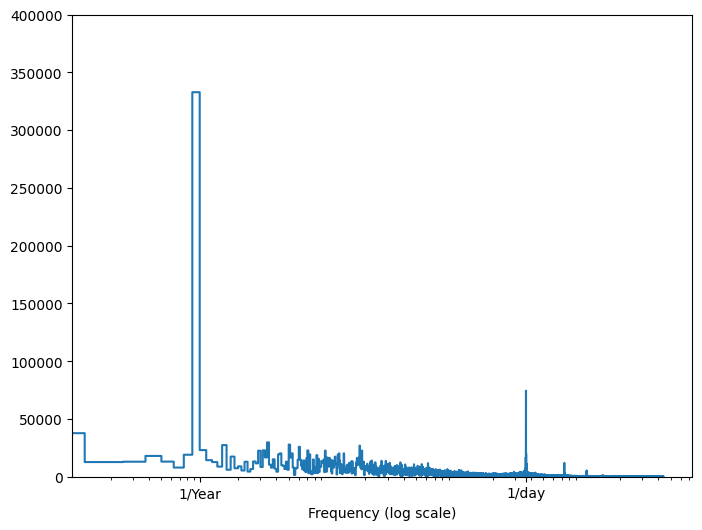
Bu bilgilere sahip değilseniz, Fast Fourier Dönüşümü ile öznitelikleri çıkararak hangi frekansların önemli olduğunu belirleyebilirsiniz. Varsayımları kontrol etmek için, zaman içindeki sıcaklığın tf.signal.rfft . 1/year ve 1/day civarındaki frekanslardaki bariz tepe noktalarına dikkat edin:
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
verileri böl
Eğitim, doğrulama ve test setleri için (70%, 20%, 10%) bir bölme kullanacaksınız. Verilerin bölünmeden önce rastgele karıştırılmadığına dikkat edin. Bu iki nedenden dolayıdır:
- Verileri ardışık örneklerin pencerelerine bölmenin hala mümkün olmasını sağlar.
- Model eğitildikten sonra toplanan veriler üzerinde değerlendirilerek doğrulama/test sonuçlarının daha gerçekçi olmasını sağlar.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Verileri normalleştirin
Bir sinir ağını eğitmeden önce özellikleri ölçeklendirmek önemlidir. Normalleştirme, bu ölçeklemeyi yapmanın yaygın bir yoludur: ortalamayı çıkarın ve her özelliğin standart sapmasına bölün.
Modellerin doğrulama ve test setlerindeki değerlere erişimi olmaması için ortalama ve standart sapma yalnızca eğitim verileri kullanılarak hesaplanmalıdır.
Modelin eğitim sırasında eğitim setindeki gelecek değerlere erişimi olmaması ve bu normalleştirmenin hareketli ortalamalar kullanılarak yapılması gerektiği de tartışılabilir. Bu öğreticinin odak noktası bu değildir ve doğrulama ve test setleri (biraz) dürüst ölçümler almanızı sağlar. Bu nedenle, basitlik adına bu eğitimde basit bir ortalama kullanılır.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
Şimdi, özelliklerin dağılımına bir göz atın. Bazı özelliklerin uzun kuyrukları vardır, ancak -9999 rüzgar hızı değeri gibi bariz hatalar yoktur.
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

Veri pencereleme
Bu öğreticideki modeller, verilerden ardışık örneklerden oluşan bir pencereye dayalı olarak bir dizi tahmin yapacaktır.
Giriş pencerelerinin ana özellikleri şunlardır:
- Giriş ve etiket pencerelerinin genişliği (zaman adımı sayısı).
- Aralarındaki zaman farkı.
- Hangi özelliklerin girdi, etiket veya her ikisi olarak kullanıldığı.
Bu öğretici, çeşitli modeller oluşturur (Linear, DNN, CNN ve RNN modelleri dahil) ve bunları her ikisi için de kullanır:
- Tek çıkışlı ve çoklu çıkışlı tahminler.
- Tek zamanlı adım ve çok zaman adımlı tahminler.
Bu bölüm, tüm bu modeller için yeniden kullanılabilmesi için veri pencerelemenin uygulanmasına odaklanmaktadır.
Göreve ve modelin türüne bağlı olarak, çeşitli veri pencereleri oluşturmak isteyebilirsiniz. İşte bazı örnekler:
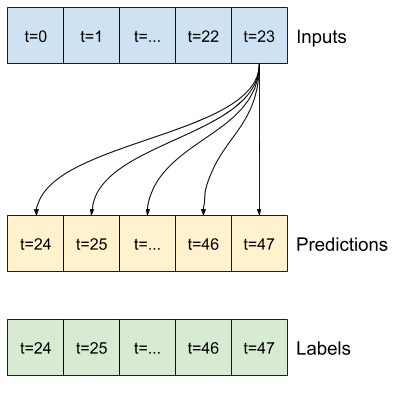
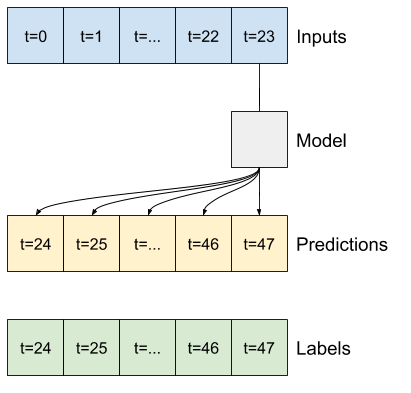
Örneğin, 24 saatlik geçmiş verili 24 saat ilerisi için tek bir tahmin yapmak için şöyle bir pencere tanımlayabilirsiniz:
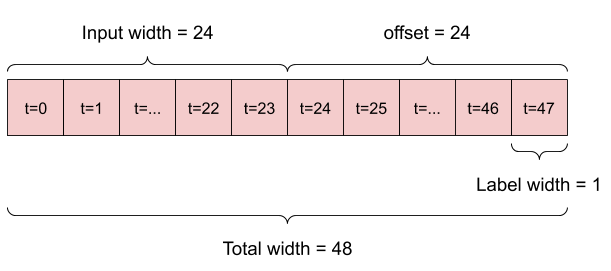
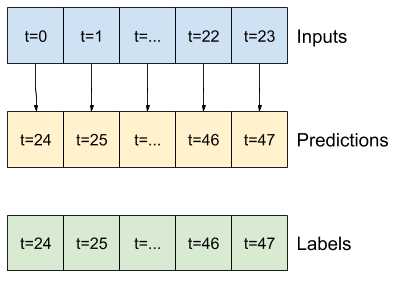
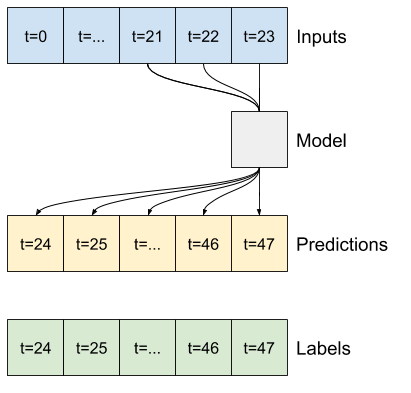
Altı saatlik geçmiş veriliyken bir saat ileriyi tahmin eden bir modelin şöyle bir pencereye ihtiyacı olacaktır:

Bu bölümün geri kalanı bir WindowGenerator sınıfını tanımlar. Bu sınıf şunları yapabilir:
- İndeksleri ve ofsetleri yukarıdaki şemalarda gösterildiği gibi kullanın.
- Özellik pencerelerini
(features, labels)çiftlerine ayırın. - Ortaya çıkan pencerelerin içeriğini çizin.
-
tf.data.Datasets kullanarak eğitim, değerlendirme ve test verilerinden bu pencerelerin gruplarını verimli bir şekilde oluşturun.
1. İndeksler ve ofsetler
WindowGenerator sınıfını oluşturarak başlayın. __init__ yöntemi, giriş ve etiket endeksleri için gerekli tüm mantığı içerir.
Ayrıca eğitim, değerlendirme ve DataFrames testini girdi olarak alır. Bunlar daha sonra pencerelerin tf.data.Dataset 'lerine dönüştürülecektir.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Bu bölümün başındaki şemalarda gösterilen 2 pencereyi oluşturmak için gereken kod:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']yer tutucu25 l10n-yer
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Böl
Ardışık girdilerin bir listesi verildiğinde, split_window yöntemi onları bir girdi penceresine ve bir etiket penceresine dönüştürür.
Daha önce tanımladığınız w2 örneği şu şekilde bölünecektir:
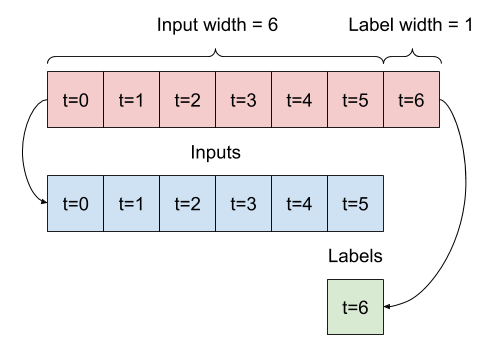
Bu şema, verilerin features eksenini göstermez, ancak bu split_window işlevi aynı zamanda label_columns da işler, böylece hem tek çıkışlı hem de çoklu çıkışlı örnekler için kullanılabilir.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Denemek:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
Tipik olarak, TensorFlow'daki veriler, en dıştaki dizinin örnekler arasında olduğu ("parti" boyutu) diziler halinde paketlenir. Ortadaki indeksler "zaman" veya "uzay" (genişlik, yükseklik) boyut(lar)ıdır. En içteki indeksler özelliklerdir.
Yukarıdaki kod, her bir zaman adımında 19 özelliğe sahip üç adet 7'lik adım penceresinden oluşan bir toplu iş aldı. Bunları 6 zamanlı adım 19 özellikli girişler ve 1 zamanlı adım 1 özellik etiketi grubuna böler. WindowGenerator , label_columns=['T (degC)'] ile başlatıldığından, etiketin yalnızca bir özelliği vardır. Başlangıçta bu öğretici, tek çıktı etiketlerini tahmin eden modeller oluşturacaktır.
3. Konu
Bölünmüş pencerenin basit bir şekilde görselleştirilmesine izin veren bir çizim yöntemi:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
Bu çizim, öğenin başvurduğu zamana dayalı olarak girdileri, etiketleri ve (daha sonra) tahminleri hizalar:
w2.plot()
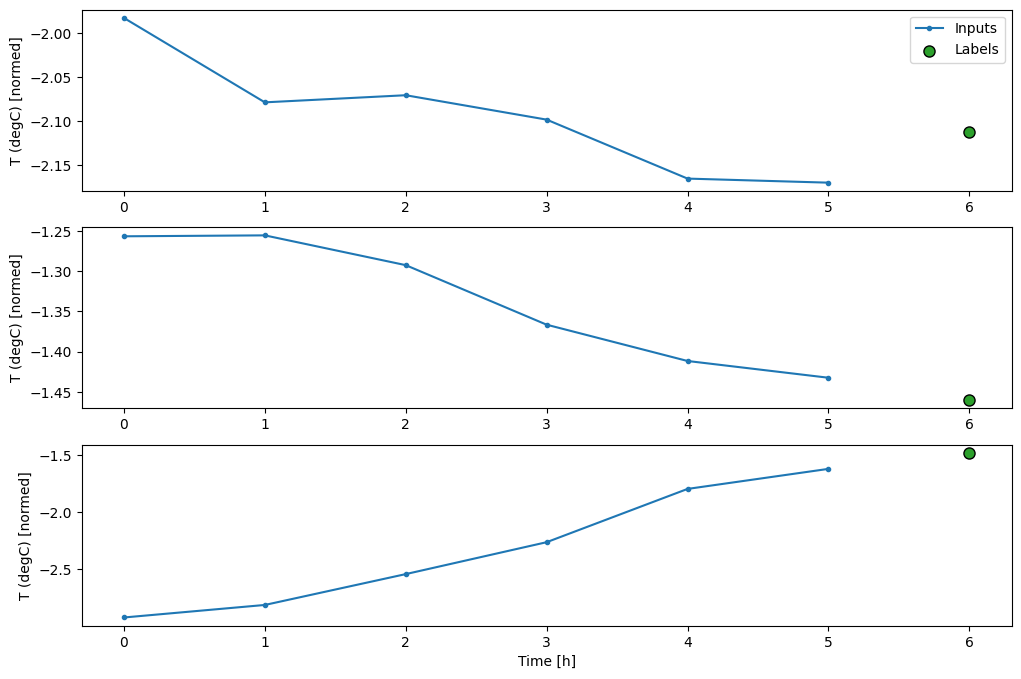
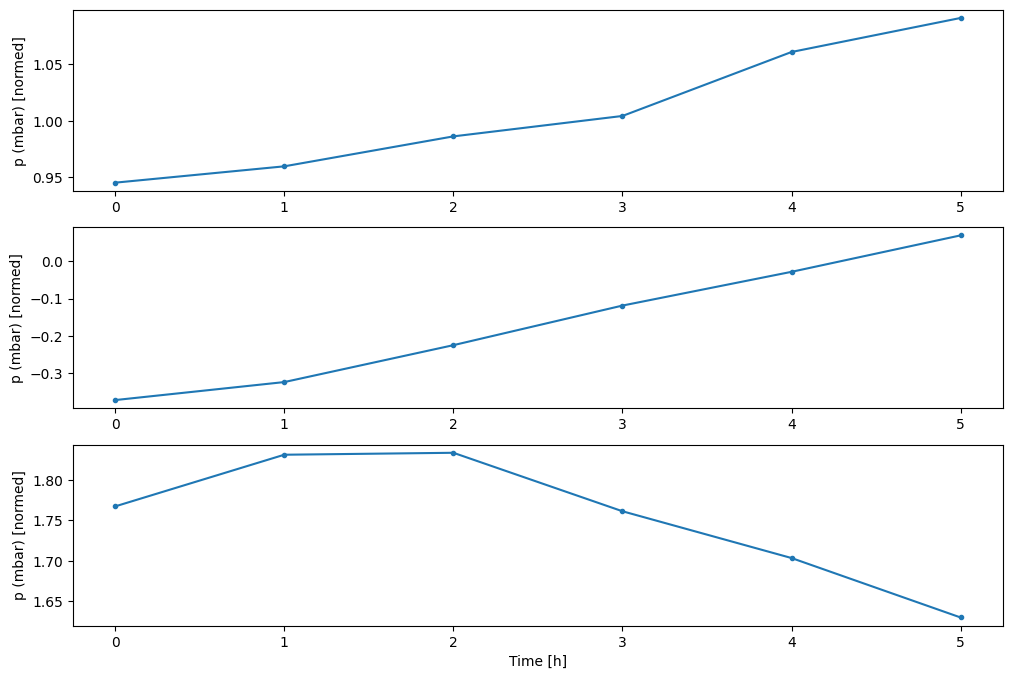
Diğer sütunları çizebilirsiniz, ancak örnek pencere w2 konfigürasyonunda yalnızca T (degC) sütunu için etiketler bulunur.
w2.plot(plot_col='p (mbar)')
4. tf.data.Dataset s oluşturun
Son olarak, bu make_dataset yöntemi bir zaman serisi DataFrame alır ve bunu tf.keras.utils.timeseries_dataset_from_array işlevini kullanarak (input_window, label_window) çiftlerinden oluşan bir tf.data.Dataset dönüştürür:
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
WindowGenerator nesnesi eğitim, doğrulama ve test verilerini tutar.
Daha önce tanımladığınız make_dataset yöntemini kullanarak bunlara tf.data.Dataset s olarak erişmek için özellikler ekleyin. Ayrıca, kolay erişim ve çizim için standart bir örnek toplu iş ekleyin:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Artık WindowGenerator nesnesi, tf.data.Dataset nesnelerine erişmenizi sağlar, böylece verileri kolayca yineleyebilirsiniz.
Dataset.element_spec özelliği, veri kümesi öğelerinin yapısını, veri türlerini ve şekillerini size söyler.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
Bir Dataset üzerinde yineleme yapmak, somut yığınlar verir:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Tek adımlı modeller
Bu tür veriler üzerinde oluşturabileceğiniz en basit model, tek bir özelliğin değerini, yalnızca mevcut koşullara dayalı olarak geleceğe 1 adım (bir saat) öngören modeldir.
Bu nedenle, bir saat sonraki T (degC) değerini tahmin etmek için modeller oluşturarak başlayın.
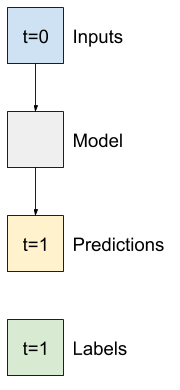
Bu tek adımlı (input, label) çiftleri üretmek için bir WindowGenerator nesnesi yapılandırın:
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
window nesnesi, eğitim, doğrulama ve test kümelerinden tf.data.Dataset 'ler oluşturarak veri yığınları üzerinde kolayca yineleme yapmanıza olanak tanır.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
taban çizgisi
Eğitilebilir bir model oluşturmadan önce, sonraki daha karmaşık modellerle karşılaştırma noktası olarak bir performans temeline sahip olmak iyi olacaktır.
Bu ilk görev, tüm özelliklerin mevcut değeri göz önüne alındığında, bir saat sonraki sıcaklığı tahmin etmektir. Mevcut değerler, mevcut sıcaklığı içerir.
Bu nedenle, "Değişiklik yok" tahmininde bulunarak, yalnızca geçerli sıcaklığı tahmin olarak döndüren bir modelle başlayın. Sıcaklık yavaş değiştiği için bu makul bir temeldir. Elbette, gelecekte daha fazla tahminde bulunursanız, bu temel daha az işe yarayacaktır.
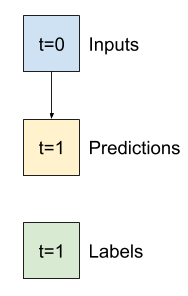
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Bu modeli somutlaştırın ve değerlendirin:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
Bu, bazı performans ölçütlerini yazdırdı, ancak bunlar size modelin ne kadar iyi performans gösterdiğine dair bir fikir vermiyor.
WindowGenerator bir çizim yöntemi vardır, ancak çizimler yalnızca tek bir örnekle çok ilginç olmayacaktır.
Bu nedenle, bir seferde 24 saat ardışık girdiler ve etiketler üreten daha geniş bir WindowGenerator oluşturun. Yeni wide_window değişkeni, modelin çalışma şeklini değiştirmez. Model, tek bir giriş zaman adımına dayalı olarak geleceğe bir saatlik tahminler yapmaya devam ediyor. Burada time ekseni batch ekseni gibi hareket eder: her tahmin, zaman adımları arasında etkileşim olmadan bağımsız olarak yapılır:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
Bu genişletilmiş pencere, herhangi bir kod değişikliği olmaksızın doğrudan aynı baseline modele geçirilebilir. Bu mümkündür çünkü girdiler ve etiketler aynı sayıda zaman adımına sahiptir ve taban çizgisi girdiyi çıktıya iletir:
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
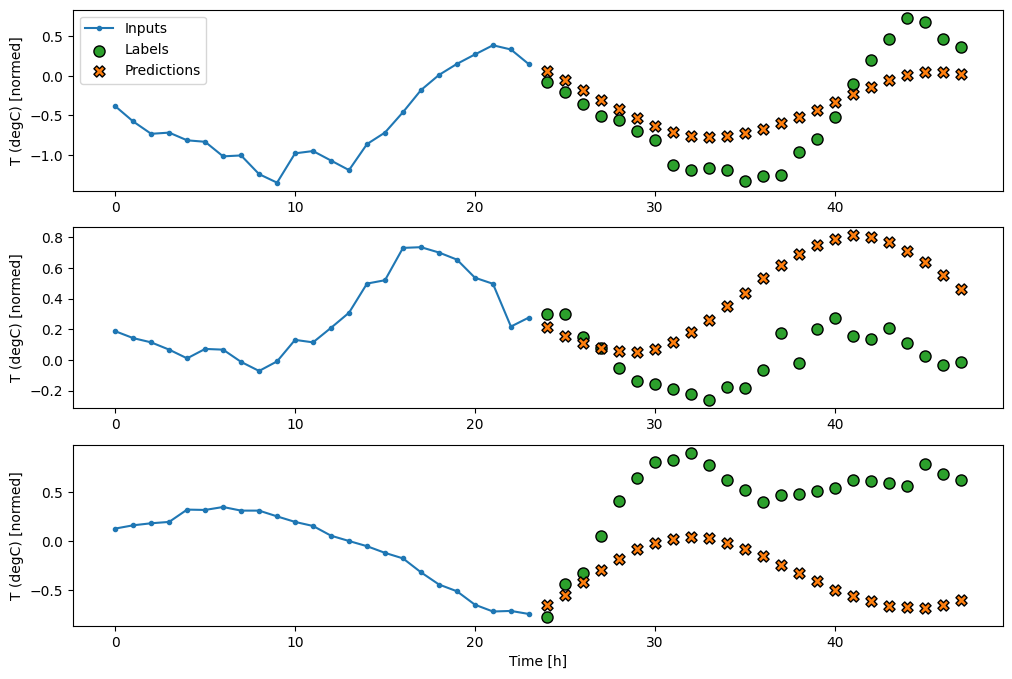
Temel modelin tahminlerini çizerek, etiketlerin bir saat sağa kaydırıldığına dikkat edin:
wide_window.plot(baseline)
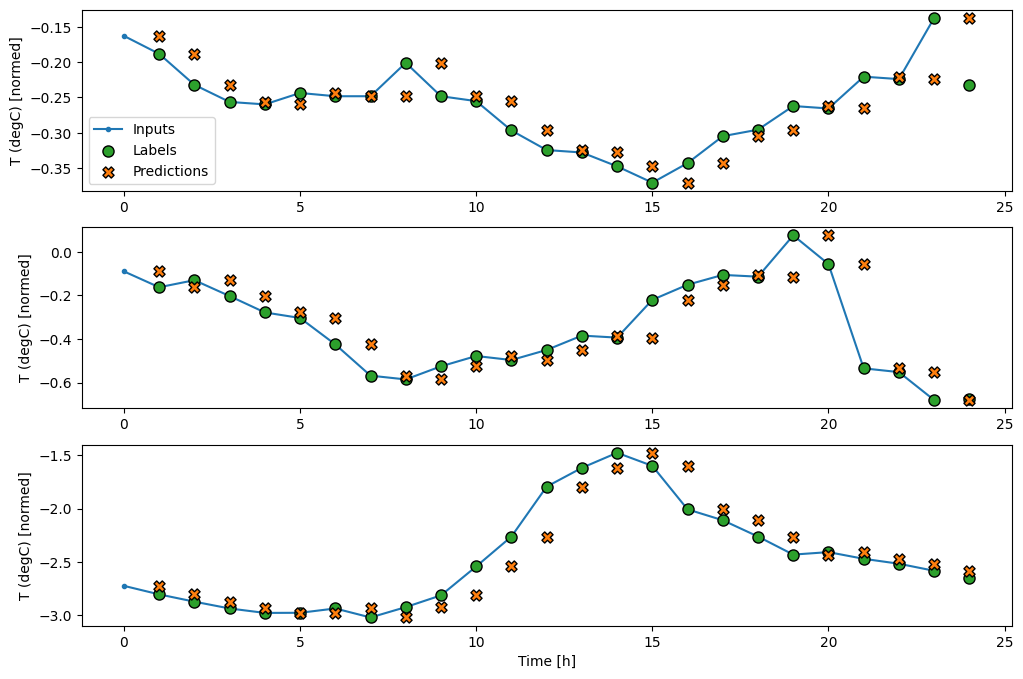
Üç örnekten oluşan yukarıdaki grafiklerde tek adımlı model 24 saat boyunca çalıştırılır. Bu biraz açıklamayı hak ediyor:
- Mavi
Inputssatırı, her zaman adımındaki giriş sıcaklığını gösterir. Model tüm özellikleri alır, bu grafik sadece sıcaklığı gösterir. - Yeşil
Labelsnoktaları, hedef tahmin değerini gösterir. Bu noktalar, giriş zamanında değil, tahmin zamanında gösterilir. Bu nedenle etiket aralığı girişlere göre 1 adım kaydırılır. - Turuncu
Predictionsçarpıları, modelin her bir çıktı zaman adımı için tahminidir. Model mükemmel bir şekilde tahmin ediyor olsaydı, tahminler doğrudanLabels.
Doğrusal model
Bu göreve uygulayabileceğiniz en basit eğitilebilir model, girdi ve çıktı arasına doğrusal dönüşüm eklemektir. Bu durumda, bir zaman adımından elde edilen çıktı yalnızca o adıma bağlıdır:

activation seti olmayan bir tf.keras.layers.Dense katmanı, doğrusal bir modeldir. Katman yalnızca (batch, time, inputs) verisinin son eksenini (toplu (batch, time, units) e dönüştürür; batch ve time eksenlerinde her kaleme bağımsız olarak uygulanır.
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
Bu öğretici birçok modeli eğitir, bu nedenle eğitim prosedürünü bir işleve paketleyin:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Modeli eğitin ve performansını değerlendirin:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
baseline model gibi, doğrusal model de geniş pencere kümelerinde çağrılabilir. Bu şekilde kullanıldığında model, ardışık zaman adımlarında bir dizi bağımsız tahmin yapar. time ekseni, başka bir batch ekseni gibi davranır. Her zaman adımında tahminler arasında etkileşim yoktur.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
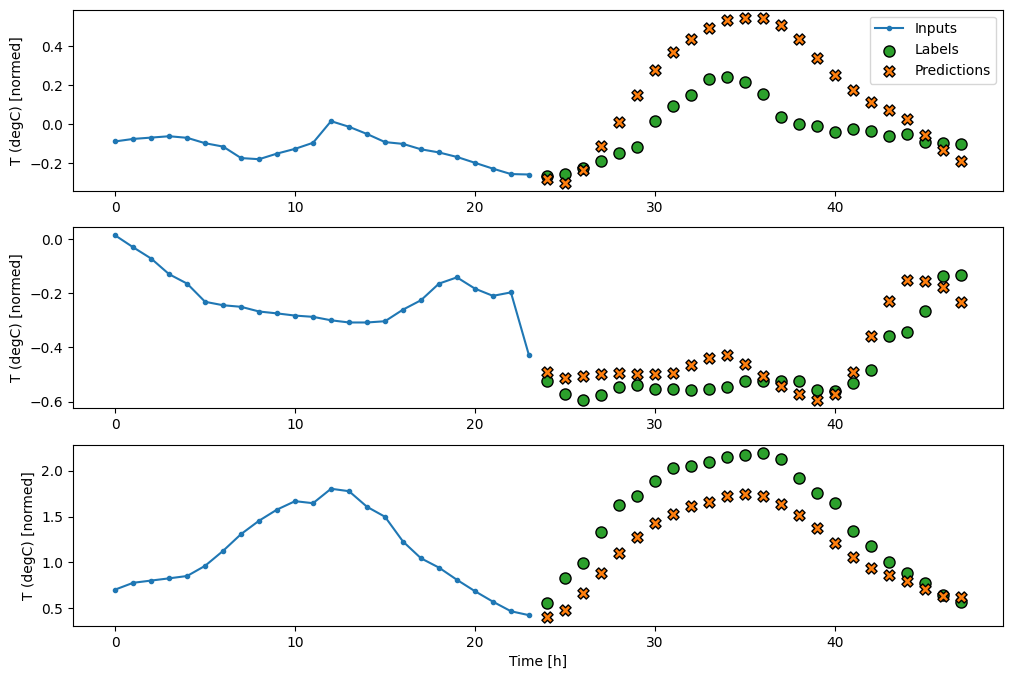
wide_window örnek tahminlerinin grafiği burada, çoğu durumda tahminin yalnızca giriş sıcaklığını döndürmekten açıkça daha iyi olduğunu, ancak birkaç durumda daha kötü olduğunu not edin:
wide_window.plot(linear)
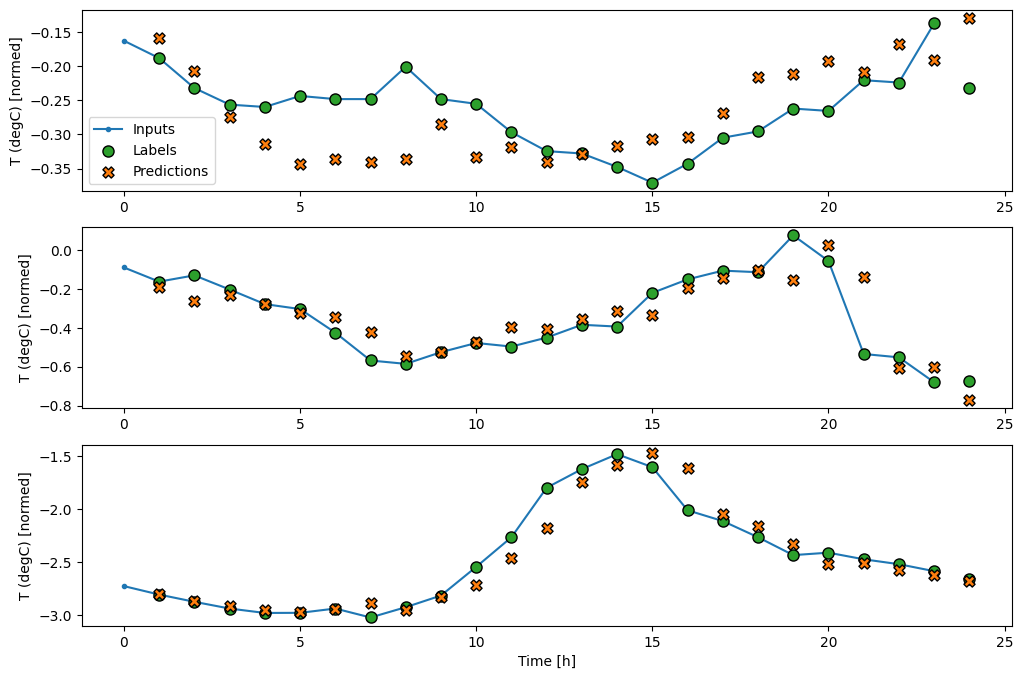
Doğrusal modellerin bir avantajı, yorumlanmalarının nispeten basit olmasıdır. Katmanın ağırlıklarını çıkarabilir ve her bir girdiye atanan ağırlığı görselleştirebilirsiniz:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
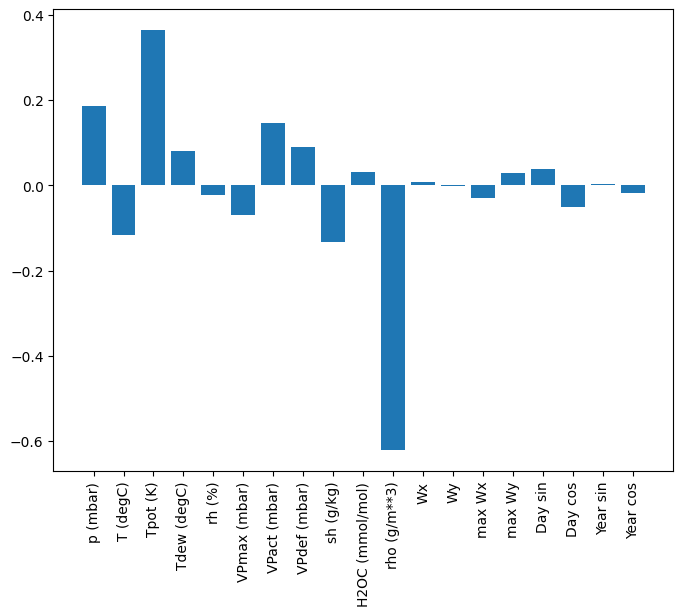
Bazen model, T (degC) girişine en fazla ağırlığı bile koymaz. Bu, rastgele başlatmanın risklerinden biridir.
Yoğun
Aslında birden çok zaman adımında çalışan modelleri uygulamadan önce, daha derin, daha güçlü, tek girdi adımlı modellerin performansını kontrol etmeye değer.
Girdi ve çıktı arasında birkaç Dense katmanı istiflemesi dışında, linear modele benzer bir model aşağıda verilmiştir:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
Çok adımlı yoğun
Tek adımlı bir model, girdilerinin mevcut değerleri için bağlam içermez. Giriş özelliklerinin zaman içinde nasıl değiştiğini göremez. Bu sorunu çözmek için modelin tahminlerde bulunurken birden çok zaman adımına erişmesi gerekir:
baseline , linear ve dense modeller, her bir zaman adımını bağımsız olarak ele aldı. Burada model, tek bir çıktı üretmek için girdi olarak birden çok zaman adımı alacaktır.
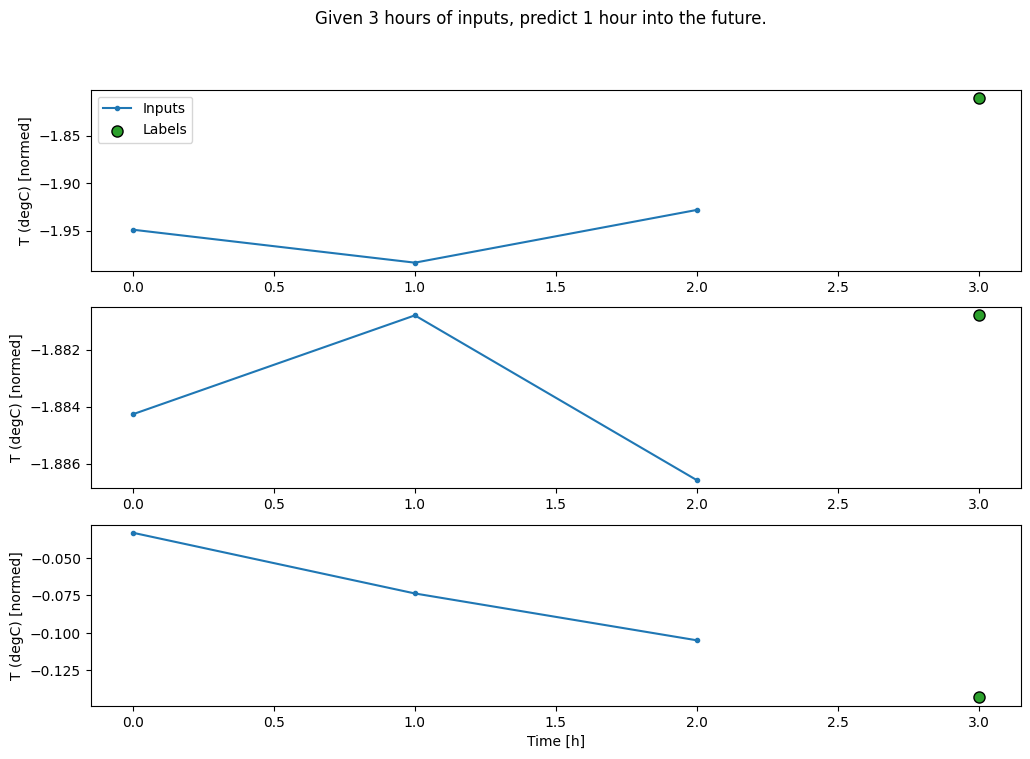
Üç saatlik girdiler ve bir saatlik etiketler üretecek bir WindowGenerator oluşturun:
Window 'ın shift parametresinin iki pencerenin sonuna göre olduğuna dikkat edin.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']yer tutucu66 l10n-yer
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
Modelin ilk katmanı olarak bir tf.keras.layers.Flatten ekleyerek dense bir modeli çoklu giriş adımlı bir pencerede eğitebilirsiniz:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
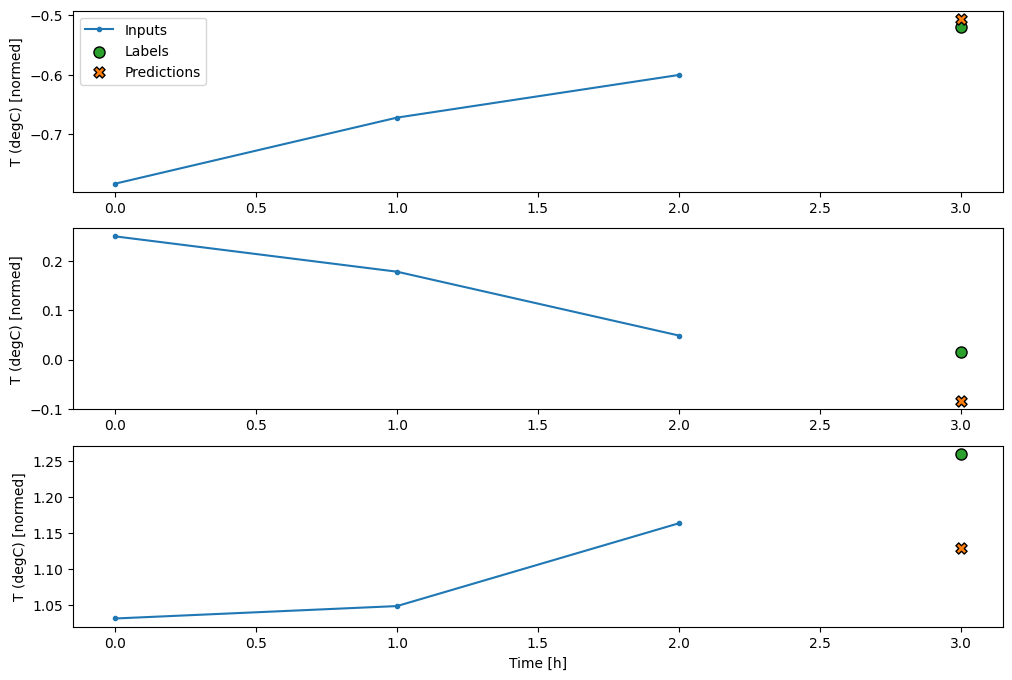
Bu yaklaşımın ana dezavantajı, ortaya çıkan modelin yalnızca tam olarak bu şekle sahip giriş pencerelerinde yürütülebilmesidir.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
Bir sonraki bölümdeki evrişim modelleri bu sorunu giderir.
Evrişim sinir ağı
Bir evrişim katmanı ( tf.keras.layers.Conv1D ) ayrıca her tahmine girdi olarak birden çok zaman adımı alır.
Aşağıda multi_step_dense ile aynı model, bir multi_step_dense yeniden yazılmıştır.
Değişiklikleri not edin:
-
tf.keras.layers.Flattenve ilktf.keras.layers.Dense, birtf.keras.layers.Conv1Dile değiştirilir. - Evrişim zaman eksenini çıktısında tuttuğundan
tf.keras.layers.Reshapeartık gerekli değildir.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Modelin beklenen şekle sahip çıktılar ürettiğini kontrol etmek için örnek bir toplu iş üzerinde çalıştırın:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Bunu conv_window üzerinde eğitin ve değerlendirin ve multi_step_dense modeline benzer bir performans vermelidir.
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
Bu conv_model ve multi_step_dense modeli arasındaki fark, conv_model herhangi bir uzunluktaki girdilerde çalıştırılabilmesidir. Evrişim katmanı, kayan bir girdi penceresine uygulanır:
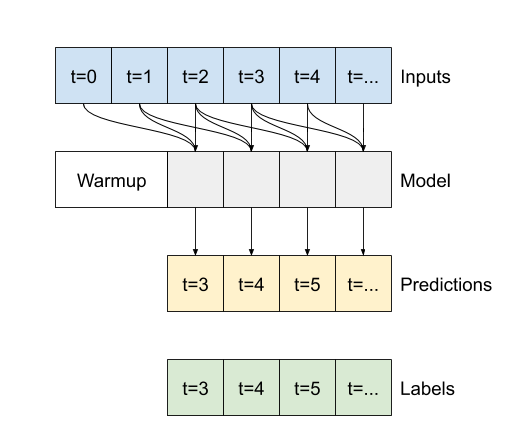
Daha geniş girdide çalıştırırsanız, daha geniş çıktı üretir:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
Çıkışın girişten daha kısa olduğuna dikkat edin. Eğitim veya çizim çalışması yapmak için etiketlere ve aynı uzunluğa sahip tahmine ihtiyacınız var. Bu nedenle, etiket ve tahmin uzunluklarının eşleşmesi için birkaç ekstra giriş süresi adımıyla geniş pencereler oluşturmak için bir WindowGenerator oluşturun:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']yer tutucu85 l10n-yer
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
Artık modelin tahminlerini daha geniş bir pencerede çizebilirsiniz. İlk tahminden önceki 3 giriş zamanı adımına dikkat edin. Buradaki her tahmin, önceki 3 zaman adımına dayanmaktadır:
wide_conv_window.plot(conv_model)
tekrarlayan sinir ağı
Tekrarlayan Sinir Ağı (RNN), zaman serisi verilerine çok uygun bir sinir ağı türüdür. RNN'ler, bir zaman serisini adım adım işler ve zaman adımından zaman adımına kadar bir iç durumu korur.
Bir RNN öğreticisi ile Metin oluşturma ve Keras kılavuzu ile Tekrarlayan Sinir Ağları (RNN) hakkında daha fazla bilgi edinebilirsiniz.
Bu öğreticide, Uzun Kısa Süreli Bellek ( tf.keras.layers.LSTM ) adlı bir RNN katmanı kullanacaksınız.
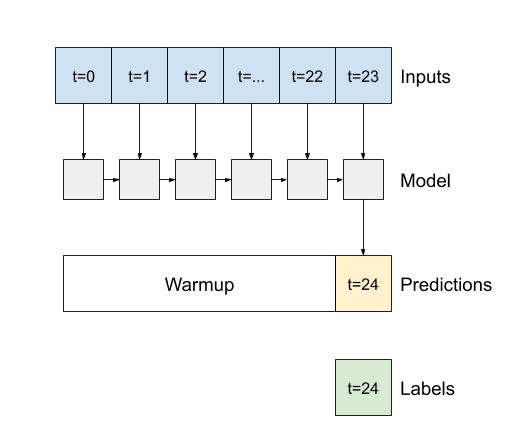
tf.keras.layers.LSTM RNN katmanları için önemli bir yapıcı argümanı, return_sequences argümanıdır. Bu ayar, katmanı iki yoldan biriyle yapılandırabilir:
- Varsayılan olarak
Falseise, katman yalnızca son zaman adımının çıktısını döndürür ve modele tek bir tahmin yapmadan önce dahili durumunu ısıtması için zaman verir:
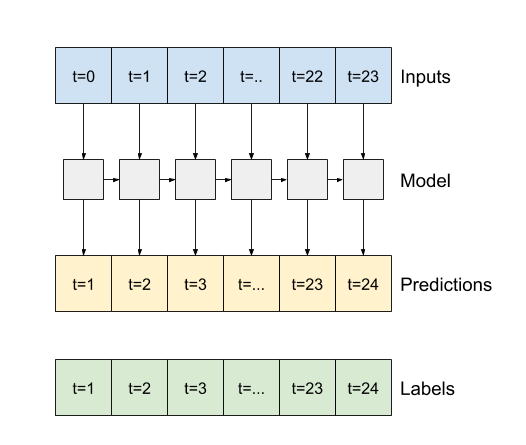
-
Trueise, katman her girdi için bir çıktı döndürür. Bu, aşağıdakiler için yararlıdır:- RNN katmanlarını istifleme.
- Bir modeli aynı anda birden çok zaman adımında eğitmek.
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
return_sequences=True ile model bir seferde 24 saatlik veri üzerinde eğitilebilir.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
wide_window.plot(lstm_model)
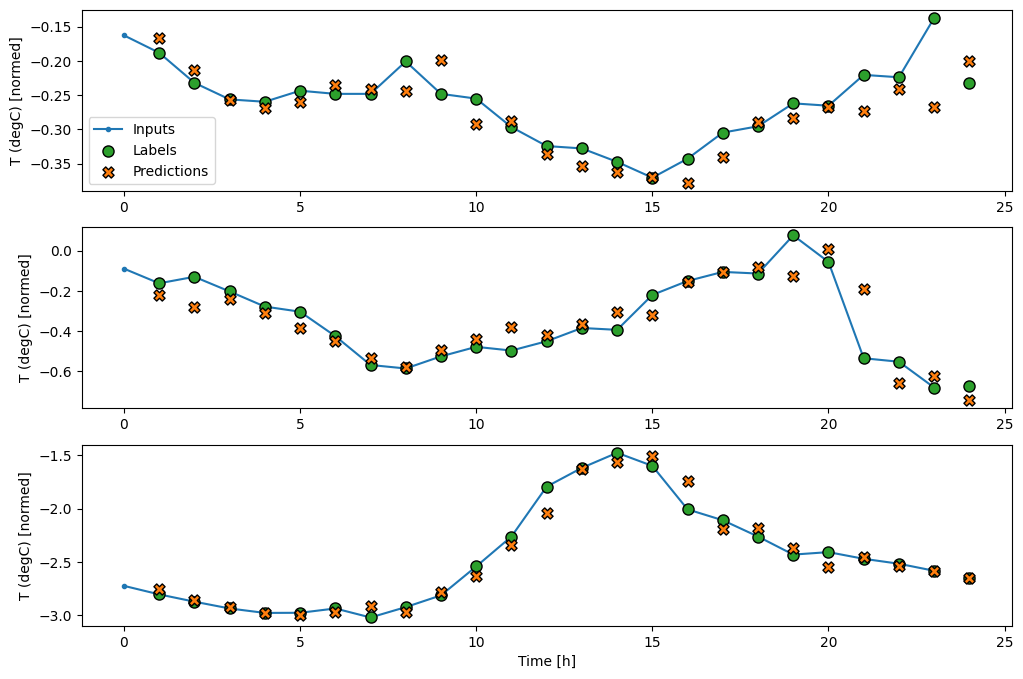
Verim
Bu veri seti ile tipik olarak modellerin her biri bir öncekinden biraz daha iyi sonuç verir:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()

for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
Çok çıkışlı modeller
Şimdiye kadarki modellerin tümü, tek bir zaman adımı için tek bir çıktı özelliği olan T (degC) öngördü.
Bu modellerin tümü, çıktı katmanındaki birimlerin sayısı değiştirilerek ve eğitim pencereleri labels tüm özellikleri içerecek şekilde ayarlanarak ( example_labels ) birden fazla özelliği tahmin edecek şekilde dönüştürülebilir:
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Etiketlerin features ekseninin artık 1 yerine girişlerle aynı derinliğe sahip olduğuna dikkat edin.
temel
Aynı temel model ( Baseline ) burada kullanılabilir, ancak bu sefer belirli bir label_index seçmek yerine tüm özellikler tekrarlanır:
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
Yoğun
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
RNN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
Gelişmiş: Artık bağlantılar
Daha önceki Baseline modeli, dizinin zaman adımından zaman adımına büyük ölçüde değişmediği gerçeğinden yararlandı. Bu öğreticide şimdiye kadar eğitilen her model rastgele başlatıldı ve ardından çıktının önceki zaman adımına göre küçük bir değişiklik olduğunu öğrenmek zorunda kaldı.
Dikkatli bir başlatma ile bu sorunun üstesinden gelebilseniz de, bunu model yapısına eklemek daha kolaydır.
Zaman serisi analizinde, bir sonraki değeri tahmin etmek yerine, değerin bir sonraki zaman adımında nasıl değişeceğini tahmin eden modeller oluşturmak yaygındır. Benzer şekilde, derin öğrenmedeki artık ağlar (veya ResNet'ler) her katmanın modelin birikim sonucuna eklendiği mimarilere atıfta bulunur.
Değişimin küçük olması gerektiği bilgisinden bu şekilde yararlanırsınız.
Esasen bu, modeli Baseline ile eşleşecek şekilde başlatır. Bu görev için modellerin biraz daha iyi performansla daha hızlı yakınsamasına yardımcı olur.
Bu yaklaşım, bu öğreticide tartışılan herhangi bir modelle birlikte kullanılabilir.
Burada, LSTM modeline uygulanmaktadır, ilk tahmin edilen değişikliklerin küçük olmasını sağlamak ve kalan bağlantıya aşırı güç vermemek için tf.initializers.zeros kullanımına dikkat edin. zeros yalnızca son katmanda kullanıldığından, buradaki gradyanlar için simetriyi bozma endişesi yoktur.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
Verim
İşte bu çok çıkışlı modellerin genel performansı.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
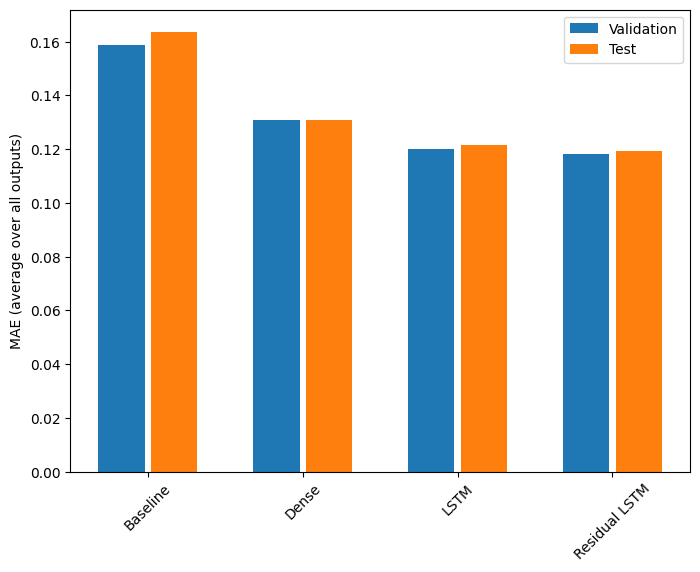
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
Yukarıdaki performansların tüm model çıktılarında ortalaması alınır.
Çok adımlı modeller
Önceki bölümlerdeki hem tek çıkışlı hem de çoklu çıkışlı modeller, geleceğe bir saat olmak üzere tek zaman adımlı tahminler yaptı.
Bu bölüm, çoklu zaman adımlı tahminler yapmak için bu modellerin nasıl genişletileceğini inceler.
Çok adımlı bir tahminde, modelin bir dizi gelecekteki değeri tahmin etmeyi öğrenmesi gerekir. Bu nedenle, yalnızca tek bir gelecek noktanın tahmin edildiği tek adımlı bir modelin aksine, çok adımlı bir model gelecekteki değerlerin bir dizisini tahmin eder.
Buna iki kaba yaklaşım var:
- Tüm zaman serisinin bir kerede tahmin edildiği tek atış tahminleri.
- Modelin yalnızca tek adımlı tahminler yaptığı ve çıktısının girdisi olarak geri beslendiği otoregresif tahminler.
Bu bölümde tüm modeller, tüm çıktı zaman adımlarındaki tüm özellikleri tahmin edecektir.
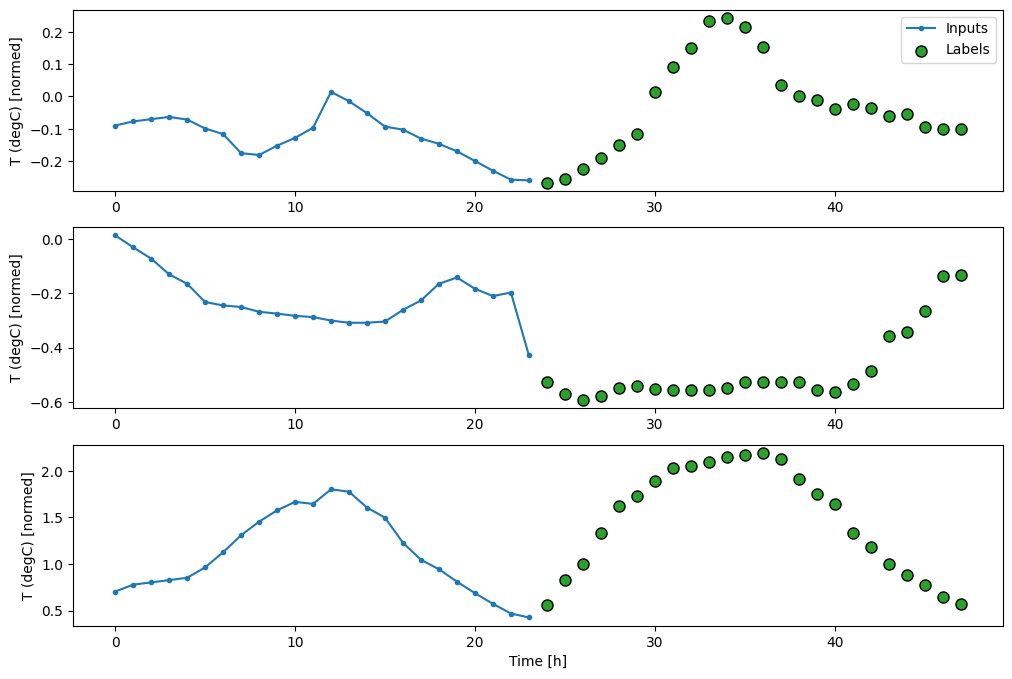
Çok adımlı model için eğitim verileri yine saatlik örneklerden oluşur. Bununla birlikte, burada modeller, geçmişin 24 saati veriliyken, 24 saat ileriyi tahmin etmeyi öğreneceklerdir.
İşte veri kümesinden bu dilimleri oluşturan bir Window nesnesi:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
taban çizgileri
Bu görev için basit bir temel, gerekli sayıda çıkış zamanı adımı için son giriş zamanı adımını tekrarlamaktır:
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
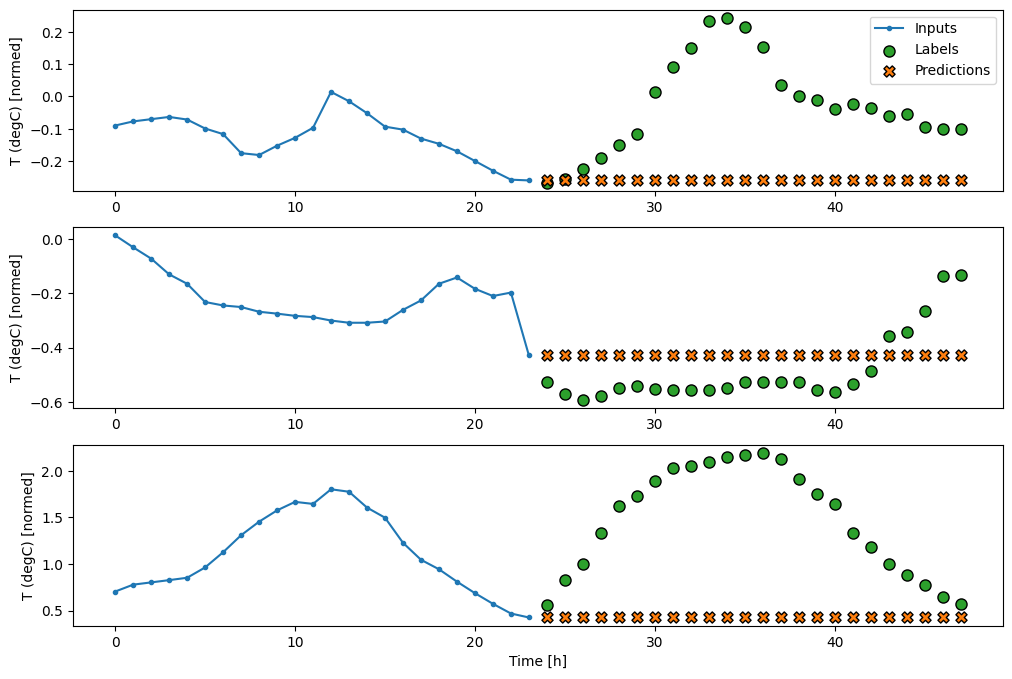
Bu görev, geçmiş 24 saat verili olarak 24 saat ileriyi tahmin etmek olduğundan, yarının benzer olacağını varsayarak bir önceki günü tekrarlamak bir başka basit yaklaşımdır:
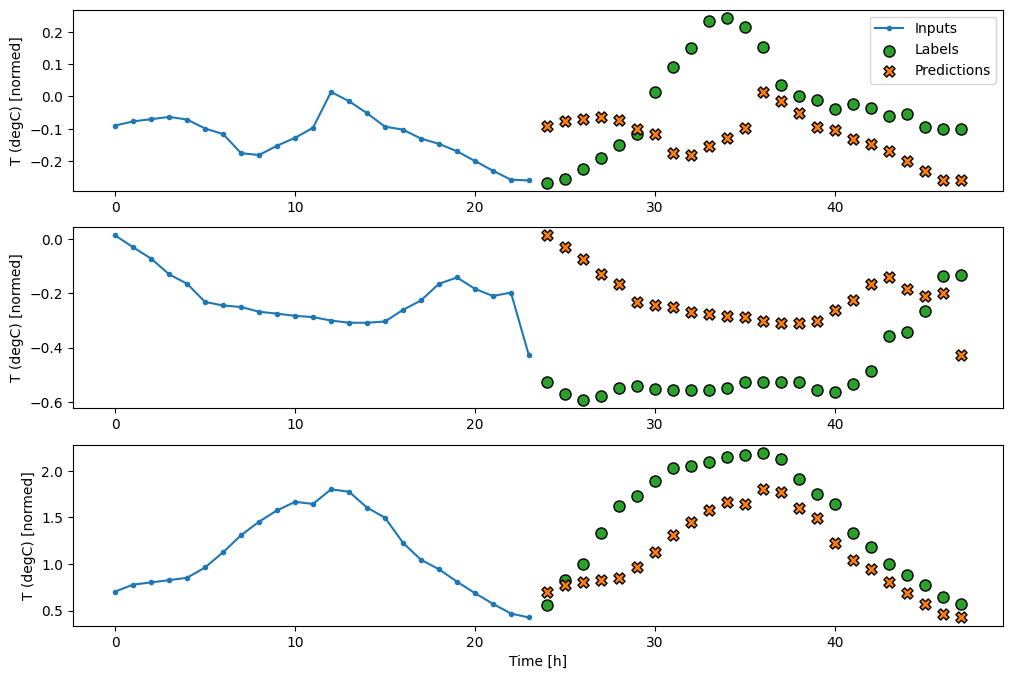
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
Tek çekim modeller
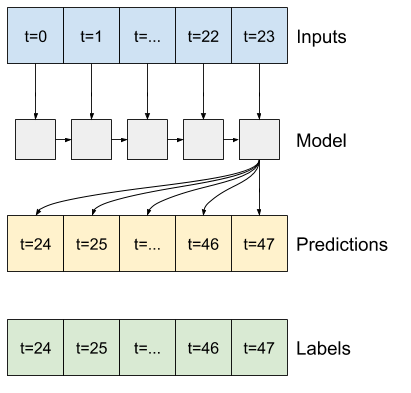
Bu soruna bir üst düzey yaklaşım, modelin tüm dizi tahminini tek bir adımda yaptığı "tek atış" modeli kullanmaktır.
Bu, OUT_STEPS*features çıktı birimlerine sahip bir tf.keras.layers.Dense olarak verimli bir şekilde uygulanabilir. Modelin sadece bu çıktıyı gerekli (OUTPUT_STEPS, features) olacak şekilde yeniden şekillendirmesi gerekiyor.
Doğrusal
Son girdi zaman adımına dayalı basit bir doğrusal model, her iki taban çizgisinden de daha iyi sonuç verir, ancak gücü düşüktür. Modelin, doğrusal bir projeksiyon ile tek bir giriş zaman adımından OUTPUT_STEPS zaman adımlarını tahmin etmesi gerekir. Büyük olasılıkla günün saatine ve yılın saatine dayalı olarak, davranışın yalnızca düşük boyutlu bir dilimini yakalayabilir.
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
Yoğun
Giriş ve çıkış arasına bir tf.keras.layers.Dense eklemek, doğrusal modele daha fazla güç verir, ancak yine de yalnızca tek bir giriş zaman adımına dayanır.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
CNN
Evrişimli bir model, işlerin zaman içinde nasıl değiştiğini görebildiği için, yoğun modelden daha iyi performansa yol açabilecek sabit genişlikli bir geçmişe dayalı tahminler yapar:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
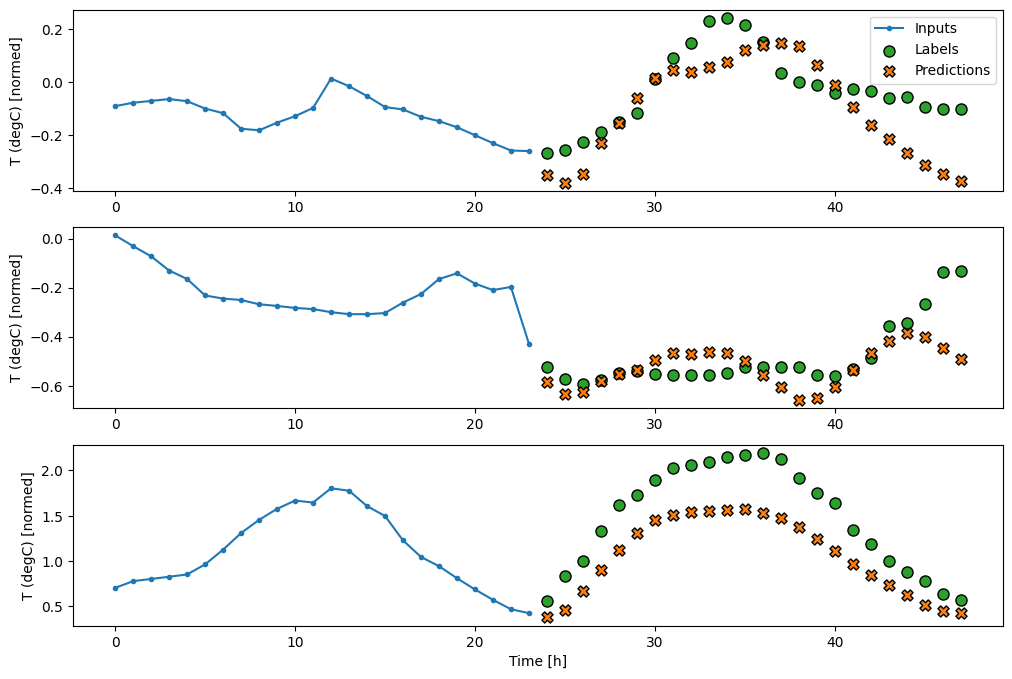
RNN
Yinelenen bir model, modelin yaptığı tahminlerle ilgiliyse, uzun bir girdi geçmişi kullanmayı öğrenebilir. Burada model, sonraki 24 saat için tek bir tahmin yapmadan önce 24 saat boyunca dahili durumu biriktirecektir.
Bu tek çekim biçiminde, LSTM'nin yalnızca son zaman adımında bir çıktı üretmesi gerekir, bu nedenle tf.keras.layers.LSTM içinde tf.keras.layers.LSTM return_sequences=False öğesini ayarlayın.
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
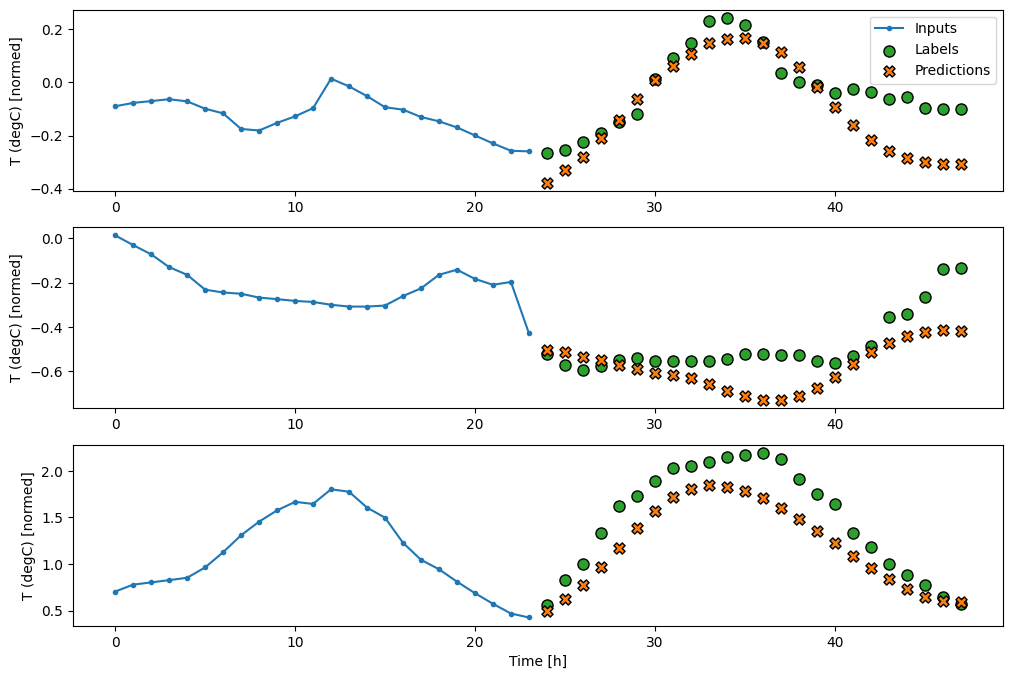
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
Gelişmiş: Otoregresif model
Yukarıdaki modellerin tümü, tüm çıktı sırasını tek bir adımda tahmin eder.
Bazı durumlarda, modelin bu tahmini bireysel zaman adımlarına ayırması faydalı olabilir. Ardından, her modelin çıktısı, her adımda kendi içine geri beslenebilir ve klasik Tekrarlayan Sinir Ağları İle Dizi Oluşturmada olduğu gibi, bir öncekine göre koşullandırılmış tahminler yapılabilir.
Bu model stilinin açık bir avantajı, değişken uzunlukta çıktı üretecek şekilde ayarlanabilmesidir.
Bu öğreticinin ilk yarısında eğitilen tek adımlı çok çıkışlı modellerden herhangi birini alabilir ve otoregresif bir geri bildirim döngüsünde çalıştırabilirsiniz, ancak burada bunu yapmak için açıkça eğitilmiş bir model oluşturmaya odaklanacaksınız.
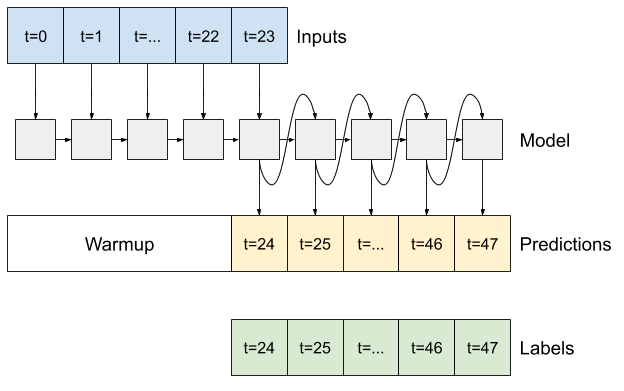
RNN
Bu öğretici yalnızca bir otoregresif RNN modeli oluşturur, ancak bu model, tek bir zaman adımı çıktısı almak üzere tasarlanmış herhangi bir modele uygulanabilir.
Model, daha önceki tek adımlı LSTM modelleriyle aynı temel forma sahip olacaktır: bir tf.keras.layers.LSTM katmanı, ardından LSTM katmanının çıktılarını model tahminlerine dönüştüren bir tf.keras.layers.Dense katmanı.
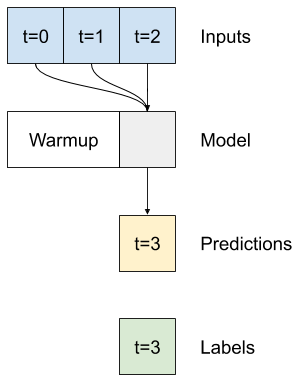
Bir tf.keras.layers.LSTM , sizin için durum ve sıralama sonuçlarını yöneten daha yüksek seviye tf.keras.layers.RNN içine sarılmış bir tf.keras.layers.LSTMCell (Keras ile Tekrarlayan Sinir Ağlarına (RNN) göz atın) ayrıntılar için kılavuz).
Bu durumda, modelin her adım için girdileri manuel olarak yönetmesi gerekir, bu nedenle alt düzey, tek zamanlı adım arabirimi için doğrudan tf.keras.layers.LSTMCell kullanır.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
Bu modelin ihtiyaç duyduğu ilk yöntem, girdilere dayalı olarak dahili durumunu başlatmak için bir warmup yöntemidir. Eğitildikten sonra, bu durum girdi geçmişinin ilgili kısımlarını yakalayacaktır. Bu, daha önceki tek adımlı LSTM modeline eşdeğerdir:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
Bu yöntem, tek bir zaman adımlı tahmin ve LSTM dahili durumunu döndürür:
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
RNN durumu ve bir ilk tahminle, şimdi girdi olarak her adımda tahminleri besleyen modeli yinelemeye devam edebilirsiniz.
Çıktı tahminlerini toplamak için en basit yaklaşım, döngüden sonra bir Python listesi ve bir tf.stack kullanmaktır.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Bu modeli örnek girdilerde test edin:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
Şimdi modeli eğitin:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
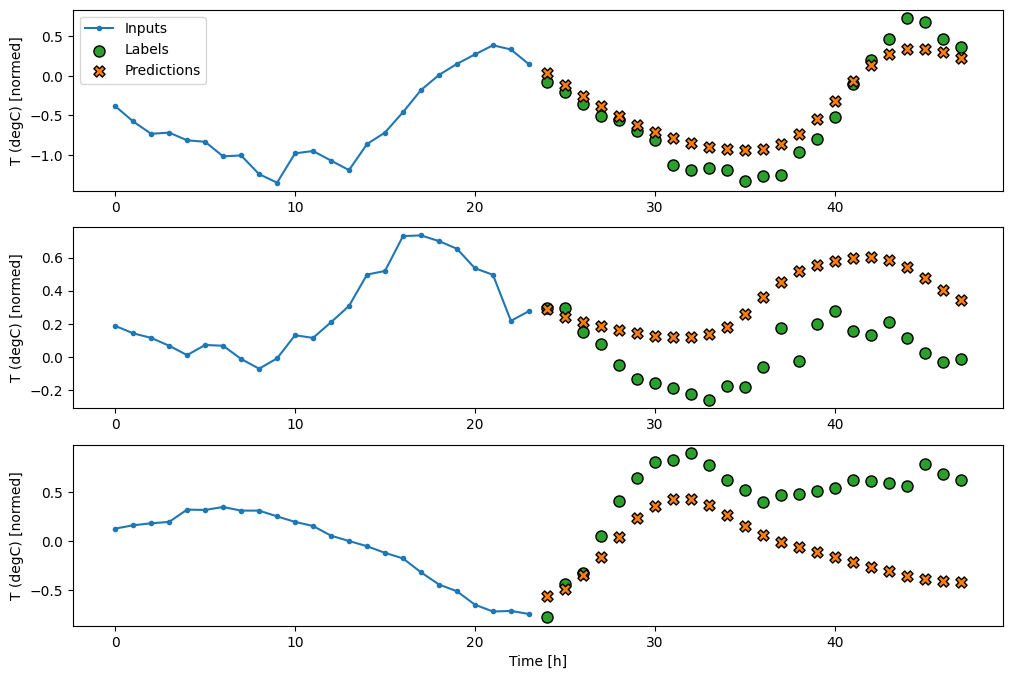
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
Verim
Bu problemde model karmaşıklığının bir fonksiyonu olarak açıkça azalan getiriler vardır:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
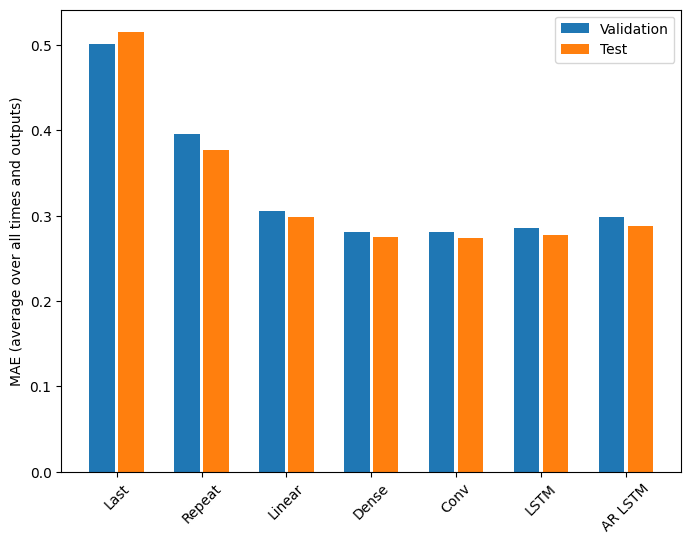
Bu öğreticinin ilk yarısındaki çok çıkışlı modellerin metrikleri, tüm çıkış özelliklerinde ortalama performansı gösterir. Bu performanslar benzerdir ancak aynı zamanda çıktı zaman adımlarının ortalaması alınır.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
Yoğun bir modelden evrişimli ve tekrarlayan modellere geçerken elde edilen kazanımlar (eğer varsa) yalnızca yüzde birkaçtır ve otoregresif model açıkça daha kötü performans göstermiştir. Bu nedenle, bu daha karmaşık yaklaşımlar, bu problem üzerinde uğraşmaya değmeyebilir, ancak denemeden bilmenin bir yolu yoktu ve bu modeller probleminiz için yardımcı olabilir.
Sonraki adımlar
Bu eğitim, TensorFlow kullanılarak zaman serisi tahminine hızlı bir giriş niteliğindeydi.
Daha fazla bilgi edinmek için şu adrese bakın:
- Scikit-Learn, Keras ve TensorFlow ile Uygulamalı Makine Öğrenimi , 2. Baskı, Bölüm 15.
- Python ile Derin Öğrenmenin 6. Bölümü .
- Udacity'nin derin öğrenme için TensorFlow'a girişinin 8. Dersi, alıştırma not defterleri de dahil.
Ayrıca, TensorFlow'da herhangi bir klasik zaman serisi modelini uygulayabileceğinizi unutmayın; bu eğitim yalnızca TensorFlow'un yerleşik işlevselliğine odaklanır.
