پیش بینی سری های زمانی

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

این آموزش مقدمه ای بر پیش بینی سری های زمانی با استفاده از TensorFlow است. چند سبک مختلف از مدل‌ها از جمله شبکه‌های عصبی کانولوشنال و بازگشتی (CNN و RNN) ایجاد می‌کند.

این در دو بخش اصلی با زیر بخش ها پوشش داده شده است:

• پیش بینی برای یک مرحله زمانی:
  • یک ویژگی واحد
  • همه ویژگی ها
• پیش بینی چند مرحله
  • تک شات: پیش بینی ها را یکباره انجام دهید.
  • Autoregressive: هر بار یک پیش بینی انجام دهید و خروجی را به مدل برگردانید.

برپایی

import os
import datetime

import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf

mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False

مجموعه داده آب و هوا

این آموزش از مجموعه داده سری زمانی آب و هوا استفاده می کند که توسط موسسه بیوژئوشیمی Max Planck ثبت شده است.

این مجموعه داده شامل 14 ویژگی مختلف مانند دمای هوا، فشار اتمسفر و رطوبت است. اینها از سال 2003 هر 10 دقیقه جمع‌آوری می‌شوند. برای کارآمدی، فقط از داده‌های جمع‌آوری‌شده بین سال‌های 2009 و 2016 استفاده خواهید کرد. این بخش از مجموعه داده‌ها توسط فرانسوا شولت برای کتاب یادگیری عمیق با پایتون تهیه شده است.

zip_path = tf.keras.utils.get_file(
    origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
    fname='jena_climate_2009_2016.csv.zip',
    extract=True)
csv_path, _ = os.path.splitext(zip_path)

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip
13574144/13568290 [==============================] - 1s 0us/step
13582336/13568290 [==============================] - 1s 0us/step

این آموزش فقط به پیش بینی های ساعتی می پردازد ، بنابراین با نمونه گیری فرعی داده ها از فواصل 10 دقیقه ای تا فواصل یک ساعته شروع کنید:

df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]

date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')

بیایید نگاهی به داده ها بیندازیم. این چند ردیف اول است:

df.head()

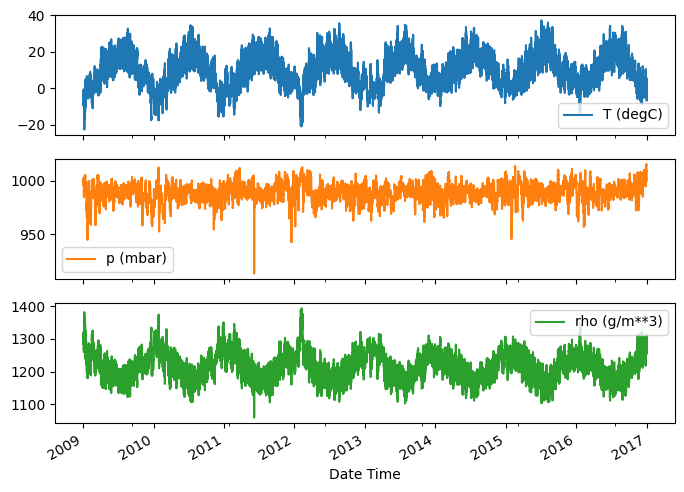
در اینجا تکامل چند ویژگی در طول زمان آورده شده است:

plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)

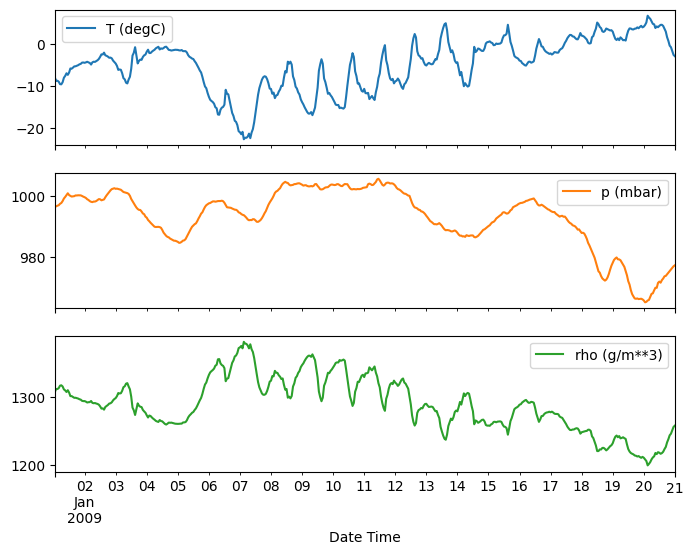
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)

بازرسی و پاکسازی

سپس به آمار مجموعه داده نگاه کنید:

df.describe().transpose()

سرعت باد

یکی از مواردی که باید برجسته شود، مقدار min سرعت باد ( wv (m/s) ) و حداکثر مقدار ( max. wv (m/s) ) ستون‌ها است. این -9999 احتمالاً اشتباه است.

یک ستون جهت باد جداگانه وجود دارد، بنابراین سرعت باید بزرگتر از صفر باشد ( >=0 ). آن را با صفر جایگزین کنید:

wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0

max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0

# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()

0.0

مهندسی ویژگی

قبل از ورود به ساخت یک مدل، مهم است که داده‌های خود را درک کنید و مطمئن شوید که داده‌های قالب‌بندی مناسب مدل را ارسال می‌کنید.

باد

آخرین ستون داده ها، wd (deg) جهت باد را بر حسب واحد درجه نشان می دهد. زاویه ها ورودی های مدل خوبی را ایجاد نمی کنند: 360 درجه و 0 درجه باید نزدیک به هم باشند و به آرامی به اطراف بپیچند. اگر باد نمی وزد، مسیر نباید مهم باشد.

در حال حاضر توزیع داده های باد به این صورت است:

plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')

Text(0, 0.5, 'Wind Velocity [m/s]')

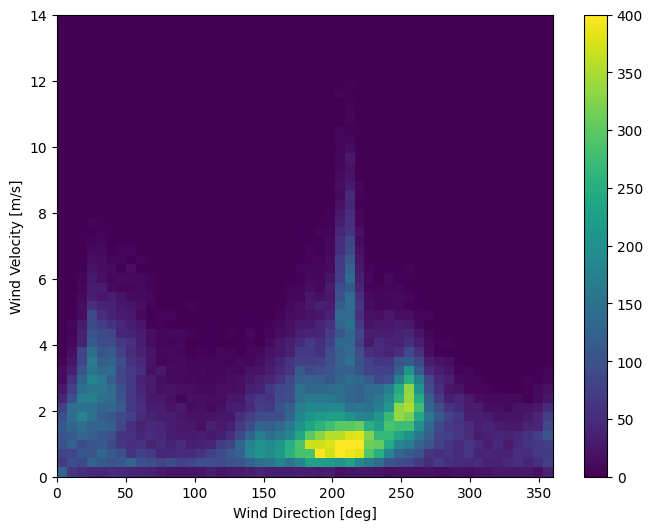
اما اگر ستون‌های جهت و سرعت باد را به بردار باد تبدیل کنید، تفسیر آن برای مدل آسان‌تر خواهد بود:

wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')

# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180

# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)

# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)

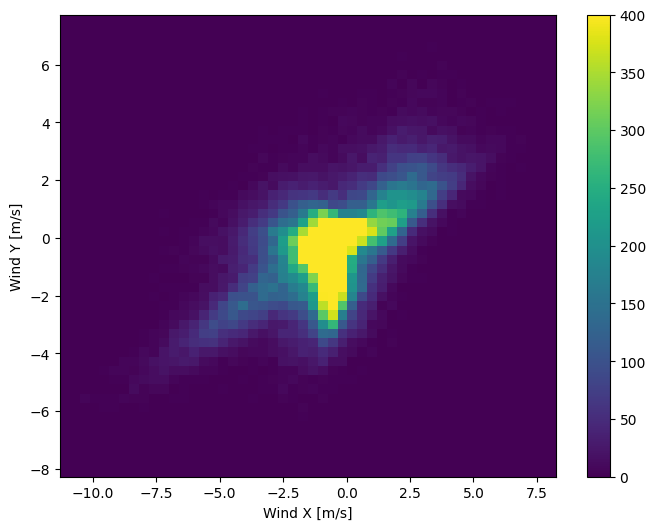
توزیع بردارهای باد برای مدل برای تفسیر صحیح بسیار ساده تر است:

plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')

(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)

زمان

به طور مشابه، ستون Date Time بسیار مفید است، اما نه به این شکل رشته ای. با تبدیل آن به ثانیه شروع کنید:

timestamp_s = date_time.map(pd.Timestamp.timestamp)

مشابه جهت باد، زمان بر حسب ثانیه ورودی مدل مفیدی نیست. به عنوان داده های آب و هوا، دارای تناوب روزانه و سالانه واضح است. راه های زیادی وجود دارد که می توانید با تناوب مقابله کنید.

می‌توانید سیگنال‌های قابل استفاده را با استفاده از تبدیل‌های سینوسی و کسینوس برای پاک کردن سیگنال‌های «زمان روز» و «زمان سال» دریافت کنید:

day = 24*60*60
year = (365.2425)*day

df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))

plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')

Text(0.5, 1.0, 'Time of day signal')

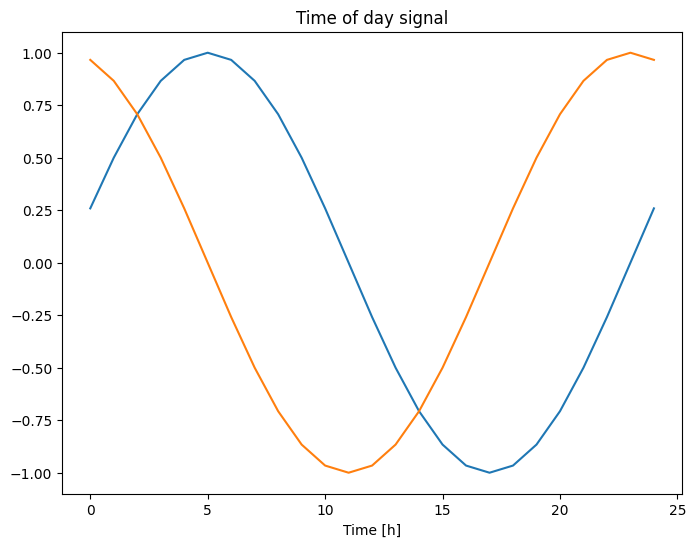
این به مدل امکان دسترسی به مهمترین ویژگی های فرکانس را می دهد. در این مورد شما از قبل می دانستید که کدام فرکانس ها مهم هستند.

اگر آن اطلاعات را ندارید، می توانید با استخراج ویژگی ها با تبدیل فوریه سریع تعیین کنید که کدام فرکانس مهم است. برای بررسی مفروضات، در اینجا tf.signal.rfft دما در طول زمان آمده است. به پیک های آشکار در فرکانس های نزدیک به 1/year و 1/day توجه کنید:

fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))

n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)

f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')

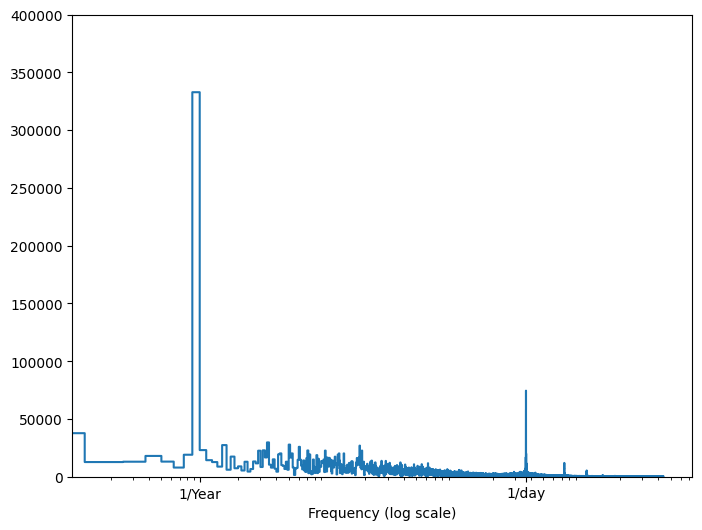
داده ها را تقسیم کنید

شما از یک تقسیم (70%, 20%, 10%) برای مجموعه های آموزشی، اعتبار سنجی و تست استفاده خواهید کرد. توجه داشته باشید که داده ها قبل از تقسیم به طور تصادفی با هم مخلوط نمی شوند. این به دو دلیل است:

1. این تضمین می کند که خرد کردن داده ها در پنجره های نمونه های متوالی هنوز امکان پذیر است.
2. این تضمین می‌کند که نتایج اعتبارسنجی/آزمون واقعی‌تر هستند و بر اساس داده‌های جمع‌آوری‌شده پس از آموزش مدل ارزیابی می‌شوند.

column_indices = {name: i for i, name in enumerate(df.columns)}

n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]

num_features = df.shape[1]

داده ها را عادی کنید

قبل از آموزش شبکه عصبی، مقیاس‌بندی ویژگی‌ها مهم است. عادی سازی یک روش رایج برای انجام این مقیاس است: میانگین را کم کنید و بر انحراف استاندارد هر ویژگی تقسیم کنید.

میانگین و انحراف معیار فقط باید با استفاده از داده های آموزشی محاسبه شود تا مدل ها به مقادیر موجود در مجموعه های اعتبار سنجی و آزمایش دسترسی نداشته باشند.

همچنین قابل بحث است که مدل نباید هنگام آموزش به مقادیر آینده در مجموعه آموزشی دسترسی داشته باشد و این نرمال سازی باید با استفاده از میانگین های متحرک انجام شود. تمرکز این آموزش این نیست، و مجموعه‌های آزمایش و اعتبارسنجی تضمین می‌کنند که معیارهای (تا حدودی) صادقانه را دریافت می‌کنید. بنابراین، به منظور سادگی، این آموزش از یک میانگین ساده استفاده می کند.

train_mean = train_df.mean()
train_std = train_df.std()

train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std

اکنون، به توزیع ویژگی‌ها نگاه کنید. برخی از ویژگی ها دارای دم بلند هستند، اما هیچ خطای آشکاری مانند مقدار -9999 سرعت باد وجود ندارد.

df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

پنجره سازی داده ها

مدل های موجود در این آموزش مجموعه ای از پیش بینی ها را بر اساس پنجره ای از نمونه های متوالی از داده ها انجام می دهند.

ویژگی های اصلی پنجره های ورودی عبارتند از:

• عرض (تعداد مراحل زمانی) پنجره های ورودی و برچسب.
• فاصله زمانی بین آنها.
• کدام ویژگی به عنوان ورودی، برچسب یا هر دو استفاده می شود.

این آموزش مدل‌های مختلفی را می‌سازد (از جمله مدل‌های Linear، DNN، CNN و RNN)، و از آنها برای هر دو استفاده می‌کند:

• پیش بینی های تک خروجی و چند خروجی .
• پیش بینی های تک مرحله ای و چند مرحله ای .

این بخش بر پیاده سازی پنجره سازی داده ها تمرکز دارد تا بتوان از آن برای همه آن مدل ها استفاده مجدد کرد.

بسته به کار و نوع مدل ممکن است بخواهید پنجره های داده مختلفی تولید کنید. در اینجا چند نمونه آورده شده است:

1. به عنوان مثال، برای انجام یک پیش‌بینی واحد در 24 ساعت آینده، با توجه به 24 ساعت تاریخ، می‌توانید پنجره‌ای مانند این تعریف کنید:

   

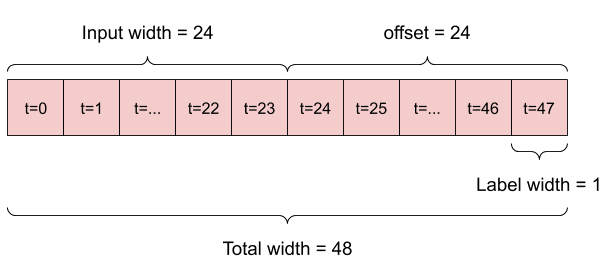
2. مدلی که یک ساعت آینده را با توجه به شش ساعت تاریخ پیش بینی می کند، به پنجره ای مانند این نیاز دارد:

   

بقیه این بخش یک کلاس WindowGenerator را تعریف می کند. این کلاس می تواند:

1. شاخص ها و آفست ها را همانطور که در نمودارهای بالا نشان داده شده است، مدیریت کنید.
2. پنجره های ویژگی ها را به جفت (features, labels) تقسیم کنید.
3. محتوای پنجره های حاصل را رسم کنید.
4. با استفاده از tf.data.Dataset s، دسته هایی از این پنجره ها را از داده های آموزش، ارزیابی و آزمایش تولید کنید.

1. شاخص ها و افست ها

با ایجاد کلاس WindowGenerator شروع کنید. متد __init__ شامل تمام منطق لازم برای شاخص های ورودی و برچسب است.

همچنین آموزش، ارزیابی و تست DataFrames را به عنوان ورودی می گیرد. اینها بعداً به tf.data.Dataset ویندوز تبدیل خواهند شد.

class WindowGenerator():
  def __init__(self, input_width, label_width, shift,
               train_df=train_df, val_df=val_df, test_df=test_df,
               label_columns=None):
    # Store the raw data.
    self.train_df = train_df
    self.val_df = val_df
    self.test_df = test_df

    # Work out the label column indices.
    self.label_columns = label_columns
    if label_columns is not None:
      self.label_columns_indices = {name: i for i, name in
                                    enumerate(label_columns)}
    self.column_indices = {name: i for i, name in
                           enumerate(train_df.columns)}

    # Work out the window parameters.
    self.input_width = input_width
    self.label_width = label_width
    self.shift = shift

    self.total_window_size = input_width + shift

    self.input_slice = slice(0, input_width)
    self.input_indices = np.arange(self.total_window_size)[self.input_slice]

    self.label_start = self.total_window_size - self.label_width
    self.labels_slice = slice(self.label_start, None)
    self.label_indices = np.arange(self.total_window_size)[self.labels_slice]

  def __repr__(self):
    return '\n'.join([
        f'Total window size: {self.total_window_size}',
        f'Input indices: {self.input_indices}',
        f'Label indices: {self.label_indices}',
        f'Label column name(s): {self.label_columns}'])

در اینجا کد ایجاد 2 پنجره نشان داده شده در نمودارها در ابتدای این بخش وجود دارد:

w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
                     label_columns=['T (degC)'])
w1

Total window size: 48
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [47]
Label column name(s): ['T (degC)']

w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
                     label_columns=['T (degC)'])
w2

Total window size: 7
Input indices: [0 1 2 3 4 5]
Label indices: [6]
Label column name(s): ['T (degC)']

2. تقسیم

با توجه به لیستی از ورودی های متوالی، روش split_window آنها را به پنجره ای از ورودی ها و پنجره ای از برچسب ها تبدیل می کند.

مثال w2 که قبلا تعریف کردید به شکل زیر تقسیم می شود:

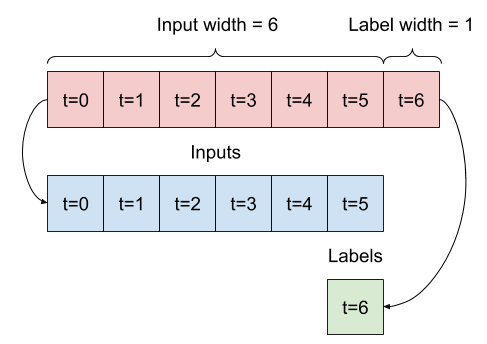
این نمودار محور features داده‌ها را نشان نمی‌دهد، اما این تابع split_window همچنین label_columns را مدیریت می‌کند، بنابراین می‌توان از آن برای نمونه‌های تک خروجی و چند خروجی استفاده کرد.

def split_window(self, features):
  inputs = features[:, self.input_slice, :]
  labels = features[:, self.labels_slice, :]
  if self.label_columns is not None:
    labels = tf.stack(
        [labels[:, :, self.column_indices[name]] for name in self.label_columns],
        axis=-1)

  # Slicing doesn't preserve static shape information, so set the shapes
  # manually. This way the `tf.data.Datasets` are easier to inspect.
  inputs.set_shape([None, self.input_width, None])
  labels.set_shape([None, self.label_width, None])

  return inputs, labels

WindowGenerator.split_window = split_window

آن را امتحان کنید:

# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
                           np.array(train_df[100:100+w2.total_window_size]),
                           np.array(train_df[200:200+w2.total_window_size])])

example_inputs, example_labels = w2.split_window(example_window)

print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')

All shapes are: (batch, time, features)
Window shape: (3, 7, 19)
Inputs shape: (3, 6, 19)
Labels shape: (3, 1, 1)

به طور معمول، داده‌ها در TensorFlow در آرایه‌هایی بسته‌بندی می‌شوند که بیرونی‌ترین شاخص در بین نمونه‌ها قرار دارد (بعد دسته‌ای). شاخص‌های میانی، ابعاد «زمان» یا «فضا» (عرض، ارتفاع) هستند. درونی ترین شاخص ها ویژگی ها هستند.

کد بالا دسته‌ای از سه پنجره 7-زمان گام با 19 ویژگی در هر مرحله زمانی را انتخاب کرد. آن‌ها را به دسته‌ای از ورودی‌های 19 ویژگی 6 مرحله‌ای و برچسب ویژگی 1 مرحله‌ای 1 بار تقسیم می‌کند. برچسب فقط یک ویژگی دارد زیرا WindowGenerator با label_columns=['T (degC)'] مقداردهی اولیه شده است. در ابتدا، این آموزش مدل هایی را می سازد که برچسب های خروجی واحد را پیش بینی می کنند.

3. طرح

در اینجا یک روش نمودار وجود دارد که امکان تجسم ساده پنجره تقسیم را فراهم می کند:

w2.example = example_inputs, example_labels

def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
  inputs, labels = self.example
  plt.figure(figsize=(12, 8))
  plot_col_index = self.column_indices[plot_col]
  max_n = min(max_subplots, len(inputs))
  for n in range(max_n):
    plt.subplot(max_n, 1, n+1)
    plt.ylabel(f'{plot_col} [normed]')
    plt.plot(self.input_indices, inputs[n, :, plot_col_index],
             label='Inputs', marker='.', zorder=-10)

    if self.label_columns:
      label_col_index = self.label_columns_indices.get(plot_col, None)
    else:
      label_col_index = plot_col_index

    if label_col_index is None:
      continue

    plt.scatter(self.label_indices, labels[n, :, label_col_index],
                edgecolors='k', label='Labels', c='#2ca02c', s=64)
    if model is not None:
      predictions = model(inputs)
      plt.scatter(self.label_indices, predictions[n, :, label_col_index],
                  marker='X', edgecolors='k', label='Predictions',
                  c='#ff7f0e', s=64)

    if n == 0:
      plt.legend()

  plt.xlabel('Time [h]')

WindowGenerator.plot = plot

این نمودار ورودی‌ها، برچسب‌ها و (بعدا) پیش‌بینی‌ها را بر اساس زمانی که مورد به آن اشاره دارد، تراز می‌کند:

w2.plot()

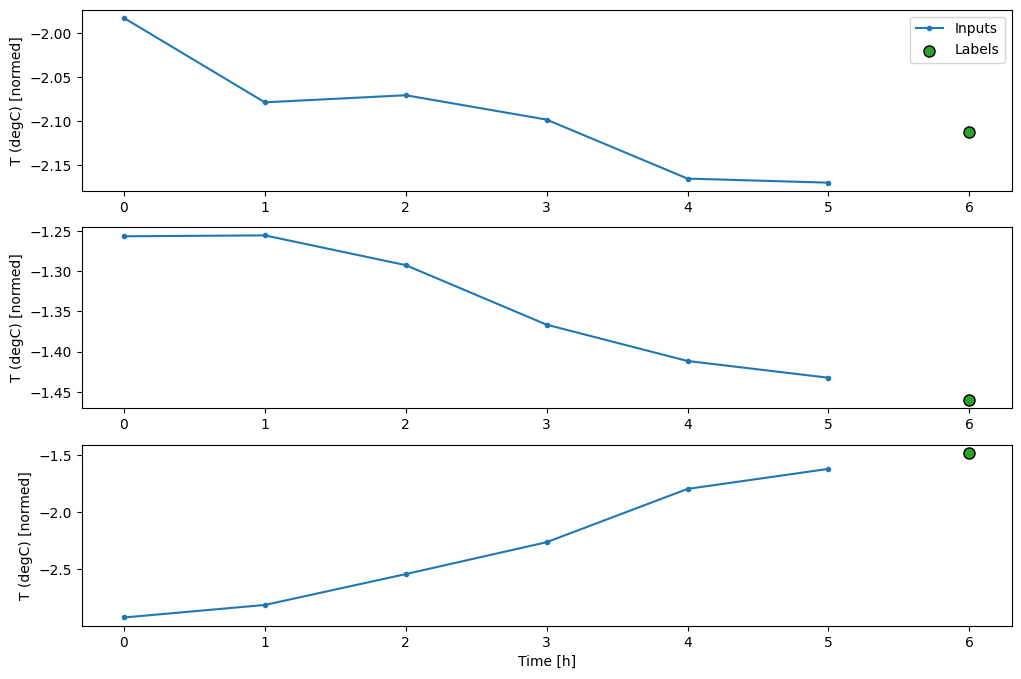
می‌توانید ستون‌های دیگر را رسم کنید، اما پیکربندی w2 پنجره نمونه فقط دارای برچسب‌هایی برای ستون T (degC) است.

w2.plot(plot_col='p (mbar)')

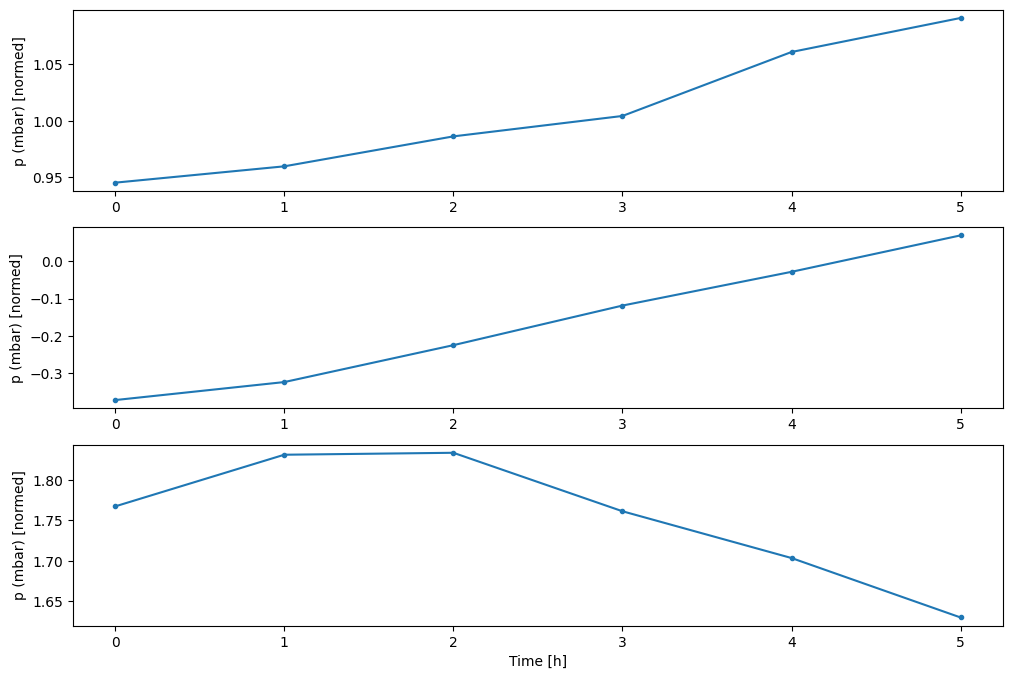
4. tf.data.Dataset s را ایجاد کنید

در نهایت، این متد make_dataset یک سری زمانی DataFrame می گیرد و آن را با استفاده از تابع tf.keras.utils.timeseries_dataset_from_array به یک tf.data.Dataset از (input_window, label_window) تبدیل می کند:

def make_dataset(self, data):
  data = np.array(data, dtype=np.float32)
  ds = tf.keras.utils.timeseries_dataset_from_array(
      data=data,
      targets=None,
      sequence_length=self.total_window_size,
      sequence_stride=1,
      shuffle=True,
      batch_size=32,)

  ds = ds.map(self.split_window)

  return ds

WindowGenerator.make_dataset = make_dataset

شی WindowGenerator داده های آموزشی، اعتبارسنجی و آزمایش را در خود نگه می دارد.

با استفاده از روش make_dataset که قبلاً تعریف کردید، ویژگی هایی را برای دسترسی به آنها به عنوان tf.data.Dataset s اضافه کنید. همچنین، برای دسترسی آسان و ترسیم، یک دسته نمونه استاندارد اضافه کنید:

@property
def train(self):
  return self.make_dataset(self.train_df)

@property
def val(self):
  return self.make_dataset(self.val_df)

@property
def test(self):
  return self.make_dataset(self.test_df)

@property
def example(self):
  """Get and cache an example batch of `inputs, labels` for plotting."""
  result = getattr(self, '_example', None)
  if result is None:
    # No example batch was found, so get one from the `.train` dataset
    result = next(iter(self.train))
    # And cache it for next time
    self._example = result
  return result

WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example

اکنون، شی WindowGenerator به شما امکان دسترسی به اشیاء tf.data.Dataset را می دهد، بنابراین می توانید به راحتی روی داده ها تکرار کنید.

ویژگی Dataset.element_spec ساختار، انواع داده ها و اشکال عناصر مجموعه داده را به شما می گوید.

# Each element is an (inputs, label) pair.
w2.train.element_spec

(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None),
 TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))

با تکرار روی یک Dataset ، دسته های بتن به دست می آیند:

for example_inputs, example_labels in w2.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 6, 19)
Labels shape (batch, time, features): (32, 1, 1)

مدل های تک مرحله ای

ساده‌ترین مدلی که می‌توانید بر اساس این نوع داده‌ها بسازید، مدلی است که ارزش یک ویژگی را پیش‌بینی می‌کند - 1 گام زمانی (یک ساعت) در آینده فقط بر اساس شرایط فعلی.

بنابراین، با ساخت مدل‌هایی برای پیش‌بینی مقدار T (degC) یک ساعت بعد شروع کنید.

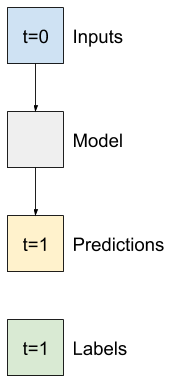
یک شی WindowGenerator را برای تولید این جفت های تک مرحله ای (input, label) پیکربندی کنید:

single_step_window = WindowGenerator(
    input_width=1, label_width=1, shift=1,
    label_columns=['T (degC)'])
single_step_window

Total window size: 2
Input indices: [0]
Label indices: [1]
Label column name(s): ['T (degC)']

شی window tf.data.Dataset s را از مجموعه های آموزشی، اعتبار سنجی و آزمایش ایجاد می کند و به شما این امکان را می دهد که به راحتی روی دسته ای از داده ها تکرار کنید.

for example_inputs, example_labels in single_step_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 1, 19)
Labels shape (batch, time, features): (32, 1, 1)

خط پایه

قبل از ساخت یک مدل آموزش پذیر، خوب است که یک خط پایه عملکرد به عنوان نقطه ای برای مقایسه با مدل های پیچیده تر بعدی داشته باشید.

اولین کار این است که با توجه به ارزش فعلی همه ویژگی‌ها، دمای یک ساعت بعد را پیش‌بینی کنیم. مقادیر فعلی شامل دمای فعلی است.

بنابراین، با مدلی شروع کنید که فقط دمای فعلی را به عنوان پیش‌بینی برمی‌گرداند و «بدون تغییر» را پیش‌بینی می‌کند. این یک خط پایه معقول است زیرا دما به آرامی تغییر می کند. البته، اگر در آینده پیش‌بینی بیشتری انجام دهید، این خط پایه کمتر کار خواهد کرد.

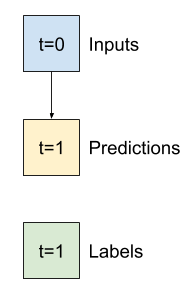
class Baseline(tf.keras.Model):
  def __init__(self, label_index=None):
    super().__init__()
    self.label_index = label_index

  def call(self, inputs):
    if self.label_index is None:
      return inputs
    result = inputs[:, :, self.label_index]
    return result[:, :, tf.newaxis]

نمونه سازی و ارزیابی این مدل:

baseline = Baseline(label_index=column_indices['T (degC)'])

baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785

این چند معیار عملکرد را نشان می‌دهد، اما این معیارها به شما احساس خوبی نسبت به عملکرد مدل نمی‌دهد.

WindowGenerator یک روش نمودار دارد، اما نمودارها تنها با یک نمونه خیلی جالب نخواهند بود.

بنابراین، یک WindowGenerator گسترده‌تر ایجاد کنید که 24 ساعت ورودی‌ها و برچسب‌های متوالی را در یک زمان برای ویندوز ایجاد می‌کند. متغیر wide_window جدید نحوه عملکرد مدل را تغییر نمی دهد. این مدل هنوز یک ساعت آینده را بر اساس یک مرحله زمانی ورودی پیش‌بینی می‌کند. در اینجا، محور time مانند محور batch عمل می کند: هر پیش بینی به طور مستقل و بدون تعامل بین مراحل زمانی انجام می شود:

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1,
    label_columns=['T (degC)'])

wide_window

Total window size: 25
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
Label column name(s): ['T (degC)']

این پنجره گسترش یافته را می توان مستقیماً به همان مدل baseline بدون تغییر کد ارسال کرد. این امکان پذیر است زیرا ورودی ها و برچسب ها تعداد مراحل زمانی یکسانی دارند و خط مبنا فقط ورودی را به خروجی ارسال می کند:

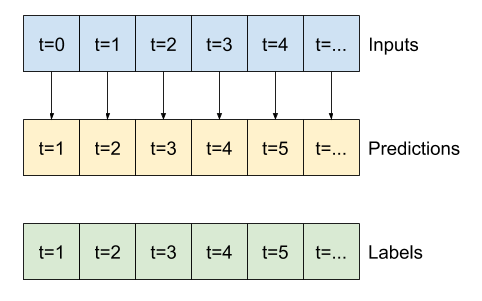
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

با ترسیم پیش‌بینی‌های مدل پایه، توجه کنید که فقط برچسب‌ها یک ساعت به سمت راست جابه‌جا می‌شوند:

wide_window.plot(baseline)

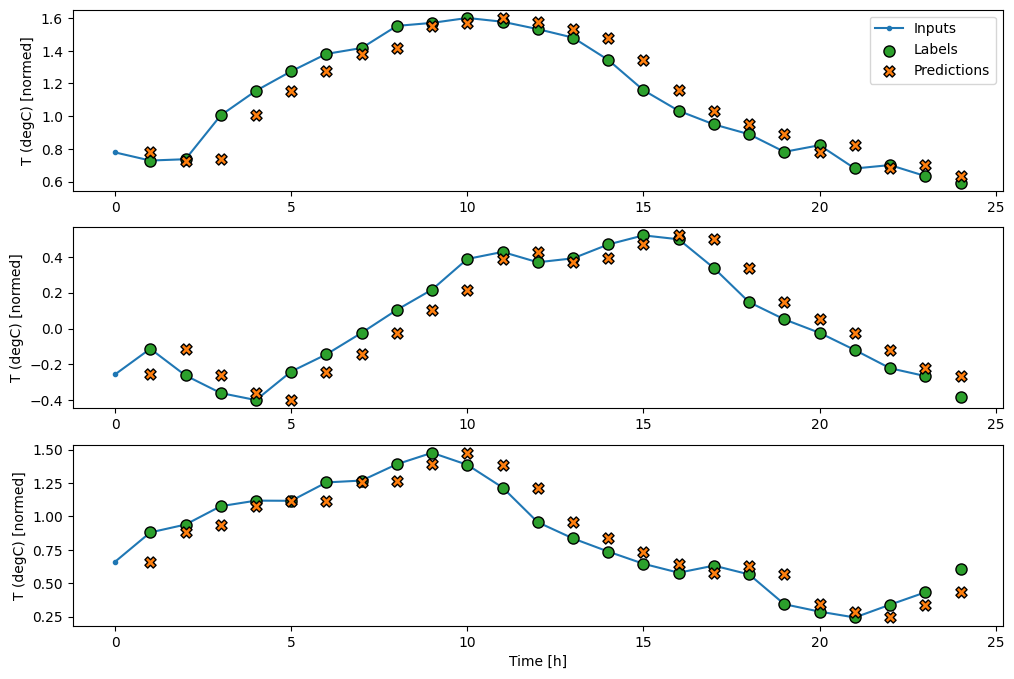
در نمودارهای سه نمونه فوق، مدل تک مرحله ای در طول 24 ساعت اجرا می شود. این سزاوار توضیح است:

• خط آبی Inputs ها دمای ورودی را در هر مرحله زمانی نشان می دهد. مدل تمام ویژگی ها را دریافت می کند، این نمودار فقط دما را نشان می دهد.
• نقاط سبز رنگ Labels مقدار پیش بینی هدف را نشان می دهد. این نقاط در زمان پیش‌بینی نشان داده می‌شوند، نه در زمان ورودی. به همین دلیل است که محدوده برچسب ها نسبت به ورودی ها 1 مرحله تغییر می کند.
• ضربدرهای نارنجی Predictions ، پیش بینی های مدل برای هر مرحله زمانی خروجی هستند. اگر مدل کاملاً پیش‌بینی می‌کرد، پیش‌بینی‌ها مستقیماً روی Labels قرار می‌گرفتند.

مدل خطی

ساده ترین مدل آموزش پذیری که می توانید برای این کار اعمال کنید، درج تبدیل خطی بین ورودی و خروجی است. در این مورد خروجی یک مرحله زمانی فقط به آن مرحله بستگی دارد:

یک لایه tf.keras.layers.Dense بدون مجموعه activation یک مدل خطی است. لایه فقط آخرین محور داده ها را از (batch, time, inputs) به (batch, time, units) . به طور مستقل برای هر آیتم در محورهای batch و time اعمال می شود.

linear = tf.keras.Sequential([
    tf.keras.layers.Dense(units=1)
])

print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)

Input shape: (32, 1, 19)
Output shape: (32, 1, 1)

این آموزش مدل های زیادی را آموزش می دهد، بنابراین روند آموزش را در یک تابع بسته بندی کنید:

MAX_EPOCHS = 20

def compile_and_fit(model, window, patience=2):
  early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
                                                    patience=patience,
                                                    mode='min')

  model.compile(loss=tf.losses.MeanSquaredError(),
                optimizer=tf.optimizers.Adam(),
                metrics=[tf.metrics.MeanAbsoluteError()])

  history = model.fit(window.train, epochs=MAX_EPOCHS,
                      validation_data=window.val,
                      callbacks=[early_stopping])
  return history

آموزش مدل و ارزیابی عملکرد آن:

history = compile_and_fit(linear, single_step_window)

val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858
Epoch 2/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711
Epoch 3/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690
Epoch 4/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692
Epoch 5/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685
Epoch 6/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687
Epoch 7/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680
Epoch 8/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683
Epoch 9/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684
439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684

مانند مدل baseline ، مدل خطی را می توان در دسته هایی از پنجره های عریض فراخوانی کرد. با استفاده از این روش، مدل مجموعه ای از پیش بینی های مستقل را در گام های زمانی متوالی انجام می دهد. محور time مانند یک محور batch دیگر عمل می کند. هیچ تعاملی بین پیش بینی ها در هر مرحله زمانی وجود ندارد.

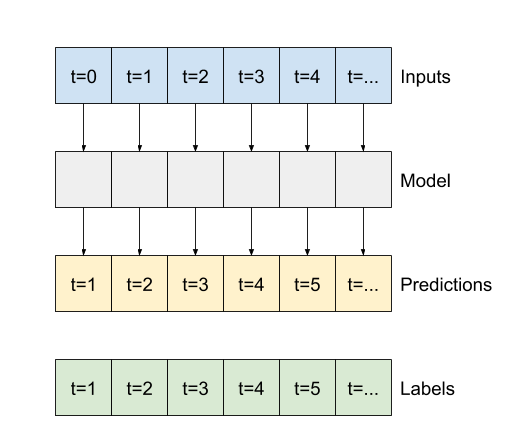
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

در اینجا نمودار نمونه‌ای از پیش‌بینی‌های آن در wide_window است، توجه داشته باشید که چگونه پیش‌بینی در بسیاری از موارد به وضوح بهتر از بازگرداندن دمای ورودی است، اما در چند مورد بدتر است:

wide_window.plot(linear)

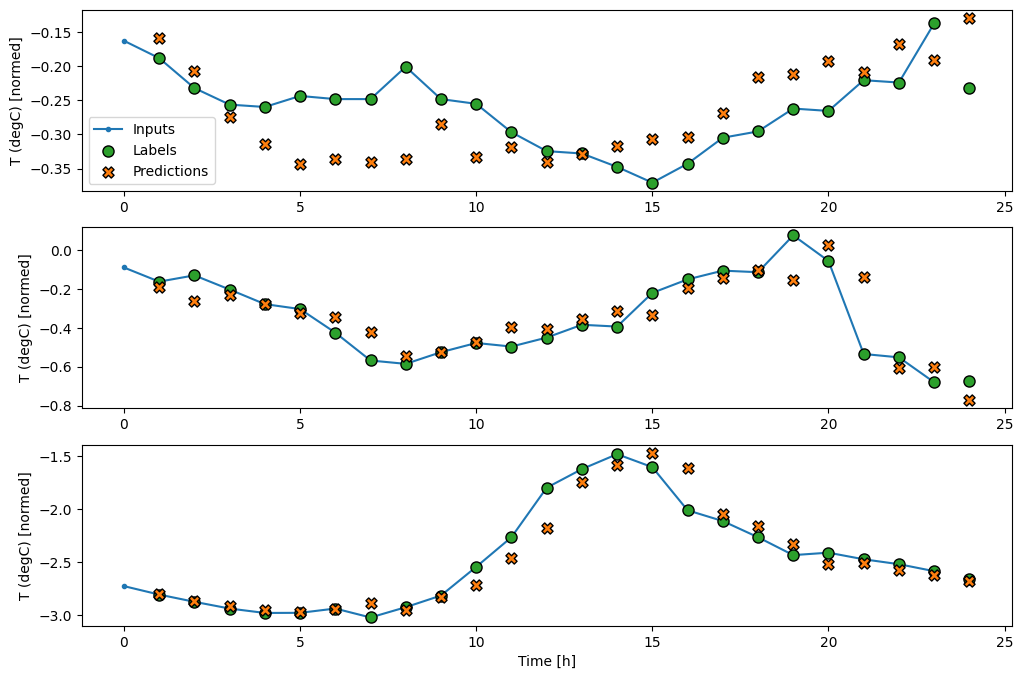
یکی از مزیت های مدل های خطی این است که تفسیر آنها نسبتاً ساده است. می توانید وزن های لایه را بیرون بکشید و وزن اختصاص داده شده به هر ورودی را تجسم کنید:

plt.bar(x = range(len(train_df.columns)),
        height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)

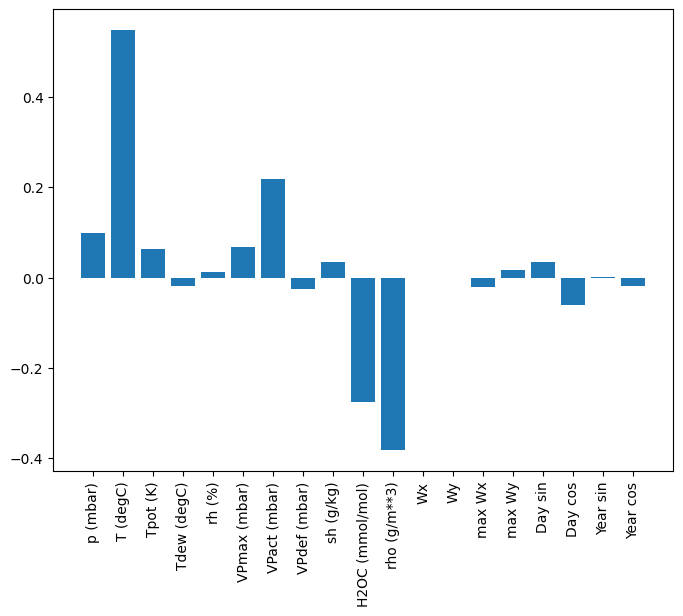
گاهی اوقات مدل حتی بیشترین وزن را روی ورودی T (degC) نمی گذارد. این یکی از خطرات اولیه سازی تصادفی است.

متراکم

قبل از استفاده از مدل‌هایی که در واقع بر روی چندین مرحله زمانی عمل می‌کنند، ارزش بررسی عملکرد مدل‌های گام ورودی عمیق‌تر، قوی‌تر و تک ورودی را دارد.

در اینجا مدلی شبیه به مدل linear است، با این تفاوت که چند لایه Dense بین ورودی و خروجی قرار می‌دهد:

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=1)
])

history = compile_and_fit(dense, single_step_window)

val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666
Epoch 2/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610
Epoch 3/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618
Epoch 4/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582
Epoch 5/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581
Epoch 6/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579
Epoch 7/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580
439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580

متراکم چند مرحله ای

یک مدل تک مرحله ای هیچ زمینه ای برای مقادیر جاری ورودی های خود ندارد. نمی تواند ببیند که چگونه ویژگی های ورودی در طول زمان تغییر می کنند. برای رفع این مشکل، مدل نیاز به دسترسی به چندین مرحله زمانی هنگام پیش‌بینی دارد:

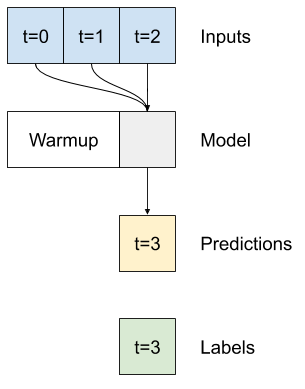
مدل های baseline ، linear و dense هر مرحله زمانی به طور مستقل انجام می شود. در اینجا مدل چندین مرحله زمانی را به عنوان ورودی برای تولید یک خروجی انجام می دهد.

یک WindowGenerator ایجاد کنید که دسته‌ای از ورودی‌های سه ساعته و برچسب‌های یک ساعته تولید می‌کند:

توجه داشته باشید که پارامتر shift Window نسبت به انتهای دو پنجره است.

CONV_WIDTH = 3
conv_window = WindowGenerator(
    input_width=CONV_WIDTH,
    label_width=1,
    shift=1,
    label_columns=['T (degC)'])

conv_window

Total window size: 4
Input indices: [0 1 2]
Label indices: [3]
Label column name(s): ['T (degC)']

conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")

Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')

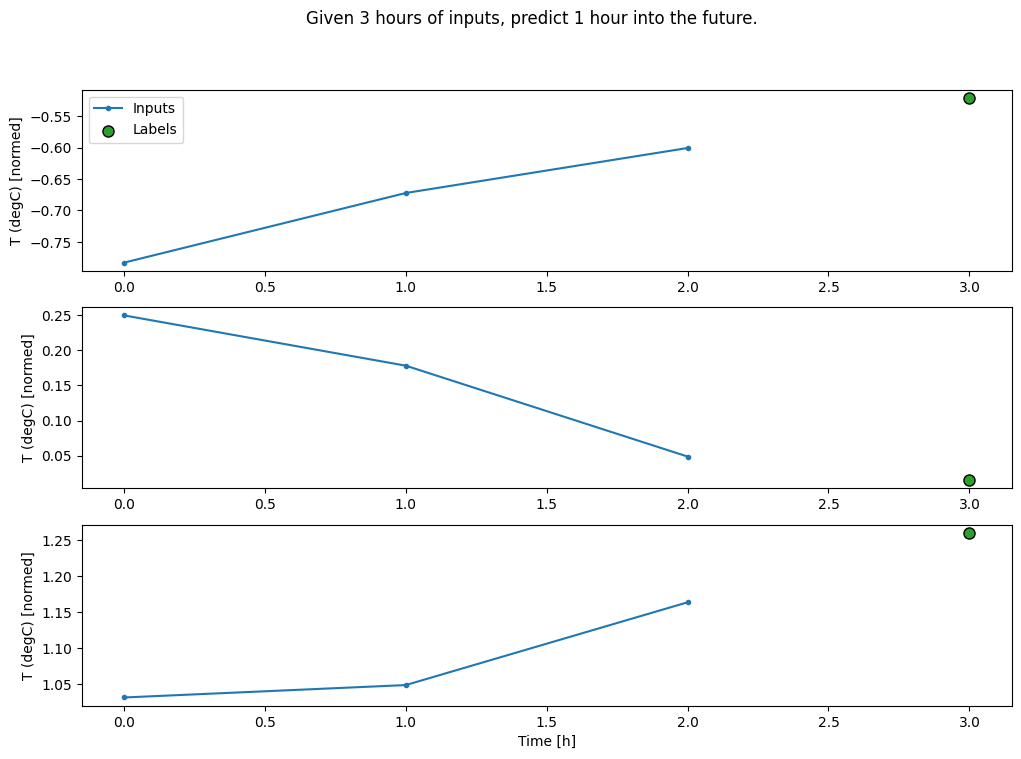
می‌توانید با افزودن یک tf.keras.layers.Flatten به عنوان اولین لایه مدل، یک مدل dense را روی یک پنجره چند مرحله‌ای ورودی آموزش دهید:

multi_step_dense = tf.keras.Sequential([
    # Shape: (time, features) => (time*features)
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
    # Add back the time dimension.
    # Shape: (outputs) => (1, outputs)
    tf.keras.layers.Reshape([1, -1]),
])

print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)

Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

history = compile_and_fit(multi_step_dense, conv_window)

IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609

conv_window.plot(multi_step_dense)

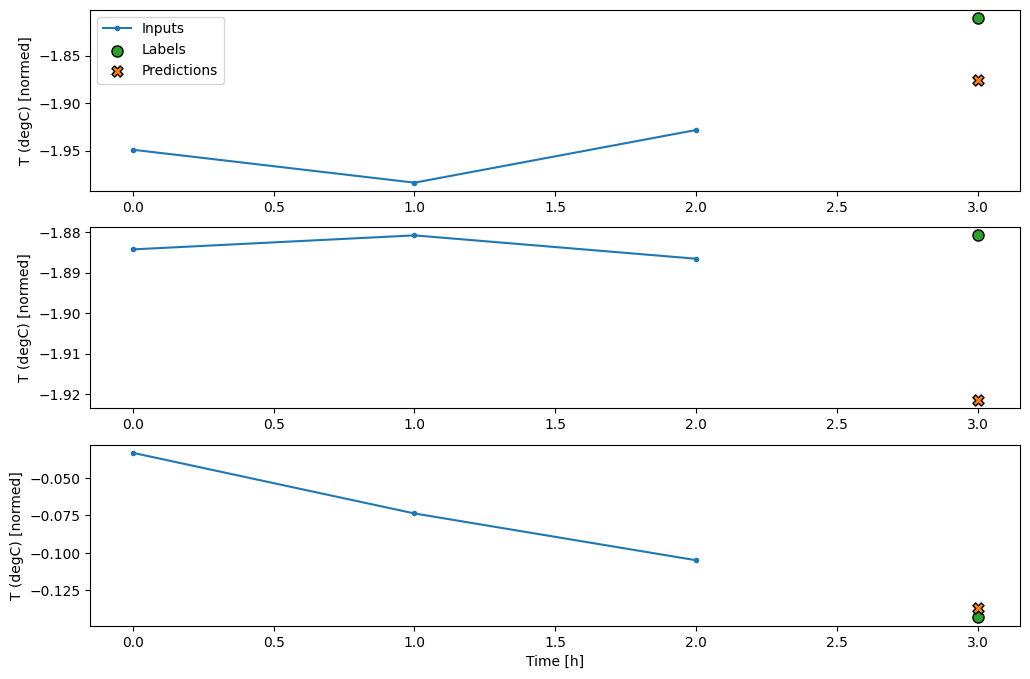
جنبه منفی اصلی این رویکرد این است که مدل به دست آمده را فقط می توان روی پنجره های ورودی دقیقاً به این شکل اجرا کرد.

print('Input shape:', wide_window.example[0].shape)
try:
  print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
  print(f'\n{type(e).__name__}:{e}')

Input shape: (32, 24, 19)

ValueError:Exception encountered when calling layer "sequential_2" (type Sequential).

Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456)

Call arguments received:
  • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32)
  • training=None
  • mask=None

مدل های کانولوشن در بخش بعدی این مشکل را برطرف می کنند.

شبکه عصبی پیچیدگی

یک لایه کانولوشن ( tf.keras.layers.Conv1D ) نیز چندین مرحله زمانی را به عنوان ورودی برای هر پیش بینی انجام می دهد.

در زیر همان مدل multi_step_dense است که با کانولوشن دوباره نوشته شده است.

به تغییرات توجه کنید:

• tf.keras.layers.Flatten و اولین tf.keras.layers.Dense با tf.keras.layers.Conv1D جایگزین می شوند.
• tf.keras.layers.Reshape دیگر ضروری نیست زیرا کانولوشن محور زمان را در خروجی خود نگه می دارد.

conv_model = tf.keras.Sequential([
    tf.keras.layers.Conv1D(filters=32,
                           kernel_size=(CONV_WIDTH,),
                           activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
])

آن را روی یک دسته نمونه اجرا کنید تا بررسی کنید که مدل خروجی هایی با شکل مورد انتظار تولید می کند:

print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)

Conv model on `conv_window`
Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

آن را در conv_window آموزش و ارزیابی کنید و باید عملکردی مشابه مدل multi_step_dense .

history = compile_and_fit(conv_model, conv_window)

IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)

438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568

تفاوت بین این conv_model و مدل multi_step_dense این است که conv_model را می توان بر روی ورودی های با هر طولی اجرا کرد. لایه کانولوشن به یک پنجره کشویی از ورودی ها اعمال می شود:

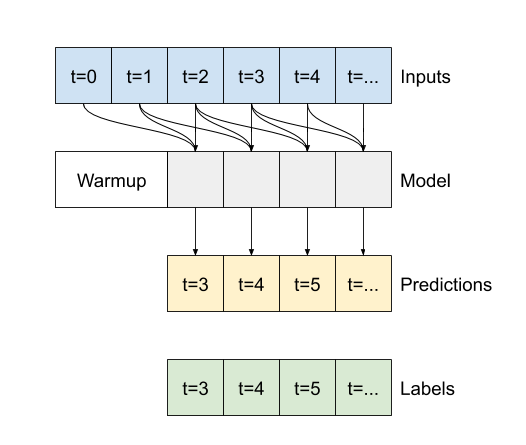
اگر آن را روی ورودی گسترده تر اجرا کنید، خروجی وسیع تری تولید می کند:

print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)

Wide window
Input shape: (32, 24, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 22, 1)

توجه داشته باشید که خروجی کوتاهتر از ورودی است. برای اینکه آموزش یا ترسیم کار انجام شود، به برچسب‌ها و پیش‌بینی نیاز دارید که طول یکسانی داشته باشند. بنابراین یک WindowGenerator تا پنجره های عریض با چند مرحله زمانی ورودی اضافی تولید کند تا طول برچسب و پیش بینی مطابقت داشته باشند:

LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
    input_width=INPUT_WIDTH,
    label_width=LABEL_WIDTH,
    shift=1,
    label_columns=['T (degC)'])

wide_conv_window

Total window size: 27
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25]
Label indices: [ 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26]
Label column name(s): ['T (degC)']

print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)

Wide conv window
Input shape: (32, 26, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 24, 1)

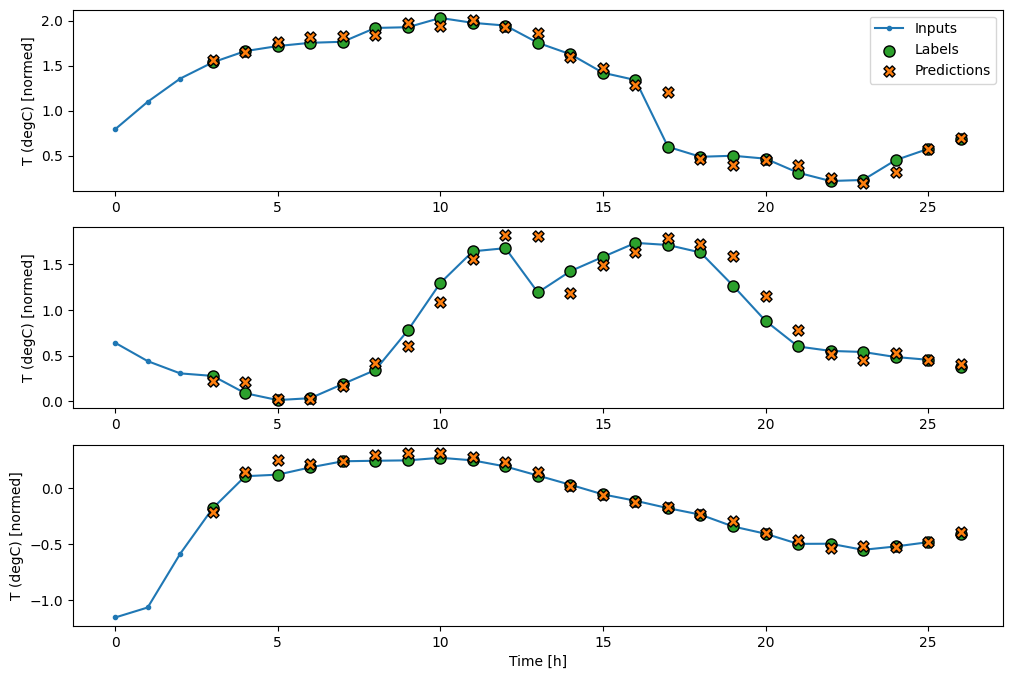
اکنون می‌توانید پیش‌بینی‌های مدل را در یک پنجره وسیع‌تر رسم کنید. به 3 مرحله زمانی ورودی قبل از اولین پیش بینی توجه کنید. هر پیش‌بینی در اینجا بر اساس 3 مرحله زمانی قبلی است:

wide_conv_window.plot(conv_model)

شبکه عصبی مکرر

شبکه عصبی بازگشتی (RNN) نوعی شبکه عصبی است که برای داده های سری زمانی مناسب است. RNN ها یک سری زمانی را گام به گام پردازش می کنند و یک حالت داخلی را از مرحله زمانی به مرحله دیگر حفظ می کنند.

می‌توانید در نسل متن با آموزش RNN و شبکه‌های عصبی بازگشتی (RNN) با راهنمای Keras اطلاعات بیشتری کسب کنید.

در این آموزش، از یک لایه RNN به نام حافظه کوتاه مدت طولانی ( tf.keras.layers.LSTM ) استفاده خواهید کرد.

یک آرگومان سازنده مهم برای تمام لایه‌های Keras RNN، مانند tf.keras.layers.LSTM ، آرگومان return_sequences است. این تنظیم می تواند لایه را به یکی از دو روش پیکربندی کند:

1. اگر False ، پیش‌فرض باشد، لایه تنها خروجی مرحله زمانی نهایی را برمی‌گرداند و به مدل زمان می‌دهد تا قبل از انجام یک پیش‌بینی، حالت داخلی خود را گرم کند:

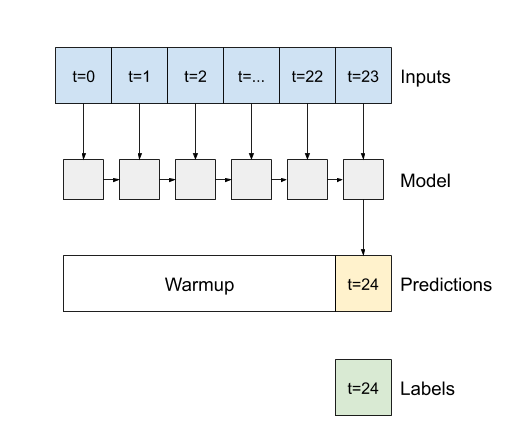
1. اگر True باشد، لایه برای هر ورودی یک خروجی برمی‌گرداند. این برای:
   • انباشتن لایه های RNN.
   • آموزش یک مدل در چند مرحله زمانی به طور همزمان.

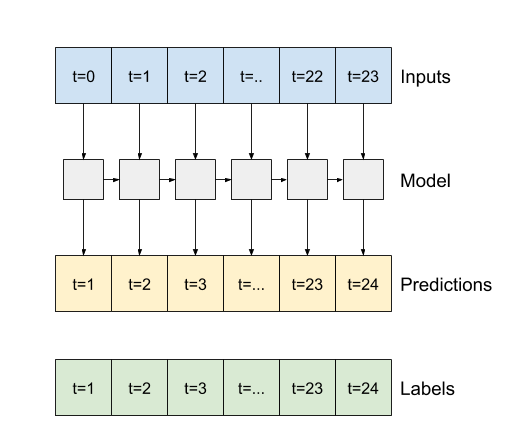
lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=1)
])

با return_sequences=True ، مدل را می توان بر روی 24 ساعت داده در یک زمان آموزش داد.

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509

wide_window.plot(lstm_model)

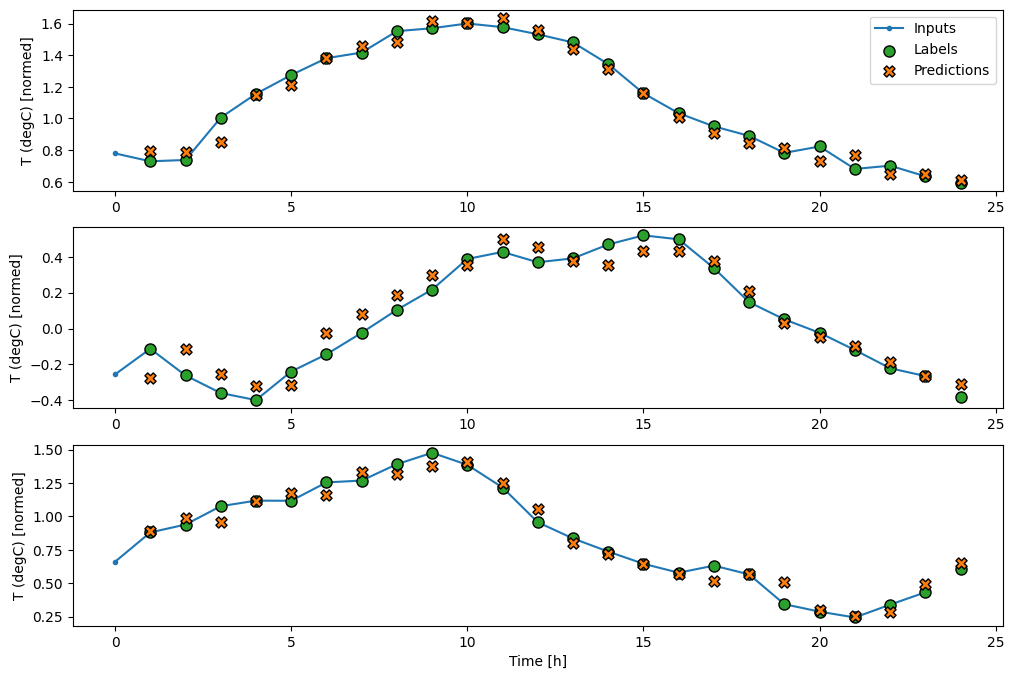
کارایی

با این مجموعه داده معمولاً هر یک از مدل‌ها کمی بهتر از مدل قبلی عمل می‌کنند:

x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
_ = plt.legend()

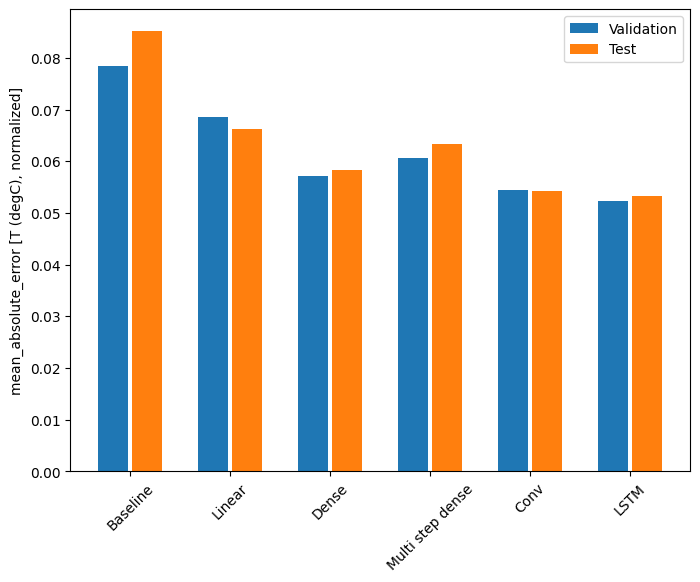
for name, value in performance.items():
  print(f'{name:12s}: {value[1]:0.4f}')

Baseline    : 0.0852
Linear      : 0.0666
Dense       : 0.0573
Multi step dense: 0.0586
Conv        : 0.0577
LSTM        : 0.0518

مدل های چند خروجی

همه مدل‌ها تا کنون یک ویژگی خروجی واحد، T (degC) را برای یک مرحله زمانی پیش‌بینی کرده‌اند.

همه این مدل‌ها را می‌توان برای پیش‌بینی ویژگی‌های متعدد تنها با تغییر تعداد واحدها در لایه خروجی و تنظیم پنجره‌های آموزشی برای گنجاندن همه ویژگی‌ها در labels ( example_labels ) تبدیل کرد.

single_step_window = WindowGenerator(
    # `WindowGenerator` returns all features as labels if you 
    # don't set the `label_columns` argument.
    input_width=1, label_width=1, shift=1)

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

for example_inputs, example_labels in wide_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 24, 19)
Labels shape (batch, time, features): (32, 24, 19)

در بالا توجه داشته باشید که محور features برچسب‌ها به جای 1 ، اکنون همان عمق ورودی‌ها را دارد.

خط پایه

در اینجا می توان از همان مدل پایه ( Baseline ) استفاده کرد، اما این بار به جای انتخاب یک label_index خاص، همه ویژگی ها را تکرار می کند:

baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589

متراکم

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(dense, single_step_window)

IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302

RNN

%%time
wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)

print()

438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205

CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s
Wall time: 2min 8s

پیشرفته: اتصالات باقیمانده

مدل Baseline قبلی از این واقعیت استفاده کرد که توالی از مرحله زمانی به مرحله زمانی به شدت تغییر نمی کند. هر مدلی که تا کنون در این آموزش آموزش داده شده است، به طور تصادفی مقداردهی اولیه شده است، و سپس باید یاد می گیرد که خروجی یک تغییر کوچک نسبت به مرحله زمانی قبلی است.

در حالی که می توانید با مقداردهی اولیه دقیق این مشکل را حل کنید، ساختن آن در ساختار مدل ساده تر است.

در تجزیه و تحلیل سری های زمانی معمول است که مدل هایی بسازند که به جای پیش بینی مقدار بعدی، پیش بینی کنند که مقدار در مرحله زمانی بعدی چگونه تغییر می کند. به طور مشابه، شبکه‌های باقیمانده – یا ResNets – در یادگیری عمیق به معماری‌هایی اشاره می‌کنند که هر لایه به نتیجه انباشته مدل اضافه می‌کند.

اینگونه است که شما از این آگاهی که تغییر باید کوچک باشد بهره می برید.

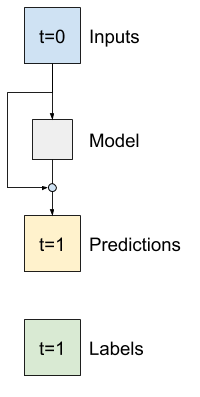
در اصل، این مدل را برای مطابقت با Baseline مقداردهی اولیه می کند. برای این کار به مدل‌ها کمک می‌کند سریع‌تر و با عملکرد کمی بهتر همگرا شوند.

این رویکرد را می توان در ارتباط با هر مدلی که در این آموزش مورد بحث قرار گرفته است استفاده کرد.

در اینجا، برای مدل LSTM اعمال می شود، به استفاده از tf.initializers.zeros توجه داشته باشید تا اطمینان حاصل کنید که تغییرات اولیه پیش بینی شده اندک هستند و اتصال باقی مانده را تحت تأثیر قرار نمی دهند. در اینجا هیچ نگرانی برای شکستن تقارن برای گرادیان وجود ندارد، زیرا zeros فقط در آخرین لایه استفاده می شوند.

class ResidualWrapper(tf.keras.Model):
  def __init__(self, model):
    super().__init__()
    self.model = model

  def call(self, inputs, *args, **kwargs):
    delta = self.model(inputs, *args, **kwargs)

    # The prediction for each time step is the input
    # from the previous time step plus the delta
    # calculated by the model.
    return inputs + delta

%%time
residual_lstm = ResidualWrapper(
    tf.keras.Sequential([
    tf.keras.layers.LSTM(32, return_sequences=True),
    tf.keras.layers.Dense(
        num_features,
        # The predicted deltas should start small.
        # Therefore, initialize the output layer with zeros.
        kernel_initializer=tf.initializers.zeros())
]))

history = compile_and_fit(residual_lstm, wide_window)

IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()

438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179

CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s
Wall time: 43.1 s

کارایی

در اینجا عملکرد کلی این مدل های چند خروجی آورده شده است.

x = np.arange(len(performance))
width = 0.3

metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()

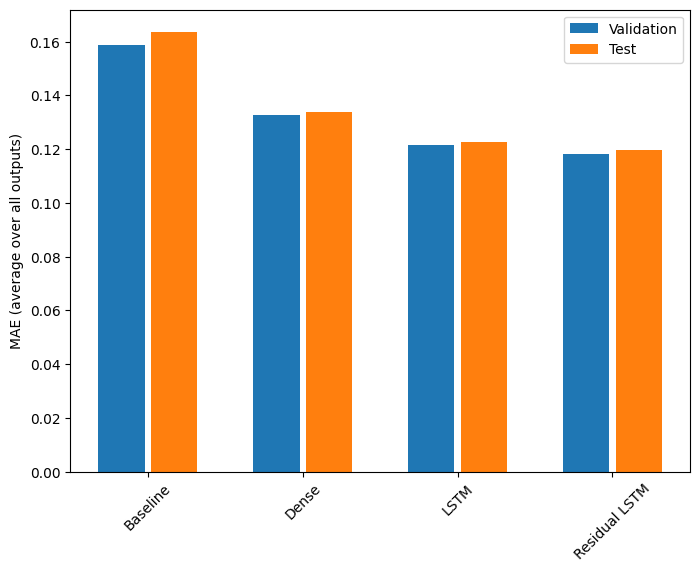
for name, value in performance.items():
  print(f'{name:15s}: {value[1]:0.4f}')

Baseline       : 0.1638
Dense          : 0.1311
LSTM           : 0.1214
Residual LSTM  : 0.1194

عملکردهای فوق در تمام خروجی های مدل به طور میانگین محاسبه می شوند.

مدل های چند مرحله ای

هر دو مدل تک‌خروجی و چند خروجی در بخش‌های قبلی، پیش‌بینی‌های تک‌خروجی را، یک ساعت بعد، انجام دادند.

این بخش به چگونگی گسترش این مدل‌ها برای پیش‌بینی چند مرحله زمانی می‌پردازد .

در یک پیش‌بینی چند مرحله‌ای، مدل باید بیاموزد که محدوده‌ای از مقادیر آینده را پیش‌بینی کند. بنابراین، بر خلاف مدل تک مرحله ای، که در آن تنها یک نقطه آینده پیش بینی می شود، یک مدل چند مرحله ای دنباله ای از مقادیر آینده را پیش بینی می کند.

دو رویکرد تقریبی در این مورد وجود دارد:

1. پیش بینی های تک شات که در آن کل سری زمانی به یکباره پیش بینی می شود.
2. پیش بینی های خودرگرسیون که در آن مدل فقط پیش بینی های تک مرحله ای را انجام می دهد و خروجی آن به عنوان ورودی آن بازخورد داده می شود.

در این بخش همه مدل ها تمام ویژگی ها را در تمام مراحل زمانی خروجی پیش بینی می کنند.

برای مدل چند مرحله ای، داده های آموزشی دوباره از نمونه های ساعتی تشکیل شده است. با این حال، در اینجا، مدل ها یاد می گیرند که 24 ساعت آینده را با توجه به 24 ساعت گذشته پیش بینی کنند.

در اینجا یک شی Window وجود دارد که این برش ها را از مجموعه داده تولید می کند:

OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
                               label_width=OUT_STEPS,
                               shift=OUT_STEPS)

multi_window.plot()
multi_window

Total window size: 48
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47]
Label column name(s): None

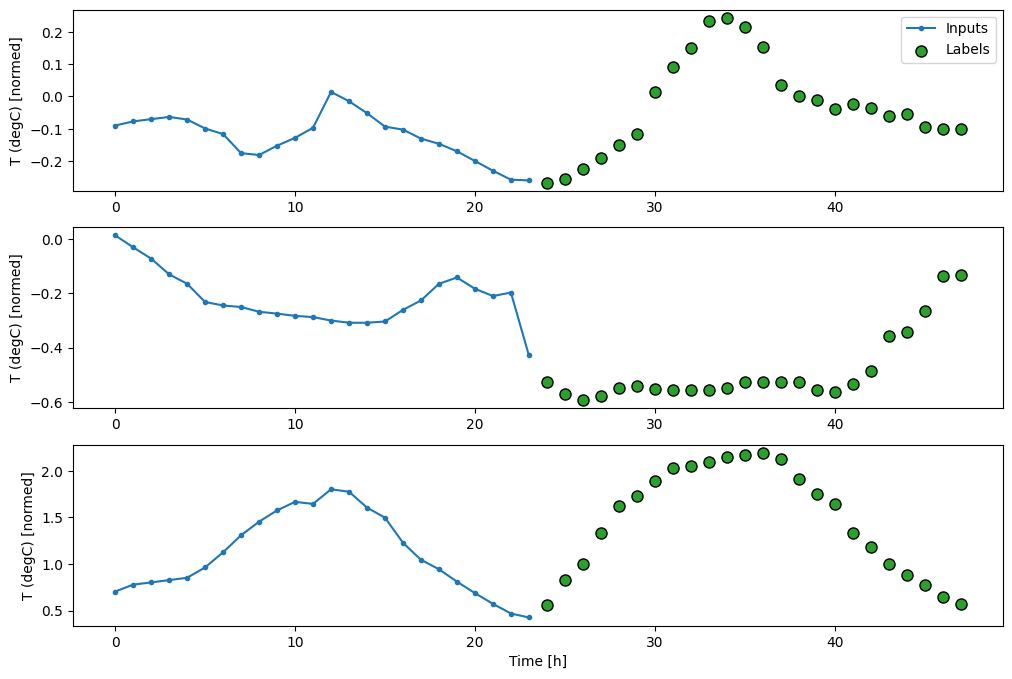
خطوط پایه

یک خط پایه ساده برای این کار تکرار آخرین مرحله زمانی ورودی برای تعداد مورد نیاز مراحل زمانی خروجی است:

class MultiStepLastBaseline(tf.keras.Model):
  def call(self, inputs):
    return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])

last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
                      metrics=[tf.metrics.MeanAbsoluteError()])

multi_val_performance = {}
multi_performance = {}

multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)

437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007

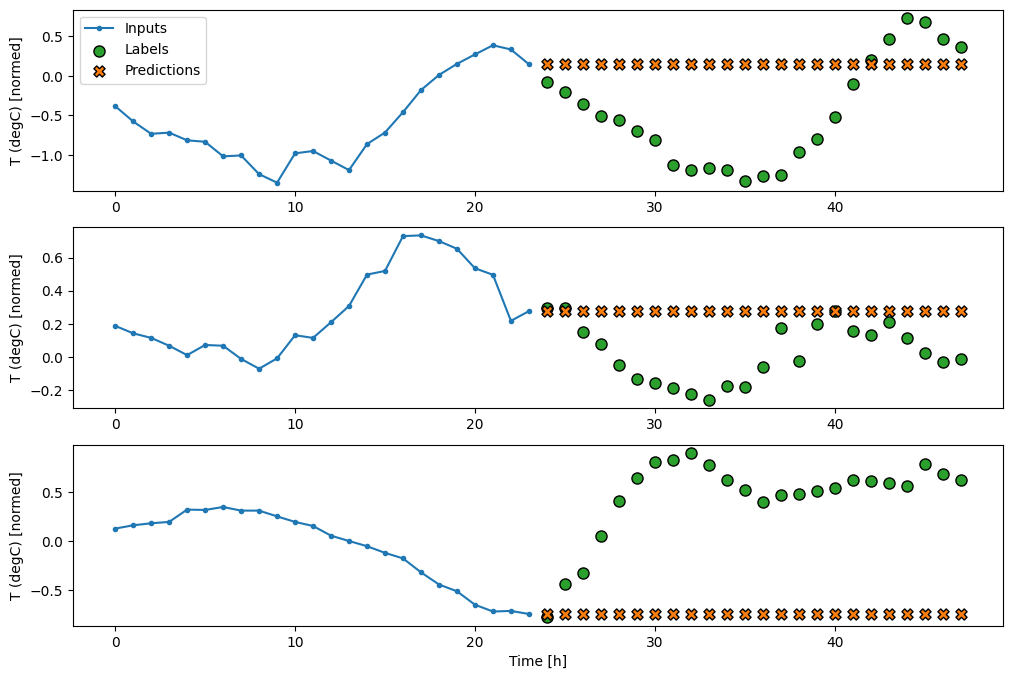
از آنجایی که این کار پیش بینی 24 ساعت آینده است، با توجه به 24 ساعت گذشته، روش ساده دیگر تکرار روز قبل است، با فرض اینکه فردا مشابه باشد:

class RepeatBaseline(tf.keras.Model):
  def call(self, inputs):
    return inputs

repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
                        metrics=[tf.metrics.MeanAbsoluteError()])

multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)

437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959

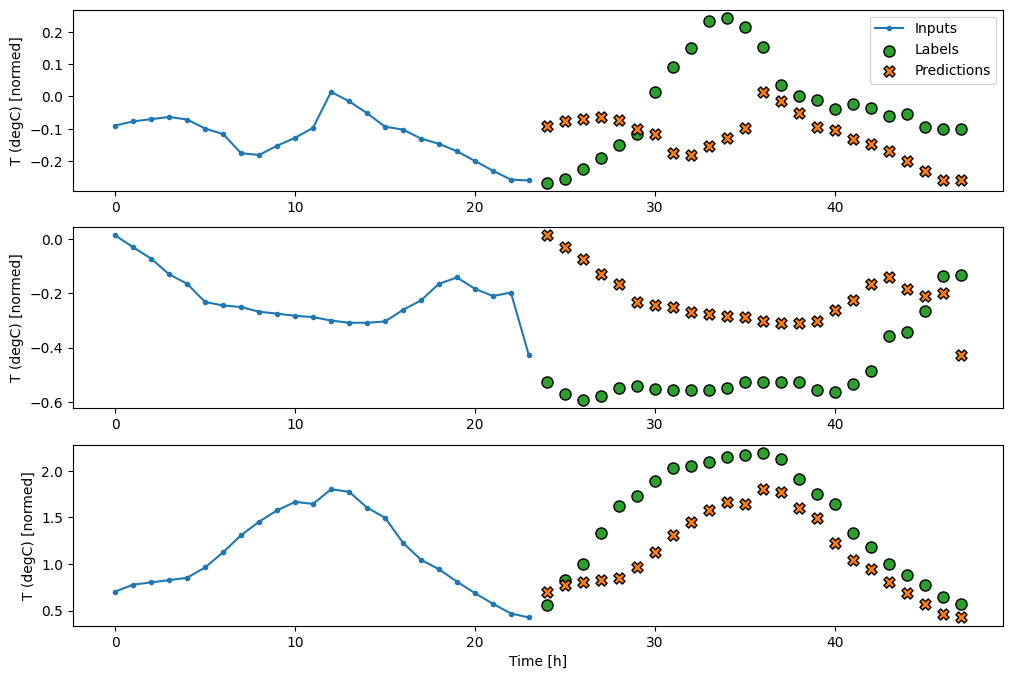
مدل های تک شات

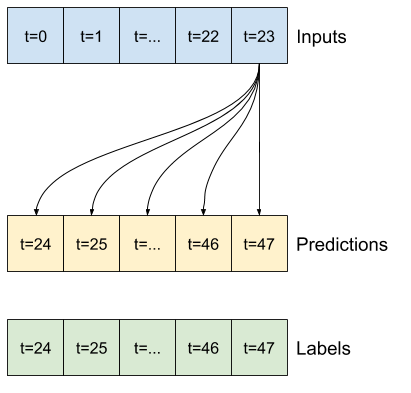
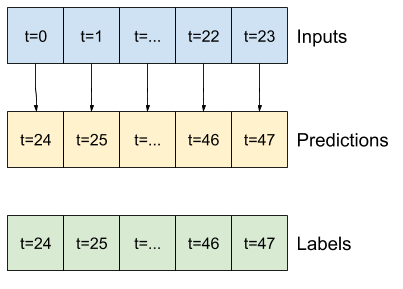
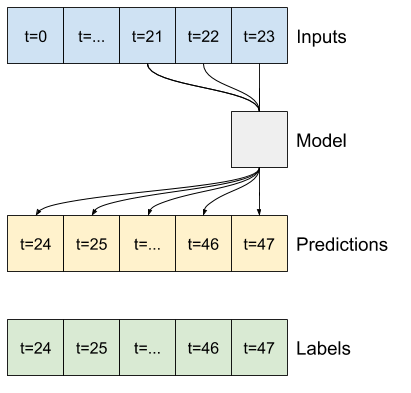
یکی از رویکردهای سطح بالا برای این مشکل استفاده از مدل "تک شات" است که در آن مدل کل توالی را در یک مرحله پیش بینی می کند.

این را می توان به طور موثر به عنوان tf.keras.layers.Dense با OUT_STEPS*features واحدهای خروجی پیاده سازی کرد. مدل فقط باید آن خروجی را به مقدار مورد نیاز تغییر شکل دهد (OUTPUT_STEPS, features) .

خطی

یک مدل خطی ساده مبتنی بر آخرین مرحله زمانی ورودی بهتر از هر یک از خطوط پایه است، اما قدرت کمتری دارد. مدل نیاز به پیش‌بینی OUTPUT_STEPS گام‌های زمانی دارد، از یک مرحله زمانی ورودی تکی با یک طرح خطی. این فقط می تواند یک برش کم بعدی از رفتار را به تصویر بکشد که احتمالاً عمدتاً بر اساس زمان روز و زمان سال است.

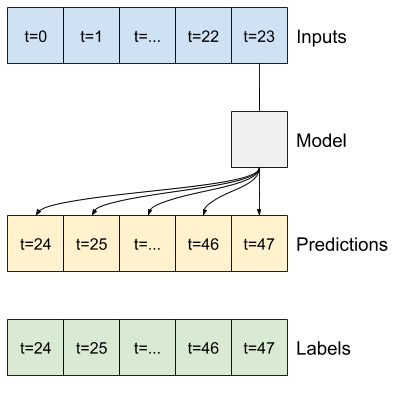
multi_linear_model = tf.keras.Sequential([
    # Take the last time-step.
    # Shape [batch, time, features] => [batch, 1, features]
    tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
    # Shape => [batch, 1, out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_linear_model, multi_window)

IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)

437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053

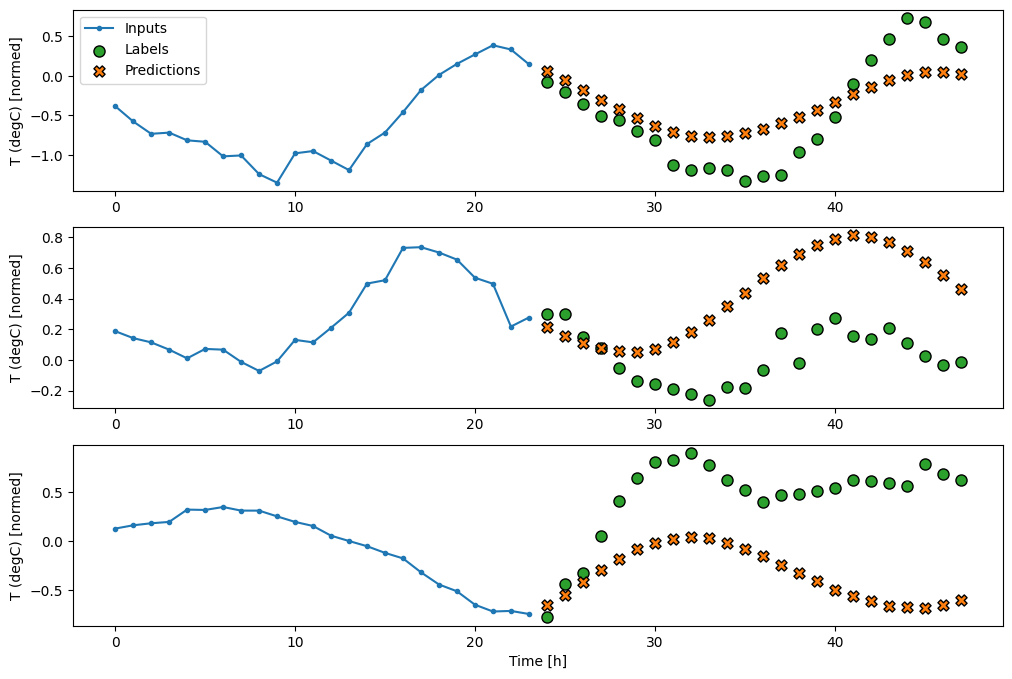
متراکم

افزودن tf.keras.layers.Dense بین ورودی و خروجی به مدل خطی قدرت بیشتری می‌دهد، اما همچنان تنها بر اساس یک مرحله زمانی ورودی است.

multi_dense_model = tf.keras.Sequential([
    # Take the last time step.
    # Shape [batch, time, features] => [batch, 1, features]
    tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
    # Shape => [batch, 1, dense_units]
    tf.keras.layers.Dense(512, activation='relu'),
    # Shape => [batch, out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_dense_model, multi_window)

IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)

437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837

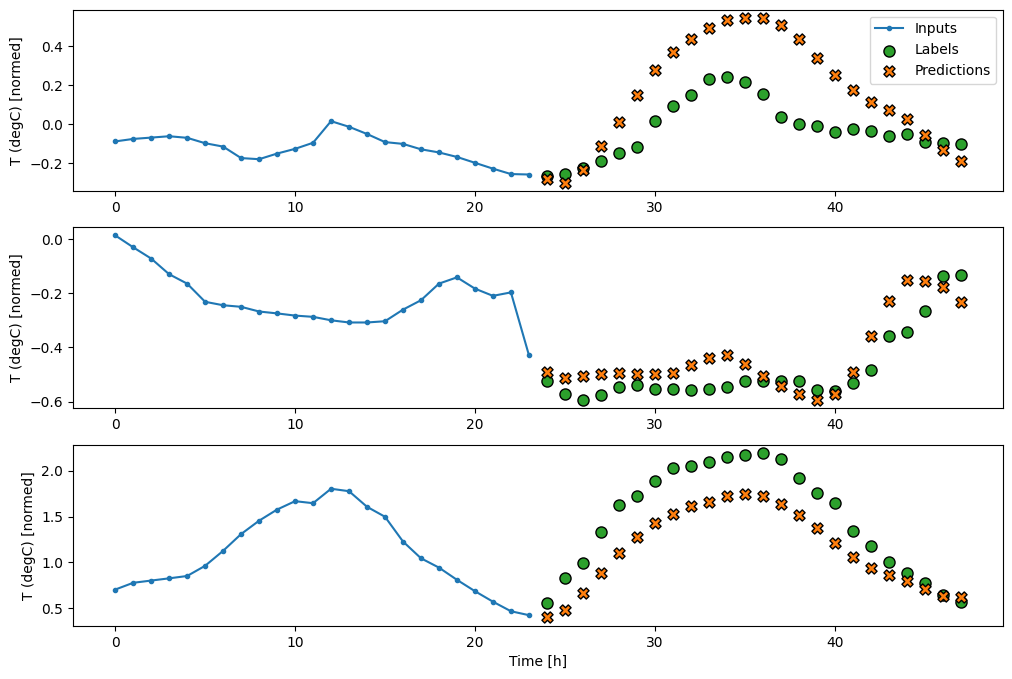
CNN

یک مدل کانولوشنال پیش‌بینی‌هایی را بر اساس یک تاریخچه با عرض ثابت انجام می‌دهد، که ممکن است به عملکرد بهتری نسبت به مدل متراکم منجر شود، زیرا می‌تواند ببیند که چگونه چیزها در طول زمان تغییر می‌کنند:

CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
    # Shape [batch, time, features] => [batch, CONV_WIDTH, features]
    tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
    # Shape => [batch, 1, conv_units]
    tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
    # Shape => [batch, 1,  out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_conv_model, multi_window)

IPython.display.clear_output()

multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
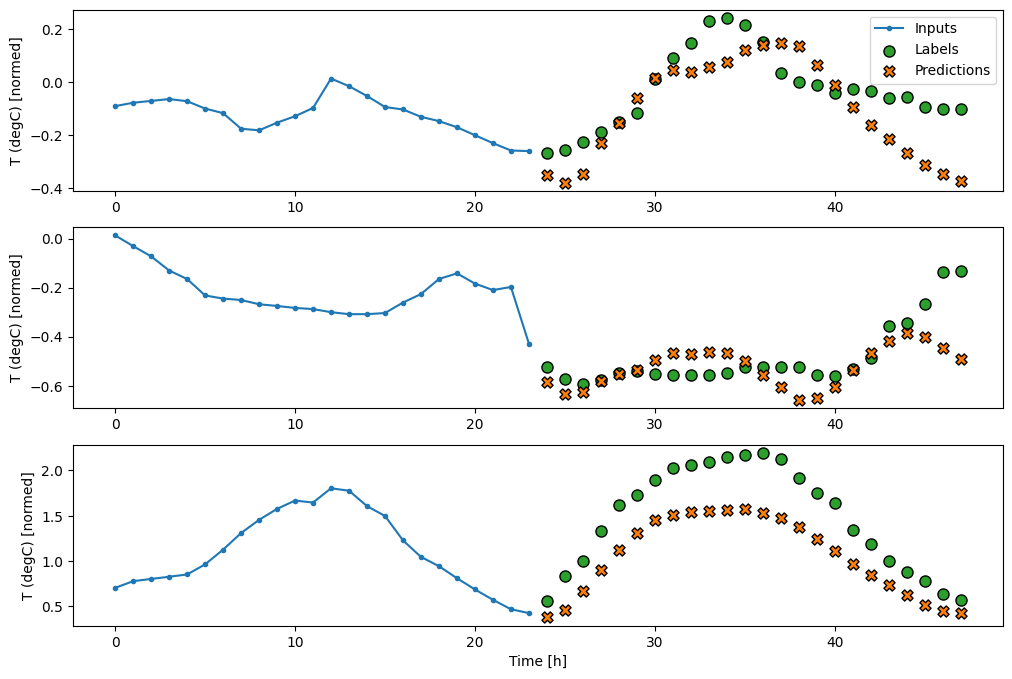
multi_window.plot(multi_conv_model)

437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833

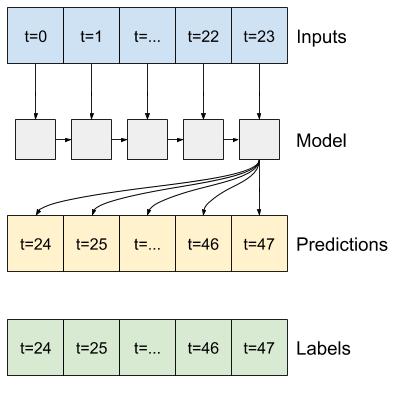
RNN

یک مدل تکرارشونده می‌تواند یاد بگیرد که از تاریخچه طولانی ورودی‌ها استفاده کند، اگر با پیش‌بینی‌هایی که مدل انجام می‌دهد مرتبط باشد. در اینجا مدل حالت داخلی را به مدت 24 ساعت جمع می کند، قبل از اینکه یک پیش بینی برای 24 ساعت آینده انجام دهد.

در این قالب تک شات، LSTM فقط نیاز به تولید خروجی در آخرین مرحله زمانی دارد، بنابراین return_sequences=False را در tf.keras.layers.LSTM کنید.

multi_lstm_model = tf.keras.Sequential([
    # Shape [batch, time, features] => [batch, lstm_units].
    # Adding more `lstm_units` just overfits more quickly.
    tf.keras.layers.LSTM(32, return_sequences=False),
    # Shape => [batch, out_steps*features].
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features].
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_lstm_model, multi_window)

IPython.display.clear_output()

multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)

437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863

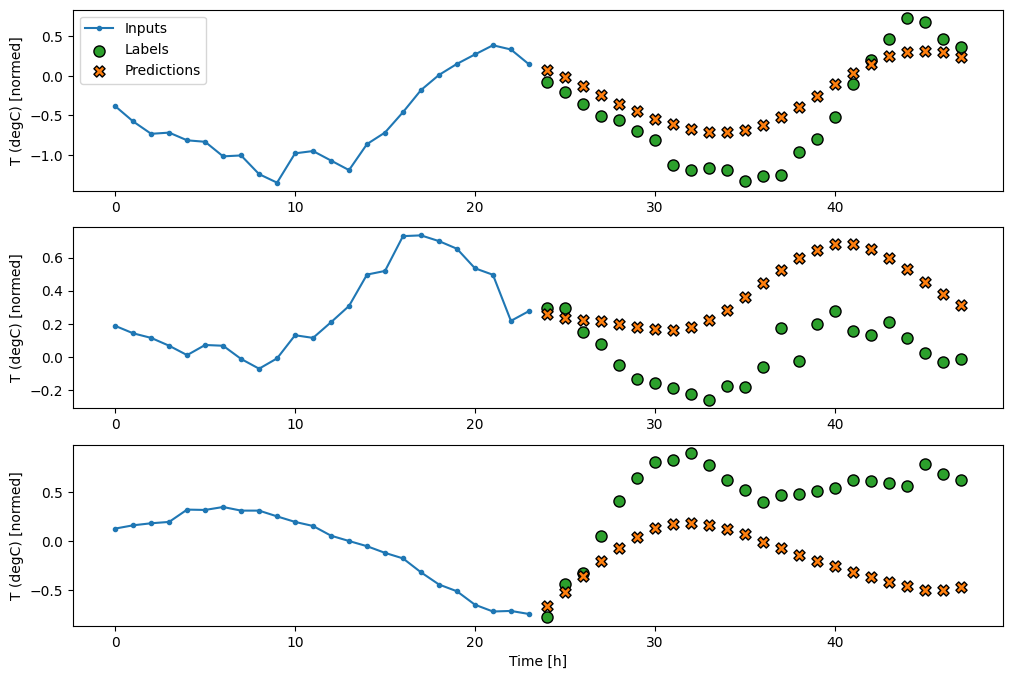
پیشرفته: مدل خودرگرسیون

مدل های بالا همگی کل توالی خروجی را در یک مرحله پیش بینی می کنند.

در برخی موارد ممکن است برای مدل مفید باشد که این پیش‌بینی را به مراحل زمانی جداگانه تجزیه کند. سپس، خروجی هر مدل می‌تواند در هر مرحله به خودش بازگردانده شود و پیش‌بینی‌ها را می‌توان مشروط به مرحله قبلی کرد، مانند توالی‌های کلاسیک تولیدکننده با شبکه‌های عصبی مکرر .

یکی از مزیت های واضح این سبک مدل این است که می توان آن را برای تولید خروجی با طول های متفاوت تنظیم کرد.

می‌توانید هر یک از مدل‌های چند خروجی تک مرحله‌ای را که در نیمه اول این آموزش آموزش داده شده‌اند انتخاب کنید و در یک حلقه بازخورد خودکار رگرسیون اجرا کنید، اما در اینجا روی ساختن مدلی تمرکز خواهید کرد که به صراحت برای انجام این کار آموزش دیده است.

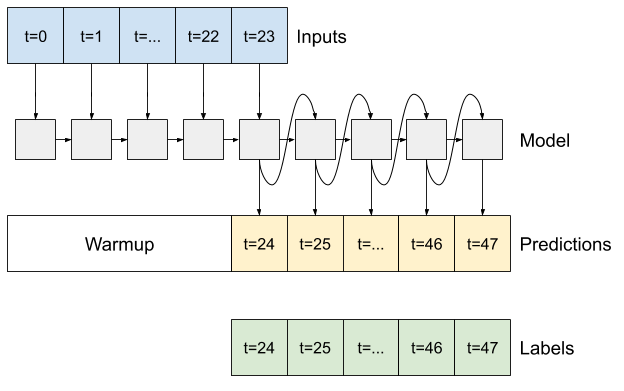
RNN

این آموزش فقط یک مدل RNN اتورگرسیو می سازد، اما این الگو را می توان برای هر مدلی که برای خروجی یک مرحله زمانی طراحی شده است، اعمال کرد.

این مدل همان شکل اولیه مدل های LSTM تک مرحله ای قبلی را خواهد داشت: یک لایه tf.keras.layers.LSTM و به دنبال آن یک لایه tf.keras.layers.Dense که خروجی های لایه LSTM را به پیش بینی های مدل تبدیل می کند.

یک tf.keras.layers.LSTM یک سلول tf.keras.layers.LSTMC است که در سطح بالاتر tf.keras.layers.LSTMCell پیچیده شده است که نتایج حالت و ترتیب را برای شما مدیریت می کند (شبکه های عصبی tf.keras.layers.RNN (RNN) را با Keras بررسی کنید. راهنمای جزئیات).

در این حالت، مدل باید ورودی‌های هر مرحله را به صورت دستی مدیریت کند، بنابراین از tf.keras.layers.LSTMCell مستقیماً برای سطح پایین‌تر و رابط مرحله زمانی تک استفاده می‌کند.

class FeedBack(tf.keras.Model):
  def __init__(self, units, out_steps):
    super().__init__()
    self.out_steps = out_steps
    self.units = units
    self.lstm_cell = tf.keras.layers.LSTMCell(units)
    # Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
    self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
    self.dense = tf.keras.layers.Dense(num_features)

feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)

اولین روشی که این مدل به آن نیاز دارد یک روش warmup کردن برای مقداردهی اولیه حالت داخلی آن بر اساس ورودی ها است. پس از آموزش، این حالت بخش های مربوطه از تاریخچه ورودی را ضبط می کند. این معادل مدل LSTM تک مرحله ای قبلی است:

def warmup(self, inputs):
  # inputs.shape => (batch, time, features)
  # x.shape => (batch, lstm_units)
  x, *state = self.lstm_rnn(inputs)

  # predictions.shape => (batch, features)
  prediction = self.dense(x)
  return prediction, state

FeedBack.warmup = warmup

این روش یک پیش‌بینی مرحله زمانی و وضعیت داخلی LSTM را برمی‌گرداند:

prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape

TensorShape([32, 19])

با وضعیت RNN و یک پیش‌بینی اولیه، اکنون می‌توانید به تکرار مدل ادامه دهید که پیش‌بینی‌ها را در هر مرحله به عقب به عنوان ورودی تغذیه می‌کند.

ساده ترین روش برای جمع آوری پیش بینی های خروجی استفاده از یک لیست پایتون و یک tf.stack بعد از حلقه است.

def call(self, inputs, training=None):
  # Use a TensorArray to capture dynamically unrolled outputs.
  predictions = []
  # Initialize the LSTM state.
  prediction, state = self.warmup(inputs)

  # Insert the first prediction.
  predictions.append(prediction)

  # Run the rest of the prediction steps.
  for n in range(1, self.out_steps):
    # Use the last prediction as input.
    x = prediction
    # Execute one lstm step.
    x, state = self.lstm_cell(x, states=state,
                              training=training)
    # Convert the lstm output to a prediction.
    prediction = self.dense(x)
    # Add the prediction to the output.
    predictions.append(prediction)

  # predictions.shape => (time, batch, features)
  predictions = tf.stack(predictions)
  # predictions.shape => (batch, time, features)
  predictions = tf.transpose(predictions, [1, 0, 2])
  return predictions

FeedBack.call = call

این مدل را روی ورودی های نمونه آزمایش کنید:

print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)

Output shape (batch, time, features):  (32, 24, 19)

حالا مدل را آموزش دهید:

history = compile_and_fit(feedback_model, multi_window)

IPython.display.clear_output()

multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)

437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011

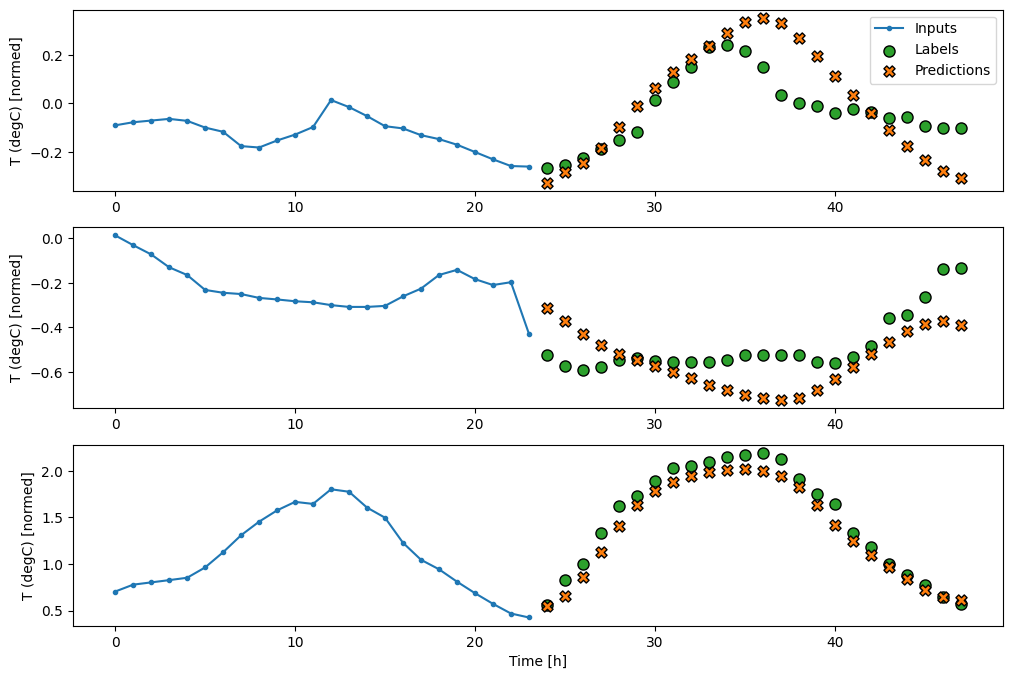
کارایی

به وضوح بازدهی کاهشی به عنوان تابعی از پیچیدگی مدل در این مشکل وجود دارد:

x = np.arange(len(multi_performance))
width = 0.3

metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]

plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
           rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()

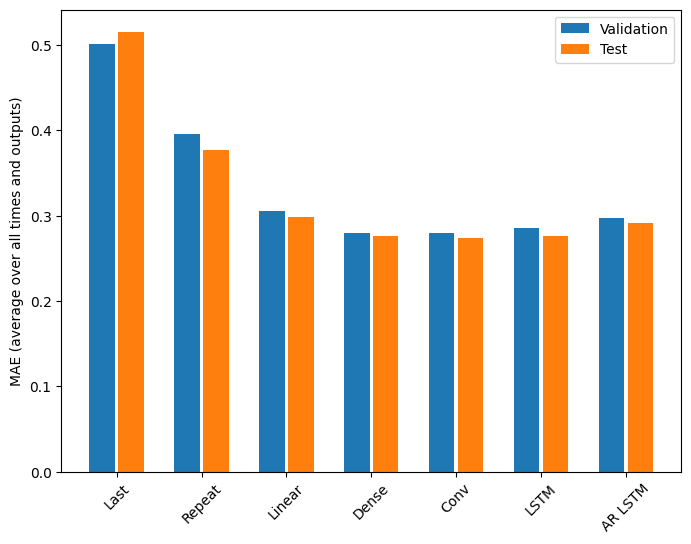
معیارهای مدل های چند خروجی در نیمه اول این آموزش میانگین عملکرد را در همه ویژگی های خروجی نشان می دهد. این عملکردها مشابه هستند، اما در طول مراحل زمانی خروجی نیز میانگین می‌شوند.

for name, value in multi_performance.items():
  print(f'{name:8s}: {value[1]:0.4f}')

Last    : 0.5157
Repeat  : 0.3774
Linear  : 0.2977
Dense   : 0.2781
Conv    : 0.2796
LSTM    : 0.2767
AR LSTM : 0.2901

دستاوردهای به دست آمده از مدل متراکم به مدل های کانولوشنال و بازگشتی تنها چند درصد (در صورت وجود) است و مدل خودرگرسیون به وضوح بدتر عمل کرد. بنابراین این رویکردهای پیچیده‌تر ممکن است ارزشی برای حل این مشکل نداشته باشند، اما راهی برای دانستن بدون تلاش وجود نداشت و این مدل‌ها می‌توانند برای مشکل شما مفید باشند.

مراحل بعدی

این آموزش مقدمه ای سریع برای پیش بینی سری های زمانی با استفاده از TensorFlow بود.

برای کسب اطلاعات بیشتر به ادامه مطلب مراجعه کنید:

• فصل 15 یادگیری ماشینی عملی با Scikit-Learn، Keras و TensorFlow ، ویرایش دوم.
• فصل 6 یادگیری عمیق با پایتون .
• درس 8 مقدمه Udacity برای TensorFlow برای یادگیری عمیق ، از جمله دفترچه‌های تمرین .

همچنین، به یاد داشته باشید که می توانید هر مدل سری زمانی کلاسیک را در TensorFlow پیاده سازی کنید - این آموزش فقط بر روی عملکرد داخلی TensorFlow تمرکز دارد.