 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
מדריך זה הוא מבוא לחיזוי סדרות זמן באמצעות TensorFlow. זה בונה כמה סגנונות שונים של מודלים, כולל רשתות עצביות קונבולוציוניות וחוזרות (CNNs ו-RNNs).
זה מכוסה בשני חלקים עיקריים, עם סעיפים משנה:
- תחזית לשלב זמן בודד:
- תכונה בודדת.
- כל התכונות.
- תחזית שלבים מרובים:
- צילום יחיד: בצע את התחזיות בבת אחת.
- אוטורגרסיבי: בצע חיזוי אחד בכל פעם והזן את הפלט בחזרה למודל.
להכין
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
מערך מזג האוויר
הדרכה זו משתמשת במערך נתונים מסדרת זמן של מזג אוויר שתועדה על ידי מכון מקס פלנק לביוגיאוכימיה .
מערך נתונים זה מכיל 14 תכונות שונות כגון טמפרטורת אוויר, לחץ אטמוספרי ולחות. אלה נאספו כל 10 דקות, החל משנת 2003. לצורך יעילות, תשתמש רק בנתונים שנאספו בין 2009 ל-2016. חלק זה של מערך הנתונים הוכן על ידי פרנסואה צ'ולט עבור ספרו Deep Learning with Python .
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
מדריך זה יעסוק רק בתחזיות לפי שעה , אז התחל בדגימת משנה של הנתונים ממרווחים של 10 דקות למרווחים של שעה אחת:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
בואו נסתכל על הנתונים. להלן השורות הראשונות:
df.head()
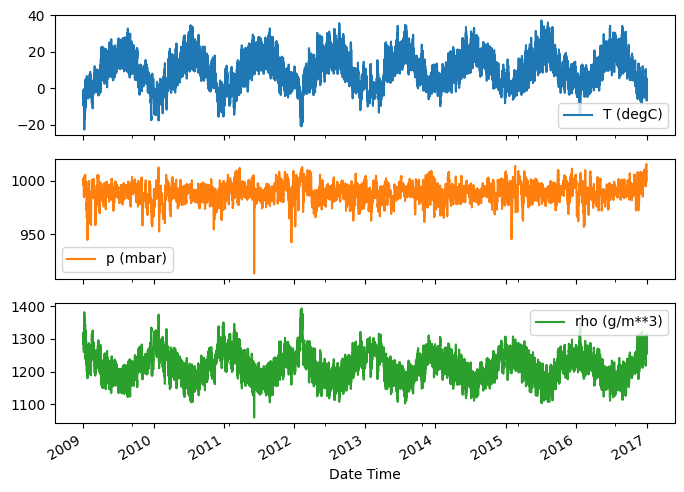
להלן ההתפתחות של כמה תכונות לאורך זמן:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
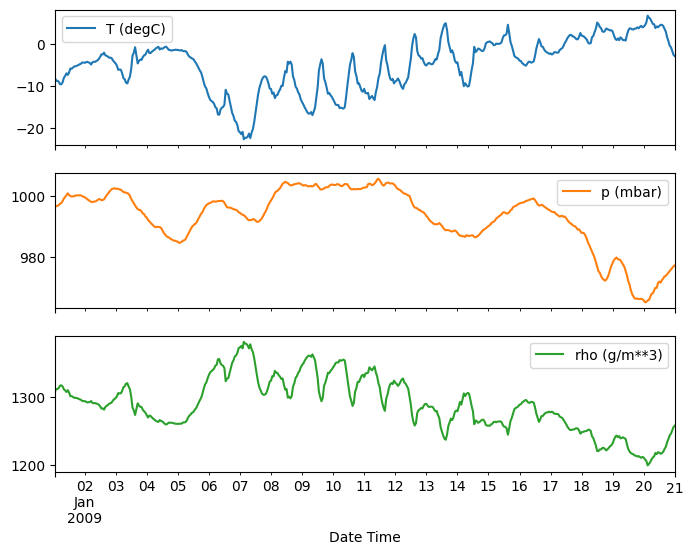
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
לבדוק ולנקות
לאחר מכן, עיין בסטטיסטיקה של מערך הנתונים:
df.describe().transpose()
מהירות הרוח
דבר אחד שצריך לבלוט הוא הערך min של מהירות הרוח ( wv (m/s) ) והערך המקסימלי ( max. wv (m/s) ) . סביר להניח -9999 זה שגוי.
יש עמודת כיוון רוח נפרדת, כך שהמהירות צריכה להיות גדולה מאפס ( >=0 ). החלף אותו באפסים:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
הנדסת תכונות
לפני שצולל לבניית מודל, חשוב להבין את הנתונים שלך ולהיות בטוח שאתה מעביר את המודל בפורמט מתאים.
רוּחַ
העמודה האחרונה של הנתונים, wd (deg) -נותנת את כיוון הרוח ביחידות של מעלות. זוויות אינן מהוות כניסות טובות לדגם: 360° ו-0° צריכות להיות קרובות אחת לשניה ולהתעטף בצורה חלקה. הכיוון לא צריך להיות משנה אם הרוח לא נושבת.
כרגע ההתפלגות של נתוני הרוח נראית כך:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
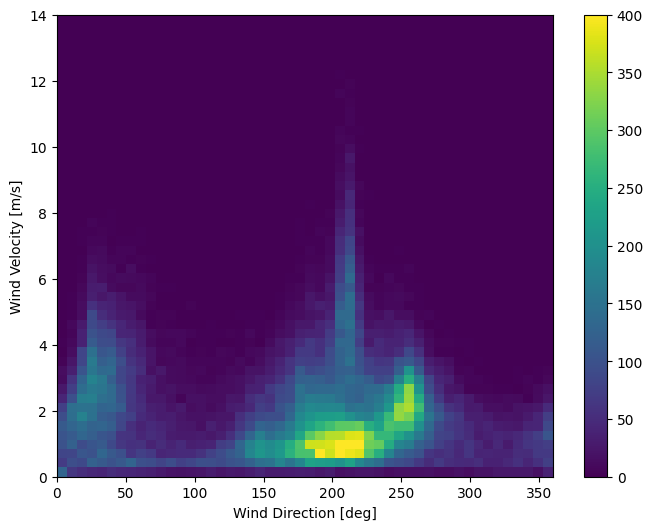
אבל זה יהיה קל יותר למודל לפרש אם תמיר את עמודות כיוון הרוח והמהירות לוקטור רוח:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
ההתפלגות של וקטורי הרוח היא הרבה יותר פשוטה עבור המודל לפרש נכון:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
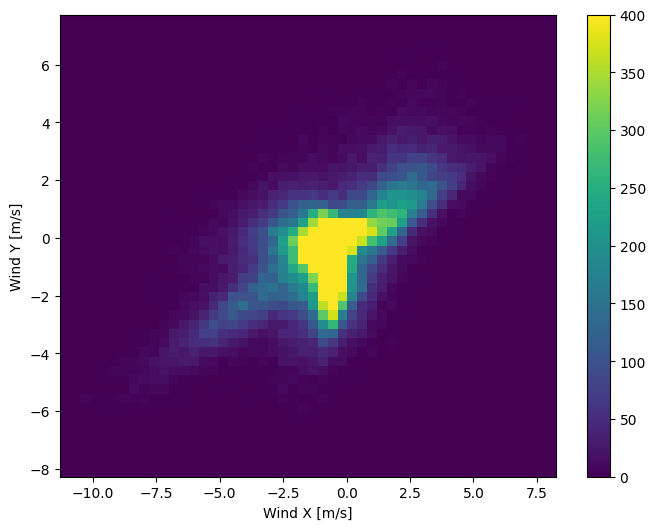
זְמַן
באופן דומה, העמודה Date Time שימושית מאוד, אבל לא בצורת מחרוזת זו. התחל על ידי המרתו לשניות:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
בדומה לכיוון הרוח, הזמן בשניות אינו קלט שימושי בדגם. בהיותם נתוני מזג אוויר, יש להם מחזוריות יומית ושנתית ברורה. ישנן דרכים רבות להתמודד עם מחזוריות.
אתה יכול לקבל אותות שמיש על ידי שימוש בהמרות סינוס וקוסינוס כדי לנקות אותות "שעה ביום" ו"זמן בשנה":
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
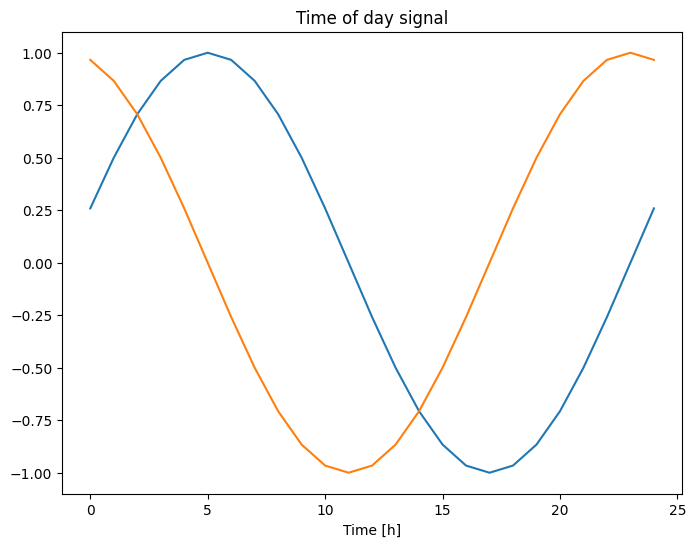
זה נותן לדגם גישה לתכונות התדר החשובות ביותר. במקרה זה ידעת מבעוד מועד אילו תדרים חשובים.
אם אין לך מידע זה, אתה יכול לקבוע אילו תדרים חשובים על ידי חילוץ תכונות עם Fast Fourier Transform . כדי לבדוק את ההנחות, הנה ה- tf.signal.rfft של הטמפרטורה לאורך זמן. שימו לב לשיאים הברורים בתדרים הקרובים ל 1/year ו 1/day :
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')

פצל את הנתונים
אתה תשתמש בחלוקה (70%, 20%, 10%) עבור מערכי ההדרכה, האימות והמבחנים. שימו לב שהנתונים לא עוברים ערבוב אקראי לפני הפיצול. זה משתי סיבות:
- זה מבטיח שקיצוץ הנתונים לחלונות של דגימות עוקבות עדיין אפשרי.
- זה מבטיח שתוצאות האימות/בדיקה יהיו מציאותיות יותר, תוך הערכה על פי הנתונים שנאספו לאחר הכשרת המודל.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
נרמל את הנתונים
חשוב להתאים תכונות לפני אימון רשת עצבית. נורמליזציה היא דרך נפוצה לעשות קנה מידה זה: מפחיתים את הממוצע ומחלקים בסטיית התקן של כל תכונה.
יש לחשב את הממוצע ואת סטיית התקן רק באמצעות נתוני האימון כך שלמודלים אין גישה לערכים בערכות האימות והבדיקות.
אפשר גם לטעון שלמודל לא צריכה להיות גישה לערכים עתידיים במערך האימונים בעת האימון, ושנורמליזציה זו צריכה להיעשות באמצעות ממוצעים נעים. זה לא המוקד של המדריך הזה, וערכות האימות והבדיקות מבטיחות שתקבל מדדים כנים (קצת). אז, למען הפשטות, הדרכה זו משתמשת בממוצע פשוט.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
כעת, הציצו בהפצת התכונות. לחלק מהתכונות יש זנבות ארוכים, אבל אין שגיאות ברורות כמו ערך מהירות הרוח -9999 .
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

חלונות נתונים
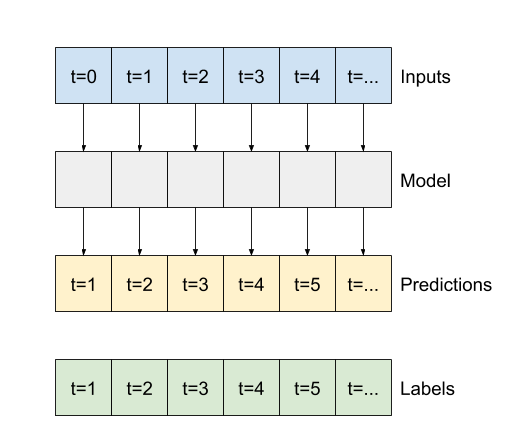
המודלים במדריך זה יבצעו קבוצה של תחזיות על סמך חלון של דגימות עוקבות מהנתונים.
המאפיינים העיקריים של חלונות הקלט הם:
- הרוחב (מספר שלבי הזמן) של חלונות הקלט והתווית.
- קיזוז הזמן ביניהם.
- אילו תכונות משמשות כקלט, תוויות או שניהם.
מדריך זה בונה מגוון דגמים (כולל דגמי ליניארי, DNN, CNN ו-RNN), ומשתמש בשניהם:
- חיזויים של פלט בודד ורב פלט .
- תחזיות של צעדים חד-פעמיים ורב-פעמיים .
סעיף זה מתמקד ביישום חלונות הנתונים כך שניתן לעשות בו שימוש חוזר עבור כל הדגמים הללו.
בהתאם למשימה ולסוג הדגם, ייתכן שתרצה ליצור מגוון חלונות נתונים. הנה כמה דוגמאות:
לדוגמה, כדי לבצע תחזית בודדת 24 שעות לעתיד, בהינתן 24 שעות של היסטוריה, תוכל להגדיר חלון כזה:
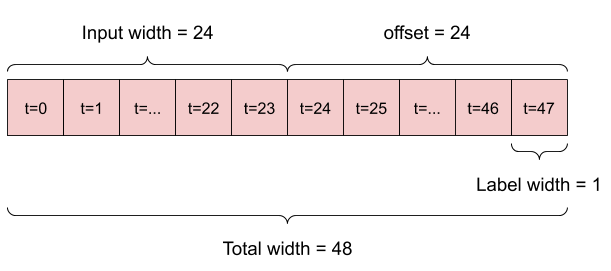
מודל שעושה תחזית שעה אחת לעתיד, בהינתן שש שעות של היסטוריה, יצטרך חלון כזה:

שאר החלק הזה מגדיר מחלקה של WindowGenerator . שיעור זה יכול:
- טפל באינדקסים ובקיזוזים כפי שמוצג בתרשימים למעלה.
- פיצול חלונות של תכונות לזוגות
(features, labels). - תכנן את התוכן של החלונות שהתקבלו.
- הפק ביעילות קבוצות של חלונות אלה מנתוני ההדרכה, ההערכה והבדיקה, באמצעות
tf.data.Datasets.
1. אינדקסים וקיזוזים
התחל ביצירת המחלקה WindowGenerator . שיטת __init__ כוללת את כל ההיגיון הדרוש עבור מדדי הקלט והתוויות.
זה גם לוקח את ההדרכה, ההערכה והבדיקה של DataFrames כקלט. אלה יומרו ל- tf.data.Dataset s של חלונות מאוחר יותר.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
הנה קוד ליצירת 2 החלונות המוצגים בתרשימים בתחילת סעיף זה:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. פיצול
בהינתן רשימה של קלט רצוף, שיטת split_window תמיר אותם לחלון קלט וחלון של תוויות.
הדוגמה של w2 שתגדיר קודם תפוצל כך:
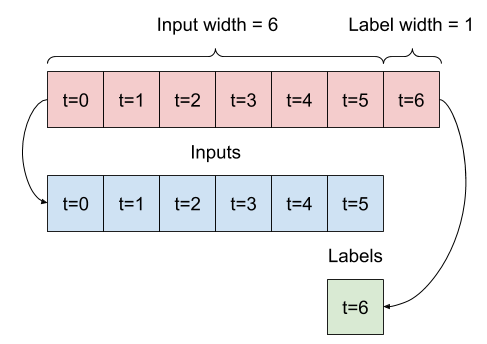
דיאגרמה זו אינה מציגה את ציר features של הנתונים, אך פונקציית split_window זו מטפלת גם ב- label_columns כך שניתן להשתמש בה הן לדוגמאות של פלט יחיד והן לדוגמאות ריבוי פלט.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
נסה את זה:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
בדרך כלל, הנתונים ב-TensorFlow נארזים במערכים שבהם האינדקס החיצוני ביותר הוא על פני דוגמאות (המימד "אצווה"). המדדים האמצעיים הם הממדים של "זמן" או "מרחב" (רוחב, גובה). המדדים הפנימיים ביותר הם התכונות.
הקוד שלמעלה לקח אצווה של שלושה חלונות של 7 פעמים עם 19 תכונות בכל שלב זמן. זה מחלק אותם לקבוצה של כניסות של 6-פעמים של 19 תכונות, ותווית שלב 1 של תכונות. לתווית יש רק תכונה אחת מכיוון שה- WindowGenerator אותחל עם label_columns=['T (degC)'] . בתחילה, מדריך זה יבנה מודלים המנבאים תוויות פלט בודדות.
3. עלילה
להלן שיטת עלילה המאפשרת הדמיה פשוטה של החלון המפוצל:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
העלילה הזו מיישרת קלט, תוויות וחיזוי (מאוחר יותר) על סמך הזמן שהפריט מתייחס אליו:
w2.plot()
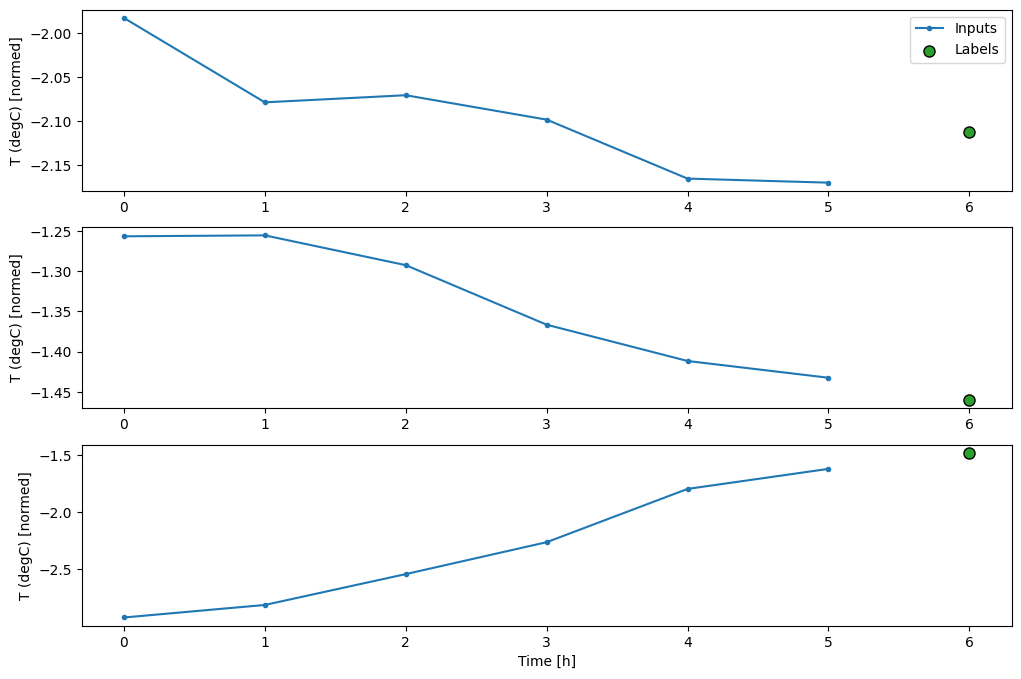
אתה יכול לשרטט את העמודות האחרות, אבל לתצורת חלון w2 לדוגמה יש תוויות רק עבור העמודה T (degC) .
w2.plot(plot_col='p (mbar)')
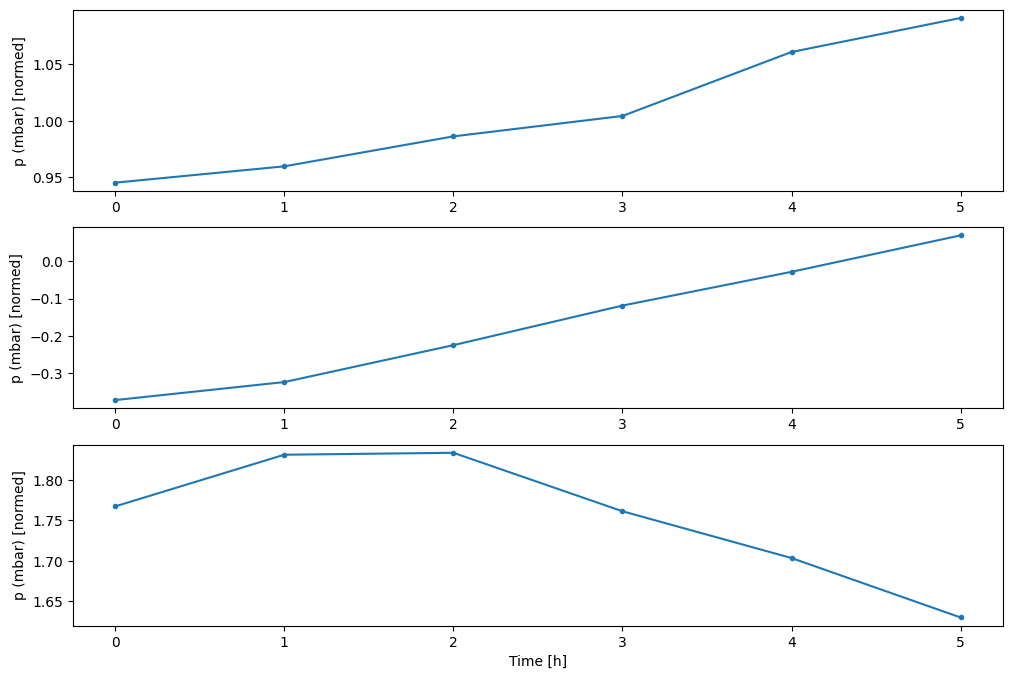
4. צור tf.data.Dataset s
לבסוף, שיטת make_dataset זו תיקח סדרת זמן DataFrame ותמיר אותו ל- tf.data.Dataset של זוגות (input_window, label_window) באמצעות הפונקציה tf.keras.utils.timeseries_dataset_from_array :
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
האובייקט WindowGenerator מכיל נתוני הדרכה, אימות ובדיקה.
הוסף מאפיינים לגישה אליהם כ- tf.data.Dataset s באמצעות שיטת make_dataset שהגדרת קודם לכן. כמו כן, הוסף אצווה דוגמה סטנדרטית לגישה נוחה ותכנון:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
כעת, האובייקט WindowGenerator נותן לך גישה לאובייקטים tf.data.Dataset , כך שתוכל לעבור בקלות על הנתונים.
המאפיין Dataset.element_spec אומר לך את המבנה, סוגי הנתונים והצורות של רכיבי הנתונים.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
איטרציה על Dataset מניב קבוצות בטון:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
דגמי צעד בודד
המודל הפשוט ביותר שאתה יכול לבנות על סוג זה של נתונים הוא כזה שמנבא ערך של תכונה בודדת - צעד זמן אחד (שעה אחת) לעתיד בהתבסס רק על התנאים הנוכחיים.
אז, התחל בבניית מודלים כדי לחזות את ערך ה- T (degC) שעה אחת לעתיד.
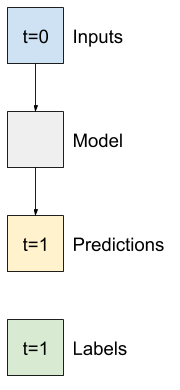
קבע את התצורה של אובייקט WindowGenerator כדי לייצר את צמדי הצעדים האלה (input, label) :
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
אובייקט window יוצר tf.data.Dataset s ממערכי ההדרכה, האימות והבדיקות, ומאפשר לך לחזור בקלות על אצווה של נתונים.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
קו בסיס
לפני בניית מודל הניתן לאימון, יהיה טוב שיהיה קו בסיס ביצועים כנקודת השוואה עם הדגמים המאוחרים יותר המסובכים יותר.
משימה ראשונה זו היא לחזות טמפרטורה שעה אחת לעתיד, בהתחשב בערך הנוכחי של כל התכונות. הערכים הנוכחיים כוללים את הטמפרטורה הנוכחית.
אז, התחל עם מודל שרק מחזיר את הטמפרטורה הנוכחית בתור החיזוי, מנבא "ללא שינוי". זהו קו בסיס סביר מכיוון שהטמפרטורה משתנה לאט. כמובן, קו הבסיס הזה יעבוד פחות טוב אם תבצע תחזית נוספת בעתיד.
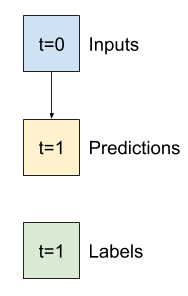
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
הצג והעריך את המודל הזה:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
זה הדפיס כמה מדדי ביצועים, אבל אלה לא נותנים לך הרגשה עד כמה המודל מצליח.
ל- WindowGenerator יש שיטת עלילה, אבל העלילות לא יהיו מעניינות במיוחד עם מדגם בודד בלבד.
אז, צור WindowGenerator רחב יותר שיוצר חלונות 24 שעות של קלט ותוויות רצופות בכל פעם. המשתנה wide_window החדש לא משנה את אופן הפעולה של המודל. המודל עדיין עושה תחזיות שעה אחת לעתיד על סמך שלב זמן קלט בודד. כאן, ציר time פועל כמו ציר batch : כל חיזוי מתבצע באופן עצמאי ללא אינטראקציה בין שלבי זמן:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
ניתן להעביר חלון מורחב זה ישירות לאותו מודל baseline ללא שינויי קוד. זה אפשרי מכיוון שלכניסות והתוויות יש את אותו מספר שלבי זמן, וקו הבסיס פשוט מעביר את הקלט לפלט:
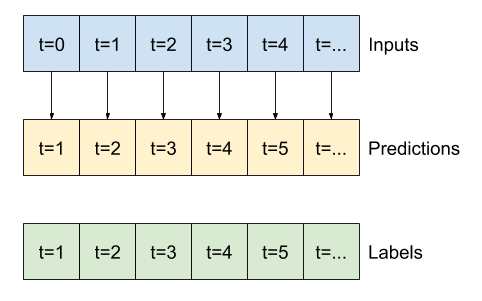
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
על ידי שרטוט התחזיות של מודל הבסיס, שימו לב שזה פשוט התוויות המוזזות ימינה בשעה אחת:
wide_window.plot(baseline)
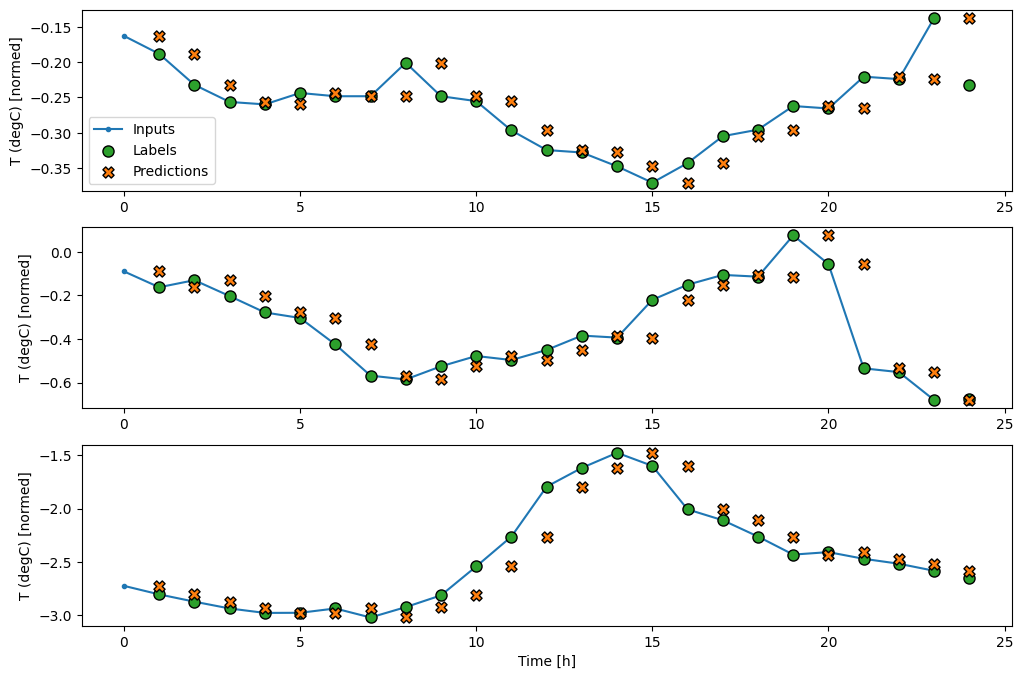
בתרשים של שלוש דוגמאות לעיל, מודל הצעד הבודד מופעל על פני 24 שעות. זה ראוי להסבר:
- קו
Inputsהכחול מציג את טמפרטורת הכניסה בכל שלב בזמן. הדגם מקבל את כל התכונות, העלילה הזו מציגה רק את הטמפרטורה. - נקודות
Labelsהירוקות מציגות את ערך חיזוי היעד. נקודות אלו מוצגות בזמן החיזוי, לא בזמן הקלט. זו הסיבה שטווח התוויות מוסט שלב אחד ביחס לכניסות. - צלבי החיזויים הכתומים הם
Predictionsהמודל עבור כל שלב בזמן הפלט. אם המודל היה חוזה בצורה מושלמת, התחזיות היו נוחתות ישירות עלLabels.
דגם ליניארי
המודל הניתן לאימון הפשוט ביותר שתוכל ליישם במשימה זו הוא הוספת טרנספורמציה ליניארית בין הקלט והפלט. במקרה זה הפלט משלב זמן תלוי רק בשלב זה:

שכבה tf.keras.layers.Dense ללא סט activation היא מודל ליניארי. השכבה הופכת רק את הציר האחרון של הנתונים מ- (batch, time, inputs) ל- (batch, time, units) ; הוא מיושם באופן עצמאי על כל פריט על פני ציר batch time .
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
הדרכה זו מכשירה דגמים רבים, אז ארוז את הליך ההדרכה לפונקציה:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
אימן את המודל והעריך את ביצועיו:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
כמו מודל baseline , ניתן לקרוא למודל הליניארי על קבוצות של חלונות רחבים. בשימוש כך המודל יוצר קבוצה של תחזיות עצמאיות על שלבי זמן עוקבים. ציר time פועל כמו ציר batch אחר. אין אינטראקציות בין התחזיות בכל שלב בזמן.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
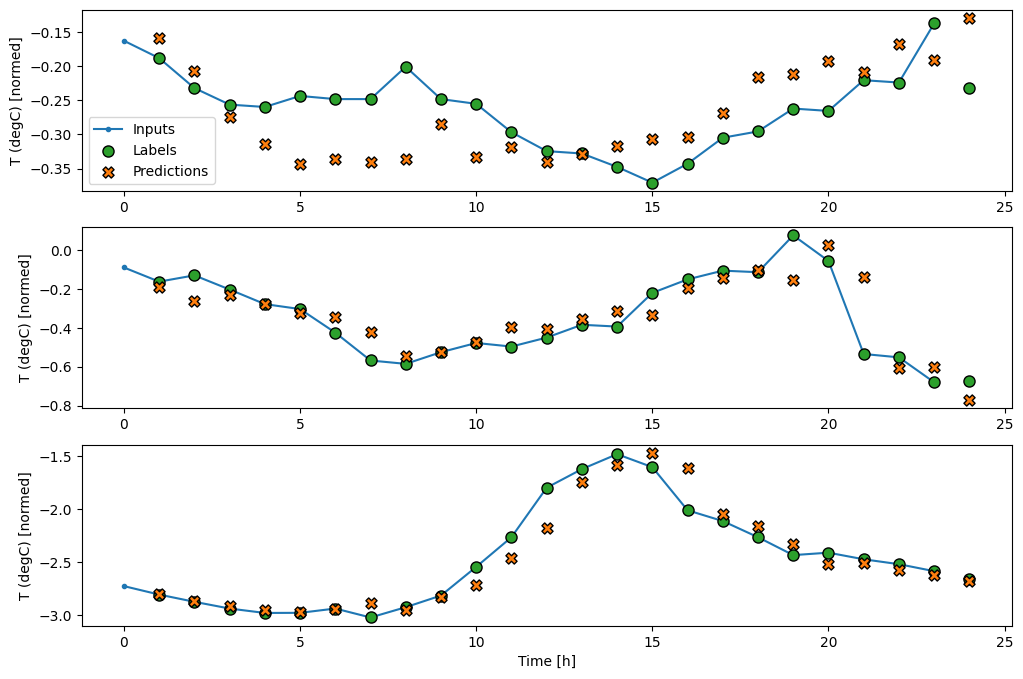
הנה העלילה של תחזיות הדוגמה שלו ב- wide_window , שימו לב כיצד במקרים רבים החיזוי בבירור טוב יותר מאשר רק החזרת טמפרטורת הקלט, אך במקרים בודדים זה גרוע יותר:
wide_window.plot(linear)
יתרון אחד למודלים ליניאריים הוא שהם פשוטים יחסית לפירוש. אתה יכול לשלוף את משקולות השכבה ולדמיין את המשקל שהוקצה לכל קלט:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
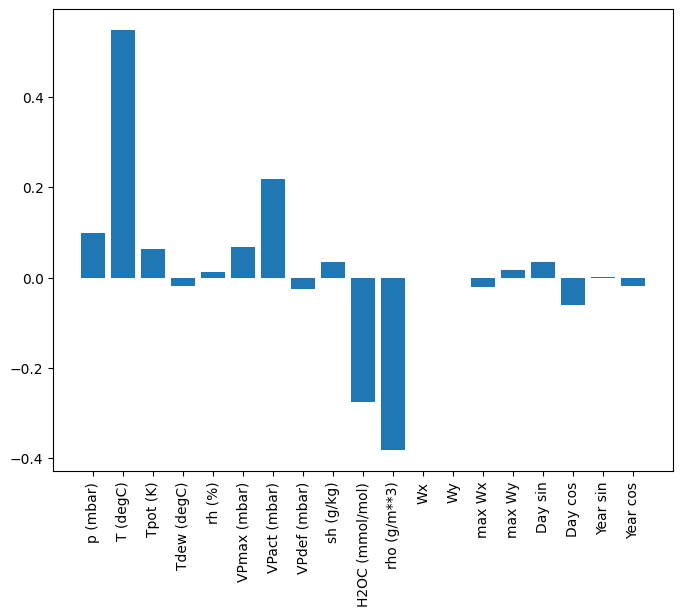
לפעמים הדגם אפילו לא שם את המשקל הרב ביותר על הקלט T (degC) . זהו אחד הסיכונים של אתחול אקראי.
צָפוּף
לפני יישום מודלים שפועלים בפועל על מספר שלבי זמן, כדאי לבדוק את הביצועים של מודלים עמוקים יותר, חזקים יותר, עם שלבי קלט בודדים.
הנה מודל דומה למודל linear , אלא שהוא מערם כמה שכבות Dense בין הקלט והפלט:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
צפוף רב שלבים
למודל חד-פעמי אין הקשר לערכים הנוכחיים של התשומות שלו. הוא לא יכול לראות כיצד תכונות הקלט משתנות לאורך זמן. כדי לטפל בבעיה זו, המודל זקוק לגישה למספר שלבי זמן בעת ביצוע תחזיות:
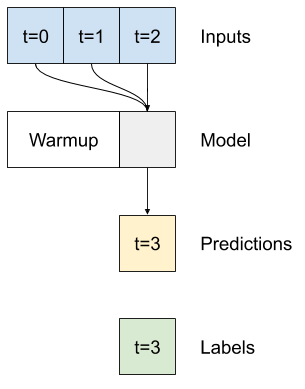
המודלים baseline , linear dense טופלו בכל צעד זמן באופן עצמאי. כאן המודל ייקח מספר שלבי זמן כקלט כדי לייצר פלט בודד.
צור WindowGenerator שיפיק אצווה של קלט של שלוש שעות ותוויות של שעה אחת:
שימו לב שפרמטר shift של Window הוא ביחס לסוף שני החלונות.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
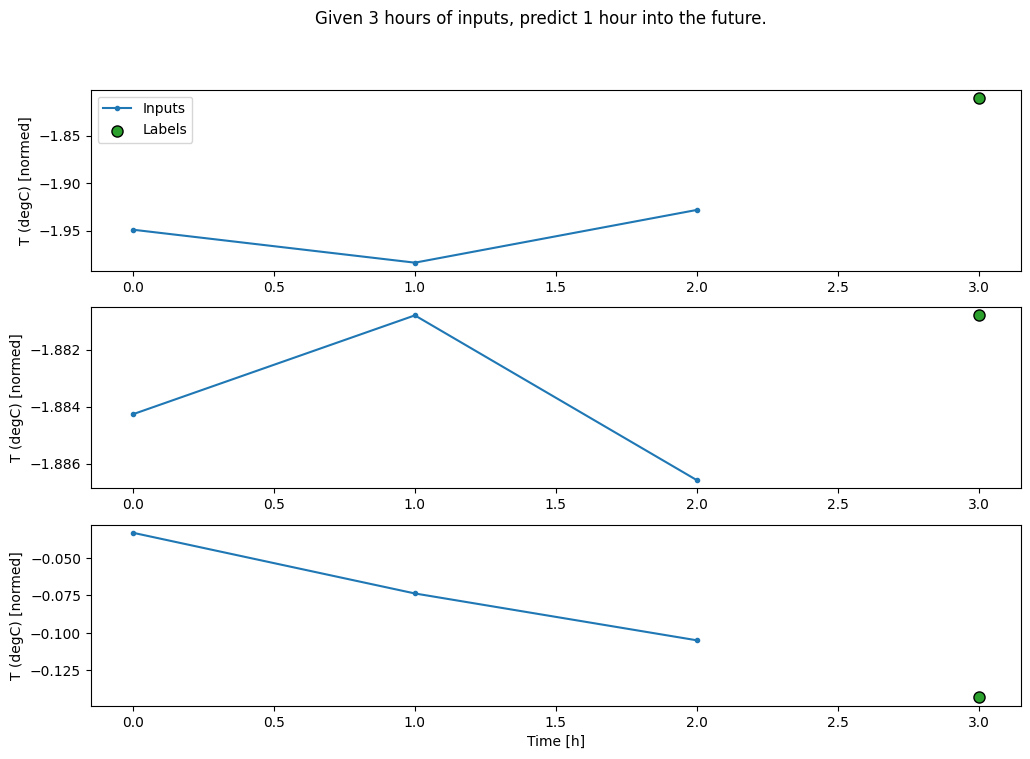
אתה יכול לאמן מודל dense על חלון שלבים מרובה קלט על ידי הוספת tf.keras.layers.Flatten כשכבה הראשונה של המודל:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
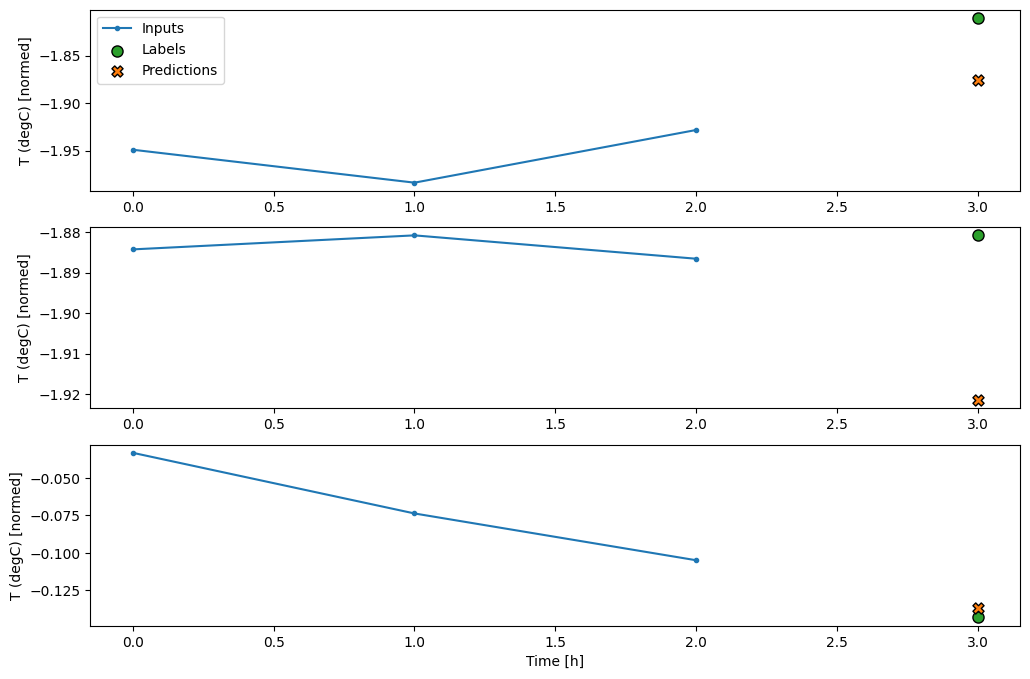
הצד השלילי העיקרי של גישה זו הוא שניתן להפעיל את המודל המתקבל רק על חלונות קלט בעלי צורה זו בדיוק.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
המודלים הקונבולוציוניים בסעיף הבא פותרים בעיה זו.
רשת נוירונים של Convolution
שכבת קונבולציה ( tf.keras.layers.Conv1D ) גם לוקחת מספר שלבי זמן כקלט לכל חיזוי.
להלן אותו דגם כמו multi_step_dense , שנכתב מחדש עם קונבולציה.
שימו לב לשינויים:
-
tf.keras.layers.Flattentf.keras.layers.Denseהראשונות מוחלפות ב-tf.keras.layers.Conv1D. - אין צורך יותר
tf.keras.layers.Reshapeשומרת על ציר הזמן בפלט שלה.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
הפעל אותו על אצווה לדוגמה כדי לבדוק שהמודל מייצר פלטים עם הצורה הצפויה:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
אמן והעריך אותו ב- conv_window והוא אמור לתת ביצועים דומים למודל multi_step_dense .
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
ההבדל בין conv_model זה למודל multi_step_dense הוא שניתן להפעיל את conv_model על כניסות בכל אורך. השכבה הקונבולוציונית מוחלת על חלון הזזה של כניסות:
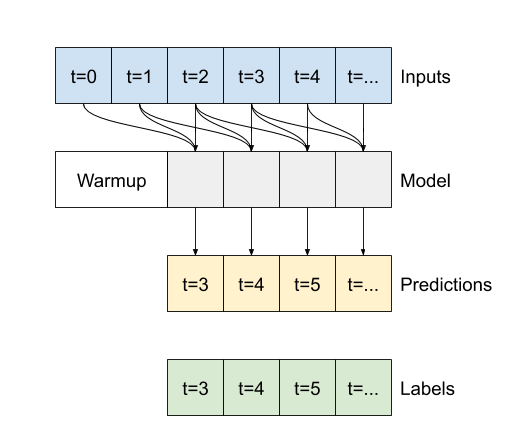
אם אתה מפעיל אותו על קלט רחב יותר, הוא מייצר פלט רחב יותר:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
שימו לב שהפלט קצר יותר מהקלט. כדי שהאימונים או התכנון יעבדו, אתה צריך שהתוויות והניבוי יהיו באותו אורך. אז בנו WindowGenerator כדי לייצר חלונות רחבים עם כמה שלבי זמן קלט נוספים כך שהתווית ואורכי החיזוי תואמים:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
כעת, אתה יכול לשרטט את התחזיות של המודל על חלון רחב יותר. שימו לב ל-3 שלבי זמן הקלט לפני החיזוי הראשון. כל תחזית כאן מבוססת על 3 שלבי הזמן הקודמים:
wide_conv_window.plot(conv_model)
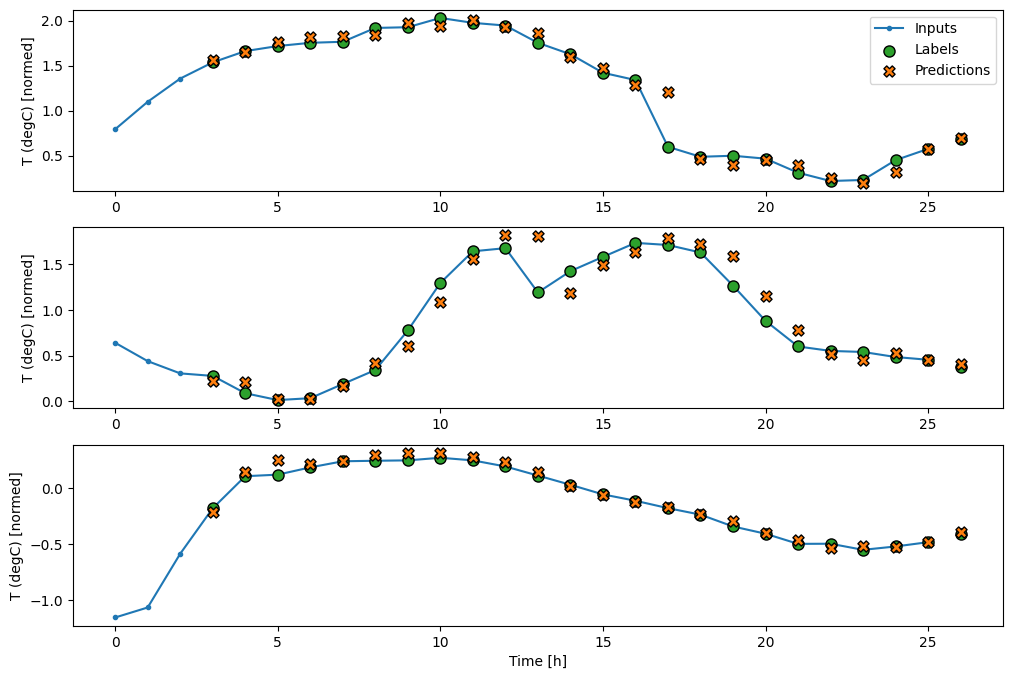
רשת נוירונים חוזרת
רשת עצבית חוזרת (RNN) היא סוג של רשת עצבית המתאימה היטב לנתוני סדרות זמן. RNNs מעבדים סדרת זמן צעד אחר צעד, שומרים על מצב פנימי משלב זמן לשלב זמן.
אתה יכול ללמוד עוד בדור הטקסט עם הדרכה של RNN ובמדריך הרשתות העצביות החוזרות (RNN) עם Keras .
במדריך זה, תשתמש בשכבת RNN הנקראת זיכרון ארוך טווח קצר ( tf.keras.layers.LSTM ).
ארגומנט בנאי חשוב עבור כל שכבות RNN של Keras, כגון tf.keras.layers.LSTM , הוא הארגומנט return_sequences . הגדרה זו יכולה להגדיר את השכבה באחת משתי דרכים:
- אם
False, ברירת המחדל, השכבה מחזירה רק את הפלט של שלב הזמן הסופי, ונותנת למודל זמן להתחמם במצבו הפנימי לפני ביצוע חיזוי בודד:
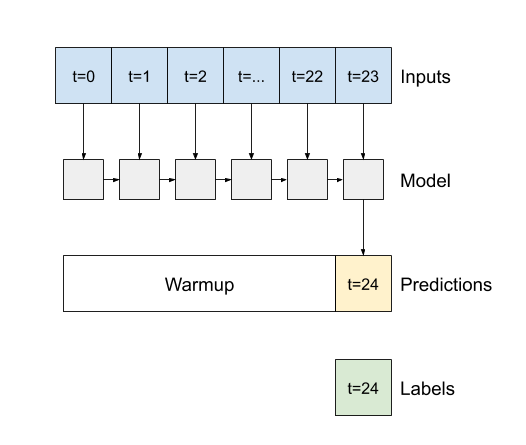
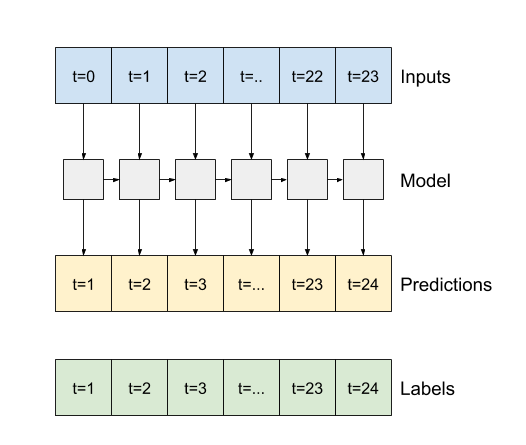
- אם
True, השכבה מחזירה פלט עבור כל קלט. זה שימושי עבור:- ערימת שכבות RNN.
- אימון מודל על מספר שלבי זמן בו זמנית.
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
עם return_sequences=True , ניתן לאמן את המודל על 24 שעות של נתונים בכל פעם.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
wide_window.plot(lstm_model)
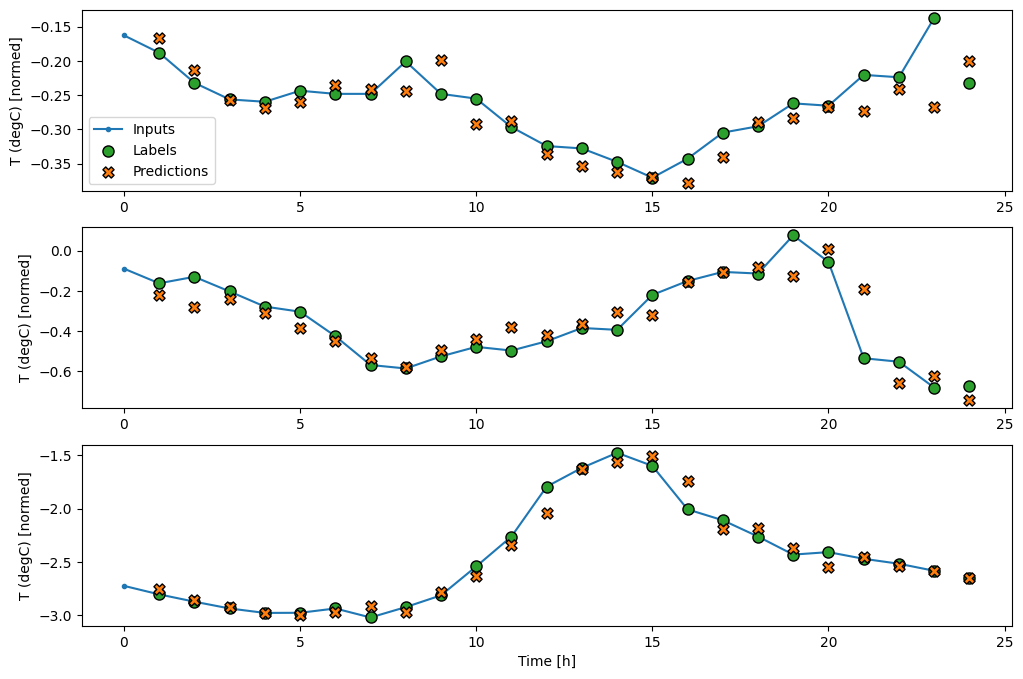
ביצועים
עם מערך הנתונים הזה, בדרך כלל, כל אחד מהדגמים מצליח מעט יותר מזה שלפניו:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
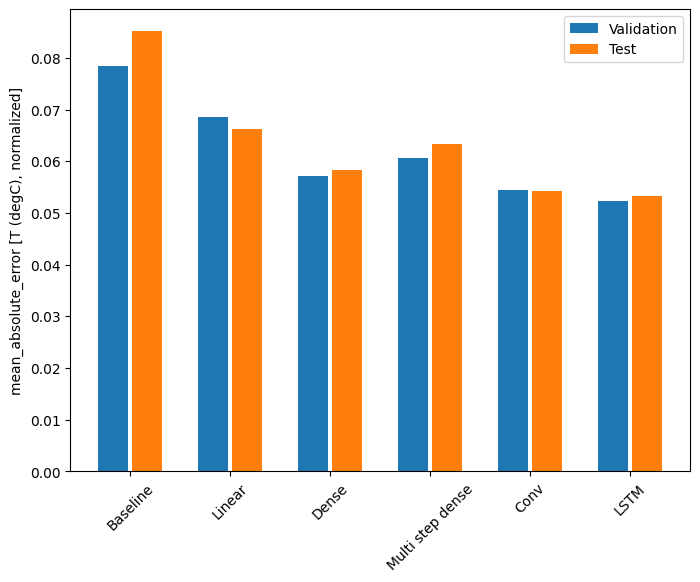
for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
דגמים מרובי פלט
הדגמים עד כה חזו תכונת פלט בודדת, T (degC) , עבור שלב זמן בודד.
ניתן להמיר את כל המודלים הללו לחיזוי תכונות מרובות רק על ידי שינוי מספר היחידות בשכבת הפלט והתאמת חלונות ההדרכה כך שיכללו את כל התכונות labels ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
שים לב לעיל שלציר features של התוויות יש כעת אותו עומק כמו הכניסות, במקום 1 .
קו בסיס
ניתן להשתמש באותו מודל בסיס ( Baseline ) כאן, אך הפעם לחזור על כל התכונות במקום לבחור label_index ספציפי:
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
צָפוּף
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
RNN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
מתקדם: חיבורים שיוריים
מודל Baseline מקודם ניצל את העובדה שהרצף אינו משתנה באופן דרסטי משלב זמן לשלב. כל דגם שהוכשר במדריך הזה עד כה אותחל באקראי, ואז היה צריך ללמוד שהפלט הוא שינוי קטן משלב הזמן הקודם.
אמנם אתה יכול לעקוף את הבעיה עם אתחול קפדני, אבל זה פשוט יותר לבנות את זה במבנה המודל.
מקובל בניתוח סדרות זמן לבנות מודלים שבמקום לחזות את הערך הבא, מנבאים כיצד הערך ישתנה בשלב הזמן הבא. באופן דומה, רשתות שיוריות - או ResNets - בלמידה עמוקה מתייחסות לארכיטקטורות שבהן כל שכבה מוסיפה לתוצאה המצטברת של המודל.
כך מנצלים את הידיעה שהשינוי צריך להיות קטן.
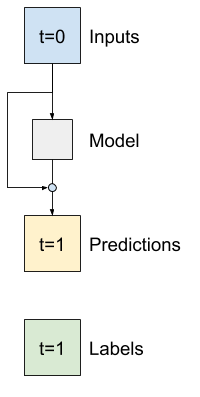
בעיקרו של דבר, זה מאתחל את המודל כך שיתאים ל- Baseline . עבור משימה זו זה עוזר לדגמים להתכנס מהר יותר, עם ביצועים מעט טובים יותר.
ניתן להשתמש בגישה זו בשילוב עם כל מודל שנדון במדריך זה.
כאן, הוא מיושם על מודל LSTM, שים לב לשימוש ב- tf.initializers.zeros כדי להבטיח שהשינויים החזויים הראשוניים קטנים, ואינם גוברים על החיבור השיורי. אין כאן דאגות לשבירת סימטריה לשיפועים, מכיוון zeros משמשים רק בשכבה האחרונה.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
ביצועים
להלן הביצועים הכוללים של דגמי ריבוי פלטים אלה.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
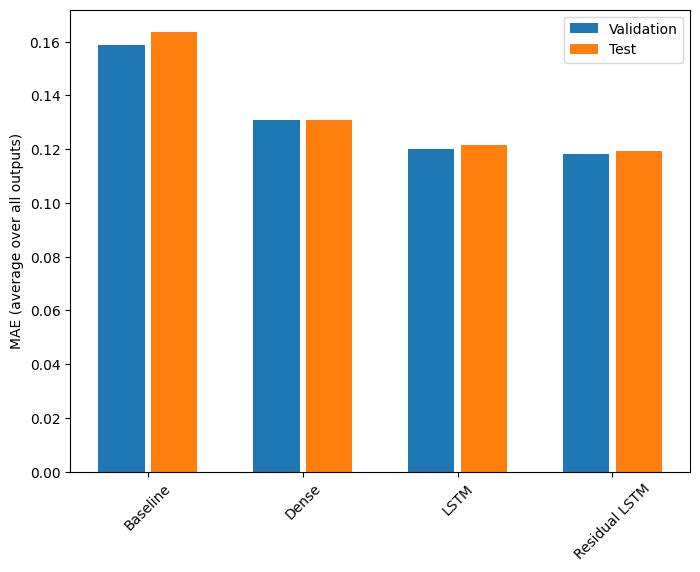
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
הביצועים שלעיל מוערכים בממוצע על פני כל תפוקות הדגם.
דגמים מרובי שלבים
גם המודלים של פלט יחיד וגם של ריבוי פלט בסעיפים הקודמים עשו תחזיות של צעד זמן בודד , שעה אחת לתוך העתיד.
חלק זה בוחן כיצד להרחיב את המודלים הללו כדי לבצע חיזויים מרובים של צעדי זמן .
בתחזית רב-שלבית, המודל צריך ללמוד לחזות טווח של ערכים עתידיים. לפיכך, בניגוד למודל של צעד אחד, שבו רק נקודה עתידית אחת חזויה, מודל רב-שלבי מנבא רצף של הערכים העתידיים.
ישנן שתי גישות גסות לכך:
- תחזיות של צילום בודד שבו כל סדרת הזמן נחזו בבת אחת.
- חיזויים אוטורגרסיביים שבהם המודל מבצע רק תחזיות צעד בודד והפלט שלו מוזן בחזרה כקלט שלו.
בסעיף זה כל הדגמים ינבאו את כל התכונות בכל שלבי זמן הפלט .
עבור המודל הרב-שלבי, נתוני ההדרכה מורכבים שוב מדגימות שעתיות. עם זאת, כאן, המודלים ילמדו לחזות 24 שעות אל העתיד, בהינתן 24 שעות מהעבר.
להלן אובייקט Window שיוצר את הפרוסות הללו ממערך הנתונים:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
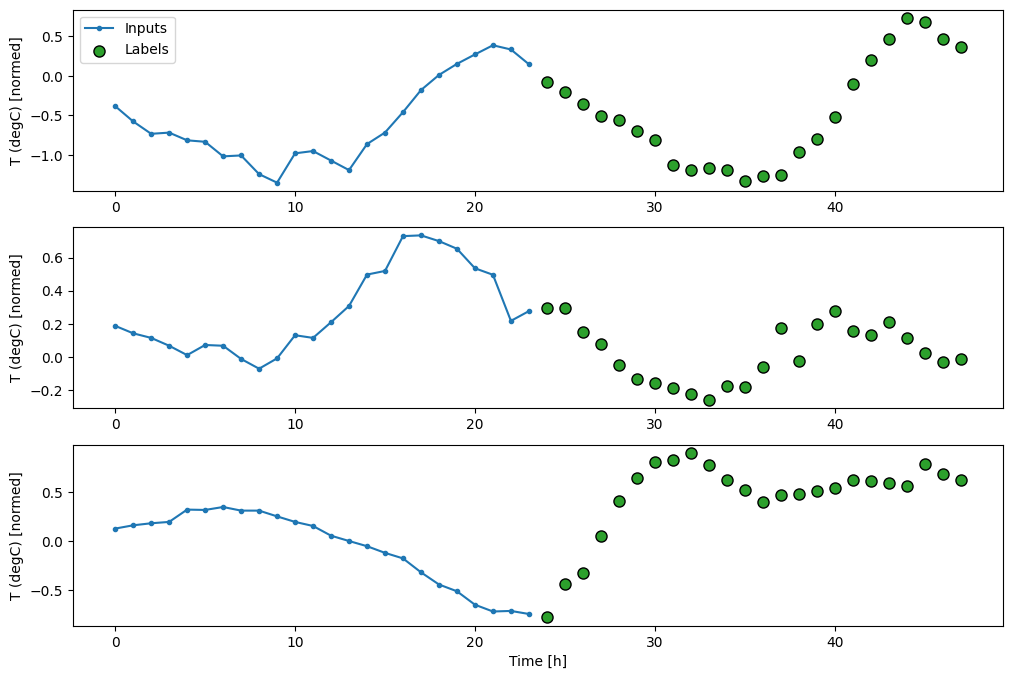
קווי בסיס
קו בסיס פשוט למשימה זו הוא לחזור על שלב זמן הקלט האחרון עבור המספר הנדרש של שלבי זמן הפלט:
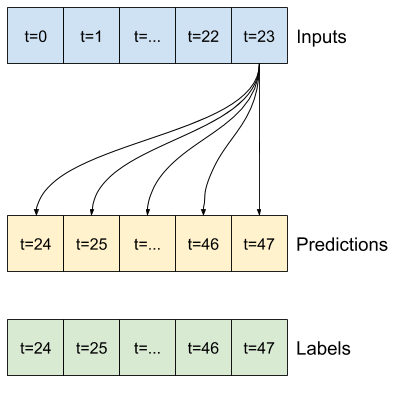
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
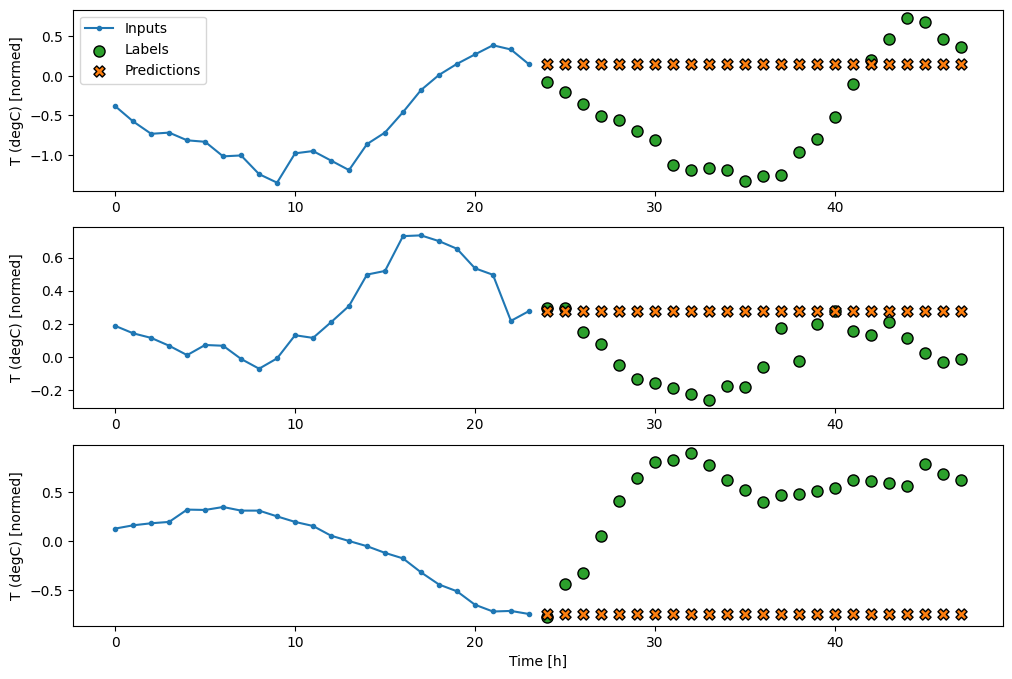
מכיוון שמשימה זו היא לחזות 24 שעות לעתיד, בהינתן 24 שעות מהעבר, גישה פשוטה נוספת היא לחזור על היום הקודם, בהנחה שמחר יהיה דומה:
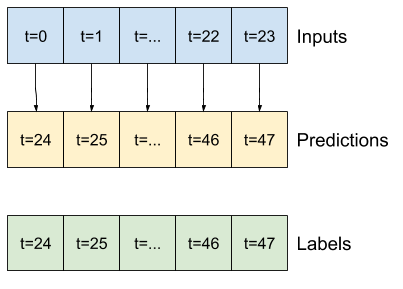
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
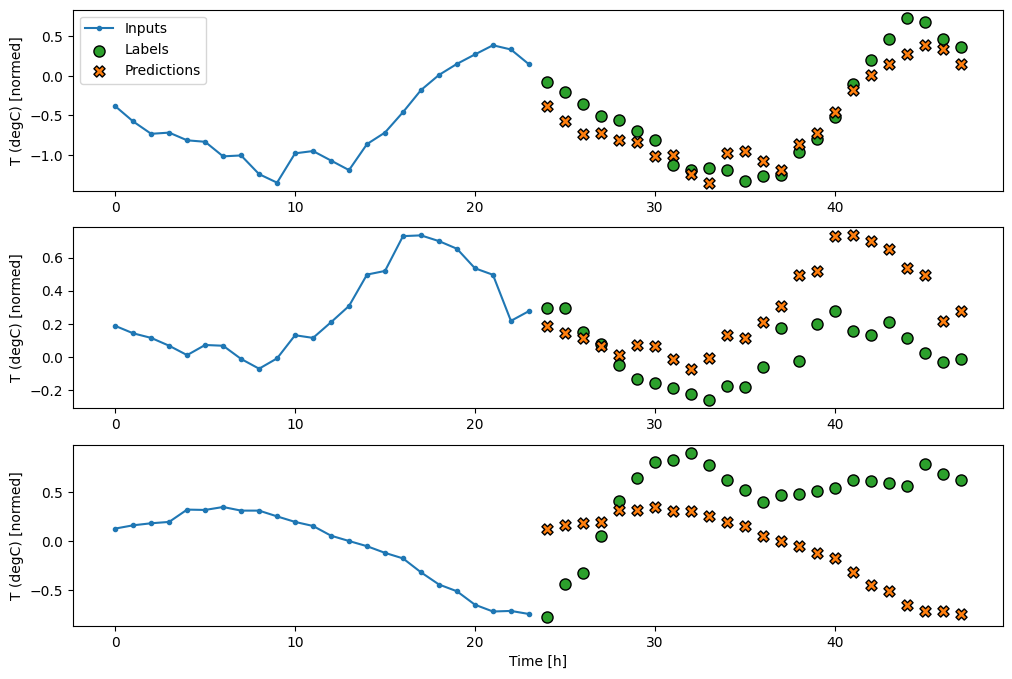
דגמים עם צילום בודד
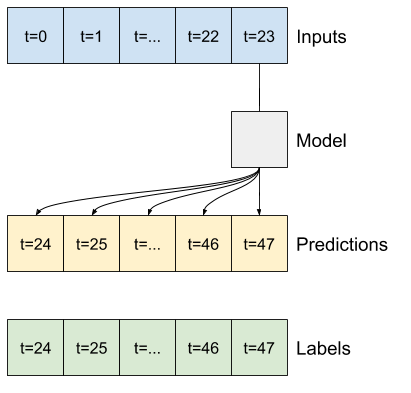
גישה אחת ברמה גבוהה לבעיה זו היא להשתמש במודל "ירייה בודדת", כאשר המודל מבצע את חיזוי הרצף כולו בשלב אחד.
ניתן ליישם זאת ביעילות כ- tf.keras.layers.Dense עם OUT_STEPS*features יחידות פלט. המודל רק צריך לעצב מחדש את הפלט (OUTPUT_STEPS, features) .
ליניארי
מודל ליניארי פשוט המבוסס על שלב זמן הקלט האחרון עושה טוב יותר מכל אחת מהקו הבסיס, אבל הוא בעל עוצמה נמוכה. המודל צריך לחזות OUTPUT_STEPS שלבי זמן, משלב זמן קלט בודד עם השלכה ליניארית. זה יכול לתפוס רק נתח נמוך של ההתנהגות, ככל הנראה מבוסס בעיקר על השעה ביום והשעה בשנה.
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053

צָפוּף
הוספת tf.keras.layers.Dense בין הקלט לפלט מעניקה למודל הליניארי יותר כוח, אך עדיין מבוססת רק על שלב זמן קלט בודד.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
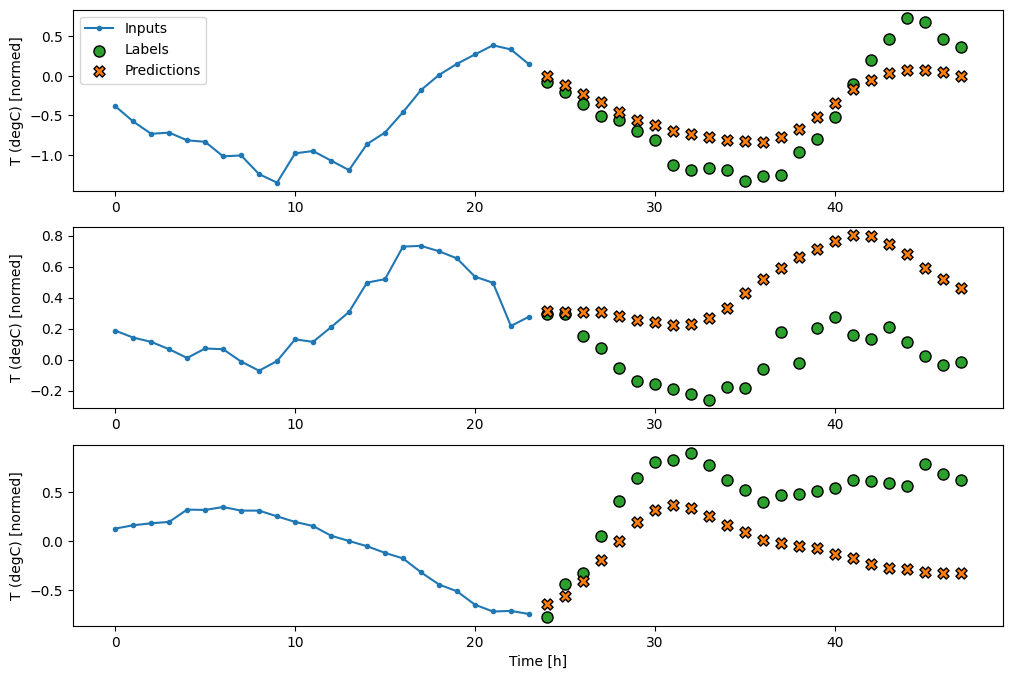
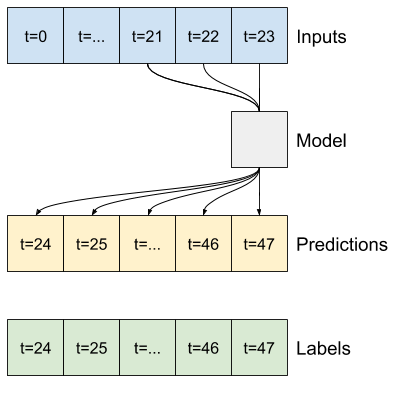
CNN
מודל קונבולוציוני יוצר תחזיות על סמך היסטוריה ברוחב קבוע, מה שעשוי להוביל לביצועים טובים יותר מהמודל הצפוף מכיוון שהוא יכול לראות כיצד דברים משתנים לאורך זמן:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
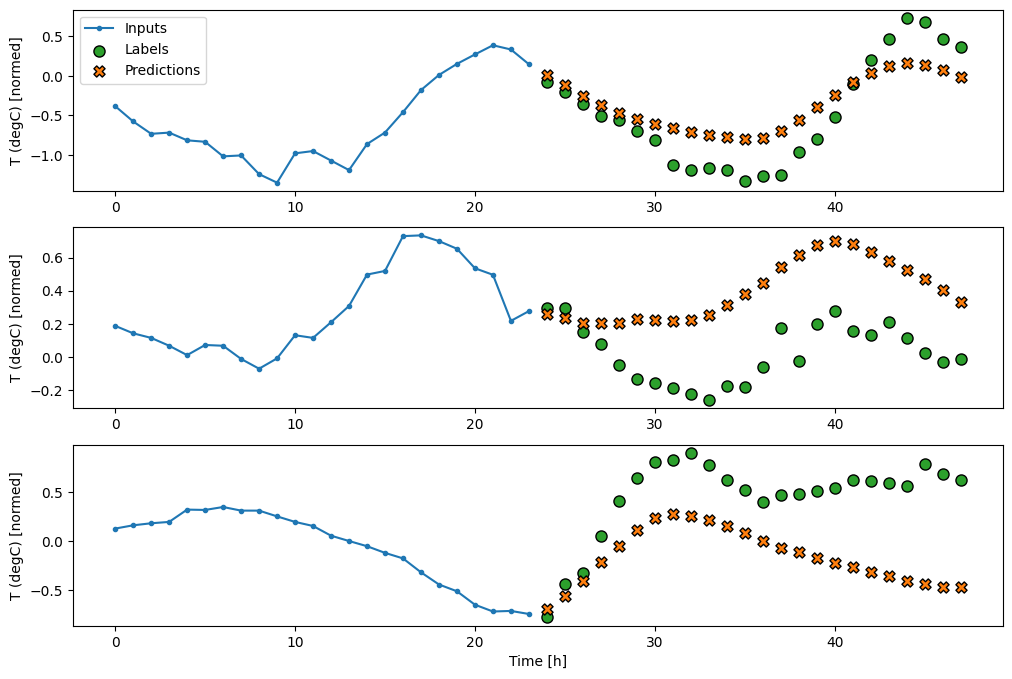
RNN
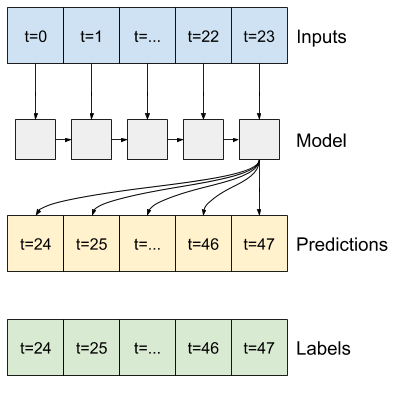
מודל חוזר יכול ללמוד להשתמש בהיסטוריה ארוכה של תשומות, אם זה רלוונטי לתחזיות שהמודל עושה. כאן המודל יצבור מצב פנימי במשך 24 שעות, לפני ביצוע חיזוי בודד ל-24 השעות הבאות.
בפורמט של צילום יחיד זה, ה-LSTM צריך להפיק פלט רק בשלב הזמן האחרון, אז הגדר return_sequences=False ב- tf.keras.layers.LSTM .
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
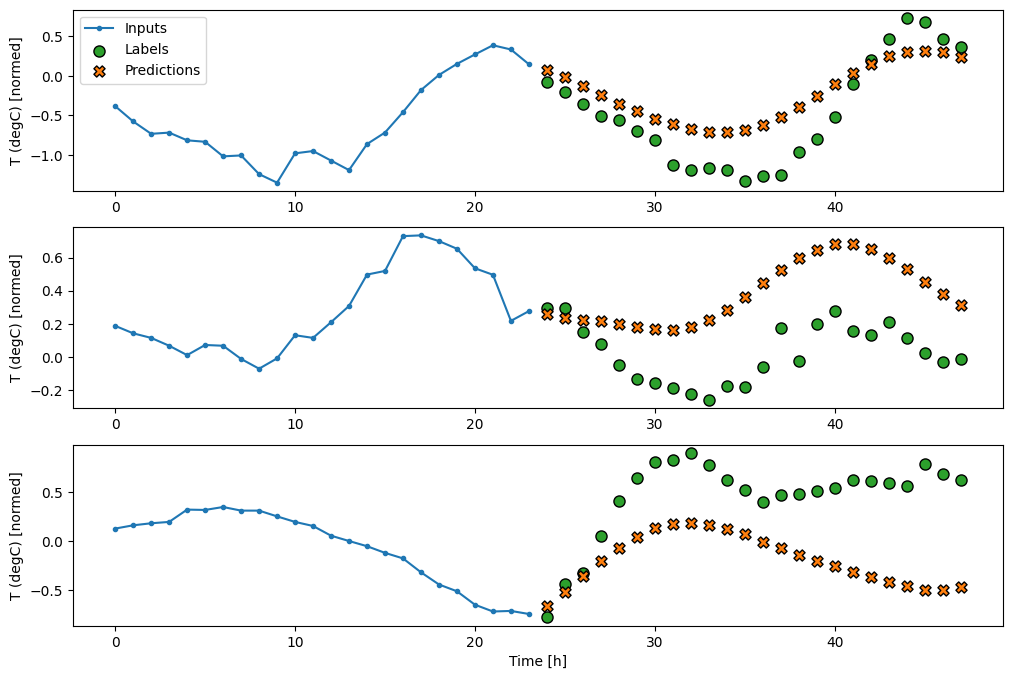
מתקדם: דגם אוטורגרסיבי
המודלים שלעיל כולם חוזים את רצף הפלט כולו בשלב אחד.
במקרים מסוימים עשוי להיות מועיל למודל לפרק את החיזוי הזה לשלבי זמן בודדים. לאחר מכן, ניתן להזין את הפלט של כל דגם בחזרה לתוך עצמו בכל שלב וניתן לבצע תחזיות בתנאי הקודם, כמו בגרסה הקלאסית של Generating Sequences With Recurrent Neural Networks .
יתרון אחד ברור לסגנון הדגם הזה הוא שניתן להגדיר אותו לייצר פלט באורך משתנה.
אתה יכול לקחת כל אחד מהמודלים מרובי-השלבים הבודדים שהוכשרו במחצית הראשונה של המדריך הזה ולרוץ בלולאת משוב אוטורגרסיבית, אבל כאן תתמקד בבניית מודל שעבר הכשרה מפורשת לעשות זאת.
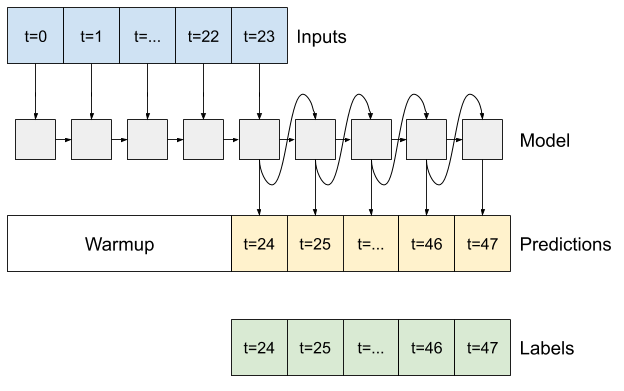
RNN
מדריך זה בונה רק מודל RNN אוטורגרסיבי, אך ניתן ליישם את הדפוס הזה על כל מודל שתוכנן להפיק שלב זמן בודד.
למודל תהיה אותה צורה בסיסית כמו מודלים LSTM חד-שלביים מקודמים: שכבת tf.keras.layers.LSTM ואחריה שכבה tf.keras.layers.Dense הממירה את הפלטים של שכבת LSTM לחיזוי מודל.
tf.keras.layers.LSTM הוא תא tf.keras.layers.LSTMCell עטוף ברמה הגבוהה יותר tf.keras.layers.RNN שמנהל עבורך את המצב ואת תוצאות הרצף (בדוק את הרשתות העצביות החוזרות (RNN) עם Keras מדריך לפרטים).
במקרה זה, המודל צריך לנהל באופן ידני את התשומות עבור כל שלב, ולכן הוא משתמש ב- tf.keras.layers.LSTMCell ישירות עבור ממשק שלב של פעם אחת ברמה נמוכה יותר.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
השיטה הראשונה שמודל זה צריך היא שיטת warmup כדי לאתחל את המצב הפנימי שלו בהתבסס על התשומות. לאחר הכשרה, מצב זה יתפוס את החלקים הרלוונטיים של היסטוריית הקלט. זה שווה ערך למודל LSTM חד-שלבי מקודם:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
שיטה זו מחזירה חיזוי צעד-זמן בודד ואת המצב הפנימי של ה- LSTM :
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
עם המצב של ה- RNN , ותחזית ראשונית, כעת תוכל להמשיך לחזור על המודל ולהזין את התחזיות בכל צעד אחורה כקלט.
הגישה הפשוטה ביותר לאיסוף תחזיות הפלט היא להשתמש ברשימת Python וב- tf.stack לאחר הלולאה.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
הפעל את המודל הזה במבחן על הכניסות לדוגמה:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
כעת, אמנו את הדגם:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
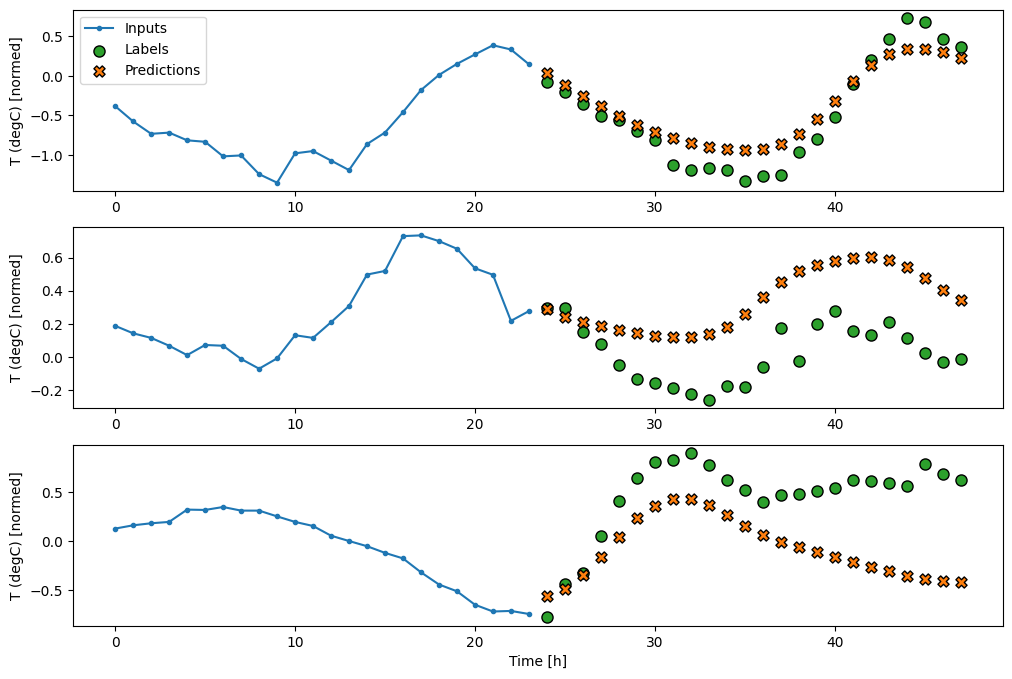
ביצועים
ישנן תשואות פוחתות בבירור כפונקציה של מורכבות המודל בבעיה זו:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
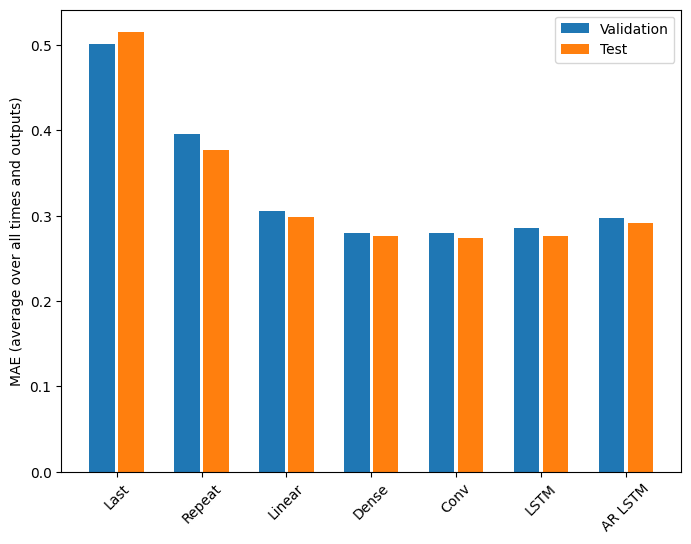
המדדים עבור דגמי ריבוי פלטים במחצית הראשונה של מדריך זה מציגים את הביצועים הממוצעים בכל תכונות הפלט. ביצועים אלה דומים אך גם בממוצע לאורך שלבי זמן הפלט.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
הרווחים שהושגו במעבר מדגם צפוף לדגמים קונבולוציוניים וחוזרים הם אחוזים בודדים בלבד (אם בכלל), והמודל האוטו-רגרסיב הביצועים גרועים יותר. אז אולי הגישות המורכבות יותר האלה לא יועילו לבעיה הזו , אבל לא הייתה דרך לדעת בלי לנסות, והמודלים האלה יכולים להיות מועילים לבעיה שלך .
הצעדים הבאים
מדריך זה היה מבוא מהיר לחיזוי סדרות זמן באמצעות TensorFlow.
למידע נוסף, עיין ב:
- פרק 15 של למידת מכונה מעשית עם Scikit-Learn, Keras ו- TensorFlow , מהדורה 2.
- פרק 6 של למידה עמוקה עם Python .
- שיעור 8 במבוא של Udacity ל-TensorFlow ללמידה עמוקה , כולל מחברות התרגילים .
כמו כן, זכור שאתה יכול ליישם כל מודל סדרת זמן קלאסי ב-TensorFlow - הדרכה זו רק מתמקדת בפונקציונליות המובנית של TensorFlow.
