Previsione di serie temporali

Visualizza su TensorFlow.org

Esegui in Google Colab

Visualizza l'origine su GitHub

Scarica quaderno

Questo tutorial è un'introduzione alla previsione di serie temporali utilizzando TensorFlow. Costruisce alcuni stili diversi di modelli tra cui reti neurali convoluzionali e ricorrenti (CNN e RNN).

Questo è trattato in due parti principali, con sottosezioni:

• Previsione per un singolo passaggio temporale:
  • Una sola caratteristica.
  • Tutte le funzionalità.
• Prevedere più passaggi:
  • Colpo singolo: fai le previsioni tutte in una volta.
  • Autoregressivo: crea una previsione alla volta e invia l'output al modello.

Impostare

import os
import datetime

import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf

mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False

Il set di dati meteorologici

Questo tutorial utilizza una serie di dati meteorologici registrati dal Max Planck Institute for Biogeochemistry .

Questo set di dati contiene 14 diverse caratteristiche come temperatura dell'aria, pressione atmosferica e umidità. Questi sono stati raccolti ogni 10 minuti, a partire dal 2003. Per motivi di efficienza, utilizzerai solo i dati raccolti tra il 2009 e il 2016. Questa sezione del set di dati è stata preparata da François Chollet per il suo libro Deep Learning with Python .

zip_path = tf.keras.utils.get_file(
    origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
    fname='jena_climate_2009_2016.csv.zip',
    extract=True)
csv_path, _ = os.path.splitext(zip_path)

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip
13574144/13568290 [==============================] - 1s 0us/step
13582336/13568290 [==============================] - 1s 0us/step

Questo tutorial si occuperà solo di previsioni orarie , quindi inizia sottocampionando i dati da intervalli di 10 minuti a intervalli di un'ora:

df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]

date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')

Diamo uno sguardo ai dati. Ecco le prime righe:

df.head()

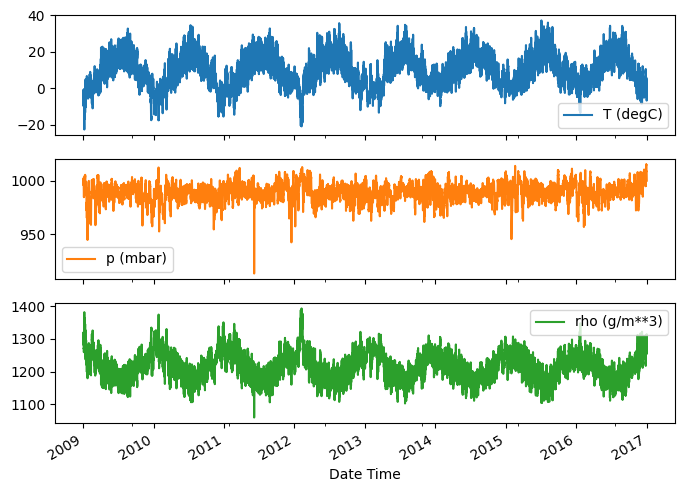
Ecco l'evoluzione di alcune funzionalità nel tempo:

plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)

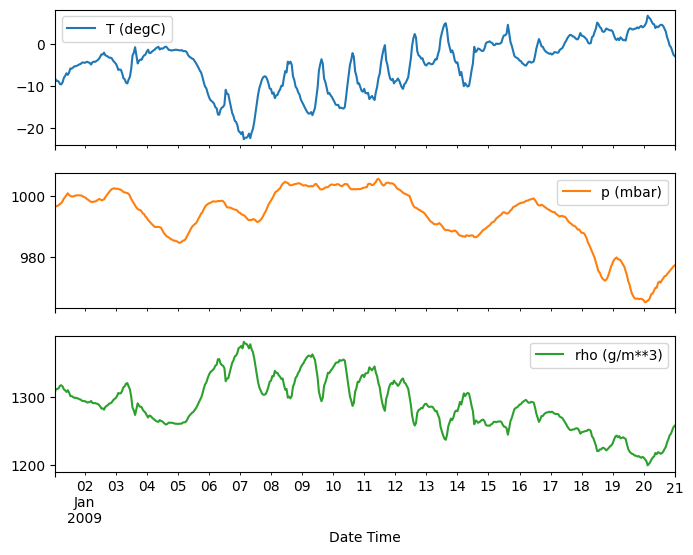
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)

Ispezionare e pulire

Quindi, guarda le statistiche del set di dati:

df.describe().transpose()

Velocità del vento

Una cosa che dovrebbe risaltare è il valore min delle colonne della velocità del vento ( wv (m/s) ) e il valore massimo ( max. wv (m/s) ). Questo -9999 è probabilmente errato.

C'è una colonna separata per la direzione del vento, quindi la velocità dovrebbe essere maggiore di zero ( >=0 ). Sostituiscilo con zeri:

wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0

max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0

# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()

0.0

Ingegneria delle funzionalità

Prima di immergerti nella creazione di un modello, è importante comprendere i tuoi dati e assicurarti di passare il modello con dati formattati in modo appropriato.

Vento

L'ultima colonna dei dati, wd (deg) fornisce la direzione del vento in unità di gradi. Gli angoli non sono buoni input del modello: 360° e 0° dovrebbero essere vicini l'uno all'altro e avvolgersi senza intoppi. La direzione non dovrebbe importare se il vento non soffia.

In questo momento la distribuzione dei dati sul vento è simile a questa:

plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')

Text(0, 0.5, 'Wind Velocity [m/s]')

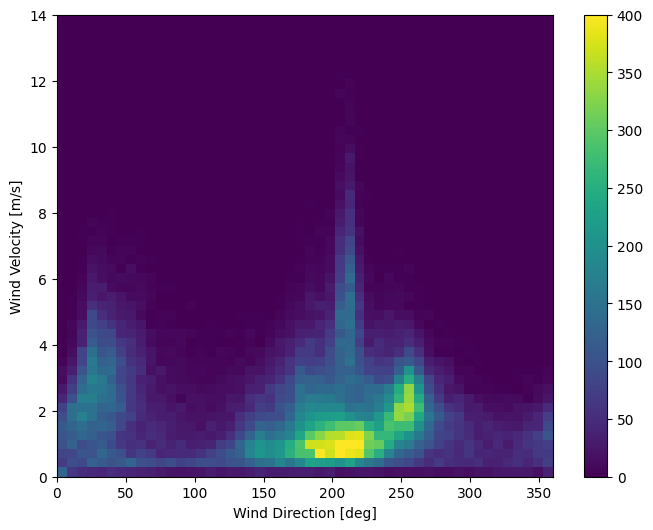
Ma questo sarà più facile da interpretare per il modello se si convertono le colonne della direzione del vento e della velocità in un vettore del vento:

wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')

# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180

# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)

# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)

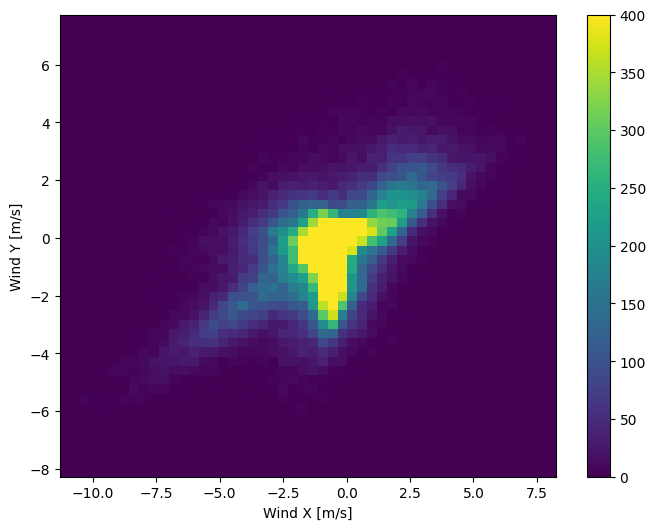
La distribuzione dei vettori del vento è molto più semplice da interpretare correttamente per il modello:

plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')

(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)

Volta

Allo stesso modo, la colonna Date Time è molto utile, ma non in questa forma di stringa. Inizia convertendolo in secondi:

timestamp_s = date_time.map(pd.Timestamp.timestamp)

Simile alla direzione del vento, il tempo in secondi non è un utile input del modello. Essendo dati meteorologici, ha una chiara periodicità giornaliera e annuale. Ci sono molti modi in cui potresti affrontare la periodicità.

È possibile ottenere segnali utilizzabili utilizzando le trasformazioni seno e coseno per cancellare i segnali "Ora del giorno" e "Ora dell'anno":

day = 24*60*60
year = (365.2425)*day

df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))

plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')

Text(0.5, 1.0, 'Time of day signal')

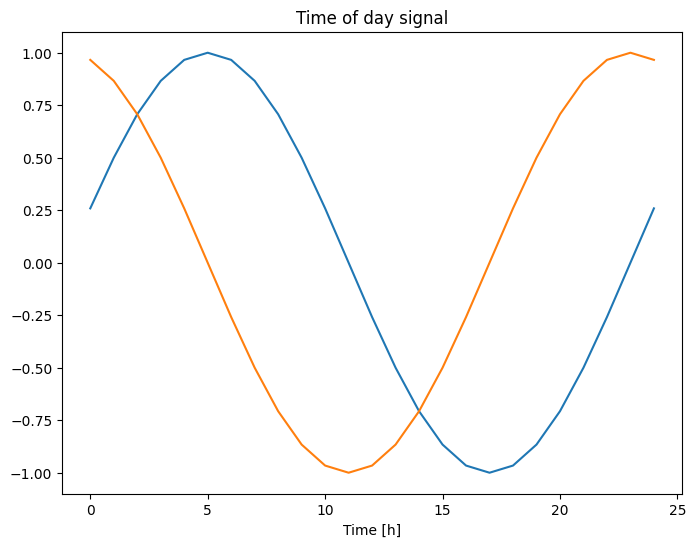
Questo dà al modello l'accesso alle caratteristiche di frequenza più importanti. In questo caso sapevi in ​​anticipo quali frequenze erano importanti.

Se non disponi di tali informazioni, puoi determinare quali frequenze sono importanti estraendo le funzionalità con Trasformata di Fourier veloce . Per verificare le ipotesi, ecco il tf.signal.rfft della temperatura nel tempo. Nota i picchi evidenti a frequenze vicine a 1/year e 1/day :

fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))

n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)

f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')

Dividi i dati

Utilizzerai una suddivisione (70%, 20%, 10%) per i set di addestramento, convalida e test. Nota che i dati non vengono mescolati casualmente prima di essere suddivisi. Questo per due motivi:

1. Garantisce che sia ancora possibile suddividere i dati in finestre di campioni consecutivi.
2. Garantisce che i risultati della convalida/test siano più realistici, essendo valutati sui dati raccolti dopo che il modello è stato addestrato.

column_indices = {name: i for i, name in enumerate(df.columns)}

n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]

num_features = df.shape[1]

Normalizza i dati

È importante ridimensionare le funzionalità prima di addestrare una rete neurale. La normalizzazione è un modo comune per eseguire questo ridimensionamento: sottrarre la media e dividere per la deviazione standard di ciascuna caratteristica.

La media e la deviazione standard devono essere calcolate solo utilizzando i dati di addestramento in modo che i modelli non abbiano accesso ai valori nei set di validazione e test.

È anche discutibile che il modello non dovrebbe avere accesso ai valori futuri nel set di allenamento durante l'allenamento e che questa normalizzazione dovrebbe essere eseguita utilizzando le medie mobili. Questo non è l'obiettivo di questo tutorial e i set di convalida e test assicurano di ottenere metriche (in qualche modo) oneste. Quindi, nell'interesse della semplicità, questo tutorial utilizza una media semplice.

train_mean = train_df.mean()
train_std = train_df.std()

train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std

Ora, dai un'occhiata alla distribuzione delle funzionalità. Alcune funzioni hanno code lunghe, ma non ci sono errori evidenti come il valore di velocità del vento -9999 .

df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

Finestratura dei dati

I modelli in questo tutorial eseguiranno una serie di previsioni basate su una finestra di campioni consecutivi dai dati.

Le caratteristiche principali delle finestre di input sono:

• La larghezza (numero di fasi temporali) delle finestre di input ed etichetta.
• La differenza di tempo tra di loro.
• Quali funzioni vengono utilizzate come input, etichette o entrambi.

Questo tutorial crea una varietà di modelli (inclusi i modelli Linear, DNN, CNN e RNN) e li usa per entrambi:

• Previsioni a output singolo e multi output .
• Previsioni a passo singolo e a più passi .

Questa sezione si concentra sull'implementazione della finestra di dati in modo che possa essere riutilizzata per tutti questi modelli.

A seconda dell'attività e del tipo di modello, potresti voler generare una varietà di finestre di dati. Ecco alcuni esempi:

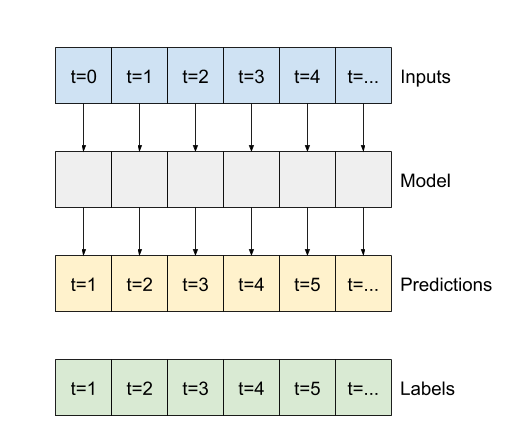
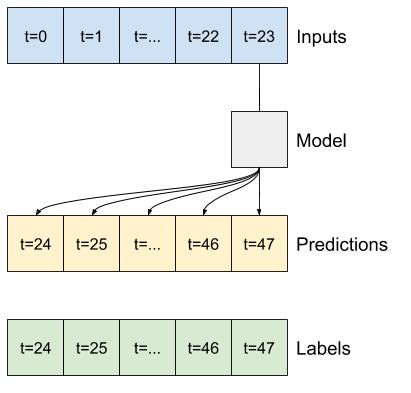
1. Ad esempio, per fare una singola previsione 24 ore nel futuro, date 24 ore di cronologia, potresti definire una finestra come questa:

   

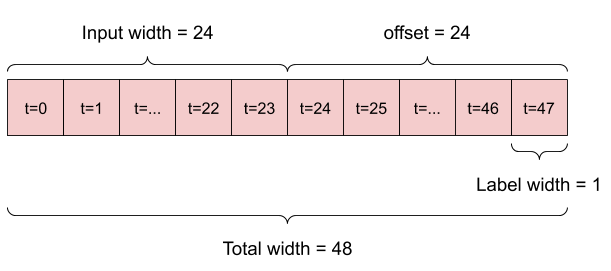
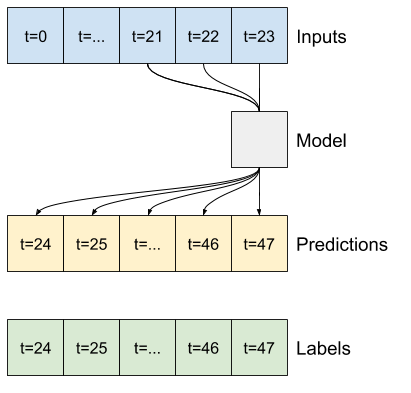
2. Un modello che fa una previsione un'ora nel futuro, date sei ore di storia, avrebbe bisogno di una finestra come questa:

   

Il resto di questa sezione definisce una classe WindowGenerator . Questa classe può:

1. Gestire gli indici e gli offset come mostrato nei diagrammi sopra.
2. Dividi le finestre di funzionalità in coppie (features, labels) .
3. Traccia il contenuto delle finestre risultanti.
4. Genera in modo efficiente batch di queste finestre dai dati di addestramento, valutazione e test, utilizzando tf.data.Dataset s.

1. Indici e offset

Inizia creando la classe WindowGenerator . Il metodo __init__ include tutta la logica necessaria per gli indici di input e di etichetta.

Prende anche la formazione, la valutazione e il test dei DataFrame come input. Questi verranno convertiti in tf.data.Dataset s di Windows in seguito.

class WindowGenerator():
  def __init__(self, input_width, label_width, shift,
               train_df=train_df, val_df=val_df, test_df=test_df,
               label_columns=None):
    # Store the raw data.
    self.train_df = train_df
    self.val_df = val_df
    self.test_df = test_df

    # Work out the label column indices.
    self.label_columns = label_columns
    if label_columns is not None:
      self.label_columns_indices = {name: i for i, name in
                                    enumerate(label_columns)}
    self.column_indices = {name: i for i, name in
                           enumerate(train_df.columns)}

    # Work out the window parameters.
    self.input_width = input_width
    self.label_width = label_width
    self.shift = shift

    self.total_window_size = input_width + shift

    self.input_slice = slice(0, input_width)
    self.input_indices = np.arange(self.total_window_size)[self.input_slice]

    self.label_start = self.total_window_size - self.label_width
    self.labels_slice = slice(self.label_start, None)
    self.label_indices = np.arange(self.total_window_size)[self.labels_slice]

  def __repr__(self):
    return '\n'.join([
        f'Total window size: {self.total_window_size}',
        f'Input indices: {self.input_indices}',
        f'Label indices: {self.label_indices}',
        f'Label column name(s): {self.label_columns}'])

Ecco il codice per creare le 2 finestre mostrate nei diagrammi all'inizio di questa sezione:

w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
                     label_columns=['T (degC)'])
w1

Total window size: 48
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [47]
Label column name(s): ['T (degC)']

w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
                     label_columns=['T (degC)'])
w2

Total window size: 7
Input indices: [0 1 2 3 4 5]
Label indices: [6]
Label column name(s): ['T (degC)']

2. Dividi

Dato un elenco di input consecutivi, il metodo split_window li convertirà in una finestra di input e in una finestra di etichette.

L'esempio w2 che hai definito in precedenza sarà suddiviso in questo modo:

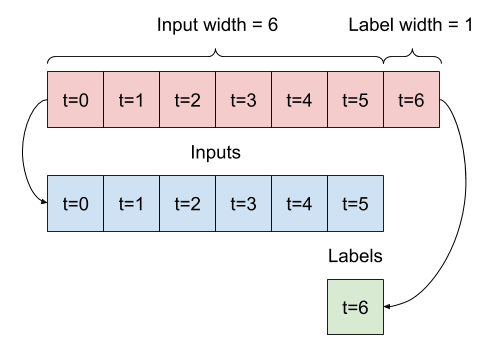
Questo diagramma non mostra l'asse delle features dei dati, ma questa funzione split_window gestisce anche label_columns in modo che possa essere utilizzata sia per gli esempi a output singolo che per quelli multi-output.

def split_window(self, features):
  inputs = features[:, self.input_slice, :]
  labels = features[:, self.labels_slice, :]
  if self.label_columns is not None:
    labels = tf.stack(
        [labels[:, :, self.column_indices[name]] for name in self.label_columns],
        axis=-1)

  # Slicing doesn't preserve static shape information, so set the shapes
  # manually. This way the `tf.data.Datasets` are easier to inspect.
  inputs.set_shape([None, self.input_width, None])
  labels.set_shape([None, self.label_width, None])

  return inputs, labels

WindowGenerator.split_window = split_window

Provalo:

# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
                           np.array(train_df[100:100+w2.total_window_size]),
                           np.array(train_df[200:200+w2.total_window_size])])

example_inputs, example_labels = w2.split_window(example_window)

print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')

All shapes are: (batch, time, features)
Window shape: (3, 7, 19)
Inputs shape: (3, 6, 19)
Labels shape: (3, 1, 1)

In genere, i dati in TensorFlow vengono compressi in matrici in cui l'indice più esterno si trova tra gli esempi (la dimensione "batch"). Gli indici centrali sono le dimensioni "tempo" o "spazio" (larghezza, altezza). Gli indici più interni sono le caratteristiche.

Il codice sopra ha richiesto un batch di tre finestre di 7 passaggi temporali con 19 funzionalità per ogni passaggio temporale. Li divide in un batch di 6 input di funzionalità del passaggio 19 e un'etichetta di funzionalità del passaggio 1 di 1 volta. L'etichetta ha solo una funzione perché WindowGenerator è stato inizializzato con label_columns=['T (degC)'] . Inizialmente, questo tutorial creerà modelli che prevedono etichette di output singolo.

3. Trama

Ecco un metodo di trama che consente una semplice visualizzazione della finestra divisa:

w2.example = example_inputs, example_labels

def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
  inputs, labels = self.example
  plt.figure(figsize=(12, 8))
  plot_col_index = self.column_indices[plot_col]
  max_n = min(max_subplots, len(inputs))
  for n in range(max_n):
    plt.subplot(max_n, 1, n+1)
    plt.ylabel(f'{plot_col} [normed]')
    plt.plot(self.input_indices, inputs[n, :, plot_col_index],
             label='Inputs', marker='.', zorder=-10)

    if self.label_columns:
      label_col_index = self.label_columns_indices.get(plot_col, None)
    else:
      label_col_index = plot_col_index

    if label_col_index is None:
      continue

    plt.scatter(self.label_indices, labels[n, :, label_col_index],
                edgecolors='k', label='Labels', c='#2ca02c', s=64)
    if model is not None:
      predictions = model(inputs)
      plt.scatter(self.label_indices, predictions[n, :, label_col_index],
                  marker='X', edgecolors='k', label='Predictions',
                  c='#ff7f0e', s=64)

    if n == 0:
      plt.legend()

  plt.xlabel('Time [h]')

WindowGenerator.plot = plot

Questo grafico allinea input, etichette e (successive) previsioni in base al tempo a cui si riferisce l'elemento:

w2.plot()

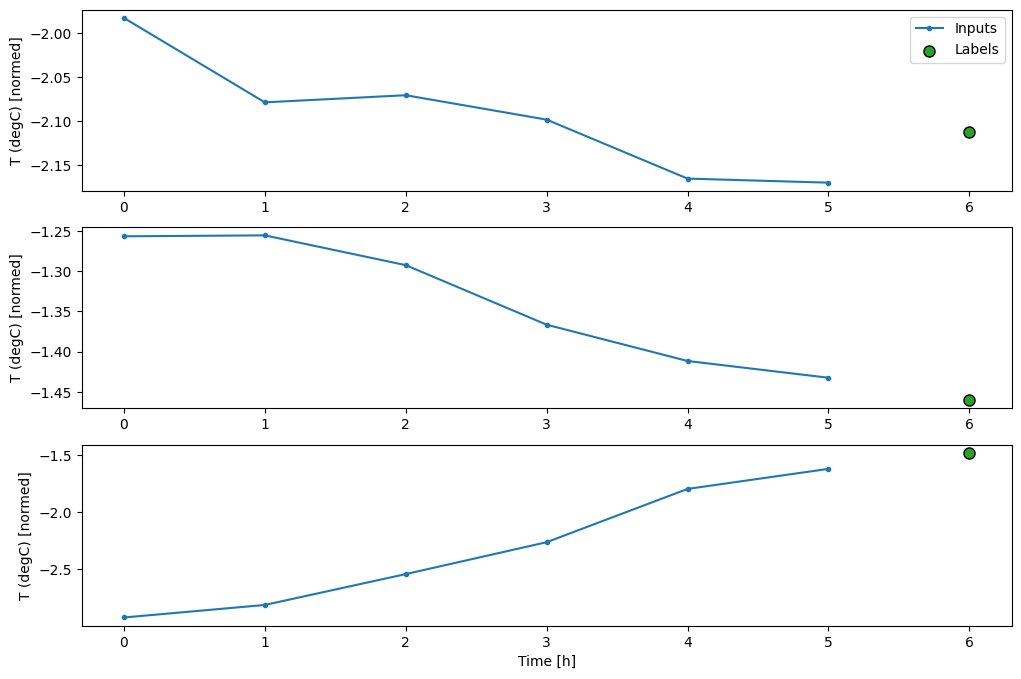
È possibile tracciare le altre colonne, ma la configurazione w2 della finestra di esempio ha solo etichette per la colonna T (degC) .

w2.plot(plot_col='p (mbar)')

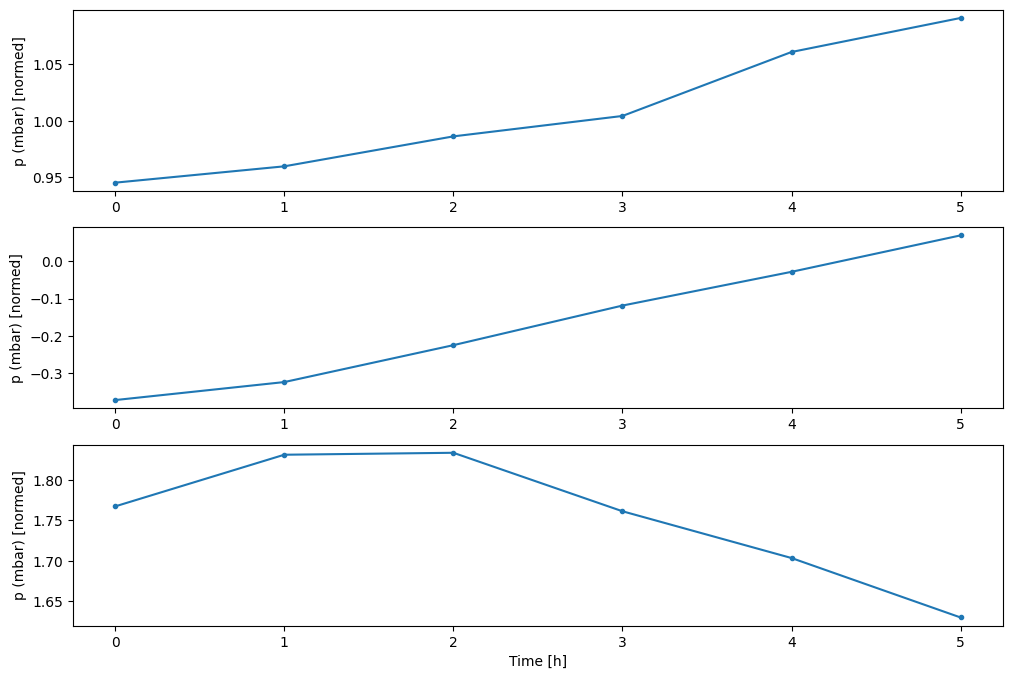
4. Creare tf.data.Dataset s

Infine, questo metodo make_dataset prenderà una serie temporale DataFrame e lo convertirà in un tf.data.Dataset di coppie (input_window, label_window) usando la funzione tf.keras.utils.timeseries_dataset_from_array :

def make_dataset(self, data):
  data = np.array(data, dtype=np.float32)
  ds = tf.keras.utils.timeseries_dataset_from_array(
      data=data,
      targets=None,
      sequence_length=self.total_window_size,
      sequence_stride=1,
      shuffle=True,
      batch_size=32,)

  ds = ds.map(self.split_window)

  return ds

WindowGenerator.make_dataset = make_dataset

L'oggetto WindowGenerator contiene dati di addestramento, convalida e test.

Aggiungi proprietà per accedervi come tf.data.Dataset s usando il metodo make_dataset che hai definito in precedenza. Inoltre, aggiungi un batch di esempio standard per un facile accesso e tracciatura:

@property
def train(self):
  return self.make_dataset(self.train_df)

@property
def val(self):
  return self.make_dataset(self.val_df)

@property
def test(self):
  return self.make_dataset(self.test_df)

@property
def example(self):
  """Get and cache an example batch of `inputs, labels` for plotting."""
  result = getattr(self, '_example', None)
  if result is None:
    # No example batch was found, so get one from the `.train` dataset
    result = next(iter(self.train))
    # And cache it for next time
    self._example = result
  return result

WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example

Ora, l'oggetto WindowGenerator ti dà accesso agli oggetti tf.data.Dataset , così puoi facilmente scorrere i dati.

La proprietà Dataset.element_spec indica la struttura, i tipi di dati e le forme degli elementi del set di dati.

# Each element is an (inputs, label) pair.
w2.train.element_spec

(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None),
 TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))

L'iterazione su un Dataset di dati produce batch concreti:

for example_inputs, example_labels in w2.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 6, 19)
Labels shape (batch, time, features): (32, 1, 1)

Modelli a passo singolo

Il modello più semplice che puoi costruire su questo tipo di dati è quello che prevede il valore di una singola caratteristica: 1 passo temporale (un'ora) nel futuro in base solo alle condizioni attuali.

Quindi, inizia costruendo modelli per prevedere il valore T (degC) un'ora nel futuro.

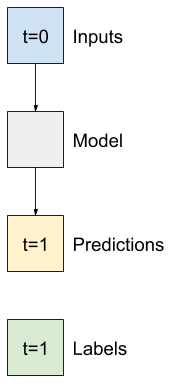
Configura un oggetto WindowGenerator per produrre queste coppie a passaggio singolo (input, label) :

single_step_window = WindowGenerator(
    input_width=1, label_width=1, shift=1,
    label_columns=['T (degC)'])
single_step_window

Total window size: 2
Input indices: [0]
Label indices: [1]
Label column name(s): ['T (degC)']

L'oggetto window crea tf.data.Dataset s dai set di addestramento, convalida e test, consentendo di scorrere facilmente su batch di dati.

for example_inputs, example_labels in single_step_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 1, 19)
Labels shape (batch, time, features): (32, 1, 1)

Linea di base

Prima di costruire un modello addestrabile sarebbe bene avere una linea di base delle prestazioni come punto di confronto con i modelli successivi più complicati.

Questo primo compito è prevedere la temperatura un'ora nel futuro, dato il valore attuale di tutte le caratteristiche. I valori attuali includono la temperatura attuale.

Quindi, inizia con un modello che restituisce solo la temperatura attuale come previsione, prevedendo "Nessun cambiamento". Questa è una linea di base ragionevole poiché la temperatura cambia lentamente. Naturalmente, questa linea di base funzionerà meno bene se si effettua una previsione ulteriormente in futuro.

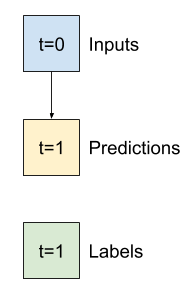
class Baseline(tf.keras.Model):
  def __init__(self, label_index=None):
    super().__init__()
    self.label_index = label_index

  def call(self, inputs):
    if self.label_index is None:
      return inputs
    result = inputs[:, :, self.label_index]
    return result[:, :, tf.newaxis]

Istanziare e valutare questo modello:

baseline = Baseline(label_index=column_indices['T (degC)'])

baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785

Ciò ha stampato alcune metriche delle prestazioni, ma quelle non ti danno un'idea di quanto bene stia andando il modello.

WindowGenerator ha un metodo plot, ma i grafici non saranno molto interessanti con un solo campione.

Quindi, crea un WindowGenerator più ampio che genera Windows 24 ore di input ed etichette consecutive alla volta. La nuova variabile wide_window non cambia il modo in cui opera il modello. Il modello continua a fare previsioni per un'ora nel futuro sulla base di un singolo passaggio temporale di input. In questo caso, l'asse time agisce come l'asse batch : ogni previsione viene effettuata in modo indipendente senza alcuna interazione tra i passaggi temporali:

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1,
    label_columns=['T (degC)'])

wide_window

Total window size: 25
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
Label column name(s): ['T (degC)']

Questa finestra espansa può essere passata direttamente allo stesso modello di baseline senza modifiche al codice. Ciò è possibile perché gli input e le etichette hanno lo stesso numero di fasi temporali e la linea di base inoltra semplicemente l'input all'output:

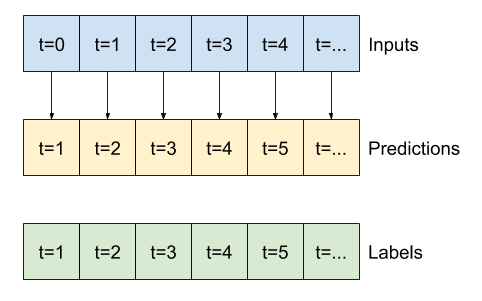
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

Tracciando le previsioni del modello di base, nota che sono semplicemente le etichette spostate a destra di un'ora:

wide_window.plot(baseline)

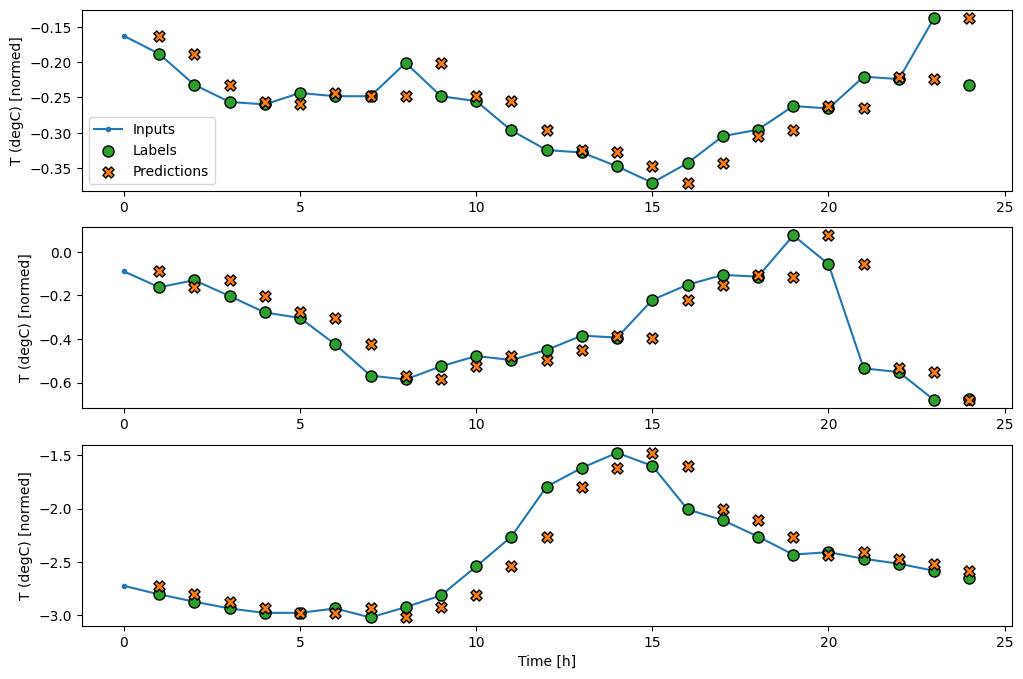
Nei grafici sopra di tre esempi, il modello a passo singolo viene eseguito nel corso di 24 ore. Questo merita qualche spiegazione:

• La linea blu Inputs mostra la temperatura di ingresso in ogni fase. Il modello riceve tutte le caratteristiche, questo grafico mostra solo la temperatura.
• I punti Labels verdi mostrano il valore di previsione target. Questi punti vengono visualizzati all'ora della previsione, non all'ora di input. Ecco perché la gamma di etichette viene spostata di 1 passo rispetto agli ingressi.
• Le croci di Predictions arancioni sono le previsioni del modello per ogni fase temporale di output. Se il modello prevedesse perfettamente le previsioni atterrerebbero direttamente sulle Labels .

Modello lineare

Il modello addestrabile più semplice che puoi applicare a questa attività consiste nell'inserire una trasformazione lineare tra l'input e l'output. In questo caso l'uscita da un passo temporale dipende solo da quel passo:

Uno strato tf.keras.layers.Dense senza set di activation è un modello lineare. Il livello trasforma solo l'ultimo asse dei dati da (batch, time, inputs) a (batch, time, units) ; viene applicato indipendentemente a ogni articolo lungo l'asse del batch e del time .

linear = tf.keras.Sequential([
    tf.keras.layers.Dense(units=1)
])

print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)

Input shape: (32, 1, 19)
Output shape: (32, 1, 1)

Questo tutorial addestra molti modelli, quindi impacchetta la procedura di addestramento in una funzione:

MAX_EPOCHS = 20

def compile_and_fit(model, window, patience=2):
  early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
                                                    patience=patience,
                                                    mode='min')

  model.compile(loss=tf.losses.MeanSquaredError(),
                optimizer=tf.optimizers.Adam(),
                metrics=[tf.metrics.MeanAbsoluteError()])

  history = model.fit(window.train, epochs=MAX_EPOCHS,
                      validation_data=window.val,
                      callbacks=[early_stopping])
  return history

Addestrare il modello e valutarne le prestazioni:

history = compile_and_fit(linear, single_step_window)

val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858
Epoch 2/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711
Epoch 3/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690
Epoch 4/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692
Epoch 5/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685
Epoch 6/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687
Epoch 7/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680
Epoch 8/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683
Epoch 9/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684
439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684

Come il modello di baseline , il modello lineare può essere richiamato su lotti di ampie finestre. Usato in questo modo, il modello effettua un insieme di previsioni indipendenti su fasi temporali consecutive. L'asse del time agisce come un altro asse batch . Non ci sono interazioni tra le previsioni in ogni fase temporale.

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

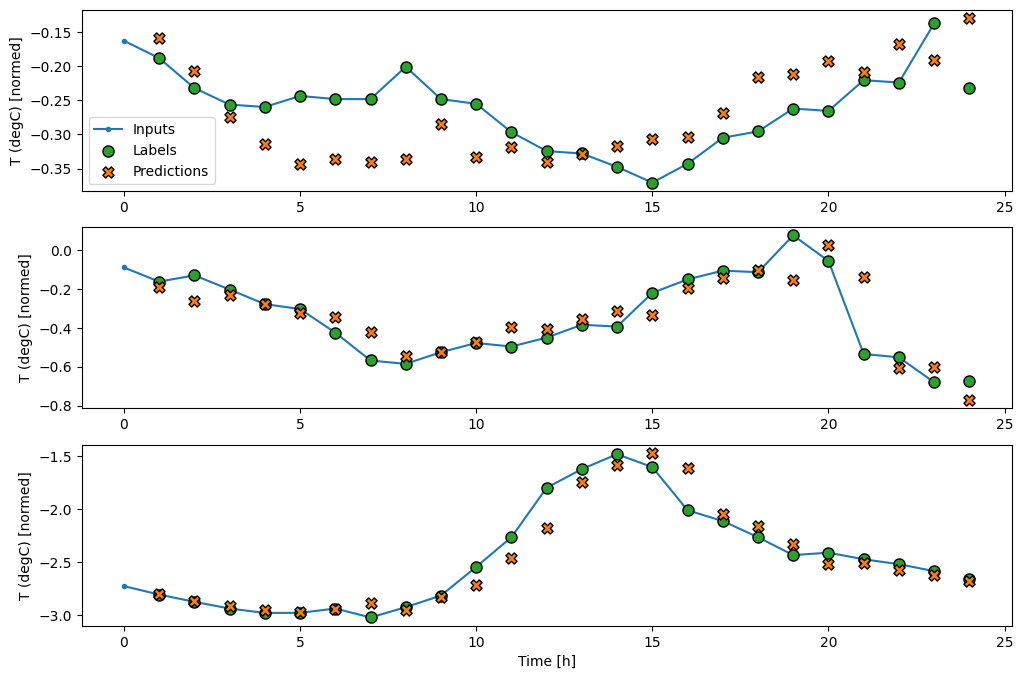
Ecco la trama delle sue previsioni di esempio su wide_window , nota come in molti casi la previsione è chiaramente migliore della semplice restituzione della temperatura di input, ma in alcuni casi è peggio:

wide_window.plot(linear)

Un vantaggio dei modelli lineari è che sono relativamente semplici da interpretare. Puoi estrarre i pesi del livello e visualizzare il peso assegnato a ciascun input:

plt.bar(x = range(len(train_df.columns)),
        height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)

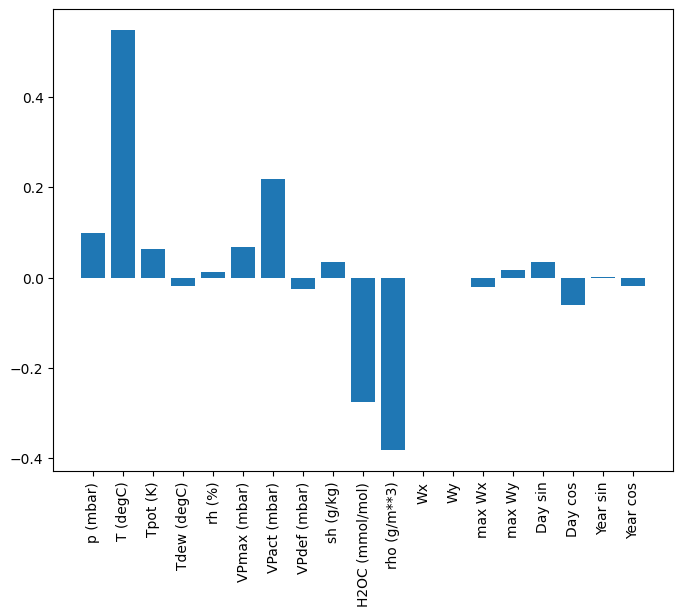
A volte il modello non dà nemmeno il massimo peso sull'input T (degC) . Questo è uno dei rischi dell'inizializzazione casuale.

Denso

Prima di applicare modelli che operano effettivamente su più fasi temporali, vale la pena verificare le prestazioni di modelli a fasi di ingresso singolo più profonde, più potenti.

Ecco un modello simile al modello linear , tranne per il fatto che impila diversi strati Dense tra l'input e l'output:

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=1)
])

history = compile_and_fit(dense, single_step_window)

val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666
Epoch 2/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610
Epoch 3/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618
Epoch 4/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582
Epoch 5/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581
Epoch 6/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579
Epoch 7/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580
439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580

Denso a più gradini

Un modello single-time-step non ha contesto per i valori correnti dei suoi input. Non può vedere come cambiano le funzioni di input nel tempo. Per risolvere questo problema, il modello ha bisogno di accedere a più fasi temporali quando si effettuano previsioni:

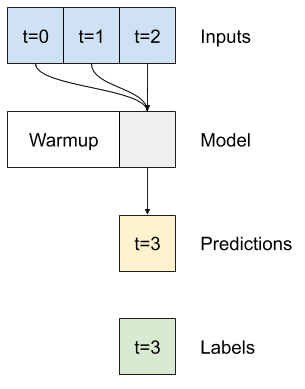
I modelli di baseline , linear e dense hanno gestito ogni fase temporale in modo indipendente. Qui il modello richiederà più passaggi temporali come input per produrre un singolo output.

Crea un WindowGenerator che produrrà lotti di input di tre ore ed etichette di un'ora:

Si noti che il parametro di shift della Window è relativo alla fine delle due finestre.

CONV_WIDTH = 3
conv_window = WindowGenerator(
    input_width=CONV_WIDTH,
    label_width=1,
    shift=1,
    label_columns=['T (degC)'])

conv_window

Total window size: 4
Input indices: [0 1 2]
Label indices: [3]
Label column name(s): ['T (degC)']

conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")

Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')

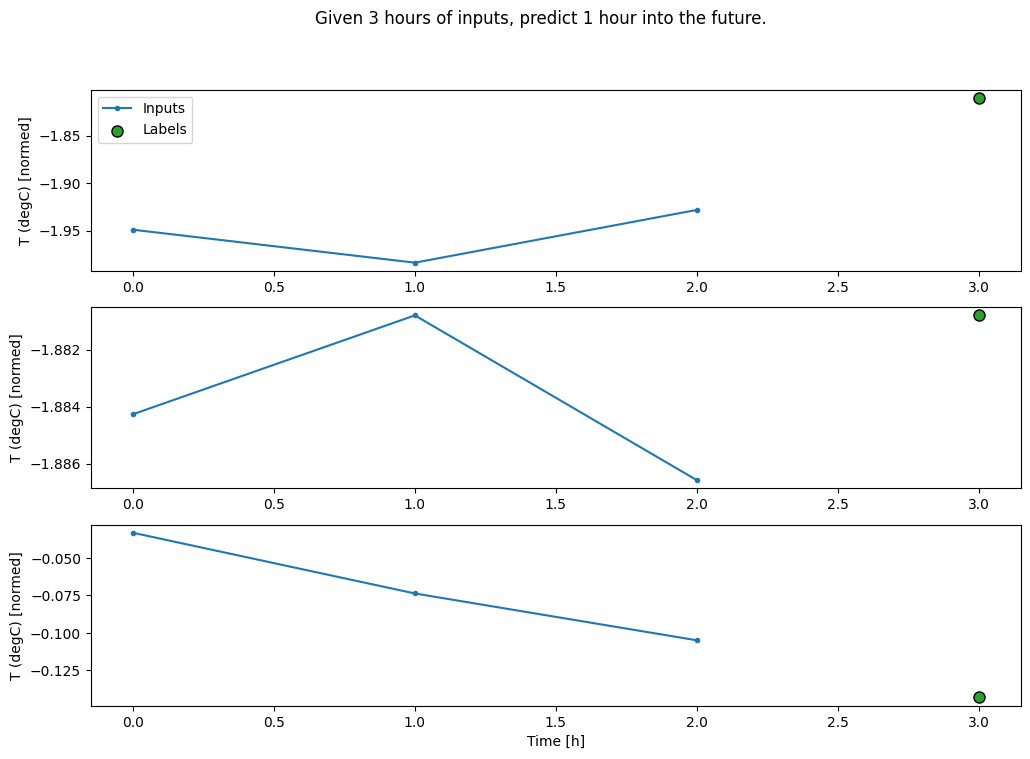
Puoi addestrare un modello dense su una finestra a più passaggi di input aggiungendo un tf.keras.layers.Flatten come primo livello del modello:

multi_step_dense = tf.keras.Sequential([
    # Shape: (time, features) => (time*features)
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
    # Add back the time dimension.
    # Shape: (outputs) => (1, outputs)
    tf.keras.layers.Reshape([1, -1]),
])

print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)

Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

history = compile_and_fit(multi_step_dense, conv_window)

IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609

conv_window.plot(multi_step_dense)

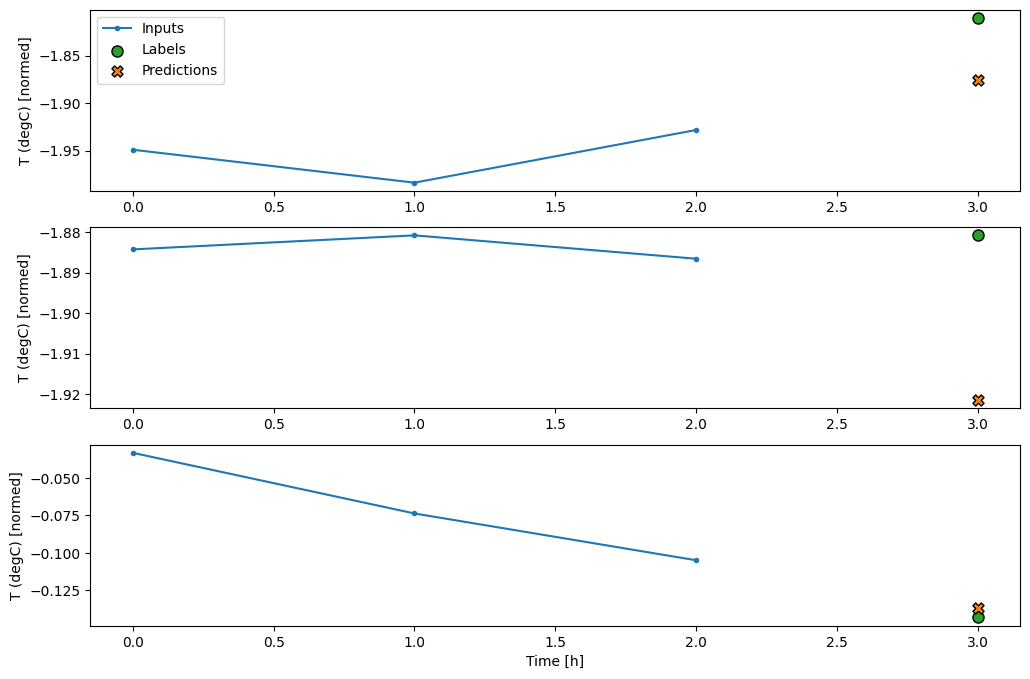
Il principale svantaggio di questo approccio è che il modello risultante può essere eseguito solo su finestre di input di esattamente questa forma.

print('Input shape:', wide_window.example[0].shape)
try:
  print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
  print(f'\n{type(e).__name__}:{e}')

Input shape: (32, 24, 19)

ValueError:Exception encountered when calling layer "sequential_2" (type Sequential).

Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456)

Call arguments received:
  • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32)
  • training=None
  • mask=None

I modelli convoluzionali nella sezione successiva risolvono questo problema.

Rete neurale di convoluzione

Un livello di convoluzione ( tf.keras.layers.Conv1D ) richiede anche più passaggi temporali come input per ciascuna previsione.

Di seguito è riportato lo stesso modello di multi_step_dense , riscritto con una convoluzione.

Nota le modifiche:

• Il tf.keras.layers.Flatten e il primo tf.keras.layers.Dense sono sostituiti da un tf.keras.layers.Conv1D .
• Il tf.keras.layers.Reshape non è più necessario poiché la convoluzione mantiene l'asse del tempo nel suo output.

conv_model = tf.keras.Sequential([
    tf.keras.layers.Conv1D(filters=32,
                           kernel_size=(CONV_WIDTH,),
                           activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
])

Eseguilo su un batch di esempio per verificare che il modello produca output con la forma prevista:

print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)

Conv model on `conv_window`
Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

Addestralo e valutalo su conv_window e dovrebbe fornire prestazioni simili al modello multi_step_dense .

history = compile_and_fit(conv_model, conv_window)

IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)

438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568

La differenza tra questo conv_model e il modello multi_step_dense è che conv_model può essere eseguito su input di qualsiasi lunghezza. Il livello convoluzionale viene applicato a una finestra scorrevole di input:

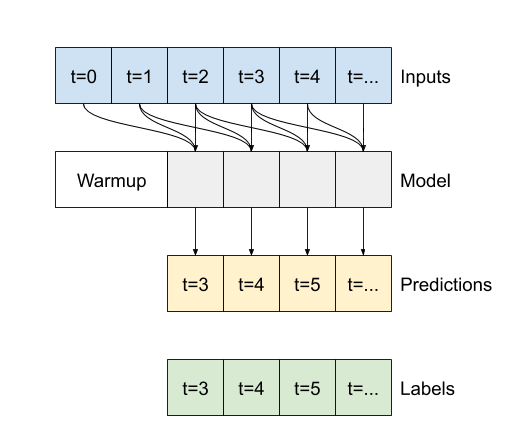
Se lo esegui su un input più ampio, produce un output più ampio:

print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)

Wide window
Input shape: (32, 24, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 22, 1)

Si noti che l'output è più breve dell'input. Per fare in modo che la formazione o il disegno funzionino, è necessario che le etichette e la previsione abbiano la stessa lunghezza. Quindi crea un WindowGenerator per produrre ampie finestre con alcuni passaggi di tempo di input aggiuntivi in ​​modo che le lunghezze dell'etichetta e della previsione corrispondano:

LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
    input_width=INPUT_WIDTH,
    label_width=LABEL_WIDTH,
    shift=1,
    label_columns=['T (degC)'])

wide_conv_window

Total window size: 27
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25]
Label indices: [ 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26]
Label column name(s): ['T (degC)']

print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)

Wide conv window
Input shape: (32, 26, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 24, 1)

Ora puoi tracciare le previsioni del modello su una finestra più ampia. Prendere nota dei 3 passaggi temporali di input prima della prima previsione. Ogni previsione qui si basa sui 3 passaggi temporali precedenti:

wide_conv_window.plot(conv_model)

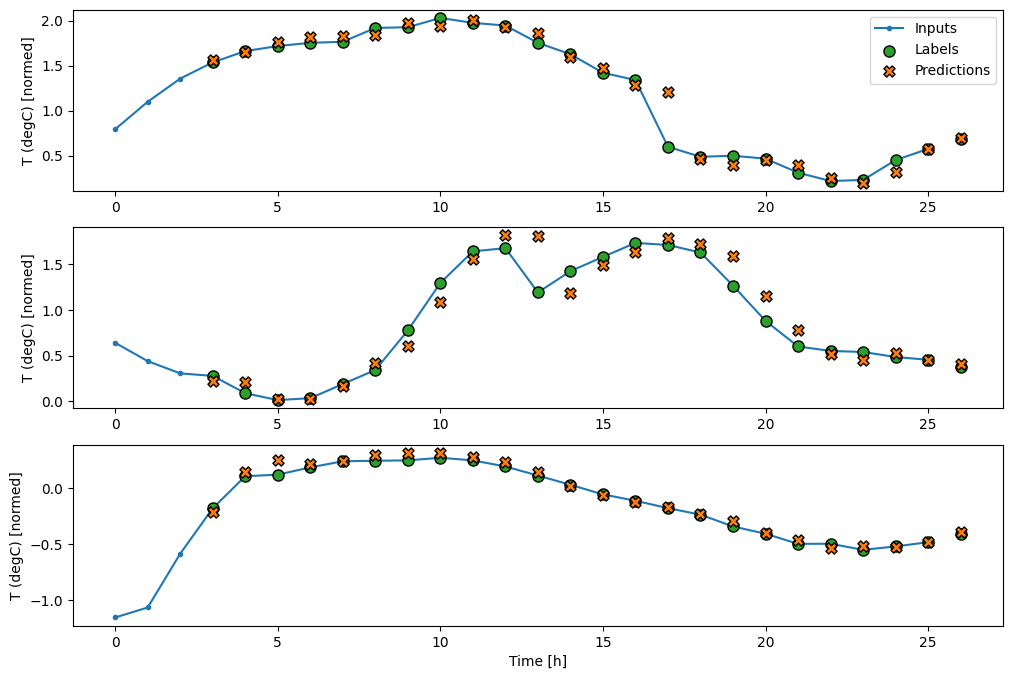
Rete neurale ricorrente

Una rete neurale ricorrente (RNN) è un tipo di rete neurale adatta ai dati di serie temporali. Gli RNN elaborano una serie temporale passo dopo passo, mantenendo uno stato interno da un passo temporale all'altro.

Puoi saperne di più nella Generazione di testo con un tutorial RNN e nella guida Recurrent Neural Networks (RNN) with Keras .

In questo tutorial, utilizzerai un livello RNN chiamato memoria a lungo termine ( tf.keras.layers.LSTM ).

Un importante argomento del costruttore per tutti i livelli RNN Keras, come tf.keras.layers.LSTM , è l'argomento return_sequences . Questa impostazione può configurare il livello in uno dei due modi seguenti:

1. Se False , l'impostazione predefinita, il livello restituisce solo l'output del passaggio temporale finale, dando al modello il tempo di riscaldare il suo stato interno prima di effettuare una singola previsione:

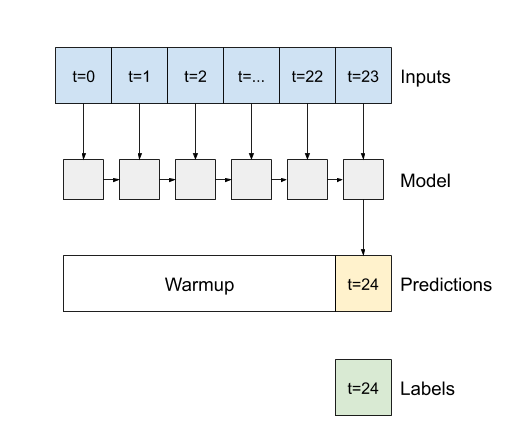
1. Se True , il livello restituisce un output per ogni input. Questo è utile per:
   • Impilare i livelli RNN.
   • Addestrare un modello su più fasi temporali contemporaneamente.

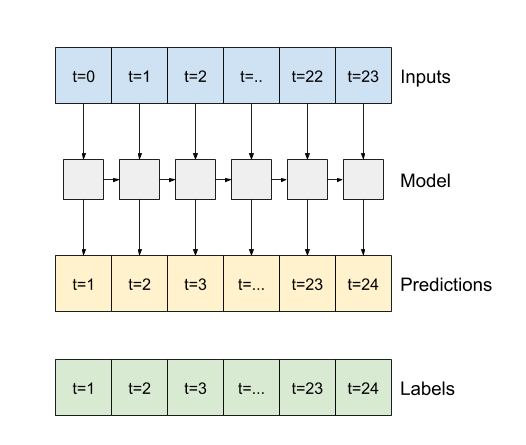
lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=1)
])

Con return_sequences=True , il modello può essere addestrato su 24 ore di dati alla volta.

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509

wide_window.plot(lstm_model)

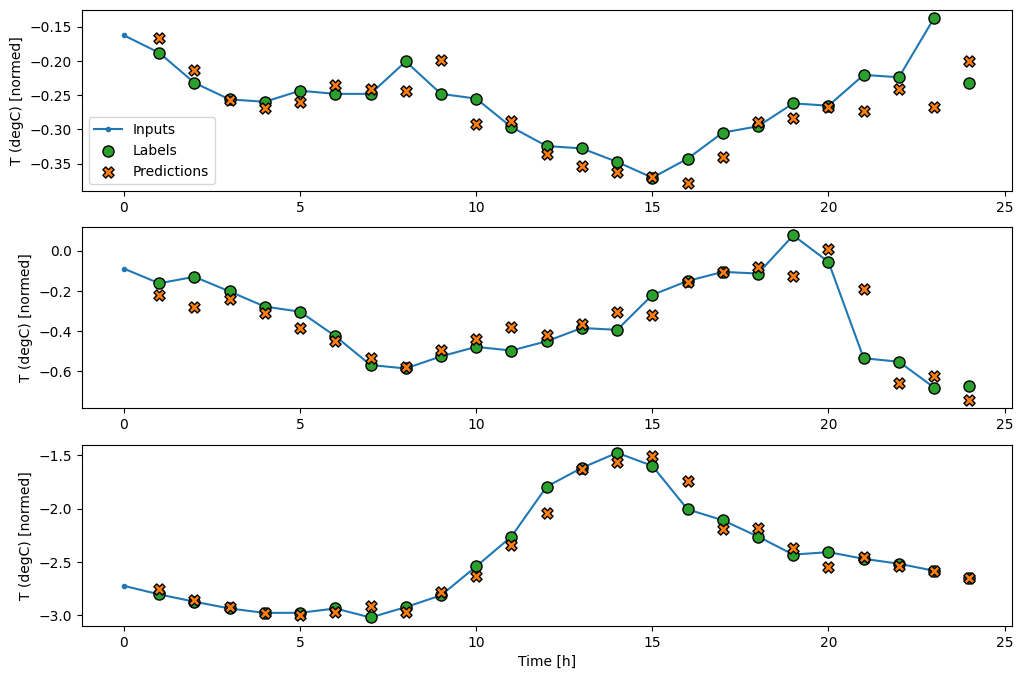
Prestazione

Con questo set di dati in genere ciascuno dei modelli fa leggermente meglio di quello precedente:

x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
_ = plt.legend()

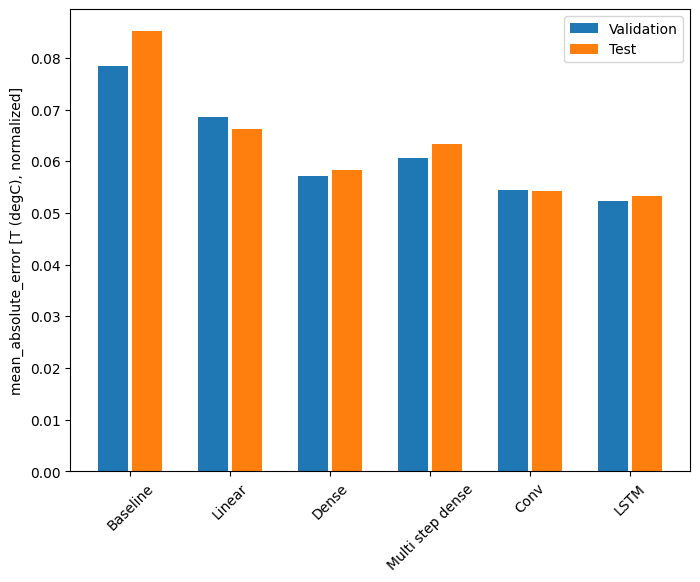
for name, value in performance.items():
  print(f'{name:12s}: {value[1]:0.4f}')

Baseline    : 0.0852
Linear      : 0.0666
Dense       : 0.0573
Multi step dense: 0.0586
Conv        : 0.0577
LSTM        : 0.0518

Modelli a più uscite

Finora i modelli prevedevano tutti una singola caratteristica di output, T (degC) , per un singolo passaggio temporale.

Tutti questi modelli possono essere convertiti per prevedere più funzionalità semplicemente modificando il numero di unità nel livello di output e regolando le finestre di addestramento per includere tutte le funzionalità nelle labels ( example_labels ):

single_step_window = WindowGenerator(
    # `WindowGenerator` returns all features as labels if you 
    # don't set the `label_columns` argument.
    input_width=1, label_width=1, shift=1)

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

for example_inputs, example_labels in wide_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 24, 19)
Labels shape (batch, time, features): (32, 24, 19)

Notare sopra che l'asse delle features delle etichette ora ha la stessa profondità degli input, invece di 1 .

Linea di base

Lo stesso modello di base ( Baseline ) può essere utilizzato qui, ma questa volta ripetendo tutte le funzionalità invece di selezionare un label_index specifico:

baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589

Denso

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(dense, single_step_window)

IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302

RNN

%%time
wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)

print()

438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205

CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s
Wall time: 2min 8s

Avanzato: Connessioni residue

Il modello Baseline di prima ha sfruttato il fatto che la sequenza non cambia drasticamente da un passaggio temporale all'altro. Ogni modello addestrato in questo tutorial finora è stato inizializzato in modo casuale, quindi è stato necessario apprendere che l'output è una piccola modifica rispetto al passaggio temporale precedente.

Sebbene sia possibile aggirare questo problema con un'attenta inizializzazione, è più semplice integrarlo nella struttura del modello.

È comune nell'analisi delle serie temporali creare modelli che, invece di prevedere il valore successivo, prevedono come cambierà il valore nel passaggio temporale successivo. Allo stesso modo, le reti residue, o ResNet, nel deep learning si riferiscono ad architetture in cui ogni livello si aggiunge al risultato cumulativo del modello.

È così che approfitti della consapevolezza che il cambiamento dovrebbe essere piccolo.

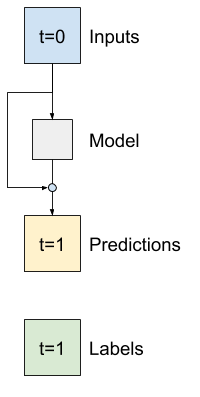
In sostanza, questo inizializza il modello in modo che corrisponda a Baseline . Per questo compito aiuta i modelli a convergere più velocemente, con prestazioni leggermente migliori.

Questo approccio può essere utilizzato insieme a qualsiasi modello discusso in questo tutorial.

Qui, viene applicato al modello LSTM, si noti l'uso di tf.initializers.zeros per garantire che le modifiche iniziali previste siano piccole e non prevalgano sulla connessione residua. Non ci sono problemi di rottura della simmetria per i gradienti qui, poiché gli zeros vengono utilizzati solo sull'ultimo livello.

class ResidualWrapper(tf.keras.Model):
  def __init__(self, model):
    super().__init__()
    self.model = model

  def call(self, inputs, *args, **kwargs):
    delta = self.model(inputs, *args, **kwargs)

    # The prediction for each time step is the input
    # from the previous time step plus the delta
    # calculated by the model.
    return inputs + delta

%%time
residual_lstm = ResidualWrapper(
    tf.keras.Sequential([
    tf.keras.layers.LSTM(32, return_sequences=True),
    tf.keras.layers.Dense(
        num_features,
        # The predicted deltas should start small.
        # Therefore, initialize the output layer with zeros.
        kernel_initializer=tf.initializers.zeros())
]))

history = compile_and_fit(residual_lstm, wide_window)

IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()

438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179

CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s
Wall time: 43.1 s

Prestazione

Ecco le prestazioni complessive di questi modelli multi-uscita.

x = np.arange(len(performance))
width = 0.3

metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()

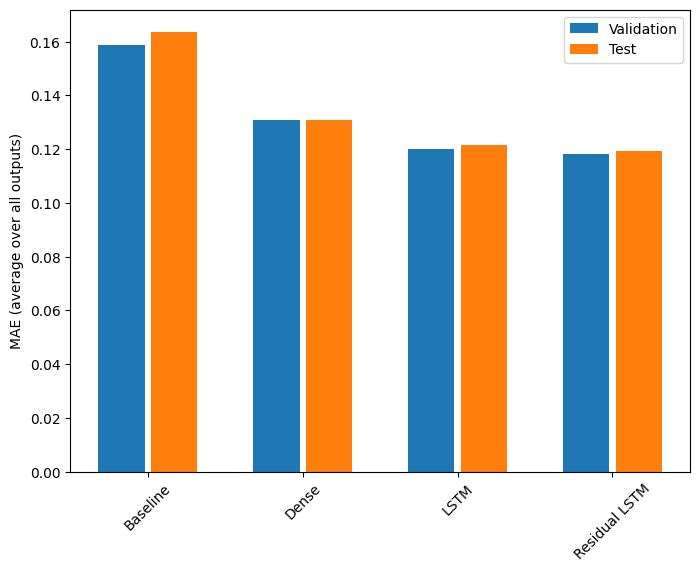
for name, value in performance.items():
  print(f'{name:15s}: {value[1]:0.4f}')

Baseline       : 0.1638
Dense          : 0.1311
LSTM           : 0.1214
Residual LSTM  : 0.1194

Le prestazioni di cui sopra sono mediate su tutti gli output del modello.

Modelli a più fasi

Sia i modelli a output singolo che quelli a output multiplo nelle sezioni precedenti hanno effettuato previsioni di singoli passaggi temporali , un'ora nel futuro.

In questa sezione viene illustrato come espandere questi modelli per effettuare previsioni di più fasi temporali .

In una previsione a più fasi, il modello deve imparare a prevedere una serie di valori futuri. Pertanto, a differenza di un modello a fase singola, in cui è previsto un solo punto futuro, un modello a più fasi prevede una sequenza di valori futuri.

Ci sono due approcci approssimativi a questo:

1. Pronostici a colpo singolo in cui l'intera serie temporale viene prevista contemporaneamente.
2. Previsioni autoregressive in cui il modello effettua solo previsioni a passo singolo e il suo output viene restituito come input.

In questa sezione tutti i modelli prevederanno tutte le caratteristiche in tutti i passaggi temporali di output .

Per il modello a più fasi, i dati di addestramento sono nuovamente costituiti da campioni orari. Tuttavia, qui, i modelli impareranno a prevedere 24 ore nel futuro, date 24 ore del passato.

Ecco un oggetto Window che genera queste sezioni dal set di dati:

OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
                               label_width=OUT_STEPS,
                               shift=OUT_STEPS)

multi_window.plot()
multi_window

Total window size: 48
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47]
Label column name(s): None

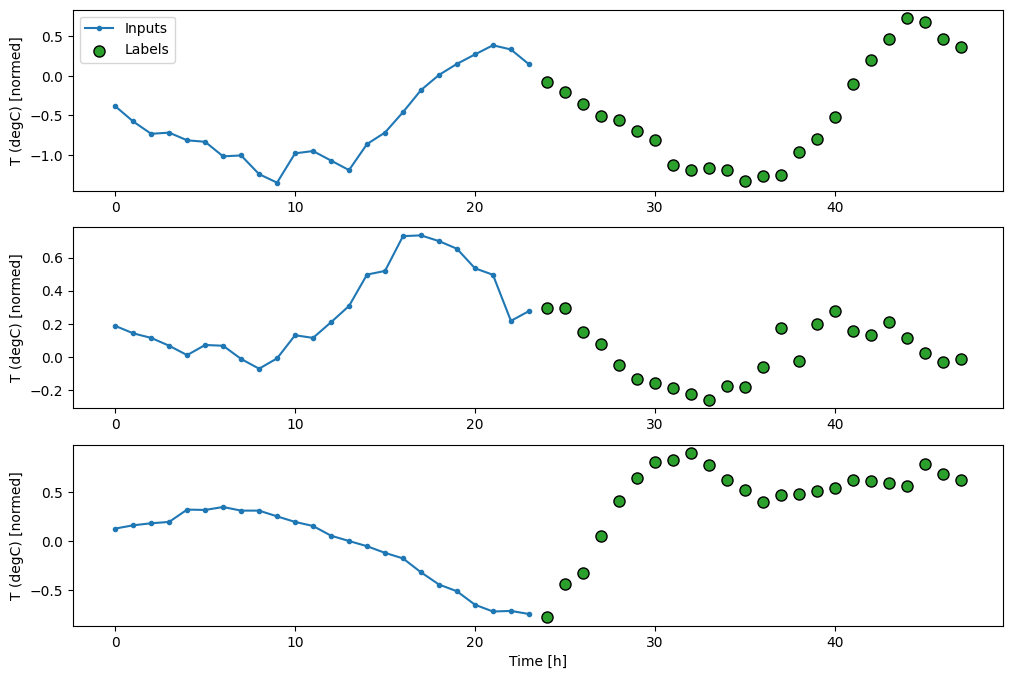
Linee di base

Una semplice linea di base per questa attività consiste nel ripetere l'ultimo passaggio temporale di input per il numero richiesto di passaggi temporali di output:

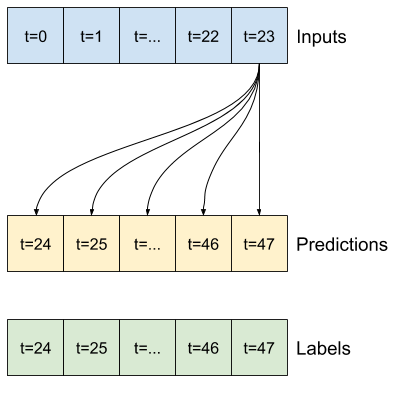
class MultiStepLastBaseline(tf.keras.Model):
  def call(self, inputs):
    return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])

last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
                      metrics=[tf.metrics.MeanAbsoluteError()])

multi_val_performance = {}
multi_performance = {}

multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)

437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007

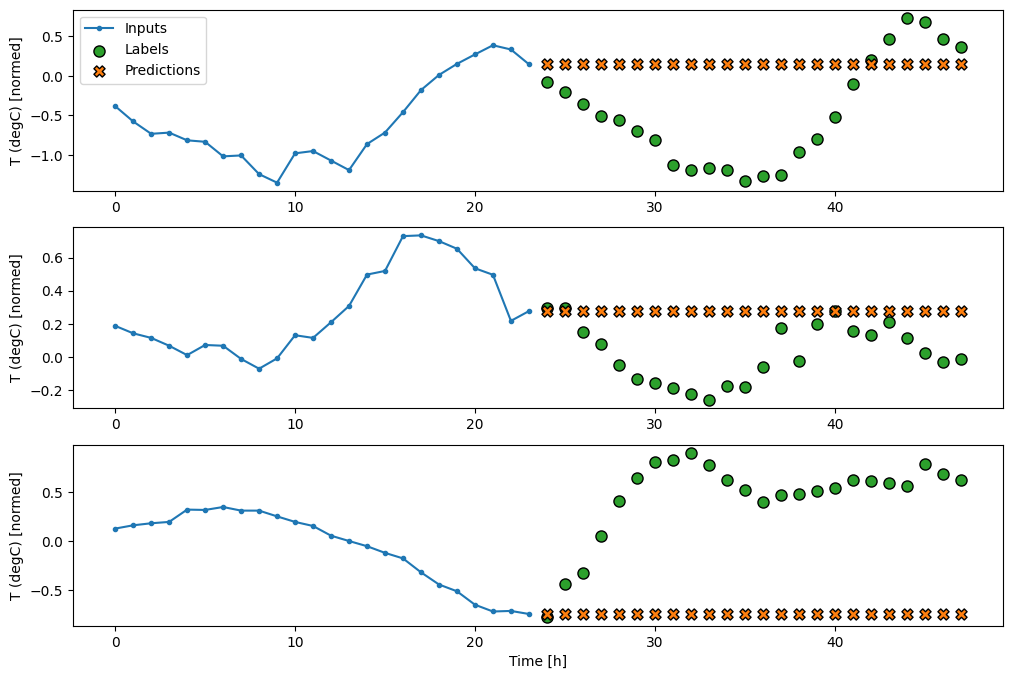
Poiché questo compito è prevedere 24 ore nel futuro, date 24 ore del passato, un altro approccio semplice consiste nel ripetere il giorno precedente, supponendo che il domani sarà simile:

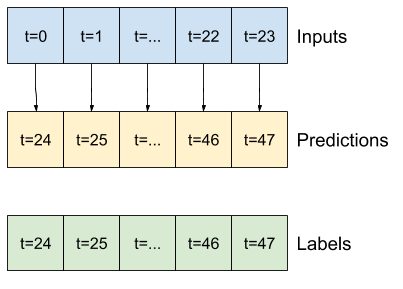
class RepeatBaseline(tf.keras.Model):
  def call(self, inputs):
    return inputs

repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
                        metrics=[tf.metrics.MeanAbsoluteError()])

multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)

437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959

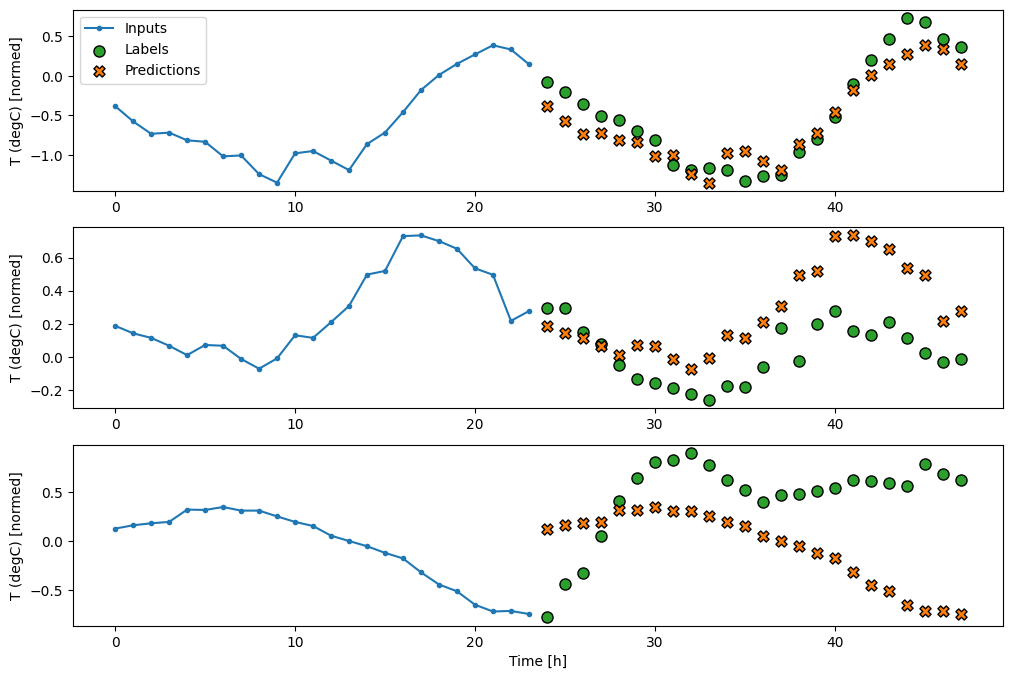
Modelli a scatto singolo

Un approccio di alto livello a questo problema consiste nell'utilizzare un modello "single-shot", in cui il modello effettua la previsione dell'intera sequenza in un unico passaggio.

Questo può essere implementato in modo efficiente come tf.keras.layers.Dense con OUT_STEPS*features unità di output. Il modello deve solo rimodellare l'output nel modo richiesto (OUTPUT_STEPS, features) .

Lineare

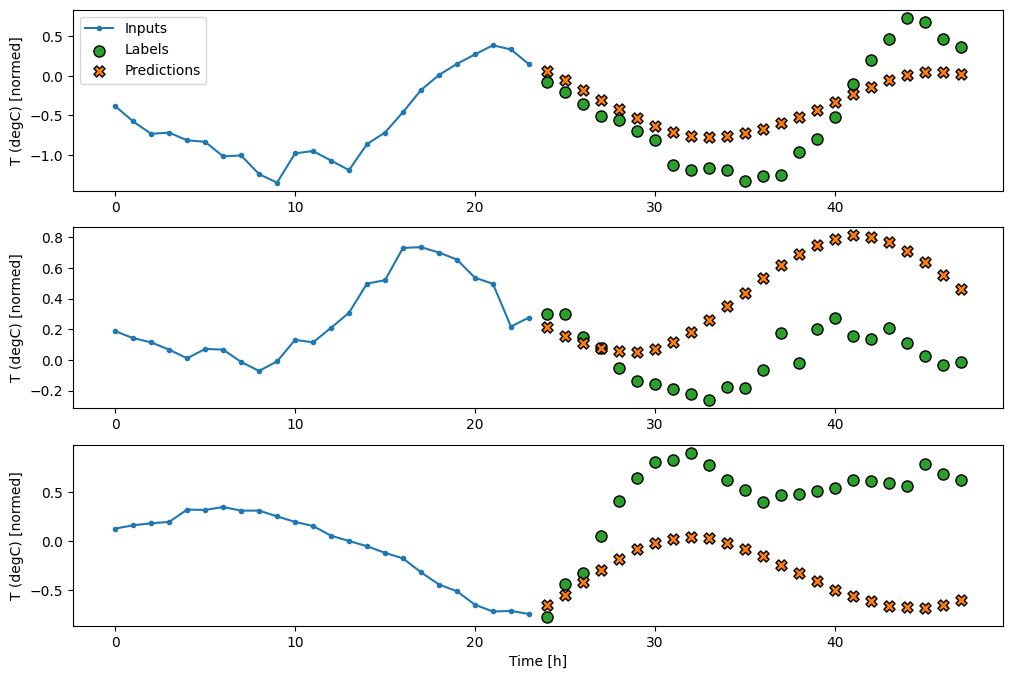
Un semplice modello lineare basato sull'ultimo passaggio temporale di input funziona meglio di entrambe le linee di base, ma è sottodimensionato. Il modello deve prevedere i passaggi temporali OUTPUT_STEPS , da un singolo passaggio temporale di input con una proiezione lineare. Può catturare solo una fetta a bassa dimensione del comportamento, probabilmente basata principalmente sull'ora del giorno e sul periodo dell'anno.

multi_linear_model = tf.keras.Sequential([
    # Take the last time-step.
    # Shape [batch, time, features] => [batch, 1, features]
    tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
    # Shape => [batch, 1, out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_linear_model, multi_window)

IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)

437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053

Denso

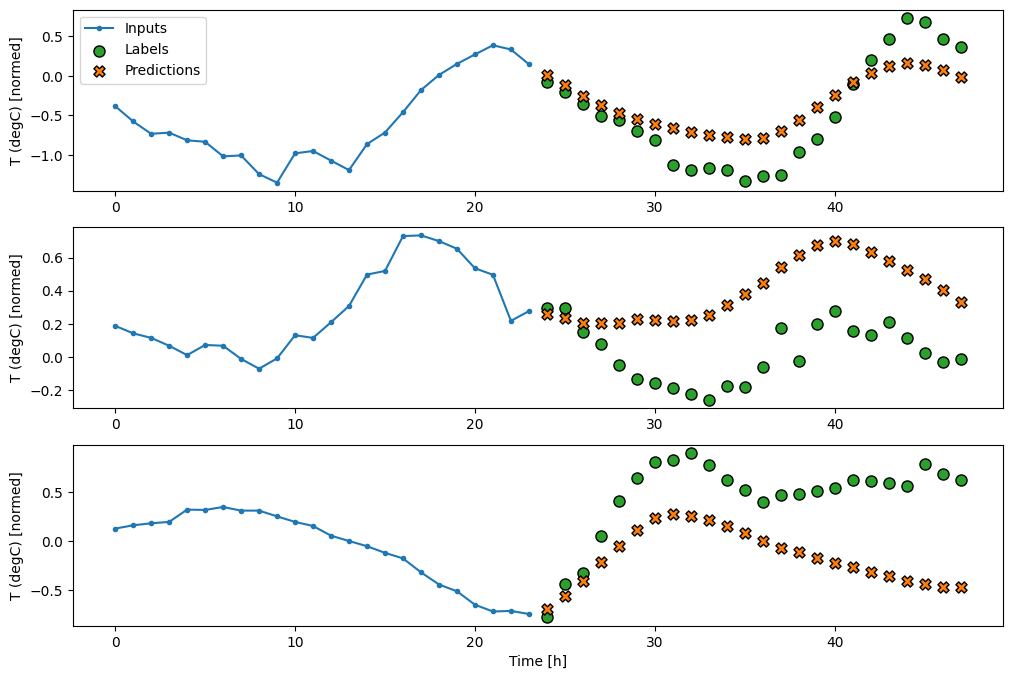
L'aggiunta di un tf.keras.layers.Dense tra l'input e l'output fornisce più potenza al modello lineare, ma si basa ancora solo su un singolo passo temporale di input.

multi_dense_model = tf.keras.Sequential([
    # Take the last time step.
    # Shape [batch, time, features] => [batch, 1, features]
    tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
    # Shape => [batch, 1, dense_units]
    tf.keras.layers.Dense(512, activation='relu'),
    # Shape => [batch, out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_dense_model, multi_window)

IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)

437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837

CNN

Un modello convoluzionale effettua previsioni basate su una cronologia a larghezza fissa, che può portare a prestazioni migliori rispetto al modello denso poiché può vedere come cambiano le cose nel tempo:

CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
    # Shape [batch, time, features] => [batch, CONV_WIDTH, features]
    tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
    # Shape => [batch, 1, conv_units]
    tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
    # Shape => [batch, 1,  out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_conv_model, multi_window)

IPython.display.clear_output()

multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)

437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833

RNN

Un modello ricorrente può imparare a utilizzare una lunga storia di input, se è rilevante per le previsioni che il modello sta facendo. Qui il modello accumulerà lo stato interno per 24 ore, prima di fare una singola previsione per le 24 ore successive.

In questo formato single-shot, LSTM deve produrre un output solo nell'ultimo passaggio temporale, quindi imposta return_sequences=False in tf.keras.layers.LSTM .

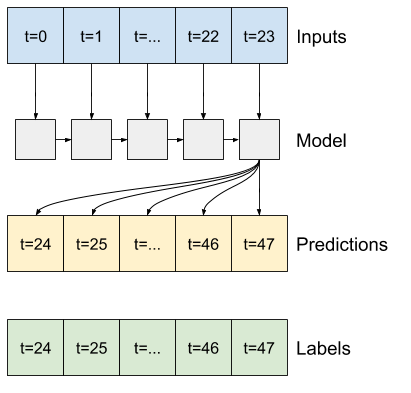
multi_lstm_model = tf.keras.Sequential([
    # Shape [batch, time, features] => [batch, lstm_units].
    # Adding more `lstm_units` just overfits more quickly.
    tf.keras.layers.LSTM(32, return_sequences=False),
    # Shape => [batch, out_steps*features].
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features].
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_lstm_model, multi_window)

IPython.display.clear_output()

multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)

437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863

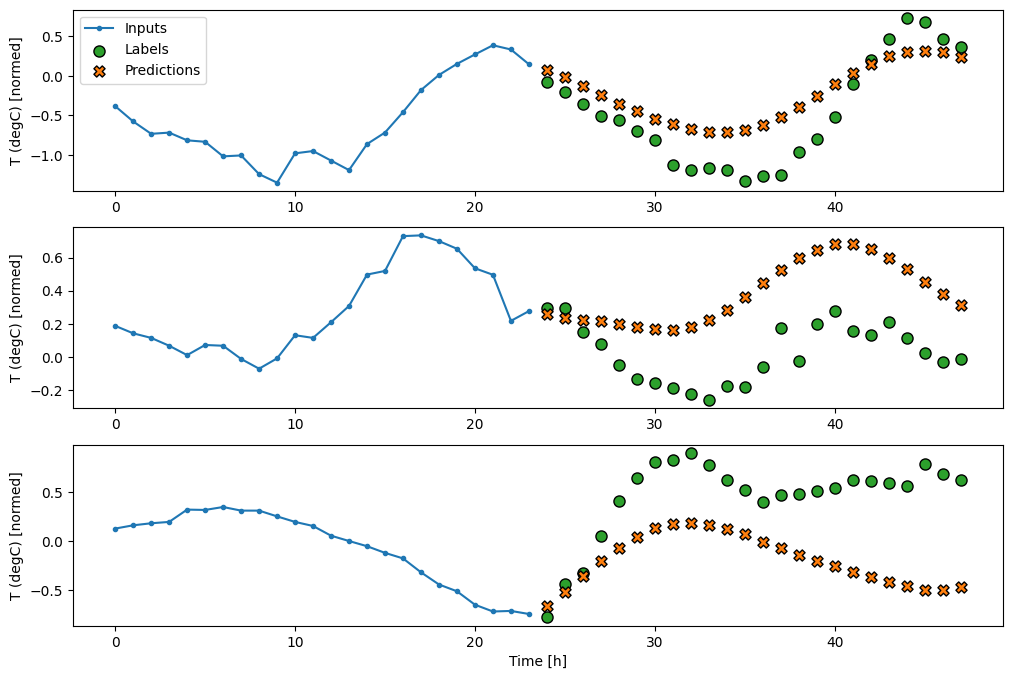
Avanzato: modello autoregressivo

Tutti i modelli di cui sopra prevedono l'intera sequenza di output in un unico passaggio.

In alcuni casi può essere utile che il modello scomponga questa previsione in singoli passaggi temporali. Quindi, l'output di ciascun modello può essere reimmesso in se stesso ad ogni passaggio e le previsioni possono essere fatte condizionate dal precedente, come nel classico Generating Sequences With Recurrent Neural Networks .

Un chiaro vantaggio di questo stile di modello è che può essere impostato per produrre output con una lunghezza variabile.

Potresti prendere uno qualsiasi dei modelli multi-output a passaggio singolo addestrati nella prima metà di questo tutorial ed eseguire in un ciclo di feedback autoregressivo, ma qui ti concentrerai sulla creazione di un modello che è stato esplicitamente addestrato per farlo.

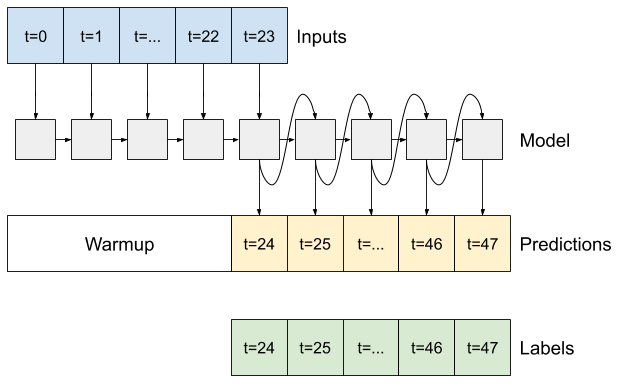
RNN

Questo tutorial crea solo un modello RNN autoregressivo, ma questo modello può essere applicato a qualsiasi modello progettato per generare un singolo passaggio temporale.

Il modello avrà la stessa forma di base dei modelli LSTM a passaggio singolo dei precedenti: un livello tf.keras.layers.LSTM seguito da un livello tf.keras.layers.Dense che converte gli output del livello LSTM in previsioni del modello.

Un tf.keras.layers.LSTM è un tf.keras.layers.LSTMCell racchiuso nel livello superiore tf.keras.layers.RNN che gestisce lo stato e i risultati della sequenza per te (controlla le reti neurali ricorrenti (RNN) con Keras guida per i dettagli).

In questo caso, il modello deve gestire manualmente gli input per ogni passaggio, quindi utilizza tf.keras.layers.LSTMCell direttamente per l'interfaccia a singolo passaggio temporale di livello inferiore.

class FeedBack(tf.keras.Model):
  def __init__(self, units, out_steps):
    super().__init__()
    self.out_steps = out_steps
    self.units = units
    self.lstm_cell = tf.keras.layers.LSTMCell(units)
    # Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
    self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
    self.dense = tf.keras.layers.Dense(num_features)

feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)

Il primo metodo di cui ha bisogno questo modello è un metodo di warmup per inizializzare il suo stato interno in base agli input. Una volta addestrato, questo stato acquisirà le parti rilevanti della cronologia di input. Questo è equivalente al modello LSTM a passaggio singolo di prima:

def warmup(self, inputs):
  # inputs.shape => (batch, time, features)
  # x.shape => (batch, lstm_units)
  x, *state = self.lstm_rnn(inputs)

  # predictions.shape => (batch, features)
  prediction = self.dense(x)
  return prediction, state

FeedBack.warmup = warmup

Questo metodo restituisce una singola previsione del passo temporale e lo stato interno LSTM :

prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape

TensorShape([32, 19])

Con lo stato RNN e una previsione iniziale è ora possibile continuare a iterare il modello alimentando le previsioni ad ogni passo indietro come input.

L'approccio più semplice per raccogliere le previsioni di output consiste nell'usare un elenco Python e un tf.stack dopo il ciclo.

def call(self, inputs, training=None):
  # Use a TensorArray to capture dynamically unrolled outputs.
  predictions = []
  # Initialize the LSTM state.
  prediction, state = self.warmup(inputs)

  # Insert the first prediction.
  predictions.append(prediction)

  # Run the rest of the prediction steps.
  for n in range(1, self.out_steps):
    # Use the last prediction as input.
    x = prediction
    # Execute one lstm step.
    x, state = self.lstm_cell(x, states=state,
                              training=training)
    # Convert the lstm output to a prediction.
    prediction = self.dense(x)
    # Add the prediction to the output.
    predictions.append(prediction)

  # predictions.shape => (time, batch, features)
  predictions = tf.stack(predictions)
  # predictions.shape => (batch, time, features)
  predictions = tf.transpose(predictions, [1, 0, 2])
  return predictions

FeedBack.call = call

Eseguire il test di questo modello sugli input di esempio:

print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)

Output shape (batch, time, features):  (32, 24, 19)

Ora, addestra il modello:

history = compile_and_fit(feedback_model, multi_window)

IPython.display.clear_output()

multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)

437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011

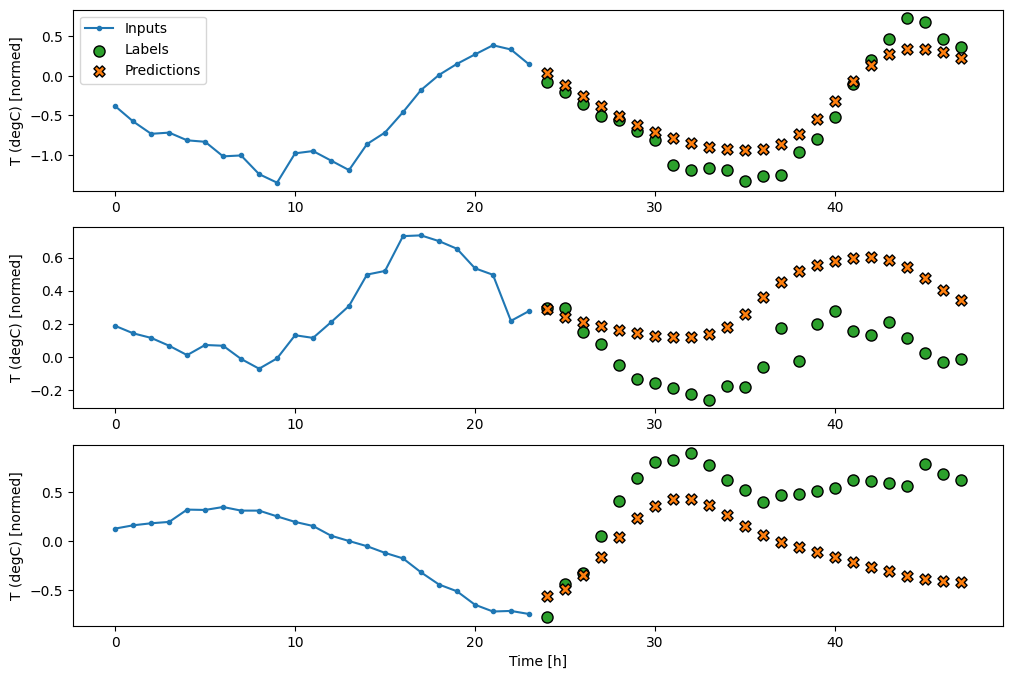
Prestazione

Ci sono chiaramente rendimenti decrescenti in funzione della complessità del modello su questo problema:

x = np.arange(len(multi_performance))
width = 0.3

metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]

plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
           rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()

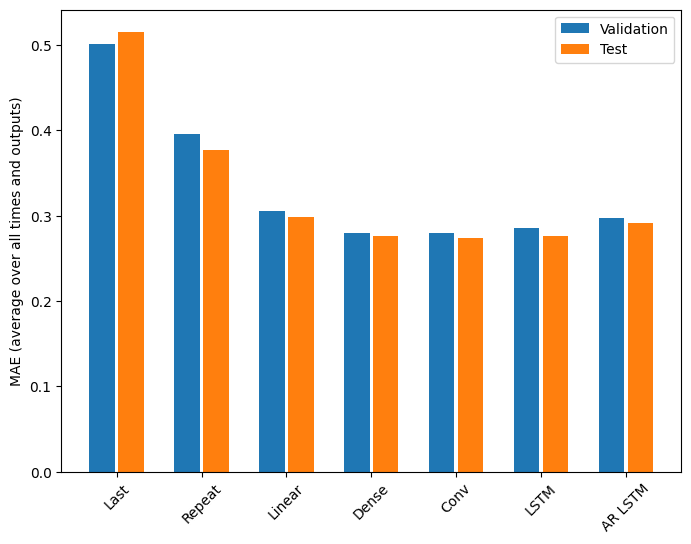
Le metriche per i modelli multi-output nella prima metà di questo tutorial mostrano le prestazioni medie di tutte le funzionalità di output. Queste prestazioni sono simili, ma sono anche mediate nei vari passaggi temporali di output.

for name, value in multi_performance.items():
  print(f'{name:8s}: {value[1]:0.4f}')

Last    : 0.5157
Repeat  : 0.3774
Linear  : 0.2977
Dense   : 0.2781
Conv    : 0.2796
LSTM    : 0.2767
AR LSTM : 0.2901

I guadagni ottenuti passando da un modello denso a modelli convoluzionali e ricorrenti sono solo una piccola percentuale (se presente) e il modello autoregressivo ha ottenuto risultati nettamente peggiori. Quindi questi approcci più complessi potrebbero non valere la pena su questo problema, ma non c'era modo di saperlo senza provare e questi modelli potrebbero essere utili per il tuo problema.

Prossimi passi

Questo tutorial è stata una rapida introduzione alla previsione di serie temporali utilizzando TensorFlow.

Per saperne di più, fare riferimento a:

• Capitolo 15 di Machine Learning pratico con Scikit-Learn, Keras e TensorFlow , 2a edizione.
• Capitolo 6 di Deep Learning con Python .
• Lezione 8 dell'introduzione di Udacity a TensorFlow per il deep learning , inclusi i quaderni degli esercizi .

Inoltre, ricorda che puoi implementare qualsiasi modello di serie temporali classico in TensorFlow: questo tutorial si concentra solo sulla funzionalità integrata di TensorFlow.