التنبؤ بالسلاسل الزمنية

عرض على TensorFlow.org

تشغيل في Google Colab

عرض المصدر على جيثب

تحميل دفتر

هذا البرنامج التعليمي عبارة عن مقدمة للتنبؤ بالسلاسل الزمنية باستخدام TensorFlow. يبني عدة أنماط مختلفة من النماذج بما في ذلك الشبكات العصبية التلافيفية والمتكررة (CNNs و RNNs).

يتم تغطية ذلك في جزأين رئيسيين ، مع أقسام فرعية:

• التنبؤ لخطوة زمنية واحدة:
  • ميزة واحدة.
  • كل المميزات.
• توقع خطوات متعددة:
  • لقطة واحدة: قم بعمل التنبؤات كلها مرة واحدة.
  • الانحدار التلقائي: قم بعمل تنبؤ واحد في كل مرة وأعد الإخراج إلى النموذج.

يثبت

import os
import datetime

import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf

mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False

مجموعة بيانات الطقس

يستخدم هذا البرنامج التعليمي مجموعة بيانات متسلسلة زمنية للطقس سجلها معهد ماكس بلانك للكيمياء الحيوية .

تحتوي مجموعة البيانات هذه على 14 ميزة مختلفة مثل درجة حرارة الهواء والضغط الجوي والرطوبة. تم جمع هذه البيانات كل 10 دقائق ، بدءًا من عام 2003. ولتحقيق الكفاءة ، ستستخدم فقط البيانات التي تم جمعها بين عامي 2009 و 2016. تم إعداد هذا القسم من مجموعة البيانات بواسطة François Chollet لكتابه Deep Learning with Python .

zip_path = tf.keras.utils.get_file(
    origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
    fname='jena_climate_2009_2016.csv.zip',
    extract=True)
csv_path, _ = os.path.splitext(zip_path)

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip
13574144/13568290 [==============================] - 1s 0us/step
13582336/13568290 [==============================] - 1s 0us/step

سيتعامل هذا البرنامج التعليمي فقط مع التوقعات كل ساعة ، لذا ابدأ بأخذ عينات فرعية للبيانات من فواصل زمنية مدتها 10 دقائق إلى فواصل زمنية مدتها ساعة واحدة:

df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]

date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')

دعنا نلقي نظرة على البيانات. فيما يلي الصفوف القليلة الأولى:

df.head()

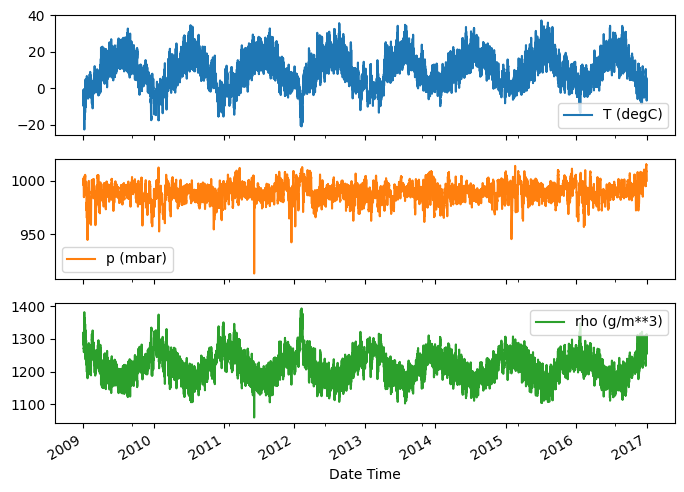
إليك تطور بعض الميزات بمرور الوقت:

plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)

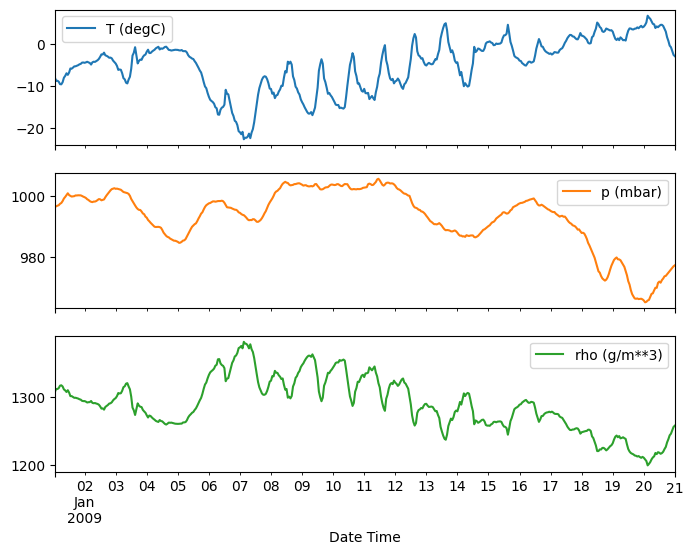
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)

فحص وتنظيف

بعد ذلك ، انظر إلى إحصائيات مجموعة البيانات:

df.describe().transpose()

سرعة الرياح

الشيء الوحيد الذي يجب أن يبرز هو القيمة min لسرعة الرياح ( wv (m/s) max. wv (m/s) ). من المحتمل أن يكون هذا -9999 خاطئًا.

يوجد عمود اتجاه رياح منفصل ، لذا يجب أن تكون السرعة أكبر من الصفر ( >=0 ). استبدلها بأصفار:

wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0

max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0

# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()

0.0

هندسة الميزات

قبل التعمق في بناء نموذج ، من المهم فهم بياناتك والتأكد من أنك تقوم بتمرير بيانات منسقة بشكل مناسب للنموذج.

ريح

العمود الأخير من البيانات ، wd (deg) يعطي اتجاه الرياح بوحدات من الدرجات. لا تقدم الزوايا مدخلات نموذجية جيدة: يجب أن تكون 360 درجة و 0 درجة قريبة من بعضها البعض وأن تلتف حولها بسلاسة. لا يجب أن يكون الاتجاه مهمًا إذا كانت الرياح لا تهب.

في الوقت الحالي ، يبدو توزيع بيانات الرياح كما يلي:

plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')

Text(0, 0.5, 'Wind Velocity [m/s]')

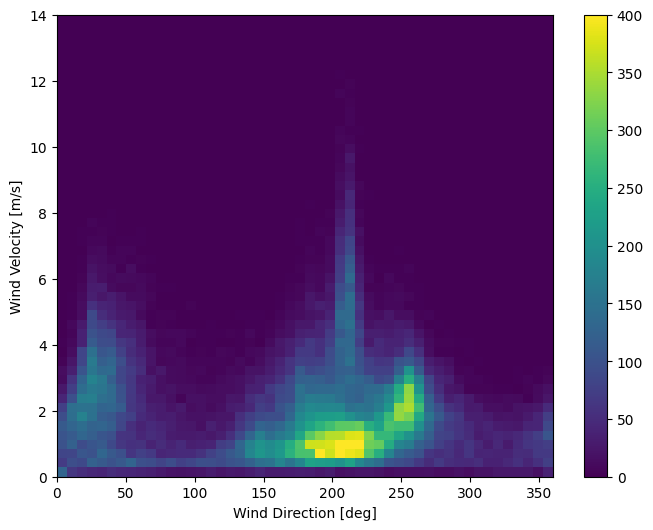
ولكن سيكون من السهل على النموذج تفسير ذلك إذا قمت بتحويل أعمدة اتجاه الرياح والسرعة إلى متجه للرياح:

wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')

# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180

# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)

# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)

يكون توزيع نواقل الرياح أبسط بكثير بالنسبة للنموذج لتفسير ما يلي بشكل صحيح:

plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')

(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)

زمن

وبالمثل ، فإن عمود Date Time مفيد للغاية ، ولكن ليس في شكل السلسلة هذا. ابدأ بتحويله إلى ثوانٍ:

timestamp_s = date_time.map(pd.Timestamp.timestamp)

على غرار اتجاه الرياح ، لا يعد الوقت بالثواني إدخالًا مفيدًا للنموذج. نظرًا لكونها بيانات الطقس ، فهي تتميز بالدورية اليومية والسنوية. هناك العديد من الطرق التي يمكنك من خلالها التعامل مع الدورية.

يمكنك الحصول على إشارات قابلة للاستخدام باستخدام تحويلات الجيب وجيب التمام لمسح إشارات "الوقت من اليوم" و "الوقت من العام":

day = 24*60*60
year = (365.2425)*day

df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))

plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')

Text(0.5, 1.0, 'Time of day signal')

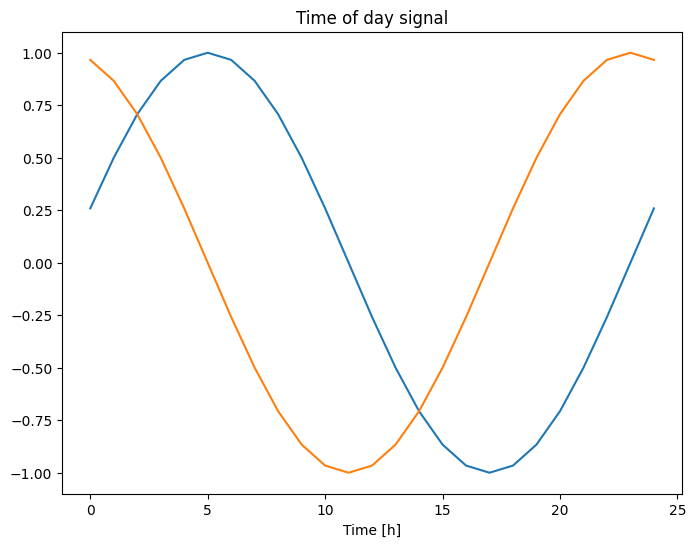
يتيح ذلك للنموذج الوصول إلى أهم ميزات التردد. في هذه الحالة ، كنت تعرف مسبقًا الترددات المهمة.

إذا لم تكن لديك هذه المعلومات ، يمكنك تحديد الترددات المهمة عن طريق استخراج الميزات باستخدام Fast Fourier Transform . للتحقق من الافتراضات ، إليك tf.signal.rfft لدرجة الحرارة بمرور الوقت. لاحظ القمم الواضحة عند الترددات القريبة من 1/year و 1/day :

fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))

n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)

f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')

تقسيم البيانات

ستستخدم تقسيمًا (70%, 20%, 10%) للتدريب والتحقق من الصحة ومجموعات الاختبار. لاحظ أن البيانات لا يتم خلطها عشوائيًا قبل التقسيم. هذا هو لسببين:

1. إنه يضمن أن تقطيع البيانات إلى نوافذ عينات متتالية لا يزال ممكنًا.
2. يضمن أن تكون نتائج التحقق / الاختبار أكثر واقعية ، حيث يتم تقييمها على البيانات التي تم جمعها بعد تدريب النموذج.

column_indices = {name: i for i, name in enumerate(df.columns)}

n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]

num_features = df.shape[1]

تطبيع البيانات

من المهم قياس الميزات قبل تدريب الشبكة العصبية. يعد التطبيع طريقة شائعة للقيام بهذا القياس: اطرح المتوسط ​​واقسم على الانحراف المعياري لكل ميزة.

يجب حساب المتوسط ​​والانحراف المعياري فقط باستخدام بيانات التدريب بحيث لا يكون للنماذج إمكانية الوصول إلى القيم الموجودة في مجموعات التحقق من الصحة والاختبار.

يمكن القول أيضًا أنه لا ينبغي للنموذج الوصول إلى القيم المستقبلية في مجموعة التدريب عند التدريب ، وأن هذا التطبيع يجب أن يتم باستخدام المتوسطات المتحركة. هذا ليس محور هذا البرنامج التعليمي ، وتضمن مجموعات التحقق والاختبار حصولك (إلى حد ما) على مقاييس صادقة. لذلك ، من أجل البساطة ، يستخدم هذا البرنامج التعليمي متوسطًا بسيطًا.

train_mean = train_df.mean()
train_std = train_df.std()

train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std

الآن ، ألق نظرة خاطفة على توزيع الميزات. بعض الميزات لها ذيول طويلة ، ولكن لا توجد أخطاء واضحة مثل قيمة سرعة الرياح -9999 .

df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

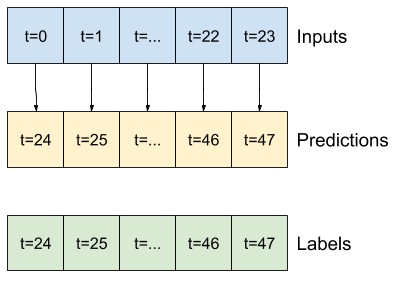
نوافذ البيانات

ستقوم النماذج في هذا البرنامج التعليمي بعمل مجموعة من التنبؤات بناءً على نافذة من العينات المتتالية من البيانات.

الميزات الرئيسية لنوافذ الإدخال هي:

• عرض (عدد الخطوات الزمنية) لإطارات الإدخال والتسمية.
• وقت الإزاحة بينهما.
• الميزات المستخدمة كمدخلات أو تسميات أو كليهما.

يبني هذا البرنامج التعليمي مجموعة متنوعة من النماذج (بما في ذلك نماذج Linear و DNN و CNN و RNN) ، ويستخدمها لكل من:

• تنبؤات أحادية الإخراج ومتعددة المخرجات .
• تنبؤات أحادية الخطوة ومتعددة الخطوات .

يركز هذا القسم على تنفيذ نوافذ البيانات بحيث يمكن إعادة استخدامها لجميع هذه النماذج.

بناءً على المهمة ونوع النموذج ، قد ترغب في إنشاء مجموعة متنوعة من نوافذ البيانات. وهنا بعض الأمثلة:

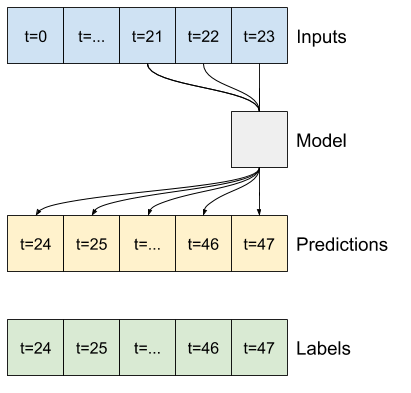
1. على سبيل المثال ، لعمل توقع واحد خلال 24 ساعة في المستقبل ، بالنظر إلى 24 ساعة من التاريخ ، يمكنك تحديد نافذة مثل هذه:

   

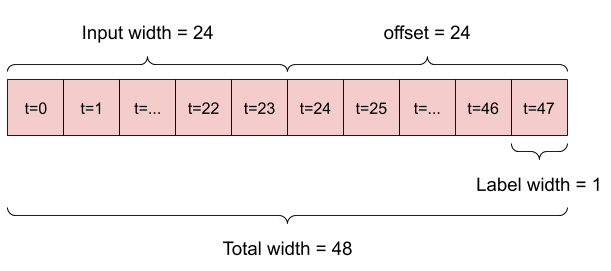
2. النموذج الذي يقوم بالتنبؤ بساعة واحدة في المستقبل ، في ظل ست ساعات من التاريخ ، سيحتاج إلى نافذة مثل هذه:

   

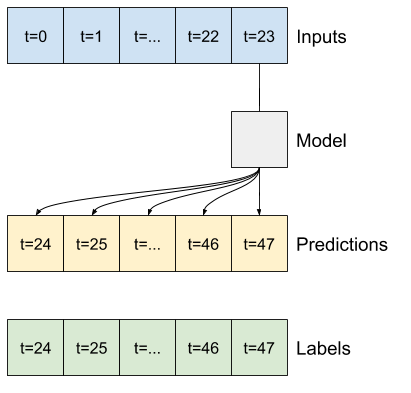
يحدد الجزء المتبقي من هذا القسم فئة WindowGenerator . يمكن لهذا الفصل:

1. تعامل مع الفهارس والإزاحات كما هو موضح في الرسوم البيانية أعلاه.
2. قسّم نوافذ الميزات إلى أزواج (features, labels) .
3. ارسم محتوى النوافذ الناتجة.
4. قم بإنشاء دفعات من هذه النوافذ بكفاءة من بيانات التدريب والتقييم والاختبار ، باستخدام tf.data.Dataset s.

1. الفهارس والتعويضات

ابدأ بإنشاء فئة WindowGenerator . تتضمن طريقة __init__ كل المنطق الضروري لمؤشرات الإدخال والتسمية.

كما يأخذ التدريب والتقييم والاختبار DataFrames كمدخلات. سيتم تحويلها إلى tf.data.Dataset s من windows لاحقًا.

class WindowGenerator():
  def __init__(self, input_width, label_width, shift,
               train_df=train_df, val_df=val_df, test_df=test_df,
               label_columns=None):
    # Store the raw data.
    self.train_df = train_df
    self.val_df = val_df
    self.test_df = test_df

    # Work out the label column indices.
    self.label_columns = label_columns
    if label_columns is not None:
      self.label_columns_indices = {name: i for i, name in
                                    enumerate(label_columns)}
    self.column_indices = {name: i for i, name in
                           enumerate(train_df.columns)}

    # Work out the window parameters.
    self.input_width = input_width
    self.label_width = label_width
    self.shift = shift

    self.total_window_size = input_width + shift

    self.input_slice = slice(0, input_width)
    self.input_indices = np.arange(self.total_window_size)[self.input_slice]

    self.label_start = self.total_window_size - self.label_width
    self.labels_slice = slice(self.label_start, None)
    self.label_indices = np.arange(self.total_window_size)[self.labels_slice]

  def __repr__(self):
    return '\n'.join([
        f'Total window size: {self.total_window_size}',
        f'Input indices: {self.input_indices}',
        f'Label indices: {self.label_indices}',
        f'Label column name(s): {self.label_columns}'])

فيما يلي رمز لإنشاء النافذتين الموضحتين في الرسوم البيانية في بداية هذا القسم:

w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
                     label_columns=['T (degC)'])
w1

Total window size: 48
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [47]
Label column name(s): ['T (degC)']

w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
                     label_columns=['T (degC)'])
w2

Total window size: 7
Input indices: [0 1 2 3 4 5]
Label indices: [6]
Label column name(s): ['T (degC)']

2. انقسام

بالنظر إلى قائمة المدخلات المتتالية ، فإن طريقة split_window إلى نافذة من المدخلات ونافذة من الملصقات.

سيتم تقسيم المثال w2 الذي حددته سابقًا على النحو التالي:

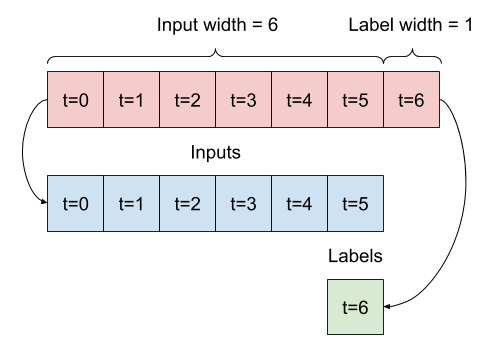
لا يُظهر هذا الرسم التخطيطي محور features البيانات ، ولكن وظيفة split_window هذه تتعامل أيضًا مع label_columns بحيث يمكن استخدامها لكل من أمثلة الإخراج الفردي والمخرجات المتعددة.

def split_window(self, features):
  inputs = features[:, self.input_slice, :]
  labels = features[:, self.labels_slice, :]
  if self.label_columns is not None:
    labels = tf.stack(
        [labels[:, :, self.column_indices[name]] for name in self.label_columns],
        axis=-1)

  # Slicing doesn't preserve static shape information, so set the shapes
  # manually. This way the `tf.data.Datasets` are easier to inspect.
  inputs.set_shape([None, self.input_width, None])
  labels.set_shape([None, self.label_width, None])

  return inputs, labels

WindowGenerator.split_window = split_window

حاول:

# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
                           np.array(train_df[100:100+w2.total_window_size]),
                           np.array(train_df[200:200+w2.total_window_size])])

example_inputs, example_labels = w2.split_window(example_window)

print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')

All shapes are: (batch, time, features)
Window shape: (3, 7, 19)
Inputs shape: (3, 6, 19)
Labels shape: (3, 1, 1)

عادةً ما يتم تجميع البيانات في TensorFlow في مصفوفات حيث يوجد الفهرس الخارجي عبر الأمثلة (بُعد "الدُفعة"). المؤشرات الوسطى هي البعد (الأبعاد) "الوقت" أو "الفضاء" (العرض ، الارتفاع). المؤشرات الأعمق هي الميزات.

أخذ الكود أعلاه مجموعة من ثلاث نوافذ خطوات 7 مرات مع 19 ميزة في كل خطوة زمنية. يقوم بتقسيمها إلى مجموعة من مدخلات 6-time-step 19-Feature ، و 1-time-time 1-feature label. تحتوي التسمية على ميزة واحدة فقط لأنه تمت تهيئة WindowGenerator باستخدام label_columns=['T (degC)'] . في البداية ، سيقوم هذا البرنامج التعليمي ببناء نماذج تتنبأ بتسميات الإخراج الفردية.

3. مؤامرة

فيما يلي طريقة الرسم التي تتيح تصورًا بسيطًا للنافذة المنقسمة:

w2.example = example_inputs, example_labels

def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
  inputs, labels = self.example
  plt.figure(figsize=(12, 8))
  plot_col_index = self.column_indices[plot_col]
  max_n = min(max_subplots, len(inputs))
  for n in range(max_n):
    plt.subplot(max_n, 1, n+1)
    plt.ylabel(f'{plot_col} [normed]')
    plt.plot(self.input_indices, inputs[n, :, plot_col_index],
             label='Inputs', marker='.', zorder=-10)

    if self.label_columns:
      label_col_index = self.label_columns_indices.get(plot_col, None)
    else:
      label_col_index = plot_col_index

    if label_col_index is None:
      continue

    plt.scatter(self.label_indices, labels[n, :, label_col_index],
                edgecolors='k', label='Labels', c='#2ca02c', s=64)
    if model is not None:
      predictions = model(inputs)
      plt.scatter(self.label_indices, predictions[n, :, label_col_index],
                  marker='X', edgecolors='k', label='Predictions',
                  c='#ff7f0e', s=64)

    if n == 0:
      plt.legend()

  plt.xlabel('Time [h]')

WindowGenerator.plot = plot

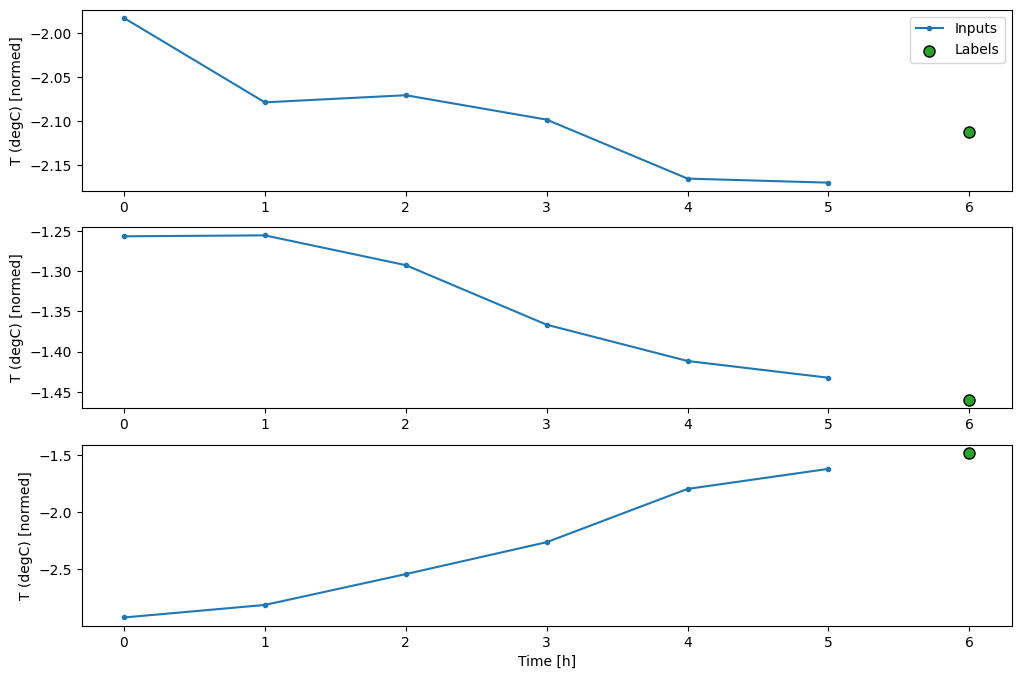
تعمل هذه المؤامرة على محاذاة المدخلات والتسميات والتنبؤات (اللاحقة) بناءً على الوقت الذي يشير إليه العنصر:

w2.plot()

يمكنك رسم الأعمدة الأخرى ، لكن نموذج تكوين النافذة w2 يحتوي فقط على تسميات لعمود T (degC) .

w2.plot(plot_col='p (mbar)')

4. قم tf.data.Dataset s

أخيرًا ، ستأخذ طريقة make_dataset هذه سلسلة زمنية DataFrame وتحولها إلى tf.data.Dataset من أزواج (input_window, label_window) باستخدام الدالة tf.keras.utils.timeseries_dataset_from_array :

def make_dataset(self, data):
  data = np.array(data, dtype=np.float32)
  ds = tf.keras.utils.timeseries_dataset_from_array(
      data=data,
      targets=None,
      sequence_length=self.total_window_size,
      sequence_stride=1,
      shuffle=True,
      batch_size=32,)

  ds = ds.map(self.split_window)

  return ds

WindowGenerator.make_dataset = make_dataset

يحتفظ كائن WindowGenerator التدريب والتحقق من الصحة والاختبار.

أضف خصائص للوصول إليها كمجموعة tf.data.Dataset باستخدام طريقة make_dataset التي حددتها مسبقًا. أضف أيضًا نموذجًا قياسيًا للدفعة لسهولة الوصول والتخطيط:

@property
def train(self):
  return self.make_dataset(self.train_df)

@property
def val(self):
  return self.make_dataset(self.val_df)

@property
def test(self):
  return self.make_dataset(self.test_df)

@property
def example(self):
  """Get and cache an example batch of `inputs, labels` for plotting."""
  result = getattr(self, '_example', None)
  if result is None:
    # No example batch was found, so get one from the `.train` dataset
    result = next(iter(self.train))
    # And cache it for next time
    self._example = result
  return result

WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example

الآن ، يمنحك كائن WindowGenerator الوصول إلى كائنات tf.data.Dataset ، بحيث يمكنك تكرار البيانات بسهولة.

تخبرك الخاصية Dataset.element_spec بالبنية وأنواع البيانات والأشكال لعناصر مجموعة البيانات.

# Each element is an (inputs, label) pair.
w2.train.element_spec

(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None),
 TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))

ينتج عن التكرار عبر مجموعة Dataset دفعات محددة:

for example_inputs, example_labels in w2.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 6, 19)
Labels shape (batch, time, features): (32, 1, 1)

نماذج خطوة واحدة

أبسط نموذج يمكنك بناؤه على هذا النوع من البيانات هو النموذج الذي يتوقع قيمة ميزة واحدة - خطوة زمنية واحدة (ساعة واحدة) في المستقبل بناءً على الظروف الحالية فقط.

لذا ، ابدأ ببناء نماذج للتنبؤ بقيمة T (degC) ساعة واحدة في المستقبل.

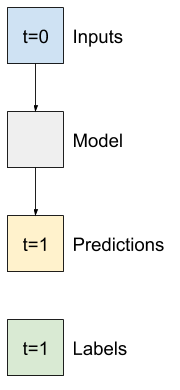
قم بتكوين كائن WindowGenerator لإنتاج هذه الأزواج المكونة من خطوة واحدة (input, label) :

single_step_window = WindowGenerator(
    input_width=1, label_width=1, shift=1,
    label_columns=['T (degC)'])
single_step_window

Total window size: 2
Input indices: [0]
Label indices: [1]
Label column name(s): ['T (degC)']

ينشئ كائن window tf.data.Dataset s من مجموعات التدريب والتحقق والاختبار ، مما يسمح لك بالتكرار بسهولة عبر مجموعات البيانات.

for example_inputs, example_labels in single_step_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 1, 19)
Labels shape (batch, time, features): (32, 1, 1)

حدود

قبل بناء نموذج قابل للتدريب ، سيكون من الجيد أن يكون لديك أساس أداء كنقطة للمقارنة مع النماذج اللاحقة الأكثر تعقيدًا.

هذه المهمة الأولى هي التنبؤ بدرجة الحرارة ساعة واحدة في المستقبل ، بالنظر إلى القيمة الحالية لجميع الميزات. تشمل القيم الحالية درجة الحرارة الحالية.

لذا ، ابدأ بنموذج يقوم فقط بإرجاع درجة الحرارة الحالية كتنبؤ ، وتوقع "لا تغيير". هذا هو خط الأساس المعقول لأن درجة الحرارة تتغير ببطء. بالطبع ، لن يعمل هذا الخط الأساسي بشكل جيد إذا أجريت تنبؤًا إضافيًا في المستقبل.

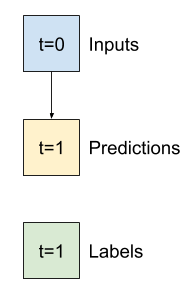
class Baseline(tf.keras.Model):
  def __init__(self, label_index=None):
    super().__init__()
    self.label_index = label_index

  def call(self, inputs):
    if self.label_index is None:
      return inputs
    result = inputs[:, :, self.label_index]
    return result[:, :, tf.newaxis]

إنشاء وتقييم هذا النموذج:

baseline = Baseline(label_index=column_indices['T (degC)'])

baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785

لقد أدى ذلك إلى طباعة بعض مقاييس الأداء ، لكن تلك المقاييس لا تمنحك إحساسًا بمدى جودة أداء النموذج.

يحتوي WindowGenerator على طريقة الرسم ، لكن المؤامرات لن تكون ممتعة للغاية بعينة واحدة فقط.

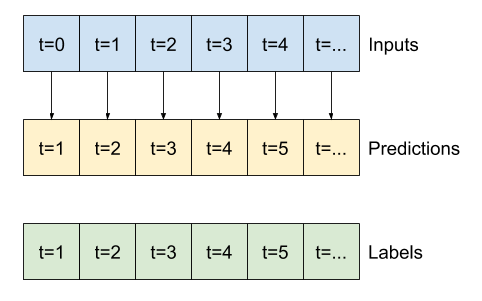
لذلك ، قم بإنشاء WindowGenerator أوسع نطاقاً يقوم بإنشاء نوافذ 24 ساعة من المدخلات والتسميات المتتالية في كل مرة. لا يغير متغير wide_window الجديد الطريقة التي يعمل بها النموذج. لا يزال النموذج يقوم بالتنبؤات لمدة ساعة واحدة في المستقبل بناءً على خطوة زمنية واحدة للإدخال. هنا ، يعمل المحور time كمحور batch : يتم إجراء كل توقع بشكل مستقل دون أي تفاعل بين خطوات الوقت:

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1,
    label_columns=['T (degC)'])

wide_window

Total window size: 25
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
Label column name(s): ['T (degC)']

يمكن تمرير هذه النافذة الموسعة مباشرة إلى نفس النموذج baseline دون أي تغييرات في التعليمات البرمجية. هذا ممكن لأن المدخلات والتسميات لها نفس عدد الخطوات الزمنية ، والخط الأساسي يعيد توجيه المدخلات إلى المخرجات:

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

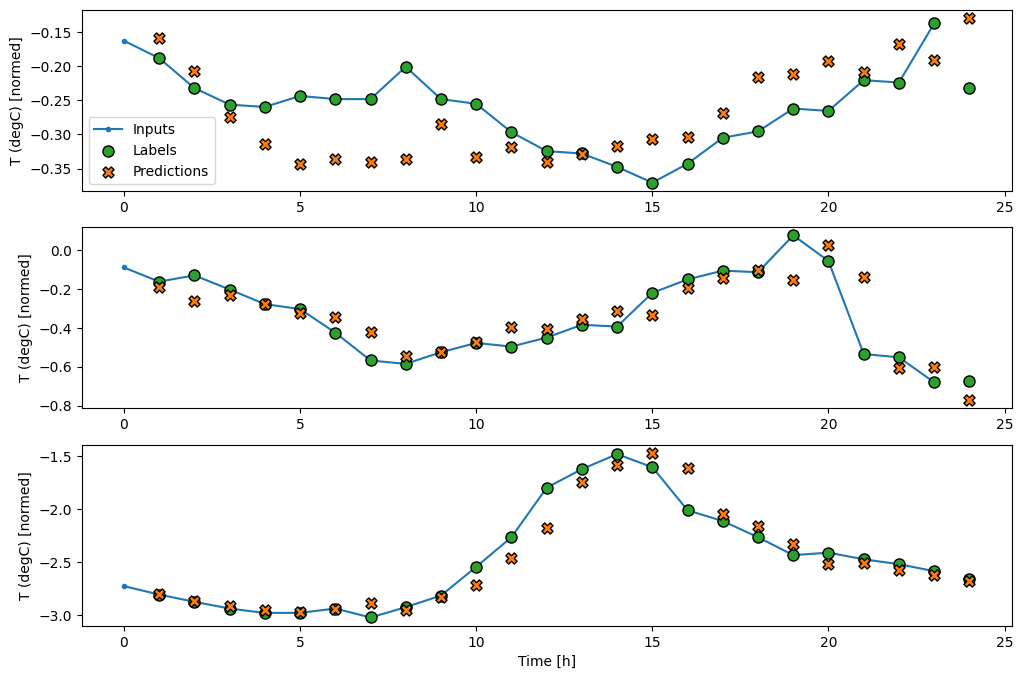
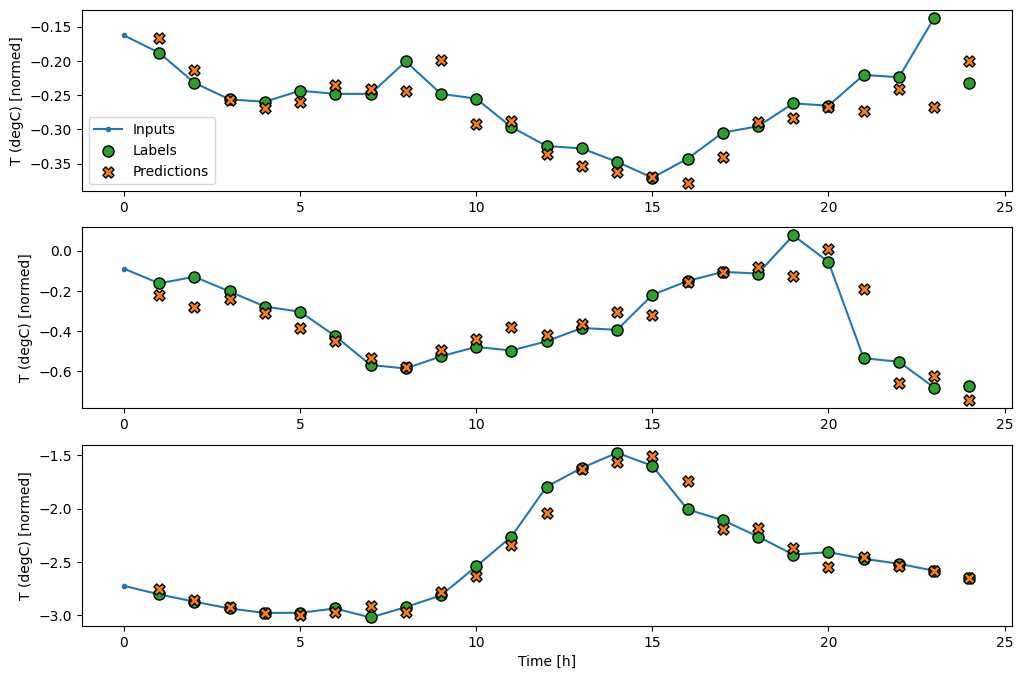
من خلال رسم تنبؤات النموذج الأساسي ، لاحظ أنه ببساطة تم تغيير الملصقات إلى اليمين بمقدار ساعة واحدة:

wide_window.plot(baseline)

في المخططات المذكورة أعلاه المكونة من ثلاثة أمثلة ، يتم تشغيل نموذج الخطوة الواحدة على مدار 24 ساعة. هذا يستحق بعض الشرح:

• يعرض خط Inputs الأزرق درجة حرارة الإدخال في كل خطوة زمنية. يتلقى النموذج جميع الميزات ، وتوضح هذه المؤامرة درجة الحرارة فقط.
• تعرض نقاط Labels الخضراء قيمة التنبؤ الهدف. تظهر هذه النقاط في وقت التنبؤ ، وليس وقت الإدخال. هذا هو السبب في أن نطاق التسميات يتم إزاحته خطوة واحدة بالنسبة للمدخلات.
• تقاطع Predictions البرتقالية هي تنبؤات النموذج لكل خطوة زمنية للإخراج. إذا كان النموذج يتنبأ بشكل مثالي ، فستهبط التنبؤات مباشرة على Labels .

نموذج خطي

أبسط نموذج قابل للتدريب يمكنك تطبيقه على هذه المهمة هو إدراج تحويل خطي بين الإدخال والإخراج. في هذه الحالة ، يعتمد الإخراج من خطوة زمنية فقط على تلك الخطوة:

طبقة tf.keras.layers.Dense . كثيفة بدون مجموعة activation هي نموذج خطي. تقوم الطبقة فقط بتحويل المحور الأخير للبيانات من (batch, time, inputs) إلى (batch, time, units) ؛ يتم تطبيقه بشكل مستقل على كل عنصر عبر محوري batch time .

linear = tf.keras.Sequential([
    tf.keras.layers.Dense(units=1)
])

print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)

Input shape: (32, 1, 19)
Output shape: (32, 1, 1)

يقوم هذا البرنامج التعليمي بتدريب العديد من النماذج ، لذلك قم بتجميع إجراءات التدريب في وظيفة:

MAX_EPOCHS = 20

def compile_and_fit(model, window, patience=2):
  early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
                                                    patience=patience,
                                                    mode='min')

  model.compile(loss=tf.losses.MeanSquaredError(),
                optimizer=tf.optimizers.Adam(),
                metrics=[tf.metrics.MeanAbsoluteError()])

  history = model.fit(window.train, epochs=MAX_EPOCHS,
                      validation_data=window.val,
                      callbacks=[early_stopping])
  return history

تدريب النموذج وتقييم أدائه:

history = compile_and_fit(linear, single_step_window)

val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858
Epoch 2/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711
Epoch 3/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690
Epoch 4/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692
Epoch 5/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685
Epoch 6/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687
Epoch 7/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680
Epoch 8/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683
Epoch 9/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684
439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684

مثل النموذج baseline ، يمكن استدعاء النموذج الخطي على دفعات من النوافذ العريضة. باستخدام هذه الطريقة ، يقوم النموذج بعمل مجموعة من التنبؤات المستقلة على خطوات زمنية متتالية. يعمل محور time كمحور batch آخر. لا توجد تفاعلات بين التوقعات في كل خطوة زمنية.

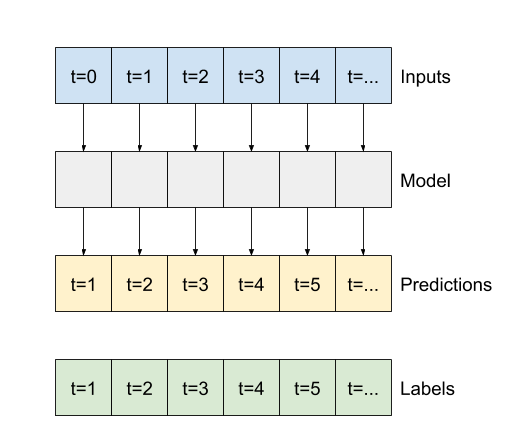
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

فيما يلي مخطط للتنبؤات النموذجية على wide_window ، لاحظ كيف أن التنبؤ في كثير من الحالات أفضل من مجرد إعادة درجة حرارة الإدخال ، لكنه أسوأ في حالات قليلة:

wide_window.plot(linear)

تتمثل إحدى ميزات النماذج الخطية في سهولة تفسيرها نسبيًا. يمكنك سحب أوزان الطبقة وتصور الوزن المخصص لكل إدخال:

plt.bar(x = range(len(train_df.columns)),
        height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)

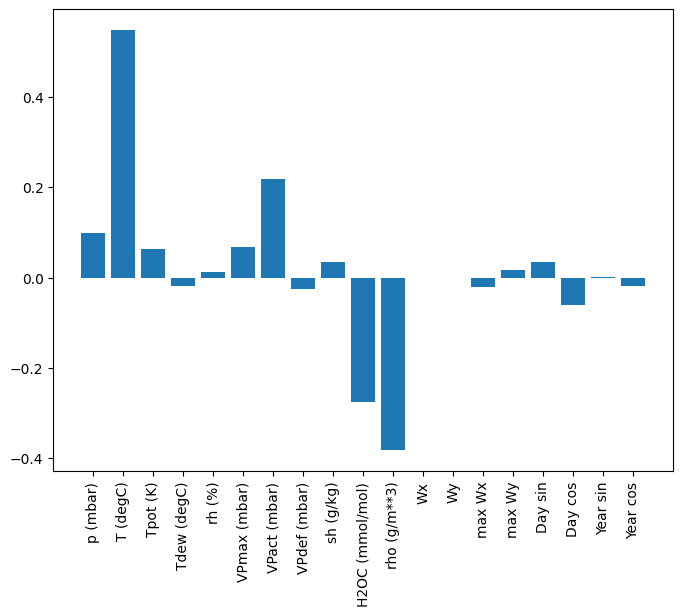
في بعض الأحيان لا يضع النموذج أكبر قدر من الوزن على الإدخال T (degC) . هذا هو أحد مخاطر التهيئة العشوائية.

كثيف

قبل تطبيق النماذج التي تعمل فعليًا وفقًا لخطوات زمنية متعددة ، من الجدير التحقق من أداء نماذج خطوة إدخال واحدة أعمق وأكثر قوة.

هذا نموذج مشابه للنموذج linear ، إلا أنه يكدس عدة طبقات Dense بين المدخلات والمخرجات:

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=1)
])

history = compile_and_fit(dense, single_step_window)

val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666
Epoch 2/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610
Epoch 3/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618
Epoch 4/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582
Epoch 5/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581
Epoch 6/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579
Epoch 7/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580
439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580

متعدد الخطوات كثيفة

لا يحتوي نموذج الخطوة الواحدة على سياق القيم الحالية لمدخلاته. لا يمكنه رؤية كيف تتغير ميزات الإدخال بمرور الوقت. لمعالجة هذه المشكلة ، يحتاج النموذج إلى الوصول إلى خطوات زمنية متعددة عند إجراء التنبؤات:

تم التعامل مع النماذج baseline linear dense في كل خطوة زمنية بشكل مستقل. سيتخذ النموذج هنا عدة خطوات زمنية كمدخلات لإنتاج مخرج واحد.

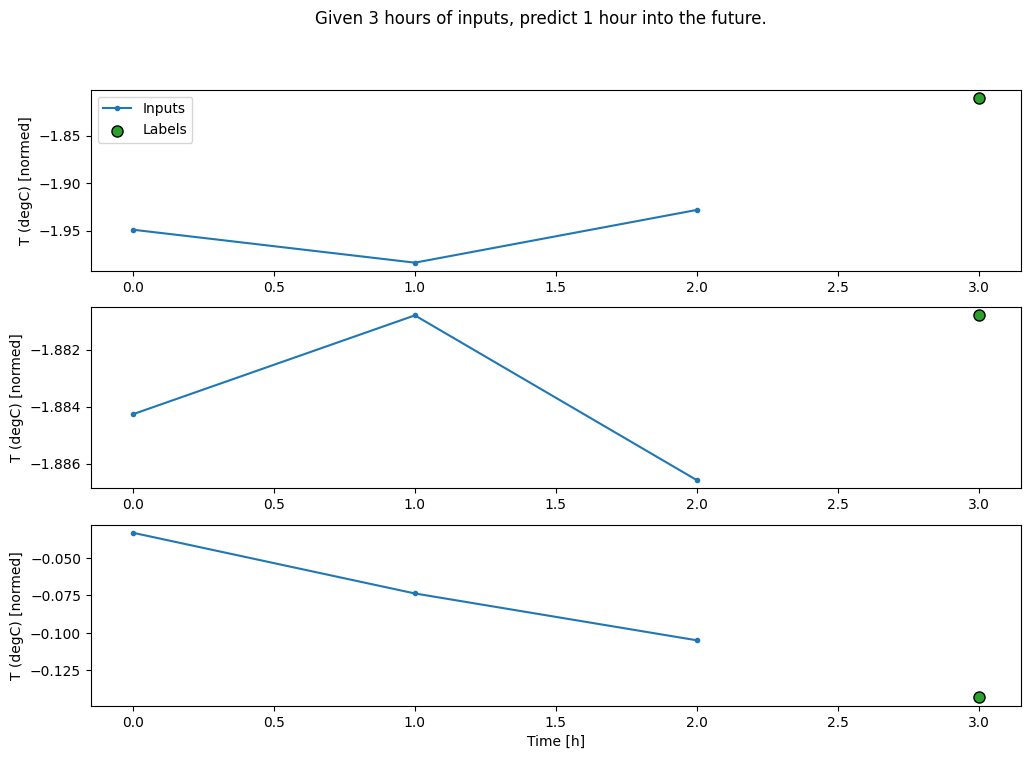
قم بإنشاء WindowGenerator الذي سينتج دفعات من المدخلات لمدة ثلاث ساعات وملصقات لمدة ساعة واحدة:

لاحظ أن معلمة shift Window مرتبطة بنهاية النافذتين.

CONV_WIDTH = 3
conv_window = WindowGenerator(
    input_width=CONV_WIDTH,
    label_width=1,
    shift=1,
    label_columns=['T (degC)'])

conv_window

Total window size: 4
Input indices: [0 1 2]
Label indices: [3]
Label column name(s): ['T (degC)']

conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")

Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')

يمكنك تدريب نموذج dense على نافذة متعددة المدخلات عن طريق إضافة tf.keras.layers.Flatten كطبقة أولى من النموذج:

multi_step_dense = tf.keras.Sequential([
    # Shape: (time, features) => (time*features)
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
    # Add back the time dimension.
    # Shape: (outputs) => (1, outputs)
    tf.keras.layers.Reshape([1, -1]),
])

print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)

Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

history = compile_and_fit(multi_step_dense, conv_window)

IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609

conv_window.plot(multi_step_dense)

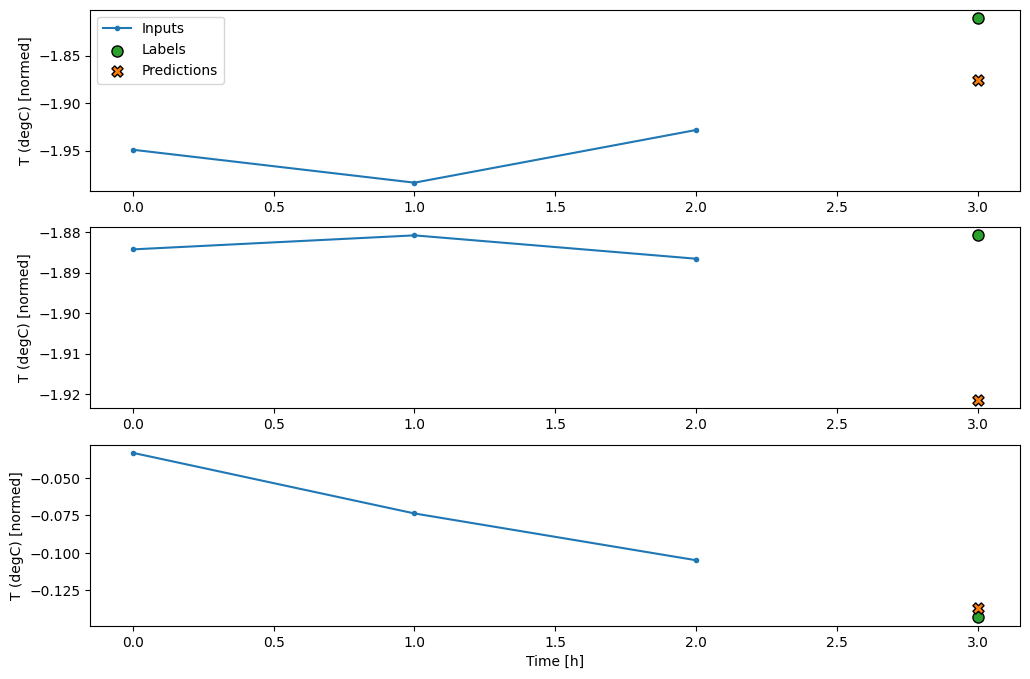
يتمثل الجانب السلبي الرئيسي لهذا الأسلوب في أنه لا يمكن تنفيذ النموذج الناتج إلا على نوافذ الإدخال من هذا الشكل بالضبط.

print('Input shape:', wide_window.example[0].shape)
try:
  print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
  print(f'\n{type(e).__name__}:{e}')

Input shape: (32, 24, 19)

ValueError:Exception encountered when calling layer "sequential_2" (type Sequential).

Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456)

Call arguments received:
  • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32)
  • training=None
  • mask=None

النماذج التلافيفية في القسم التالي تعمل على حل هذه المشكلة.

الشبكة العصبية الالتفافية

تأخذ طبقة الالتفاف ( tf.keras.layers.Conv1D ) أيضًا خطوات زمنية متعددة كمدخلات لكل تنبؤ.

يوجد أدناه نفس نموذج multi_step_dense ، معاد كتابته باستخدام الالتفاف.

لاحظ التغييرات:

• يتم استبدال tf.keras.layers.Flatten والأول tf.keras.layers.Dense بـ tf.keras.layers.Conv1D .
• لم يعد tf.keras.layers.Reshape ضروريًا لأن الالتفاف يحافظ على محور الوقت في ناتجه.

conv_model = tf.keras.Sequential([
    tf.keras.layers.Conv1D(filters=32,
                           kernel_size=(CONV_WIDTH,),
                           activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
])

قم بتشغيله على دفعة كمثال للتحقق من أن النموذج ينتج مخرجات بالشكل المتوقع:

print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)

Conv model on `conv_window`
Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

قم بتدريبه وتقييمه على conv_window ويجب أن يعطي أداء مشابهًا لنموذج multi_step_dense .

history = compile_and_fit(conv_model, conv_window)

IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)

438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568

يتمثل الاختلاف بين نموذج multi_step_dense هذا ونموذج كثرة الخطوات المتعددة في أنه يمكن تشغيل conv_model conv_model مدخلات بأي طول. يتم تطبيق الطبقة التلافيفية على نافذة منزلقة من المدخلات:

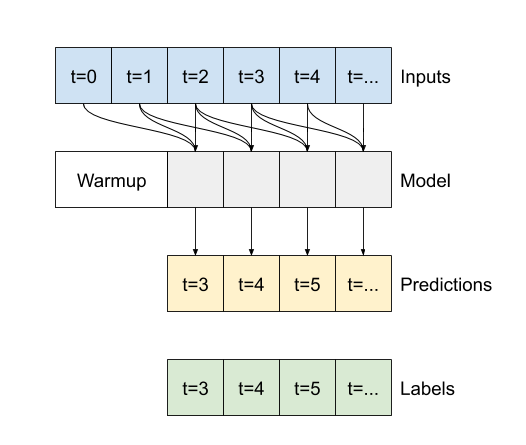
إذا قمت بتشغيله على مدخلات أوسع ، فإنه ينتج مخرجات أوسع:

print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)

Wide window
Input shape: (32, 24, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 22, 1)

لاحظ أن الإخراج أقصر من المدخلات. لإجراء التدريب أو التخطيط ، تحتاج إلى أن يكون للتسميات والتنبؤ نفس الطول. لذلك ، قم ببناء WindowGenerator لإنتاج نوافذ عريضة مع بضع خطوات زمنية إضافية للإدخال بحيث يتطابق أطوال التسمية والتنبؤ:

LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
    input_width=INPUT_WIDTH,
    label_width=LABEL_WIDTH,
    shift=1,
    label_columns=['T (degC)'])

wide_conv_window

Total window size: 27
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25]
Label indices: [ 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26]
Label column name(s): ['T (degC)']

print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)

Wide conv window
Input shape: (32, 26, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 24, 1)

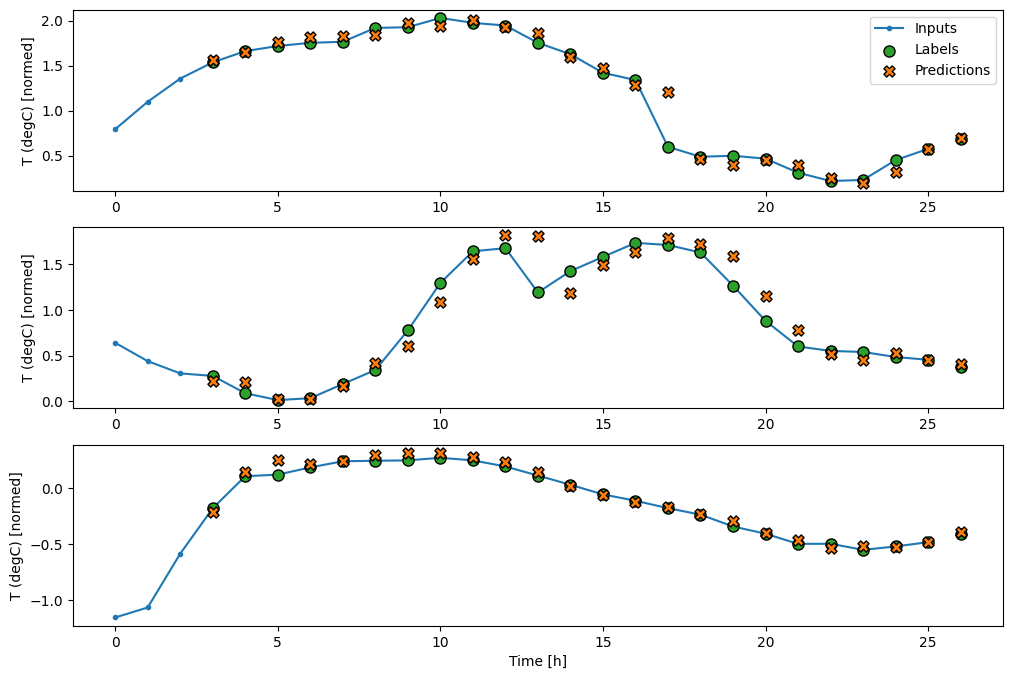
الآن ، يمكنك رسم تنبؤات النموذج على نافذة أوسع. لاحظ خطوات وقت الإدخال الثلاث قبل التوقع الأول. يعتمد كل توقع هنا على 3 خطوات زمنية سابقة:

wide_conv_window.plot(conv_model)

الشبكة العصبية المتكررة

الشبكة العصبية المتكررة (RNN) هي نوع من الشبكات العصبية مناسبة تمامًا لبيانات السلاسل الزمنية. تعالج RNNs سلسلة زمنية خطوة بخطوة ، مما يحافظ على الحالة الداخلية من خطوة إلى أخرى.

يمكنك معرفة المزيد في إنشاء النص باستخدام برنامج تعليمي لـ RNN والشبكات العصبية المتكررة (RNN) مع دليل Keras .

في هذا البرنامج التعليمي ، ستستخدم طبقة RNN تسمى الذاكرة طويلة المدى ( tf.keras.layers.LSTM ).

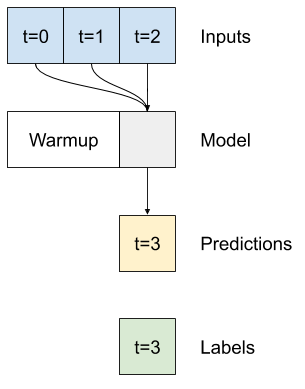
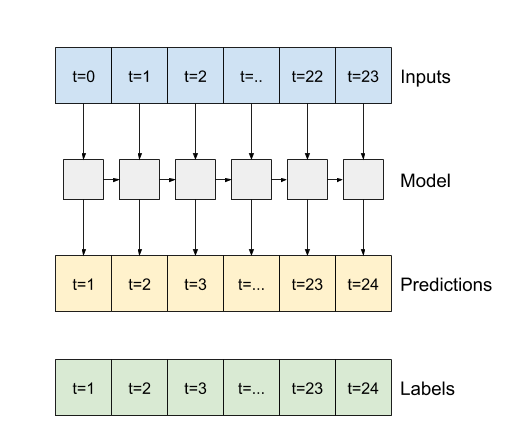
وسيطة منشئ مهمة لجميع طبقات Keras RNN ، مثل tf.keras.layers.LSTM ، هي وسيطة return_sequences . يمكن لهذا الإعداد تكوين الطبقة بإحدى طريقتين:

1. إذا كانت القيمة False الافتراضية ، فإن الطبقة تُرجع فقط ناتج الخطوة الزمنية النهائية ، مما يمنح النموذج وقتًا لتسخين حالته الداخلية قبل إجراء توقع واحد:

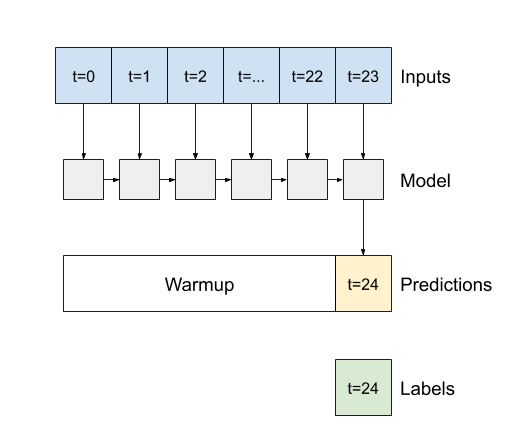
1. إذا كان True ، تقوم الطبقة بإرجاع مخرجات لكل إدخال. هذا مفيد لـ:
   • تكديس طبقات RNN.
   • تدريب نموذج على خطوات زمنية متعددة في وقت واحد.

lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=1)
])

باستخدام return_sequences=True ، يمكن تدريب النموذج على 24 ساعة من البيانات في كل مرة.

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509

wide_window.plot(lstm_model)

أداء

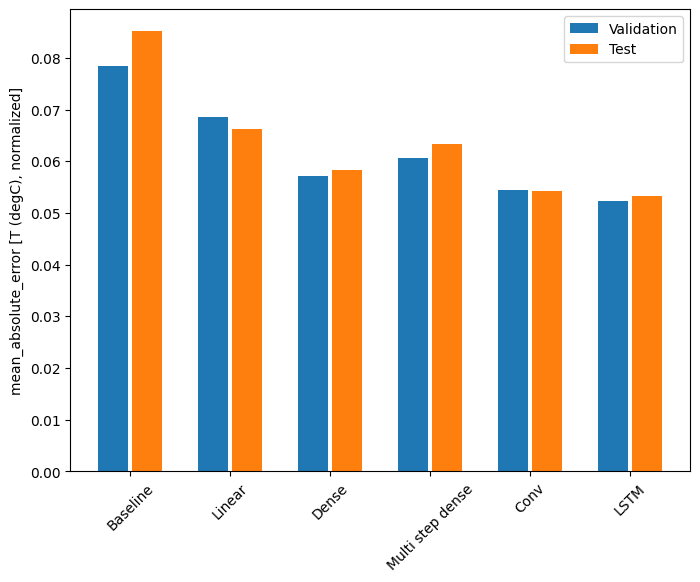
باستخدام مجموعة البيانات هذه ، عادةً ما يكون أداء كل نموذج أفضل قليلاً من النموذج السابق له:

x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
_ = plt.legend()

for name, value in performance.items():
  print(f'{name:12s}: {value[1]:0.4f}')

Baseline    : 0.0852
Linear      : 0.0666
Dense       : 0.0573
Multi step dense: 0.0586
Conv        : 0.0577
LSTM        : 0.0518

نماذج متعددة المخرجات

توقعت جميع النماذج حتى الآن ميزة خرج واحدة ، T (degC) ، لخطوة زمنية واحدة.

يمكن تحويل كل هذه النماذج للتنبؤ بالعديد من الميزات فقط عن طريق تغيير عدد الوحدات في طبقة الإخراج وضبط نوافذ التدريب لتشمل جميع الميزات في labels ( example_labels ):

single_step_window = WindowGenerator(
    # `WindowGenerator` returns all features as labels if you 
    # don't set the `label_columns` argument.
    input_width=1, label_width=1, shift=1)

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

for example_inputs, example_labels in wide_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 24, 19)
Labels shape (batch, time, features): (32, 24, 19)

لاحظ أعلاه أن محور features الخاص بالتسميات له الآن نفس عمق المدخلات ، بدلاً من 1 .

حدود

يمكن استخدام نفس النموذج الأساسي ( Baseline ) هنا ، ولكن هذه المرة تكرار جميع الميزات بدلاً من تحديد label_index معين:

baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589

كثيف

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(dense, single_step_window)

IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302

RNN

%%time
wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)

print()

438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205

CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s
Wall time: 2min 8s

متقدم: الوصلات المتبقية

استفاد نموذج Baseline السابق من حقيقة أن التسلسل لا يتغير بشكل كبير من خطوة زمنية إلى أخرى. كل نموذج تم تدريبه في هذا البرنامج التعليمي حتى الآن تمت تهيئته بشكل عشوائي ، ومن ثم كان عليه أن يتعلم أن الناتج هو تغيير بسيط عن الخطوة الزمنية السابقة.

بينما يمكنك التغلب على هذه المشكلة من خلال التهيئة الدقيقة ، فمن الأسهل بناء هذا في بنية النموذج.

من الشائع في تحليل السلاسل الزمنية بناء نماذج بدلاً من توقع القيمة التالية ، توقع كيف ستتغير القيمة في الخطوة الزمنية التالية. وبالمثل ، تشير الشبكات المتبقية - أو شبكات ResNets - في التعلم العميق إلى البنى التي تضيف فيها كل طبقة إلى النتيجة المتراكمة للنموذج.

هذه هي الطريقة التي تستفيد بها من معرفة أن التغيير يجب أن يكون صغيراً.

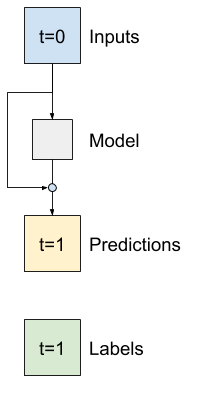
بشكل أساسي ، يؤدي هذا إلى تهيئة النموذج لمطابقة Baseline . بالنسبة لهذه المهمة ، تساعد النماذج على التقارب بشكل أسرع ، مع أداء أفضل قليلاً.

يمكن استخدام هذا النهج جنبًا إلى جنب مع أي نموذج تمت مناقشته في هذا البرنامج التعليمي.

هنا ، يتم تطبيقه على نموذج LSTM ، لاحظ استخدام tf.initializers.zeros للتأكد من أن التغييرات الأولية المتوقعة صغيرة ، ولا تغلب على الاتصال المتبقي. لا توجد مخاوف تتعلق بكسر التناسق للتدرجات هنا ، حيث يتم استخدام zeros فقط في الطبقة الأخيرة.

class ResidualWrapper(tf.keras.Model):
  def __init__(self, model):
    super().__init__()
    self.model = model

  def call(self, inputs, *args, **kwargs):
    delta = self.model(inputs, *args, **kwargs)

    # The prediction for each time step is the input
    # from the previous time step plus the delta
    # calculated by the model.
    return inputs + delta

%%time
residual_lstm = ResidualWrapper(
    tf.keras.Sequential([
    tf.keras.layers.LSTM(32, return_sequences=True),
    tf.keras.layers.Dense(
        num_features,
        # The predicted deltas should start small.
        # Therefore, initialize the output layer with zeros.
        kernel_initializer=tf.initializers.zeros())
]))

history = compile_and_fit(residual_lstm, wide_window)

IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()

438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179

CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s
Wall time: 43.1 s

أداء

هنا هو الأداء العام لهذه النماذج متعددة المخرجات.

x = np.arange(len(performance))
width = 0.3

metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()

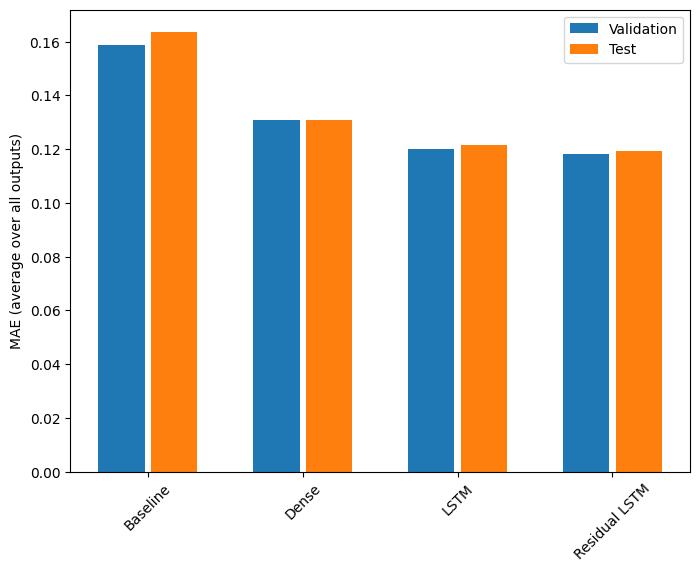
for name, value in performance.items():
  print(f'{name:15s}: {value[1]:0.4f}')

Baseline       : 0.1638
Dense          : 0.1311
LSTM           : 0.1214
Residual LSTM  : 0.1194

يتم حساب متوسط ​​الأداء أعلاه عبر جميع مخرجات النموذج.

نماذج متعددة الخطوات

قدم كلا النموذجين أحادي المخرجات ونماذج المخرجات المتعددة في الأقسام السابقة تنبؤات بخطوة زمنية واحدة ، بعد ساعة واحدة من المستقبل.

يبحث هذا القسم في كيفية توسيع هذه النماذج لعمل تنبؤات متعددة الخطوات .

في التنبؤ متعدد الخطوات ، يحتاج النموذج إلى تعلم كيفية التنبؤ بمجموعة من القيم المستقبلية. وبالتالي ، على عكس نموذج الخطوة الواحدة ، حيث يتم توقع نقطة مستقبلية واحدة فقط ، يتنبأ نموذج متعدد الخطوات بتسلسل القيم المستقبلية.

هناك طريقتان تقريبية لهذا:

1. تنبؤات اللقطة الواحدة حيث يتم توقع السلسلة الزمنية بأكملها مرة واحدة.
2. تنبؤات الانحدار التلقائي حيث يقوم النموذج فقط بعمل تنبؤات من خطوة واحدة ويتم إرجاع مخرجاته كمدخلاته.

في هذا القسم ، ستتنبأ جميع النماذج بجميع الميزات عبر جميع خطوات وقت الإخراج .

بالنسبة للنموذج متعدد الخطوات ، تتكون بيانات التدريب مرة أخرى من عينات كل ساعة. ومع ذلك ، هنا ، ستتعلم النماذج التنبؤ بـ 24 ساعة في المستقبل ، بالنظر إلى 24 ساعة من الماضي.

إليك كائن Window يقوم بإنشاء هذه الشرائح من مجموعة البيانات:

OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
                               label_width=OUT_STEPS,
                               shift=OUT_STEPS)

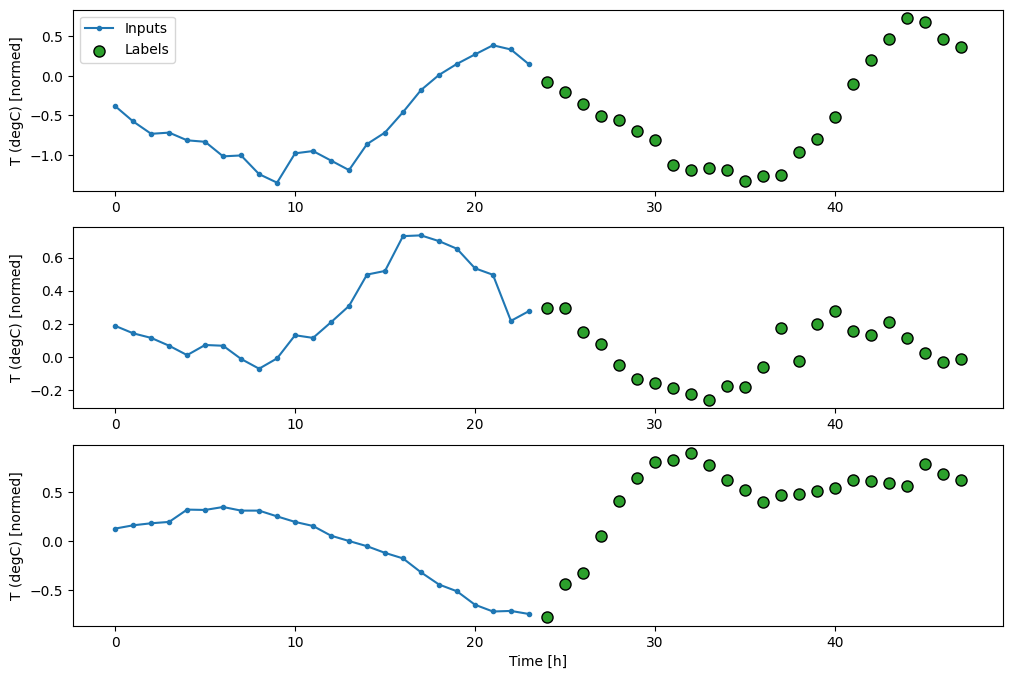
multi_window.plot()
multi_window

Total window size: 48
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47]
Label column name(s): None

خطوط الأساس

يتمثل خط الأساس البسيط لهذه المهمة في تكرار الخطوة الأخيرة لوقت الإدخال للعدد المطلوب من خطوات وقت الإخراج:

class MultiStepLastBaseline(tf.keras.Model):
  def call(self, inputs):
    return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])

last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
                      metrics=[tf.metrics.MeanAbsoluteError()])

multi_val_performance = {}
multi_performance = {}

multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)

437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007

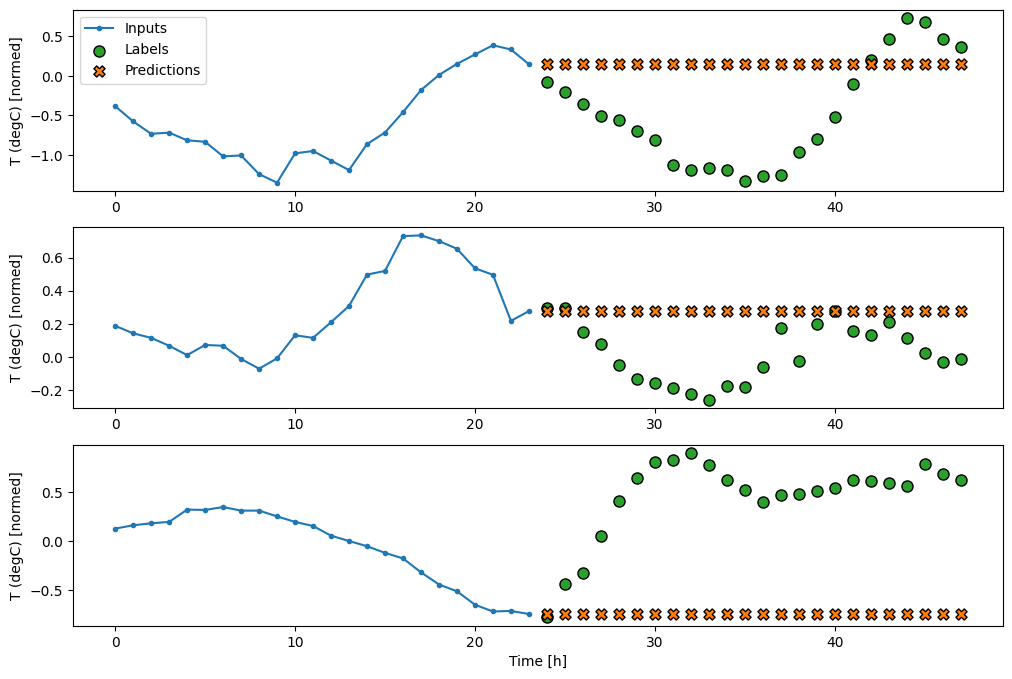
نظرًا لأن هذه المهمة هي التنبؤ بـ 24 ساعة في المستقبل ، بالنظر إلى 24 ساعة من الماضي ، هناك طريقة بسيطة أخرى تتمثل في تكرار اليوم السابق ، بافتراض أن الغد سيكون مشابهًا:

class RepeatBaseline(tf.keras.Model):
  def call(self, inputs):
    return inputs

repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
                        metrics=[tf.metrics.MeanAbsoluteError()])

multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)

437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959

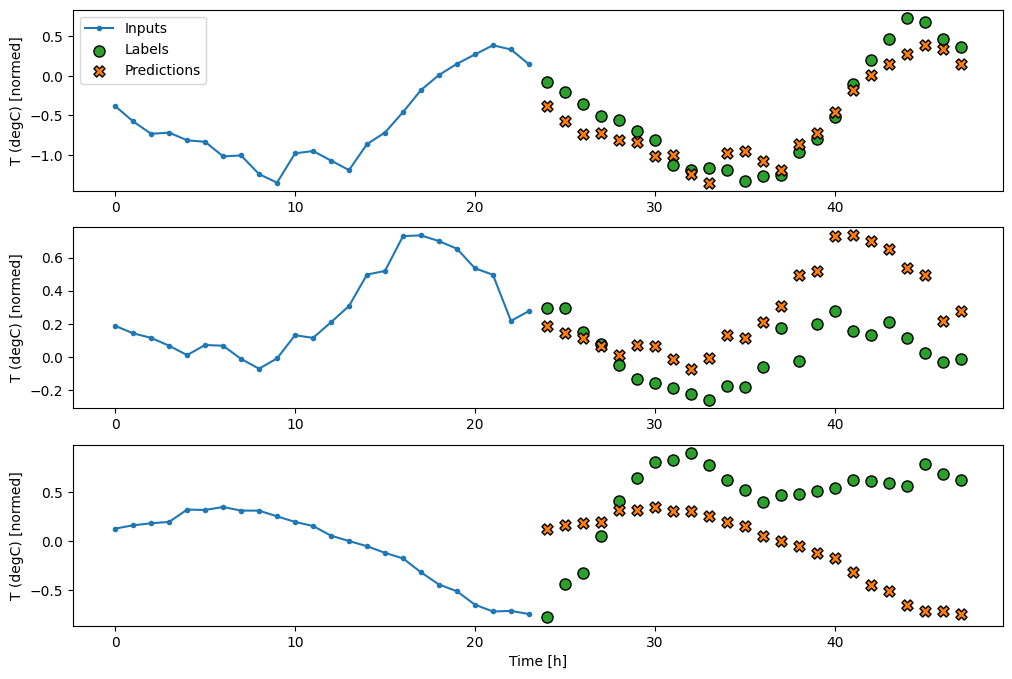
نماذج اللقطة الواحدة

تتمثل إحدى المقاربات عالية المستوى لهذه المشكلة في استخدام نموذج "اللقطة الواحدة" ، حيث يقوم النموذج بالتنبؤ بالتسلسل بأكمله في خطوة واحدة.

يمكن تنفيذ ذلك بكفاءة باعتباره tf.keras.layers.Dense مع OUT_STEPS*features بوحدات الإخراج. يحتاج النموذج فقط إلى إعادة تشكيل هذا الإخراج إلى المطلوب (OUTPUT_STEPS, features) .

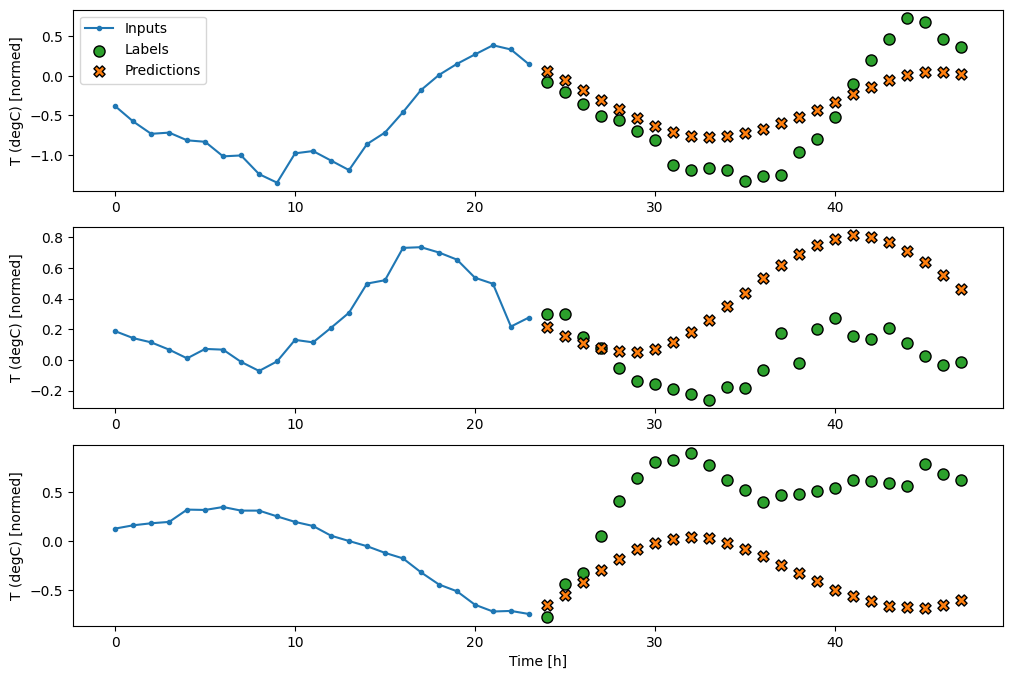
خطي

يعمل النموذج الخطي البسيط المستند إلى الخطوة الزمنية الأخيرة للإدخال بشكل أفضل من أي من خط الأساس ، ولكنه ضعيف. يحتاج النموذج إلى التنبؤ بالخطوات الزمنية OUTPUT_STEPS ، من خطوة وقت إدخال واحدة مع إسقاط خطي. يمكنه فقط التقاط شريحة منخفضة الأبعاد من السلوك ، ومن المحتمل أن يعتمد بشكل أساسي على الوقت من اليوم والوقت من السنة.

multi_linear_model = tf.keras.Sequential([
    # Take the last time-step.
    # Shape [batch, time, features] => [batch, 1, features]
    tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
    # Shape => [batch, 1, out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_linear_model, multi_window)

IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)

437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053

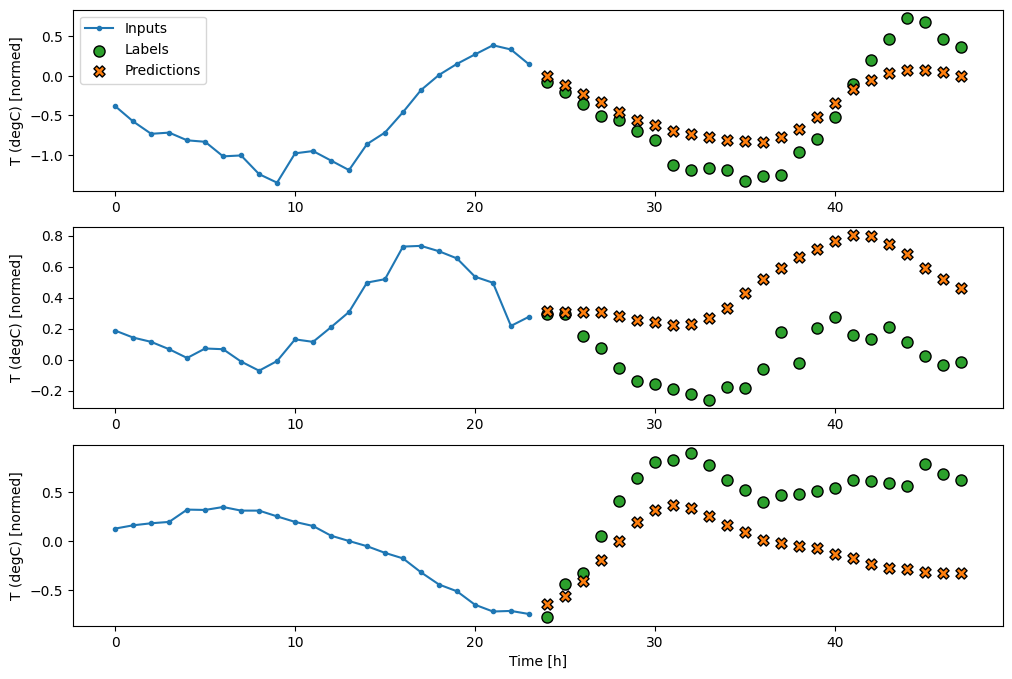
كثيف

إضافة tf.keras.layers.Dense . كثيفة بين المدخلات والمخرجات تعطي النموذج الخطي مزيدًا من القوة ، لكنها لا تزال تعتمد فقط على خطوة زمنية واحدة للإدخال.

multi_dense_model = tf.keras.Sequential([
    # Take the last time step.
    # Shape [batch, time, features] => [batch, 1, features]
    tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
    # Shape => [batch, 1, dense_units]
    tf.keras.layers.Dense(512, activation='relu'),
    # Shape => [batch, out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_dense_model, multi_window)

IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)

437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837

سي إن إن

يقوم النموذج التلافيفي بعمل تنبؤات بناءً على تاريخ ثابت العرض ، مما قد يؤدي إلى أداء أفضل من النموذج الكثيف لأنه يمكنه رؤية كيف تتغير الأشياء بمرور الوقت:

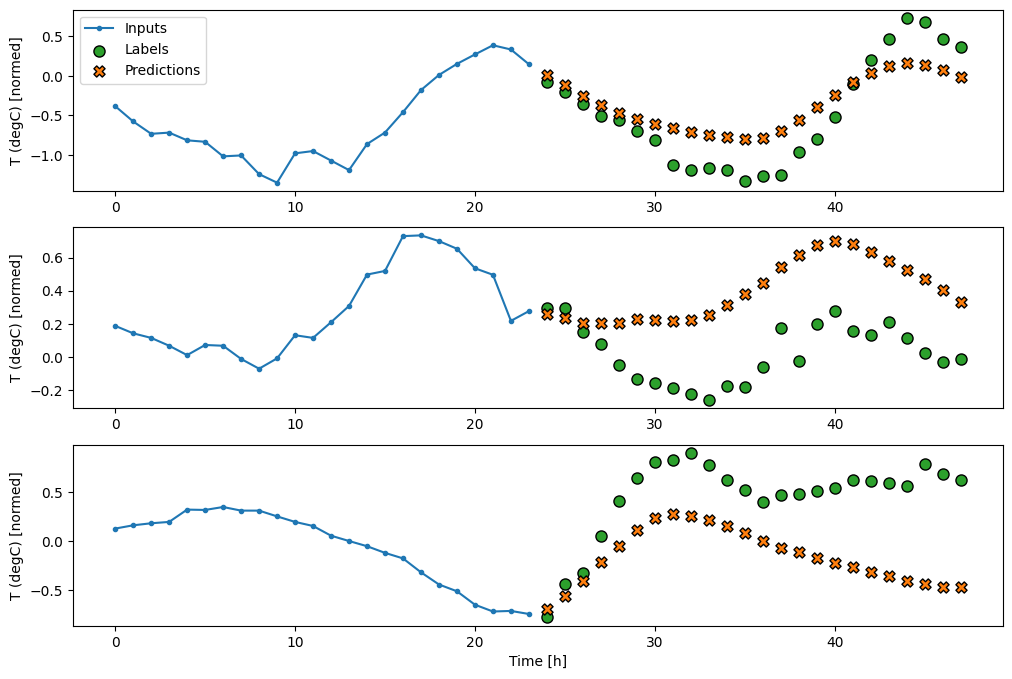
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
    # Shape [batch, time, features] => [batch, CONV_WIDTH, features]
    tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
    # Shape => [batch, 1, conv_units]
    tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
    # Shape => [batch, 1,  out_steps*features]
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features]
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_conv_model, multi_window)

IPython.display.clear_output()

multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)

437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833

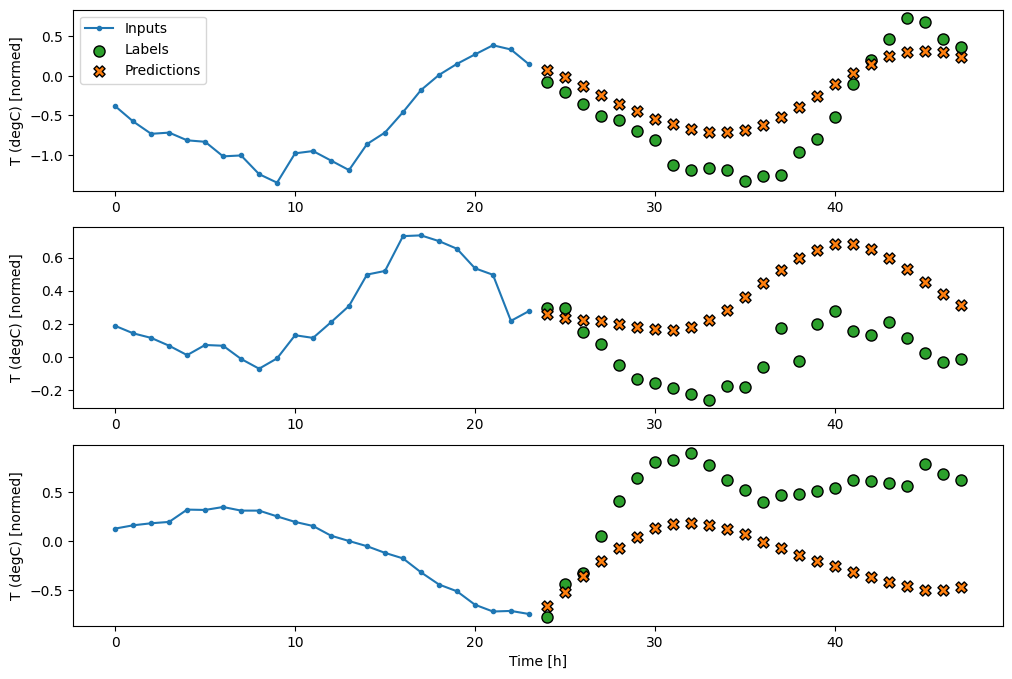
RNN

يمكن أن يتعلم النموذج المتكرر استخدام تاريخ طويل من المدخلات ، إذا كان وثيق الصلة بالتنبؤات التي يقوم بها النموذج. هنا سيتراكم النموذج الحالة الداخلية لمدة 24 ساعة ، قبل إجراء توقع واحد لمدة 24 ساعة القادمة.

في تنسيق اللقطة المفردة هذا ، يحتاج LSTM فقط إلى إنتاج مخرجات في الخطوة الزمنية الأخيرة ، لذا قم بتعيين return_sequences=False في tf.keras.layers.LSTM .

multi_lstm_model = tf.keras.Sequential([
    # Shape [batch, time, features] => [batch, lstm_units].
    # Adding more `lstm_units` just overfits more quickly.
    tf.keras.layers.LSTM(32, return_sequences=False),
    # Shape => [batch, out_steps*features].
    tf.keras.layers.Dense(OUT_STEPS*num_features,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features].
    tf.keras.layers.Reshape([OUT_STEPS, num_features])
])

history = compile_and_fit(multi_lstm_model, multi_window)

IPython.display.clear_output()

multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)

437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863

متقدم: نموذج الانحدار التلقائي

تتنبأ جميع النماذج المذكورة أعلاه بتسلسل الإخراج بالكامل في خطوة واحدة.

في بعض الحالات ، قد يكون من المفيد للنموذج تحليل هذا التوقع إلى خطوات زمنية فردية. بعد ذلك ، يمكن تغذية مخرجات كل نموذج مرة أخرى في نفسه في كل خطوة ويمكن جعل التنبؤات مشروطة بالخطوة السابقة ، كما هو الحال في إنشاء التسلسلات الكلاسيكية مع الشبكات العصبية المتكررة .

تتمثل إحدى الميزات الواضحة لهذا النمط من النموذج في أنه يمكن إعداده لإنتاج مخرجات بطول متفاوت.

يمكنك أن تأخذ أيًا من النماذج متعددة المخرجات المكونة من خطوة واحدة والتي تم تدريبها في النصف الأول من هذا البرنامج التعليمي وتشغيلها في حلقة ردود فعل الانحدار التلقائي ، ولكن هنا ستركز على بناء نموذج تم تدريبه بشكل صريح للقيام بذلك.

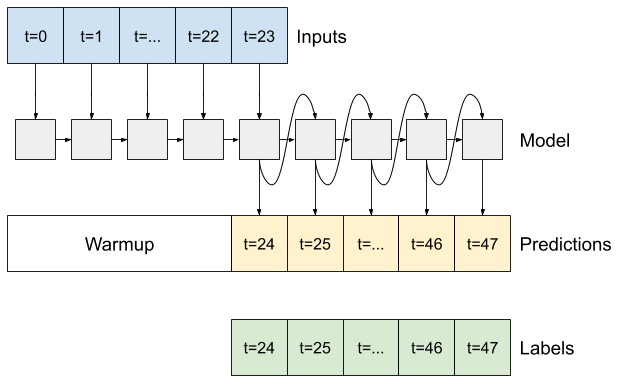
RNN

يبني هذا البرنامج التعليمي نموذج RNN ذاتي الانحدار فقط ، ولكن يمكن تطبيق هذا النمط على أي نموذج تم تصميمه لإخراج خطوة زمنية واحدة.

سيكون للنموذج نفس الشكل الأساسي لنماذج LSTM ذات الخطوة الواحدة من السابق: طبقة tf.keras.layers.LSTM متبوعة بـ tf.keras.layers.Dense طبقة كثيفة تحول مخرجات طبقة LSTM إلى تنبؤات نموذجية.

إن tf.keras.layers.LSTM عبارة عن tf.keras.layers.LSTMCell ملفوفة في المستوى الأعلى tf.keras.layers.RNN الذي يدير نتائج الحالة والتسلسل نيابةً عنك (راجع الشبكات العصبية المتكررة (RNN) باستخدام Keras دليل للحصول على التفاصيل).

في هذه الحالة ، يجب على النموذج إدارة المدخلات يدويًا لكل خطوة ، لذلك يستخدم tf.keras.layers.LSTMCell مباشرةً للواجهة ذات المستوى الأدنى ، وواجهة الخطوة الواحدة.

class FeedBack(tf.keras.Model):
  def __init__(self, units, out_steps):
    super().__init__()
    self.out_steps = out_steps
    self.units = units
    self.lstm_cell = tf.keras.layers.LSTMCell(units)
    # Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
    self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
    self.dense = tf.keras.layers.Dense(num_features)

feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)

الطريقة الأولى التي يحتاجها هذا النموذج هي طريقة warmup لتهيئة حالته الداخلية بناءً على المدخلات. بمجرد التدريب ، ستلتقط هذه الحالة الأجزاء ذات الصلة من سجل الإدخال. هذا يعادل نموذج LSTM الخطوة من سابقًا:

def warmup(self, inputs):
  # inputs.shape => (batch, time, features)
  # x.shape => (batch, lstm_units)
  x, *state = self.lstm_rnn(inputs)

  # predictions.shape => (batch, features)
  prediction = self.dense(x)
  return prediction, state

FeedBack.warmup = warmup

تُرجع هذه الطريقة تنبؤًا بخطوة زمنية واحدة والحالة الداخلية لـ LSTM :

prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape

TensorShape([32, 19])

مع حالة RNN ، والتنبؤ الأولي ، يمكنك الآن متابعة تكرار النموذج الذي يغذي التنبؤات في كل خطوة إلى الوراء كمدخل.

إن أبسط طريقة لتجميع تنبؤات المخرجات هي استخدام قائمة Python و tf.stack بعد الحلقة.

def call(self, inputs, training=None):
  # Use a TensorArray to capture dynamically unrolled outputs.
  predictions = []
  # Initialize the LSTM state.
  prediction, state = self.warmup(inputs)

  # Insert the first prediction.
  predictions.append(prediction)

  # Run the rest of the prediction steps.
  for n in range(1, self.out_steps):
    # Use the last prediction as input.
    x = prediction
    # Execute one lstm step.
    x, state = self.lstm_cell(x, states=state,
                              training=training)
    # Convert the lstm output to a prediction.
    prediction = self.dense(x)
    # Add the prediction to the output.
    predictions.append(prediction)

  # predictions.shape => (time, batch, features)
  predictions = tf.stack(predictions)
  # predictions.shape => (batch, time, features)
  predictions = tf.transpose(predictions, [1, 0, 2])
  return predictions

FeedBack.call = call

اختبر هذا النموذج على مدخلات المثال:

print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)

Output shape (batch, time, features):  (32, 24, 19)

الآن ، قم بتدريب النموذج:

history = compile_and_fit(feedback_model, multi_window)

IPython.display.clear_output()

multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
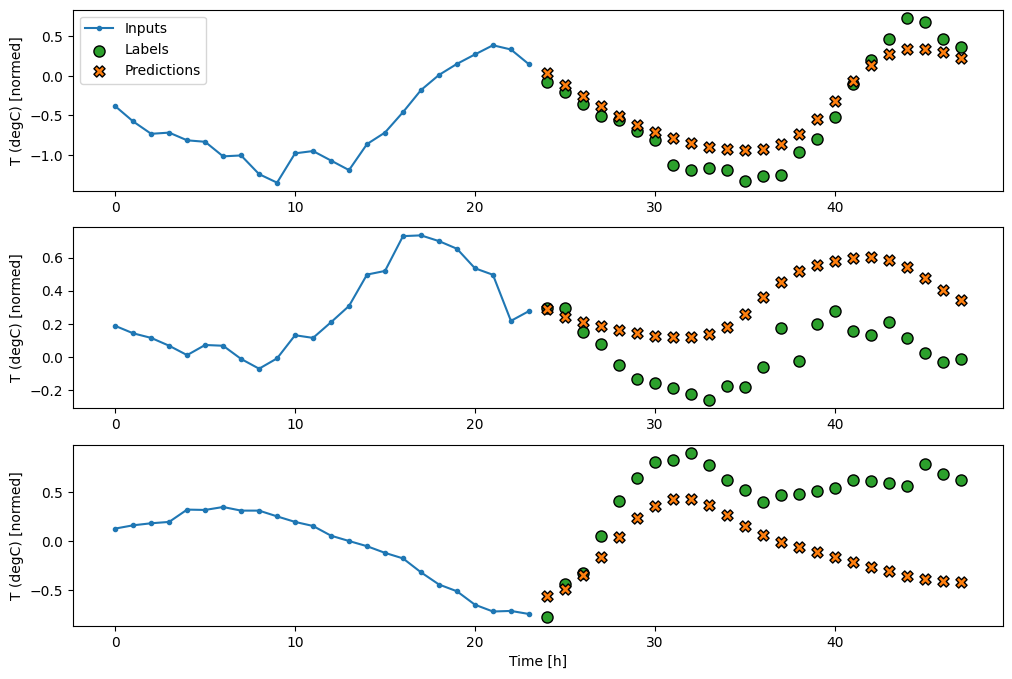
multi_window.plot(feedback_model)

437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011

أداء

هناك عوائد متناقصة بشكل واضح كدالة لتعقيد النموذج في هذه المشكلة:

x = np.arange(len(multi_performance))
width = 0.3

metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]

plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
           rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()

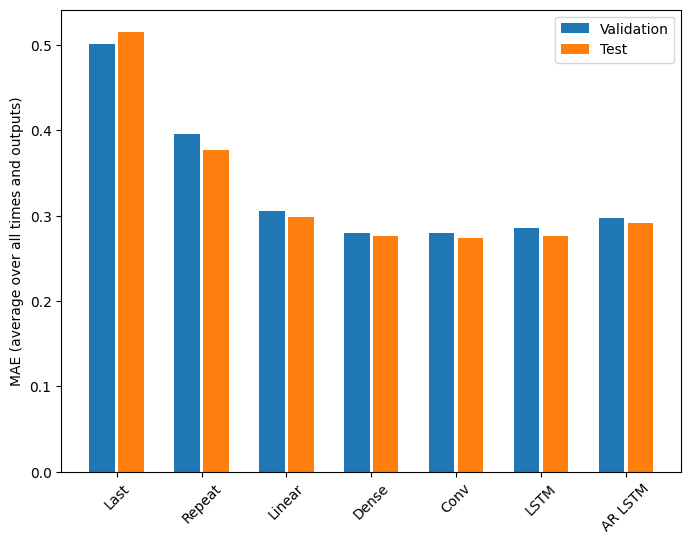
تُظهر مقاييس النماذج متعددة المخرجات في النصف الأول من هذا البرنامج التعليمي متوسط ​​الأداء عبر جميع ميزات الإخراج. هذه العروض متشابهة ولكن أيضًا تم حساب متوسطها عبر خطوات وقت الإخراج.

for name, value in multi_performance.items():
  print(f'{name:8s}: {value[1]:0.4f}')

Last    : 0.5157
Repeat  : 0.3774
Linear  : 0.2977
Dense   : 0.2781
Conv    : 0.2796
LSTM    : 0.2767
AR LSTM : 0.2901

المكاسب التي تحققت من نموذج كثيف إلى نماذج تلافيفية ومتكررة ليست سوى نسبة قليلة (إن وجدت) ، وكان أداء نموذج الانحدار الذاتي أسوأ بشكل واضح. لذلك قد لا تكون هذه الأساليب الأكثر تعقيدًا مفيدة أثناء حل هذه المشكلة ، ولكن لا توجد طريقة لمعرفة ذلك دون محاولة ، وقد تكون هذه النماذج مفيدة لمشكلتك .

الخطوات التالية

كان هذا البرنامج التعليمي بمثابة مقدمة سريعة للتنبؤ بالسلاسل الزمنية باستخدام TensorFlow.

لمعرفة المزيد ، يرجى الرجوع إلى:

• الفصل 15 من التعلم الآلي العملي باستخدام Scikit-Learn و Keras و TensorFlow ، الإصدار الثاني.
• الفصل السادس من التعلم العميق مع بايثون .
• الدرس 8 من مقدمة Udacity إلى TensorFlow للتعلم العميق ، بما في ذلك دفاتر التمارين .

تذكر أيضًا أنه يمكنك تنفيذ أي نموذج سلسلة زمنية كلاسيكية في TensorFlow - يركز هذا البرنامج التعليمي فقط على الوظائف المضمنة في TensorFlow.