 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Hướng dẫn này trình bày cách phân loại tập dữ liệu mất cân bằng cao, trong đó số lượng ví dụ trong một lớp nhiều hơn rất nhiều các ví dụ trong lớp khác. Bạn sẽ làm việc với bộ dữ liệu Phát hiện Gian lận Thẻ Tín dụng được lưu trữ trên Kaggle. Mục đích là để phát hiện chỉ 492 giao dịch gian lận trong tổng số 284.807 giao dịch. Bạn sẽ sử dụng Keras để xác định trọng số của mô hình và lớp để giúp mô hình học hỏi từ dữ liệu không cân bằng. .
Hướng dẫn này chứa mã hoàn chỉnh để:
- Tải tệp CSV bằng Pandas.
- Tạo tập hợp đào tạo, xác nhận và kiểm tra.
- Xác định và đào tạo một mô hình bằng Keras (bao gồm cả thiết lập trọng số của lớp).
- Đánh giá mô hình bằng cách sử dụng các thước đo khác nhau (bao gồm cả độ chính xác và thu hồi).
- Hãy thử các kỹ thuật phổ biến để xử lý dữ liệu mất cân bằng như:
- Trọng số lớp
- Lấy mẫu quá mức
Thành lập
import tensorflow as tf
from tensorflow import keras
import os
import tempfile
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
Xử lý và thăm dò dữ liệu
Tải xuống bộ dữ liệu Gian lận thẻ tín dụng Kaggle
Pandas là một thư viện Python với nhiều tiện ích hữu ích để tải và làm việc với dữ liệu có cấu trúc. Nó có thể được sử dụng để tải xuống CSV vào một Pandas DataFrame .
file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()
Kiểm tra sự mất cân bằng nhãn lớp
Hãy xem xét sự mất cân bằng tập dữ liệu:
neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n'.format(
total, pos, 100 * pos / total))
Examples:
Total: 284807
Positive: 492 (0.17% of total)
Điều này cho thấy một phần nhỏ các mẫu dương tính.
Làm sạch, tách và chuẩn hóa dữ liệu
Dữ liệu thô có một số vấn đề. Đầu tiên, cột Time và Amount quá thay đổi để sử dụng trực tiếp. Thả cột Time (vì không rõ nghĩa của nó) và lấy nhật ký của cột Amount để giảm phạm vi của nó.
cleaned_df = raw_df.copy()
# You don't want the `Time` column.
cleaned_df.pop('Time')
# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Ammount'] = np.log(cleaned_df.pop('Amount')+eps)
Chia tập dữ liệu thành các tập huấn luyện, xác thực và thử nghiệm. Bộ xác nhận được sử dụng trong quá trình điều chỉnh mô hình để đánh giá tổn thất và bất kỳ số liệu nào, tuy nhiên, mô hình không phù hợp với dữ liệu này. Bộ thử nghiệm hoàn toàn không được sử dụng trong giai đoạn huấn luyện và chỉ được sử dụng ở phần cuối để đánh giá mức độ tổng quát của mô hình đối với dữ liệu mới. Điều này đặc biệt quan trọng với các bộ dữ liệu không cân bằng trong đó việc trang bị quá nhiều là một mối quan tâm đáng kể do thiếu dữ liệu đào tạo.
# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
Chuẩn hóa các tính năng đầu vào bằng sklearn StandardScaler. Điều này sẽ đặt giá trị trung bình thành 0 và độ lệch chuẩn thành 1.
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
Training labels shape: (182276,) Validation labels shape: (45569,) Test labels shape: (56962,) Training features shape: (182276, 29) Validation features shape: (45569, 29) Test features shape: (56962, 29)
Nhìn vào phân phối dữ liệu
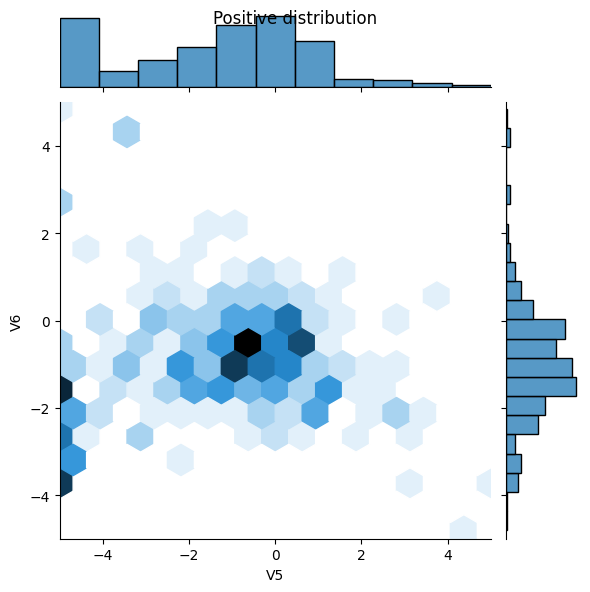
Tiếp theo, hãy so sánh sự phân bố của các ví dụ tích cực và tiêu cực trên một vài tính năng. Những câu hỏi hay để tự hỏi bản thân vào thời điểm này là:
- Những phân phối này có ý nghĩa không?
- Đúng. Bạn đã chuẩn hóa đầu vào và chúng chủ yếu tập trung trong phạm vi
+/- 2.
- Đúng. Bạn đã chuẩn hóa đầu vào và chúng chủ yếu tập trung trong phạm vi
- Bạn có thể thấy sự khác biệt giữa các bản phân phối?
- Có, các ví dụ tích cực chứa tỷ lệ giá trị cực đoan cao hơn nhiều.
pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)
sns.jointplot(x=pos_df['V5'], y=pos_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")
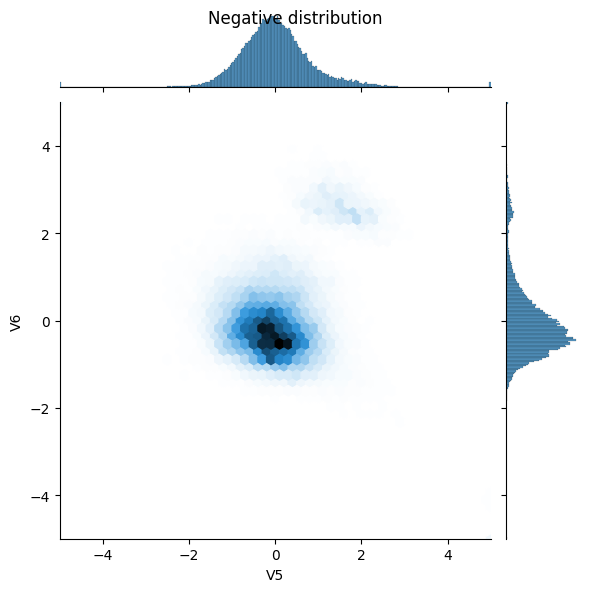
sns.jointplot(x=neg_df['V5'], y=neg_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")
Xác định mô hình và số liệu
Xác định một chức năng tạo ra một mạng nơ-ron đơn giản với một lớp ẩn được kết nối dày đặc, một lớp bỏ trang để giảm việc trang bị quá mức và một lớp sigmoid đầu ra trả về xác suất một giao dịch là gian lận:
METRICS = [
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.BinaryAccuracy(name='accuracy'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc'),
keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]
def make_model(metrics=METRICS, output_bias=None):
if output_bias is not None:
output_bias = tf.keras.initializers.Constant(output_bias)
model = keras.Sequential([
keras.layers.Dense(
16, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid',
bias_initializer=output_bias),
])
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.BinaryCrossentropy(),
metrics=metrics)
return model
Hiểu các chỉ số hữu ích
Lưu ý rằng có một số chỉ số được xác định ở trên có thể được mô hình tính toán sẽ hữu ích khi đánh giá hiệu suất.
- Âm tính giả và dương tính giả là các mẫu được phân loại không chính xác
- Âm tính thực sự và dương tính thực sự là các mẫu đã được phân loại chính xác
- Độ chính xác là tỷ lệ phần trăm các ví dụ được phân loại chính xác> \(\frac{\text{true samples} }{\text{total samples} }\)
- Độ chính xác là phần trăm số dương tính dự đoán đã được phân loại chính xác> \(\frac{\text{true positives} }{\text{true positives + false positives} }\)
- Nhớ lại là tỷ lệ phần trăm dương tính thực tế đã được phân loại chính xác> \(\frac{\text{true positives} }{\text{true positives + false negatives} }\)
- AUC đề cập đến Khu vực dưới đường cong của đường cong đặc tính hoạt động của máy thu (ROC-AUC). Số liệu này bằng với xác suất mà bộ phân loại sẽ xếp hạng mẫu dương ngẫu nhiên cao hơn mẫu phủ định ngẫu nhiên.
- AUPRC đề cập đến Khu vực nằm dưới đường cong của đường cong thu hồi độ chính xác. Chỉ số này tính toán các cặp truy lại chính xác cho các ngưỡng xác suất khác nhau.
Đọc thêm:
- Đúng so với Sai và Tích cực so với Tiêu cực
- Sự chính xác
- Độ chính xác và thu hồi
- ROC-AUC
- Mối quan hệ giữa độ chính xác-thu hồi và đường cong ROC
Mô hình cơ sở
Xây dựng mô hình
Bây giờ, hãy tạo và đào tạo mô hình của bạn bằng cách sử dụng hàm đã được xác định trước đó. Lưu ý rằng mô hình vừa vặn bằng cách sử dụng kích thước lô lớn hơn mặc định là 2048, điều này quan trọng để đảm bảo rằng mỗi lô có khả năng chứa một vài mẫu dương tính. Nếu quy mô lô quá nhỏ, họ sẽ không có giao dịch gian lận nào để rút kinh nghiệm.
EPOCHS = 100
BATCH_SIZE = 2048
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_prc',
verbose=1,
patience=10,
mode='max',
restore_best_weights=True)
model = make_model()
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 480
dropout (Dropout) (None, 16) 0
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 497
Trainable params: 497
Non-trainable params: 0
_________________________________________________________________
Chạy thử mô hình:
model.predict(train_features[:10])
array([[0.9466284 ],
[0.7211031 ],
[0.60527885],
[0.8335568 ],
[0.5909625 ],
[0.6751574 ],
[0.6623665 ],
[0.81066036],
[0.50712407],
[0.8296292 ]], dtype=float32)
Tùy chọn: Đặt độ chệch ban đầu chính xác.
Những phỏng đoán ban đầu không phải là tuyệt vời. Bạn biết rằng tập dữ liệu là không cân bằng. Đặt độ chệch của lớp đầu ra để phản ánh điều đó (Xem: Công thức đào tạo mạng thần kinh: "init well" ). Điều này có thể giúp ích cho sự hội tụ ban đầu.
Với khởi tạo thiên vị mặc định, tổn thất sẽ là về math.log(2) = 0.69314
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 1.2781
Có thể bắt nguồn từ thiên vị chính xác để đặt:
\[ p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) \]
\[ b_0 = -log_e(1/p_0 - 1) \]
\[ b_0 = log_e(pos/neg)\]
initial_bias = np.log([pos/neg])
initial_bias
array([-6.35935934])
Đặt đó là độ chệch ban đầu và mô hình sẽ đưa ra những phỏng đoán ban đầu hợp lý hơn nhiều.
Nó phải ở gần: pos/total = 0.0018
model = make_model(output_bias=initial_bias)
model.predict(train_features[:10])
array([[2.3598122e-05],
[1.5476024e-03],
[6.8338902e-04],
[9.4873342e-04],
[1.0742771e-03],
[7.7475846e-04],
[1.2199467e-03],
[5.5399281e-04],
[1.6213538e-03],
[3.0470363e-04]], dtype=float32)
Với việc khởi tạo này, tổn thất ban đầu sẽ xấp xỉ:
\[-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317\]
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.0200
Tổn thất ban đầu này ít hơn khoảng 50 lần so với nếu có khi khởi tạo ngây thơ.
Bằng cách này, mô hình không cần dành vài kỷ nguyên đầu tiên mà chỉ cần biết rằng những ví dụ tích cực khó có thể xảy ra. Điều này cũng giúp bạn dễ dàng đọc được các biểu đồ về tổn thất trong quá trình huấn luyện.
Kiểm tra trọng lượng ban đầu
Để làm cho các lần chạy huấn luyện khác nhau dễ so sánh hơn, hãy giữ trọng số của mô hình ban đầu này trong tệp điểm kiểm tra và tải chúng vào từng mô hình trước khi huấn luyện:
initial_weights = os.path.join(tempfile.mkdtemp(), 'initial_weights')
model.save_weights(initial_weights)
Xác nhận rằng bản sửa lỗi thiên vị có ích
Trước khi tiếp tục, hãy nhanh chóng xác nhận rằng quá trình khởi tạo thiên vị cẩn thận thực sự có ích.
Đào tạo mô hình trong 20 kỷ nguyên, có và không có khởi tạo cẩn thận này, và so sánh các tổn thất:
model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
def plot_loss(history, label, n):
# Use a log scale on y-axis to show the wide range of values.
plt.semilogy(history.epoch, history.history['loss'],
color=colors[n], label='Train ' + label)
plt.semilogy(history.epoch, history.history['val_loss'],
color=colors[n], label='Val ' + label,
linestyle="--")
plt.xlabel('Epoch')
plt.ylabel('Loss')
plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)
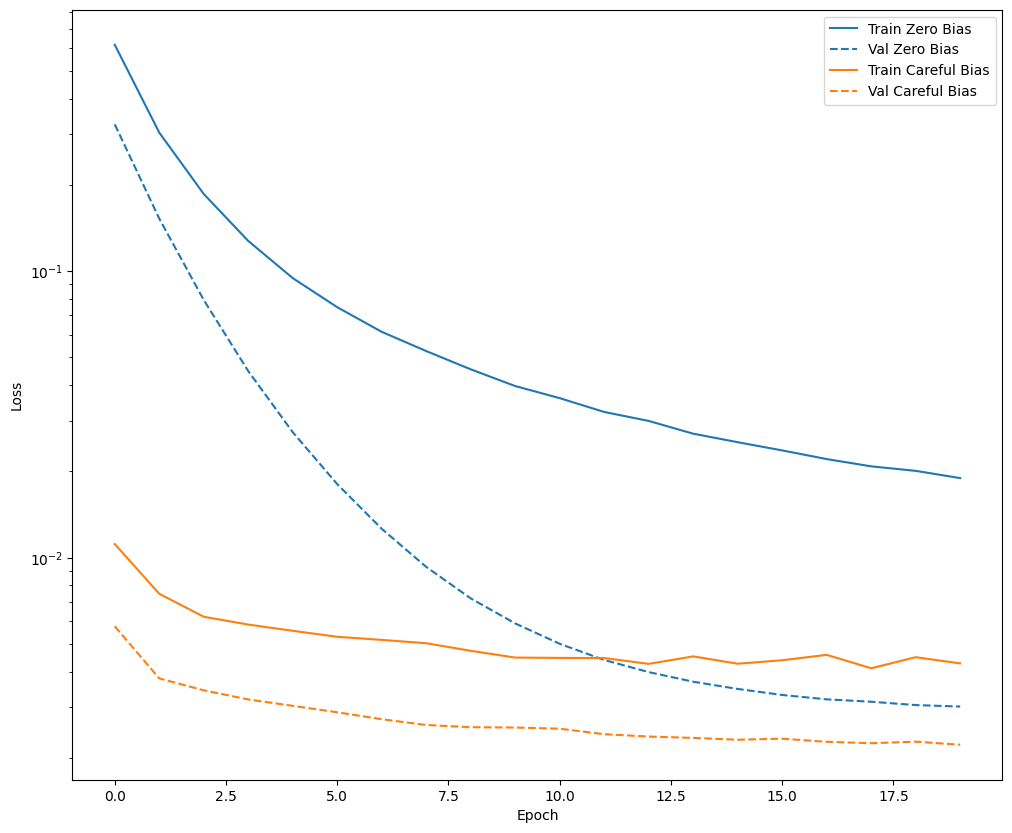
Hình trên cho thấy rõ ràng: Về vấn đề mất xác thực, đối với vấn đề này, việc khởi tạo cẩn thận này mang lại một lợi thế rõ ràng.
Đào tạo mô hình
model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels))
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 0.0161 - tp: 64.0000 - fp: 9.0000 - tn: 227425.0000 - fn: 347.0000 - accuracy: 0.9984 - precision: 0.8767 - recall: 0.1557 - auc: 0.6148 - prc: 0.1692 - val_loss: 0.0115 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7205 - val_prc: 0.2571 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0087 - tp: 49.0000 - fp: 11.0000 - tn: 181940.0000 - fn: 276.0000 - accuracy: 0.9984 - precision: 0.8167 - recall: 0.1508 - auc: 0.8085 - prc: 0.3735 - val_loss: 0.0054 - val_tp: 35.0000 - val_fp: 6.0000 - val_tn: 45477.0000 - val_fn: 51.0000 - val_accuracy: 0.9987 - val_precision: 0.8537 - val_recall: 0.4070 - val_auc: 0.9065 - val_prc: 0.6598 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0061 - tp: 126.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 199.0000 - accuracy: 0.9988 - precision: 0.8235 - recall: 0.3877 - auc: 0.8997 - prc: 0.6187 - val_loss: 0.0046 - val_tp: 55.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 31.0000 - val_accuracy: 0.9991 - val_precision: 0.8730 - val_recall: 0.6395 - val_auc: 0.9063 - val_prc: 0.6941 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 172.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 153.0000 - accuracy: 0.9990 - precision: 0.8473 - recall: 0.5292 - auc: 0.9068 - prc: 0.6448 - val_loss: 0.0044 - val_tp: 58.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 28.0000 - val_accuracy: 0.9992 - val_precision: 0.8788 - val_recall: 0.6744 - val_auc: 0.9064 - val_prc: 0.7114 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 167.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 158.0000 - accuracy: 0.9990 - precision: 0.8477 - recall: 0.5138 - auc: 0.9134 - prc: 0.6215 - val_loss: 0.0043 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7181 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 193.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 132.0000 - accuracy: 0.9991 - precision: 0.8733 - recall: 0.5938 - auc: 0.9198 - prc: 0.6760 - val_loss: 0.0042 - val_tp: 59.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 27.0000 - val_accuracy: 0.9992 - val_precision: 0.8806 - val_recall: 0.6860 - val_auc: 0.9064 - val_prc: 0.7370 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 183.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 142.0000 - accuracy: 0.9991 - precision: 0.8592 - recall: 0.5631 - auc: 0.9202 - prc: 0.6737 - val_loss: 0.0042 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7463 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 171.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 154.0000 - accuracy: 0.9990 - precision: 0.8465 - recall: 0.5262 - auc: 0.9156 - prc: 0.6574 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7480 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 196.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8711 - recall: 0.6031 - auc: 0.9218 - prc: 0.6799 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7550 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 173.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 152.0000 - accuracy: 0.9990 - precision: 0.8650 - recall: 0.5323 - auc: 0.9048 - prc: 0.6520 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9122 - val_prc: 0.7598 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 190.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8597 - recall: 0.5846 - auc: 0.9172 - prc: 0.6779 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9065 - val_prc: 0.7595 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 192.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 133.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.5908 - auc: 0.9281 - prc: 0.7312 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9123 - val_prc: 0.7648 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 185.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 140.0000 - accuracy: 0.9991 - precision: 0.8565 - recall: 0.5692 - auc: 0.9328 - prc: 0.7222 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7615 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 183.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 142.0000 - accuracy: 0.9990 - precision: 0.8472 - recall: 0.5631 - auc: 0.9295 - prc: 0.6770 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7670 Epoch 15/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 194.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8700 - recall: 0.5969 - auc: 0.9344 - prc: 0.7233 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7672 Epoch 16/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 207.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8697 - recall: 0.6369 - auc: 0.9329 - prc: 0.7194 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7694 Epoch 17/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 190.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8716 - recall: 0.5846 - auc: 0.9345 - prc: 0.7265 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7705 Epoch 18/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8622 - recall: 0.5969 - auc: 0.9344 - prc: 0.7199 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7725 Epoch 19/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 205.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8613 - recall: 0.6308 - auc: 0.9346 - prc: 0.7266 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7739 Epoch 20/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 207.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8809 - recall: 0.6369 - auc: 0.9421 - prc: 0.7634 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7729 Epoch 21/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0040 - tp: 204.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8644 - recall: 0.6277 - auc: 0.9360 - prc: 0.7340 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7756 Epoch 22/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 207.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8884 - recall: 0.6369 - auc: 0.9328 - prc: 0.7277 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7773 Epoch 23/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0041 - tp: 191.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8527 - recall: 0.5877 - auc: 0.9375 - prc: 0.7280 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8857 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7790 Epoch 24/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 196.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6031 - auc: 0.9375 - prc: 0.7466 - val_loss: 0.0038 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7762 Epoch 25/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 204.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8681 - recall: 0.6277 - auc: 0.9467 - prc: 0.7480 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9123 - val_prc: 0.7789 Epoch 26/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8661 - recall: 0.5969 - auc: 0.9360 - prc: 0.7292 - val_loss: 0.0038 - val_tp: 60.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8955 - val_recall: 0.6977 - val_auc: 0.9123 - val_prc: 0.7783 Epoch 27/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8776 - recall: 0.6400 - auc: 0.9376 - prc: 0.7632 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7772 Epoch 28/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 202.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 123.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6215 - auc: 0.9408 - prc: 0.7638 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7808 Epoch 29/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 214.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8807 - recall: 0.6585 - auc: 0.9347 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7806 Epoch 30/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 197.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 128.0000 - accuracy: 0.9991 - precision: 0.8640 - recall: 0.6062 - auc: 0.9346 - prc: 0.7489 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7804 Epoch 31/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 213.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 112.0000 - accuracy: 0.9992 - precision: 0.8659 - recall: 0.6554 - auc: 0.9407 - prc: 0.7615 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7809 Epoch 32/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9407 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7821 Epoch 33/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 210.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 115.0000 - accuracy: 0.9992 - precision: 0.8787 - recall: 0.6462 - auc: 0.9392 - prc: 0.7642 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7826 Epoch 34/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9423 - prc: 0.7759 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7830 Epoch 35/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 35.0000 - tn: 181916.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8566 - recall: 0.6431 - auc: 0.9407 - prc: 0.7381 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 36/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 204.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8831 - recall: 0.6277 - auc: 0.9407 - prc: 0.7587 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 37/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8672 - recall: 0.6431 - auc: 0.9345 - prc: 0.7386 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7849 Epoch 38/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 198.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.6092 - auc: 0.9454 - prc: 0.7488 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7844 Epoch 39/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 209.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8782 - recall: 0.6431 - auc: 0.9407 - prc: 0.7419 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 40/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 198.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8761 - recall: 0.6092 - auc: 0.9546 - prc: 0.7644 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7835 Epoch 41/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8745 - recall: 0.6431 - auc: 0.9377 - prc: 0.7587 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7827 Epoch 42/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 195.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8667 - recall: 0.6000 - auc: 0.9345 - prc: 0.7436 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7834 Epoch 43/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8655 - recall: 0.6338 - auc: 0.9500 - prc: 0.7699 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 44/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8927 - recall: 0.6400 - auc: 0.9438 - prc: 0.7625 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7841 Epoch 45/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 205.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8686 - recall: 0.6308 - auc: 0.9422 - prc: 0.7519 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7847 Epoch 46/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 206.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8766 - recall: 0.6338 - auc: 0.9423 - prc: 0.7529 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7843 Epoch 47/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 219.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8866 - recall: 0.6738 - auc: 0.9377 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7871 Epoch 48/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8729 - recall: 0.6338 - auc: 0.9393 - prc: 0.7676 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7854 Epoch 49/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 215.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 110.0000 - accuracy: 0.9992 - precision: 0.8811 - recall: 0.6615 - auc: 0.9407 - prc: 0.7618 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9125 - val_prc: 0.7855 Epoch 50/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 214.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8699 - recall: 0.6585 - auc: 0.9377 - prc: 0.7727 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7858 Epoch 51/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 219.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8795 - recall: 0.6738 - auc: 0.9393 - prc: 0.7889 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7876 Epoch 52/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 217.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8967 - recall: 0.6677 - auc: 0.9439 - prc: 0.7812 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7887 Epoch 53/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 206.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8803 - recall: 0.6338 - auc: 0.9362 - prc: 0.7734 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 54/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 223.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 102.0000 - accuracy: 0.9993 - precision: 0.8814 - recall: 0.6862 - auc: 0.9438 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7877 Epoch 55/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 220.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 105.0000 - accuracy: 0.9993 - precision: 0.8943 - recall: 0.6769 - auc: 0.9439 - prc: 0.7866 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 56/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 209.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8970 - recall: 0.6431 - auc: 0.9392 - prc: 0.7613 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 57/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0033 - tp: 221.0000 - fp: 23.0000 - tn: 181928.0000 - fn: 104.0000 - accuracy: 0.9993 - precision: 0.9057 - recall: 0.6800 - auc: 0.9516 - prc: 0.7954 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 58/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8851 - recall: 0.6400 - auc: 0.9485 - prc: 0.7746 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7875 Epoch 59/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 216.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 109.0000 - accuracy: 0.9992 - precision: 0.8780 - recall: 0.6646 - auc: 0.9531 - prc: 0.7928 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7883 Epoch 60/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 211.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8719 - recall: 0.6492 - auc: 0.9469 - prc: 0.7808 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7882 Epoch 61/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 201.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 124.0000 - accuracy: 0.9992 - precision: 0.8933 - recall: 0.6185 - auc: 0.9424 - prc: 0.7720 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7881 Epoch 62/100 81/90 [==========================>...] - ETA: 0s - loss: 0.0034 - tp: 196.0000 - fp: 21.0000 - tn: 165565.0000 - fn: 106.0000 - accuracy: 0.9992 - precision: 0.9032 - recall: 0.6490 - auc: 0.9413 - prc: 0.7849Restoring model weights from the end of the best epoch: 52. 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 211.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8941 - recall: 0.6492 - auc: 0.9423 - prc: 0.7828 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7860 Epoch 62: early stopping
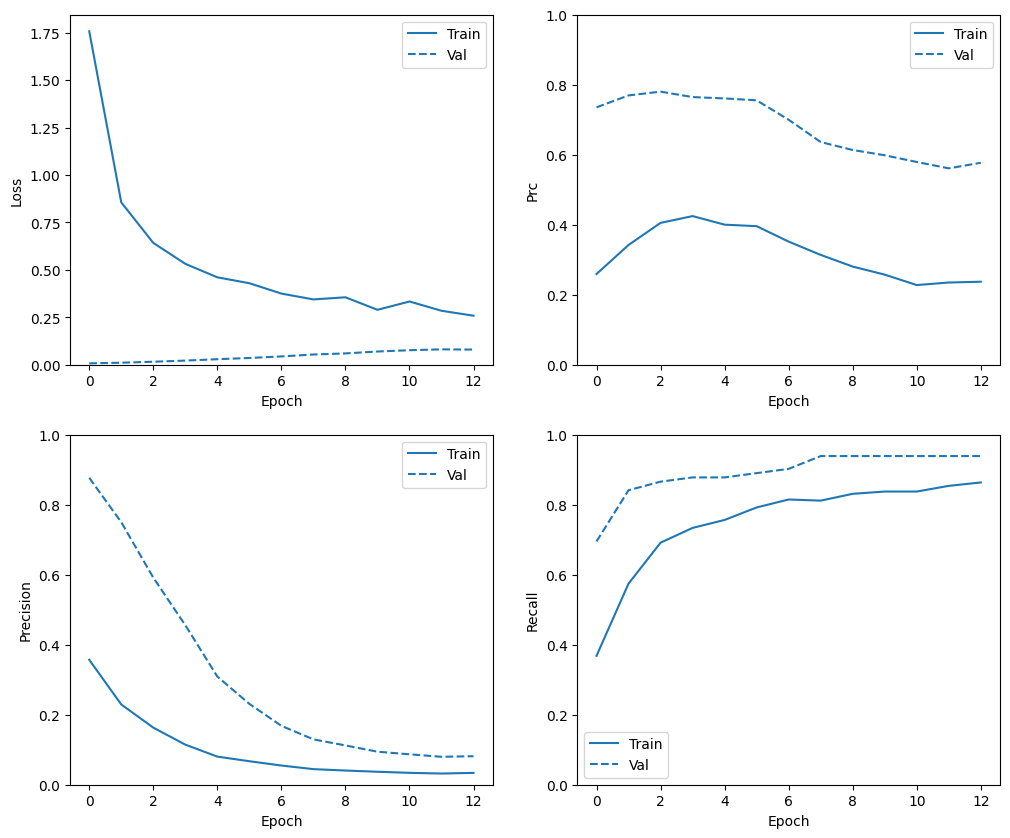
Kiểm tra lịch sử đào tạo
Trong phần này, bạn sẽ đưa ra các biểu đồ về độ chính xác và mất mát của mô hình của bạn trên tập hợp đào tạo và xác nhận. Những điều này rất hữu ích để kiểm tra xem có mặc quá nhiều hay không, bạn có thể tìm hiểu thêm trong phần hướng dẫn Overfit và underfit .
Ngoài ra, bạn có thể tạo các biểu đồ này cho bất kỳ số liệu nào bạn đã tạo ở trên. Các phủ định sai được đưa vào làm ví dụ.
def plot_metrics(history):
metrics = ['loss', 'prc', 'precision', 'recall']
for n, metric in enumerate(metrics):
name = metric.replace("_"," ").capitalize()
plt.subplot(2,2,n+1)
plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
color=colors[0], linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
if metric == 'loss':
plt.ylim([0, plt.ylim()[1]])
elif metric == 'auc':
plt.ylim([0.8,1])
else:
plt.ylim([0,1])
plt.legend();
plot_metrics(baseline_history)
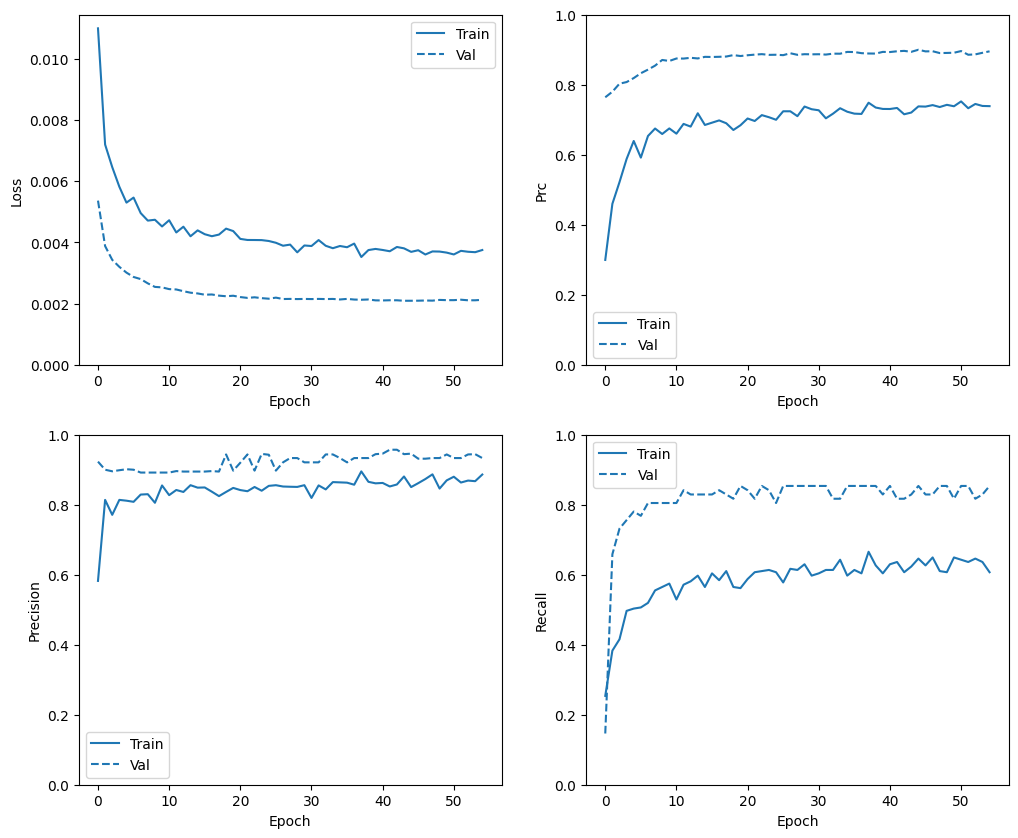
Đánh giá các chỉ số
Bạn có thể sử dụng ma trận nhầm lẫn để tóm tắt các nhãn thực tế so với các nhãn được dự đoán, trong đó trục X là nhãn được dự đoán và trục Y là nhãn thực tế:
train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)
def plot_cm(labels, predictions, p=0.5):
cm = confusion_matrix(labels, predictions > p)
plt.figure(figsize=(5,5))
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion matrix @{:.2f}'.format(p))
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
Đánh giá mô hình của bạn trên tập dữ liệu thử nghiệm và hiển thị kết quả cho các chỉ số bạn đã tạo ở trên:
baseline_results = model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_baseline)
loss : 0.0024895435199141502 tp : 59.0 fp : 7.0 tn : 56874.0 fn : 22.0 accuracy : 0.9994909167289734 precision : 0.8939393758773804 recall : 0.7283950448036194 auc : 0.9318439960479736 prc : 0.8204483985900879 Legitimate Transactions Detected (True Negatives): 56874 Legitimate Transactions Incorrectly Detected (False Positives): 7 Fraudulent Transactions Missed (False Negatives): 22 Fraudulent Transactions Detected (True Positives): 59 Total Fraudulent Transactions: 81
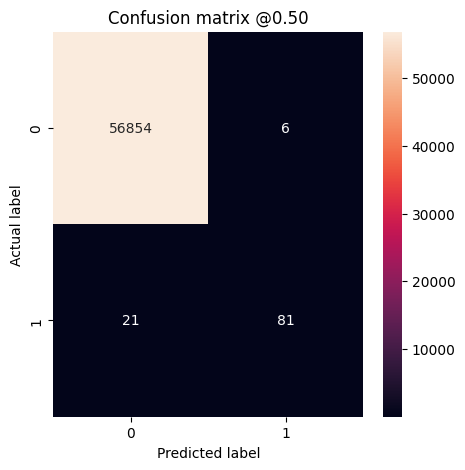
Nếu mô hình đã dự đoán mọi thứ một cách hoàn hảo, thì đây sẽ là một ma trận đường chéo trong đó các giá trị ngoài đường chéo chính, cho biết các dự đoán không chính xác, sẽ bằng không. Trong trường hợp này, ma trận cho thấy rằng bạn có tương đối ít xác thực sai, có nghĩa là có tương đối ít giao dịch hợp pháp bị gắn cờ không chính xác. Tuy nhiên, bạn có thể muốn có ít âm tính giả hơn mặc dù chi phí tăng số lượng âm tính giả. Việc đánh đổi này có thể thích hợp hơn vì âm tính giả sẽ cho phép thực hiện các giao dịch gian lận, trong khi dương tính giả có thể khiến khách hàng gửi email đến yêu cầu họ xác minh hoạt động thẻ của mình.
Lập kế hoạch cho ROC
Bây giờ vẽ sơ đồ ROC . Biểu đồ này hữu ích vì nó cho thấy, trong nháy mắt, phạm vi hiệu suất mà mô hình có thể đạt được chỉ bằng cách điều chỉnh ngưỡng đầu ra.
def plot_roc(name, labels, predictions, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,20])
plt.ylim([80,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
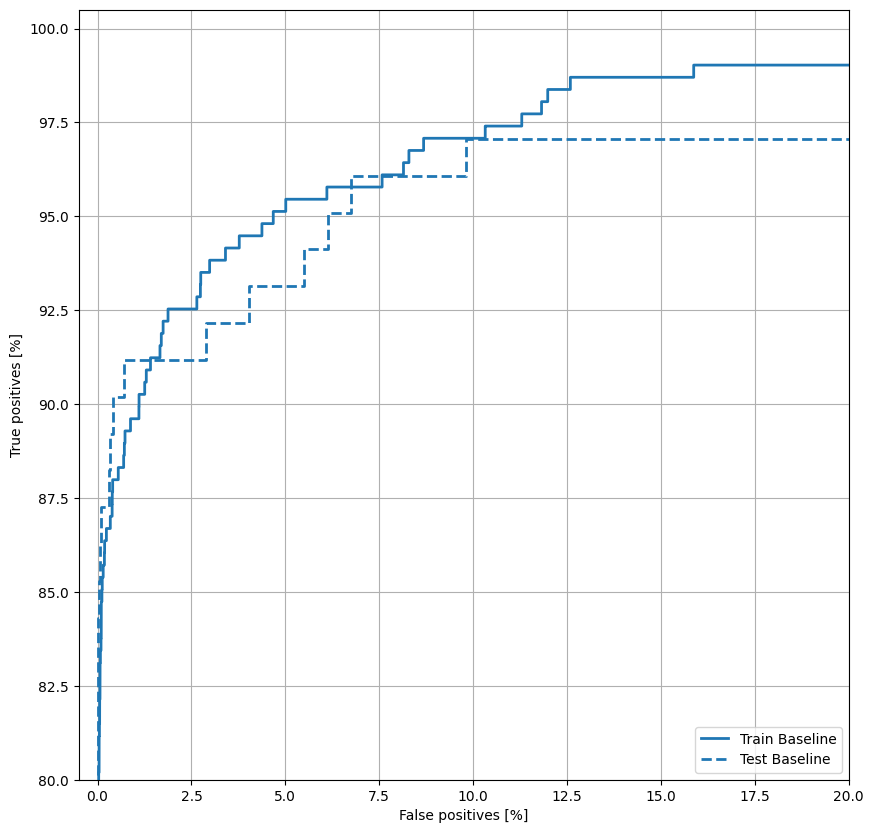
Lập đồ thị AUPRC
Bây giờ vẽ AUPRC . Diện tích dưới đường cong thu hồi độ chính xác nội suy, thu được bằng cách vẽ biểu đồ (thu hồi, độ chính xác) cho các giá trị khác nhau của ngưỡng phân loại. Tùy thuộc vào cách nó được tính toán, PR AUC có thể tương đương với độ chính xác trung bình của mô hình.
def plot_prc(name, labels, predictions, **kwargs):
precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
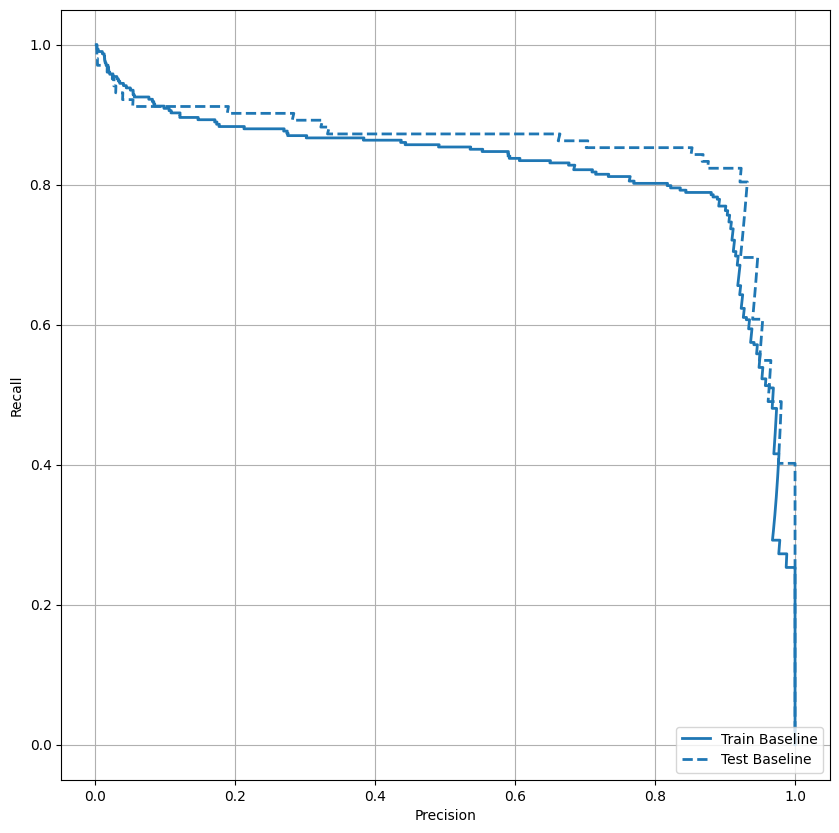
Có vẻ như độ chính xác tương đối cao, nhưng độ thu hồi và diện tích dưới đường cong ROC (AUC) không cao như bạn có thể muốn. Bộ phân loại thường phải đối mặt với những thách thức khi cố gắng tối đa hóa cả độ chính xác và khả năng thu hồi, điều này đặc biệt đúng khi làm việc với bộ dữ liệu không cân bằng. Điều quan trọng là phải xem xét chi phí của các loại lỗi khác nhau trong bối cảnh của vấn đề mà bạn quan tâm. Trong ví dụ này, âm sai (một giao dịch gian lận bị bỏ qua) có thể gây ra chi phí tài chính, trong khi dương tính giả (một giao dịch bị gắn cờ không chính xác là gian lận) có thể làm giảm hạnh phúc của người dùng.
Trọng lượng hạng
Tính trọng lượng lớp
Mục đích là để xác định các giao dịch gian lận, nhưng bạn không có nhiều mẫu tích cực để làm việc, vì vậy bạn sẽ muốn bộ phân loại có trọng lượng lớn đối với một số ví dụ có sẵn. Bạn có thể làm điều này bằng cách chuyển trọng số Keras cho mỗi lớp thông qua một tham số. Những điều này sẽ khiến mô hình "chú ý nhiều hơn" đến các ví dụ từ một lớp ít được đại diện.
# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))
Weight for class 0: 0.50 Weight for class 1: 289.44
Huấn luyện một mô hình với các trọng lượng của lớp
Bây giờ hãy thử đào tạo lại và đánh giá mô hình với trọng số lớp để xem điều đó ảnh hưởng như thế nào đến các dự đoán.
weighted_model = make_model()
weighted_model.load_weights(initial_weights)
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels),
# The class weights go here
class_weight=class_weight)
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 4.1298 - tp: 59.0000 - fp: 11.0000 - tn: 238821.0000 - fn: 347.0000 - accuracy: 0.9985 - precision: 0.8429 - recall: 0.1453 - auc: 0.6238 - prc: 0.1649 - val_loss: 0.0119 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7124 - val_prc: 0.0294 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 1.8711 - tp: 69.0000 - fp: 54.0000 - tn: 181897.0000 - fn: 256.0000 - accuracy: 0.9983 - precision: 0.5610 - recall: 0.2123 - auc: 0.8178 - prc: 0.2117 - val_loss: 0.0060 - val_tp: 56.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 30.0000 - val_accuracy: 0.9991 - val_precision: 0.8485 - val_recall: 0.6512 - val_auc: 0.9427 - val_prc: 0.6870 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.8666 - tp: 187.0000 - fp: 198.0000 - tn: 181753.0000 - fn: 138.0000 - accuracy: 0.9982 - precision: 0.4857 - recall: 0.5754 - auc: 0.9075 - prc: 0.4912 - val_loss: 0.0077 - val_tp: 65.0000 - val_fp: 19.0000 - val_tn: 45464.0000 - val_fn: 21.0000 - val_accuracy: 0.9991 - val_precision: 0.7738 - val_recall: 0.7558 - val_auc: 0.9564 - val_prc: 0.6924 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.6876 - tp: 218.0000 - fp: 530.0000 - tn: 181421.0000 - fn: 107.0000 - accuracy: 0.9965 - precision: 0.2914 - recall: 0.6708 - auc: 0.9152 - prc: 0.5102 - val_loss: 0.0109 - val_tp: 68.0000 - val_fp: 39.0000 - val_tn: 45444.0000 - val_fn: 18.0000 - val_accuracy: 0.9987 - val_precision: 0.6355 - val_recall: 0.7907 - val_auc: 0.9661 - val_prc: 0.6926 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.5229 - tp: 240.0000 - fp: 1102.0000 - tn: 180849.0000 - fn: 85.0000 - accuracy: 0.9935 - precision: 0.1788 - recall: 0.7385 - auc: 0.9395 - prc: 0.5228 - val_loss: 0.0154 - val_tp: 70.0000 - val_fp: 79.0000 - val_tn: 45404.0000 - val_fn: 16.0000 - val_accuracy: 0.9979 - val_precision: 0.4698 - val_recall: 0.8140 - val_auc: 0.9657 - val_prc: 0.7023 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.4753 - tp: 251.0000 - fp: 1839.0000 - tn: 180112.0000 - fn: 74.0000 - accuracy: 0.9895 - precision: 0.1201 - recall: 0.7723 - auc: 0.9336 - prc: 0.4297 - val_loss: 0.0213 - val_tp: 70.0000 - val_fp: 156.0000 - val_tn: 45327.0000 - val_fn: 16.0000 - val_accuracy: 0.9962 - val_precision: 0.3097 - val_recall: 0.8140 - val_auc: 0.9654 - val_prc: 0.6742 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3870 - tp: 270.0000 - fp: 2554.0000 - tn: 179397.0000 - fn: 55.0000 - accuracy: 0.9857 - precision: 0.0956 - recall: 0.8308 - auc: 0.9463 - prc: 0.3800 - val_loss: 0.0269 - val_tp: 70.0000 - val_fp: 264.0000 - val_tn: 45219.0000 - val_fn: 16.0000 - val_accuracy: 0.9939 - val_precision: 0.2096 - val_recall: 0.8140 - val_auc: 0.9651 - val_prc: 0.6116 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3942 - tp: 268.0000 - fp: 3219.0000 - tn: 178732.0000 - fn: 57.0000 - accuracy: 0.9820 - precision: 0.0769 - recall: 0.8246 - auc: 0.9434 - prc: 0.3273 - val_loss: 0.0337 - val_tp: 70.0000 - val_fp: 355.0000 - val_tn: 45128.0000 - val_fn: 16.0000 - val_accuracy: 0.9919 - val_precision: 0.1647 - val_recall: 0.8140 - val_auc: 0.9682 - val_prc: 0.5918 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3886 - tp: 271.0000 - fp: 3845.0000 - tn: 178106.0000 - fn: 54.0000 - accuracy: 0.9786 - precision: 0.0658 - recall: 0.8338 - auc: 0.9397 - prc: 0.2995 - val_loss: 0.0386 - val_tp: 70.0000 - val_fp: 406.0000 - val_tn: 45077.0000 - val_fn: 16.0000 - val_accuracy: 0.9907 - val_precision: 0.1471 - val_recall: 0.8140 - val_auc: 0.9756 - val_prc: 0.5889 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2951 - tp: 281.0000 - fp: 4348.0000 - tn: 177603.0000 - fn: 44.0000 - accuracy: 0.9759 - precision: 0.0607 - recall: 0.8646 - auc: 0.9623 - prc: 0.2826 - val_loss: 0.0441 - val_tp: 72.0000 - val_fp: 464.0000 - val_tn: 45019.0000 - val_fn: 14.0000 - val_accuracy: 0.9895 - val_precision: 0.1343 - val_recall: 0.8372 - val_auc: 0.9748 - val_prc: 0.5895 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2703 - tp: 280.0000 - fp: 4697.0000 - tn: 177254.0000 - fn: 45.0000 - accuracy: 0.9740 - precision: 0.0563 - recall: 0.8615 - auc: 0.9660 - prc: 0.2589 - val_loss: 0.0490 - val_tp: 72.0000 - val_fp: 552.0000 - val_tn: 44931.0000 - val_fn: 14.0000 - val_accuracy: 0.9876 - val_precision: 0.1154 - val_recall: 0.8372 - val_auc: 0.9762 - val_prc: 0.5902 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3358 - tp: 278.0000 - fp: 5262.0000 - tn: 176689.0000 - fn: 47.0000 - accuracy: 0.9709 - precision: 0.0502 - recall: 0.8554 - auc: 0.9468 - prc: 0.2368 - val_loss: 0.0534 - val_tp: 74.0000 - val_fp: 597.0000 - val_tn: 44886.0000 - val_fn: 12.0000 - val_accuracy: 0.9866 - val_precision: 0.1103 - val_recall: 0.8605 - val_auc: 0.9752 - val_prc: 0.5848 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2833 - tp: 286.0000 - fp: 5502.0000 - tn: 176449.0000 - fn: 39.0000 - accuracy: 0.9696 - precision: 0.0494 - recall: 0.8800 - auc: 0.9582 - prc: 0.2572 - val_loss: 0.0563 - val_tp: 74.0000 - val_fp: 616.0000 - val_tn: 44867.0000 - val_fn: 12.0000 - val_accuracy: 0.9862 - val_precision: 0.1072 - val_recall: 0.8605 - val_auc: 0.9748 - val_prc: 0.5678 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2969 - tp: 280.0000 - fp: 5630.0000 - tn: 176321.0000 - fn: 45.0000 - accuracy: 0.9689 - precision: 0.0474 - recall: 0.8615 - auc: 0.9594 - prc: 0.2374 - val_loss: 0.0597 - val_tp: 74.0000 - val_fp: 644.0000 - val_tn: 44839.0000 - val_fn: 12.0000 - val_accuracy: 0.9856 - val_precision: 0.1031 - val_recall: 0.8605 - val_auc: 0.9741 - val_prc: 0.5627 Epoch 15/100 90/90 [==============================] - ETA: 0s - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224Restoring model weights from the end of the best epoch: 5. 90/90 [==============================] - 1s 7ms/step - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224 - val_loss: 0.0621 - val_tp: 74.0000 - val_fp: 665.0000 - val_tn: 44818.0000 - val_fn: 12.0000 - val_accuracy: 0.9851 - val_precision: 0.1001 - val_recall: 0.8605 - val_auc: 0.9771 - val_prc: 0.5550 Epoch 15: early stopping
Kiểm tra lịch sử đào tạo
plot_metrics(weighted_history)
Đánh giá các chỉ số
train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)
weighted_results = weighted_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_weighted)
loss : 0.014327289536595345 tp : 69.0 fp : 88.0 tn : 56793.0 fn : 12.0 accuracy : 0.9982444643974304 precision : 0.4394904375076294 recall : 0.8518518805503845 auc : 0.9410961866378784 prc : 0.7397712469100952 Legitimate Transactions Detected (True Negatives): 56793 Legitimate Transactions Incorrectly Detected (False Positives): 88 Fraudulent Transactions Missed (False Negatives): 12 Fraudulent Transactions Detected (True Positives): 69 Total Fraudulent Transactions: 81
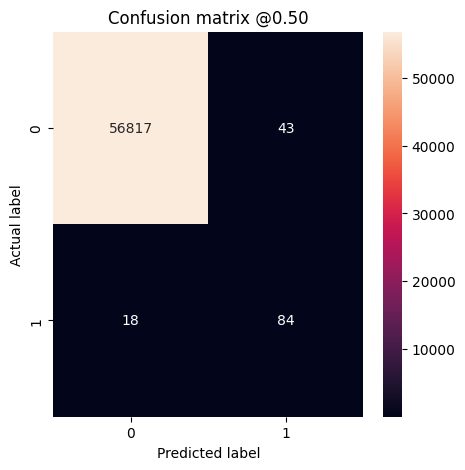
Ở đây bạn có thể thấy rằng với các trọng số cùng loại, độ chính xác và độ chính xác thấp hơn vì có nhiều dương tính giả hơn, nhưng ngược lại, thu hồi và AUC cao hơn vì mô hình cũng tìm thấy nhiều dương tính thật hơn. Mặc dù có độ chính xác thấp hơn, mô hình này có khả năng thu hồi cao hơn (và xác định được nhiều giao dịch gian lận hơn). Tất nhiên, có cái giá phải trả cho cả hai loại lỗi (bạn sẽ không muốn gây lỗi cho người dùng bằng cách gắn cờ quá nhiều giao dịch hợp pháp là gian lận). Hãy cẩn thận xem xét sự cân bằng giữa các loại lỗi khác nhau này đối với ứng dụng của bạn.
Lập kế hoạch cho ROC
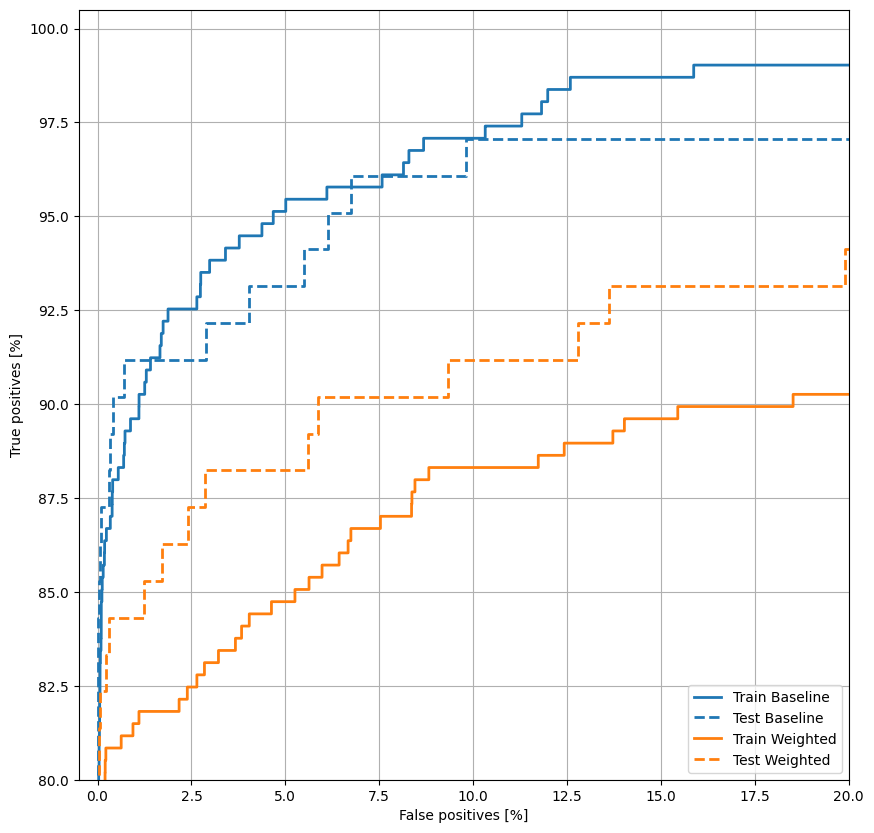
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
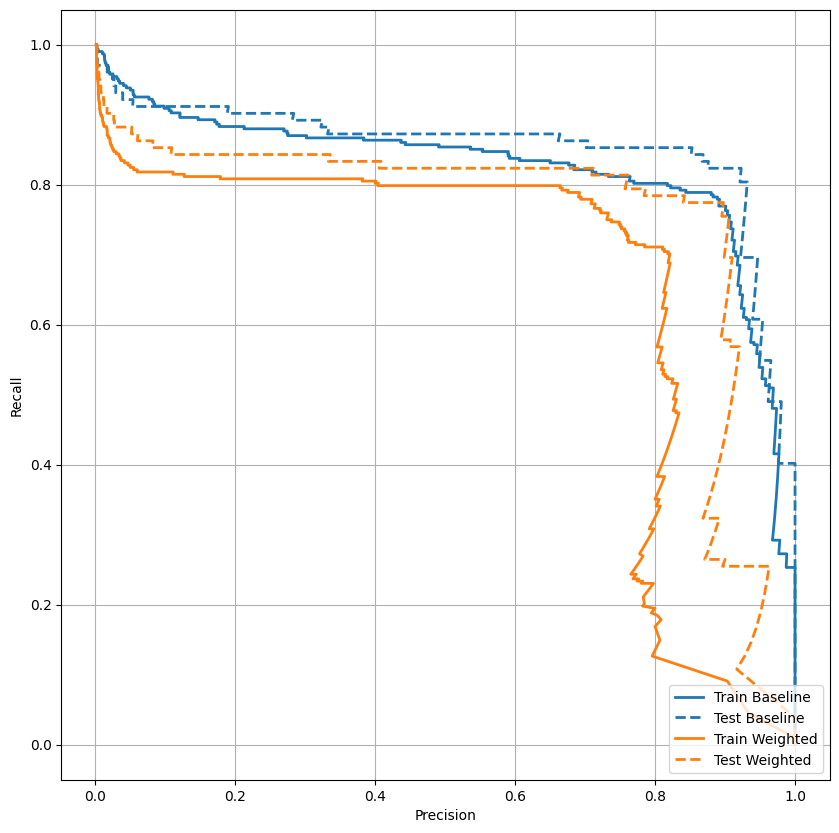
Lập đồ thị AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
Lấy mẫu quá mức
Lấy mẫu mực cho tầng lớp thiểu số
Một cách tiếp cận liên quan sẽ là lấy mẫu lại tập dữ liệu bằng cách lấy mẫu quá mức cho lớp thiểu số.
pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]
pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]
Sử dụng NumPy
Bạn có thể cân bằng tập dữ liệu theo cách thủ công bằng cách chọn đúng số lượng chỉ số ngẫu nhiên từ các ví dụ tích cực:
ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))
res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]
res_pos_features.shape
(181951, 29)
resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)
order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]
resampled_features.shape
(363902, 29)
Sử dụng tf.data
Nếu bạn đang sử dụng tf.data , cách dễ nhất để tạo ra các ví dụ cân bằng là bắt đầu với một tập dữ liệu positive và negative , và hợp nhất chúng. Xem hướng dẫn tf.data để biết thêm ví dụ.
BUFFER_SIZE = 100000
def make_ds(features, labels):
ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
ds = ds.shuffle(BUFFER_SIZE).repeat()
return ds
pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)
Mỗi tập dữ liệu cung cấp các cặp (feature, label) :
for features, label in pos_ds.take(1):
print("Features:\n", features.numpy())
print()
print("Label: ", label.numpy())
Features: [ 0.56826828 1.24841849 -2.52251105 3.84165891 0.05052604 -0.7621795 -1.43118352 0.43296139 -1.85102109 -2.50477555 3.20133397 -3.52460861 -0.95133935 -5. -1.93144512 -0.7302767 -2.46735228 0.21827555 -1.45046438 0.21081234 0.39176826 -0.23558789 -0.03611637 -0.62063738 0.3686766 0.23622961 1.2242418 0.75555829 -1.45589162] Label: 1
Hợp nhất cả hai với nhau bằng tf.data.Dataset.sample_from_datasets :
resampled_ds = tf.data.Dataset.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)
for features, label in resampled_ds.take(1):
print(label.numpy().mean())
0.50732421875
Để sử dụng tập dữ liệu này, bạn sẽ cần số bước cho mỗi kỷ nguyên.
Định nghĩa về "kỷ nguyên" trong trường hợp này ít rõ ràng hơn. Giả sử đó là số lô bắt buộc để xem mỗi ví dụ phủ định một lần:
resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch
278.0
Đào tạo về dữ liệu được lấy mẫu quá mức
Bây giờ, hãy thử đào tạo mô hình với tập dữ liệu được lấy mẫu lại thay vì sử dụng trọng số lớp để xem các phương pháp này so sánh như thế nào.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2)
resampled_history = resampled_model.fit(
resampled_ds,
epochs=EPOCHS,
steps_per_epoch=resampled_steps_per_epoch,
callbacks=[early_stopping],
validation_data=val_ds)
Epoch 1/100 278/278 [==============================] - 10s 32ms/step - loss: 0.5508 - tp: 214194.0000 - fp: 51114.0000 - tn: 290615.0000 - fn: 70383.0000 - accuracy: 0.8060 - precision: 0.8073 - recall: 0.7527 - auc: 0.8600 - prc: 0.8879 - val_loss: 0.2279 - val_tp: 73.0000 - val_fp: 969.0000 - val_tn: 44514.0000 - val_fn: 13.0000 - val_accuracy: 0.9785 - val_precision: 0.0701 - val_recall: 0.8488 - val_auc: 0.9551 - val_prc: 0.7044 Epoch 2/100 278/278 [==============================] - 8s 28ms/step - loss: 0.2235 - tp: 253877.0000 - fp: 15743.0000 - tn: 268530.0000 - fn: 31194.0000 - accuracy: 0.9176 - precision: 0.9416 - recall: 0.8906 - auc: 0.9658 - prc: 0.9746 - val_loss: 0.1367 - val_tp: 73.0000 - val_fp: 777.0000 - val_tn: 44706.0000 - val_fn: 13.0000 - val_accuracy: 0.9827 - val_precision: 0.0859 - val_recall: 0.8488 - val_auc: 0.9596 - val_prc: 0.7072 Epoch 3/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1785 - tp: 258572.0000 - fp: 9840.0000 - tn: 274878.0000 - fn: 26054.0000 - accuracy: 0.9370 - precision: 0.9633 - recall: 0.9085 - auc: 0.9773 - prc: 0.9827 - val_loss: 0.1023 - val_tp: 72.0000 - val_fp: 699.0000 - val_tn: 44784.0000 - val_fn: 14.0000 - val_accuracy: 0.9844 - val_precision: 0.0934 - val_recall: 0.8372 - val_auc: 0.9632 - val_prc: 0.7032 Epoch 4/100 278/278 [==============================] - 8s 29ms/step - loss: 0.1571 - tp: 260447.0000 - fp: 8085.0000 - tn: 276389.0000 - fn: 24423.0000 - accuracy: 0.9429 - precision: 0.9699 - recall: 0.9143 - auc: 0.9826 - prc: 0.9863 - val_loss: 0.0869 - val_tp: 74.0000 - val_fp: 701.0000 - val_tn: 44782.0000 - val_fn: 12.0000 - val_accuracy: 0.9844 - val_precision: 0.0955 - val_recall: 0.8605 - val_auc: 0.9633 - val_prc: 0.6972 Epoch 5/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1440 - tp: 261457.0000 - fp: 7449.0000 - tn: 277093.0000 - fn: 23345.0000 - accuracy: 0.9459 - precision: 0.9723 - recall: 0.9180 - auc: 0.9855 - prc: 0.9883 - val_loss: 0.0774 - val_tp: 73.0000 - val_fp: 679.0000 - val_tn: 44804.0000 - val_fn: 13.0000 - val_accuracy: 0.9848 - val_precision: 0.0971 - val_recall: 0.8488 - val_auc: 0.9645 - val_prc: 0.6971 Epoch 6/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1349 - tp: 262460.0000 - fp: 6942.0000 - tn: 277723.0000 - fn: 22219.0000 - accuracy: 0.9488 - precision: 0.9742 - recall: 0.9220 - auc: 0.9876 - prc: 0.9896 - val_loss: 0.0718 - val_tp: 74.0000 - val_fp: 624.0000 - val_tn: 44859.0000 - val_fn: 12.0000 - val_accuracy: 0.9860 - val_precision: 0.1060 - val_recall: 0.8605 - val_auc: 0.9645 - val_prc: 0.6891 Epoch 7/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1264 - tp: 263166.0000 - fp: 6780.0000 - tn: 278253.0000 - fn: 21145.0000 - accuracy: 0.9510 - precision: 0.9749 - recall: 0.9256 - auc: 0.9895 - prc: 0.9909 - val_loss: 0.0672 - val_tp: 75.0000 - val_fp: 602.0000 - val_tn: 44881.0000 - val_fn: 11.0000 - val_accuracy: 0.9865 - val_precision: 0.1108 - val_recall: 0.8721 - val_auc: 0.9670 - val_prc: 0.6822 Epoch 8/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1190 - tp: 264216.0000 - fp: 6569.0000 - tn: 278270.0000 - fn: 20289.0000 - accuracy: 0.9528 - precision: 0.9757 - recall: 0.9287 - auc: 0.9910 - prc: 0.9920 - val_loss: 0.0628 - val_tp: 74.0000 - val_fp: 570.0000 - val_tn: 44913.0000 - val_fn: 12.0000 - val_accuracy: 0.9872 - val_precision: 0.1149 - val_recall: 0.8605 - val_auc: 0.9671 - val_prc: 0.6830 Epoch 9/100 278/278 [==============================] - 9s 31ms/step - loss: 0.1125 - tp: 264562.0000 - fp: 6339.0000 - tn: 279137.0000 - fn: 19306.0000 - accuracy: 0.9550 - precision: 0.9766 - recall: 0.9320 - auc: 0.9924 - prc: 0.9930 - val_loss: 0.0576 - val_tp: 74.0000 - val_fp: 544.0000 - val_tn: 44939.0000 - val_fn: 12.0000 - val_accuracy: 0.9878 - val_precision: 0.1197 - val_recall: 0.8605 - val_auc: 0.9672 - val_prc: 0.6828 Epoch 10/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1064 - tp: 266549.0000 - fp: 6112.0000 - tn: 278323.0000 - fn: 18360.0000 - accuracy: 0.9570 - precision: 0.9776 - recall: 0.9356 - auc: 0.9934 - prc: 0.9937 - val_loss: 0.0544 - val_tp: 74.0000 - val_fp: 541.0000 - val_tn: 44942.0000 - val_fn: 12.0000 - val_accuracy: 0.9879 - val_precision: 0.1203 - val_recall: 0.8605 - val_auc: 0.9638 - val_prc: 0.6827 Epoch 11/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1005 - tp: 267048.0000 - fp: 6123.0000 - tn: 278896.0000 - fn: 17277.0000 - accuracy: 0.9589 - precision: 0.9776 - recall: 0.9392 - auc: 0.9943 - prc: 0.9944 - val_loss: 0.0493 - val_tp: 74.0000 - val_fp: 500.0000 - val_tn: 44983.0000 - val_fn: 12.0000 - val_accuracy: 0.9888 - val_precision: 0.1289 - val_recall: 0.8605 - val_auc: 0.9578 - val_prc: 0.6761 Epoch 12/100 277/278 [============================>.] - ETA: 0s - loss: 0.0950 - tp: 266855.0000 - fp: 6079.0000 - tn: 277677.0000 - fn: 16685.0000 - accuracy: 0.9599 - precision: 0.9777 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949Restoring model weights from the end of the best epoch: 2. 278/278 [==============================] - 8s 29ms/step - loss: 0.0950 - tp: 267815.0000 - fp: 6094.0000 - tn: 278693.0000 - fn: 16742.0000 - accuracy: 0.9599 - precision: 0.9778 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949 - val_loss: 0.0451 - val_tp: 74.0000 - val_fp: 468.0000 - val_tn: 45015.0000 - val_fn: 12.0000 - val_accuracy: 0.9895 - val_precision: 0.1365 - val_recall: 0.8605 - val_auc: 0.9581 - val_prc: 0.6683 Epoch 12: early stopping
Nếu quá trình đào tạo đang xem xét toàn bộ tập dữ liệu trên mỗi bản cập nhật gradient, việc lấy mẫu quá mức này về cơ bản sẽ giống với trọng số lớp.
Nhưng khi huấn luyện mô hình theo lô, như bạn đã làm ở đây, dữ liệu được lấy mẫu quá mức cung cấp tín hiệu gradient mượt mà hơn: Thay vì mỗi ví dụ tích cực được hiển thị trong một lô với trọng lượng lớn, chúng được hiển thị thành nhiều lô khác nhau mỗi lần với một trọng lượng nhỏ.
Tín hiệu gradient mượt mà hơn này giúp cho việc huấn luyện mô hình dễ dàng hơn.
Kiểm tra lịch sử đào tạo
Lưu ý rằng phân phối của các chỉ số sẽ khác nhau ở đây, vì dữ liệu đào tạo có phân phối hoàn toàn khác với dữ liệu kiểm tra và xác thực.
plot_metrics(resampled_history)
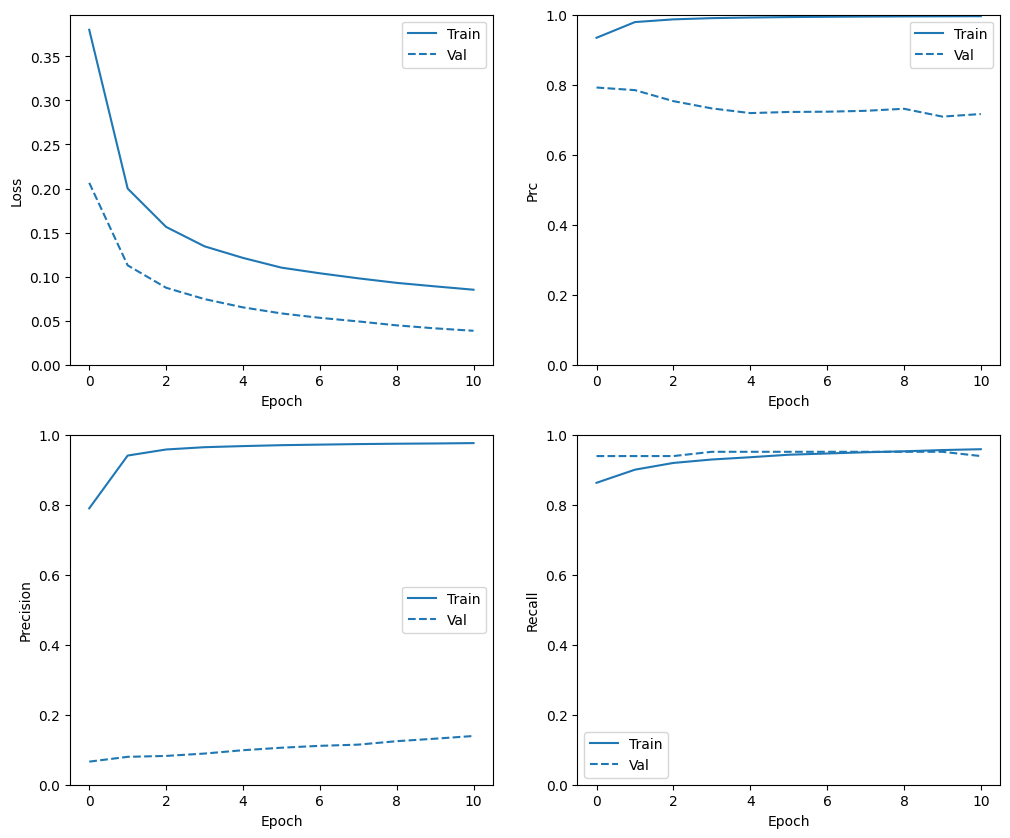
Đào tạo lại
Bởi vì việc đào tạo dễ dàng hơn trên dữ liệu cân bằng, quy trình đào tạo trên có thể nhanh chóng quá mức.
Vì vậy, hãy chia nhỏ các kỷ nguyên để cung cấp cho tf.keras.callbacks.EarlyStopping quyền kiểm soát tốt hơn đối với thời điểm ngừng đào tạo.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
resampled_history = resampled_model.fit(
resampled_ds,
# These are not real epochs
steps_per_epoch=20,
epochs=10*EPOCHS,
callbacks=[early_stopping],
validation_data=(val_ds))
Epoch 1/1000 20/20 [==============================] - 3s 73ms/step - loss: 2.0114 - tp: 3382.0000 - fp: 5181.0000 - tn: 60589.0000 - fn: 17377.0000 - accuracy: 0.7393 - precision: 0.3950 - recall: 0.1629 - auc: 0.6308 - prc: 0.3325 - val_loss: 0.4343 - val_tp: 7.0000 - val_fp: 5042.0000 - val_tn: 40441.0000 - val_fn: 79.0000 - val_accuracy: 0.8876 - val_precision: 0.0014 - val_recall: 0.0814 - val_auc: 0.2282 - val_prc: 0.0012 Epoch 2/1000 20/20 [==============================] - 1s 33ms/step - loss: 1.2163 - tp: 7466.0000 - fp: 5137.0000 - tn: 15257.0000 - fn: 13100.0000 - accuracy: 0.5548 - precision: 0.5924 - recall: 0.3630 - auc: 0.4763 - prc: 0.5716 - val_loss: 0.4539 - val_tp: 36.0000 - val_fp: 5893.0000 - val_tn: 39590.0000 - val_fn: 50.0000 - val_accuracy: 0.8696 - val_precision: 0.0061 - val_recall: 0.4186 - val_auc: 0.6494 - val_prc: 0.0054 Epoch 3/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.7406 - tp: 12289.0000 - fp: 5509.0000 - tn: 14872.0000 - fn: 8290.0000 - accuracy: 0.6631 - precision: 0.6905 - recall: 0.5972 - auc: 0.6803 - prc: 0.7580 - val_loss: 0.4611 - val_tp: 75.0000 - val_fp: 6273.0000 - val_tn: 39210.0000 - val_fn: 11.0000 - val_accuracy: 0.8621 - val_precision: 0.0118 - val_recall: 0.8721 - val_auc: 0.9293 - val_prc: 0.4539 Epoch 4/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.5071 - tp: 15891.0000 - fp: 5370.0000 - tn: 15013.0000 - fn: 4686.0000 - accuracy: 0.7545 - precision: 0.7474 - recall: 0.7723 - auc: 0.8298 - prc: 0.8757 - val_loss: 0.4451 - val_tp: 78.0000 - val_fp: 5505.0000 - val_tn: 39978.0000 - val_fn: 8.0000 - val_accuracy: 0.8790 - val_precision: 0.0140 - val_recall: 0.9070 - val_auc: 0.9443 - val_prc: 0.6777 Epoch 5/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.4284 - tp: 17046.0000 - fp: 5072.0000 - tn: 15496.0000 - fn: 3346.0000 - accuracy: 0.7945 - precision: 0.7707 - recall: 0.8359 - auc: 0.8827 - prc: 0.9151 - val_loss: 0.4140 - val_tp: 77.0000 - val_fp: 4338.0000 - val_tn: 41145.0000 - val_fn: 9.0000 - val_accuracy: 0.9046 - val_precision: 0.0174 - val_recall: 0.8953 - val_auc: 0.9463 - val_prc: 0.6903 Epoch 6/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3836 - tp: 17606.0000 - fp: 4362.0000 - tn: 16113.0000 - fn: 2879.0000 - accuracy: 0.8232 - precision: 0.8014 - recall: 0.8595 - auc: 0.9080 - prc: 0.9336 - val_loss: 0.3824 - val_tp: 77.0000 - val_fp: 3314.0000 - val_tn: 42169.0000 - val_fn: 9.0000 - val_accuracy: 0.9271 - val_precision: 0.0227 - val_recall: 0.8953 - val_auc: 0.9475 - val_prc: 0.6752 Epoch 7/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3574 - tp: 17856.0000 - fp: 3894.0000 - tn: 16553.0000 - fn: 2657.0000 - accuracy: 0.8401 - precision: 0.8210 - recall: 0.8705 - auc: 0.9208 - prc: 0.9432 - val_loss: 0.3538 - val_tp: 76.0000 - val_fp: 2592.0000 - val_tn: 42891.0000 - val_fn: 10.0000 - val_accuracy: 0.9429 - val_precision: 0.0285 - val_recall: 0.8837 - val_auc: 0.9486 - val_prc: 0.6819 Epoch 8/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3377 - tp: 17766.0000 - fp: 3483.0000 - tn: 17067.0000 - fn: 2644.0000 - accuracy: 0.8504 - precision: 0.8361 - recall: 0.8705 - auc: 0.9280 - prc: 0.9481 - val_loss: 0.3271 - val_tp: 76.0000 - val_fp: 2047.0000 - val_tn: 43436.0000 - val_fn: 10.0000 - val_accuracy: 0.9549 - val_precision: 0.0358 - val_recall: 0.8837 - val_auc: 0.9497 - val_prc: 0.6910 Epoch 9/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3188 - tp: 17749.0000 - fp: 2855.0000 - tn: 17547.0000 - fn: 2809.0000 - accuracy: 0.8617 - precision: 0.8614 - recall: 0.8634 - auc: 0.9360 - prc: 0.9539 - val_loss: 0.3051 - val_tp: 74.0000 - val_fp: 1657.0000 - val_tn: 43826.0000 - val_fn: 12.0000 - val_accuracy: 0.9634 - val_precision: 0.0427 - val_recall: 0.8605 - val_auc: 0.9514 - val_prc: 0.7022 Epoch 10/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3046 - tp: 17772.0000 - fp: 2599.0000 - tn: 17841.0000 - fn: 2748.0000 - accuracy: 0.8695 - precision: 0.8724 - recall: 0.8661 - auc: 0.9402 - prc: 0.9570 - val_loss: 0.2860 - val_tp: 74.0000 - val_fp: 1398.0000 - val_tn: 44085.0000 - val_fn: 12.0000 - val_accuracy: 0.9691 - val_precision: 0.0503 - val_recall: 0.8605 - val_auc: 0.9527 - val_prc: 0.6997 Epoch 11/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2937 - tp: 17673.0000 - fp: 2352.0000 - tn: 18273.0000 - fn: 2662.0000 - accuracy: 0.8776 - precision: 0.8825 - recall: 0.8691 - auc: 0.9447 - prc: 0.9595 - val_loss: 0.2687 - val_tp: 73.0000 - val_fp: 1235.0000 - val_tn: 44248.0000 - val_fn: 13.0000 - val_accuracy: 0.9726 - val_precision: 0.0558 - val_recall: 0.8488 - val_auc: 0.9534 - val_prc: 0.7066 Epoch 12/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2813 - tp: 17721.0000 - fp: 2109.0000 - tn: 18523.0000 - fn: 2607.0000 - accuracy: 0.8849 - precision: 0.8936 - recall: 0.8718 - auc: 0.9485 - prc: 0.9621 - val_loss: 0.2524 - val_tp: 73.0000 - val_fp: 1098.0000 - val_tn: 44385.0000 - val_fn: 13.0000 - val_accuracy: 0.9756 - val_precision: 0.0623 - val_recall: 0.8488 - val_auc: 0.9539 - val_prc: 0.7094 Epoch 13/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2706 - tp: 18031.0000 - fp: 1869.0000 - tn: 18502.0000 - fn: 2558.0000 - accuracy: 0.8919 - precision: 0.9061 - recall: 0.8758 - auc: 0.9520 - prc: 0.9652 - val_loss: 0.2395 - val_tp: 73.0000 - val_fp: 1037.0000 - val_tn: 44446.0000 - val_fn: 13.0000 - val_accuracy: 0.9770 - val_precision: 0.0658 - val_recall: 0.8488 - val_auc: 0.9549 - val_prc: 0.7119 Epoch 14/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2665 - tp: 18087.0000 - fp: 1748.0000 - tn: 18567.0000 - fn: 2558.0000 - accuracy: 0.8949 - precision: 0.9119 - recall: 0.8761 - auc: 0.9525 - prc: 0.9661 - val_loss: 0.2283 - val_tp: 73.0000 - val_fp: 972.0000 - val_tn: 44511.0000 - val_fn: 13.0000 - val_accuracy: 0.9784 - val_precision: 0.0699 - val_recall: 0.8488 - val_auc: 0.9556 - val_prc: 0.7045 Epoch 15/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2589 - tp: 18064.0000 - fp: 1630.0000 - tn: 18830.0000 - fn: 2436.0000 - accuracy: 0.9007 - precision: 0.9172 - recall: 0.8812 - auc: 0.9560 - prc: 0.9676 - val_loss: 0.2180 - val_tp: 73.0000 - val_fp: 941.0000 - val_tn: 44542.0000 - val_fn: 13.0000 - val_accuracy: 0.9791 - val_precision: 0.0720 - val_recall: 0.8488 - val_auc: 0.9563 - val_prc: 0.7069 Epoch 16/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2495 - tp: 18132.0000 - fp: 1481.0000 - tn: 18926.0000 - fn: 2421.0000 - accuracy: 0.9047 - precision: 0.9245 - recall: 0.8822 - auc: 0.9587 - prc: 0.9695 - val_loss: 0.2079 - val_tp: 73.0000 - val_fp: 905.0000 - val_tn: 44578.0000 - val_fn: 13.0000 - val_accuracy: 0.9799 - val_precision: 0.0746 - val_recall: 0.8488 - val_auc: 0.9565 - val_prc: 0.7110 Epoch 17/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2435 - tp: 18047.0000 - fp: 1378.0000 - tn: 19144.0000 - fn: 2391.0000 - accuracy: 0.9080 - precision: 0.9291 - recall: 0.8830 - auc: 0.9601 - prc: 0.9706 - val_loss: 0.1990 - val_tp: 73.0000 - val_fp: 882.0000 - val_tn: 44601.0000 - val_fn: 13.0000 - val_accuracy: 0.9804 - val_precision: 0.0764 - val_recall: 0.8488 - val_auc: 0.9568 - val_prc: 0.7118 Epoch 18/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2396 - tp: 18223.0000 - fp: 1289.0000 - tn: 19075.0000 - fn: 2373.0000 - accuracy: 0.9106 - precision: 0.9339 - recall: 0.8848 - auc: 0.9612 - prc: 0.9714 - val_loss: 0.1911 - val_tp: 73.0000 - val_fp: 870.0000 - val_tn: 44613.0000 - val_fn: 13.0000 - val_accuracy: 0.9806 - val_precision: 0.0774 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7148 Epoch 19/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2324 - tp: 18179.0000 - fp: 1205.0000 - tn: 19254.0000 - fn: 2322.0000 - accuracy: 0.9139 - precision: 0.9378 - recall: 0.8867 - auc: 0.9633 - prc: 0.9728 - val_loss: 0.1839 - val_tp: 73.0000 - val_fp: 857.0000 - val_tn: 44626.0000 - val_fn: 13.0000 - val_accuracy: 0.9809 - val_precision: 0.0785 - val_recall: 0.8488 - val_auc: 0.9576 - val_prc: 0.7165 Epoch 20/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2318 - tp: 18119.0000 - fp: 1224.0000 - tn: 19279.0000 - fn: 2338.0000 - accuracy: 0.9130 - precision: 0.9367 - recall: 0.8857 - auc: 0.9640 - prc: 0.9728 - val_loss: 0.1758 - val_tp: 73.0000 - val_fp: 823.0000 - val_tn: 44660.0000 - val_fn: 13.0000 - val_accuracy: 0.9817 - val_precision: 0.0815 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7185 Epoch 21/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2233 - tp: 18041.0000 - fp: 1074.0000 - tn: 19514.0000 - fn: 2331.0000 - accuracy: 0.9169 - precision: 0.9438 - recall: 0.8856 - auc: 0.9660 - prc: 0.9745 - val_loss: 0.1690 - val_tp: 73.0000 - val_fp: 813.0000 - val_tn: 44670.0000 - val_fn: 13.0000 - val_accuracy: 0.9819 - val_precision: 0.0824 - val_recall: 0.8488 - val_auc: 0.9578 - val_prc: 0.7211 Epoch 22/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2193 - tp: 18258.0000 - fp: 1013.0000 - tn: 19414.0000 - fn: 2275.0000 - accuracy: 0.9197 - precision: 0.9474 - recall: 0.8892 - auc: 0.9666 - prc: 0.9753 - val_loss: 0.1634 - val_tp: 73.0000 - val_fp: 817.0000 - val_tn: 44666.0000 - val_fn: 13.0000 - val_accuracy: 0.9818 - val_precision: 0.0820 - val_recall: 0.8488 - val_auc: 0.9580 - val_prc: 0.7123 Epoch 23/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2114 - tp: 18439.0000 - fp: 993.0000 - tn: 19417.0000 - fn: 2111.0000 - accuracy: 0.9242 - precision: 0.9489 - recall: 0.8973 - auc: 0.9696 - prc: 0.9774 - val_loss: 0.1577 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9584 - val_prc: 0.7122 Epoch 24/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2076 - tp: 18459.0000 - fp: 896.0000 - tn: 19582.0000 - fn: 2023.0000 - accuracy: 0.9287 - precision: 0.9537 - recall: 0.9012 - auc: 0.9694 - prc: 0.9776 - val_loss: 0.1528 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9587 - val_prc: 0.7129 Epoch 25/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2044 - tp: 18340.0000 - fp: 907.0000 - tn: 19664.0000 - fn: 2049.0000 - accuracy: 0.9278 - precision: 0.9529 - recall: 0.8995 - auc: 0.9707 - prc: 0.9783 - val_loss: 0.1483 - val_tp: 73.0000 - val_fp: 800.0000 - val_tn: 44683.0000 - val_fn: 13.0000 - val_accuracy: 0.9822 - val_precision: 0.0836 - val_recall: 0.8488 - val_auc: 0.9591 - val_prc: 0.7054 Epoch 26/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1997 - tp: 18293.0000 - fp: 918.0000 - tn: 19749.0000 - fn: 2000.0000 - accuracy: 0.9288 - precision: 0.9522 - recall: 0.9014 - auc: 0.9722 - prc: 0.9788 - val_loss: 0.1433 - val_tp: 73.0000 - val_fp: 788.0000 - val_tn: 44695.0000 - val_fn: 13.0000 - val_accuracy: 0.9824 - val_precision: 0.0848 - val_recall: 0.8488 - val_auc: 0.9590 - val_prc: 0.7059 Epoch 27/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1987 - tp: 18562.0000 - fp: 848.0000 - tn: 19530.0000 - fn: 2020.0000 - accuracy: 0.9300 - precision: 0.9563 - recall: 0.9019 - auc: 0.9720 - prc: 0.9791 - val_loss: 0.1394 - val_tp: 73.0000 - val_fp: 784.0000 - val_tn: 44699.0000 - val_fn: 13.0000 - val_accuracy: 0.9825 - val_precision: 0.0852 - val_recall: 0.8488 - val_auc: 0.9595 - val_prc: 0.7062 Epoch 28/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1944 - tp: 18320.0000 - fp: 828.0000 - tn: 19823.0000 - fn: 1989.0000 - accuracy: 0.9312 - precision: 0.9568 - recall: 0.9021 - auc: 0.9734 - prc: 0.9798 - val_loss: 0.1351 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9598 - val_prc: 0.7079 Epoch 29/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1933 - tp: 18455.0000 - fp: 827.0000 - tn: 19704.0000 - fn: 1974.0000 - accuracy: 0.9316 - precision: 0.9571 - recall: 0.9034 - auc: 0.9732 - prc: 0.9797 - val_loss: 0.1313 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9599 - val_prc: 0.7094 Epoch 30/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1910 - tp: 18417.0000 - fp: 768.0000 - tn: 19858.0000 - fn: 1917.0000 - accuracy: 0.9344 - precision: 0.9600 - recall: 0.9057 - auc: 0.9740 - prc: 0.9802 - val_loss: 0.1282 - val_tp: 73.0000 - val_fp: 759.0000 - val_tn: 44724.0000 - val_fn: 13.0000 - val_accuracy: 0.9831 - val_precision: 0.0877 - val_recall: 0.8488 - val_auc: 0.9602 - val_prc: 0.7094 Epoch 31/1000 20/20 [==============================] - ETA: 0s - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811Restoring model weights from the end of the best epoch: 21. 20/20 [==============================] - 1s 34ms/step - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811 - val_loss: 0.1246 - val_tp: 73.0000 - val_fp: 742.0000 - val_tn: 44741.0000 - val_fn: 13.0000 - val_accuracy: 0.9834 - val_precision: 0.0896 - val_recall: 0.8488 - val_auc: 0.9597 - val_prc: 0.7095 Epoch 31: early stopping
Kiểm tra lại lịch sử đào tạo
plot_metrics(resampled_history)
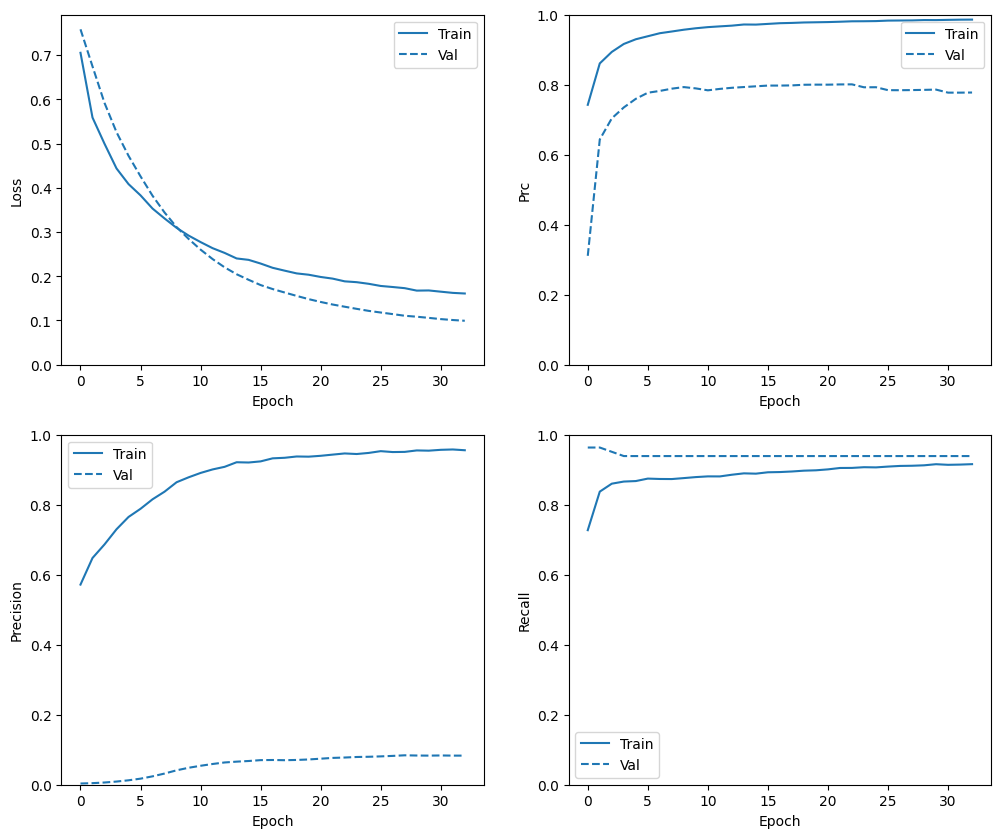
Đánh giá các chỉ số
train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)
resampled_results = resampled_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_resampled)
loss : 0.16882120072841644 tp : 71.0 fp : 1032.0 tn : 55849.0 fn : 10.0 accuracy : 0.9817070960998535 precision : 0.06436990201473236 recall : 0.8765432238578796 auc : 0.9518552422523499 prc : 0.7423797845840454 Legitimate Transactions Detected (True Negatives): 55849 Legitimate Transactions Incorrectly Detected (False Positives): 1032 Fraudulent Transactions Missed (False Negatives): 10 Fraudulent Transactions Detected (True Positives): 71 Total Fraudulent Transactions: 81
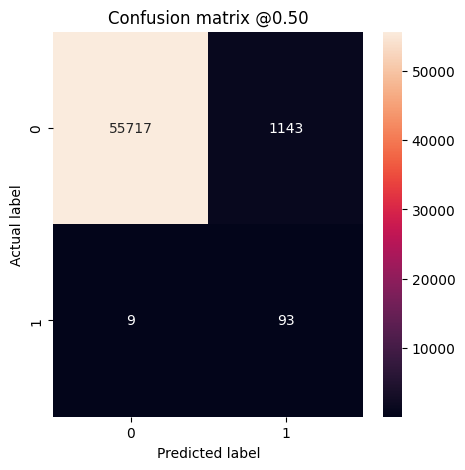
Lập kế hoạch cho ROC
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
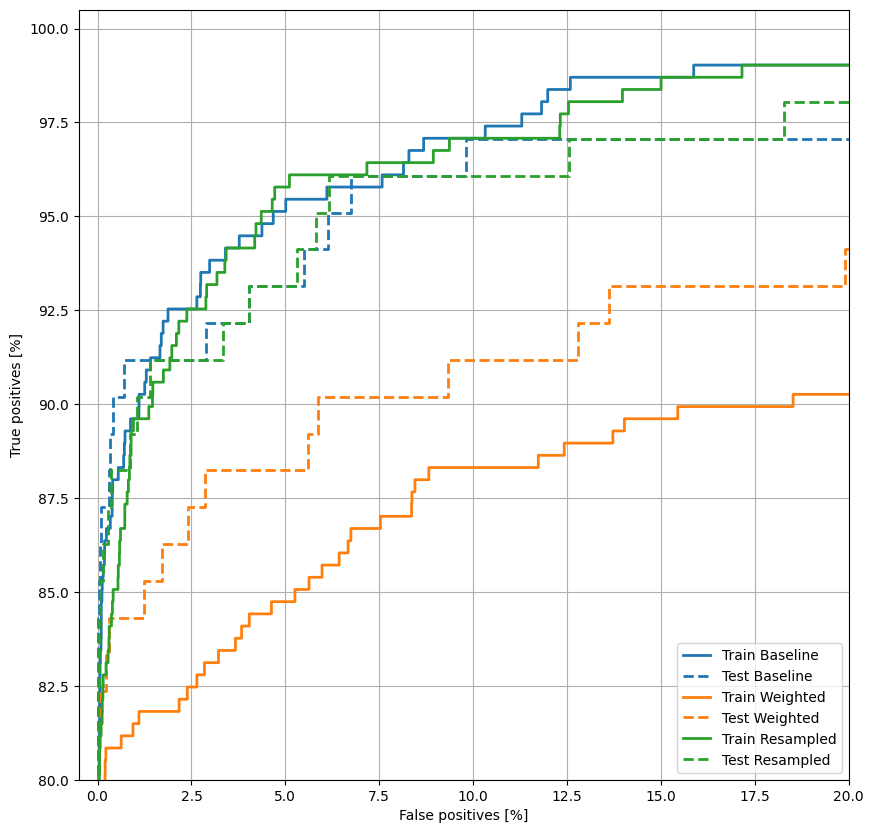
Lập đồ thị AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
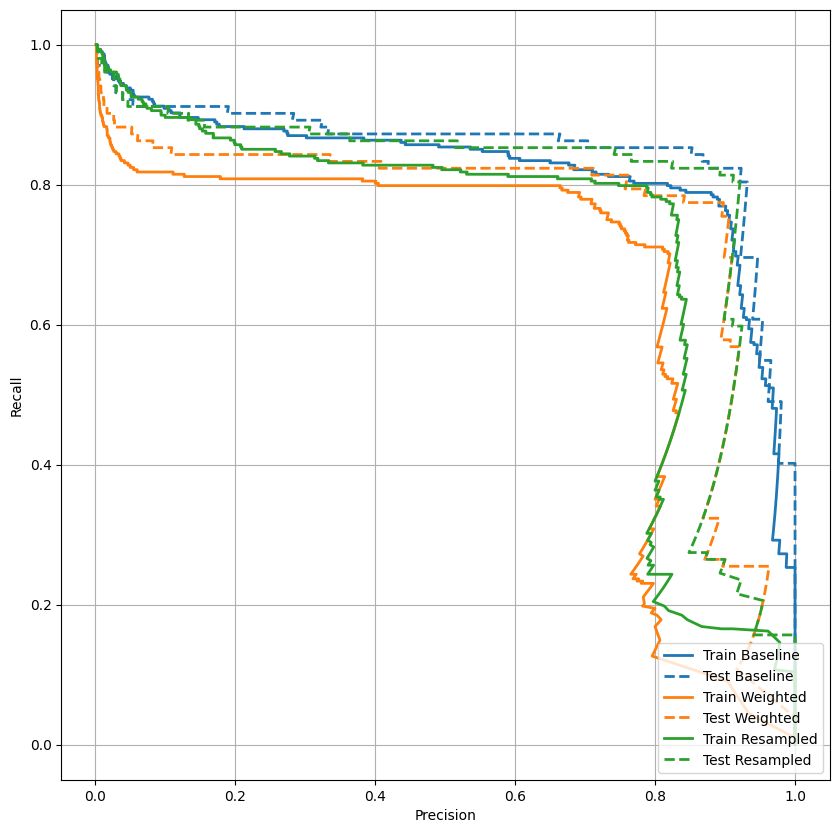
Áp dụng hướng dẫn này cho vấn đề của bạn
Phân loại dữ liệu không cân bằng là một nhiệm vụ vốn đã khó khăn vì có rất ít mẫu để học từ đó. Bạn phải luôn bắt đầu với dữ liệu trước và cố gắng hết sức để thu thập càng nhiều mẫu càng tốt và đưa ra suy nghĩ đáng kể về những tính năng nào có thể có liên quan để mô hình có thể tận dụng tối đa tầng lớp thiểu số của bạn. Tại một số thời điểm, mô hình của bạn có thể gặp khó khăn để cải thiện và mang lại kết quả như mong muốn, vì vậy, điều quan trọng là phải ghi nhớ bối cảnh vấn đề của bạn và sự cân bằng giữa các loại lỗi khác nhau.
