 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Tutorial ini menunjukkan bagaimana mengklasifikasikan dataset yang sangat tidak seimbang di mana jumlah contoh di satu kelas jauh lebih banyak daripada contoh di kelas lain. Anda akan bekerja dengan kumpulan data Deteksi Penipuan Kartu Kredit yang dihosting di Kaggle. Tujuannya adalah untuk mendeteksi hanya 492 transaksi penipuan dari total 284.807 transaksi. Anda akan menggunakan Keras untuk menentukan model dan bobot kelas untuk membantu model belajar dari data yang tidak seimbang. .
Tutorial ini berisi kode lengkap untuk:
- Muat file CSV menggunakan Pandas.
- Buat rangkaian pelatihan, validasi, dan pengujian.
- Tentukan dan latih model menggunakan Keras (termasuk pengaturan bobot kelas).
- Evaluasi model menggunakan berbagai metrik (termasuk presisi dan ingatan).
- Cobalah teknik umum untuk menangani data yang tidak seimbang seperti:
- Pembobotan kelas
- Pengambilan sampel berlebih
Mempersiapkan
import tensorflow as tf
from tensorflow import keras
import os
import tempfile
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
Pemrosesan dan eksplorasi data
Unduh kumpulan data Penipuan Kartu Kredit Kaggle
Pandas adalah pustaka Python dengan banyak utilitas bermanfaat untuk memuat dan bekerja dengan data terstruktur. Ini dapat digunakan untuk mengunduh CSV ke dalam Pandas DataFrame .
file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()
Periksa ketidakseimbangan label kelas
Mari kita lihat ketidakseimbangan dataset:
neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n'.format(
total, pos, 100 * pos / total))
Examples:
Total: 284807
Positive: 492 (0.17% of total)
Hal ini menunjukkan fraksi kecil dari sampel positif.
Bersihkan, pisahkan, dan normalkan data
Data mentah memiliki beberapa masalah. Pertama, kolom Time dan Amount terlalu bervariasi untuk digunakan secara langsung. Jatuhkan kolom Time (karena tidak jelas artinya) dan ambil log kolom Amount untuk mengurangi jangkauannya.
cleaned_df = raw_df.copy()
# You don't want the `Time` column.
cleaned_df.pop('Time')
# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Ammount'] = np.log(cleaned_df.pop('Amount')+eps)
Pisahkan dataset menjadi train, validasi, dan set test. Set validasi digunakan selama pemasangan model untuk mengevaluasi kerugian dan metrik apa pun, namun model tidak sesuai dengan data ini. Set tes sama sekali tidak digunakan selama fase pelatihan dan hanya digunakan di akhir untuk mengevaluasi seberapa baik model digeneralisasi ke data baru. Hal ini sangat penting dengan set data yang tidak seimbang di mana overfitting menjadi perhatian yang signifikan dari kurangnya data pelatihan.
# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
Normalisasikan fitur input menggunakan sklearn StandardScaler. Ini akan mengatur mean ke 0 dan standar deviasi ke 1.
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
Training labels shape: (182276,) Validation labels shape: (45569,) Test labels shape: (56962,) Training features shape: (182276, 29) Validation features shape: (45569, 29) Test features shape: (56962, 29)
Perhatikan distribusi datanya
Selanjutnya bandingkan distribusi contoh positif dan negatif pada beberapa fitur. Pertanyaan yang bagus untuk ditanyakan pada diri sendiri pada saat ini adalah:
- Apakah distribusi ini masuk akal?
- Ya. Anda telah menormalkan input dan ini sebagian besar terkonsentrasi di kisaran
+/- 2.
- Ya. Anda telah menormalkan input dan ini sebagian besar terkonsentrasi di kisaran
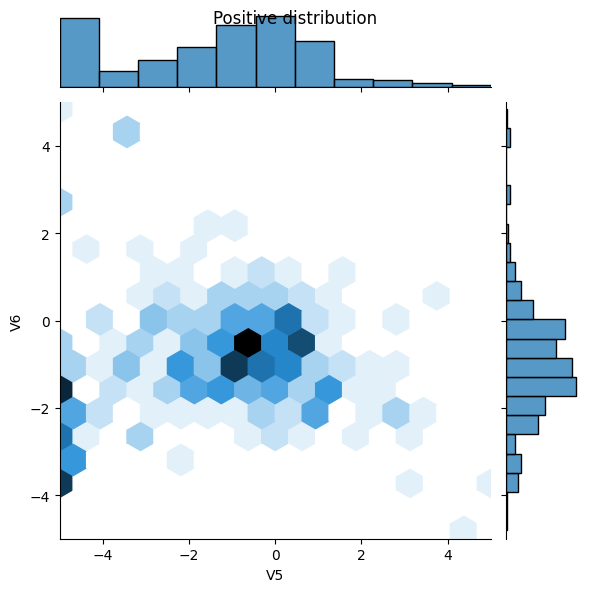
- Dapatkah Anda melihat perbedaan antara distribusi?
- Ya, contoh-contoh positif mengandung tingkat nilai ekstrim yang jauh lebih tinggi.
pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)
sns.jointplot(x=pos_df['V5'], y=pos_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")
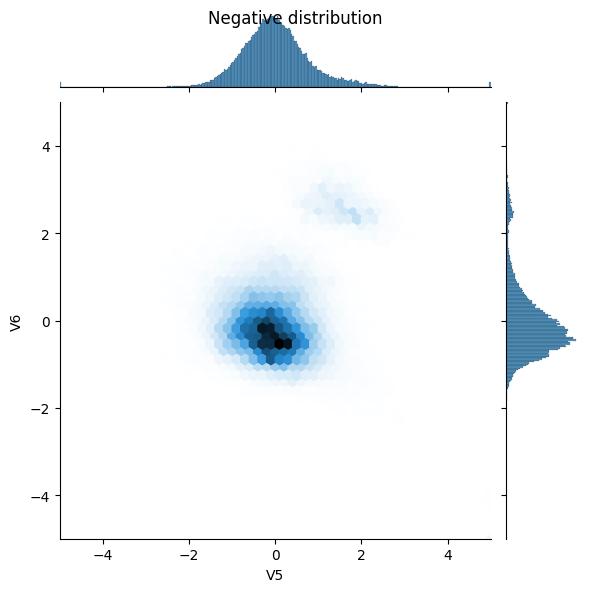
sns.jointplot(x=neg_df['V5'], y=neg_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")
Tentukan model dan metrik
Tentukan fungsi yang membuat jaringan saraf sederhana dengan lapisan tersembunyi yang terhubung secara padat, lapisan putus sekolah untuk mengurangi overfitting, dan lapisan sigmoid keluaran yang mengembalikan kemungkinan transaksi yang curang:
METRICS = [
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.BinaryAccuracy(name='accuracy'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc'),
keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]
def make_model(metrics=METRICS, output_bias=None):
if output_bias is not None:
output_bias = tf.keras.initializers.Constant(output_bias)
model = keras.Sequential([
keras.layers.Dense(
16, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid',
bias_initializer=output_bias),
])
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.BinaryCrossentropy(),
metrics=metrics)
return model
Memahami metrik yang berguna
Perhatikan bahwa ada beberapa metrik yang ditentukan di atas yang dapat dihitung oleh model yang akan membantu saat mengevaluasi kinerja.
- Negatif palsu dan positif palsu adalah sampel yang salah diklasifikasikan
- Negatif sejati dan positif sejati adalah sampel yang diklasifikasikan dengan benar
- Akurasi adalah persentase contoh yang diklasifikasikan dengan benar > \(\frac{\text{true samples} }{\text{total samples} }\)
- Presisi adalah persentase prediksi positif yang diklasifikasikan dengan benar > \(\frac{\text{true positives} }{\text{true positives + false positives} }\)
- Ingat adalah persentase positif aktual yang diklasifikasikan dengan benar > \(\frac{\text{true positives} }{\text{true positives + false negatives} }\)
- AUC mengacu pada Area Di Bawah Kurva dari kurva Karakteristik Operasi Penerima (ROC-AUC). Metrik ini sama dengan probabilitas bahwa pengklasifikasi akan memberi peringkat sampel positif acak lebih tinggi daripada sampel negatif acak.
- AUPRC mengacu pada Area Di Bawah Kurva Precision-Recall Curve. Metrik ini menghitung pasangan presisi-recall untuk ambang probabilitas yang berbeda.
Baca lebih lajut:
- Benar vs. Salah dan Positif vs. Negatif
- Ketepatan
- Presisi dan Recall
- ROC-AUC
- Hubungan antara Precision-Recall dan Kurva ROC
Model dasar
Bangun modelnya
Sekarang buat dan latih model Anda menggunakan fungsi yang telah ditentukan sebelumnya. Perhatikan bahwa model cocok menggunakan ukuran batch standar yang lebih besar dari 2048, ini penting untuk memastikan bahwa setiap batch memiliki peluang yang layak untuk mengandung beberapa sampel positif. Jika ukuran batch terlalu kecil, mereka kemungkinan tidak akan memiliki transaksi penipuan untuk dipelajari.
EPOCHS = 100
BATCH_SIZE = 2048
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_prc',
verbose=1,
patience=10,
mode='max',
restore_best_weights=True)
model = make_model()
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 480
dropout (Dropout) (None, 16) 0
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 497
Trainable params: 497
Non-trainable params: 0
_________________________________________________________________
Uji coba model:
model.predict(train_features[:10])
array([[0.9466284 ],
[0.7211031 ],
[0.60527885],
[0.8335568 ],
[0.5909625 ],
[0.6751574 ],
[0.6623665 ],
[0.81066036],
[0.50712407],
[0.8296292 ]], dtype=float32)
Opsional: Tetapkan bias awal yang benar.
Tebakan awal ini tidak bagus. Anda tahu dataset tidak seimbang. Atur bias layer output untuk mencerminkan hal itu (Lihat: A Recipe for Training Neural Networks: "init well" ). Ini dapat membantu dengan konvergensi awal.
Dengan inisialisasi bias default, kerugiannya adalah tentang math.log(2) = 0.69314
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 1.2781
Bias yang benar untuk ditetapkan dapat diturunkan dari:
\[ p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) \]
\[ b_0 = -log_e(1/p_0 - 1) \]
\[ b_0 = log_e(pos/neg)\]
initial_bias = np.log([pos/neg])
initial_bias
array([-6.35935934])
Tetapkan itu sebagai bias awal, dan model akan memberikan tebakan awal yang jauh lebih masuk akal.
Seharusnya dekat: pos/total = 0.0018
model = make_model(output_bias=initial_bias)
model.predict(train_features[:10])
array([[2.3598122e-05],
[1.5476024e-03],
[6.8338902e-04],
[9.4873342e-04],
[1.0742771e-03],
[7.7475846e-04],
[1.2199467e-03],
[5.5399281e-04],
[1.6213538e-03],
[3.0470363e-04]], dtype=float32)
Dengan inisialisasi ini, kerugian awal harus kira-kira:
\[-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317\]
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.0200
Kerugian awal ini sekitar 50 kali lebih kecil daripada jika dengan inisialisasi naif.
Dengan cara ini model tidak perlu menghabiskan beberapa zaman pertama hanya belajar bahwa contoh-contoh positif tidak mungkin. Ini juga memudahkan untuk membaca plot kerugian selama pelatihan.
Pos pemeriksaan bobot awal
Untuk membuat berbagai pelatihan berjalan lebih sebanding, simpan bobot model awal ini dalam file pos pemeriksaan, dan muat ke setiap model sebelum pelatihan:
initial_weights = os.path.join(tempfile.mkdtemp(), 'initial_weights')
model.save_weights(initial_weights)
Konfirmasikan bahwa perbaikan bias membantu
Sebelum melanjutkan, konfirmasikan dengan cepat bahwa inisialisasi bias yang hati-hati benar-benar membantu.
Latih model selama 20 epoch, dengan dan tanpa inisialisasi yang cermat ini, dan bandingkan kerugiannya:
model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
def plot_loss(history, label, n):
# Use a log scale on y-axis to show the wide range of values.
plt.semilogy(history.epoch, history.history['loss'],
color=colors[n], label='Train ' + label)
plt.semilogy(history.epoch, history.history['val_loss'],
color=colors[n], label='Val ' + label,
linestyle="--")
plt.xlabel('Epoch')
plt.ylabel('Loss')
plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)
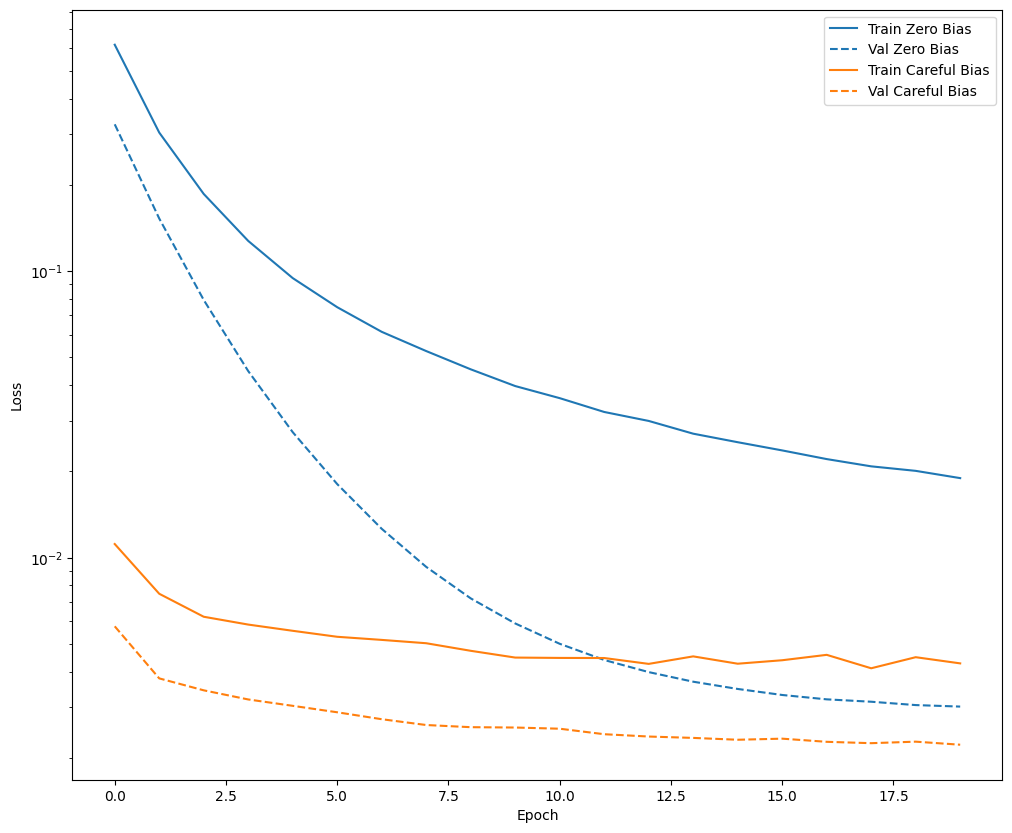
Gambar di atas memperjelas: Dalam hal kehilangan validasi, pada masalah ini, inisialisasi yang cermat ini memberikan keuntungan yang jelas.
Latih modelnya
model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels))
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 0.0161 - tp: 64.0000 - fp: 9.0000 - tn: 227425.0000 - fn: 347.0000 - accuracy: 0.9984 - precision: 0.8767 - recall: 0.1557 - auc: 0.6148 - prc: 0.1692 - val_loss: 0.0115 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7205 - val_prc: 0.2571 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0087 - tp: 49.0000 - fp: 11.0000 - tn: 181940.0000 - fn: 276.0000 - accuracy: 0.9984 - precision: 0.8167 - recall: 0.1508 - auc: 0.8085 - prc: 0.3735 - val_loss: 0.0054 - val_tp: 35.0000 - val_fp: 6.0000 - val_tn: 45477.0000 - val_fn: 51.0000 - val_accuracy: 0.9987 - val_precision: 0.8537 - val_recall: 0.4070 - val_auc: 0.9065 - val_prc: 0.6598 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0061 - tp: 126.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 199.0000 - accuracy: 0.9988 - precision: 0.8235 - recall: 0.3877 - auc: 0.8997 - prc: 0.6187 - val_loss: 0.0046 - val_tp: 55.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 31.0000 - val_accuracy: 0.9991 - val_precision: 0.8730 - val_recall: 0.6395 - val_auc: 0.9063 - val_prc: 0.6941 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 172.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 153.0000 - accuracy: 0.9990 - precision: 0.8473 - recall: 0.5292 - auc: 0.9068 - prc: 0.6448 - val_loss: 0.0044 - val_tp: 58.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 28.0000 - val_accuracy: 0.9992 - val_precision: 0.8788 - val_recall: 0.6744 - val_auc: 0.9064 - val_prc: 0.7114 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 167.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 158.0000 - accuracy: 0.9990 - precision: 0.8477 - recall: 0.5138 - auc: 0.9134 - prc: 0.6215 - val_loss: 0.0043 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7181 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 193.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 132.0000 - accuracy: 0.9991 - precision: 0.8733 - recall: 0.5938 - auc: 0.9198 - prc: 0.6760 - val_loss: 0.0042 - val_tp: 59.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 27.0000 - val_accuracy: 0.9992 - val_precision: 0.8806 - val_recall: 0.6860 - val_auc: 0.9064 - val_prc: 0.7370 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 183.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 142.0000 - accuracy: 0.9991 - precision: 0.8592 - recall: 0.5631 - auc: 0.9202 - prc: 0.6737 - val_loss: 0.0042 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7463 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 171.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 154.0000 - accuracy: 0.9990 - precision: 0.8465 - recall: 0.5262 - auc: 0.9156 - prc: 0.6574 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7480 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 196.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8711 - recall: 0.6031 - auc: 0.9218 - prc: 0.6799 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7550 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 173.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 152.0000 - accuracy: 0.9990 - precision: 0.8650 - recall: 0.5323 - auc: 0.9048 - prc: 0.6520 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9122 - val_prc: 0.7598 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 190.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8597 - recall: 0.5846 - auc: 0.9172 - prc: 0.6779 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9065 - val_prc: 0.7595 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 192.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 133.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.5908 - auc: 0.9281 - prc: 0.7312 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9123 - val_prc: 0.7648 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 185.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 140.0000 - accuracy: 0.9991 - precision: 0.8565 - recall: 0.5692 - auc: 0.9328 - prc: 0.7222 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7615 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 183.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 142.0000 - accuracy: 0.9990 - precision: 0.8472 - recall: 0.5631 - auc: 0.9295 - prc: 0.6770 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7670 Epoch 15/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 194.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8700 - recall: 0.5969 - auc: 0.9344 - prc: 0.7233 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7672 Epoch 16/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 207.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8697 - recall: 0.6369 - auc: 0.9329 - prc: 0.7194 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7694 Epoch 17/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 190.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8716 - recall: 0.5846 - auc: 0.9345 - prc: 0.7265 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7705 Epoch 18/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8622 - recall: 0.5969 - auc: 0.9344 - prc: 0.7199 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7725 Epoch 19/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 205.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8613 - recall: 0.6308 - auc: 0.9346 - prc: 0.7266 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7739 Epoch 20/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 207.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8809 - recall: 0.6369 - auc: 0.9421 - prc: 0.7634 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7729 Epoch 21/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0040 - tp: 204.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8644 - recall: 0.6277 - auc: 0.9360 - prc: 0.7340 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7756 Epoch 22/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 207.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8884 - recall: 0.6369 - auc: 0.9328 - prc: 0.7277 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7773 Epoch 23/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0041 - tp: 191.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8527 - recall: 0.5877 - auc: 0.9375 - prc: 0.7280 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8857 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7790 Epoch 24/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 196.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6031 - auc: 0.9375 - prc: 0.7466 - val_loss: 0.0038 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7762 Epoch 25/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 204.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8681 - recall: 0.6277 - auc: 0.9467 - prc: 0.7480 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9123 - val_prc: 0.7789 Epoch 26/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8661 - recall: 0.5969 - auc: 0.9360 - prc: 0.7292 - val_loss: 0.0038 - val_tp: 60.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8955 - val_recall: 0.6977 - val_auc: 0.9123 - val_prc: 0.7783 Epoch 27/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8776 - recall: 0.6400 - auc: 0.9376 - prc: 0.7632 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7772 Epoch 28/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 202.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 123.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6215 - auc: 0.9408 - prc: 0.7638 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7808 Epoch 29/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 214.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8807 - recall: 0.6585 - auc: 0.9347 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7806 Epoch 30/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 197.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 128.0000 - accuracy: 0.9991 - precision: 0.8640 - recall: 0.6062 - auc: 0.9346 - prc: 0.7489 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7804 Epoch 31/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 213.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 112.0000 - accuracy: 0.9992 - precision: 0.8659 - recall: 0.6554 - auc: 0.9407 - prc: 0.7615 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7809 Epoch 32/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9407 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7821 Epoch 33/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 210.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 115.0000 - accuracy: 0.9992 - precision: 0.8787 - recall: 0.6462 - auc: 0.9392 - prc: 0.7642 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7826 Epoch 34/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9423 - prc: 0.7759 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7830 Epoch 35/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 35.0000 - tn: 181916.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8566 - recall: 0.6431 - auc: 0.9407 - prc: 0.7381 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 36/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 204.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8831 - recall: 0.6277 - auc: 0.9407 - prc: 0.7587 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 37/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8672 - recall: 0.6431 - auc: 0.9345 - prc: 0.7386 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7849 Epoch 38/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 198.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.6092 - auc: 0.9454 - prc: 0.7488 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7844 Epoch 39/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 209.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8782 - recall: 0.6431 - auc: 0.9407 - prc: 0.7419 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 40/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 198.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8761 - recall: 0.6092 - auc: 0.9546 - prc: 0.7644 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7835 Epoch 41/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8745 - recall: 0.6431 - auc: 0.9377 - prc: 0.7587 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7827 Epoch 42/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 195.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8667 - recall: 0.6000 - auc: 0.9345 - prc: 0.7436 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7834 Epoch 43/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8655 - recall: 0.6338 - auc: 0.9500 - prc: 0.7699 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 44/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8927 - recall: 0.6400 - auc: 0.9438 - prc: 0.7625 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7841 Epoch 45/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 205.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8686 - recall: 0.6308 - auc: 0.9422 - prc: 0.7519 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7847 Epoch 46/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 206.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8766 - recall: 0.6338 - auc: 0.9423 - prc: 0.7529 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7843 Epoch 47/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 219.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8866 - recall: 0.6738 - auc: 0.9377 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7871 Epoch 48/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8729 - recall: 0.6338 - auc: 0.9393 - prc: 0.7676 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7854 Epoch 49/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 215.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 110.0000 - accuracy: 0.9992 - precision: 0.8811 - recall: 0.6615 - auc: 0.9407 - prc: 0.7618 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9125 - val_prc: 0.7855 Epoch 50/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 214.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8699 - recall: 0.6585 - auc: 0.9377 - prc: 0.7727 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7858 Epoch 51/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 219.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8795 - recall: 0.6738 - auc: 0.9393 - prc: 0.7889 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7876 Epoch 52/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 217.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8967 - recall: 0.6677 - auc: 0.9439 - prc: 0.7812 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7887 Epoch 53/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 206.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8803 - recall: 0.6338 - auc: 0.9362 - prc: 0.7734 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 54/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 223.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 102.0000 - accuracy: 0.9993 - precision: 0.8814 - recall: 0.6862 - auc: 0.9438 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7877 Epoch 55/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 220.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 105.0000 - accuracy: 0.9993 - precision: 0.8943 - recall: 0.6769 - auc: 0.9439 - prc: 0.7866 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 56/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 209.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8970 - recall: 0.6431 - auc: 0.9392 - prc: 0.7613 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 57/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0033 - tp: 221.0000 - fp: 23.0000 - tn: 181928.0000 - fn: 104.0000 - accuracy: 0.9993 - precision: 0.9057 - recall: 0.6800 - auc: 0.9516 - prc: 0.7954 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 58/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8851 - recall: 0.6400 - auc: 0.9485 - prc: 0.7746 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7875 Epoch 59/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 216.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 109.0000 - accuracy: 0.9992 - precision: 0.8780 - recall: 0.6646 - auc: 0.9531 - prc: 0.7928 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7883 Epoch 60/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 211.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8719 - recall: 0.6492 - auc: 0.9469 - prc: 0.7808 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7882 Epoch 61/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 201.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 124.0000 - accuracy: 0.9992 - precision: 0.8933 - recall: 0.6185 - auc: 0.9424 - prc: 0.7720 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7881 Epoch 62/100 81/90 [==========================>...] - ETA: 0s - loss: 0.0034 - tp: 196.0000 - fp: 21.0000 - tn: 165565.0000 - fn: 106.0000 - accuracy: 0.9992 - precision: 0.9032 - recall: 0.6490 - auc: 0.9413 - prc: 0.7849Restoring model weights from the end of the best epoch: 52. 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 211.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8941 - recall: 0.6492 - auc: 0.9423 - prc: 0.7828 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7860 Epoch 62: early stopping
Periksa riwayat pelatihan
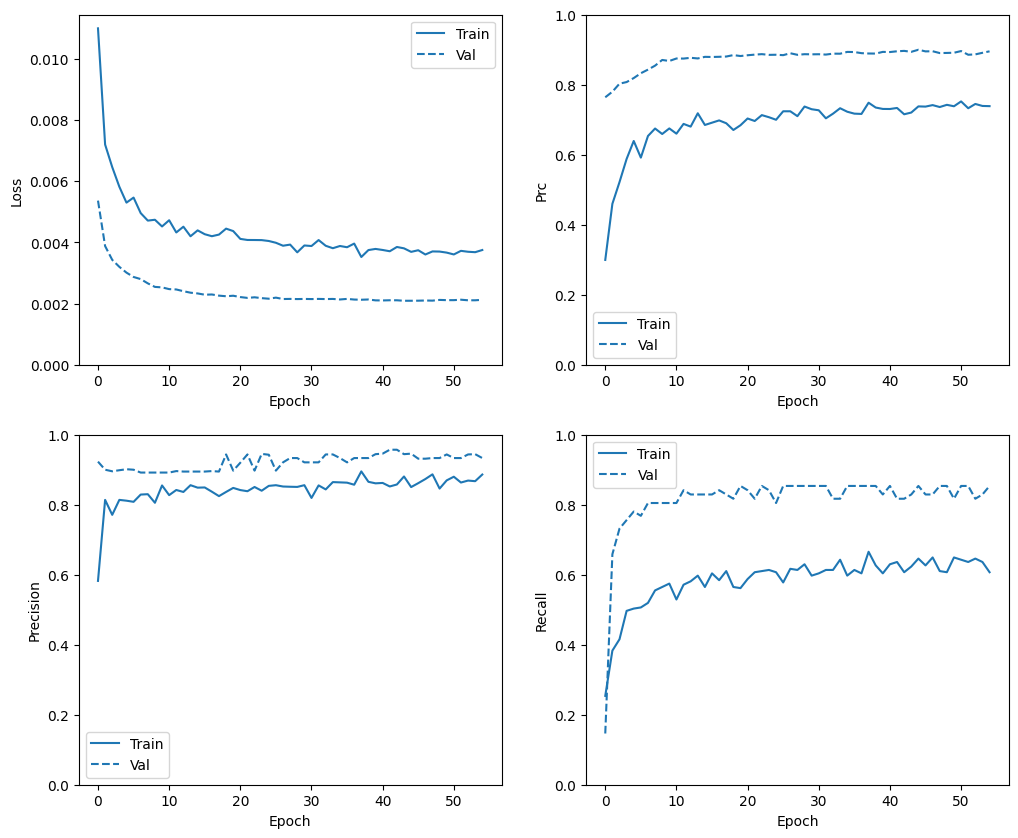
Di bagian ini, Anda akan menghasilkan plot akurasi dan kehilangan model Anda pada set pelatihan dan validasi. Ini berguna untuk memeriksa overfitting, yang dapat Anda pelajari lebih lanjut di tutorial Overfit dan underfit .
Selain itu, Anda dapat membuat plot ini untuk salah satu metrik yang Anda buat di atas. Negatif palsu dimasukkan sebagai contoh.
def plot_metrics(history):
metrics = ['loss', 'prc', 'precision', 'recall']
for n, metric in enumerate(metrics):
name = metric.replace("_"," ").capitalize()
plt.subplot(2,2,n+1)
plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
color=colors[0], linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
if metric == 'loss':
plt.ylim([0, plt.ylim()[1]])
elif metric == 'auc':
plt.ylim([0.8,1])
else:
plt.ylim([0,1])
plt.legend();
plot_metrics(baseline_history)
Evaluasi metrik
Anda dapat menggunakan matriks konfusi untuk meringkas label aktual vs. yang diprediksi, di mana sumbu X adalah label yang diprediksi dan sumbu Y adalah label yang sebenarnya:
train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)
def plot_cm(labels, predictions, p=0.5):
cm = confusion_matrix(labels, predictions > p)
plt.figure(figsize=(5,5))
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion matrix @{:.2f}'.format(p))
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
Evaluasi model Anda pada kumpulan data pengujian dan tampilkan hasil untuk metrik yang Anda buat di atas:
baseline_results = model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_baseline)
loss : 0.0024895435199141502 tp : 59.0 fp : 7.0 tn : 56874.0 fn : 22.0 accuracy : 0.9994909167289734 precision : 0.8939393758773804 recall : 0.7283950448036194 auc : 0.9318439960479736 prc : 0.8204483985900879 Legitimate Transactions Detected (True Negatives): 56874 Legitimate Transactions Incorrectly Detected (False Positives): 7 Fraudulent Transactions Missed (False Negatives): 22 Fraudulent Transactions Detected (True Positives): 59 Total Fraudulent Transactions: 81
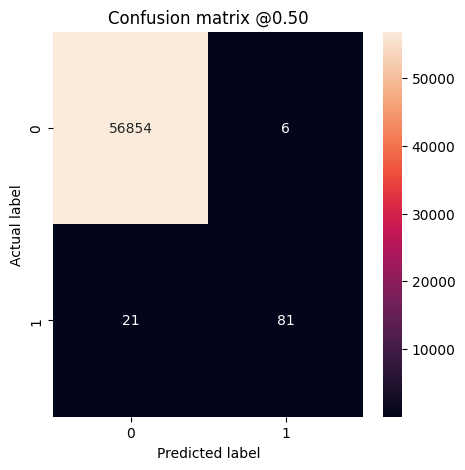
Jika model telah memprediksi semuanya dengan sempurna, ini akan menjadi matriks diagonal di mana nilai di luar diagonal utama, yang menunjukkan prediksi yang salah, akan menjadi nol. Dalam hal ini matriks menunjukkan bahwa Anda memiliki hasil positif palsu yang relatif sedikit, artinya ada relatif sedikit transaksi sah yang ditandai secara tidak benar. Namun, Anda mungkin ingin memiliki lebih sedikit negatif palsu meskipun biaya untuk meningkatkan jumlah positif palsu. Pertukaran ini mungkin lebih disukai karena negatif palsu akan memungkinkan transaksi penipuan dilakukan, sedangkan positif palsu dapat menyebabkan email dikirim ke pelanggan untuk meminta mereka memverifikasi aktivitas kartu mereka.
Rencanakan ROC
Sekarang plot ROC . Plot ini berguna karena menunjukkan, sekilas, kisaran kinerja yang dapat dicapai model hanya dengan menyetel ambang keluaran.
def plot_roc(name, labels, predictions, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,20])
plt.ylim([80,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
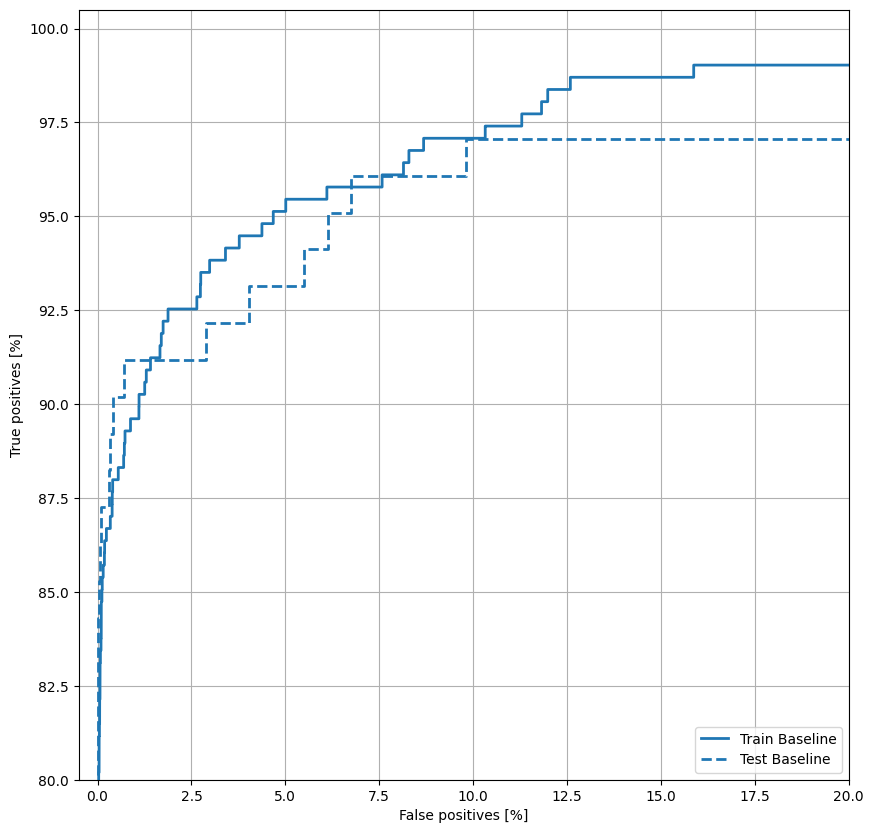
Plot AUPRC
Sekarang plot AUPRC . Area di bawah kurva presisi-recall interpolasi, diperoleh dengan memplot (recall, presisi) poin untuk nilai-nilai yang berbeda dari ambang klasifikasi. Bergantung pada cara penghitungannya, PR AUC mungkin setara dengan presisi rata-rata model.
def plot_prc(name, labels, predictions, **kwargs):
precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
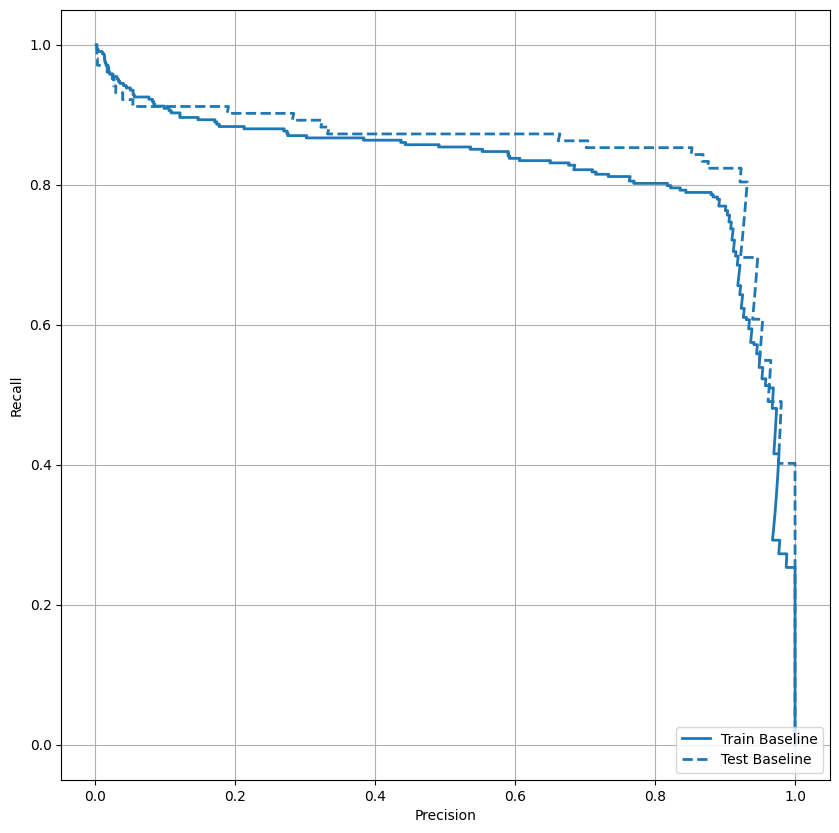
Sepertinya presisinya relatif tinggi, tetapi daya ingat dan area di bawah kurva ROC (AUC) tidak setinggi yang Anda inginkan. Pengklasifikasi sering menghadapi tantangan saat mencoba memaksimalkan presisi dan ingatan, yang terutama benar saat bekerja dengan kumpulan data yang tidak seimbang. Penting untuk mempertimbangkan biaya dari berbagai jenis kesalahan dalam konteks masalah yang Anda pedulikan. Dalam contoh ini, negatif palsu (transaksi penipuan tidak terjawab) mungkin memiliki biaya finansial, sementara positif palsu (transaksi salah ditandai sebagai penipuan) dapat mengurangi kebahagiaan pengguna.
Bobot kelas
Hitung bobot kelas
Tujuannya adalah untuk mengidentifikasi transaksi penipuan, tetapi Anda tidak memiliki banyak sampel positif untuk digunakan, jadi Anda ingin pengklasifikasi sangat mempertimbangkan beberapa contoh yang tersedia. Anda dapat melakukan ini dengan melewatkan bobot Keras untuk setiap kelas melalui sebuah parameter. Ini akan menyebabkan model "lebih memperhatikan" contoh dari kelas yang kurang terwakili.
# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))
Weight for class 0: 0.50 Weight for class 1: 289.44
Latih model dengan bobot kelas
Sekarang coba latih ulang dan evaluasi model dengan bobot kelas untuk melihat bagaimana hal itu memengaruhi prediksi.
weighted_model = make_model()
weighted_model.load_weights(initial_weights)
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels),
# The class weights go here
class_weight=class_weight)
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 4.1298 - tp: 59.0000 - fp: 11.0000 - tn: 238821.0000 - fn: 347.0000 - accuracy: 0.9985 - precision: 0.8429 - recall: 0.1453 - auc: 0.6238 - prc: 0.1649 - val_loss: 0.0119 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7124 - val_prc: 0.0294 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 1.8711 - tp: 69.0000 - fp: 54.0000 - tn: 181897.0000 - fn: 256.0000 - accuracy: 0.9983 - precision: 0.5610 - recall: 0.2123 - auc: 0.8178 - prc: 0.2117 - val_loss: 0.0060 - val_tp: 56.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 30.0000 - val_accuracy: 0.9991 - val_precision: 0.8485 - val_recall: 0.6512 - val_auc: 0.9427 - val_prc: 0.6870 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.8666 - tp: 187.0000 - fp: 198.0000 - tn: 181753.0000 - fn: 138.0000 - accuracy: 0.9982 - precision: 0.4857 - recall: 0.5754 - auc: 0.9075 - prc: 0.4912 - val_loss: 0.0077 - val_tp: 65.0000 - val_fp: 19.0000 - val_tn: 45464.0000 - val_fn: 21.0000 - val_accuracy: 0.9991 - val_precision: 0.7738 - val_recall: 0.7558 - val_auc: 0.9564 - val_prc: 0.6924 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.6876 - tp: 218.0000 - fp: 530.0000 - tn: 181421.0000 - fn: 107.0000 - accuracy: 0.9965 - precision: 0.2914 - recall: 0.6708 - auc: 0.9152 - prc: 0.5102 - val_loss: 0.0109 - val_tp: 68.0000 - val_fp: 39.0000 - val_tn: 45444.0000 - val_fn: 18.0000 - val_accuracy: 0.9987 - val_precision: 0.6355 - val_recall: 0.7907 - val_auc: 0.9661 - val_prc: 0.6926 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.5229 - tp: 240.0000 - fp: 1102.0000 - tn: 180849.0000 - fn: 85.0000 - accuracy: 0.9935 - precision: 0.1788 - recall: 0.7385 - auc: 0.9395 - prc: 0.5228 - val_loss: 0.0154 - val_tp: 70.0000 - val_fp: 79.0000 - val_tn: 45404.0000 - val_fn: 16.0000 - val_accuracy: 0.9979 - val_precision: 0.4698 - val_recall: 0.8140 - val_auc: 0.9657 - val_prc: 0.7023 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.4753 - tp: 251.0000 - fp: 1839.0000 - tn: 180112.0000 - fn: 74.0000 - accuracy: 0.9895 - precision: 0.1201 - recall: 0.7723 - auc: 0.9336 - prc: 0.4297 - val_loss: 0.0213 - val_tp: 70.0000 - val_fp: 156.0000 - val_tn: 45327.0000 - val_fn: 16.0000 - val_accuracy: 0.9962 - val_precision: 0.3097 - val_recall: 0.8140 - val_auc: 0.9654 - val_prc: 0.6742 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3870 - tp: 270.0000 - fp: 2554.0000 - tn: 179397.0000 - fn: 55.0000 - accuracy: 0.9857 - precision: 0.0956 - recall: 0.8308 - auc: 0.9463 - prc: 0.3800 - val_loss: 0.0269 - val_tp: 70.0000 - val_fp: 264.0000 - val_tn: 45219.0000 - val_fn: 16.0000 - val_accuracy: 0.9939 - val_precision: 0.2096 - val_recall: 0.8140 - val_auc: 0.9651 - val_prc: 0.6116 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3942 - tp: 268.0000 - fp: 3219.0000 - tn: 178732.0000 - fn: 57.0000 - accuracy: 0.9820 - precision: 0.0769 - recall: 0.8246 - auc: 0.9434 - prc: 0.3273 - val_loss: 0.0337 - val_tp: 70.0000 - val_fp: 355.0000 - val_tn: 45128.0000 - val_fn: 16.0000 - val_accuracy: 0.9919 - val_precision: 0.1647 - val_recall: 0.8140 - val_auc: 0.9682 - val_prc: 0.5918 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3886 - tp: 271.0000 - fp: 3845.0000 - tn: 178106.0000 - fn: 54.0000 - accuracy: 0.9786 - precision: 0.0658 - recall: 0.8338 - auc: 0.9397 - prc: 0.2995 - val_loss: 0.0386 - val_tp: 70.0000 - val_fp: 406.0000 - val_tn: 45077.0000 - val_fn: 16.0000 - val_accuracy: 0.9907 - val_precision: 0.1471 - val_recall: 0.8140 - val_auc: 0.9756 - val_prc: 0.5889 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2951 - tp: 281.0000 - fp: 4348.0000 - tn: 177603.0000 - fn: 44.0000 - accuracy: 0.9759 - precision: 0.0607 - recall: 0.8646 - auc: 0.9623 - prc: 0.2826 - val_loss: 0.0441 - val_tp: 72.0000 - val_fp: 464.0000 - val_tn: 45019.0000 - val_fn: 14.0000 - val_accuracy: 0.9895 - val_precision: 0.1343 - val_recall: 0.8372 - val_auc: 0.9748 - val_prc: 0.5895 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2703 - tp: 280.0000 - fp: 4697.0000 - tn: 177254.0000 - fn: 45.0000 - accuracy: 0.9740 - precision: 0.0563 - recall: 0.8615 - auc: 0.9660 - prc: 0.2589 - val_loss: 0.0490 - val_tp: 72.0000 - val_fp: 552.0000 - val_tn: 44931.0000 - val_fn: 14.0000 - val_accuracy: 0.9876 - val_precision: 0.1154 - val_recall: 0.8372 - val_auc: 0.9762 - val_prc: 0.5902 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3358 - tp: 278.0000 - fp: 5262.0000 - tn: 176689.0000 - fn: 47.0000 - accuracy: 0.9709 - precision: 0.0502 - recall: 0.8554 - auc: 0.9468 - prc: 0.2368 - val_loss: 0.0534 - val_tp: 74.0000 - val_fp: 597.0000 - val_tn: 44886.0000 - val_fn: 12.0000 - val_accuracy: 0.9866 - val_precision: 0.1103 - val_recall: 0.8605 - val_auc: 0.9752 - val_prc: 0.5848 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2833 - tp: 286.0000 - fp: 5502.0000 - tn: 176449.0000 - fn: 39.0000 - accuracy: 0.9696 - precision: 0.0494 - recall: 0.8800 - auc: 0.9582 - prc: 0.2572 - val_loss: 0.0563 - val_tp: 74.0000 - val_fp: 616.0000 - val_tn: 44867.0000 - val_fn: 12.0000 - val_accuracy: 0.9862 - val_precision: 0.1072 - val_recall: 0.8605 - val_auc: 0.9748 - val_prc: 0.5678 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2969 - tp: 280.0000 - fp: 5630.0000 - tn: 176321.0000 - fn: 45.0000 - accuracy: 0.9689 - precision: 0.0474 - recall: 0.8615 - auc: 0.9594 - prc: 0.2374 - val_loss: 0.0597 - val_tp: 74.0000 - val_fp: 644.0000 - val_tn: 44839.0000 - val_fn: 12.0000 - val_accuracy: 0.9856 - val_precision: 0.1031 - val_recall: 0.8605 - val_auc: 0.9741 - val_prc: 0.5627 Epoch 15/100 90/90 [==============================] - ETA: 0s - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224Restoring model weights from the end of the best epoch: 5. 90/90 [==============================] - 1s 7ms/step - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224 - val_loss: 0.0621 - val_tp: 74.0000 - val_fp: 665.0000 - val_tn: 44818.0000 - val_fn: 12.0000 - val_accuracy: 0.9851 - val_precision: 0.1001 - val_recall: 0.8605 - val_auc: 0.9771 - val_prc: 0.5550 Epoch 15: early stopping
Periksa riwayat pelatihan
plot_metrics(weighted_history)
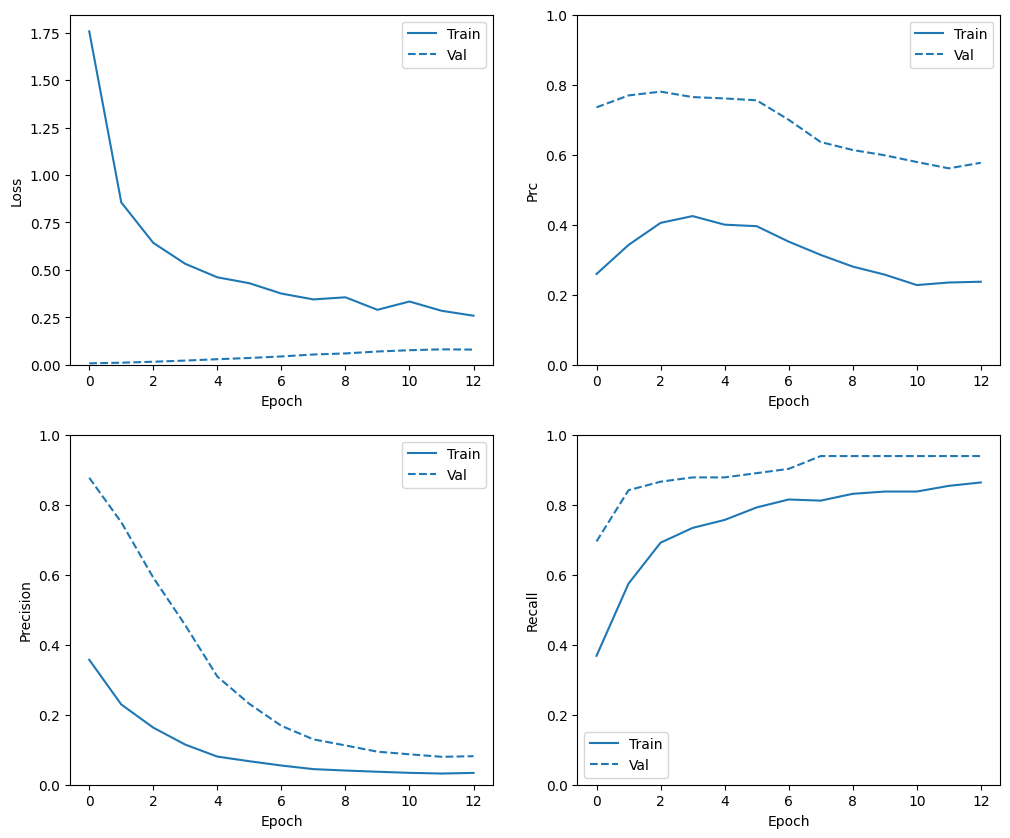
Evaluasi metrik
train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)
weighted_results = weighted_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_weighted)
loss : 0.014327289536595345 tp : 69.0 fp : 88.0 tn : 56793.0 fn : 12.0 accuracy : 0.9982444643974304 precision : 0.4394904375076294 recall : 0.8518518805503845 auc : 0.9410961866378784 prc : 0.7397712469100952 Legitimate Transactions Detected (True Negatives): 56793 Legitimate Transactions Incorrectly Detected (False Positives): 88 Fraudulent Transactions Missed (False Negatives): 12 Fraudulent Transactions Detected (True Positives): 69 Total Fraudulent Transactions: 81
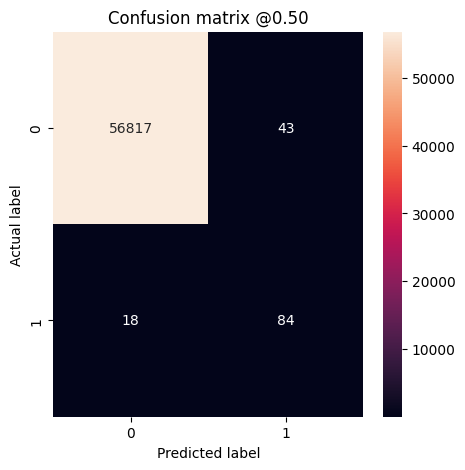
Di sini Anda dapat melihat bahwa dengan bobot kelas akurasi dan presisi lebih rendah karena lebih banyak positif palsu, tetapi sebaliknya recall dan AUC lebih tinggi karena model juga menemukan lebih banyak positif benar. Meskipun memiliki akurasi yang lebih rendah, model ini memiliki daya ingat yang lebih tinggi (dan mengidentifikasi lebih banyak transaksi penipuan). Tentu saja, ada biaya untuk kedua jenis kesalahan (Anda juga tidak ingin mengganggu pengguna dengan menandai terlalu banyak transaksi yang sah sebagai penipuan). Pertimbangkan dengan cermat pertukaran antara berbagai jenis kesalahan ini untuk aplikasi Anda.
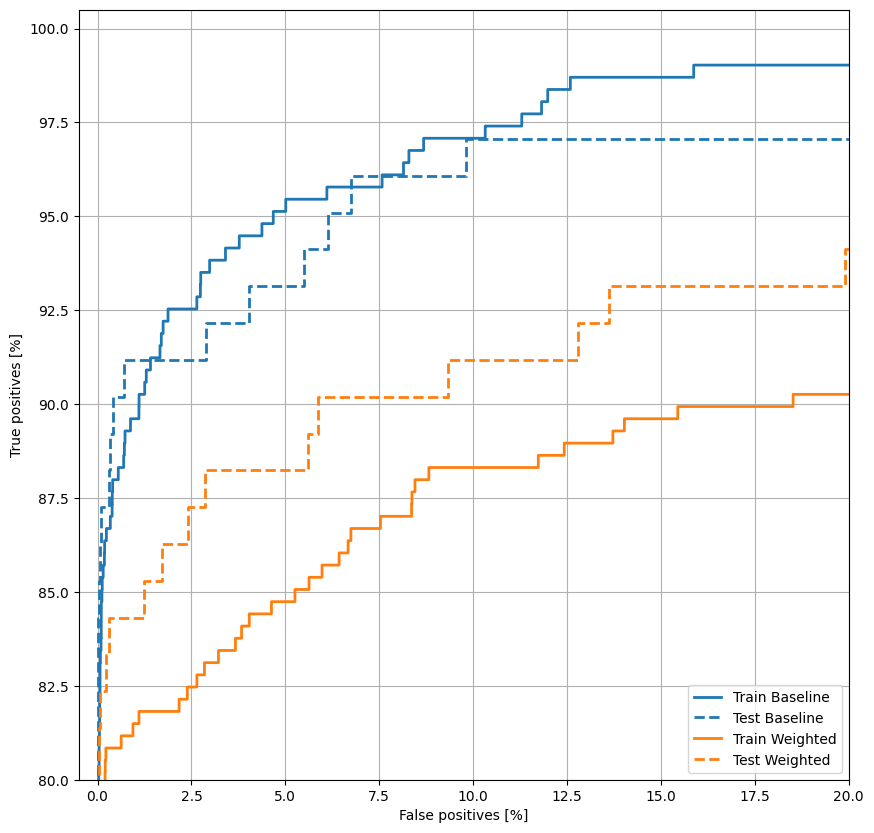
Rencanakan ROC
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
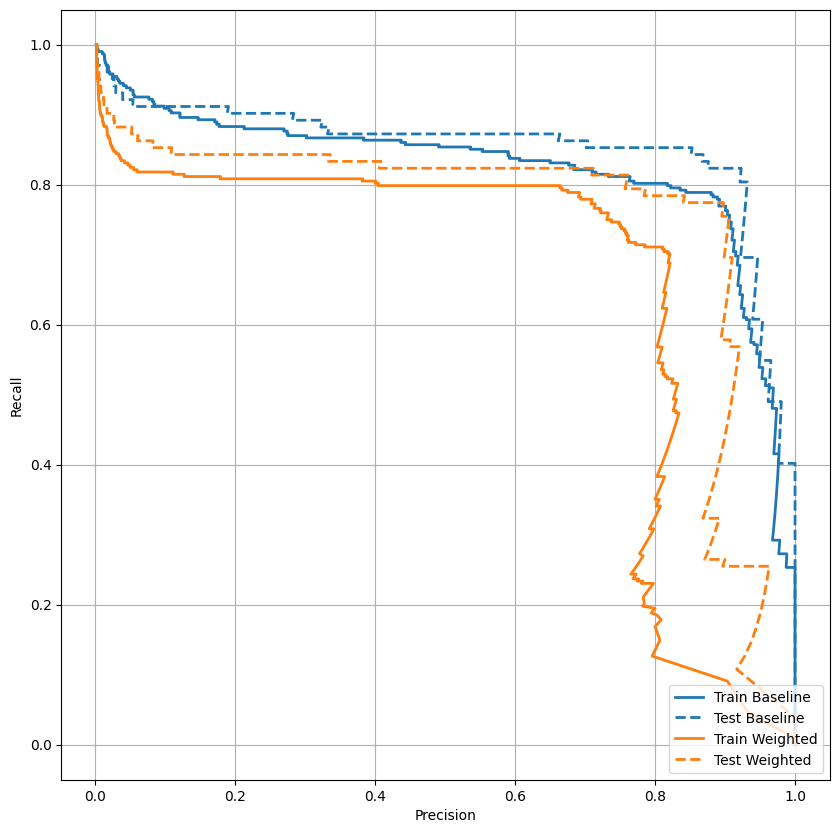
Plot AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
Pengambilan sampel berlebih
Oversample kelas minoritas
Pendekatan terkait adalah dengan mengambil sampel ulang dataset dengan melakukan oversampling kelas minoritas.
pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]
pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]
Menggunakan NumPy
Anda dapat menyeimbangkan kumpulan data secara manual dengan memilih jumlah indeks acak yang tepat dari contoh positif:
ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))
res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]
res_pos_features.shape
(181951, 29)
resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)
order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]
resampled_features.shape
(363902, 29)
Menggunakan tf.data
Jika Anda menggunakan tf.data , cara termudah untuk menghasilkan contoh yang seimbang adalah memulai dengan kumpulan data positive dan negative , dan menggabungkannya. Lihat panduan tf.data untuk lebih banyak contoh.
BUFFER_SIZE = 100000
def make_ds(features, labels):
ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
ds = ds.shuffle(BUFFER_SIZE).repeat()
return ds
pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)
Setiap kumpulan data menyediakan (feature, label) pasangan:
for features, label in pos_ds.take(1):
print("Features:\n", features.numpy())
print()
print("Label: ", label.numpy())
Features: [ 0.56826828 1.24841849 -2.52251105 3.84165891 0.05052604 -0.7621795 -1.43118352 0.43296139 -1.85102109 -2.50477555 3.20133397 -3.52460861 -0.95133935 -5. -1.93144512 -0.7302767 -2.46735228 0.21827555 -1.45046438 0.21081234 0.39176826 -0.23558789 -0.03611637 -0.62063738 0.3686766 0.23622961 1.2242418 0.75555829 -1.45589162] Label: 1
Gabungkan keduanya menggunakan tf.data.Dataset.sample_from_datasets :
resampled_ds = tf.data.Dataset.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)
for features, label in resampled_ds.take(1):
print(label.numpy().mean())
0.50732421875
Untuk menggunakan kumpulan data ini, Anda memerlukan jumlah langkah per epoch.
Definisi "zaman" dalam hal ini kurang jelas. Katakanlah itu jumlah batch yang diperlukan untuk melihat setiap contoh negatif satu kali:
resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch
278.0
Latih data yang di-oversampling
Sekarang coba latih model dengan kumpulan data yang disampel ulang alih-alih menggunakan bobot kelas untuk melihat bagaimana metode ini dibandingkan.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2)
resampled_history = resampled_model.fit(
resampled_ds,
epochs=EPOCHS,
steps_per_epoch=resampled_steps_per_epoch,
callbacks=[early_stopping],
validation_data=val_ds)
Epoch 1/100 278/278 [==============================] - 10s 32ms/step - loss: 0.5508 - tp: 214194.0000 - fp: 51114.0000 - tn: 290615.0000 - fn: 70383.0000 - accuracy: 0.8060 - precision: 0.8073 - recall: 0.7527 - auc: 0.8600 - prc: 0.8879 - val_loss: 0.2279 - val_tp: 73.0000 - val_fp: 969.0000 - val_tn: 44514.0000 - val_fn: 13.0000 - val_accuracy: 0.9785 - val_precision: 0.0701 - val_recall: 0.8488 - val_auc: 0.9551 - val_prc: 0.7044 Epoch 2/100 278/278 [==============================] - 8s 28ms/step - loss: 0.2235 - tp: 253877.0000 - fp: 15743.0000 - tn: 268530.0000 - fn: 31194.0000 - accuracy: 0.9176 - precision: 0.9416 - recall: 0.8906 - auc: 0.9658 - prc: 0.9746 - val_loss: 0.1367 - val_tp: 73.0000 - val_fp: 777.0000 - val_tn: 44706.0000 - val_fn: 13.0000 - val_accuracy: 0.9827 - val_precision: 0.0859 - val_recall: 0.8488 - val_auc: 0.9596 - val_prc: 0.7072 Epoch 3/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1785 - tp: 258572.0000 - fp: 9840.0000 - tn: 274878.0000 - fn: 26054.0000 - accuracy: 0.9370 - precision: 0.9633 - recall: 0.9085 - auc: 0.9773 - prc: 0.9827 - val_loss: 0.1023 - val_tp: 72.0000 - val_fp: 699.0000 - val_tn: 44784.0000 - val_fn: 14.0000 - val_accuracy: 0.9844 - val_precision: 0.0934 - val_recall: 0.8372 - val_auc: 0.9632 - val_prc: 0.7032 Epoch 4/100 278/278 [==============================] - 8s 29ms/step - loss: 0.1571 - tp: 260447.0000 - fp: 8085.0000 - tn: 276389.0000 - fn: 24423.0000 - accuracy: 0.9429 - precision: 0.9699 - recall: 0.9143 - auc: 0.9826 - prc: 0.9863 - val_loss: 0.0869 - val_tp: 74.0000 - val_fp: 701.0000 - val_tn: 44782.0000 - val_fn: 12.0000 - val_accuracy: 0.9844 - val_precision: 0.0955 - val_recall: 0.8605 - val_auc: 0.9633 - val_prc: 0.6972 Epoch 5/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1440 - tp: 261457.0000 - fp: 7449.0000 - tn: 277093.0000 - fn: 23345.0000 - accuracy: 0.9459 - precision: 0.9723 - recall: 0.9180 - auc: 0.9855 - prc: 0.9883 - val_loss: 0.0774 - val_tp: 73.0000 - val_fp: 679.0000 - val_tn: 44804.0000 - val_fn: 13.0000 - val_accuracy: 0.9848 - val_precision: 0.0971 - val_recall: 0.8488 - val_auc: 0.9645 - val_prc: 0.6971 Epoch 6/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1349 - tp: 262460.0000 - fp: 6942.0000 - tn: 277723.0000 - fn: 22219.0000 - accuracy: 0.9488 - precision: 0.9742 - recall: 0.9220 - auc: 0.9876 - prc: 0.9896 - val_loss: 0.0718 - val_tp: 74.0000 - val_fp: 624.0000 - val_tn: 44859.0000 - val_fn: 12.0000 - val_accuracy: 0.9860 - val_precision: 0.1060 - val_recall: 0.8605 - val_auc: 0.9645 - val_prc: 0.6891 Epoch 7/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1264 - tp: 263166.0000 - fp: 6780.0000 - tn: 278253.0000 - fn: 21145.0000 - accuracy: 0.9510 - precision: 0.9749 - recall: 0.9256 - auc: 0.9895 - prc: 0.9909 - val_loss: 0.0672 - val_tp: 75.0000 - val_fp: 602.0000 - val_tn: 44881.0000 - val_fn: 11.0000 - val_accuracy: 0.9865 - val_precision: 0.1108 - val_recall: 0.8721 - val_auc: 0.9670 - val_prc: 0.6822 Epoch 8/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1190 - tp: 264216.0000 - fp: 6569.0000 - tn: 278270.0000 - fn: 20289.0000 - accuracy: 0.9528 - precision: 0.9757 - recall: 0.9287 - auc: 0.9910 - prc: 0.9920 - val_loss: 0.0628 - val_tp: 74.0000 - val_fp: 570.0000 - val_tn: 44913.0000 - val_fn: 12.0000 - val_accuracy: 0.9872 - val_precision: 0.1149 - val_recall: 0.8605 - val_auc: 0.9671 - val_prc: 0.6830 Epoch 9/100 278/278 [==============================] - 9s 31ms/step - loss: 0.1125 - tp: 264562.0000 - fp: 6339.0000 - tn: 279137.0000 - fn: 19306.0000 - accuracy: 0.9550 - precision: 0.9766 - recall: 0.9320 - auc: 0.9924 - prc: 0.9930 - val_loss: 0.0576 - val_tp: 74.0000 - val_fp: 544.0000 - val_tn: 44939.0000 - val_fn: 12.0000 - val_accuracy: 0.9878 - val_precision: 0.1197 - val_recall: 0.8605 - val_auc: 0.9672 - val_prc: 0.6828 Epoch 10/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1064 - tp: 266549.0000 - fp: 6112.0000 - tn: 278323.0000 - fn: 18360.0000 - accuracy: 0.9570 - precision: 0.9776 - recall: 0.9356 - auc: 0.9934 - prc: 0.9937 - val_loss: 0.0544 - val_tp: 74.0000 - val_fp: 541.0000 - val_tn: 44942.0000 - val_fn: 12.0000 - val_accuracy: 0.9879 - val_precision: 0.1203 - val_recall: 0.8605 - val_auc: 0.9638 - val_prc: 0.6827 Epoch 11/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1005 - tp: 267048.0000 - fp: 6123.0000 - tn: 278896.0000 - fn: 17277.0000 - accuracy: 0.9589 - precision: 0.9776 - recall: 0.9392 - auc: 0.9943 - prc: 0.9944 - val_loss: 0.0493 - val_tp: 74.0000 - val_fp: 500.0000 - val_tn: 44983.0000 - val_fn: 12.0000 - val_accuracy: 0.9888 - val_precision: 0.1289 - val_recall: 0.8605 - val_auc: 0.9578 - val_prc: 0.6761 Epoch 12/100 277/278 [============================>.] - ETA: 0s - loss: 0.0950 - tp: 266855.0000 - fp: 6079.0000 - tn: 277677.0000 - fn: 16685.0000 - accuracy: 0.9599 - precision: 0.9777 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949Restoring model weights from the end of the best epoch: 2. 278/278 [==============================] - 8s 29ms/step - loss: 0.0950 - tp: 267815.0000 - fp: 6094.0000 - tn: 278693.0000 - fn: 16742.0000 - accuracy: 0.9599 - precision: 0.9778 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949 - val_loss: 0.0451 - val_tp: 74.0000 - val_fp: 468.0000 - val_tn: 45015.0000 - val_fn: 12.0000 - val_accuracy: 0.9895 - val_precision: 0.1365 - val_recall: 0.8605 - val_auc: 0.9581 - val_prc: 0.6683 Epoch 12: early stopping
Jika proses pelatihan mempertimbangkan seluruh dataset pada setiap pembaruan gradien, oversampling ini pada dasarnya akan identik dengan pembobotan kelas.
Namun saat melatih model secara batch, seperti yang Anda lakukan di sini, data yang di-oversampling memberikan sinyal gradien yang lebih halus: Alih-alih setiap contoh positif ditampilkan dalam satu batch dengan bobot besar, mereka ditampilkan dalam banyak batch berbeda setiap kali dengan berat kecil.
Sinyal gradien yang lebih halus ini memudahkan untuk melatih model.
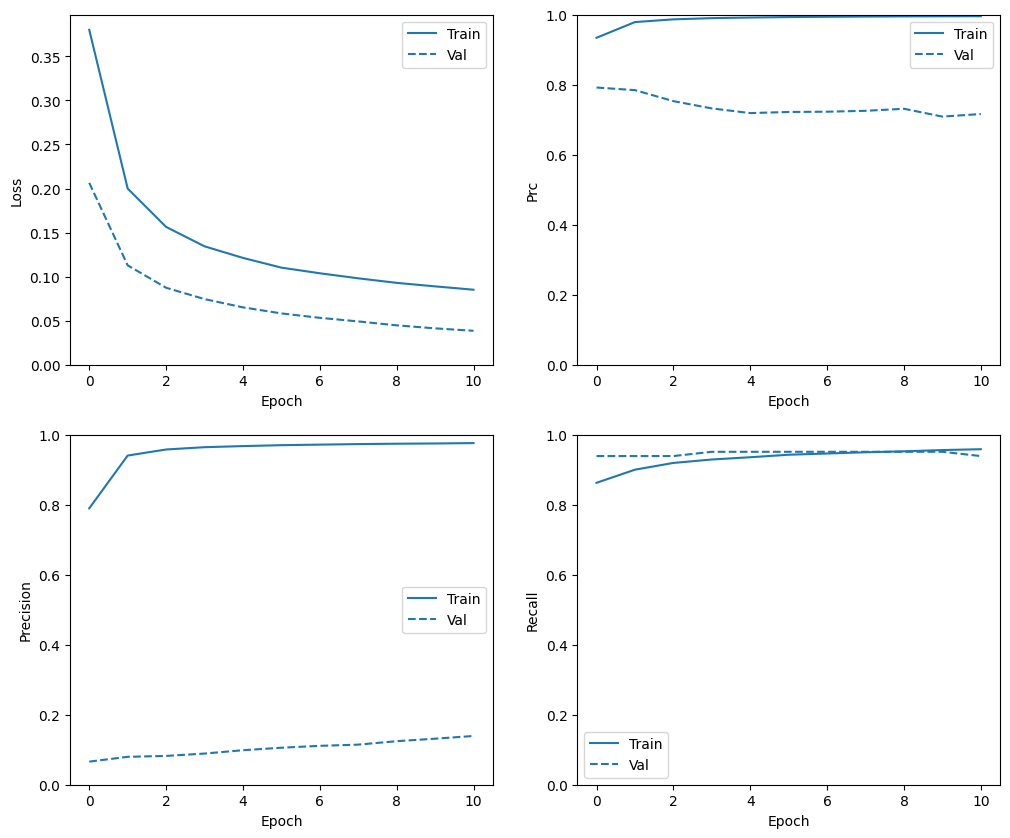
Periksa riwayat pelatihan
Perhatikan bahwa distribusi metrik akan berbeda di sini, karena data pelatihan memiliki distribusi yang sama sekali berbeda dari data validasi dan pengujian.
plot_metrics(resampled_history)
Latih ulang
Karena pelatihan lebih mudah pada data yang seimbang, prosedur pelatihan di atas mungkin terlalu cepat.
Jadi, pisahkan epoch untuk memberikan kontrol yang lebih baik kepada tf.keras.callbacks.EarlyStopping kapan harus menghentikan pelatihan.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
resampled_history = resampled_model.fit(
resampled_ds,
# These are not real epochs
steps_per_epoch=20,
epochs=10*EPOCHS,
callbacks=[early_stopping],
validation_data=(val_ds))
Epoch 1/1000 20/20 [==============================] - 3s 73ms/step - loss: 2.0114 - tp: 3382.0000 - fp: 5181.0000 - tn: 60589.0000 - fn: 17377.0000 - accuracy: 0.7393 - precision: 0.3950 - recall: 0.1629 - auc: 0.6308 - prc: 0.3325 - val_loss: 0.4343 - val_tp: 7.0000 - val_fp: 5042.0000 - val_tn: 40441.0000 - val_fn: 79.0000 - val_accuracy: 0.8876 - val_precision: 0.0014 - val_recall: 0.0814 - val_auc: 0.2282 - val_prc: 0.0012 Epoch 2/1000 20/20 [==============================] - 1s 33ms/step - loss: 1.2163 - tp: 7466.0000 - fp: 5137.0000 - tn: 15257.0000 - fn: 13100.0000 - accuracy: 0.5548 - precision: 0.5924 - recall: 0.3630 - auc: 0.4763 - prc: 0.5716 - val_loss: 0.4539 - val_tp: 36.0000 - val_fp: 5893.0000 - val_tn: 39590.0000 - val_fn: 50.0000 - val_accuracy: 0.8696 - val_precision: 0.0061 - val_recall: 0.4186 - val_auc: 0.6494 - val_prc: 0.0054 Epoch 3/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.7406 - tp: 12289.0000 - fp: 5509.0000 - tn: 14872.0000 - fn: 8290.0000 - accuracy: 0.6631 - precision: 0.6905 - recall: 0.5972 - auc: 0.6803 - prc: 0.7580 - val_loss: 0.4611 - val_tp: 75.0000 - val_fp: 6273.0000 - val_tn: 39210.0000 - val_fn: 11.0000 - val_accuracy: 0.8621 - val_precision: 0.0118 - val_recall: 0.8721 - val_auc: 0.9293 - val_prc: 0.4539 Epoch 4/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.5071 - tp: 15891.0000 - fp: 5370.0000 - tn: 15013.0000 - fn: 4686.0000 - accuracy: 0.7545 - precision: 0.7474 - recall: 0.7723 - auc: 0.8298 - prc: 0.8757 - val_loss: 0.4451 - val_tp: 78.0000 - val_fp: 5505.0000 - val_tn: 39978.0000 - val_fn: 8.0000 - val_accuracy: 0.8790 - val_precision: 0.0140 - val_recall: 0.9070 - val_auc: 0.9443 - val_prc: 0.6777 Epoch 5/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.4284 - tp: 17046.0000 - fp: 5072.0000 - tn: 15496.0000 - fn: 3346.0000 - accuracy: 0.7945 - precision: 0.7707 - recall: 0.8359 - auc: 0.8827 - prc: 0.9151 - val_loss: 0.4140 - val_tp: 77.0000 - val_fp: 4338.0000 - val_tn: 41145.0000 - val_fn: 9.0000 - val_accuracy: 0.9046 - val_precision: 0.0174 - val_recall: 0.8953 - val_auc: 0.9463 - val_prc: 0.6903 Epoch 6/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3836 - tp: 17606.0000 - fp: 4362.0000 - tn: 16113.0000 - fn: 2879.0000 - accuracy: 0.8232 - precision: 0.8014 - recall: 0.8595 - auc: 0.9080 - prc: 0.9336 - val_loss: 0.3824 - val_tp: 77.0000 - val_fp: 3314.0000 - val_tn: 42169.0000 - val_fn: 9.0000 - val_accuracy: 0.9271 - val_precision: 0.0227 - val_recall: 0.8953 - val_auc: 0.9475 - val_prc: 0.6752 Epoch 7/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3574 - tp: 17856.0000 - fp: 3894.0000 - tn: 16553.0000 - fn: 2657.0000 - accuracy: 0.8401 - precision: 0.8210 - recall: 0.8705 - auc: 0.9208 - prc: 0.9432 - val_loss: 0.3538 - val_tp: 76.0000 - val_fp: 2592.0000 - val_tn: 42891.0000 - val_fn: 10.0000 - val_accuracy: 0.9429 - val_precision: 0.0285 - val_recall: 0.8837 - val_auc: 0.9486 - val_prc: 0.6819 Epoch 8/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3377 - tp: 17766.0000 - fp: 3483.0000 - tn: 17067.0000 - fn: 2644.0000 - accuracy: 0.8504 - precision: 0.8361 - recall: 0.8705 - auc: 0.9280 - prc: 0.9481 - val_loss: 0.3271 - val_tp: 76.0000 - val_fp: 2047.0000 - val_tn: 43436.0000 - val_fn: 10.0000 - val_accuracy: 0.9549 - val_precision: 0.0358 - val_recall: 0.8837 - val_auc: 0.9497 - val_prc: 0.6910 Epoch 9/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3188 - tp: 17749.0000 - fp: 2855.0000 - tn: 17547.0000 - fn: 2809.0000 - accuracy: 0.8617 - precision: 0.8614 - recall: 0.8634 - auc: 0.9360 - prc: 0.9539 - val_loss: 0.3051 - val_tp: 74.0000 - val_fp: 1657.0000 - val_tn: 43826.0000 - val_fn: 12.0000 - val_accuracy: 0.9634 - val_precision: 0.0427 - val_recall: 0.8605 - val_auc: 0.9514 - val_prc: 0.7022 Epoch 10/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3046 - tp: 17772.0000 - fp: 2599.0000 - tn: 17841.0000 - fn: 2748.0000 - accuracy: 0.8695 - precision: 0.8724 - recall: 0.8661 - auc: 0.9402 - prc: 0.9570 - val_loss: 0.2860 - val_tp: 74.0000 - val_fp: 1398.0000 - val_tn: 44085.0000 - val_fn: 12.0000 - val_accuracy: 0.9691 - val_precision: 0.0503 - val_recall: 0.8605 - val_auc: 0.9527 - val_prc: 0.6997 Epoch 11/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2937 - tp: 17673.0000 - fp: 2352.0000 - tn: 18273.0000 - fn: 2662.0000 - accuracy: 0.8776 - precision: 0.8825 - recall: 0.8691 - auc: 0.9447 - prc: 0.9595 - val_loss: 0.2687 - val_tp: 73.0000 - val_fp: 1235.0000 - val_tn: 44248.0000 - val_fn: 13.0000 - val_accuracy: 0.9726 - val_precision: 0.0558 - val_recall: 0.8488 - val_auc: 0.9534 - val_prc: 0.7066 Epoch 12/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2813 - tp: 17721.0000 - fp: 2109.0000 - tn: 18523.0000 - fn: 2607.0000 - accuracy: 0.8849 - precision: 0.8936 - recall: 0.8718 - auc: 0.9485 - prc: 0.9621 - val_loss: 0.2524 - val_tp: 73.0000 - val_fp: 1098.0000 - val_tn: 44385.0000 - val_fn: 13.0000 - val_accuracy: 0.9756 - val_precision: 0.0623 - val_recall: 0.8488 - val_auc: 0.9539 - val_prc: 0.7094 Epoch 13/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2706 - tp: 18031.0000 - fp: 1869.0000 - tn: 18502.0000 - fn: 2558.0000 - accuracy: 0.8919 - precision: 0.9061 - recall: 0.8758 - auc: 0.9520 - prc: 0.9652 - val_loss: 0.2395 - val_tp: 73.0000 - val_fp: 1037.0000 - val_tn: 44446.0000 - val_fn: 13.0000 - val_accuracy: 0.9770 - val_precision: 0.0658 - val_recall: 0.8488 - val_auc: 0.9549 - val_prc: 0.7119 Epoch 14/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2665 - tp: 18087.0000 - fp: 1748.0000 - tn: 18567.0000 - fn: 2558.0000 - accuracy: 0.8949 - precision: 0.9119 - recall: 0.8761 - auc: 0.9525 - prc: 0.9661 - val_loss: 0.2283 - val_tp: 73.0000 - val_fp: 972.0000 - val_tn: 44511.0000 - val_fn: 13.0000 - val_accuracy: 0.9784 - val_precision: 0.0699 - val_recall: 0.8488 - val_auc: 0.9556 - val_prc: 0.7045 Epoch 15/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2589 - tp: 18064.0000 - fp: 1630.0000 - tn: 18830.0000 - fn: 2436.0000 - accuracy: 0.9007 - precision: 0.9172 - recall: 0.8812 - auc: 0.9560 - prc: 0.9676 - val_loss: 0.2180 - val_tp: 73.0000 - val_fp: 941.0000 - val_tn: 44542.0000 - val_fn: 13.0000 - val_accuracy: 0.9791 - val_precision: 0.0720 - val_recall: 0.8488 - val_auc: 0.9563 - val_prc: 0.7069 Epoch 16/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2495 - tp: 18132.0000 - fp: 1481.0000 - tn: 18926.0000 - fn: 2421.0000 - accuracy: 0.9047 - precision: 0.9245 - recall: 0.8822 - auc: 0.9587 - prc: 0.9695 - val_loss: 0.2079 - val_tp: 73.0000 - val_fp: 905.0000 - val_tn: 44578.0000 - val_fn: 13.0000 - val_accuracy: 0.9799 - val_precision: 0.0746 - val_recall: 0.8488 - val_auc: 0.9565 - val_prc: 0.7110 Epoch 17/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2435 - tp: 18047.0000 - fp: 1378.0000 - tn: 19144.0000 - fn: 2391.0000 - accuracy: 0.9080 - precision: 0.9291 - recall: 0.8830 - auc: 0.9601 - prc: 0.9706 - val_loss: 0.1990 - val_tp: 73.0000 - val_fp: 882.0000 - val_tn: 44601.0000 - val_fn: 13.0000 - val_accuracy: 0.9804 - val_precision: 0.0764 - val_recall: 0.8488 - val_auc: 0.9568 - val_prc: 0.7118 Epoch 18/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2396 - tp: 18223.0000 - fp: 1289.0000 - tn: 19075.0000 - fn: 2373.0000 - accuracy: 0.9106 - precision: 0.9339 - recall: 0.8848 - auc: 0.9612 - prc: 0.9714 - val_loss: 0.1911 - val_tp: 73.0000 - val_fp: 870.0000 - val_tn: 44613.0000 - val_fn: 13.0000 - val_accuracy: 0.9806 - val_precision: 0.0774 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7148 Epoch 19/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2324 - tp: 18179.0000 - fp: 1205.0000 - tn: 19254.0000 - fn: 2322.0000 - accuracy: 0.9139 - precision: 0.9378 - recall: 0.8867 - auc: 0.9633 - prc: 0.9728 - val_loss: 0.1839 - val_tp: 73.0000 - val_fp: 857.0000 - val_tn: 44626.0000 - val_fn: 13.0000 - val_accuracy: 0.9809 - val_precision: 0.0785 - val_recall: 0.8488 - val_auc: 0.9576 - val_prc: 0.7165 Epoch 20/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2318 - tp: 18119.0000 - fp: 1224.0000 - tn: 19279.0000 - fn: 2338.0000 - accuracy: 0.9130 - precision: 0.9367 - recall: 0.8857 - auc: 0.9640 - prc: 0.9728 - val_loss: 0.1758 - val_tp: 73.0000 - val_fp: 823.0000 - val_tn: 44660.0000 - val_fn: 13.0000 - val_accuracy: 0.9817 - val_precision: 0.0815 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7185 Epoch 21/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2233 - tp: 18041.0000 - fp: 1074.0000 - tn: 19514.0000 - fn: 2331.0000 - accuracy: 0.9169 - precision: 0.9438 - recall: 0.8856 - auc: 0.9660 - prc: 0.9745 - val_loss: 0.1690 - val_tp: 73.0000 - val_fp: 813.0000 - val_tn: 44670.0000 - val_fn: 13.0000 - val_accuracy: 0.9819 - val_precision: 0.0824 - val_recall: 0.8488 - val_auc: 0.9578 - val_prc: 0.7211 Epoch 22/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2193 - tp: 18258.0000 - fp: 1013.0000 - tn: 19414.0000 - fn: 2275.0000 - accuracy: 0.9197 - precision: 0.9474 - recall: 0.8892 - auc: 0.9666 - prc: 0.9753 - val_loss: 0.1634 - val_tp: 73.0000 - val_fp: 817.0000 - val_tn: 44666.0000 - val_fn: 13.0000 - val_accuracy: 0.9818 - val_precision: 0.0820 - val_recall: 0.8488 - val_auc: 0.9580 - val_prc: 0.7123 Epoch 23/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2114 - tp: 18439.0000 - fp: 993.0000 - tn: 19417.0000 - fn: 2111.0000 - accuracy: 0.9242 - precision: 0.9489 - recall: 0.8973 - auc: 0.9696 - prc: 0.9774 - val_loss: 0.1577 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9584 - val_prc: 0.7122 Epoch 24/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2076 - tp: 18459.0000 - fp: 896.0000 - tn: 19582.0000 - fn: 2023.0000 - accuracy: 0.9287 - precision: 0.9537 - recall: 0.9012 - auc: 0.9694 - prc: 0.9776 - val_loss: 0.1528 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9587 - val_prc: 0.7129 Epoch 25/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2044 - tp: 18340.0000 - fp: 907.0000 - tn: 19664.0000 - fn: 2049.0000 - accuracy: 0.9278 - precision: 0.9529 - recall: 0.8995 - auc: 0.9707 - prc: 0.9783 - val_loss: 0.1483 - val_tp: 73.0000 - val_fp: 800.0000 - val_tn: 44683.0000 - val_fn: 13.0000 - val_accuracy: 0.9822 - val_precision: 0.0836 - val_recall: 0.8488 - val_auc: 0.9591 - val_prc: 0.7054 Epoch 26/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1997 - tp: 18293.0000 - fp: 918.0000 - tn: 19749.0000 - fn: 2000.0000 - accuracy: 0.9288 - precision: 0.9522 - recall: 0.9014 - auc: 0.9722 - prc: 0.9788 - val_loss: 0.1433 - val_tp: 73.0000 - val_fp: 788.0000 - val_tn: 44695.0000 - val_fn: 13.0000 - val_accuracy: 0.9824 - val_precision: 0.0848 - val_recall: 0.8488 - val_auc: 0.9590 - val_prc: 0.7059 Epoch 27/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1987 - tp: 18562.0000 - fp: 848.0000 - tn: 19530.0000 - fn: 2020.0000 - accuracy: 0.9300 - precision: 0.9563 - recall: 0.9019 - auc: 0.9720 - prc: 0.9791 - val_loss: 0.1394 - val_tp: 73.0000 - val_fp: 784.0000 - val_tn: 44699.0000 - val_fn: 13.0000 - val_accuracy: 0.9825 - val_precision: 0.0852 - val_recall: 0.8488 - val_auc: 0.9595 - val_prc: 0.7062 Epoch 28/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1944 - tp: 18320.0000 - fp: 828.0000 - tn: 19823.0000 - fn: 1989.0000 - accuracy: 0.9312 - precision: 0.9568 - recall: 0.9021 - auc: 0.9734 - prc: 0.9798 - val_loss: 0.1351 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9598 - val_prc: 0.7079 Epoch 29/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1933 - tp: 18455.0000 - fp: 827.0000 - tn: 19704.0000 - fn: 1974.0000 - accuracy: 0.9316 - precision: 0.9571 - recall: 0.9034 - auc: 0.9732 - prc: 0.9797 - val_loss: 0.1313 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9599 - val_prc: 0.7094 Epoch 30/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1910 - tp: 18417.0000 - fp: 768.0000 - tn: 19858.0000 - fn: 1917.0000 - accuracy: 0.9344 - precision: 0.9600 - recall: 0.9057 - auc: 0.9740 - prc: 0.9802 - val_loss: 0.1282 - val_tp: 73.0000 - val_fp: 759.0000 - val_tn: 44724.0000 - val_fn: 13.0000 - val_accuracy: 0.9831 - val_precision: 0.0877 - val_recall: 0.8488 - val_auc: 0.9602 - val_prc: 0.7094 Epoch 31/1000 20/20 [==============================] - ETA: 0s - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811Restoring model weights from the end of the best epoch: 21. 20/20 [==============================] - 1s 34ms/step - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811 - val_loss: 0.1246 - val_tp: 73.0000 - val_fp: 742.0000 - val_tn: 44741.0000 - val_fn: 13.0000 - val_accuracy: 0.9834 - val_precision: 0.0896 - val_recall: 0.8488 - val_auc: 0.9597 - val_prc: 0.7095 Epoch 31: early stopping
Periksa kembali riwayat pelatihan
plot_metrics(resampled_history)
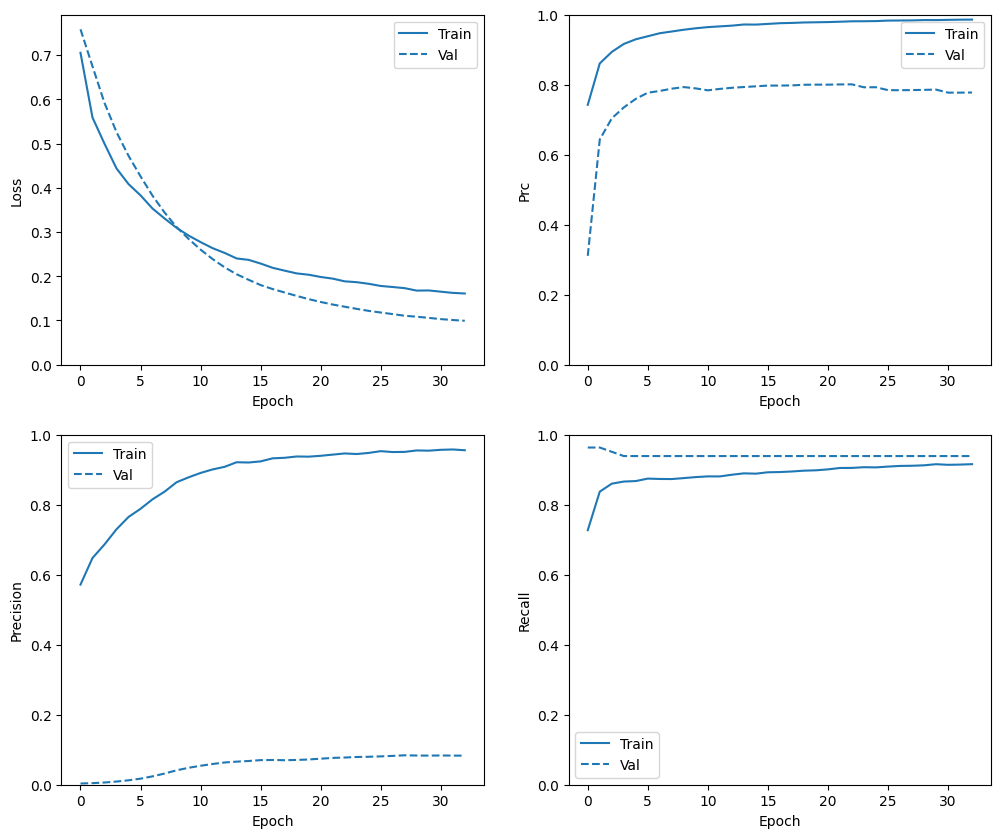
Evaluasi metrik
train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)
resampled_results = resampled_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_resampled)
loss : 0.16882120072841644 tp : 71.0 fp : 1032.0 tn : 55849.0 fn : 10.0 accuracy : 0.9817070960998535 precision : 0.06436990201473236 recall : 0.8765432238578796 auc : 0.9518552422523499 prc : 0.7423797845840454 Legitimate Transactions Detected (True Negatives): 55849 Legitimate Transactions Incorrectly Detected (False Positives): 1032 Fraudulent Transactions Missed (False Negatives): 10 Fraudulent Transactions Detected (True Positives): 71 Total Fraudulent Transactions: 81
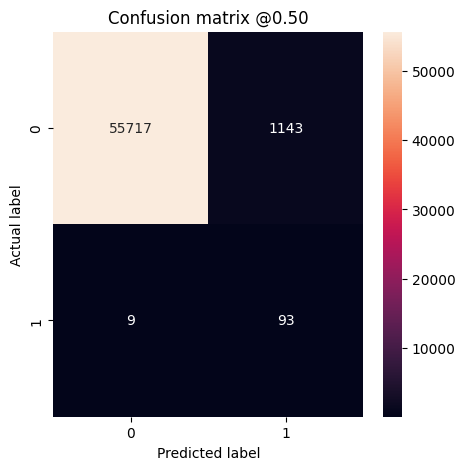
Rencanakan ROC
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
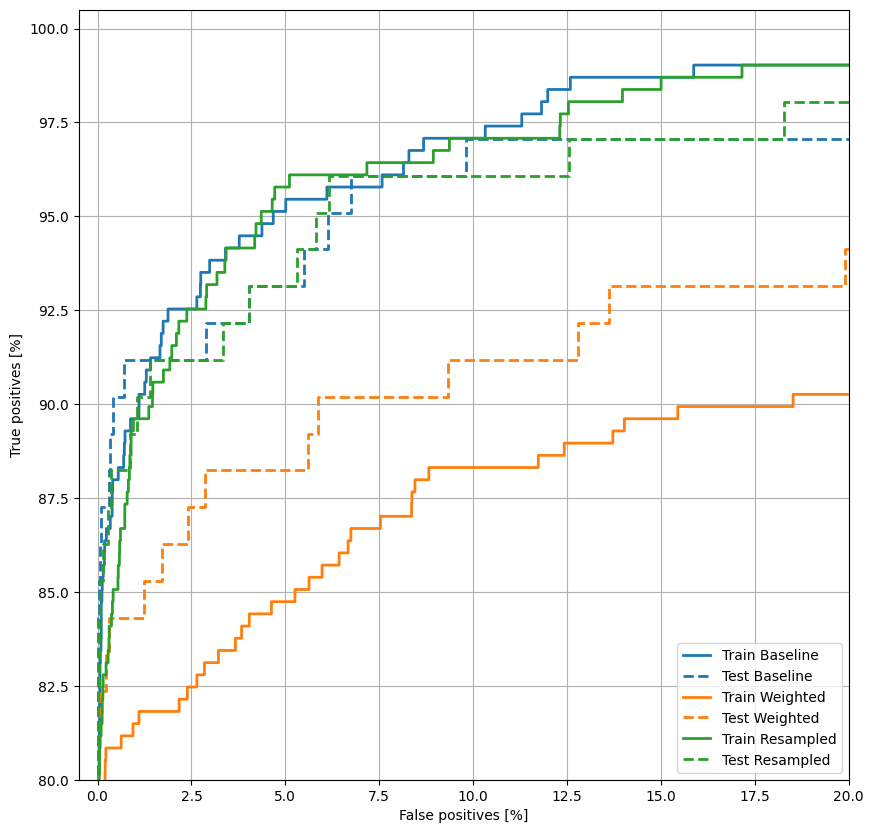
Plot AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
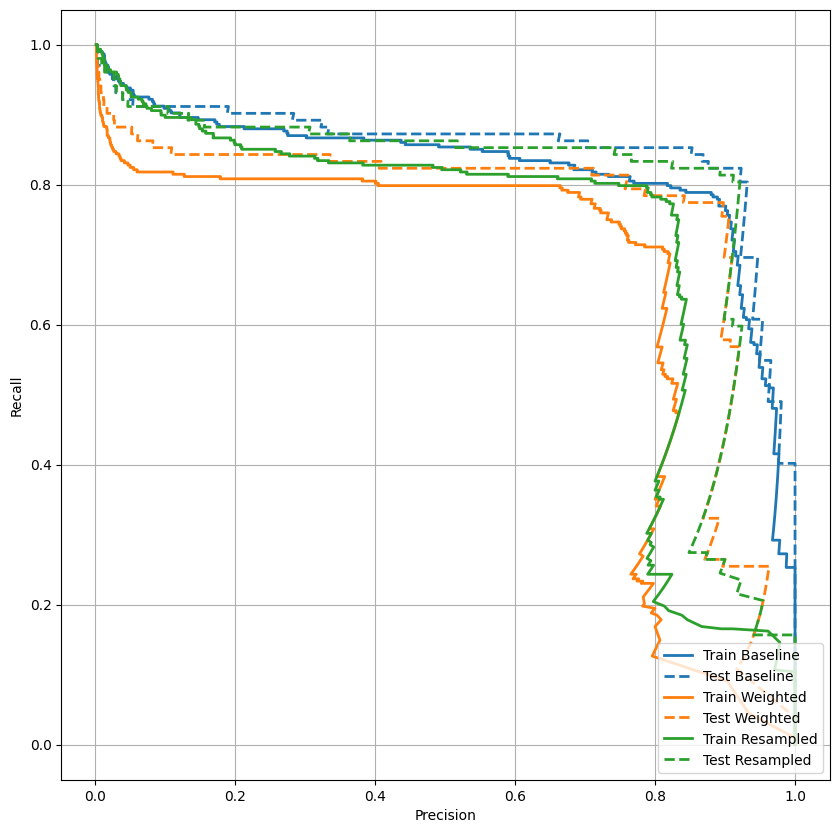
Menerapkan tutorial ini untuk masalah Anda
Klasifikasi data yang tidak seimbang adalah tugas yang sulit karena hanya ada sedikit sampel untuk dipelajari. Anda harus selalu memulai dengan data terlebih dahulu dan melakukan yang terbaik untuk mengumpulkan sampel sebanyak mungkin dan memberikan pemikiran substansial tentang fitur apa yang mungkin relevan sehingga model dapat memaksimalkan kelas minoritas Anda. Pada titik tertentu model Anda mungkin kesulitan untuk meningkatkan dan memberikan hasil yang Anda inginkan, jadi penting untuk mengingat konteks masalah Anda dan pertukaran antara berbagai jenis kesalahan.
