 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Ten samouczek pokazuje, jak zaimplementować metodę Actor-Critic przy użyciu TensorFlow do szkolenia agenta w środowisku Open AI Gym CartPole-V0. Zakłada się, że czytelnik ma pewną wiedzę na temat gradientowych metod uczenia się przez wzmocnienie.
Metody aktora-krytyka
Metody aktora-krytyka to metody uczenia się różnic czasowych (TD) , które reprezentują funkcję polityki niezależną od funkcji wartości.
Funkcja polityki (lub polityka) zwraca rozkład prawdopodobieństwa działań, które agent może podjąć na podstawie danego stanu. Funkcja wartości określa oczekiwany zwrot dla agenta rozpoczynającego się w danym stanie i działającego zgodnie z określoną polityką w nieskończoność.
W metodzie Aktor-Krytyk określamy politykę jako aktora , który proponuje zestaw możliwych działań w danym stanie, a funkcję wartości szacunkowej określamy jako krytyka , który ocenia działania podjęte przez aktora w oparciu o daną politykę .
W tym samouczku zarówno aktor , jak i krytyk będą reprezentowani za pomocą jednej sieci neuronowej z dwoma wyjściami.
KoszykPolak-v0
W środowisku CartPole-v0 kij jest przymocowany do wózka poruszającego się po torze pozbawionym tarcia. Słup zaczyna się pionowo, a celem agenta jest zapobieganie jego przewróceniu poprzez przyłożenie siły -1 lub +1 do wózka. Nagroda +1 jest przyznawana za każdy krok, w którym słupek pozostaje w pozycji pionowej. Epizod kończy się, gdy (1) drążek znajduje się więcej niż 15 stopni od pionu lub (2) wózek przesunie się o więcej niż 2,4 jednostki od środka.
Problem jest uważany za „rozwiązany”, gdy średnia łączna nagroda za odcinek osiąga 195 w ciągu 100 kolejnych prób.
Ustawiać
Zaimportuj niezbędne pakiety i skonfiguruj ustawienia globalne.
pip install gympip install pyglet
# Install additional packages for visualizationsudo apt-get install -y xvfb python-opengl > /dev/null 2>&1pip install pyvirtualdisplay > /dev/null 2>&1pip install git+https://github.com/tensorflow/docs > /dev/null 2>&1
import collections
import gym
import numpy as np
import statistics
import tensorflow as tf
import tqdm
from matplotlib import pyplot as plt
from tensorflow.keras import layers
from typing import Any, List, Sequence, Tuple
# Create the environment
env = gym.make("CartPole-v0")
# Set seed for experiment reproducibility
seed = 42
env.seed(seed)
tf.random.set_seed(seed)
np.random.seed(seed)
# Small epsilon value for stabilizing division operations
eps = np.finfo(np.float32).eps.item()
Model
Aktor i Krytyk będą modelowane za pomocą jednej sieci neuronowej, która generuje odpowiednio prawdopodobieństwa działania i wartość krytyczną. W tym samouczku do zdefiniowania modelu używane są klasy podrzędne modelu.
Podczas przejścia do przodu model przyjmie stan jako dane wejściowe i wygeneruje zarówno prawdopodobieństwa działania, jak i wartość krytyczną \(V\), która modeluje funkcję wartości zależnej od stanu . Celem jest wyszkolenie modelu, który wybiera działania w oparciu o \(\pi\) , która maksymalizuje oczekiwany zwrot .
Dla Cartpole-v0 istnieją cztery wartości reprezentujące stan: odpowiednio pozycja wózka, prędkość wózka, kąt biegunowy i prędkość biegunowa. Agent może wykonać dwie akcje, aby popchnąć wózek odpowiednio w lewo (0) i w prawo (1).
Więcej informacji można znaleźć na stronie wiki CartPole-v0 OpenAI Gym .
class ActorCritic(tf.keras.Model):
"""Combined actor-critic network."""
def __init__(
self,
num_actions: int,
num_hidden_units: int):
"""Initialize."""
super().__init__()
self.common = layers.Dense(num_hidden_units, activation="relu")
self.actor = layers.Dense(num_actions)
self.critic = layers.Dense(1)
def call(self, inputs: tf.Tensor) -> Tuple[tf.Tensor, tf.Tensor]:
x = self.common(inputs)
return self.actor(x), self.critic(x)
num_actions = env.action_space.n # 2
num_hidden_units = 128
model = ActorCritic(num_actions, num_hidden_units)
Trening
Aby przeszkolić agenta, wykonaj następujące kroki:
- Uruchom agenta w środowisku, aby zbierać dane treningowe na odcinek.
- Oblicz oczekiwany zwrot w każdym kroku czasowym.
- Oblicz stratę dla połączonego modelu aktor-krytyk.
- Obliczanie gradientów i aktualizacja parametrów sieci.
- Powtarzaj 1-4, aż zostanie osiągnięte kryterium sukcesu lub maksymalna liczba odcinków.
1. Zbieranie danych treningowych
Podobnie jak w przypadku uczenia nadzorowanego, aby trenować model aktor-krytyczny, musisz mieć dane szkoleniowe. Aby jednak zebrać takie dane, model musiałby zostać „uruchomiony” w środowisku.
Dane treningowe są zbierane dla każdego odcinka. Następnie w każdym kroku czasowym przebieg modelu będzie wykonywany na stanie środowiska w celu wygenerowania prawdopodobieństw działania i wartości krytycznej w oparciu o aktualną politykę sparametryzowaną przez wagi modelu.
Następne działanie będzie próbkowane z prawdopodobieństw działania wygenerowanych przez model, które następnie zostaną zastosowane w środowisku, powodując wygenerowanie następnego stanu i nagrody.
Proces ten jest zaimplementowany w funkcji run_episode , która wykorzystuje operacje TensorFlow, dzięki czemu można go później skompilować w wykres TensorFlow w celu szybszego trenowania. Zauważ, że tf.TensorArray s były używane do obsługi iteracji Tensor na tablicach o zmiennej długości.
# Wrap OpenAI Gym's `env.step` call as an operation in a TensorFlow function.
# This would allow it to be included in a callable TensorFlow graph.
def env_step(action: np.ndarray) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
"""Returns state, reward and done flag given an action."""
state, reward, done, _ = env.step(action)
return (state.astype(np.float32),
np.array(reward, np.int32),
np.array(done, np.int32))
def tf_env_step(action: tf.Tensor) -> List[tf.Tensor]:
return tf.numpy_function(env_step, [action],
[tf.float32, tf.int32, tf.int32])
def run_episode(
initial_state: tf.Tensor,
model: tf.keras.Model,
max_steps: int) -> Tuple[tf.Tensor, tf.Tensor, tf.Tensor]:
"""Runs a single episode to collect training data."""
action_probs = tf.TensorArray(dtype=tf.float32, size=0, dynamic_size=True)
values = tf.TensorArray(dtype=tf.float32, size=0, dynamic_size=True)
rewards = tf.TensorArray(dtype=tf.int32, size=0, dynamic_size=True)
initial_state_shape = initial_state.shape
state = initial_state
for t in tf.range(max_steps):
# Convert state into a batched tensor (batch size = 1)
state = tf.expand_dims(state, 0)
# Run the model and to get action probabilities and critic value
action_logits_t, value = model(state)
# Sample next action from the action probability distribution
action = tf.random.categorical(action_logits_t, 1)[0, 0]
action_probs_t = tf.nn.softmax(action_logits_t)
# Store critic values
values = values.write(t, tf.squeeze(value))
# Store log probability of the action chosen
action_probs = action_probs.write(t, action_probs_t[0, action])
# Apply action to the environment to get next state and reward
state, reward, done = tf_env_step(action)
state.set_shape(initial_state_shape)
# Store reward
rewards = rewards.write(t, reward)
if tf.cast(done, tf.bool):
break
action_probs = action_probs.stack()
values = values.stack()
rewards = rewards.stack()
return action_probs, values, rewards
2. Obliczanie oczekiwanych zwrotów
Sekwencja nagród dla każdego kroku \(t\), \(\{r_{t}\}^{T}_{t=1}\) zebrana podczas jednego odcinka jest konwertowana na sekwencję oczekiwanych zwrotów \(\{G_{t}\}^{T}_{t=1}\) , w której suma nagród jest brana z bieżącego kroku czasowego \(t\) do \(T\) , a każda nagroda jest mnożona przez wykładniczo malejący współczynnik dyskontowy \(\gamma\):
\[G_{t} = \sum^{T}_{t'=t} \gamma^{t'-t}r_{t'}\]
Ponieważ \(\gamma\in(0,1)\), nagrody dalej od bieżącego kroku czasowego mają mniejszą wagę.
Intuicyjnie oczekiwany zwrot oznacza po prostu, że nagrody teraz są lepsze niż nagrody później. W sensie matematycznym ma zapewnić zbieżność sumy nagród.
Aby ustabilizować szkolenie, wynikowa sekwencja zwrotów jest również standaryzowana (tj. ma zerową średnią i odchylenie standardowe jednostki).
def get_expected_return(
rewards: tf.Tensor,
gamma: float,
standardize: bool = True) -> tf.Tensor:
"""Compute expected returns per timestep."""
n = tf.shape(rewards)[0]
returns = tf.TensorArray(dtype=tf.float32, size=n)
# Start from the end of `rewards` and accumulate reward sums
# into the `returns` array
rewards = tf.cast(rewards[::-1], dtype=tf.float32)
discounted_sum = tf.constant(0.0)
discounted_sum_shape = discounted_sum.shape
for i in tf.range(n):
reward = rewards[i]
discounted_sum = reward + gamma * discounted_sum
discounted_sum.set_shape(discounted_sum_shape)
returns = returns.write(i, discounted_sum)
returns = returns.stack()[::-1]
if standardize:
returns = ((returns - tf.math.reduce_mean(returns)) /
(tf.math.reduce_std(returns) + eps))
return returns
3. Strata aktora-krytyka
Ponieważ używany jest hybrydowy model aktor-krytyczny, wybrana funkcja straty jest kombinacją strat aktora i krytyka dla treningu, jak pokazano poniżej:
\[L = L_{actor} + L_{critic}\]
Utrata aktora
Strata aktora jest oparta na gradientach polityki z krytykiem jako punktem odniesienia zależną od stanu i obliczana na podstawie szacunków dla pojedynczej próby (na odcinek).
\[L_{actor} = -\sum^{T}_{t=1} \log\pi_{\theta}(a_{t} | s_{t})[G(s_{t}, a_{t}) - V^{\pi}_{\theta}(s_{t})]\]
gdzie:
- \(T\): liczba kroków czasowych na odcinek, która może się różnić w każdym odcinku
- \(s_{t}\): stan w kroku czasowym \(t\)
- \(a_{t}\): wybrana akcja w kroku czasowym \(t\) podany stan \(s\)
- \(\pi_{\theta}\): jest polisą (aktorem) sparametryzowaną przez \(\theta\)
- \(V^{\pi}_{\theta}\): jest funkcją wartości (critic) również sparametryzowaną przez \(\theta\)
- \(G = G_{t}\): oczekiwany zwrot dla danego stanu, para akcji w kroku czasowym \(t\)
Do sumy dodaje się ujemny termin, ponieważ chodzi o maksymalizację prawdopodobieństwa działań przynoszących wyższe nagrody poprzez minimalizację łącznej straty.
Korzyść
Termin \(G - V\) w naszym sformułowaniu \(L_{actor}\) nazywany jest przewagą , która wskazuje, o ile lepsze działanie ma dany stan w porównaniu z działaniem losowym wybranym zgodnie z polityką \(\pi\) dla tego stanu.
Chociaż możliwe jest wykluczenie linii bazowej, może to skutkować dużą zmiennością podczas treningu. A fajną rzeczą w wyborze krytycznego \(V\) jako punktu odniesienia jest to, że wytrenowano go tak, aby był jak najbliżej \(G\), co prowadzi do mniejszej wariancji.
Ponadto bez krytyka algorytm próbowałby zwiększyć prawdopodobieństwa działań podejmowanych w danym stanie w oparciu o oczekiwany zwrot, co może nie mieć większego znaczenia, jeśli względne prawdopodobieństwa między działaniami pozostają takie same.
Załóżmy na przykład, że dwa działania dla danego stanu przyniosą taki sam oczekiwany zwrot. Bez krytyka algorytm próbowałby podnieść prawdopodobieństwo tych działań na podstawie celu \(J\). Z krytykiem może się okazać, że nie ma żadnej przewagi (\(G - V = 0\)), a więc nie ma korzyści ze zwiększenia prawdopodobieństw działań, a algorytm ustawiłby gradienty na zero.
Krytyczna strata
Trening \(V\) , aby był jak najbliżej \(G\) można ustawić jako problem regresji z następującą funkcją straty:
\[L_{critic} = L_{\delta}(G, V^{\pi}_{\theta})\]
gdzie \(L_{\delta}\) to strata Hubera , która jest mniej wrażliwa na wartości odstające w danych niż utrata kwadratu błędu.
huber_loss = tf.keras.losses.Huber(reduction=tf.keras.losses.Reduction.SUM)
def compute_loss(
action_probs: tf.Tensor,
values: tf.Tensor,
returns: tf.Tensor) -> tf.Tensor:
"""Computes the combined actor-critic loss."""
advantage = returns - values
action_log_probs = tf.math.log(action_probs)
actor_loss = -tf.math.reduce_sum(action_log_probs * advantage)
critic_loss = huber_loss(values, returns)
return actor_loss + critic_loss
4. Definiowanie etapu treningu do aktualizacji parametrów
Wszystkie powyższe kroki są połączone w krok treningowy, który jest uruchamiany w każdym odcinku. Wszystkie kroki prowadzące do funkcji utraty są wykonywane z kontekstem tf.GradientTape , aby umożliwić automatyczne różnicowanie.
W tym samouczku zastosowano optymalizator Adam do zastosowania gradientów do parametrów modelu.
Na tym etapie obliczana jest również suma niezdyskontowanych nagród, episode_reward . Ta wartość zostanie później wykorzystana do oceny, czy spełnione jest kryterium sukcesu.
Kontekst tf.function jest stosowany do funkcji train_step , dzięki czemu można ją skompilować w wywoływalny wykres TensorFlow, co może prowadzić do 10-krotnego przyspieszenia uczenia.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.01)
@tf.function
def train_step(
initial_state: tf.Tensor,
model: tf.keras.Model,
optimizer: tf.keras.optimizers.Optimizer,
gamma: float,
max_steps_per_episode: int) -> tf.Tensor:
"""Runs a model training step."""
with tf.GradientTape() as tape:
# Run the model for one episode to collect training data
action_probs, values, rewards = run_episode(
initial_state, model, max_steps_per_episode)
# Calculate expected returns
returns = get_expected_return(rewards, gamma)
# Convert training data to appropriate TF tensor shapes
action_probs, values, returns = [
tf.expand_dims(x, 1) for x in [action_probs, values, returns]]
# Calculating loss values to update our network
loss = compute_loss(action_probs, values, returns)
# Compute the gradients from the loss
grads = tape.gradient(loss, model.trainable_variables)
# Apply the gradients to the model's parameters
optimizer.apply_gradients(zip(grads, model.trainable_variables))
episode_reward = tf.math.reduce_sum(rewards)
return episode_reward
5. Uruchom pętlę treningową
Trening jest wykonywany poprzez uruchomienie etapu treningu, aż do osiągnięcia kryterium sukcesu lub maksymalnej liczby epizodów.
Bieżący zapis nagród za odcinki jest przechowywany w kolejce. Po osiągnięciu 100 prób najstarsza nagroda jest usuwana z lewego (ogonowego) końca kolejki, a najnowsza jest dodawana z przodu (z prawej). Bieżąca suma nagród jest również utrzymywana dla wydajności obliczeniowej.
W zależności od czasu pracy trening może zakończyć się w mniej niż minutę.
%%time
min_episodes_criterion = 100
max_episodes = 10000
max_steps_per_episode = 1000
# Cartpole-v0 is considered solved if average reward is >= 195 over 100
# consecutive trials
reward_threshold = 195
running_reward = 0
# Discount factor for future rewards
gamma = 0.99
# Keep last episodes reward
episodes_reward: collections.deque = collections.deque(maxlen=min_episodes_criterion)
with tqdm.trange(max_episodes) as t:
for i in t:
initial_state = tf.constant(env.reset(), dtype=tf.float32)
episode_reward = int(train_step(
initial_state, model, optimizer, gamma, max_steps_per_episode))
episodes_reward.append(episode_reward)
running_reward = statistics.mean(episodes_reward)
t.set_description(f'Episode {i}')
t.set_postfix(
episode_reward=episode_reward, running_reward=running_reward)
# Show average episode reward every 10 episodes
if i % 10 == 0:
pass # print(f'Episode {i}: average reward: {avg_reward}')
if running_reward > reward_threshold and i >= min_episodes_criterion:
break
print(f'\nSolved at episode {i}: average reward: {running_reward:.2f}!')
Episode 361: 4%|▎ | 361/10000 [01:13<32:33, 4.93it/s, episode_reward=182, running_reward=195] Solved at episode 361: average reward: 195.14! CPU times: user 2min 46s, sys: 35.4 s, total: 3min 21s Wall time: 1min 13s
Wyobrażanie sobie
Po szkoleniu dobrze byłoby zwizualizować, jak model zachowuje się w środowisku. Możesz uruchomić poniższe komórki, aby wygenerować animację GIF jednego uruchomienia odcinka modelu. Pamiętaj, że aby poprawnie renderować obrazy środowiska w Colab, OpenAI Gym wymaga zainstalowania dodatkowych pakietów.
# Render an episode and save as a GIF file
from IPython import display as ipythondisplay
from PIL import Image
from pyvirtualdisplay import Display
display = Display(visible=0, size=(400, 300))
display.start()
def render_episode(env: gym.Env, model: tf.keras.Model, max_steps: int):
screen = env.render(mode='rgb_array')
im = Image.fromarray(screen)
images = [im]
state = tf.constant(env.reset(), dtype=tf.float32)
for i in range(1, max_steps + 1):
state = tf.expand_dims(state, 0)
action_probs, _ = model(state)
action = np.argmax(np.squeeze(action_probs))
state, _, done, _ = env.step(action)
state = tf.constant(state, dtype=tf.float32)
# Render screen every 10 steps
if i % 10 == 0:
screen = env.render(mode='rgb_array')
images.append(Image.fromarray(screen))
if done:
break
return images
# Save GIF image
images = render_episode(env, model, max_steps_per_episode)
image_file = 'cartpole-v0.gif'
# loop=0: loop forever, duration=1: play each frame for 1ms
images[0].save(
image_file, save_all=True, append_images=images[1:], loop=0, duration=1)
import tensorflow_docs.vis.embed as embed
embed.embed_file(image_file)
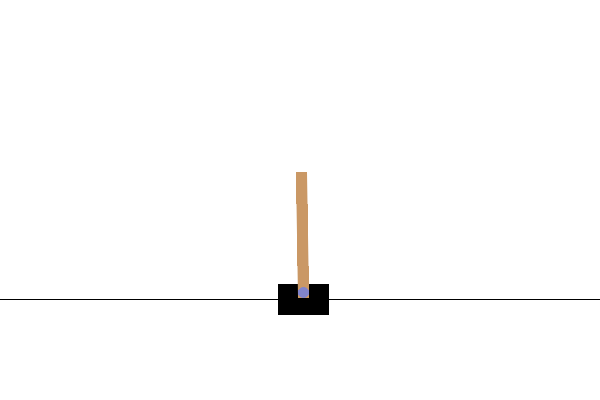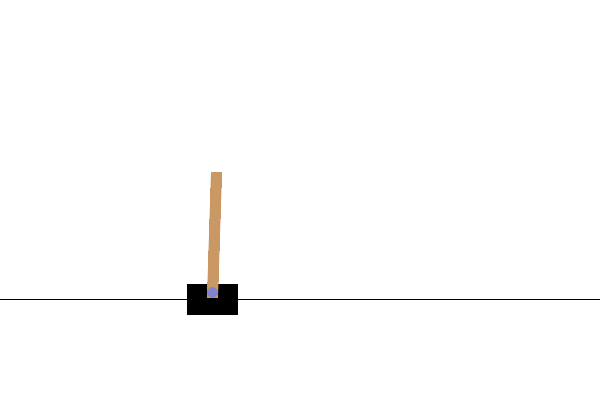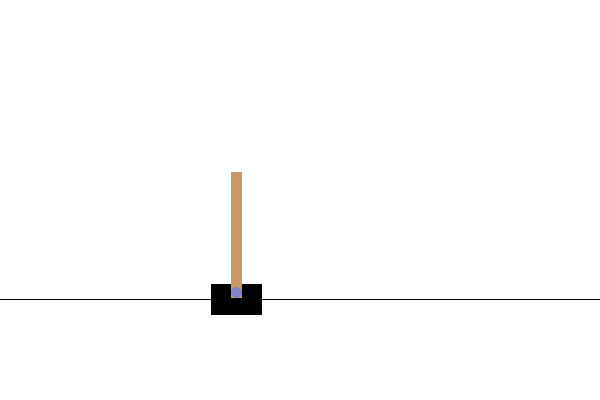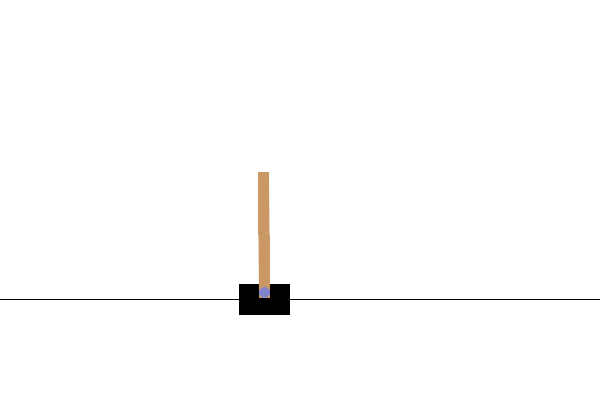
Następne kroki
Ten samouczek zademonstrował, jak zaimplementować metodę aktora-krytycznego za pomocą Tensorflow.
W następnym kroku możesz spróbować trenować model w innym środowisku w OpenAI Gym.
Aby uzyskać dodatkowe informacje dotyczące metod aktora krytycznego i problemu Cartpole-v0, możesz zapoznać się z następującymi zasobami:
- Metoda krytyka aktorskiego
- Wykład krytyka aktorskiego (CAL)
- Problem sterowania uczeniem się Cartpole [Barto, et al. 1983]
Aby uzyskać więcej przykładów uczenia się przez wzmacnianie w TensorFlow, możesz sprawdzić następujące zasoby:
