หน้านี้ได้รับการแปลโดย Cloud Translation API

ตัวเข้ารหัสอัตโนมัติแบบแปรผัน

ดูบน TensorFlow.org

ทำงานใน Google Colab

ดูแหล่งที่มาบน GitHub

ดาวน์โหลดโน๊ตบุ๊ค

สมุดบันทึกนี้สาธิตวิธีฝึก Variational Autoencoder (VAE) ( 1 , 2 ) ในชุดข้อมูล MNIST VAE เป็นความน่าจะเป็นที่ใช้กับตัวเข้ารหัสอัตโนมัติ ซึ่งเป็นโมเดลที่ใช้ข้อมูลอินพุตที่มีมิติสูงและบีบอัดให้มีขนาดเล็กลง ต่างจากตัวเข้ารหัสอัตโนมัติแบบดั้งเดิมซึ่งจับคู่อินพุตกับเวกเตอร์แฝง VAE จะจับคู่ข้อมูลที่ป้อนเข้าในพารามิเตอร์ของการแจกแจงความน่าจะเป็น เช่น ค่าเฉลี่ยและความแปรปรวนของค่าเกาส์เซียน วิธีการนี้จะสร้างพื้นที่แฝงที่มีโครงสร้างอย่างต่อเนื่องและต่อเนื่อง ซึ่งเป็นประโยชน์สำหรับการสร้างภาพ

CVAE พื้นที่แฝงของภาพ

ติดตั้ง

pip install tensorflow-probability

# to generate gifs
pip install imageio
pip install git+https://github.com/tensorflow/docs

from IPython import display

import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time

ตัวยึดตำแหน่ง36

โหลดชุดข้อมูล MNIST

ภาพ MNIST แต่ละภาพเดิมเป็นเวกเตอร์ของจำนวนเต็ม 784 จำนวน ซึ่งแต่ละภาพอยู่ระหว่าง 0-255 และแสดงถึงความเข้มของพิกเซล สร้างแบบจำลองแต่ละพิกเซลด้วยการกระจายแบบเบอร์นูลลีในแบบจำลองของเรา และทำไบนารีชุดข้อมูลแบบสแตติก

(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
11501568/11490434 [==============================] - 0s 0us/step

def preprocess_images(images):
  images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
  return np.where(images > .5, 1.0, 0.0).astype('float32')

train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)

train_size = 60000
batch_size = 32
test_size = 10000

ใช้ tf.data เพื่อแบทช์และสับเปลี่ยนข้อมูล

train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
                 .shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
                .shuffle(test_size).batch(batch_size))

กำหนดเครือข่ายตัวเข้ารหัสและตัวถอดรหัสด้วย tf.keras.Sequential

ในตัวอย่าง VAE นี้ ให้ใช้ ConvNet ขนาดเล็กสองตัวสำหรับเครือข่ายตัวเข้ารหัสและตัวถอดรหัส ในวรรณคดี เครือข่ายเหล่านี้ยังถูกอ้างถึงเป็นการอนุมาน/การรับรู้ และแบบจำลองกำเนิดตามลำดับ ใช้ tf.keras.Sequential เพื่อทำให้การใช้งานง่ายขึ้น ให้ \(x\) และ \(z\) แทนค่าการสังเกตและตัวแปรแฝงตามลำดับในคำอธิบายต่อไปนี้

เครือข่ายตัวเข้ารหัส

สิ่งนี้กำหนดการกระจายหลังโดยประมาณ \(q(z|x)\)ซึ่งใช้เป็นอินพุตการสังเกตและเอาต์พุตชุดของพารามิเตอร์สำหรับการระบุการกระจายแบบมีเงื่อนไขของการแสดงแฝง \(z\)ในตัวอย่างนี้ เพียงแค่จำลองการแจกแจงเป็นเกาส์เซียนในแนวทแยง และเครือข่ายจะแสดงค่าพารามิเตอร์เฉลี่ยและความแปรปรวนของบันทึกของเกาส์เซียนแยกตัวประกอบ ผลต่างบันทึกเอาต์พุตแทนความแปรปรวนโดยตรงเพื่อความเสถียรเชิงตัวเลข

ตัวถอดรหัสเครือข่าย

สิ่งนี้กำหนดการกระจายแบบมีเงื่อนไขของการสังเกต \(p(x|z)\)ซึ่งใช้ตัวอย่างแฝง \(z\) เป็นอินพุตและเอาต์พุตพารามิเตอร์สำหรับการกระจายแบบมีเงื่อนไขของการสังเกต จำลองการกระจายแฝงก่อน \(p(z)\) เป็นหน่วยเกาส์เซียน

เคล็ดลับการปรับพารามิเตอร์ใหม่

ในการสร้างตัวอย่าง \(z\) สำหรับตัวถอดรหัสระหว่างการฝึก คุณสามารถสุ่มตัวอย่างจากการกระจายแฝงที่กำหนดโดยพารามิเตอร์ที่ส่งออกโดยตัวเข้ารหัส โดยให้สังเกตอินพุต \(x\)อย่างไรก็ตาม การดำเนินการสุ่มตัวอย่างนี้สร้างปัญหาคอขวดเนื่องจากการแพร่กระจายย้อนกลับไม่สามารถไหลผ่านโหนดแบบสุ่มได้

ในการแก้ไขปัญหานี้ ให้ใช้เคล็ดลับการปรับพารามิเตอร์ใหม่ ในตัวอย่างของเรา คุณประมาณ \(z\) โดยใช้พารามิเตอร์ตัวถอดรหัสและพารามิเตอร์อื่น \(\epsilon\) ดังนี้:

\[z = \mu + \sigma \odot \epsilon\]

โดยที่ \(\mu\) และ \(\sigma\) แสดงถึงค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการแจกแจงแบบเกาส์เซียนตามลำดับ สามารถได้มาจากเอาต์พุตตัวถอดรหัส \(\epsilon\) ถือได้ว่าเป็นสัญญาณรบกวนแบบสุ่มที่ใช้เพื่อรักษาความสุ่มของ \(z\)สร้าง \(\epsilon\) จากการแจกแจงแบบปกติมาตรฐาน

ตัวแปรแฝง \(z\) ถูกสร้างขึ้นโดยฟังก์ชันของ \(\mu\), \(\sigma\) และ \(\epsilon\)ซึ่งจะทำให้โมเดลสามารถ backpropagate gradient ใน encoder ผ่าน \(\mu\) และ \(\sigma\) ตามลำดับ ในขณะที่ยังคงความสุ่มผ่าน \(\epsilon\).

สถาปัตยกรรมเครือข่าย

สำหรับเครือข่ายตัวเข้ารหัส ให้ใช้เลเยอร์แบบ Convolutional สองชั้น ตามด้วยเลเยอร์ที่เชื่อมต่ออย่างสมบูรณ์ ในเครือข่ายตัวถอดรหัส จำลองสถาปัตยกรรมนี้โดยใช้เลเยอร์ที่เชื่อมต่ออย่างสมบูรณ์แล้วตามด้วยเลเยอร์ทรานสโพสการบิดสามชั้น (หรือที่เรียกว่าเลเยอร์ deconvolutional ในบางบริบท) หมายเหตุ เป็นเรื่องปกติที่จะหลีกเลี่ยงการใช้แบทช์นอร์มัลไลเซชันเมื่อฝึก VAE เนื่องจากสุ่มเพิ่มเติมเนื่องจากการใช้มินิแบตช์อาจทำให้ความไม่เสถียรรุนแรงขึ้นนอกเหนือจากการสุ่มตัวอย่างจากการสุ่มตัวอย่าง

class CVAE(tf.keras.Model):
  """Convolutional variational autoencoder."""

  def __init__(self, latent_dim):
    super(CVAE, self).__init__()
    self.latent_dim = latent_dim
    self.encoder = tf.keras.Sequential(
        [
            tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
            tf.keras.layers.Conv2D(
                filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
            tf.keras.layers.Conv2D(
                filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
            tf.keras.layers.Flatten(),
            # No activation
            tf.keras.layers.Dense(latent_dim + latent_dim),
        ]
    )

    self.decoder = tf.keras.Sequential(
        [
            tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
            tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
            tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
            tf.keras.layers.Conv2DTranspose(
                filters=64, kernel_size=3, strides=2, padding='same',
                activation='relu'),
            tf.keras.layers.Conv2DTranspose(
                filters=32, kernel_size=3, strides=2, padding='same',
                activation='relu'),
            # No activation
            tf.keras.layers.Conv2DTranspose(
                filters=1, kernel_size=3, strides=1, padding='same'),
        ]
    )

  @tf.function
  def sample(self, eps=None):
    if eps is None:
      eps = tf.random.normal(shape=(100, self.latent_dim))
    return self.decode(eps, apply_sigmoid=True)

  def encode(self, x):
    mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
    return mean, logvar

  def reparameterize(self, mean, logvar):
    eps = tf.random.normal(shape=mean.shape)
    return eps * tf.exp(logvar * .5) + mean

  def decode(self, z, apply_sigmoid=False):
    logits = self.decoder(z)
    if apply_sigmoid:
      probs = tf.sigmoid(logits)
      return probs
    return logits

กำหนดฟังก์ชันการสูญเสียและตัวเพิ่มประสิทธิภาพ

VAEs ฝึกฝนโดยเพิ่มขอบเขตล่างของหลักฐาน (ELBO) ให้มากที่สุดบนความเป็นไปได้ของบันทึกระยะขอบ:

\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]

ในทางปฏิบัติ เพิ่มประสิทธิภาพการประมาณการมอนติคาร์โลตัวอย่างเดียวของความคาดหวังนี้:

\[\log p(x| z) + \log p(z) - \log q(z|x),\]

โดยที่ \(z\) ถูกสุ่มตัวอย่างจาก \(q(z|x)\)

optimizer = tf.keras.optimizers.Adam(1e-4)


def log_normal_pdf(sample, mean, logvar, raxis=1):
  log2pi = tf.math.log(2. * np.pi)
  return tf.reduce_sum(
      -.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
      axis=raxis)


def compute_loss(model, x):
  mean, logvar = model.encode(x)
  z = model.reparameterize(mean, logvar)
  x_logit = model.decode(z)
  cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
  logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
  logpz = log_normal_pdf(z, 0., 0.)
  logqz_x = log_normal_pdf(z, mean, logvar)
  return -tf.reduce_mean(logpx_z + logpz - logqz_x)


@tf.function
def train_step(model, x, optimizer):
  """Executes one training step and returns the loss.

  This function computes the loss and gradients, and uses the latter to
  update the model's parameters.
  """
  with tf.GradientTape() as tape:
    loss = compute_loss(model, x)
  gradients = tape.gradient(loss, model.trainable_variables)
  optimizer.apply_gradients(zip(gradients, model.trainable_variables))

การฝึกอบรม

เริ่มต้นด้วยการวนซ้ำชุดข้อมูล
ในระหว่างการทำซ้ำแต่ละครั้ง ให้ส่งรูปภาพไปยังตัวเข้ารหัสเพื่อรับชุดของค่าพารามิเตอร์เฉลี่ยและค่าความแปรปรวนของบันทึกของ \(q(z|x)\)หลังโดยประมาณ
จากนั้นใช้ เคล็ดลับ การปรับพารามิเตอร์ใหม่กับตัวอย่างจาก \(q(z|x)\)
สุดท้าย ส่งตัวอย่างที่ปรับพารามิเตอร์ใหม่ไปยังตัวถอดรหัสเพื่อรับบันทึกของการแจกแจงกำเนิด \(p(x|z)\)
หมายเหตุ: เนื่องจากคุณใช้ชุดข้อมูลที่โหลดโดย keras ที่มีจุดข้อมูล 60k ในชุดการฝึกและจุดข้อมูล 10k ในชุดทดสอบ ELBO ที่เป็นผลลัพธ์ของเราในชุดการทดสอบจึงสูงกว่าผลลัพธ์ที่รายงานในเอกสารประกอบเล็กน้อยซึ่งใช้ไดนามิกไบนารีของ MNIST ของ Larochelle

กำลังสร้างภาพ

หลังจากฝึกเสร็จก็ถึงเวลาสร้างภาพบางส่วน
เริ่มต้นด้วยการสุ่มตัวอย่างชุดของเวกเตอร์แฝงจากหน่วย Gaussian ก่อนการแจกแจง \(p(z)\)
จากนั้นเครื่องกำเนิดจะแปลงตัวอย่างแฝง \(z\) เป็นบันทึกของการสังเกต ให้การกระจาย \(p(x|z)\)
ที่นี่ พล็อตความน่าจะเป็นของการแจกแจงเบอร์นูลลี

epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16

# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
    shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)

def generate_and_save_images(model, epoch, test_sample):
  mean, logvar = model.encode(test_sample)
  z = model.reparameterize(mean, logvar)
  predictions = model.sample(z)
  fig = plt.figure(figsize=(4, 4))

  for i in range(predictions.shape[0]):
    plt.subplot(4, 4, i + 1)
    plt.imshow(predictions[i, :, :, 0], cmap='gray')
    plt.axis('off')

  # tight_layout minimizes the overlap between 2 sub-plots
  plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
  plt.show()

# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
  test_sample = test_batch[0:num_examples_to_generate, :, :, :]

generate_and_save_images(model, 0, test_sample)

for epoch in range(1, epochs + 1):
  start_time = time.time()
  for train_x in train_dataset:
    train_step(model, train_x, optimizer)
  end_time = time.time()

  loss = tf.keras.metrics.Mean()
  for test_x in test_dataset:
    loss(compute_loss(model, test_x))
  elbo = -loss.result()
  display.clear_output(wait=False)
  print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
        .format(epoch, elbo, end_time - start_time))
  generate_and_save_images(model, epoch, test_sample)

Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

png

แสดงภาพที่สร้างขึ้นจากยุคการฝึกครั้งสุดท้าย

def display_image(epoch_no):
  return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))

plt.imshow(display_image(epoch))
plt.axis('off')  # Display images

(-0.5, 287.5, 287.5, -0.5)

png

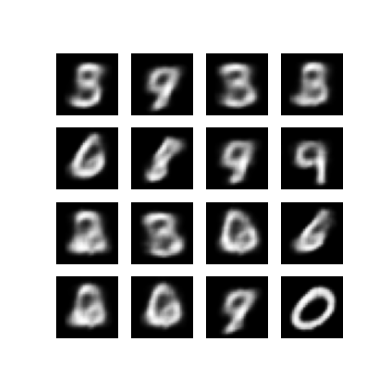
แสดง GIF แบบเคลื่อนไหวของภาพที่บันทึกไว้ทั้งหมด

anim_file = 'cvae.gif'

with imageio.get_writer(anim_file, mode='I') as writer:
  filenames = glob.glob('image*.png')
  filenames = sorted(filenames)
  for filename in filenames:
    image = imageio.imread(filename)
    writer.append_data(image)
  image = imageio.imread(filename)
  writer.append_data(image)

import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

ตัวยึดตำแหน่ง53

กิ๊ฟ

แสดงตัวเลข 2 มิติจากช่องว่างแฝง

การรันโค้ดด้านล่างจะแสดงการแจกแจงแบบต่อเนื่องของคลาสตัวเลขต่างๆ โดยที่แต่ละหลักจะแปรสภาพเป็นตัวเลขอื่นในพื้นที่แฝง 2D ใช้ ความน่าจะเป็นของ TensorFlow เพื่อสร้างการแจกแจงแบบปกติมาตรฐานสำหรับพื้นที่แฝง

def plot_latent_images(model, n, digit_size=28):
  """Plots n x n digit images decoded from the latent space."""

  norm = tfp.distributions.Normal(0, 1)
  grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
  grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
  image_width = digit_size*n
  image_height = image_width
  image = np.zeros((image_height, image_width))

  for i, yi in enumerate(grid_x):
    for j, xi in enumerate(grid_y):
      z = np.array([[xi, yi]])
      x_decoded = model.sample(z)
      digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
      image[i * digit_size: (i + 1) * digit_size,
            j * digit_size: (j + 1) * digit_size] = digit.numpy()

  plt.figure(figsize=(10, 10))
  plt.imshow(image, cmap='Greys_r')
  plt.axis('Off')
  plt.show()

plot_latent_images(model, 20)

ตัวยึดตำแหน่ง55

png

ขั้นตอนถัดไป

บทช่วยสอนนี้ได้สาธิตวิธีการใช้ตัวเข้ารหัสอัตโนมัติแบบแปรผันโดยใช้ TensorFlow

ในขั้นตอนต่อไป คุณสามารถลองปรับปรุงผลลัพธ์ของแบบจำลองโดยเพิ่มขนาดเครือข่าย ตัวอย่างเช่น คุณสามารถลองตั้งค่าพารามิเตอร์ filter สำหรับแต่ละเลเยอร์ Conv2D และ Conv2DTranspose เป็น 512 โปรดทราบว่าในการสร้างพล็อตภาพ 2D สุดท้าย คุณจะต้องคง latent_dim เป็น 2 นอกจากนี้ เวลาฝึกจะเพิ่มขึ้น เมื่อขนาดเครือข่ายเพิ่มขึ้น

คุณยังสามารถลองใช้ VAE โดยใช้ชุดข้อมูลอื่น เช่น CIFAR-10

VAE สามารถนำไปใช้ได้หลายรูปแบบและมีความซับซ้อนต่างกันไป คุณสามารถค้นหาการใช้งานเพิ่มเติมได้ในแหล่งต่อไปนี้:

หากคุณต้องการเรียนรู้เพิ่มเติมเกี่ยวกับรายละเอียดของ VAE โปรดดูที่ An Introduction to Variational Autoencoders