 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запустить в Google Colab Запустить в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
В этой записной книжке показано, как обучить вариационный автоэнкодер (VAE) ( 1 , 2 ) на наборе данных MNIST. VAE — это вероятностный подход к автоэнкодеру, модель, которая берет многомерные входные данные и сжимает их в меньшее представление. В отличие от традиционного автоэнкодера, который отображает входные данные в скрытый вектор, VAE отображает входные данные в параметры распределения вероятностей, такие как среднее значение и дисперсия гауссова. Этот подход создает непрерывное структурированное скрытое пространство, которое полезно для создания изображений.

Настраивать
pip install tensorflow-probability# to generate gifspip install imageiopip install git+https://github.com/tensorflow/docs
from IPython import display
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time
Загрузите набор данных MNIST
Каждое изображение MNIST изначально представляет собой вектор из 784 целых чисел, каждое из которых находится в диапазоне от 0 до 255 и представляет интенсивность пикселя. Смоделируйте каждый пиксель с помощью распределения Бернулли в нашей модели и статически бинаризируйте набор данных.
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
def preprocess_images(images):
images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
return np.where(images > .5, 1.0, 0.0).astype('float32')
train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)
train_size = 60000
batch_size = 32
test_size = 10000
Используйте tf.data для группирования и перемешивания данных
train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
.shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
.shuffle(test_size).batch(batch_size))
Определите сети кодировщика и декодера с помощью tf.keras.Sequential
В этом примере VAE используйте две небольшие ConvNet для сетей кодировщика и декодера. В литературе эти сети также называются моделями вывода/распознавания и генеративными моделями соответственно. Используйте tf.keras.Sequential для упрощения реализации. Пусть \(x\) и \(z\) обозначают наблюдение и скрытую переменную соответственно в следующих описаниях.
Сеть кодировщика
Это определяет приблизительное апостериорное распределение \(q(z|x)\), которое принимает в качестве входных данных наблюдение и выводит набор параметров для определения условного распределения скрытого представления \(z\). В этом примере просто смоделируйте распределение как диагональный гауссов, и сеть выводит параметры среднего значения и логарифмической дисперсии факторизованного гауссиана. Выведите логарифмическую дисперсию вместо дисперсии напрямую для численной стабильности.
Сеть декодера
Это определяет условное распределение наблюдения \(p(x|z)\), которое принимает скрытую выборку \(z\) в качестве входных данных и выводит параметры для условного распределения наблюдения. Смоделируйте скрытое распределение до \(p(z)\) как единицу Гаусса.
Трюк с репараметризацией
Чтобы сгенерировать выборку \(z\) для декодера во время обучения, вы можете выбрать из скрытого распределения, определяемого параметрами, выдаваемыми кодировщиком, с учетом входного наблюдения \(x\). Однако эта операция выборки создает узкое место, поскольку обратное распространение не может проходить через случайный узел.
Чтобы решить эту проблему, используйте трюк с репараметризацией. В нашем примере вы аппроксимируете \(z\) с помощью параметров декодера и другого параметра \(\epsilon\) следующим образом:
\[z = \mu + \sigma \odot \epsilon\]
где \(\mu\) и \(\sigma\) представляют собой среднее значение и стандартное отклонение распределения Гаусса соответственно. Они могут быть получены из вывода декодера. \(\epsilon\) можно рассматривать как случайный шум, используемый для поддержания стохастичности \(z\). Сгенерируйте \(\epsilon\) из стандартного нормального распределения.
Скрытая переменная \(z\) теперь генерируется функцией \(\mu\), \(\sigma\) и \(\epsilon\), что позволит модели распространять обратно градиенты в кодировщике через \(\mu\) и \(\sigma\) соответственно, сохраняя при этом стохастичность через \(\epsilon\).
Сетевая архитектура
Для сети кодировщика используйте два сверточных слоя, за которыми следует полносвязный слой. В сети декодера зеркально отразите эту архитектуру, используя полносвязный уровень, за которым следуют три слоя транспонирования свертки (также называемые слоями деконволюции в некоторых контекстах). Обратите внимание, что обычной практикой является избегание использования пакетной нормализации при обучении VAE, поскольку дополнительная стохастичность из-за использования мини-пакетов может усугубить нестабильность поверх стохастичности от выборки.
class CVAE(tf.keras.Model):
"""Convolutional variational autoencoder."""
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=2, padding='same',
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=2, padding='same',
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=1, padding='same'),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
Определите функцию потерь и оптимизатор
VAE тренируются, максимизируя нижнюю границу доказательств (ELBO) предельного логарифмического правдоподобия:
\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]
На практике оптимизируйте одновыборочную оценку Монте-Карло этого ожидания:
\[\log p(x| z) + \log p(z) - \log q(z|x),\]
где \(z\) выбирается из \(q(z|x)\).
optimizer = tf.keras.optimizers.Adam(1e-4)
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
def compute_loss(model, x):
mean, logvar = model.encode(x)
z = model.reparameterize(mean, logvar)
x_logit = model.decode(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
@tf.function
def train_step(model, x, optimizer):
"""Executes one training step and returns the loss.
This function computes the loss and gradients, and uses the latter to
update the model's parameters.
"""
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
Обучение
- Начните с повторения набора данных
- Во время каждой итерации передайте изображение кодировщику, чтобы получить набор параметров среднего значения и логарифмической дисперсии приблизительного апостериорного \(q(z|x)\).
- затем примените прием репараметризации к образцу из \(q(z|x)\)
- Наконец, передайте репараметризованные образцы в декодер, чтобы получить логиты генеративного распределения \(p(x|z)\).
- Примечание. Поскольку вы используете набор данных, загруженный keras, с 60 000 точек данных в обучающем наборе и 10 000 точек данных в тестовом наборе, наш результирующий показатель ELBO в тестовом наборе немного выше, чем сообщаемые результаты в литературе, в которых используется динамическая бинаризация MNIST Ларошеля.
Генерация изображений
- После обучения пришло время сгенерировать несколько изображений
- Начните с выборки набора скрытых векторов из единичного гауссовского априорного распределения \(p(z)\)
- Затем генератор преобразует скрытую выборку \(z\) в логиты наблюдения, давая распределение \(p(x|z)\)
- Здесь постройте вероятности распределений Бернулли.
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)
def generate_and_save_images(model, epoch, test_sample):
mean, logvar = model.encode(test_sample)
z = model.reparameterize(mean, logvar)
predictions = model.sample(z)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# tight_layout minimizes the overlap between 2 sub-plots
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
test_sample = test_batch[0:num_examples_to_generate, :, :, :]
generate_and_save_images(model, 0, test_sample)
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
train_step(model, train_x, optimizer)
end_time = time.time()
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
display.clear_output(wait=False)
print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
.format(epoch, elbo, end_time - start_time))
generate_and_save_images(model, epoch, test_sample)
Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

Отображение сгенерированного изображения из последней эпохи обучения
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
plt.imshow(display_image(epoch))
plt.axis('off') # Display images
(-0.5, 287.5, 287.5, -0.5)
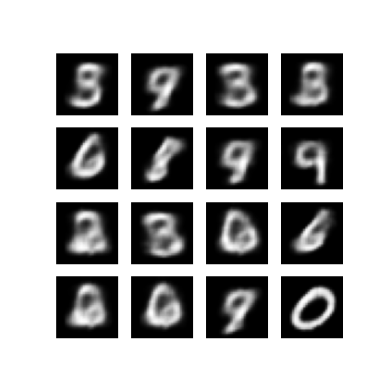
Показать анимированный GIF всех сохраненных изображений
anim_file = 'cvae.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

Отображение двумерного множества цифр из скрытого пространства
Запуск приведенного ниже кода покажет непрерывное распределение различных классов цифр, при этом каждая цифра превращается в другую в скрытом двумерном пространстве. Используйте вероятность TensorFlow , чтобы сгенерировать стандартное нормальное распределение для скрытого пространства.
def plot_latent_images(model, n, digit_size=28):
"""Plots n x n digit images decoded from the latent space."""
norm = tfp.distributions.Normal(0, 1)
grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
image_width = digit_size*n
image_height = image_width
image = np.zeros((image_height, image_width))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z = np.array([[xi, yi]])
x_decoded = model.sample(z)
digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
image[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit.numpy()
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='Greys_r')
plt.axis('Off')
plt.show()
plot_latent_images(model, 20)

Следующие шаги
В этом руководстве показано, как реализовать сверточный вариационный автоэнкодер с использованием TensorFlow.
В качестве следующего шага вы можете попытаться улучшить выходные данные модели, увеличив размер сети. Например, вы можете попробовать установить параметры filter для каждого из Conv2D и Conv2DTranspose на 512. Обратите внимание, что для создания окончательного графика скрытого 2D-изображения вам нужно оставить latent_dim 2. Кроме того, время обучения увеличится. по мере увеличения размера сети.
Вы также можете попробовать реализовать VAE, используя другой набор данных, например CIFAR-10.
VAE могут быть реализованы в нескольких различных стилях и различной сложности. Вы можете найти дополнительные реализации в следующих источниках:
- Вариационный автоэнкодер (keras.io)
- Пример VAE из руководства «Написание пользовательских слоев и моделей» (tensorflow.org)
- Вероятностные слои TFP: вариационный автоматический кодировщик
Если вы хотите узнать больше о деталях VAE, обратитесь к An Introduction to Variational Autoencoders .
