 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
W tym notatniku pokazano, jak wytrenować autokoder wariacyjny (VAE) ( 1 , 2 ) w zestawie danych MNIST. VAE to probabilistyczne podejście do autoenkodera, modelu, który pobiera dane wejściowe o dużych wymiarach i kompresuje je do mniejszej reprezentacji. W przeciwieństwie do tradycyjnego autoenkodera, który mapuje dane wejściowe na ukryty wektor, VAE mapuje dane wejściowe na parametry rozkładu prawdopodobieństwa, takie jak średnia i wariancja Gaussa. Takie podejście tworzy ciągłą, ustrukturyzowaną przestrzeń utajoną, która jest przydatna do generowania obrazu.

Ustawiać
pip install tensorflow-probability# to generate gifspip install imageiopip install git+https://github.com/tensorflow/docs
from IPython import display
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time
Załaduj zbiór danych MNIST
Każdy obraz MNIST jest oryginalnie wektorem składającym się z 784 liczb całkowitych, z których każda zawiera się w przedziale od 0 do 255 i reprezentuje intensywność piksela. Modeluj każdy piksel z rozkładem Bernoulliego w naszym modelu i statycznie zbinarizuj zestaw danych.
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
def preprocess_images(images):
images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
return np.where(images > .5, 1.0, 0.0).astype('float32')
train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)
train_size = 60000
batch_size = 32
test_size = 10000
Użyj tf.data do grupowania i tasowania danych
train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
.shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
.shuffle(test_size).batch(batch_size))
Zdefiniuj sieci kodera i dekodera za pomocą tf.keras.Sequential
W tym przykładzie VAE użyj dwóch małych sieci ConvNet dla sieci kodera i dekodera. W literaturze sieci te są również określane odpowiednio jako modele wnioskowania/rozpoznawania i modele generatywne. Użyj tf.keras.Sequential , aby uprościć implementację. Niech \(x\) i \(z\) oznaczają odpowiednio zmienną obserwacyjną i ukrytą w poniższych opisach.
Sieć enkoderów
Definiuje to przybliżony rozkład a posteriori \(q(z|x)\), który przyjmuje jako dane wejściowe obserwację i generuje zestaw parametrów do określenia rozkładu warunkowego ukrytej reprezentacji \(z\). W tym przykładzie po prostu wymodeluj rozkład jako diagonalny gaussowski, a sieć wygeneruje parametry średniej i logarytmicznej wariancji faktoryzowanego gaussowskiego. Wyprowadź wariancję logarytmiczną zamiast bezpośrednio wariancji dla stabilności numerycznej.
Sieć dekodera
Definiuje to rozkład warunkowy obserwacji \(p(x|z)\), który pobiera utajoną próbkę \(z\) jako dane wejściowe i wyprowadza parametry dla warunkowego rozkładu obserwacji. Modeluj utajony rozkład przed \(p(z)\) jako jednostkę Gaussa.
Sztuczka reparametryzacji
Aby wygenerować próbkę \(z\) dla dekodera podczas uczenia, można próbkować z ukrytego rozkładu zdefiniowanego przez parametry wyprowadzane przez koder, biorąc pod uwagę obserwację wejściową \(x\). Jednak ta operacja próbkowania tworzy wąskie gardło, ponieważ propagacja wsteczna nie może przepływać przez losowy węzeł.
Aby rozwiązać ten problem, użyj sztuczki reparametryzacji. W naszym przykładzie przybliżasz \(z\) za pomocą parametrów dekodera i innego parametru \(\epsilon\) w następujący sposób:
\[z = \mu + \sigma \odot \epsilon\]
gdzie \(\mu\) i \(\sigma\) reprezentują odpowiednio średnią i odchylenie standardowe rozkładu Gaussa. Mogą pochodzić z danych wyjściowych dekodera. \(\epsilon\) można traktować jako losowy szum używany do zachowania stochastyczności \(z\). Wygeneruj \(\epsilon\) ze standardowego rozkładu normalnego.
Utajona zmienna \(z\) jest teraz generowana przez funkcję \(\mu\), \(\sigma\) i \(\epsilon\), co umożliwiłoby modelowi propagację wsteczną gradientów w koderze odpowiednio przez \(\mu\) i \(\sigma\) przy zachowaniu stochastyczności poprzez \(\epsilon\).
Architektura sieci
W przypadku sieci kodera użyj dwóch warstw splotowych, po których następuje warstwa w pełni połączona. W sieci dekodera odwzoruj tę architekturę, używając w pełni połączonej warstwy, po której następują trzy warstwy transponujące splot (inaczej warstwy dekonwolucyjne w niektórych kontekstach). Należy zauważyć, że powszechną praktyką jest unikanie stosowania normalizacji wsadowej podczas uczenia VAE, ponieważ dodatkowa stochastyczność wynikająca z używania minipartii może pogorszyć niestabilność poza stochastycznością wynikającą z próbkowania.
class CVAE(tf.keras.Model):
"""Convolutional variational autoencoder."""
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=2, padding='same',
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=2, padding='same',
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=1, padding='same'),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
Zdefiniuj funkcję straty i optymalizator
VAE trenują poprzez maksymalizację dolnej granicy dowodu (ELBO) na marginalnym logarytmicznym prawdopodobieństwie:
\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]
W praktyce zoptymalizuj jednopróbkowe oszacowanie Monte Carlo tego oczekiwania:
\[\log p(x| z) + \log p(z) - \log q(z|x),\]
gdzie \(z\) jest próbkowany z \(q(z|x)\).
optimizer = tf.keras.optimizers.Adam(1e-4)
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
def compute_loss(model, x):
mean, logvar = model.encode(x)
z = model.reparameterize(mean, logvar)
x_logit = model.decode(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
@tf.function
def train_step(model, x, optimizer):
"""Executes one training step and returns the loss.
This function computes the loss and gradients, and uses the latter to
update the model's parameters.
"""
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
Trening
- Zacznij od iteracji po zbiorze danych
- Podczas każdej iteracji przekaż obraz do kodera, aby uzyskać zestaw parametrów średniej i logarytmicznej wariancji przybliżonego a posteriori \(q(z|x)\)
- następnie zastosuj sztuczkę reparametryzacji do próbki z \(q(z|x)\)
- Na koniec przekaż ponownie sparametryzowane próbki do dekodera w celu uzyskania logitów rozkładu generatywnego \(p(x|z)\)
- Uwaga: Ponieważ używasz zestawu danych załadowanego przez Keras z 60 000 punktów danych w zestawie uczącym i 10 000 punktów danych w zestawie testowym, nasze wynikowe ELBO w zestawie testowym jest nieco wyższe niż wyniki podane w literaturze, która wykorzystuje dynamiczną binaryzację MNIST Larochelle.
Generowanie obrazów
- Po treningu nadszedł czas na wygenerowanie kilku obrazów
- Zacznij od pobrania zbioru ukrytych wektorów z jednostki przed rozkładem Gaussa \(p(z)\)
- Generator następnie przekształci utajoną próbkę \(z\) na logity obserwacji, dając rozkład \(p(x|z)\)
- Tutaj wykreśl prawdopodobieństwa rozkładów Bernoulliego
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)
def generate_and_save_images(model, epoch, test_sample):
mean, logvar = model.encode(test_sample)
z = model.reparameterize(mean, logvar)
predictions = model.sample(z)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# tight_layout minimizes the overlap between 2 sub-plots
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
test_sample = test_batch[0:num_examples_to_generate, :, :, :]
generate_and_save_images(model, 0, test_sample)
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
train_step(model, train_x, optimizer)
end_time = time.time()
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
display.clear_output(wait=False)
print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
.format(epoch, elbo, end_time - start_time))
generate_and_save_images(model, epoch, test_sample)
Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

Wyświetl wygenerowany obraz z ostatniej epoki treningowej
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
plt.imshow(display_image(epoch))
plt.axis('off') # Display images
(-0.5, 287.5, 287.5, -0.5)
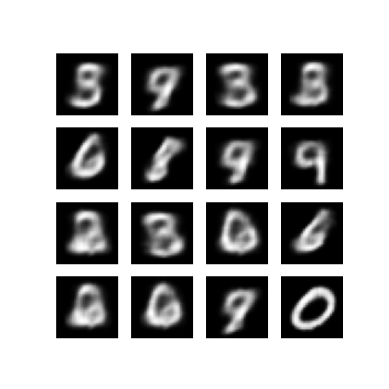
Wyświetl animowany GIF wszystkich zapisanych obrazów
anim_file = 'cvae.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

Wyświetl dwuwymiarowy rozmaitość cyfr z ukrytej przestrzeni
Uruchomienie poniższego kodu pokaże ciągły rozkład różnych klas cyfr, przy czym każda cyfra przechodzi w inną w utajonej przestrzeni 2D. Użyj prawdopodobieństwa TensorFlow , aby wygenerować standardowy rozkład normalny dla przestrzeni utajonej.
def plot_latent_images(model, n, digit_size=28):
"""Plots n x n digit images decoded from the latent space."""
norm = tfp.distributions.Normal(0, 1)
grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
image_width = digit_size*n
image_height = image_width
image = np.zeros((image_height, image_width))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z = np.array([[xi, yi]])
x_decoded = model.sample(z)
digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
image[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit.numpy()
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='Greys_r')
plt.axis('Off')
plt.show()
plot_latent_images(model, 20)

Następne kroki
Ten samouczek zademonstrował, jak zaimplementować splotowy wariacyjny autoenkoder za pomocą TensorFlow.
W następnym kroku możesz spróbować poprawić wyniki modelu, zwiększając rozmiar sieci. Na przykład możesz spróbować ustawić parametry filter dla każdej z warstw Conv2D i Conv2DTranspose na 512. Zauważ, że aby wygenerować końcowy wykres obrazu ukrytego 2D, musiałbyś ustawić latent_dim na 2. Ponadto czas uczenia się wydłużył wraz ze wzrostem rozmiaru sieci.
Możesz również spróbować wdrożyć VAE przy użyciu innego zestawu danych, takiego jak CIFAR-10.
VAE można zaimplementować w kilku różnych stylach io różnej złożoności. Dodatkowe implementacje można znaleźć w następujących źródłach:
- Autoenkoder wariacyjny (keras.io)
- Przykład VAE z przewodnika „Pisanie niestandardowych warstw i modeli” (tensorflow.org)
- Warstwy probabilistyczne TFP: wariacyjny automatyczny enkoder
Jeśli chcesz dowiedzieć się więcej o szczegółach VAE, zapoznaj się z wprowadzeniem do autokoderów odmianowych .
