 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
Questo quaderno mostra come addestrare un Variational Autoencoder (VAE) ( 1 , 2 ) sul set di dati MNIST. Un VAE è un'interpretazione probabilistica dell'autoencoder, un modello che prende dati di input di dimensioni elevate e li comprime in una rappresentazione più piccola. A differenza di un codificatore automatico tradizionale, che mappa l'input su un vettore latente, un VAE mappa i dati di input nei parametri di una distribuzione di probabilità, come la media e la varianza di una gaussiana. Questo approccio produce uno spazio latente continuo e strutturato, utile per la generazione di immagini.

Impostare
pip install tensorflow-probability# to generate gifspip install imageiopip install git+https://github.com/tensorflow/docs
from IPython import display
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time
Carica il set di dati MNIST
Ogni immagine MNIST è originariamente un vettore di 784 numeri interi, ognuno dei quali è compreso tra 0 e 255 e rappresenta l'intensità di un pixel. Modella ogni pixel con una distribuzione di Bernoulli nel nostro modello e binarizza staticamente il set di dati.
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
def preprocess_images(images):
images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
return np.where(images > .5, 1.0, 0.0).astype('float32')
train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)
train_size = 60000
batch_size = 32
test_size = 10000
Usa tf.data per raggruppare e mescolare i dati
train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
.shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
.shuffle(test_size).batch(batch_size))
Definire le reti di encoder e decoder con tf.keras.Sequential
In questo esempio VAE, utilizzare due piccole ConvNet per le reti di codificatore e decodificatore. In letteratura, queste reti sono anche denominate rispettivamente modelli di inferenza/riconoscimento e modelli generativi. Utilizzare tf.keras.Sequential per semplificare l'implementazione. Sia \(x\) e \(z\) rispettivamente l'osservazione e la variabile latente nelle seguenti descrizioni.
Rete di codificatori
Questo definisce la distribuzione a posteriori approssimativa \(q(z|x)\), che prende come input un'osservazione e restituisce un insieme di parametri per specificare la distribuzione condizionale della rappresentazione latente \(z\). In questo esempio, modella semplicemente la distribuzione come una gaussiana diagonale e la rete restituisce i parametri di media e varianza logaritmica di una gaussiana fattorizzata. Genera la varianza logaritmica invece della varianza direttamente per la stabilità numerica.
Rete di decodificatori
Questo definisce la distribuzione condizionale dell'osservazione \(p(x|z)\), che prende un campione latente \(z\) come input e restituisce i parametri per una distribuzione condizionale dell'osservazione. Modella la distribuzione latente prima \(p(z)\) come un'unità gaussiana.
Trucco di riparametrizzazione
Per generare un campione \(z\) per il decoder durante l'addestramento, è possibile campionare dalla distribuzione latente definita dai parametri emessi dal codificatore, data un'osservazione di input \(x\). Tuttavia, questa operazione di campionamento crea un collo di bottiglia perché la backpropagation non può fluire attraverso un nodo casuale.
Per risolvere questo problema, usa un trucco di riparametrizzazione. Nel nostro esempio, approssima \(z\) utilizzando i parametri del decodificatore e un altro parametro \(\epsilon\) come segue:
\[z = \mu + \sigma \odot \epsilon\]
dove \(\mu\) e \(\sigma\) rappresentano rispettivamente la media e la deviazione standard di una distribuzione gaussiana. Possono essere derivati dall'uscita del decoder. \(\epsilon\) può essere considerato come un rumore casuale utilizzato per mantenere la stocasticità di \(z\). Genera \(\epsilon\) da una distribuzione normale standard.
La variabile latente \(z\) è ora generata da una funzione di \(\mu\), \(\sigma\) e \(\epsilon\), che consentirebbe al modello di retropropagare i gradienti nell'encoder rispettivamente tramite \(\mu\) e \(\sigma\) , mantenendo la stocasticità attraverso \(\epsilon\).
Architettura di rete
Per la rete del codificatore, utilizzare due livelli convoluzionali seguiti da uno completamente connesso. Nella rete del decodificatore, rispecchia questa architettura utilizzando uno strato completamente connesso seguito da tre strati di trasposizione di convoluzione (ovvero strati deconvoluzionali in alcuni contesti). Si noti che è pratica comune evitare di utilizzare la normalizzazione batch durante l'addestramento dei VAE, poiché la stocasticità aggiuntiva dovuta all'utilizzo di mini-batch può aggravare l'instabilità oltre alla stocasticità del campionamento.
class CVAE(tf.keras.Model):
"""Convolutional variational autoencoder."""
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=2, padding='same',
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=2, padding='same',
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=1, padding='same'),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
Definire la funzione di perdita e l'ottimizzatore
I VAE si allenano massimizzando il limite inferiore dell'evidenza (ELBO) sulla probabilità logaritmica marginale:
\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]
In pratica, ottimizzare la stima Monte Carlo del singolo campione di questa aspettativa:
\[\log p(x| z) + \log p(z) - \log q(z|x),\]
dove \(z\) è campionato da \(q(z|x)\).
optimizer = tf.keras.optimizers.Adam(1e-4)
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
def compute_loss(model, x):
mean, logvar = model.encode(x)
z = model.reparameterize(mean, logvar)
x_logit = model.decode(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
@tf.function
def train_step(model, x, optimizer):
"""Executes one training step and returns the loss.
This function computes the loss and gradients, and uses the latter to
update the model's parameters.
"""
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
Formazione
- Inizia eseguendo un'iterazione sul set di dati
- Durante ogni iterazione, passare l'immagine all'encoder per ottenere una serie di parametri di media e di varianza logaritmica del \(q(z|x)\)
- quindi applica il trucco di riparametrizzazione per campionare da \(q(z|x)\)
- Passare infine i campioni riparametrizzati al decoder per ottenere i logit della distribuzione generativa \(p(x|z)\)
- Nota: poiché utilizzi il set di dati caricato da keras con 60.000 punti dati nel set di addestramento e 10.000 punti dati nel set di test, il nostro ELBO risultante sul set di test è leggermente superiore ai risultati riportati nella letteratura che utilizza la binarizzazione dinamica di MNIST di Larochelle.
Generazione di immagini
- Dopo l'allenamento, è il momento di generare alcune immagini
- Inizia campionando un insieme di vettori latenti dalla distribuzione precedente gaussiana \(p(z)\)dell'unità
- Il generatore convertirà quindi il campione latente \(z\) in logit dell'osservazione, fornendo una distribuzione \(p(x|z)\)
- Qui, traccia le probabilità delle distribuzioni di Bernoulli
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)
def generate_and_save_images(model, epoch, test_sample):
mean, logvar = model.encode(test_sample)
z = model.reparameterize(mean, logvar)
predictions = model.sample(z)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# tight_layout minimizes the overlap between 2 sub-plots
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
test_sample = test_batch[0:num_examples_to_generate, :, :, :]
generate_and_save_images(model, 0, test_sample)
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
train_step(model, train_x, optimizer)
end_time = time.time()
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
display.clear_output(wait=False)
print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
.format(epoch, elbo, end_time - start_time))
generate_and_save_images(model, epoch, test_sample)
Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

Visualizza un'immagine generata dall'ultima epoca di allenamento
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
plt.imshow(display_image(epoch))
plt.axis('off') # Display images
(-0.5, 287.5, 287.5, -0.5)
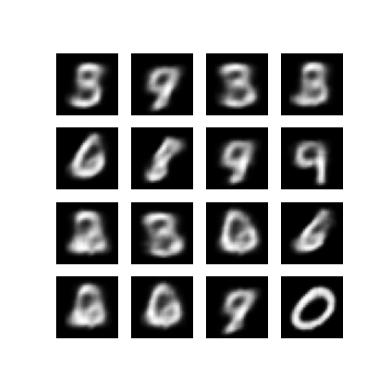
Visualizza una GIF animata di tutte le immagini salvate
anim_file = 'cvae.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

Visualizza una varietà 2D di cifre dallo spazio latente
L'esecuzione del codice seguente mostrerà una distribuzione continua delle diverse classi di cifre, con ogni cifra che si trasforma in un'altra nello spazio latente 2D. Utilizzare TensorFlow Probability per generare una distribuzione normale standard per lo spazio latente.
def plot_latent_images(model, n, digit_size=28):
"""Plots n x n digit images decoded from the latent space."""
norm = tfp.distributions.Normal(0, 1)
grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
image_width = digit_size*n
image_height = image_width
image = np.zeros((image_height, image_width))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z = np.array([[xi, yi]])
x_decoded = model.sample(z)
digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
image[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit.numpy()
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='Greys_r')
plt.axis('Off')
plt.show()
plot_latent_images(model, 20)

Prossimi passi
Questo tutorial ha dimostrato come implementare un autoencoder variazionale convoluzionale usando TensorFlow.
Come passaggio successivo, potresti provare a migliorare l'output del modello aumentando le dimensioni della rete. Ad esempio, potresti provare a impostare i parametri del filter per ciascuno dei livelli Conv2D e Conv2DTranspose su 512. Nota che per generare il grafico dell'immagine latente 2D finale, dovresti mantenere latent_dim su 2. Inoltre, il tempo di addestramento aumenterebbe all'aumentare della dimensione della rete.
Potresti anche provare a implementare un VAE utilizzando un set di dati diverso, come CIFAR-10.
I VAE possono essere implementati in diversi stili e di varia complessità. Puoi trovare ulteriori implementazioni nelle seguenti fonti:
- Codificatore automatico variazionale (keras.io)
- Esempio VAE dalla guida "Scrittura di livelli e modelli personalizzati" (tensorflow.org)
- Livelli probabilistici TFP: codificatore automatico variazionale
Se desideri saperne di più sui dettagli dei VAE, fai riferimento a An Introduction to Variational Autoencoder .
