 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Notebook ini mendemonstrasikan cara melatih Variational Autoencoder (VAE) ( 1 , 2 ) pada set data MNIST. VAE adalah pengambilan probabilistik pada autoencoder, model yang mengambil data input berdimensi tinggi dan mengompresnya menjadi representasi yang lebih kecil. Tidak seperti autoencoder tradisional, yang memetakan input ke vektor laten, VAE memetakan data input ke dalam parameter distribusi probabilitas, seperti mean dan varians Gaussian. Pendekatan ini menghasilkan ruang laten terstruktur yang berkelanjutan, yang berguna untuk pembuatan gambar.

Mempersiapkan
pip install tensorflow-probability# to generate gifspip install imageiopip install git+https://github.com/tensorflow/docs
from IPython import display
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time
Muat kumpulan data MNIST
Setiap gambar MNIST awalnya merupakan vektor dari 784 bilangan bulat, yang masing-masing antara 0-255 dan mewakili intensitas piksel. Modelkan setiap piksel dengan distribusi Bernoulli dalam model kami, dan binerisasikan kumpulan data secara statis.
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
def preprocess_images(images):
images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
return np.where(images > .5, 1.0, 0.0).astype('float32')
train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)
train_size = 60000
batch_size = 32
test_size = 10000
Gunakan tf.data untuk mengelompokkan dan mengacak data
train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
.shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
.shuffle(test_size).batch(batch_size))
Tentukan jaringan encoder dan decoder dengan tf.keras.Sequential
Dalam contoh VAE ini, gunakan dua ConvNet kecil untuk jaringan encoder dan decoder. Dalam literatur, jaringan ini juga disebut sebagai model inferensi/pengakuan dan generatif. Gunakan tf.keras.Sequential untuk menyederhanakan implementasi. Biarkan \(x\) dan \(z\) masing-masing menunjukkan observasi dan variabel laten dalam uraian berikut.
Jaringan penyandi
Ini mendefinisikan perkiraan distribusi posterior \(q(z|x)\), yang mengambil sebagai input pengamatan dan mengeluarkan serangkaian parameter untuk menentukan distribusi kondisional dari representasi laten \(z\). Dalam contoh ini, cukup modelkan distribusi sebagai Gaussian diagonal, dan jaringan mengeluarkan parameter mean dan log-varians dari Gaussian terfaktor. Keluaran log-varians alih-alih varians secara langsung untuk stabilitas numerik.
Jaringan dekoder
Ini mendefinisikan distribusi bersyarat dari observasi \(p(x|z)\), yang mengambil sampel laten \(z\) sebagai input dan mengeluarkan parameter untuk distribusi kondisional observasi. Modelkan distribusi laten sebelum \(p(z)\) sebagai unit Gaussian.
Trik parameterisasi ulang
Untuk menghasilkan sampel \(z\) untuk dekoder selama pelatihan, Anda dapat mengambil sampel dari distribusi laten yang ditentukan oleh parameter yang dikeluarkan oleh pembuat enkode, dengan pengamatan input \(x\). Namun, operasi pengambilan sampel ini menciptakan hambatan karena propagasi balik tidak dapat mengalir melalui simpul acak.
Untuk mengatasinya, gunakan trik parameterisasi ulang. Dalam contoh kami, Anda memperkirakan \(z\) menggunakan parameter dekoder dan parameter lain \(\epsilon\) sebagai berikut:
\[z = \mu + \sigma \odot \epsilon\]
di mana \(\mu\) dan \(\sigma\) masing-masing mewakili mean dan standar deviasi dari distribusi Gaussian. Mereka dapat diturunkan dari keluaran decoder. \(\epsilon\) dapat dianggap sebagai derau acak yang digunakan untuk mempertahankan stochasticity dari \(z\). Hasilkan \(\epsilon\) dari distribusi normal standar.
Variabel laten \(z\) sekarang dihasilkan oleh fungsi \(\mu\), \(\sigma\) dan \(\epsilon\), yang akan memungkinkan model untuk memundurkan gradien di encoder melalui \(\mu\) dan \(\sigma\) , sambil mempertahankan stokastisitas melalui \(\epsilon\).
Arsitektur jaringan
Untuk jaringan encoder, gunakan dua lapisan konvolusi diikuti oleh lapisan yang terhubung penuh. Dalam jaringan dekoder, cerminkan arsitektur ini dengan menggunakan lapisan yang terhubung penuh diikuti oleh tiga lapisan transpos konvolusi (alias lapisan dekonvolusi dalam beberapa konteks). Catatan, adalah praktik umum untuk menghindari penggunaan normalisasi batch saat melatih VAE, karena stokastik tambahan karena menggunakan batch mini dapat memperburuk ketidakstabilan selain stokastik dari pengambilan sampel.
class CVAE(tf.keras.Model):
"""Convolutional variational autoencoder."""
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=2, padding='same',
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=2, padding='same',
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=1, padding='same'),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
Tentukan fungsi kerugian dan pengoptimal
VAE berlatih dengan memaksimalkan batas bawah bukti (ELBO) pada kemungkinan log marjinal:
\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]
Dalam praktiknya, optimalkan estimasi sampel tunggal Monte Carlo dari ekspektasi ini:
\[\log p(x| z) + \log p(z) - \log q(z|x),\]
di mana \(z\) diambil sampelnya dari \(q(z|x)\).
optimizer = tf.keras.optimizers.Adam(1e-4)
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
def compute_loss(model, x):
mean, logvar = model.encode(x)
z = model.reparameterize(mean, logvar)
x_logit = model.decode(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
@tf.function
def train_step(model, x, optimizer):
"""Executes one training step and returns the loss.
This function computes the loss and gradients, and uses the latter to
update the model's parameters.
"""
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
Pelatihan
- Mulailah dengan mengulangi set data
- Selama setiap iterasi, teruskan gambar ke encoder untuk mendapatkan satu set parameter mean dan log-variance dari perkiraan posterior \(q(z|x)\)
- kemudian terapkan trik parameterisasi ulang ke sampel dari \(q(z|x)\)
- Terakhir, berikan sampel yang telah diparameterisasi ulang ke dekoder untuk mendapatkan logit dari distribusi generatif \(p(x|z)\)
- Catatan: Karena Anda menggunakan set data yang dimuat dengan keras dengan 60k titik data dalam set pelatihan dan 10k titik data dalam set pengujian, ELBO yang dihasilkan pada set pengujian sedikit lebih tinggi daripada hasil yang dilaporkan dalam literatur yang menggunakan binarisasi dinamis dari MNIST Larochelle.
Menghasilkan gambar
- Setelah pelatihan, saatnya untuk menghasilkan beberapa gambar
- Mulailah dengan mengambil sampel satu set vektor laten dari unit distribusi sebelumnya Gaussian \(p(z)\)
- Generator kemudian akan mengubah sampel laten \(z\) menjadi log pengamatan, memberikan distribusi \(p(x|z)\)
- Di sini, plot probabilitas distribusi Bernoulli
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)
def generate_and_save_images(model, epoch, test_sample):
mean, logvar = model.encode(test_sample)
z = model.reparameterize(mean, logvar)
predictions = model.sample(z)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# tight_layout minimizes the overlap between 2 sub-plots
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
test_sample = test_batch[0:num_examples_to_generate, :, :, :]
generate_and_save_images(model, 0, test_sample)
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
train_step(model, train_x, optimizer)
end_time = time.time()
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
display.clear_output(wait=False)
print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
.format(epoch, elbo, end_time - start_time))
generate_and_save_images(model, epoch, test_sample)
Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

Tampilkan gambar yang dihasilkan dari zaman pelatihan terakhir
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
plt.imshow(display_image(epoch))
plt.axis('off') # Display images
(-0.5, 287.5, 287.5, -0.5)
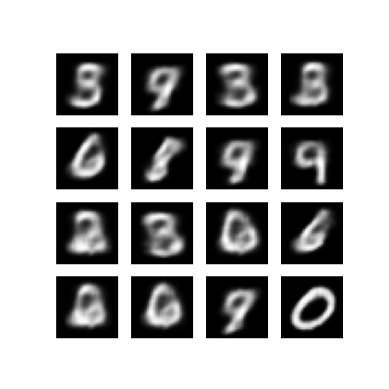
Tampilkan GIF animasi dari semua gambar yang disimpan
anim_file = 'cvae.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

Tampilkan manifold 2D digit dari ruang laten
Menjalankan kode di bawah ini akan menunjukkan distribusi berkelanjutan dari kelas digit yang berbeda, dengan setiap digit berubah menjadi yang lain melintasi ruang laten 2D. Gunakan TensorFlow Probability untuk menghasilkan distribusi normal standar untuk ruang laten.
def plot_latent_images(model, n, digit_size=28):
"""Plots n x n digit images decoded from the latent space."""
norm = tfp.distributions.Normal(0, 1)
grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
image_width = digit_size*n
image_height = image_width
image = np.zeros((image_height, image_width))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z = np.array([[xi, yi]])
x_decoded = model.sample(z)
digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
image[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit.numpy()
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='Greys_r')
plt.axis('Off')
plt.show()
plot_latent_images(model, 20)

Langkah selanjutnya
Tutorial ini telah menunjukkan cara menerapkan autoencoder variasional konvolusi menggunakan TensorFlow.
Sebagai langkah selanjutnya, Anda dapat mencoba meningkatkan keluaran model dengan meningkatkan ukuran jaringan. Misalnya, Anda dapat mencoba mengatur parameter filter untuk setiap lapisan Conv2D dan Conv2DTranspose ke 512. Perhatikan bahwa untuk menghasilkan plot gambar laten 2D akhir, Anda perlu menyimpan latent_dim ke 2. Selain itu, waktu pelatihan akan meningkat karena ukuran jaringan meningkat.
Anda juga dapat mencoba menerapkan VAE menggunakan kumpulan data yang berbeda, seperti CIFAR-10.
VAEs dapat diimplementasikan dalam beberapa gaya yang berbeda dan kompleksitas yang bervariasi. Anda dapat menemukan implementasi tambahan di sumber berikut:
- AutoEncoder Variasi (keras.io)
- Contoh VAE dari panduan "Menulis lapisan dan model khusus" (tensorflow.org)
- Lapisan Probabilistik TFP: Encoder Otomatis Variasi
Jika Anda ingin mempelajari lebih lanjut tentang detail VAE, silakan merujuk ke An Introduction to Variational Autoencoder .
