מקודד אוטומטי וריאציונלי

הצג באתר TensorFlow.org הפעל בגוגל קולאב צפה במקור ב-GitHub הורד מחברת

מחברת זו מדגים כיצד להכשיר קודן אוטומטי וריאציוני (VAE) ( 1 , 2 ) במערך הנתונים של MNIST. VAE הוא תפיסה הסתברותית של המקודד האוטומטי, מודל שלוקח נתוני קלט ממדי גבוה ודוחס אותם לייצוג קטן יותר. שלא כמו מקודד אוטומטי מסורתי, הממפה את הקלט על וקטור סמוי, VAE ממפה את נתוני הקלט לפרמטרים של התפלגות הסתברות, כגון הממוצע והשונות של גאוס. גישה זו מייצרת מרחב סמוי רציף ומובנה, אשר שימושי ליצירת תמונות.

מרחב סמוי בתמונה CVAE

להכין

pip install tensorflow-probability

# to generate gifs
pip install imageio
pip install git+https://github.com/tensorflow/docs

from IPython import display

import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time

טען את מערך הנתונים של MNIST

כל תמונת MNIST היא במקור וקטור של 784 מספרים שלמים, שכל אחד מהם הוא בין 0-255 ומייצג את העוצמה של פיקסל. דגמי כל פיקסל עם התפלגות ברנולי במודל שלנו, ובינארי סטטי של מערך הנתונים.

(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
11501568/11490434 [==============================] - 0s 0us/step

def preprocess_images(images):
  images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
  return np.where(images > .5, 1.0, 0.0).astype('float32')

train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)

train_size = 60000
batch_size = 32
test_size = 10000

השתמש ב-tf.data כדי לקבץ ולערבב את הנתונים

train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
                 .shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
                .shuffle(test_size).batch(batch_size))

הגדר את רשתות המקודד והמפענח באמצעות tf.keras.Sequential

בדוגמה זו של VAE, השתמש בשתי ConvNets קטנות עבור רשתות המקודד והמפענח. בספרות, רשתות אלו מכונות גם מודלים להסקה/הכרה ומודלים מחוללים בהתאמה. השתמש tf.keras.Sequential כדי לפשט את היישום. תנו \(x\) ול- \(z\) לציין את המשתנה התצפית והסמוי בהתאמה בתיאורים הבאים.

רשת מקודד

זה מגדיר את ההתפלגות האחורית המשוערת \(q(z|x)\), אשר לוקחת כקלט תצפית ומוציאה קבוצה של פרמטרים לציון ההתפלגות המותנית של הייצוג הסמוי \(z\). בדוגמה זו, פשוט דגלו את ההתפלגות כגאוס אלכסוני, והרשת מפלטת את הפרמטרים הממוצעים והלוג-שונות של גאוס מחולק לגורמים. פלט יומן שונות במקום השונות ישירות ליציבות מספרית.

רשת מפענח

זה מגדיר את ההתפלגות המותנית של התצפית \(p(x|z)\), שלוקחת מדגם סמוי \(z\) כקלט ומוציאה את הפרמטרים להתפלגות מותנית של התצפית. דגם את ההתפלגות הסמויה לפני \(p(z)\) כיחידה גאוסית.

טריק פרמטריזציה מחדש

כדי ליצור מדגם \(z\) עבור המפענח במהלך האימון, אתה יכול לדגום מההתפלגות הסמויה המוגדרת על ידי הפרמטרים המופקים על ידי המקודד, בהינתן תצפית קלט \(x\). עם זאת, פעולת דגימה זו יוצרת צוואר בקבוק מכיוון שההפצה לאחור לא יכולה לזרום דרך צומת אקראי.

כדי לטפל בזה, השתמש בטריק פרמטריזציה מחדש. בדוגמה שלנו, אתה \(z\) באמצעות פרמטרי המפענח ופרמטר אחר \(\epsilon\) באופן הבא:

\[z = \mu + \sigma \odot \epsilon\]

כאשר \(\mu\) ו- \(\sigma\) מייצגים את הממוצע וסטיית התקן של התפלגות גאוסית בהתאמה. ניתן להפיק אותם מפלט המפענח. ניתן להתייחס \(\epsilon\) כרעש אקראי המשמש לשמירה על הסטוקסטיות של \(z\). צור \(\epsilon\) מהתפלגות נורמלית סטנדרטית.

המשתנה הסמוי \(z\) נוצר כעת על ידי פונקציה של \(\mu\), \(\sigma\) ו- \(\epsilon\), אשר יאפשרו למודל להפיץ גרדיאנטים במקודד דרך \(\mu\) ו- \(\sigma\) בהתאמה, תוך שמירה על סטוקסטיות. \(\epsilon\).

ארכיטקטורת רשת

עבור רשת המקודד, השתמש בשתי שכבות קונבולוציוניות ואחריהן שכבה מחוברת לחלוטין. ברשת המפענח, שיקוף ארכיטקטורה זו על ידי שימוש בשכבה מחוברת מלאה ואחריה שלוש שכבות טרנספוזיציה של קונבולוציה (המכונה שכבות דקונבולוציוניות בהקשרים מסוימים). שים לב, נוהג נפוץ להימנע משימוש בנורמליזציה אצווה בעת אימון VAEs, שכן הסטוכסטיות הנוספת עקב שימוש במיני אצווה עלולה להחמיר את חוסר היציבות על הסטוכסטיות מהדגימה.

class CVAE(tf.keras.Model):
  """Convolutional variational autoencoder."""

  def __init__(self, latent_dim):
    super(CVAE, self).__init__()
    self.latent_dim = latent_dim
    self.encoder = tf.keras.Sequential(
        [
            tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
            tf.keras.layers.Conv2D(
                filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
            tf.keras.layers.Conv2D(
                filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
            tf.keras.layers.Flatten(),
            # No activation
            tf.keras.layers.Dense(latent_dim + latent_dim),
        ]
    )

    self.decoder = tf.keras.Sequential(
        [
            tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
            tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
            tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
            tf.keras.layers.Conv2DTranspose(
                filters=64, kernel_size=3, strides=2, padding='same',
                activation='relu'),
            tf.keras.layers.Conv2DTranspose(
                filters=32, kernel_size=3, strides=2, padding='same',
                activation='relu'),
            # No activation
            tf.keras.layers.Conv2DTranspose(
                filters=1, kernel_size=3, strides=1, padding='same'),
        ]
    )

  @tf.function
  def sample(self, eps=None):
    if eps is None:
      eps = tf.random.normal(shape=(100, self.latent_dim))
    return self.decode(eps, apply_sigmoid=True)

  def encode(self, x):
    mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
    return mean, logvar

  def reparameterize(self, mean, logvar):
    eps = tf.random.normal(shape=mean.shape)
    return eps * tf.exp(logvar * .5) + mean

  def decode(self, z, apply_sigmoid=False):
    logits = self.decoder(z)
    if apply_sigmoid:
      probs = tf.sigmoid(logits)
      return probs
    return logits

הגדר את פונקציית ההפסד ואת האופטימיזציה

VAEs מתאמנים על ידי מיקסום הראיות הגבול התחתון (ELBO) על הסבירות השולית ביומן:

\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]

בפועל, בצע אופטימיזציה של אומדן המדגם היחיד של מונטה קרלו של ציפייה זו:

\[\log p(x| z) + \log p(z) - \log q(z|x),\]

כאשר \(z\) נדגם מ- \(q(z|x)\).

optimizer = tf.keras.optimizers.Adam(1e-4)


def log_normal_pdf(sample, mean, logvar, raxis=1):
  log2pi = tf.math.log(2. * np.pi)
  return tf.reduce_sum(
      -.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
      axis=raxis)


def compute_loss(model, x):
  mean, logvar = model.encode(x)
  z = model.reparameterize(mean, logvar)
  x_logit = model.decode(z)
  cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
  logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
  logpz = log_normal_pdf(z, 0., 0.)
  logqz_x = log_normal_pdf(z, mean, logvar)
  return -tf.reduce_mean(logpx_z + logpz - logqz_x)


@tf.function
def train_step(model, x, optimizer):
  """Executes one training step and returns the loss.

  This function computes the loss and gradients, and uses the latter to
  update the model's parameters.
  """
  with tf.GradientTape() as tape:
    loss = compute_loss(model, x)
  gradients = tape.gradient(loss, model.trainable_variables)
  optimizer.apply_gradients(zip(gradients, model.trainable_variables))

הַדְרָכָה

  • התחל באיטרציה על מערך הנתונים
  • במהלך כל איטרציה, העבר את התמונה למקודד כדי לקבל קבוצה של פרמטרים ממוצעים ושונות יומן של ה- \(q(z|x)\)האחורי המשוער.
  • לאחר מכן החל את טריק הפרמטר מחדש לדגימה מ- \(q(z|x)\)
  • לבסוף, העבירו את הדגימות שהוגדרו מחדש למפענח כדי לקבל את הלוגיטים של ההתפלגות הגנרטיבית \(p(x|z)\)
  • הערה: מכיוון שאתה משתמש במערך הנתונים שנטען על ידי keras עם 60,000 נקודות נתונים בערכת האימון ו-10,000 נקודות נתונים במערך הבדיקות, ה-ELBO שהתקבל במערך הבדיקות גבוה מעט מהתוצאות המדווחות בספרות המשתמשת בבינאריזציה דינמית של MNIST של Larochelle.

יצירת תמונות

  • לאחר האימון, הגיע הזמן ליצור כמה תמונות
  • התחל על ידי דגימת קבוצה של וקטורים סמויים מהתפלגות קודמת גאוסית של היחידה \(p(z)\)
  • לאחר מכן, המחולל ימיר את המדגם הסמוי \(z\) ללוגיטים של התצפית, וייתן התפלגות \(p(x|z)\)
  • כאן, תכנן את ההסתברויות של התפלגויות ברנולי
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16

# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
    shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)

def generate_and_save_images(model, epoch, test_sample):
  mean, logvar = model.encode(test_sample)
  z = model.reparameterize(mean, logvar)
  predictions = model.sample(z)
  fig = plt.figure(figsize=(4, 4))

  for i in range(predictions.shape[0]):
    plt.subplot(4, 4, i + 1)
    plt.imshow(predictions[i, :, :, 0], cmap='gray')
    plt.axis('off')

  # tight_layout minimizes the overlap between 2 sub-plots
  plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
  plt.show()

# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
  test_sample = test_batch[0:num_examples_to_generate, :, :, :]

generate_and_save_images(model, 0, test_sample)

for epoch in range(1, epochs + 1):
  start_time = time.time()
  for train_x in train_dataset:
    train_step(model, train_x, optimizer)
  end_time = time.time()

  loss = tf.keras.metrics.Mean()
  for test_x in test_dataset:
    loss(compute_loss(model, test_x))
  elbo = -loss.result()
  display.clear_output(wait=False)
  print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
        .format(epoch, elbo, end_time - start_time))
  generate_and_save_images(model, epoch, test_sample)

Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

png

הצג תמונה שנוצרה מתקופת האימון האחרונה

def display_image(epoch_no):
  return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))

plt.imshow(display_image(epoch))
plt.axis('off')  # Display images

(-0.5, 287.5, 287.5, -0.5)

png

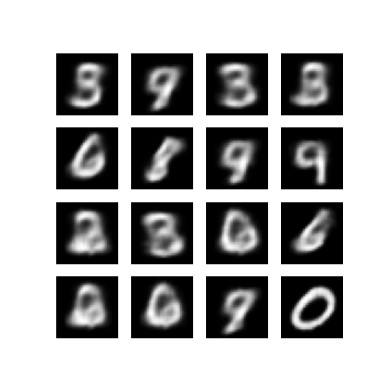
הצג GIF מונפש של כל התמונות שנשמרו

anim_file = 'cvae.gif'

with imageio.get_writer(anim_file, mode='I') as writer:
  filenames = glob.glob('image*.png')
  filenames = sorted(filenames)
  for filename in filenames:
    image = imageio.imread(filename)
    writer.append_data(image)
  image = imageio.imread(filename)
  writer.append_data(image)

import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

gif

הצג סעפת דו-ממדית של ספרות מהמרחב הסמוי

הפעלת הקוד שלהלן תציג התפלגות רציפה של מחלקות הספרות השונות, כאשר כל ספרה מתחלפת לאחרת על פני המרחב הסמוי הדו-ממדי. השתמש ב- TensorFlow Probability כדי ליצור התפלגות נורמלית סטנדרטית עבור המרחב הסמוי.

def plot_latent_images(model, n, digit_size=28):
  """Plots n x n digit images decoded from the latent space."""

  norm = tfp.distributions.Normal(0, 1)
  grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
  grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
  image_width = digit_size*n
  image_height = image_width
  image = np.zeros((image_height, image_width))

  for i, yi in enumerate(grid_x):
    for j, xi in enumerate(grid_y):
      z = np.array([[xi, yi]])
      x_decoded = model.sample(z)
      digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
      image[i * digit_size: (i + 1) * digit_size,
            j * digit_size: (j + 1) * digit_size] = digit.numpy()

  plt.figure(figsize=(10, 10))
  plt.imshow(image, cmap='Greys_r')
  plt.axis('Off')
  plt.show()

plot_latent_images(model, 20)

png

הצעדים הבאים

הדרכה זו הדגימה כיצד ליישם מקודד אוטומטי וריאציוני באמצעות TensorFlow.

כשלב הבא, תוכל לנסות לשפר את פלט הדגם על ידי הגדלת גודל הרשת. לדוגמה, אתה יכול לנסות להגדיר את פרמטרי filter עבור כל אחת Conv2D ו- Conv2DTranspose ל-512. שימו לב שכדי ליצור את עלילת התמונה הסמויה הדו-ממדית הסופית, תצטרכו לשמור את latent_dim ל-2. כמו כן, זמן האימון יגדל. ככל שגודל הרשת גדל.

אתה יכול גם לנסות ליישם VAE באמצעות מערך נתונים אחר, כגון CIFAR-10.

ניתן ליישם VAE בכמה סגנונות שונים ובמורכבות משתנה. תוכל למצוא יישומים נוספים במקורות הבאים:

אם תרצה ללמוד עוד על הפרטים של VAEs, עיין במבוא למקודדים אוטומטיים וריאציוניים .