التشفير التلقائي المتغير التلافيفي

عرض على TensorFlow.org تشغيل في Google Colab عرض المصدر على جيثب تحميل دفتر

يوضح هذا الكمبيوتر الدفتري كيفية تدريب المشفر التلقائي المتغير (VAE) ( 1 ، 2 ) على مجموعة بيانات MNIST. A VAE هو احتمالية على وحدة التشفير التلقائي ، وهو نموذج يأخذ بيانات الإدخال عالية الأبعاد ويضغطها في تمثيل أصغر. على عكس المشفر التلقائي التقليدي ، الذي يقوم بتعيين المدخلات على متجه كامن ، يقوم VAE بتعيين بيانات الإدخال في معلمات توزيع الاحتمالات ، مثل المتوسط ​​والتباين في Gaussian. ينتج عن هذا النهج مساحة كامنة مستمرة ومنظمة ، وهو أمر مفيد لتوليد الصور.

المساحة الكامنة للصورة CVAE

يثبت

pip install tensorflow-probability

# to generate gifs
pip install imageio
pip install git+https://github.com/tensorflow/docs

from IPython import display

import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time

قم بتحميل مجموعة بيانات MNIST

كل صورة MNIST هي في الأصل متجه من 784 عددًا صحيحًا ، كل منها يتراوح بين 0-255 وتمثل كثافة البكسل. قم بتكوين نموذج لكل بكسل باستخدام توزيع برنولي في نموذجنا ، وقم بترتيب مجموعة البيانات بشكل ثنائي بشكل ثابت.

(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
11501568/11490434 [==============================] - 0s 0us/step

def preprocess_images(images):
  images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
  return np.where(images > .5, 1.0, 0.0).astype('float32')

train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)

train_size = 60000
batch_size = 32
test_size = 10000

استخدم tf.data لتجميع البيانات وخلطها

train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
                 .shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
                .shuffle(test_size).batch(batch_size))

حدد شبكات التشفير وفك التشفير باستخدام tf.keras.Sequential

في مثال VAE هذا ، استخدم شبكتي ConvNets صغيرتين لشبكات التشفير وفك التشفير. في الأدبيات ، يشار إلى هذه الشبكات أيضًا باسم نماذج الاستدلال / الاعتراف والنماذج التوليدية على التوالي. استخدم tf.keras.Sequential لتبسيط التنفيذ. دع \(x\) و \(z\) تدلان على الملاحظة والمتغير الكامن على التوالي في الأوصاف التالية.

شبكة التشفير

يحدد هذا التوزيع اللاحق التقريبي \(q(z|x)\)، والذي يأخذ كمدخل ملاحظة ويخرج مجموعة من المعلمات لتحديد التوزيع الشرطي للتمثيل الكامن \(z\). في هذا المثال ، قم ببساطة بنمذجة التوزيع باعتباره Gaussian قطريًا ، وتخرج الشبكة متوسط ​​معاملات التباين في سجل Gaussian. إخراج التباين بدلاً من التباين مباشرة من أجل الاستقرار العددي.

شبكة فك

يحدد هذا التوزيع الشرطي للملاحظة \(p(x|z)\)، والذي يأخذ عينة كامنة \(z\) كمدخلات ومخرجات معلمات التوزيع الشرطي للملاحظة. نموذج التوزيع الكامن السابق \(p(z)\) كوحدة Gaussian.

خدعة الإصلاح

لإنشاء عينة \(z\) لوحدة فك الترميز أثناء التدريب ، يمكنك أخذ عينة من التوزيع الكامن المحدد بواسطة المعلمات التي تم إخراجها بواسطة المشفر ، بالنظر إلى ملاحظة الإدخال \(x\). ومع ذلك ، فإن عملية أخذ العينات هذه تخلق عنق زجاجة لأن backpropagation لا يمكن أن يتدفق عبر عقدة عشوائية.

لمعالجة هذا الأمر ، استخدم خدعة إصلاح المعايير. في مثالنا ، تقوم بتقريب \(z\) باستخدام معلمات وحدة فك الترميز ومعلمة أخرى \(\epsilon\) كما يلي:

\[z = \mu + \sigma \odot \epsilon\]

حيث يمثل \(\mu\) و \(\sigma\) المتوسط ​​والانحراف المعياري لتوزيع غاوسي على التوالي. يمكن اشتقاقها من إخراج وحدة فك التشفير. يمكن اعتبار \(\epsilon\) بمثابة ضوضاء عشوائية تُستخدم للحفاظ على العشوائية \(z\). قم بإنشاء \(\epsilon\) من توزيع عادي قياسي.

يتم الآن إنشاء المتغير الكامن \(z\) بواسطة دالة \(\mu\)و \(\sigma\) و \(\epsilon\)، مما سيمكن النموذج من إعادة نشر التدرجات في المشفر من خلال \(\mu\) و \(\sigma\) على التوالي ، مع الحفاظ على العشوائية من خلال \(\epsilon\).

هندسة الشبكات

بالنسبة لشبكة التشفير ، استخدم طبقتين تلافيفيتين متبوعين بطبقة متصلة بالكامل. في شبكة مفكك التشفير ، قم بعكس هذه البنية باستخدام طبقة متصلة بالكامل متبوعة بثلاث طبقات تحويل التفافية (تُعرف أيضًا باسم طبقات deconvolutional في بعض السياقات). لاحظ أنه من الشائع تجنب استخدام تطبيع الدُفعات عند تدريب VAEs ، نظرًا لأن العشوائية الإضافية الناتجة عن استخدام دفعات صغيرة قد تؤدي إلى تفاقم عدم الاستقرار فوق العشوائية من أخذ العينات.

class CVAE(tf.keras.Model):
  """Convolutional variational autoencoder."""

  def __init__(self, latent_dim):
    super(CVAE, self).__init__()
    self.latent_dim = latent_dim
    self.encoder = tf.keras.Sequential(
        [
            tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
            tf.keras.layers.Conv2D(
                filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
            tf.keras.layers.Conv2D(
                filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
            tf.keras.layers.Flatten(),
            # No activation
            tf.keras.layers.Dense(latent_dim + latent_dim),
        ]
    )

    self.decoder = tf.keras.Sequential(
        [
            tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
            tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
            tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
            tf.keras.layers.Conv2DTranspose(
                filters=64, kernel_size=3, strides=2, padding='same',
                activation='relu'),
            tf.keras.layers.Conv2DTranspose(
                filters=32, kernel_size=3, strides=2, padding='same',
                activation='relu'),
            # No activation
            tf.keras.layers.Conv2DTranspose(
                filters=1, kernel_size=3, strides=1, padding='same'),
        ]
    )

  @tf.function
  def sample(self, eps=None):
    if eps is None:
      eps = tf.random.normal(shape=(100, self.latent_dim))
    return self.decode(eps, apply_sigmoid=True)

  def encode(self, x):
    mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
    return mean, logvar

  def reparameterize(self, mean, logvar):
    eps = tf.random.normal(shape=mean.shape)
    return eps * tf.exp(logvar * .5) + mean

  def decode(self, z, apply_sigmoid=False):
    logits = self.decoder(z)
    if apply_sigmoid:
      probs = tf.sigmoid(logits)
      return probs
    return logits

تحديد وظيفة الخسارة والمحسن

يتدرب VAEs من خلال تعظيم الأدلة الأدنى (ELBO) على احتمالية السجل الهامشي:

\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]

من الناحية العملية ، قم بتحسين تقدير مونتي كارلو للعينة الفردية لهذا التوقع:

\[\log p(x| z) + \log p(z) - \log q(z|x),\]

حيث يتم أخذ عينات من l10n- \(z\) من \(q(z|x)\).

optimizer = tf.keras.optimizers.Adam(1e-4)


def log_normal_pdf(sample, mean, logvar, raxis=1):
  log2pi = tf.math.log(2. * np.pi)
  return tf.reduce_sum(
      -.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
      axis=raxis)


def compute_loss(model, x):
  mean, logvar = model.encode(x)
  z = model.reparameterize(mean, logvar)
  x_logit = model.decode(z)
  cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
  logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
  logpz = log_normal_pdf(z, 0., 0.)
  logqz_x = log_normal_pdf(z, mean, logvar)
  return -tf.reduce_mean(logpx_z + logpz - logqz_x)


@tf.function
def train_step(model, x, optimizer):
  """Executes one training step and returns the loss.

  This function computes the loss and gradients, and uses the latter to
  update the model's parameters.
  """
  with tf.GradientTape() as tape:
    loss = compute_loss(model, x)
  gradients = tape.gradient(loss, model.trainable_variables)
  optimizer.apply_gradients(zip(gradients, model.trainable_variables))

تمرين

  • ابدأ بالتكرار على مجموعة البيانات
  • أثناء كل تكرار ، قم بتمرير الصورة إلى المشفر للحصول على مجموعة من معلمات متوسط ​​وتباين السجل \(q(z|x)\)
  • ثم قم بتطبيق خدعة الإصلاح على عينة من \(q(z|x)\)
  • أخيرًا ، قم بتمرير العينات المعاد ضبطها إلى وحدة فك التشفير للحصول على سجلات التوزيع التوليدي \(p(x|z)\)
  • ملاحظة: نظرًا لأنك تستخدم مجموعة البيانات التي تم تحميلها بواسطة keras مع 60 ألف نقطة بيانات في مجموعة التدريب و 10 آلاف نقطة بيانات في مجموعة الاختبار ، فإن ELBO الناتج في مجموعة الاختبار أعلى قليلاً من النتائج المبلغ عنها في الأدبيات التي تستخدم ثنائية ديناميكية لـ Larochelle's MNIST.

توليد الصور

  • بعد التدريب ، حان الوقت لتوليد بعض الصور
  • ابدأ بأخذ عينات من مجموعة من النواقل الكامنة من وحدة التوزيع المسبق الغاوسي \(p(z)\)
  • سيقوم المولد بعد ذلك بتحويل العينة الكامنة \(z\) إلى سجلات الملاحظة ، مما يعطي التوزيع \(p(x|z)\)
  • هنا ، ارسم احتمالات توزيعات برنولي
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16

# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
    shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)

def generate_and_save_images(model, epoch, test_sample):
  mean, logvar = model.encode(test_sample)
  z = model.reparameterize(mean, logvar)
  predictions = model.sample(z)
  fig = plt.figure(figsize=(4, 4))

  for i in range(predictions.shape[0]):
    plt.subplot(4, 4, i + 1)
    plt.imshow(predictions[i, :, :, 0], cmap='gray')
    plt.axis('off')

  # tight_layout minimizes the overlap between 2 sub-plots
  plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
  plt.show()

# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
  test_sample = test_batch[0:num_examples_to_generate, :, :, :]

generate_and_save_images(model, 0, test_sample)

for epoch in range(1, epochs + 1):
  start_time = time.time()
  for train_x in train_dataset:
    train_step(model, train_x, optimizer)
  end_time = time.time()

  loss = tf.keras.metrics.Mean()
  for test_x in test_dataset:
    loss(compute_loss(model, test_x))
  elbo = -loss.result()
  display.clear_output(wait=False)
  print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
        .format(epoch, elbo, end_time - start_time))
  generate_and_save_images(model, epoch, test_sample)

Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

بي إن جي

اعرض صورة تم إنشاؤها من حقبة التدريب الأخيرة

def display_image(epoch_no):
  return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))

plt.imshow(display_image(epoch))
plt.axis('off')  # Display images

(-0.5, 287.5, 287.5, -0.5)

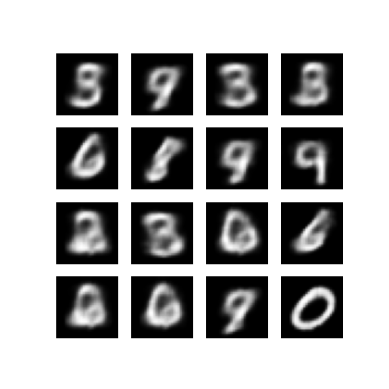
بي إن جي

عرض صورة GIF متحركة لجميع الصور المحفوظة

anim_file = 'cvae.gif'

with imageio.get_writer(anim_file, mode='I') as writer:
  filenames = glob.glob('image*.png')
  filenames = sorted(filenames)
  for filename in filenames:
    image = imageio.imread(filename)
    writer.append_data(image)
  image = imageio.imread(filename)
  writer.append_data(image)

import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

gif

عرض مشعب ثنائي الأبعاد من الأرقام من الفضاء الكامن

سيُظهر تشغيل الكود أدناه توزيعًا مستمرًا لفئات الأرقام المختلفة ، مع تحول كل رقم إلى آخر عبر المساحة الكامنة ثنائية الأبعاد. استخدم احتمالية TensorFlow لإنشاء توزيع عادي قياسي للمساحة الكامنة.

def plot_latent_images(model, n, digit_size=28):
  """Plots n x n digit images decoded from the latent space."""

  norm = tfp.distributions.Normal(0, 1)
  grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
  grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
  image_width = digit_size*n
  image_height = image_width
  image = np.zeros((image_height, image_width))

  for i, yi in enumerate(grid_x):
    for j, xi in enumerate(grid_y):
      z = np.array([[xi, yi]])
      x_decoded = model.sample(z)
      digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
      image[i * digit_size: (i + 1) * digit_size,
            j * digit_size: (j + 1) * digit_size] = digit.numpy()

  plt.figure(figsize=(10, 10))
  plt.imshow(image, cmap='Greys_r')
  plt.axis('Off')
  plt.show()

plot_latent_images(model, 20)

بي إن جي

الخطوات التالية

لقد أوضح هذا البرنامج التعليمي كيفية تنفيذ المشفر التلقائي التلافيفي المتغير باستخدام TensorFlow.

كخطوة تالية ، يمكنك محاولة تحسين إخراج النموذج عن طريق زيادة حجم الشبكة. على سبيل المثال ، يمكنك محاولة تعيين معلمات filter لكل من طبقات Conv2D و Conv2DTranspose إلى 512. لاحظ أنه من أجل إنشاء مؤامرة الصورة الكامنة ثنائية الأبعاد النهائية ، ستحتاج إلى الاحتفاظ latent_dim على 2. أيضًا ، سيزيد وقت التدريب كلما زاد حجم الشبكة.

يمكنك أيضًا تجربة تطبيق VAE باستخدام مجموعة بيانات مختلفة ، مثل CIFAR-10.

يمكن تنفيذ VAEs في عدة أنماط مختلفة ومتفاوتة التعقيد. يمكنك العثور على تطبيقات إضافية في المصادر التالية:

إذا كنت ترغب في معرفة المزيد حول تفاصيل VAEs ، فيرجى الرجوع إلى مقدمة إلى VAEs Autoencoders .