 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Ten samouczek przedstawia autokodery z trzema przykładami: podstawy, odszumianie obrazu i wykrywanie anomalii.
Autokoder to specjalny rodzaj sieci neuronowej, która jest wytrenowana do kopiowania danych wejściowych do danych wyjściowych. Na przykład, mając obraz odręcznie napisanej cyfry, autokoder najpierw koduje obraz na utajoną reprezentację o niższym wymiarze, a następnie dekoduje utajoną reprezentację z powrotem do obrazu. Autoenkoder uczy się kompresować dane, minimalizując jednocześnie błąd rekonstrukcji.
Aby dowiedzieć się więcej na temat autokoderów, rozważ przeczytanie rozdziału 14 książki Deep Learning autorstwa Iana Goodfellowa, Yoshuy Bengio i Aarona Courville'a.
Importuj TensorFlow i inne biblioteki
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
Załaduj zbiór danych
Na początek nauczysz podstawowego autokodera przy użyciu zestawu danych Fashion MNIST. Każdy obraz w tym zbiorze danych ma wymiary 28 x 28 pikseli.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print (x_train.shape)
print (x_test.shape)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz 32768/29515 [=================================] - 0s 0us/step 40960/29515 [=========================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz 26427392/26421880 [==============================] - 0s 0us/step 26435584/26421880 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz 16384/5148 [===============================================================================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz 4423680/4422102 [==============================] - 0s 0us/step 4431872/4422102 [==============================] - 0s 0us/step (60000, 28, 28) (10000, 28, 28)
Pierwszy przykład: podstawowy autokoder

Zdefiniuj autokoder z dwiema warstwami Dense: encoder , który kompresuje obrazy do 64-wymiarowego wektora utajonego oraz decoder , który rekonstruuje oryginalny obraz z przestrzeni utajonej.
Aby zdefiniować swój model, użyj interfejsu API Keras Model Subclassing .
latent_dim = 64
class Autoencoder(Model):
def __init__(self, latent_dim):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential([
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Dense(784, activation='sigmoid'),
layers.Reshape((28, 28))
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Autoencoder(latent_dim)
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
Trenuj model, używając x_train jako danych wejściowych i docelowych. encoder nauczy się kompresować zestaw danych z 784 wymiarów do przestrzeni ukrytej, a decoder nauczy się rekonstruować oryginalne obrazy. .
autoencoder.fit(x_train, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test, x_test))
Epoch 1/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0243 - val_loss: 0.0140 Epoch 2/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0116 - val_loss: 0.0106 Epoch 3/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0100 - val_loss: 0.0098 Epoch 4/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0094 - val_loss: 0.0094 Epoch 5/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0092 - val_loss: 0.0092 Epoch 6/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0091 Epoch 7/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0090 Epoch 8/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0089 - val_loss: 0.0090 Epoch 9/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 Epoch 10/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 <keras.callbacks.History at 0x7ff1d35df550>
Teraz, gdy model jest wytrenowany, przetestujmy go, kodując i dekodując obrazy z zestawu testowego.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i])
plt.title("original")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i])
plt.title("reconstructed")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

Drugi przykład: odszumianie obrazu

Autokoder można również wytrenować w usuwaniu szumu z obrazów. W następnej sekcji utworzysz zaszumioną wersję zestawu danych Fashion MNIST, stosując losowy szum do każdego obrazu. Następnie nauczysz autokodera, używając zaszumionego obrazu jako wejścia i oryginalnego obrazu jako celu.
Ponownie zaimportujmy zestaw danych, aby pominąć wprowadzone wcześniej modyfikacje.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
(60000, 28, 28, 1)
Dodawanie losowego szumu do obrazów
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
Wykreśl hałaśliwe obrazy.
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()

Zdefiniuj splotowy autokoder
W tym przykładzie wytrenujesz splotowy autokoder przy użyciu warstw Conv2D w encoder i warstw Conv2DTranspose w decoder .
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
Epoch 1/10 1875/1875 [==============================] - 8s 3ms/step - loss: 0.0169 - val_loss: 0.0107 Epoch 2/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0095 - val_loss: 0.0086 Epoch 3/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0082 - val_loss: 0.0080 Epoch 4/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0078 - val_loss: 0.0077 Epoch 5/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0076 - val_loss: 0.0075 Epoch 6/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0074 - val_loss: 0.0074 Epoch 7/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0073 - val_loss: 0.0073 Epoch 8/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0072 - val_loss: 0.0072 Epoch 9/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0071 - val_loss: 0.0071 Epoch 10/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0070 - val_loss: 0.0071 <keras.callbacks.History at 0x7ff1c45a31d0>
Rzućmy okiem na podsumowanie kodera. Zwróć uwagę, że obrazy są próbkowane w dół z 28x28 do 7x7.
autoencoder.encoder.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 14, 14, 16) 160
conv2d_1 (Conv2D) (None, 7, 7, 8) 1160
=================================================================
Total params: 1,320
Trainable params: 1,320
Non-trainable params: 0
_________________________________________________________________
Dekoder upsampluje obrazy z powrotem z 7x7 do 28x28.
autoencoder.decoder.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_transpose (Conv2DTra (None, 14, 14, 8) 584
nspose)
conv2d_transpose_1 (Conv2DT (None, 28, 28, 16) 1168
ranspose)
conv2d_2 (Conv2D) (None, 28, 28, 1) 145
=================================================================
Total params: 1,897
Trainable params: 1,897
Non-trainable params: 0
_________________________________________________________________
Wykreślanie zarówno zaszumionych obrazów, jak i odszumionych obrazów wytwarzanych przez autoenkoder.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original + noise
ax = plt.subplot(2, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
bx = plt.subplot(2, n, i + n + 1)
plt.title("reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()

Trzeci przykład: wykrywanie anomalii
Przegląd
W tym przykładzie nauczysz autokodera do wykrywania anomalii w zestawie danych EKG5000 . Ten zbiór danych zawiera 5000 elektrokardiogramów , każdy ze 140 punktami danych. Użyjesz uproszczonej wersji zestawu danych, w której każdy przykład został oznaczony jako 0 (odpowiadający nieprawidłowemu rytmowi) lub 1 (odpowiadający normalnemu rytmowi). Jesteś zainteresowany identyfikacją nieprawidłowych rytmów.
Jak wykryjesz anomalie za pomocą autokodera? Przypomnij sobie, że autokoder jest wytrenowany, aby zminimalizować błąd rekonstrukcji. Wytrenujesz autokoder tylko w normalnych rytmach, a następnie użyjesz go do zrekonstruowania wszystkich danych. Nasza hipoteza jest taka, że nieprawidłowe rytmy będą miały wyższy błąd rekonstrukcji. Następnie zaklasyfikujesz rytm jako anomalię, jeśli błąd rekonstrukcji przekroczy ustalony próg.
Załaduj dane EKG
Zbiór danych, którego będziesz używać, jest oparty na zestawie z timeeriesclassification.com .
# Download the dataset
dataframe = pd.read_csv('http://storage.googleapis.com/download.tensorflow.org/data/ecg.csv', header=None)
raw_data = dataframe.values
dataframe.head()
# The last element contains the labels
labels = raw_data[:, -1]
# The other data points are the electrocadriogram data
data = raw_data[:, 0:-1]
train_data, test_data, train_labels, test_labels = train_test_split(
data, labels, test_size=0.2, random_state=21
)
Normalizuj dane do [0,1] .
min_val = tf.reduce_min(train_data)
max_val = tf.reduce_max(train_data)
train_data = (train_data - min_val) / (max_val - min_val)
test_data = (test_data - min_val) / (max_val - min_val)
train_data = tf.cast(train_data, tf.float32)
test_data = tf.cast(test_data, tf.float32)
Uczysz autoenkoder używając tylko normalnych rytmów, które są oznaczone w tym zbiorze danych jako 1 . Oddziel normalne rytmy od nieprawidłowych rytmów.
train_labels = train_labels.astype(bool)
test_labels = test_labels.astype(bool)
normal_train_data = train_data[train_labels]
normal_test_data = test_data[test_labels]
anomalous_train_data = train_data[~train_labels]
anomalous_test_data = test_data[~test_labels]
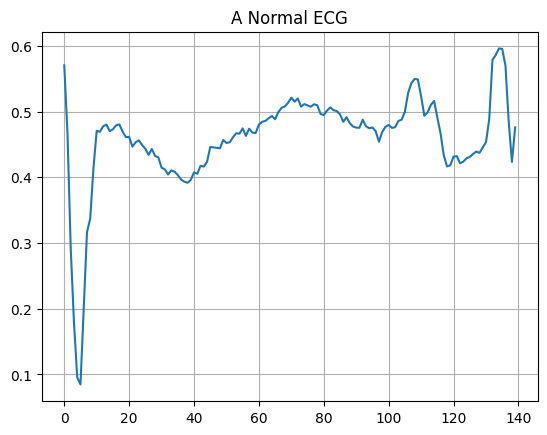
Sporządź normalne EKG.
plt.grid()
plt.plot(np.arange(140), normal_train_data[0])
plt.title("A Normal ECG")
plt.show()
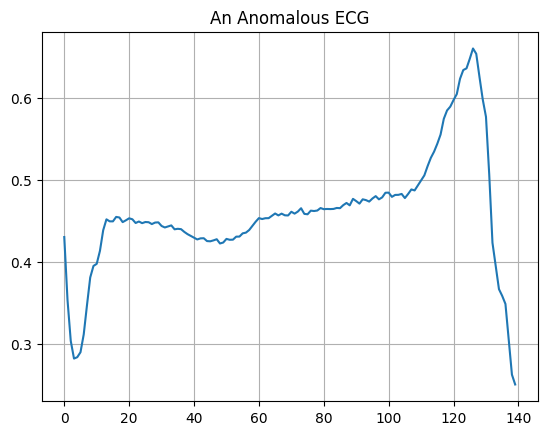
Wykreśl nieprawidłowe EKG.
plt.grid()
plt.plot(np.arange(140), anomalous_train_data[0])
plt.title("An Anomalous ECG")
plt.show()
Zbuduj model
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([
layers.Dense(16, activation="relu"),
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
autoencoder.compile(optimizer='adam', loss='mae')
Zauważ, że autokoder jest szkolony przy użyciu tylko normalnych EKG, ale jest oceniany przy użyciu pełnego zestawu testowego.
history = autoencoder.fit(normal_train_data, normal_train_data,
epochs=20,
batch_size=512,
validation_data=(test_data, test_data),
shuffle=True)
Epoch 1/20 5/5 [==============================] - 1s 33ms/step - loss: 0.0576 - val_loss: 0.0531 Epoch 2/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0552 - val_loss: 0.0514 Epoch 3/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0519 - val_loss: 0.0499 Epoch 4/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0483 - val_loss: 0.0475 Epoch 5/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0445 - val_loss: 0.0451 Epoch 6/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0409 - val_loss: 0.0432 Epoch 7/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0377 - val_loss: 0.0415 Epoch 8/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0348 - val_loss: 0.0401 Epoch 9/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0319 - val_loss: 0.0388 Epoch 10/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0293 - val_loss: 0.0378 Epoch 11/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0273 - val_loss: 0.0369 Epoch 12/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0259 - val_loss: 0.0361 Epoch 13/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0249 - val_loss: 0.0354 Epoch 14/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0239 - val_loss: 0.0346 Epoch 15/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0230 - val_loss: 0.0340 Epoch 16/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0222 - val_loss: 0.0335 Epoch 17/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0215 - val_loss: 0.0331 Epoch 18/20 5/5 [==============================] - 0s 9ms/step - loss: 0.0211 - val_loss: 0.0331 Epoch 19/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0208 - val_loss: 0.0329 Epoch 20/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0206 - val_loss: 0.0327
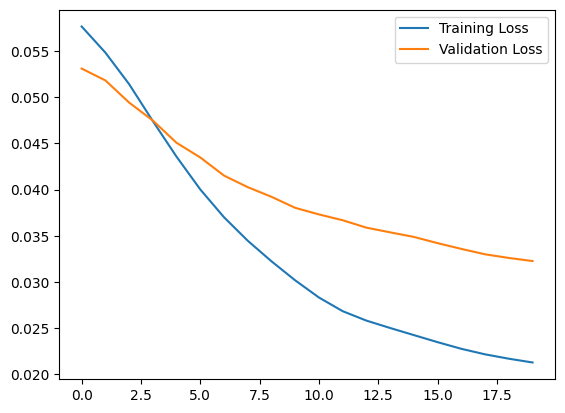
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
<matplotlib.legend.Legend at 0x7ff1d339b790>
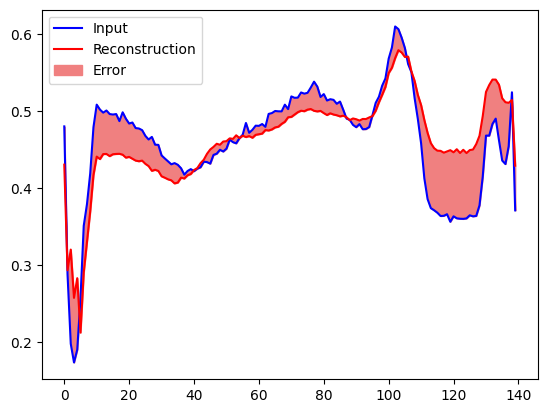
Wkrótce zaklasyfikujesz EKG jako nieprawidłowe, jeśli błąd rekonstrukcji jest większy niż jedno odchylenie standardowe od normalnych przykładów treningowych. Najpierw wykreślmy normalne EKG ze zbioru treningowego, rekonstrukcję po zakodowaniu i zdekodowaniu przez autoenkoder oraz błąd rekonstrukcji.
encoded_data = autoencoder.encoder(normal_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(normal_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], normal_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
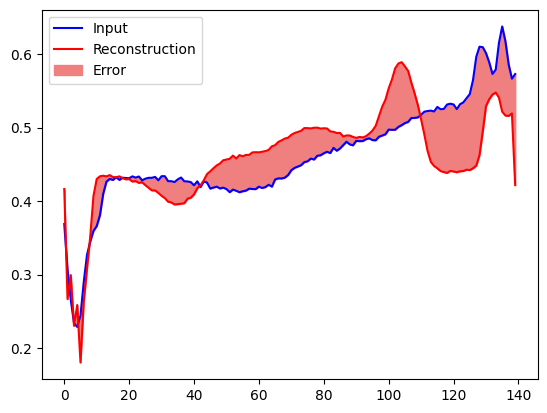
Utwórz podobny wykres, tym razem dla anomalnego przykładu testowego.
encoded_data = autoencoder.encoder(anomalous_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(anomalous_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], anomalous_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
Wykryj anomalie
Wykrywaj anomalie, obliczając, czy utrata rekonstrukcji jest większa niż ustalony próg. W tym samouczku obliczysz średni błąd średni dla normalnych przykładów ze zbioru uczącego, a następnie zaklasyfikujesz przyszłe przykłady jako anomalne, jeśli błąd rekonstrukcji jest wyższy niż jedno odchylenie standardowe ze zbioru uczącego.
Wykreśl błąd rekonstrukcji na normalnych EKG z zestawu treningowego
reconstructions = autoencoder.predict(normal_train_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_train_data)
plt.hist(train_loss[None,:], bins=50)
plt.xlabel("Train loss")
plt.ylabel("No of examples")
plt.show()

Wybierz wartość progową, która jest o jedno odchylenie standardowe powyżej średniej.
threshold = np.mean(train_loss) + np.std(train_loss)
print("Threshold: ", threshold)
Threshold: 0.03241627
Jeśli zbadasz błąd rekonstrukcji dla anomalnych przykładów w zestawie testowym, zauważysz, że większość z nich ma większy błąd rekonstrukcji niż próg. Zmieniając próg, możesz dostosować precyzję i przywołanie swojego klasyfikatora.
reconstructions = autoencoder.predict(anomalous_test_data)
test_loss = tf.keras.losses.mae(reconstructions, anomalous_test_data)
plt.hist(test_loss[None, :], bins=50)
plt.xlabel("Test loss")
plt.ylabel("No of examples")
plt.show()

Klasyfikuj EKG jako anomalię, jeśli błąd rekonstrukcji jest większy niż próg.
def predict(model, data, threshold):
reconstructions = model(data)
loss = tf.keras.losses.mae(reconstructions, data)
return tf.math.less(loss, threshold)
def print_stats(predictions, labels):
print("Accuracy = {}".format(accuracy_score(labels, predictions)))
print("Precision = {}".format(precision_score(labels, predictions)))
print("Recall = {}".format(recall_score(labels, predictions)))
preds = predict(autoencoder, test_data, threshold)
print_stats(preds, test_labels)
Accuracy = 0.944 Precision = 0.9921875 Recall = 0.9071428571428571
Następne kroki
Aby dowiedzieć się więcej o wykrywaniu anomalii za pomocą autokoderów, zapoznaj się z tym doskonałym interaktywnym przykładem zbudowanym za pomocą TensorFlow.js przez Victora Dibię. W przypadku rzeczywistego zastosowania możesz dowiedzieć się, jak Airbus wykrywa anomalie w danych telemetrycznych ISS za pomocą TensorFlow. Aby dowiedzieć się więcej o podstawach, rozważ przeczytanie tego posta na blogu autorstwa François Chollet. Więcej informacji znajdziesz w 14 rozdziale Głębokiego uczenia się Iana Goodfellowa, Yoshuy Bengio i Aarona Courville'a.
