 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
Questo tutorial introduce gli autoencoder con tre esempi: nozioni di base, denoising delle immagini e rilevamento delle anomalie.
Un autoencoder è un tipo speciale di rete neurale che viene addestrata a copiare il suo input nel suo output. Ad esempio, data l'immagine di una cifra scritta a mano, un codificatore automatico prima codifica l'immagine in una rappresentazione latente di dimensioni inferiori, quindi decodifica la rappresentazione latente in un'immagine. Un autoencoder impara a comprimere i dati riducendo al minimo l'errore di ricostruzione.
Per saperne di più sugli autoencoder, ti invitiamo a leggere il capitolo 14 di Deep Learning di Ian Goodfellow, Yoshua Bengio e Aaron Courville.
Importa TensorFlow e altre librerie
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
Carica il set di dati
Per iniziare, addestrerai l'autoencoder di base utilizzando il set di dati Fashion MNIST. Ogni immagine in questo set di dati è 28x28 pixel.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print (x_train.shape)
print (x_test.shape)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz 32768/29515 [=================================] - 0s 0us/step 40960/29515 [=========================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz 26427392/26421880 [==============================] - 0s 0us/step 26435584/26421880 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz 16384/5148 [===============================================================================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz 4423680/4422102 [==============================] - 0s 0us/step 4431872/4422102 [==============================] - 0s 0us/step (60000, 28, 28) (10000, 28, 28)
Primo esempio: codificatore automatico di base

Definire un autoencoder con due livelli Dense: un encoder , che comprime le immagini in un vettore latente a 64 dimensioni, e un decoder , che ricostruisce l'immagine originale dallo spazio latente.
Per definire il tuo modello, usa l' API Keras Model Subclassing .
latent_dim = 64
class Autoencoder(Model):
def __init__(self, latent_dim):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential([
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Dense(784, activation='sigmoid'),
layers.Reshape((28, 28))
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Autoencoder(latent_dim)
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
Addestra il modello usando x_train sia come input che come target. Il encoder imparerà a comprimere il set di dati da 784 dimensioni allo spazio latente e il decoder imparerà a ricostruire le immagini originali. .
autoencoder.fit(x_train, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test, x_test))
Epoch 1/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0243 - val_loss: 0.0140 Epoch 2/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0116 - val_loss: 0.0106 Epoch 3/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0100 - val_loss: 0.0098 Epoch 4/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0094 - val_loss: 0.0094 Epoch 5/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0092 - val_loss: 0.0092 Epoch 6/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0091 Epoch 7/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0090 Epoch 8/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0089 - val_loss: 0.0090 Epoch 9/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 Epoch 10/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 <keras.callbacks.History at 0x7ff1d35df550>
Ora che il modello è stato addestrato, testiamolo codificando e decodificando le immagini dal set di test.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i])
plt.title("original")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i])
plt.title("reconstructed")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

Secondo esempio: denoising dell'immagine

È anche possibile addestrare un codificatore automatico per rimuovere il rumore dalle immagini. Nella sezione seguente, creerai una versione rumorosa del set di dati Fashion MNIST applicando un rumore casuale a ciascuna immagine. Quindi addestrerai un codificatore automatico usando l'immagine rumorosa come input e l'immagine originale come target.
Reimportiamo il set di dati per omettere le modifiche apportate in precedenza.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
(60000, 28, 28, 1)
Aggiunta di rumore casuale alle immagini
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
Traccia le immagini rumorose.
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()

Definire un autoencoder convoluzionale
In questo esempio, addestrerai un codificatore automatico convoluzionale utilizzando i livelli Conv2D encoder e i livelli Conv2DTranspose nel decoder .
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
Epoch 1/10 1875/1875 [==============================] - 8s 3ms/step - loss: 0.0169 - val_loss: 0.0107 Epoch 2/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0095 - val_loss: 0.0086 Epoch 3/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0082 - val_loss: 0.0080 Epoch 4/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0078 - val_loss: 0.0077 Epoch 5/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0076 - val_loss: 0.0075 Epoch 6/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0074 - val_loss: 0.0074 Epoch 7/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0073 - val_loss: 0.0073 Epoch 8/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0072 - val_loss: 0.0072 Epoch 9/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0071 - val_loss: 0.0071 Epoch 10/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0070 - val_loss: 0.0071 <keras.callbacks.History at 0x7ff1c45a31d0>
Diamo un'occhiata a un riepilogo dell'encoder. Nota come le immagini vengono sottocampionate da 28x28 a 7x7.
autoencoder.encoder.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 14, 14, 16) 160
conv2d_1 (Conv2D) (None, 7, 7, 8) 1160
=================================================================
Total params: 1,320
Trainable params: 1,320
Non-trainable params: 0
_________________________________________________________________
Il decoder ricampiona le immagini da 7x7 a 28x28.
autoencoder.decoder.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_transpose (Conv2DTra (None, 14, 14, 8) 584
nspose)
conv2d_transpose_1 (Conv2DT (None, 28, 28, 16) 1168
ranspose)
conv2d_2 (Conv2D) (None, 28, 28, 1) 145
=================================================================
Total params: 1,897
Trainable params: 1,897
Non-trainable params: 0
_________________________________________________________________
Tracciare sia le immagini rumorose che le immagini denoise prodotte dall'autoencoder.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original + noise
ax = plt.subplot(2, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
bx = plt.subplot(2, n, i + n + 1)
plt.title("reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()

Terzo esempio: rilevamento delle anomalie
Panoramica
In questo esempio, addestrerai un codificatore automatico per rilevare le anomalie sul set di dati ECG5000 . Questo set di dati contiene 5.000 elettrocardiogrammi , ciascuno con 140 punti dati. Utilizzerai una versione semplificata del set di dati, in cui ogni esempio è stato etichettato come 0 (corrispondente a un ritmo anomalo) o 1 (corrispondente a un ritmo normale). Sei interessato a identificare i ritmi anormali.
Come rileverai le anomalie utilizzando un autoencoder? Ricordiamo che un autoencoder è addestrato per ridurre al minimo l'errore di ricostruzione. Addestrerai un autoencoder solo sui ritmi normali, quindi lo utilizzerai per ricostruire tutti i dati. La nostra ipotesi è che i ritmi anormali avranno un errore di ricostruzione maggiore. Classificherai quindi un ritmo come anomalia se l'errore di ricostruzione supera una soglia fissa.
Carica dati ECG
Il set di dati che utilizzerai è basato su uno di timeseriesclassification.com .
# Download the dataset
dataframe = pd.read_csv('http://storage.googleapis.com/download.tensorflow.org/data/ecg.csv', header=None)
raw_data = dataframe.values
dataframe.head()
# The last element contains the labels
labels = raw_data[:, -1]
# The other data points are the electrocadriogram data
data = raw_data[:, 0:-1]
train_data, test_data, train_labels, test_labels = train_test_split(
data, labels, test_size=0.2, random_state=21
)
Normalizza i dati su [0,1] .
min_val = tf.reduce_min(train_data)
max_val = tf.reduce_max(train_data)
train_data = (train_data - min_val) / (max_val - min_val)
test_data = (test_data - min_val) / (max_val - min_val)
train_data = tf.cast(train_data, tf.float32)
test_data = tf.cast(test_data, tf.float32)
Addestrerai l'autoencoder usando solo i ritmi normali, che sono etichettati in questo set di dati come 1 . Separare i ritmi normali da quelli anormali.
train_labels = train_labels.astype(bool)
test_labels = test_labels.astype(bool)
normal_train_data = train_data[train_labels]
normal_test_data = test_data[test_labels]
anomalous_train_data = train_data[~train_labels]
anomalous_test_data = test_data[~test_labels]
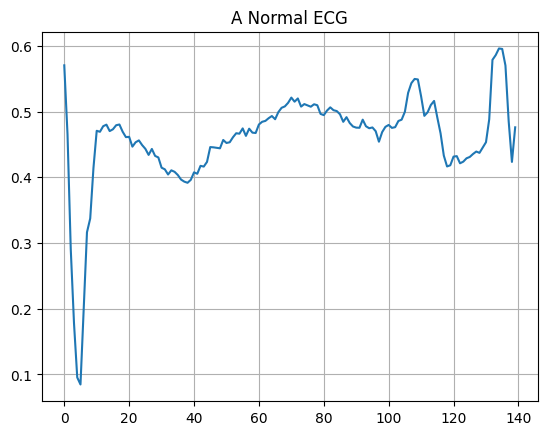
Traccia un ECG normale.
plt.grid()
plt.plot(np.arange(140), normal_train_data[0])
plt.title("A Normal ECG")
plt.show()
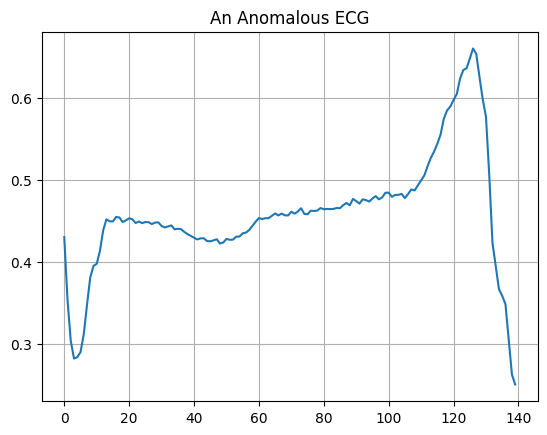
Traccia un ECG anomalo.
plt.grid()
plt.plot(np.arange(140), anomalous_train_data[0])
plt.title("An Anomalous ECG")
plt.show()
Costruisci il modello
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([
layers.Dense(16, activation="relu"),
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
autoencoder.compile(optimizer='adam', loss='mae')
Si noti che l'autocodificatore viene addestrato utilizzando solo i normali ECG, ma viene valutato utilizzando l'intero set di test.
history = autoencoder.fit(normal_train_data, normal_train_data,
epochs=20,
batch_size=512,
validation_data=(test_data, test_data),
shuffle=True)
Epoch 1/20 5/5 [==============================] - 1s 33ms/step - loss: 0.0576 - val_loss: 0.0531 Epoch 2/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0552 - val_loss: 0.0514 Epoch 3/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0519 - val_loss: 0.0499 Epoch 4/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0483 - val_loss: 0.0475 Epoch 5/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0445 - val_loss: 0.0451 Epoch 6/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0409 - val_loss: 0.0432 Epoch 7/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0377 - val_loss: 0.0415 Epoch 8/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0348 - val_loss: 0.0401 Epoch 9/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0319 - val_loss: 0.0388 Epoch 10/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0293 - val_loss: 0.0378 Epoch 11/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0273 - val_loss: 0.0369 Epoch 12/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0259 - val_loss: 0.0361 Epoch 13/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0249 - val_loss: 0.0354 Epoch 14/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0239 - val_loss: 0.0346 Epoch 15/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0230 - val_loss: 0.0340 Epoch 16/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0222 - val_loss: 0.0335 Epoch 17/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0215 - val_loss: 0.0331 Epoch 18/20 5/5 [==============================] - 0s 9ms/step - loss: 0.0211 - val_loss: 0.0331 Epoch 19/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0208 - val_loss: 0.0329 Epoch 20/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0206 - val_loss: 0.0327
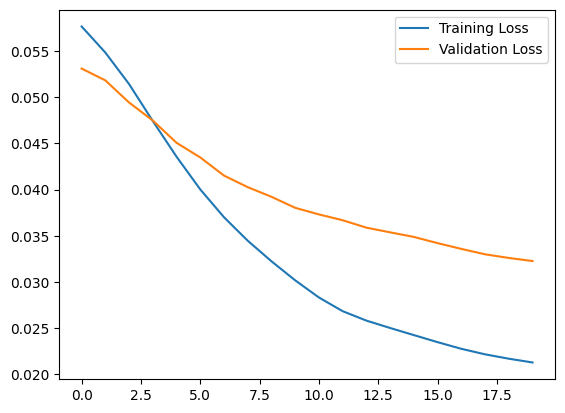
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
<matplotlib.legend.Legend at 0x7ff1d339b790>
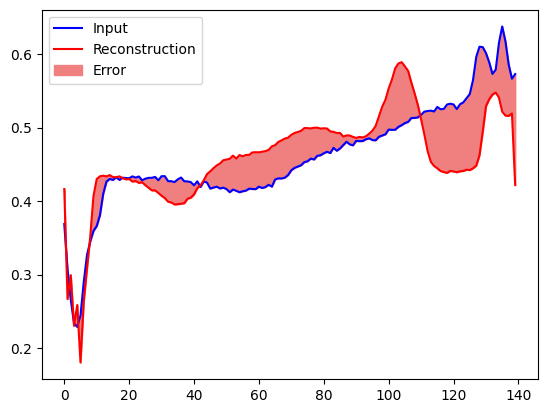
Presto classificherai un ECG come anomalo se l'errore di ricostruzione è maggiore di una deviazione standard dai normali esempi di addestramento. Per prima cosa, tracciamo un normale ECG dal set di addestramento, la ricostruzione dopo che è stato codificato e decodificato dall'autocodificatore e l'errore di ricostruzione.
encoded_data = autoencoder.encoder(normal_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(normal_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], normal_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()

Crea una trama simile, questa volta per un esempio di test anomalo.
encoded_data = autoencoder.encoder(anomalous_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(anomalous_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], anomalous_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
Rileva le anomalie
Rileva le anomalie calcolando se la perdita di ricostruzione è maggiore di una soglia fissa. In questo tutorial, calcolerai l'errore medio medio per esempi normali dal set di addestramento, quindi classificherai gli esempi futuri come anomali se l'errore di ricostruzione è maggiore di una deviazione standard dal set di addestramento.
Tracciare l'errore di ricostruzione sugli ECG normali dal set di addestramento
reconstructions = autoencoder.predict(normal_train_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_train_data)
plt.hist(train_loss[None,:], bins=50)
plt.xlabel("Train loss")
plt.ylabel("No of examples")
plt.show()

Scegli un valore di soglia che sia una deviazione standard sopra la media.
threshold = np.mean(train_loss) + np.std(train_loss)
print("Threshold: ", threshold)
Threshold: 0.03241627
Se esamini l'errore di ricostruzione per gli esempi anomali nel set di test, noterai che la maggior parte ha un errore di ricostruzione maggiore della soglia. Variando la soglia, puoi regolare la precisione e il richiamo del tuo classificatore.
reconstructions = autoencoder.predict(anomalous_test_data)
test_loss = tf.keras.losses.mae(reconstructions, anomalous_test_data)
plt.hist(test_loss[None, :], bins=50)
plt.xlabel("Test loss")
plt.ylabel("No of examples")
plt.show()

Classificare un ECG come anomalia se l'errore di ricostruzione è maggiore della soglia.
def predict(model, data, threshold):
reconstructions = model(data)
loss = tf.keras.losses.mae(reconstructions, data)
return tf.math.less(loss, threshold)
def print_stats(predictions, labels):
print("Accuracy = {}".format(accuracy_score(labels, predictions)))
print("Precision = {}".format(precision_score(labels, predictions)))
print("Recall = {}".format(recall_score(labels, predictions)))
preds = predict(autoencoder, test_data, threshold)
print_stats(preds, test_labels)
Accuracy = 0.944 Precision = 0.9921875 Recall = 0.9071428571428571
Prossimi passi
Per saperne di più sul rilevamento delle anomalie con gli autoencoder, dai un'occhiata a questo eccellente esempio interattivo creato con TensorFlow.js da Victor Dibia. Per un caso d'uso nel mondo reale, puoi scoprire come Airbus rileva le anomalie nei dati di telemetria della ISS utilizzando TensorFlow. Per saperne di più sulle basi, prendi in considerazione la lettura di questo post sul blog di François Chollet. Per maggiori dettagli, consulta il capitolo 14 di Deep Learning di Ian Goodfellow, Yoshua Bengio e Aaron Courville.
