 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Giới thiệu về gradient và hướng dẫn phân biệt tự động bao gồm mọi thứ cần thiết để tính toán gradient trong TensorFlow. Hướng dẫn này tập trung vào các tính năng sâu hơn, ít phổ biến hơn của API tf.GradientTape .
Thành lập
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
Kiểm soát ghi gradient
Trong hướng dẫn phân biệt tự động , bạn đã thấy cách kiểm soát biến và độ căng nào được băng theo dõi trong khi xây dựng phép tính gradient.
Băng cũng có các phương pháp để thao tác ghi âm.
Dừng ghi
Nếu bạn muốn dừng ghi gradient, bạn có thể sử dụng tf.GradientTape.stop_recording để tạm ngừng ghi.
Điều này có thể hữu ích để giảm chi phí nếu bạn không muốn phân biệt một hoạt động phức tạp ở giữa mô hình của mình. Điều này có thể bao gồm việc tính toán một số liệu hoặc một kết quả trung gian:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Đặt lại / bắt đầu ghi từ đầu
Nếu bạn muốn bắt đầu lại hoàn toàn, hãy sử dụng tf.GradientTape.reset . Chỉ cần thoát khỏi khối băng gradient và khởi động lại thường dễ đọc hơn, nhưng bạn có thể sử dụng phương pháp reset khi việc thoát khỏi khối băng khó hoặc không thể.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Dừng dòng chảy gradient với độ chính xác
Trái ngược với các điều khiển băng chung ở trên, hàm tf.stop_gradient chính xác hơn nhiều. Nó có thể được sử dụng để ngăn các gradient chảy dọc theo một đường cụ thể mà không cần truy cập vào chính băng:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Gradient tùy chỉnh
Trong một số trường hợp, bạn có thể muốn kiểm soát chính xác cách tính độ dốc thay vì sử dụng giá trị mặc định. Những tình huống này bao gồm:
- Không có gradient xác định cho một op mới mà bạn đang viết.
- Các tính toán mặc định không ổn định về mặt số học.
- Bạn muốn lưu vào bộ nhớ cache một tính toán đắt tiền từ chuyển tiếp.
- Bạn muốn sửa đổi một giá trị (ví dụ: sử dụng
tf.clip_by_valuehoặctf.math.round) mà không cần sửa đổi gradient.
Đối với trường hợp đầu tiên, để viết một op mới, bạn có thể sử dụng tf.RegisterGradient để thiết lập của riêng bạn (tham khảo tài liệu API để biết thêm chi tiết). (Lưu ý rằng sổ đăng ký gradient là toàn cầu, vì vậy hãy thay đổi nó một cách thận trọng.)
Đối với ba trường hợp sau, bạn có thể sử dụng tf.custom_gradient .
Đây là một ví dụ áp dụng tf.clip_by_norm cho gradient trung gian:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
Tham khảo tài liệu API trang trí tf.custom_gradient để biết thêm chi tiết.
Gradient tùy chỉnh trong SavedModel
Gradient tùy chỉnh có thể được lưu vào SavedModel bằng cách sử dụng tùy chọn tf.saved_model.SaveOptions(experimental_custom_gradients=True) .
Để được lưu vào SavedModel, hàm gradient phải có thể theo dõi được (để tìm hiểu thêm, hãy xem hướng dẫn Hiệu suất tốt hơn với tf . Chức năng).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
Lưu ý về ví dụ trên: Nếu bạn thử thay thế đoạn mã trên bằng tf.saved_model.SaveOptions(experimental_custom_gradients=False) , gradient sẽ vẫn tạo ra cùng một kết quả khi tải. Lý do là sổ đăng ký gradient vẫn chứa gradient tùy chỉnh được sử dụng trong hàm call_custom_op . Tuy nhiên, nếu bạn khởi động lại thời gian chạy sau khi lưu mà không có gradient tùy chỉnh, việc chạy mô hình được tải trong tf.GradientTape sẽ gây ra lỗi: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
Nhiều băng
Nhiều băng tương tác liền mạch.
Ví dụ: ở đây, mỗi băng đồng hồ một bộ tensors khác nhau:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
Gradient bậc cao hơn
Các hoạt động bên trong trình quản lý ngữ cảnh tf.GradientTape được ghi lại để tự động phân biệt. Nếu gradient được tính toán trong ngữ cảnh đó, thì quá trình tính toán gradient cũng được ghi lại. Kết quả là, cùng một API chính xác cũng hoạt động cho các gradient bậc cao hơn.
Ví dụ:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
Mặc dù điều đó cung cấp cho bạn đạo hàm cấp hai của một hàm vô hướng , nhưng mẫu này không tổng quát hóa để tạo ra ma trận Hessian, vì tf.GradientTape.gradient chỉ tính toán gradient của một đại lượng vô hướng. Để xây dựng ma trận Hessian , hãy đi tới ví dụ Hessian trong phần Jacobian .
"Các lệnh gọi lồng nhau tới tf.GradientTape.gradient " là một mẫu hay khi bạn tính toán đại lượng vô hướng từ một gradient và sau đó đại lượng vô hướng kết quả hoạt động như một nguồn cho phép tính gradient thứ hai, như trong ví dụ sau.
Ví dụ: Điều chỉnh độ dốc đầu vào
Nhiều mô hình dễ bị "ví dụ đối nghịch". Tập hợp các kỹ thuật này sửa đổi đầu vào của mô hình để làm nhầm lẫn đầu ra của mô hình. Cách triển khai đơn giản nhất — chẳng hạn như ví dụ Adversarial sử dụng cuộc tấn công Fast Gradient Signed Method — thực hiện một bước duy nhất dọc theo gradient của đầu ra đối với đầu vào; "gradient đầu vào".
Một kỹ thuật để tăng độ chắc chắn cho các ví dụ đối nghịch là điều hòa gradient đầu vào (Finlay & Oberman, 2019), cố gắng giảm thiểu độ lớn của gradient đầu vào. Nếu gradient đầu vào nhỏ, thì sự thay đổi trong đầu ra cũng phải nhỏ.
Dưới đây là một triển khai đơn giản của chính quy gradient đầu vào. Cách thực hiện là:
- Tính toán gradient của đầu ra đối với đầu vào bằng cách sử dụng một băng trong.
- Tính độ lớn của gradient đầu vào đó.
- Tính gradient của độ lớn đó đối với mô hình.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
Người Gia-cốp
Tất cả các ví dụ trước đã lấy gradient của một mục tiêu vô hướng đối với một số tensor nguồn.
Ma trận Jacobian biểu thị các bậc của một hàm có giá trị vectơ. Mỗi hàng chứa gradient của một trong các phần tử của vectơ.
Phương thức tf.GradientTape.jacobian cho phép bạn tính toán một cách hiệu quả ma trận Jacobian.
Lưu ý rằng:
- Giống như
gradient: Đối sốsourcescó thể là một tensor hoặc một vùng chứa tensor. - Không giống như
gradient: tensortargetphải là một tensor duy nhất.
Nguồn vô hướng
Ví dụ đầu tiên, đây là Jacobian của một vector-target đối với một nguồn vô hướng.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
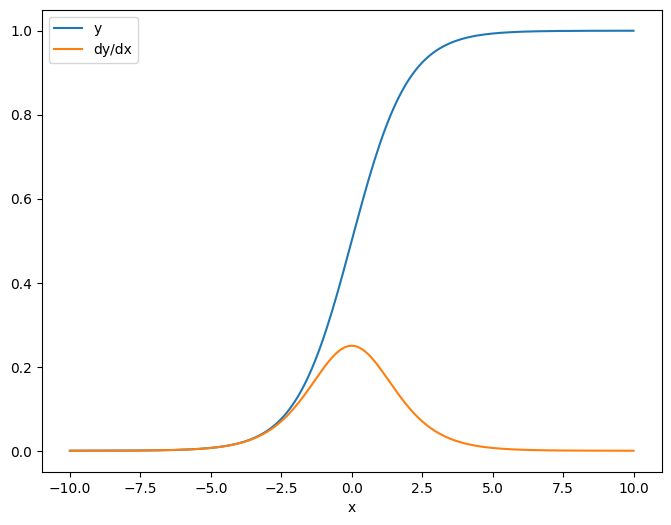
Khi bạn sử dụng Jacobian đối với một đại lượng vô hướng, kết quả có hình dạng của mục tiêu và cung cấp độ dốc của từng phần tử đối với nguồn:
print(y.shape)
print(dy_dx.shape)
(201,) (201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
Nguồn căng
Cho dù đầu vào là vô hướng hay tensor, tf.GradientTape.jacobian tính toán hiệu quả gradient của từng phần tử của nguồn đối với từng phần tử của (các) đích.
Ví dụ: đầu ra của lớp này có hình dạng là (10, 7) :
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
Và hình dạng hạt nhân của lớp là (5, 10) :
layer.kernel.shape
TensorShape([5, 10])
Hình dạng của Jacobian của đầu ra đối với hạt nhân là hai hình dạng đó được ghép với nhau:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
Nếu bạn tính tổng trên các kích thước của mục tiêu, bạn sẽ còn lại với gradient của tổng sẽ được tính toán bởi tf.GradientTape.gradient :
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
Ví dụ: Hessian
Mặc dù tf.GradientTape không cung cấp một phương pháp rõ ràng để xây dựng ma trận Hessian , nhưng có thể xây dựng một phương thức bằng phương pháp tf.GradientTape.jacobian .
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
Để sử dụng Hessian này cho một bước phương pháp Newton , trước tiên bạn phải làm phẳng các trục của nó thành một ma trận và làm phẳng gradient thành một vectơ:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
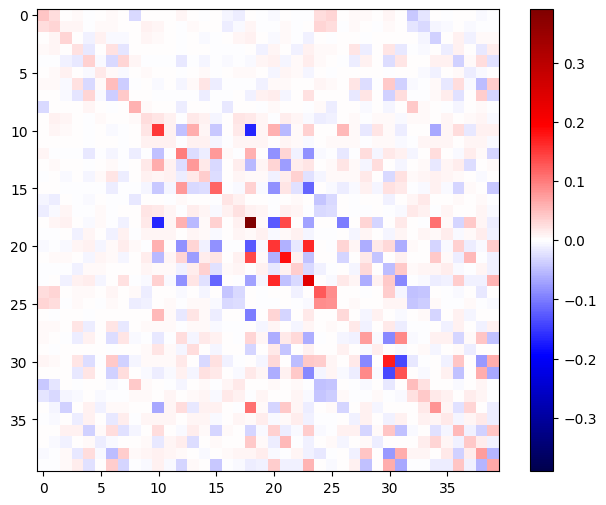
Ma trận Hessian phải là đối xứng:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
Bước cập nhật phương pháp Newton được hiển thị bên dưới:
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
Mặc dù điều này tương đối đơn giản đối với một tf.Variable duy nhất, việc áp dụng điều này cho một mô hình không tầm thường sẽ yêu cầu ghép và cắt cẩn thận để tạo ra một Hessian đầy đủ trên nhiều biến.
Batch Jacobian
Trong một số trường hợp, bạn muốn lấy Jacobian của mỗi chồng mục tiêu đối với chồng nguồn, trong đó các Jacobians cho mỗi cặp nguồn đích là độc lập.
Ví dụ, ở đây đầu vào x được định hình (batch, ins) và đầu ra y được định hình (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
Jacobian đầy đủ của y đối với x có hình dạng là (batch, ins, batch, outs) , ngay cả khi bạn chỉ muốn (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
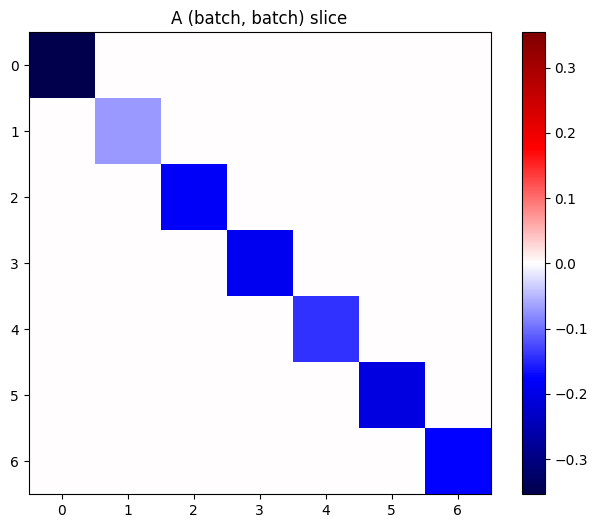
Nếu các gradient của mỗi mục trong ngăn xếp là độc lập, thì mọi lát (batch, batch) của tensor này là một ma trận đường chéo:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
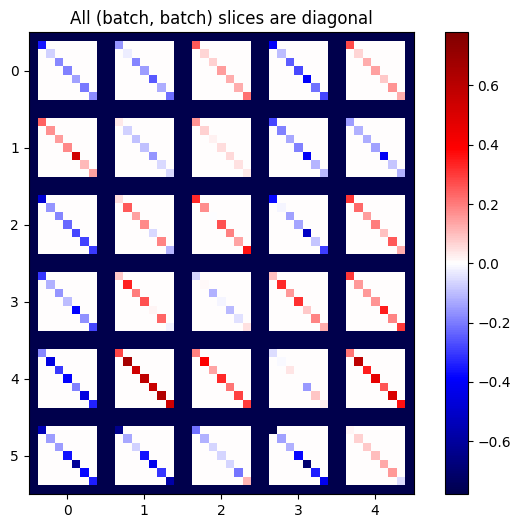
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
Để có được kết quả mong muốn, bạn có thể tính tổng trên thứ nguyên batch trùng lặp hoặc chọn các đường chéo bằng cách sử dụng tf.einsum :
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
Sẽ hiệu quả hơn nhiều nếu thực hiện phép tính mà không có thêm thứ nguyên ngay từ đầu. Phương thức tf.GradientTape.batch_jacobian thực hiện chính xác điều đó:
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
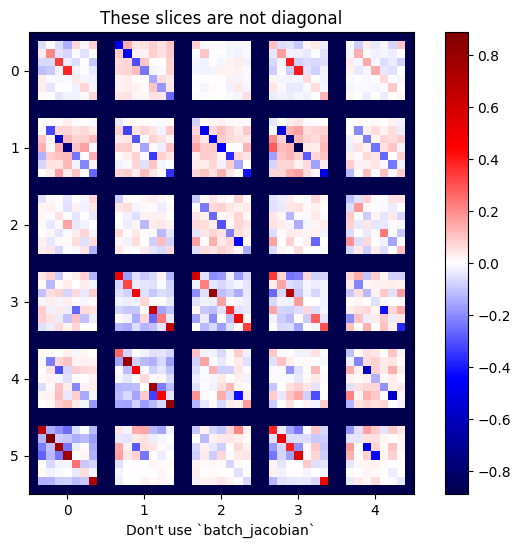
Trong trường hợp này, batch_jacobian vẫn chạy và trả về một thứ gì đó có hình dạng mong đợi, nhưng nội dung của nó có ý nghĩa không rõ ràng:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
