 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Ce didacticiel est une introduction à la prévision de séries temporelles à l'aide de TensorFlow. Il construit différents styles de modèles, notamment les réseaux de neurones convolutifs et récurrents (CNN et RNN).
Ceci est couvert en deux parties principales, avec des sous-sections :
- Prévision pour un seul pas de temps :
- Une seule fonctionnalité.
- Toutes les fonctionnalités.
- Prévoyez plusieurs étapes :
- Single-shot : Faites toutes les prédictions en même temps.
- Autorégressif : faites une prédiction à la fois et renvoyez la sortie au modèle.
Installer
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
Le jeu de données météo
Ce didacticiel utilise un ensemble de données de séries chronologiques météorologiques enregistrées par l' Institut Max Planck de biogéochimie .
Cet ensemble de données contient 14 caractéristiques différentes telles que la température de l'air, la pression atmosphérique et l'humidité. Celles-ci ont été collectées toutes les 10 minutes, à partir de 2003. Par souci d'efficacité, vous n'utiliserez que les données collectées entre 2009 et 2016. Cette partie du jeu de données a été préparée par François Chollet pour son livre Deep Learning with Python .
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
Ce didacticiel ne traitera que des prévisions horaires , alors commencez par sous-échantillonner les données d'intervalles de 10 minutes à des intervalles d'une heure :
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Jetons un coup d'œil aux données. Voici les premières lignes :
df.head()
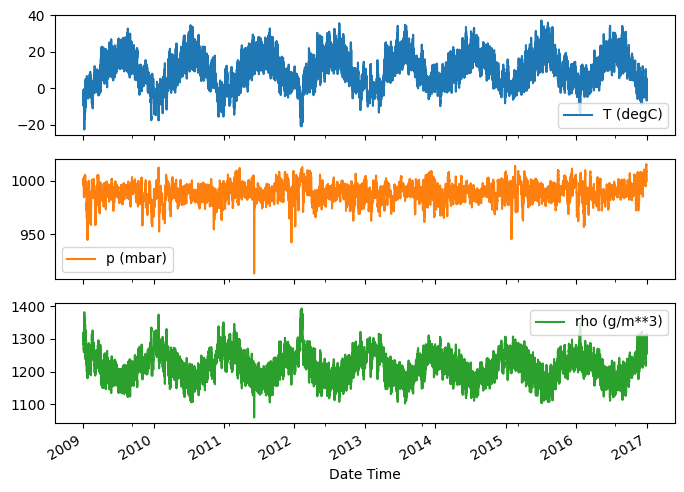
Voici l'évolution de quelques fonctionnalités au fil du temps :
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
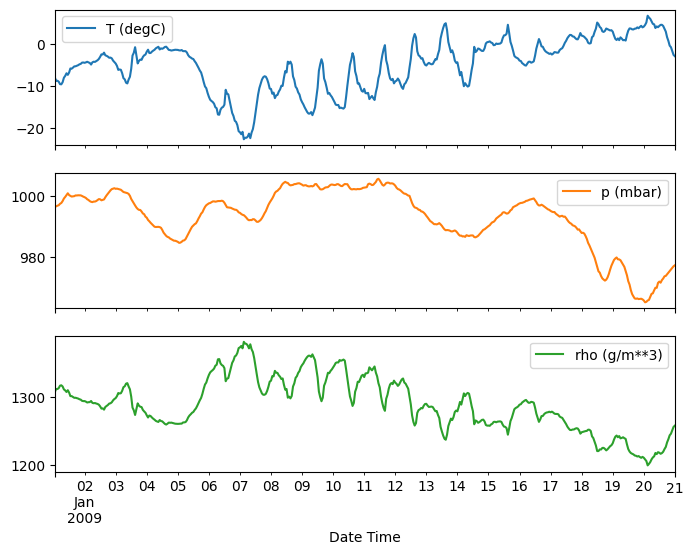
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
Inspecter et nettoyer
Ensuite, regardez les statistiques de l'ensemble de données :
df.describe().transpose()
Vitesse du vent
Une chose qui devrait se démarquer est la valeur min des colonnes de vitesse du vent ( wv (m/s) ) et la valeur maximale ( max. wv (m/s) ). Ce -9999 est probablement erroné.
Il y a une colonne de direction du vent séparée, donc la vitesse doit être supérieure à zéro ( >=0 ). Remplacez-le par des zéros :
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Ingénierie des fonctionnalités
Avant de plonger dans la création d'un modèle, il est important de comprendre vos données et de vous assurer que vous transmettez au modèle des données formatées de manière appropriée.
Vent
La dernière colonne des données, wd (deg) — donne la direction du vent en degrés. Les angles ne font pas de bonnes entrées de modèle : 360° et 0° doivent être proches l'un de l'autre et s'enrouler en douceur. La direction ne devrait pas avoir d'importance si le vent ne souffle pas.
À l'heure actuelle, la distribution des données de vent ressemble à ceci :
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
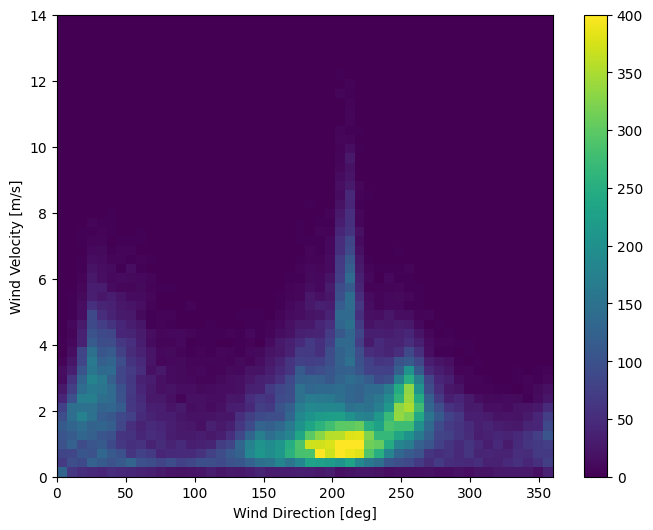
Mais cela sera plus facile à interpréter pour le modèle si vous convertissez les colonnes de direction et de vitesse du vent en un vecteur vent :
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
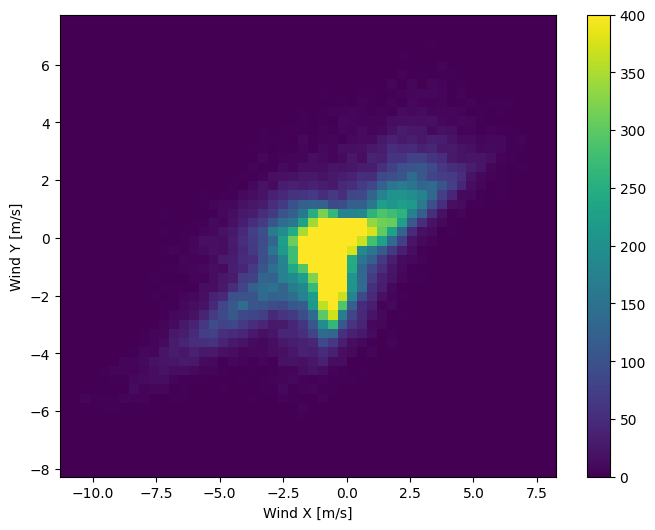
La distribution des vecteurs vent est beaucoup plus simple à interpréter correctement par le modèle :
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
Temps
De même, la colonne Date Time est très utile, mais pas sous cette forme de chaîne. Commencez par le convertir en secondes :
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Semblable à la direction du vent, le temps en secondes n'est pas une entrée de modèle utile. En tant que données météorologiques, elles ont une périodicité quotidienne et annuelle claire. Il existe de nombreuses façons de gérer la périodicité.
Vous pouvez obtenir des signaux utilisables en utilisant des transformations sinus et cosinus pour effacer les signaux « Heure de la journée » et « Période de l'année » :
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
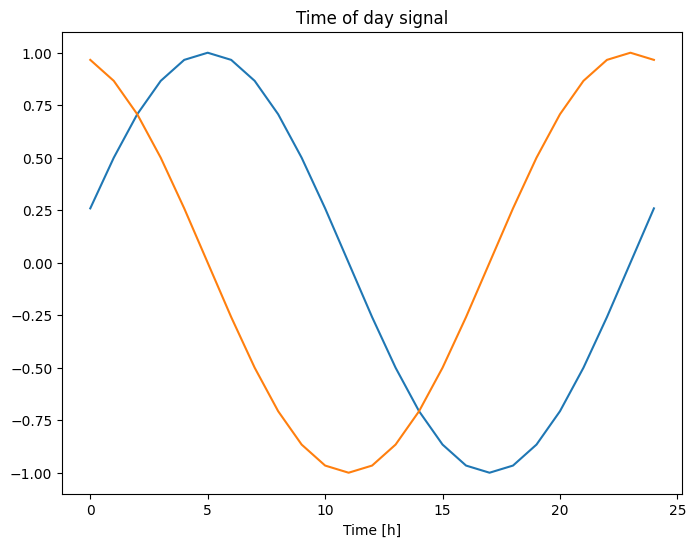
Cela donne au modèle l'accès aux caractéristiques de fréquence les plus importantes. Dans ce cas, vous saviez à l'avance quelles fréquences étaient importantes.
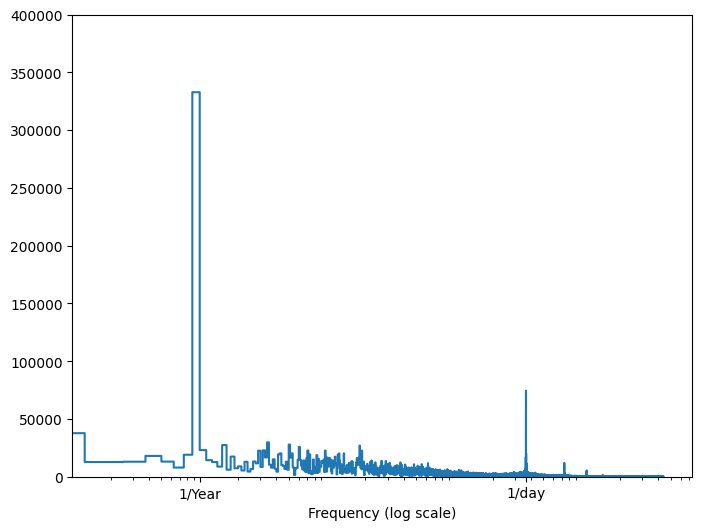
Si vous ne disposez pas de ces informations, vous pouvez déterminer quelles fréquences sont importantes en extrayant des caractéristiques avec Fast Fourier Transform . Pour vérifier les hypothèses, voici le tf.signal.rfft de la température en fonction du temps. Notez les pics évidents à des fréquences proches de 1/year et 1/day :
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
Diviser les données
Vous utiliserez une répartition (70%, 20%, 10%) pour les ensembles d'entraînement, de validation et de test. Notez que les données ne sont pas mélangées de manière aléatoire avant le fractionnement. C'est pour deux raisons:
- Il garantit que le découpage des données en fenêtres d'échantillons consécutifs est toujours possible.
- Il garantit que les résultats de validation/test sont plus réalistes, étant évalués sur les données collectées après la formation du modèle.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Normaliser les données
Il est important de mettre à l'échelle les fonctionnalités avant de former un réseau de neurones. La normalisation est une façon courante d'effectuer cette mise à l'échelle : soustrayez la moyenne et divisez par l'écart type de chaque caractéristique.
La moyenne et l'écart type ne doivent être calculés qu'à l'aide des données d'apprentissage afin que les modèles n'aient pas accès aux valeurs des ensembles de validation et de test.
On peut également soutenir que le modèle ne devrait pas avoir accès aux valeurs futures de l'ensemble de formation lors de la formation, et que cette normalisation devrait être effectuée à l'aide de moyennes mobiles. Ce n'est pas l'objet de ce didacticiel, et les ensembles de validation et de test garantissent que vous obtenez des métriques (quelque peu) honnêtes. Ainsi, dans un souci de simplicité, ce didacticiel utilise une moyenne simple.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
Maintenant, jetez un coup d'œil à la distribution des fonctionnalités. Certaines caractéristiques ont de longues queues, mais il n'y a pas d'erreurs évidentes comme la valeur de vitesse du vent -9999 .
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

Fenêtrage des données
Les modèles de ce tutoriel feront un ensemble de prédictions basées sur une fenêtre d'échantillons consécutifs à partir des données.
Les principales caractéristiques des fenêtres de saisie sont :
- La largeur (nombre de pas de temps) des fenêtres d'entrée et d'étiquette.
- Le décalage horaire entre eux.
- Quelles fonctionnalités sont utilisées comme entrées, étiquettes ou les deux.
Ce didacticiel construit une variété de modèles (y compris les modèles linéaires, DNN, CNN et RNN) et les utilise pour les deux :
- Prédictions à sortie unique et à sorties multiples .
- Prédictions à un seul pas de temps et à plusieurs pas de temps .
Cette section se concentre sur la mise en œuvre du fenêtrage des données afin qu'il puisse être réutilisé pour tous ces modèles.
Selon la tâche et le type de modèle, vous souhaiterez peut-être générer diverses fenêtres de données. Voici quelques exemples:
Par exemple, pour faire une seule prédiction 24 heures dans le futur, compte tenu de 24 heures d'historique, vous pouvez définir une fenêtre comme celle-ci :
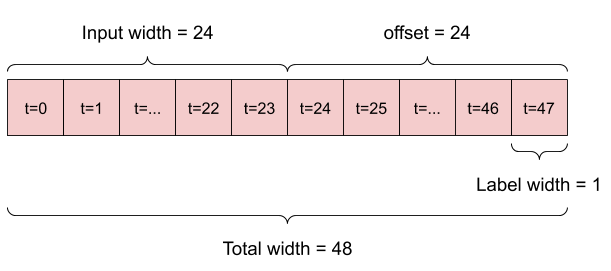
Un modèle qui fait une prédiction une heure dans le futur, compte tenu de six heures d'historique, aurait besoin d'une fenêtre comme celle-ci :

Le reste de cette section définit une classe WindowGenerator . Cette classe peut :
- Gérez les index et les décalages comme indiqué dans les schémas ci-dessus.
- Divisez les fenêtres de fonctionnalités en paires
(features, labels). - Tracez le contenu des fenêtres résultantes.
- Générez efficacement des lots de ces fenêtres à partir des données de formation, d'évaluation et de test, à l'aide
tf.data.Datasets.
1. Index et décalages
Commencez par créer la classe WindowGenerator . La méthode __init__ inclut toute la logique nécessaire pour les index d'entrée et d'étiquette.
Il prend également la formation, l'évaluation et le test DataFrames en entrée. Ceux-ci seront convertis en tf.data.Dataset s de fenêtres plus tard.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Voici le code pour créer les 2 fenêtres présentées dans les schémas au début de cette section :
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Diviser
Étant donné une liste d'entrées consécutives, la méthode split_window les convertira en une fenêtre d'entrées et une fenêtre d'étiquettes.
L'exemple w2 que vous avez défini précédemment sera divisé comme ceci :
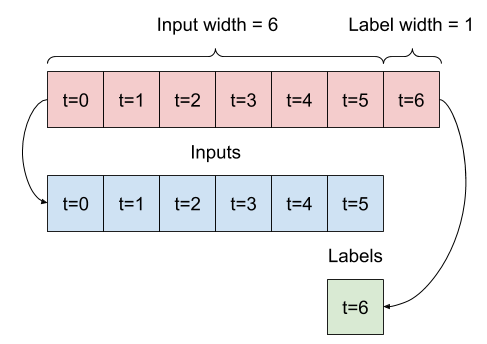
Ce diagramme ne montre pas l'axe des features des données, mais cette fonction split_window gère également les label_columns afin qu'elle puisse être utilisée à la fois pour les exemples à sortie unique et à sorties multiples.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Essaye le:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
En règle générale, les données dans TensorFlow sont regroupées dans des tableaux où l'index le plus externe se trouve dans les exemples (la dimension "lot"). Les indices du milieu sont les dimensions "temps" ou "espace" (largeur, hauteur). Les indices les plus internes sont les caractéristiques.
Le code ci-dessus a pris un lot de trois fenêtres à 7 pas de temps avec 19 fonctionnalités à chaque pas de temps. Il les divise en un lot d'entrées de 19 caractéristiques à 6 pas de temps et une étiquette de 1 caractéristique à 1 pas de temps. L'étiquette n'a qu'une seule fonctionnalité car le WindowGenerator a été initialisé avec label_columns=['T (degC)'] . Dans un premier temps, ce didacticiel créera des modèles qui prédisent des étiquettes de sortie uniques.
3. Terrain
Voici une méthode plot qui permet une visualisation simple de la fenêtre fractionnée :
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
Ce tracé aligne les entrées, les étiquettes et les prévisions (ultérieurs) en fonction de l'heure à laquelle l'élément fait référence :
w2.plot()
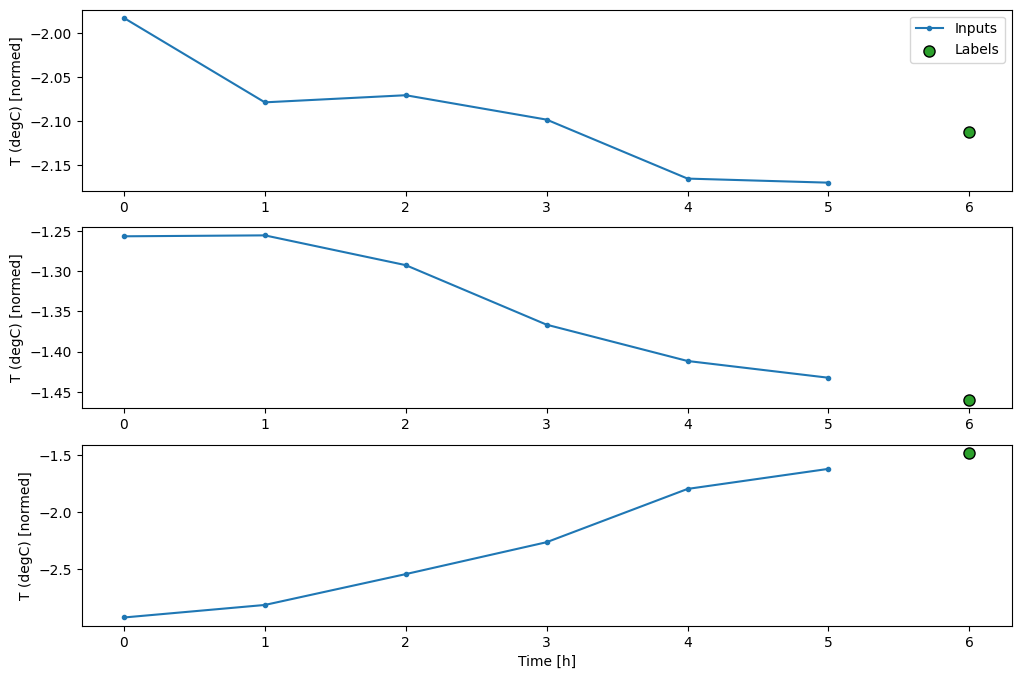
Vous pouvez tracer les autres colonnes, mais la configuration de la fenêtre d'exemple w2 n'a que des étiquettes pour la colonne T (degC) .
w2.plot(plot_col='p (mbar)')
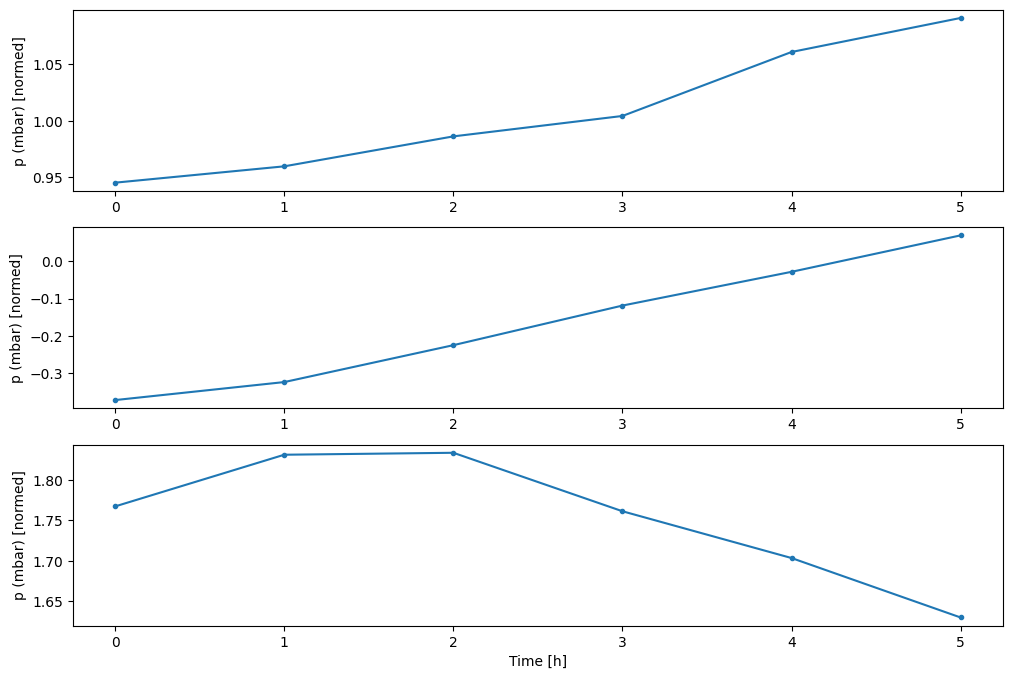
4. Créer tf.data.Dataset s
Enfin, cette méthode make_dataset prendra une série chronologique DataFrame et la convertira en un tf.data.Dataset de paires (input_window, label_window) à l'aide de la fonction tf.keras.utils.timeseries_dataset_from_array :
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
L'objet WindowGenerator contient des données de formation, de validation et de test.
Ajoutez des propriétés pour y accéder en tant que tf.data.Dataset s à l'aide de la méthode make_dataset que vous avez définie précédemment. Ajoutez également un exemple de lot standard pour un accès et un traçage faciles :
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Désormais, l'objet WindowGenerator vous donne accès aux objets tf.data.Dataset , ce qui vous permet de parcourir facilement les données.
La propriété Dataset.element_spec vous indique la structure, les types de données et les formes des éléments de l'ensemble de données.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
L'itération sur un ensemble de Dataset donne des lots concrets :
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Modèles en une seule étape
Le modèle le plus simple que vous puissiez créer à partir de ce type de données est celui qui prédit la valeur d'une seule entité — 1 pas de temps (une heure) dans le futur en se basant uniquement sur les conditions actuelles.
Alors, commencez par construire des modèles pour prédire la valeur T (degC) dans une heure dans le futur.
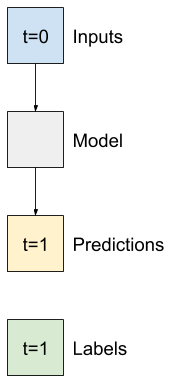
Configurez un objet WindowGenerator pour produire ces paires en une seule étape (input, label) :
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
L'objet window crée tf.data.Dataset à partir des ensembles d'entraînement, de validation et de test, ce qui vous permet d'itérer facilement sur des lots de données.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
Ligne de base
Avant de construire un modèle entraînable, il serait bon d'avoir une référence de performance comme point de comparaison avec les modèles ultérieurs plus compliqués.
Cette première tâche consiste à prédire la température dans une heure dans le futur, compte tenu de la valeur actuelle de toutes les caractéristiques. Les valeurs actuelles incluent la température actuelle.
Donc, commencez avec un modèle qui renvoie simplement la température actuelle comme prédiction, en prédisant "Pas de changement". Il s'agit d'une valeur de référence raisonnable puisque la température change lentement. Bien sûr, cette ligne de base fonctionnera moins bien si vous faites une prédiction plus loin dans le futur.
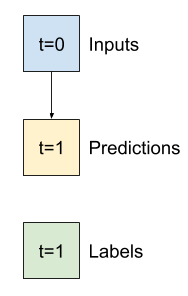
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Instanciez et évaluez ce modèle :
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
Cela a imprimé certaines mesures de performance, mais celles-ci ne vous donnent pas une idée de la performance du modèle.
Le WindowGenerator a une méthode de tracé, mais les tracés ne seront pas très intéressants avec un seul échantillon.
Créez donc un WindowGenerator plus large qui génère des fenêtres 24 heures d'entrées et d'étiquettes consécutives à la fois. La nouvelle variable wide_window ne change pas le fonctionnement du modèle. Le modèle fait toujours des prédictions une heure dans le futur sur la base d'un seul pas de temps d'entrée. Ici, l'axe des time agit comme l'axe des batch : chaque prédiction est faite indépendamment sans interaction entre les pas de temps :
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
Cette fenêtre étendue peut être transmise directement au même modèle de baseline sans aucune modification du code. Cela est possible car les entrées et les étiquettes ont le même nombre de pas de temps et la ligne de base transmet simplement l'entrée à la sortie :
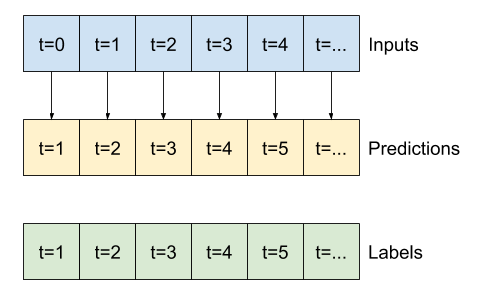
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
En traçant les prédictions du modèle de base, notez qu'il s'agit simplement des étiquettes décalées d'une heure vers la droite :
wide_window.plot(baseline)
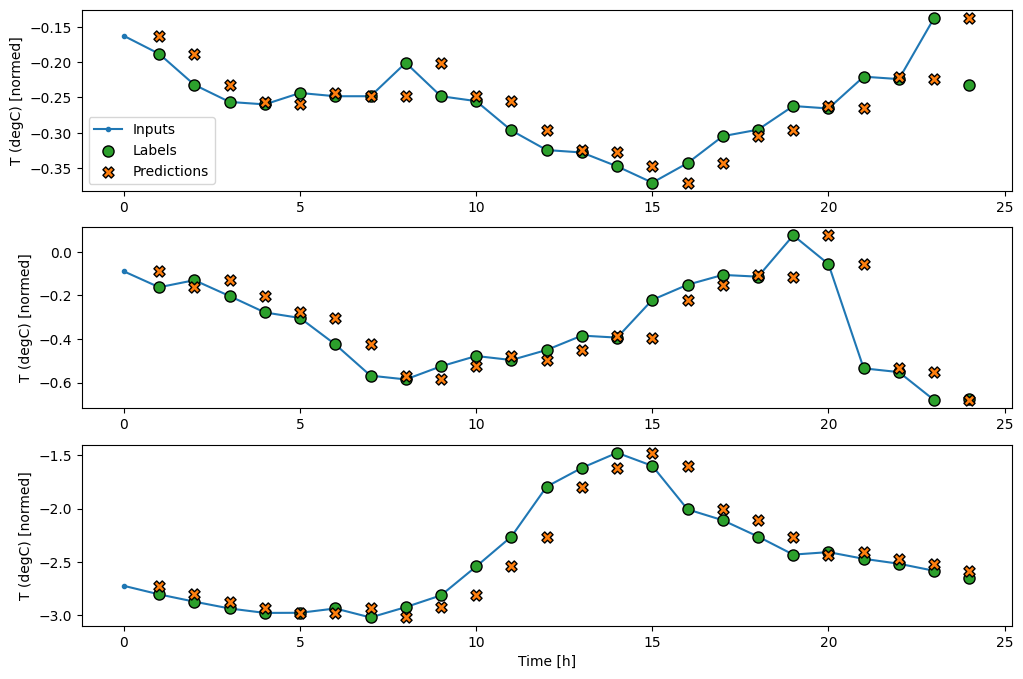
Dans les tracés ci-dessus de trois exemples, le modèle à une seule étape est exécuté sur une période de 24 heures. Cela mérite quelques explications :
- La ligne bleue
Inputsindique la température d'entrée à chaque pas de temps. Le modèle reçoit toutes les fonctionnalités, ce graphique ne montre que la température. - Les points verts des
Labelsindiquent la valeur de prédiction cible. Ces points sont affichés au moment de la prédiction, et non au moment de l'entrée. C'est pourquoi la plage d'étiquettes est décalée d'un pas par rapport aux entrées. - Les croix de
Predictionsorange correspondent aux prédictions du modèle pour chaque pas de temps de sortie. Si le modèle prévoyait parfaitement, les prédictions atterriraient directement sur lesLabels.
Modèle linéaire
Le modèle entraînable le plus simple que vous puissiez appliquer à cette tâche consiste à insérer une transformation linéaire entre l'entrée et la sortie. Dans ce cas, la sortie d'un pas de temps ne dépend que de ce pas :

Une couche tf.keras.layers.Dense sans jeu d' activation est un modèle linéaire. La couche ne transforme que le dernier axe des données de (batch, time, inputs) en (batch, time, units) ; il est appliqué indépendamment à chaque élément sur les axes de batch et de time .
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
Ce didacticiel entraîne de nombreux modèles. Regroupez donc la procédure d'entraînement dans une fonction :
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Entraînez le modèle et évaluez ses performances :
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
Comme le modèle de baseline , le modèle linéaire peut être appelé sur des lots de fenêtres larges. Utilisé de cette façon, le modèle fait un ensemble de prédictions indépendantes sur des pas de temps consécutifs. L'axe time agit comme un autre axe de batch . Il n'y a pas d'interactions entre les prédictions à chaque pas de temps.
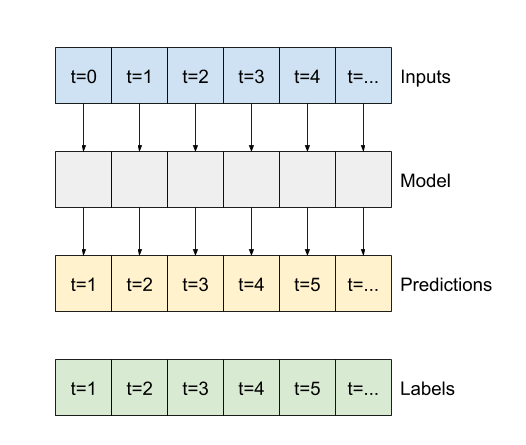
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Voici le tracé de ses exemples de prédictions sur le wide_window , notez comment, dans de nombreux cas, la prédiction est clairement meilleure que de simplement renvoyer la température d'entrée, mais dans quelques cas, c'est pire :
wide_window.plot(linear)
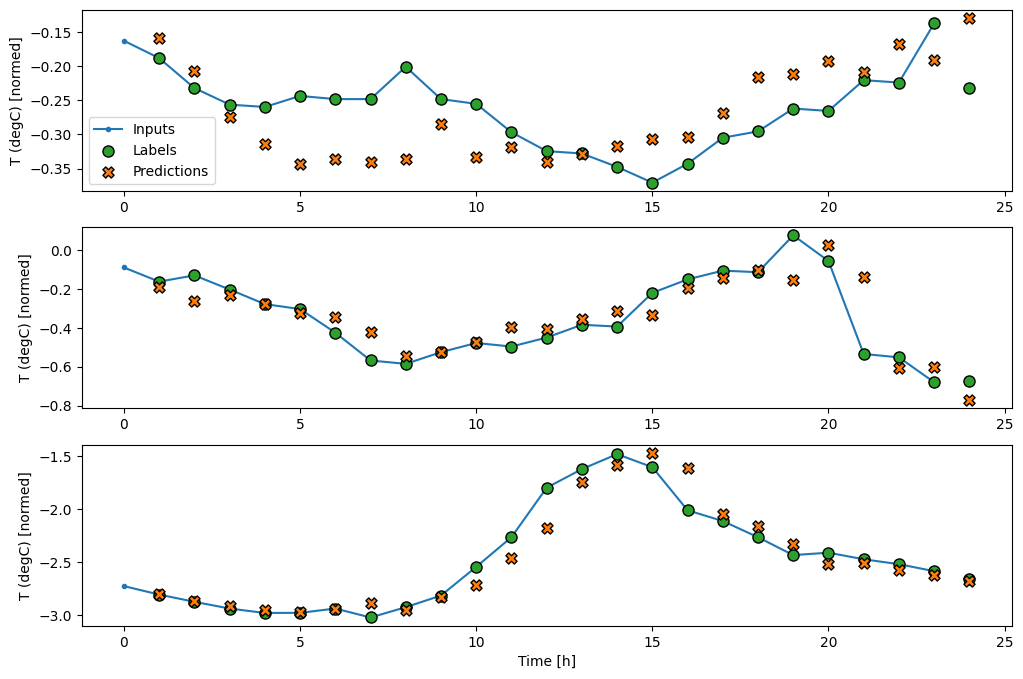
L'un des avantages des modèles linéaires est qu'ils sont relativement simples à interpréter. Vous pouvez extraire les poids de la couche et visualiser le poids attribué à chaque entrée :
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
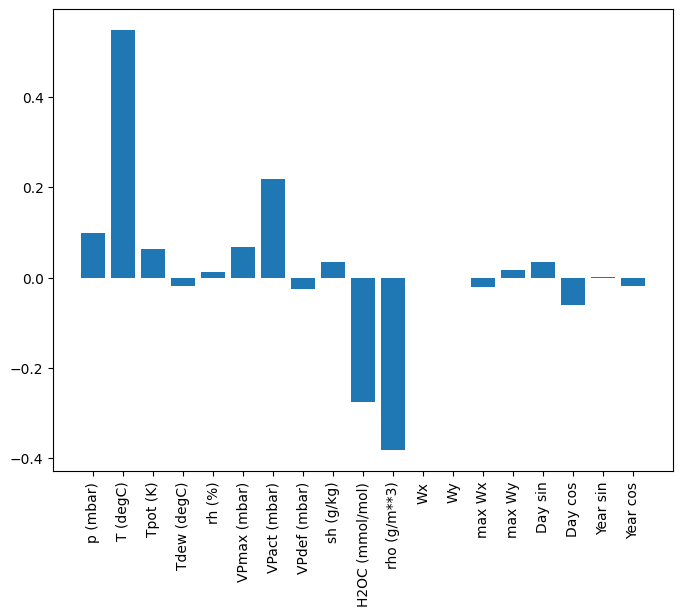
Parfois, le modèle n'accorde même pas le plus de poids à l'entrée T (degC) . C'est l'un des risques de l'initialisation aléatoire.
Dense
Avant d'appliquer des modèles qui fonctionnent réellement sur plusieurs pas de temps, il est utile de vérifier les performances de modèles plus profonds, plus puissants et à une seule étape d'entrée.
Voici un modèle similaire au modèle linear , sauf qu'il empile plusieurs couches Dense entre l'entrée et la sortie :
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
Densité en plusieurs étapes
Un modèle à pas de temps unique n'a pas de contexte pour les valeurs actuelles de ses entrées. Il ne peut pas voir comment les caractéristiques d'entrée changent au fil du temps. Pour résoudre ce problème, le modèle doit avoir accès à plusieurs pas de temps lors de la réalisation de prédictions :
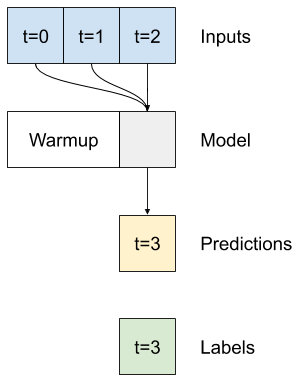
Les modèles de ligne de baseline , linear et dense ont traité chaque pas de temps indépendamment. Ici, le modèle prendra plusieurs pas de temps en entrée pour produire une seule sortie.
Créez un WindowGenerator qui produira des lots d'entrées de trois heures et d'étiquettes d'une heure :
Notez que le paramètre de shift de la Window est relatif à la fin des deux fenêtres.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
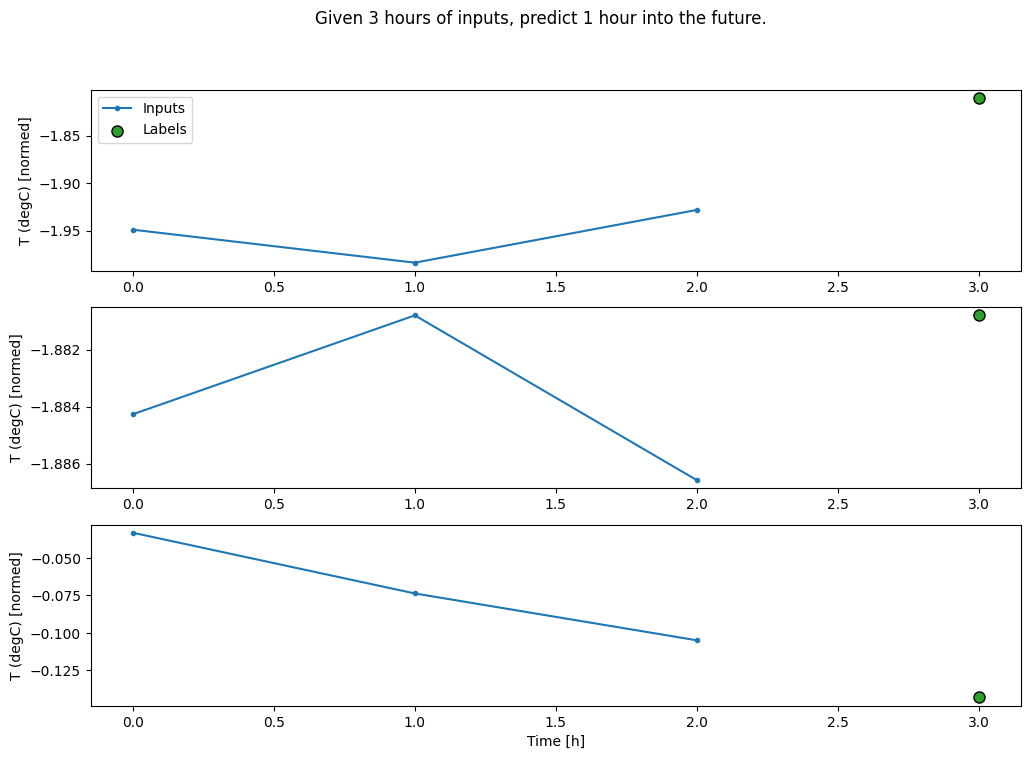
Vous pouvez entraîner un modèle dense sur une fenêtre à plusieurs étapes d'entrée en ajoutant un tf.keras.layers.Flatten comme première couche du modèle :
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
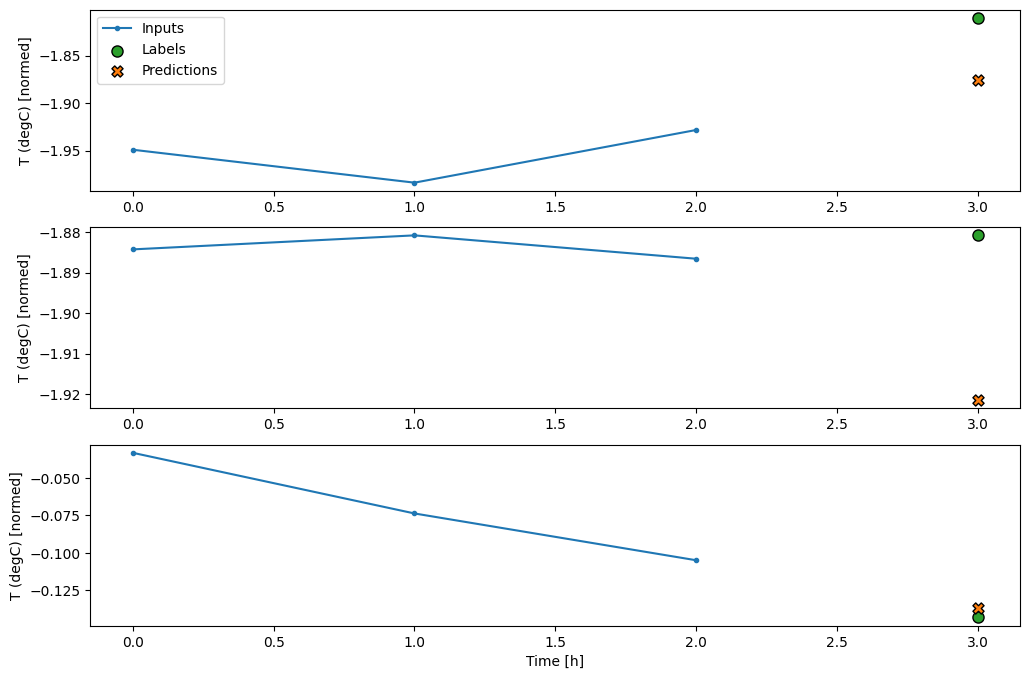
Le principal inconvénient de cette approche est que le modèle résultant ne peut être exécuté que sur des fenêtres d'entrée ayant exactement cette forme.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
Les modèles convolutifs de la section suivante corrigent ce problème.
Réseau de neurones à convolution
Une couche de convolution ( tf.keras.layers.Conv1D ) prend également plusieurs pas de temps en entrée pour chaque prédiction.
Ci-dessous, le même modèle que multi_step_dense , réécrit avec une convolution.
Notez les changements :
- Le
tf.keras.layers.Flattenet le premiertf.keras.layers.Densesont remplacés par untf.keras.layers.Conv1D. - Le
tf.keras.layers.Reshapen'est plus nécessaire puisque la convolution conserve l'axe du temps dans sa sortie.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Exécutez-le sur un exemple de lot pour vérifier que le modèle produit des sorties avec la forme attendue :
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Entraînez-le et évaluez-le sur le conv_window et il devrait donner des performances similaires au modèle multi_step_dense .
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
La différence entre ce conv_model et le modèle multi_step_dense est que le conv_model peut être exécuté sur des entrées de n'importe quelle longueur. La couche convolutive est appliquée à une fenêtre glissante d'entrées :
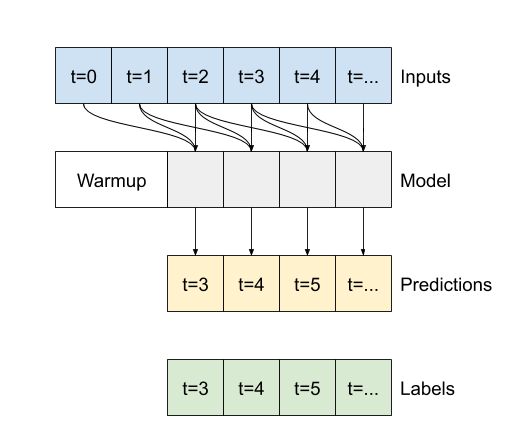
Si vous l'exécutez sur une entrée plus large, il produit une sortie plus large :
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
Notez que la sortie est plus courte que l'entrée. Pour que l'entraînement ou le traçage fonctionne, vous avez besoin que les étiquettes et la prédiction aient la même longueur. Construisez donc un WindowGenerator pour produire de larges fenêtres avec quelques pas de temps d'entrée supplémentaires afin que les longueurs d'étiquette et de prédiction correspondent :
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
Maintenant, vous pouvez tracer les prédictions du modèle sur une fenêtre plus large. Notez les 3 pas de temps d'entrée avant la première prédiction. Ici, chaque prédiction est basée sur les 3 pas de temps précédents :
wide_conv_window.plot(conv_model)
Réseau neuronal récurrent
Un réseau neuronal récurrent (RNN) est un type de réseau neuronal bien adapté aux données de séries chronologiques. Les RNN traitent une série chronologique étape par étape, en maintenant un état interne d'un pas de temps à l'autre.
Vous pouvez en savoir plus dans la génération de texte avec un didacticiel RNN et le guide Réseaux de neurones récurrents (RNN) avec Keras .
Dans ce didacticiel, vous utiliserez une couche RNN appelée Long Short-Term Memory ( tf.keras.layers.LSTM ).
Un argument de constructeur important pour toutes les couches Keras RNN, telles que tf.keras.layers.LSTM , est l'argument return_sequences . Ce paramètre peut configurer la couche de l'une des deux manières suivantes :
- Si
False, la valeur par défaut, la couche ne renvoie que la sortie du dernier pas de temps, ce qui donne au modèle le temps de réchauffer son état interne avant de faire une seule prédiction :
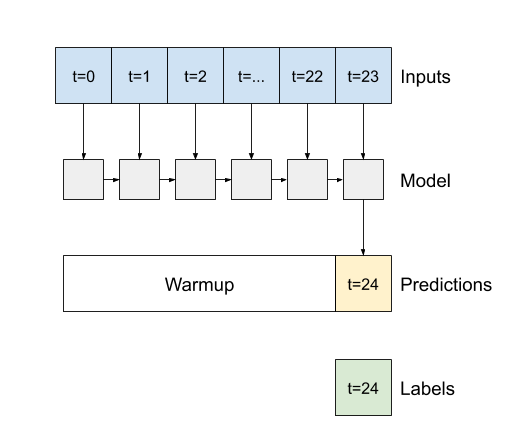
- Si
True, la couche renvoie une sortie pour chaque entrée. Ceci est utile pour :- Empiler les couches RNN.
- Entraîner un modèle sur plusieurs pas de temps simultanément.
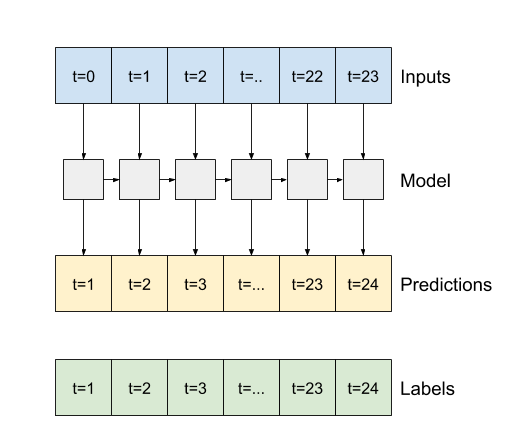
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
Avec return_sequences=True , le modèle peut être formé sur 24 heures de données à la fois.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
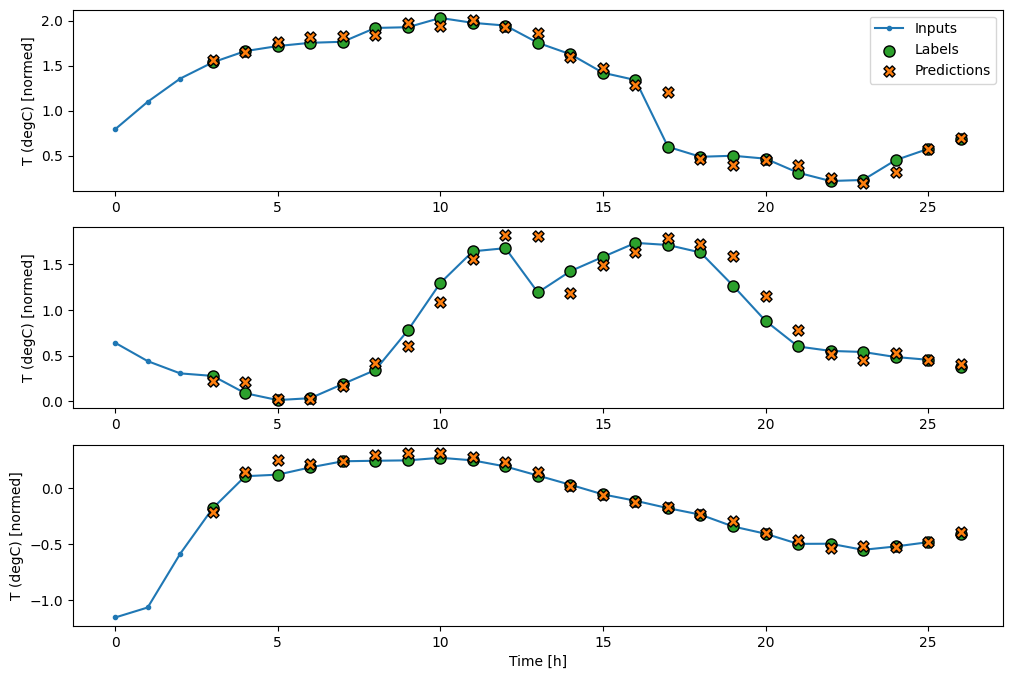
wide_window.plot(lstm_model)
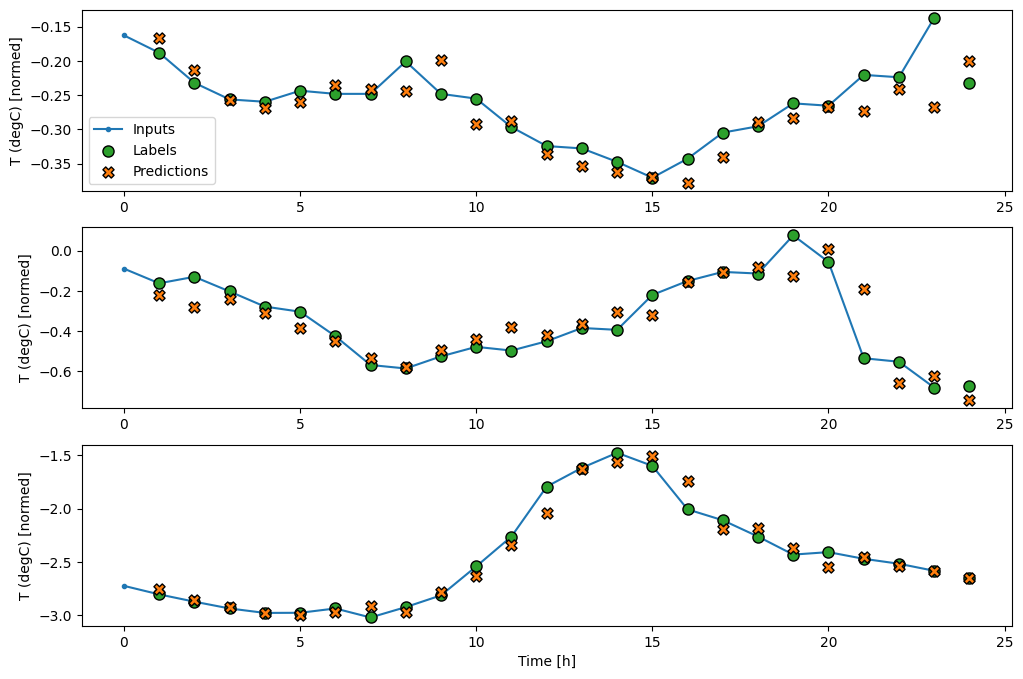
Performance
Avec cet ensemble de données, chacun des modèles fait généralement un peu mieux que celui qui le précède :
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
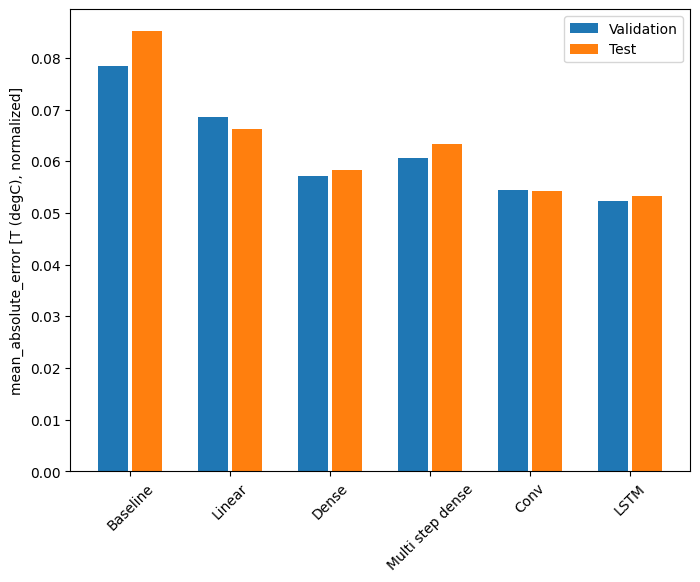
for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
Modèles multi-sorties
Jusqu'à présent, les modèles ont tous prédit une seule caractéristique de sortie, T (degC) , pour un seul pas de temps.
Tous ces modèles peuvent être convertis pour prédire plusieurs entités simplement en modifiant le nombre d'unités dans la couche de sortie et en ajustant les fenêtres d'apprentissage pour inclure toutes les entités dans les labels ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Notez ci-dessus que l'axe des features des étiquettes a maintenant la même profondeur que les entrées, au lieu de 1 .
Ligne de base
Le même modèle de référence ( Baseline ) peut être utilisé ici, mais cette fois en répétant toutes les fonctionnalités au lieu de sélectionner un label_index spécifique :
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
Dense
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
RNN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
Avancé : Connexions résiduelles
Le modèle de Baseline du précédent a profité du fait que la séquence ne change pas radicalement d'un pas de temps à l'autre. Chaque modèle formé dans ce didacticiel jusqu'à présent a été initialisé de manière aléatoire, puis a dû apprendre que la sortie est un petit changement par rapport au pas de temps précédent.
Bien que vous puissiez contourner ce problème avec une initialisation soignée, il est plus simple de l'intégrer à la structure du modèle.
Il est courant dans l'analyse des séries chronologiques de créer des modèles qui, au lieu de prédire la valeur suivante, prédisent comment la valeur changera au cours de l'étape suivante. De même, les réseaux résiduels - ou ResNets - dans l'apprentissage en profondeur font référence à des architectures où chaque couche ajoute au résultat cumulatif du modèle.
C'est ainsi que vous profitez du fait que le changement doit être minime.
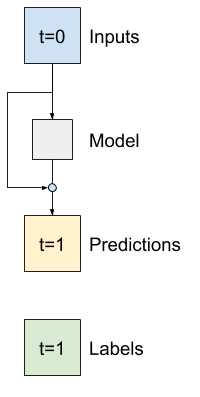
Essentiellement, cela initialise le modèle pour qu'il corresponde à la Baseline . Pour cette tâche, il aide les modèles à converger plus rapidement, avec des performances légèrement meilleures.
Cette approche peut être utilisée conjointement avec n'importe quel modèle présenté dans ce didacticiel.
Ici, il est appliqué au modèle LSTM, notez l'utilisation de tf.initializers.zeros pour s'assurer que les changements prédits initiaux sont faibles et ne surchargent pas la connexion résiduelle. Il n'y a pas de problème de rupture de symétrie pour les dégradés ici, puisque les zeros ne sont utilisés que sur la dernière couche.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
Performance
Voici les performances globales de ces modèles multi-sorties.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
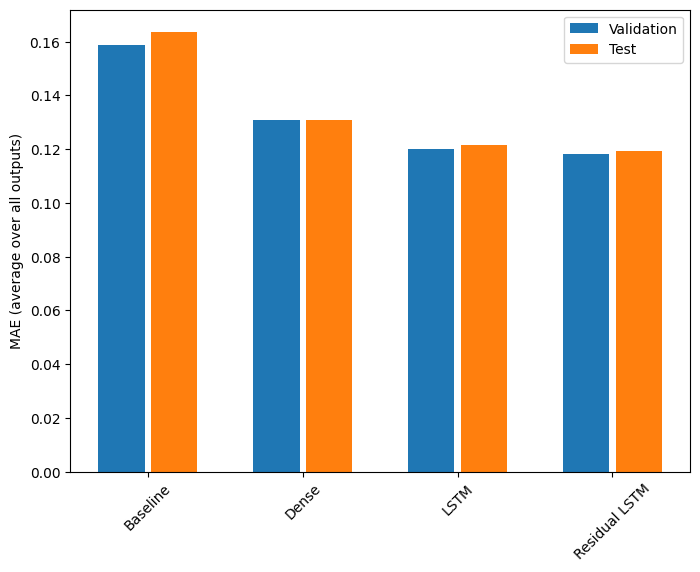
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
Les performances ci-dessus sont moyennées sur toutes les sorties du modèle.
Modèles multi-étapes
Les modèles à sortie unique et à sorties multiples dans les sections précédentes ont fait des prédictions à un seul pas de temps , une heure dans le futur.
Cette section examine comment étendre ces modèles pour faire des prédictions à plusieurs pas de temps .
Dans une prédiction en plusieurs étapes, le modèle doit apprendre à prédire une plage de valeurs futures. Ainsi, contrairement à un modèle à une seule étape, où un seul point futur est prédit, un modèle à plusieurs étapes prédit une séquence des valeurs futures.
Il existe deux approches approximatives pour cela:
- Prédictions uniques où toute la série chronologique est prédite en une seule fois.
- Prédictions autorégressives où le modèle ne fait que des prédictions en une seule étape et sa sortie est renvoyée en entrée.
Dans cette section, tous les modèles prédiront toutes les caractéristiques sur tous les pas de temps de sortie .
Pour le modèle à plusieurs étapes, les données d'apprentissage sont à nouveau constituées d'échantillons horaires. Cependant, ici, les modèles apprendront à prédire 24 heures dans le futur, étant donné 24 heures du passé.
Voici un objet Window qui génère ces tranches à partir du jeu de données :
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
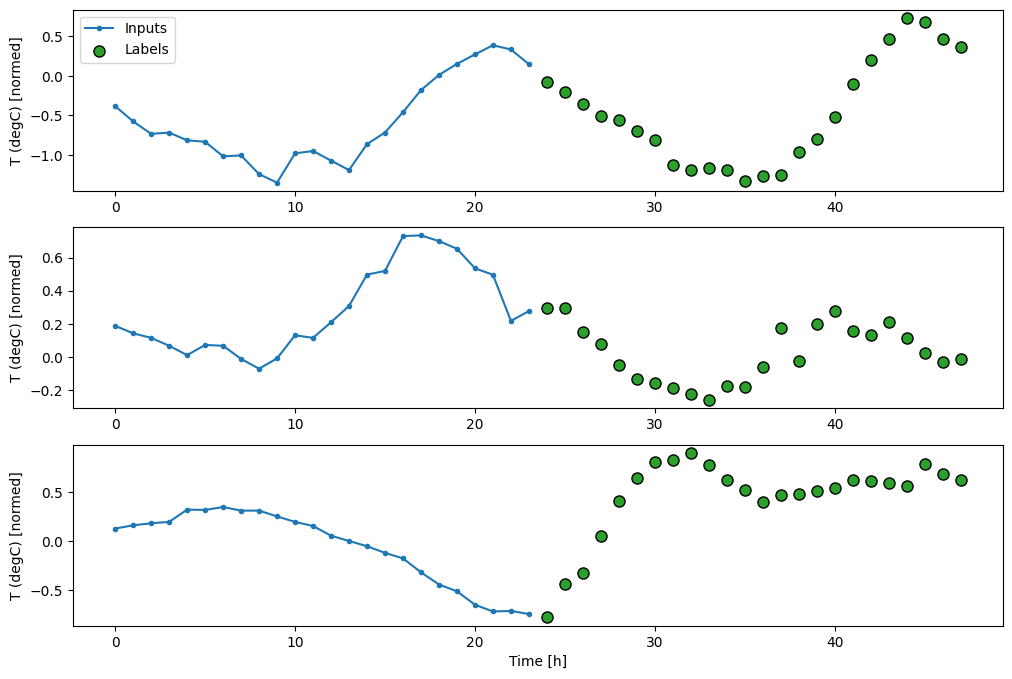
Lignes de base
Une ligne de base simple pour cette tâche consiste à répéter le dernier pas de temps d'entrée pour le nombre requis de pas de temps de sortie :
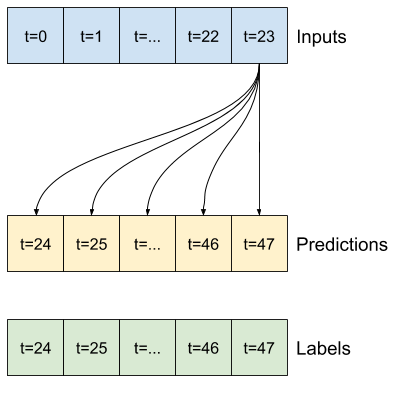
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
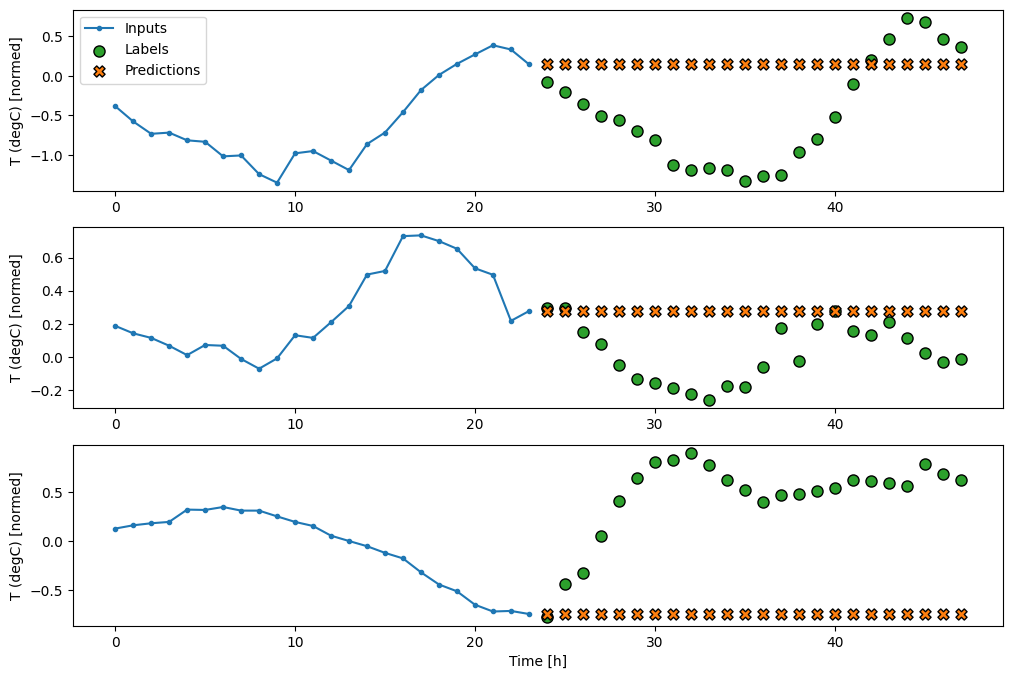
Étant donné que cette tâche consiste à prédire 24 heures dans le futur, étant donné 24 heures du passé, une autre approche simple consiste à répéter le jour précédent, en supposant que demain sera similaire :
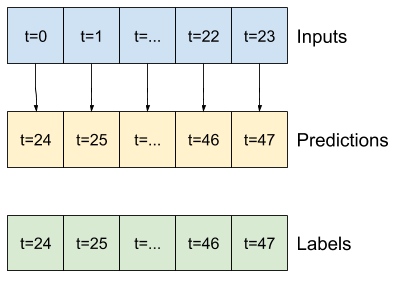
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
Modèles monocoup
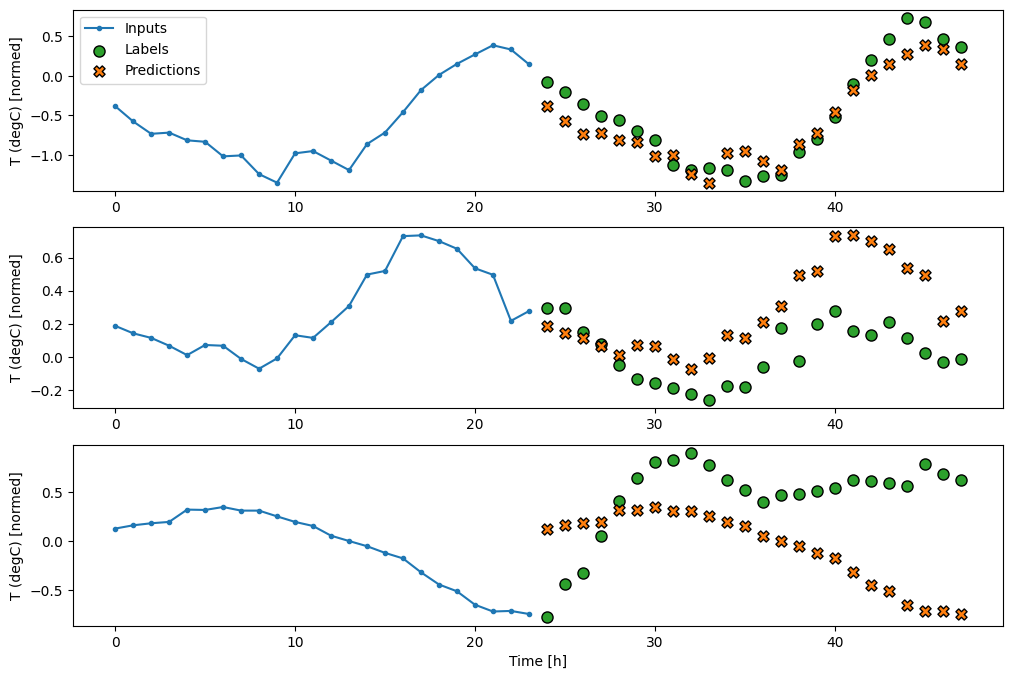
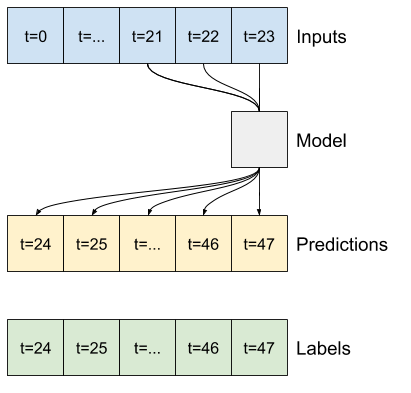
Une approche de haut niveau à ce problème consiste à utiliser un modèle "à un seul coup", où le modèle effectue la prédiction de la séquence entière en une seule étape.
Cela peut être implémenté efficacement en tant que tf.keras.layers.Dense avec OUT_STEPS*features unités de sortie. Le modèle a juste besoin de remodeler cette sortie selon les besoins (OUTPUT_STEPS, features) .
Linéaire
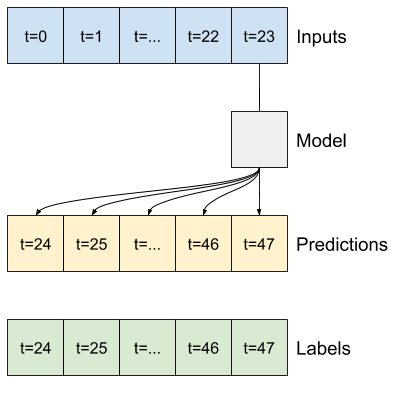
Un modèle linéaire simple basé sur le dernier pas de temps d'entrée fait mieux que l'une ou l'autre des lignes de base, mais est sous-alimenté. Le modèle doit prédire les pas de temps OUTPUT_STEPS , à partir d'un seul pas de temps d'entrée avec une projection linéaire. Il ne peut capturer qu'une tranche de faible dimension du comportement, probablement basée principalement sur l'heure de la journée et la période de l'année.
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
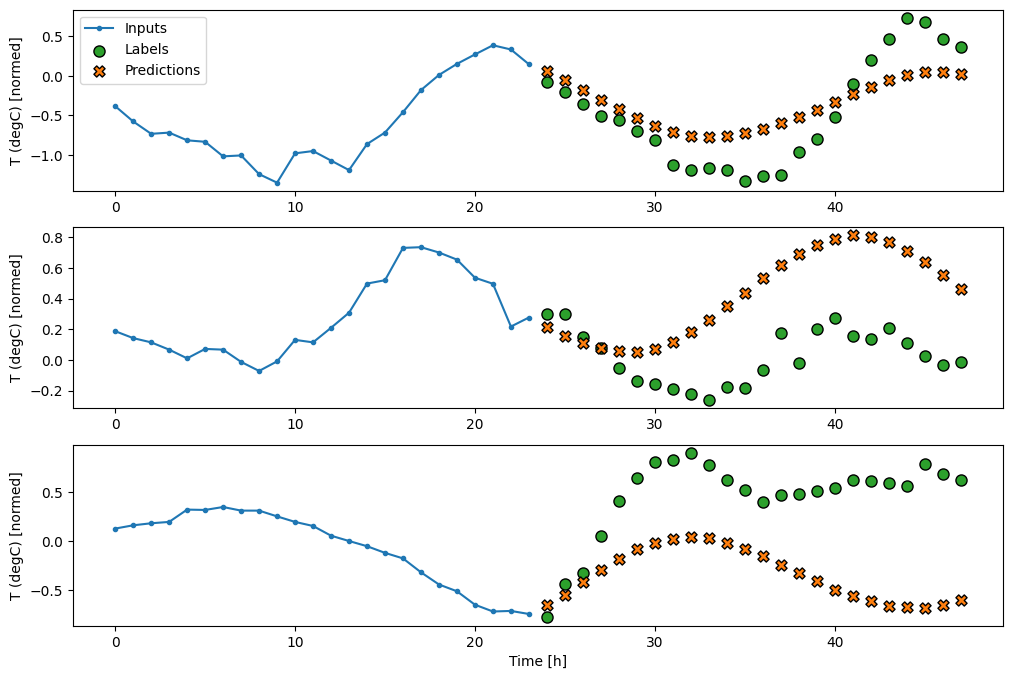
Dense
L'ajout d'un tf.keras.layers.Dense entre l'entrée et la sortie donne plus de puissance au modèle linéaire, mais n'est toujours basé que sur un seul pas de temps d'entrée.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
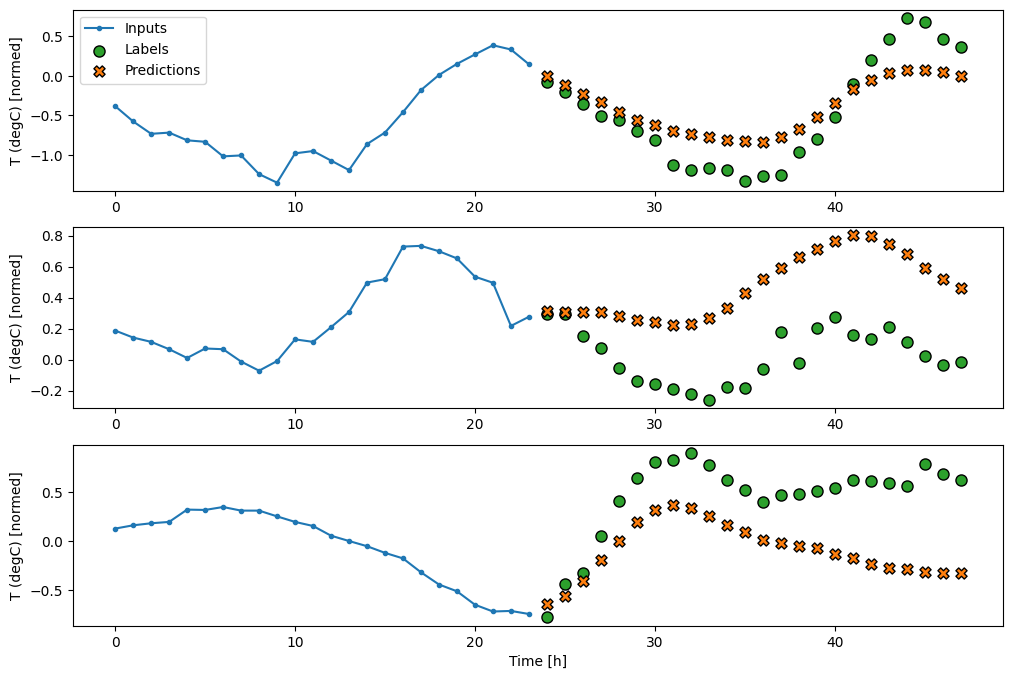
CNN
Un modèle convolutif fait des prédictions basées sur un historique à largeur fixe, ce qui peut conduire à de meilleures performances que le modèle dense car il peut voir comment les choses changent au fil du temps :
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
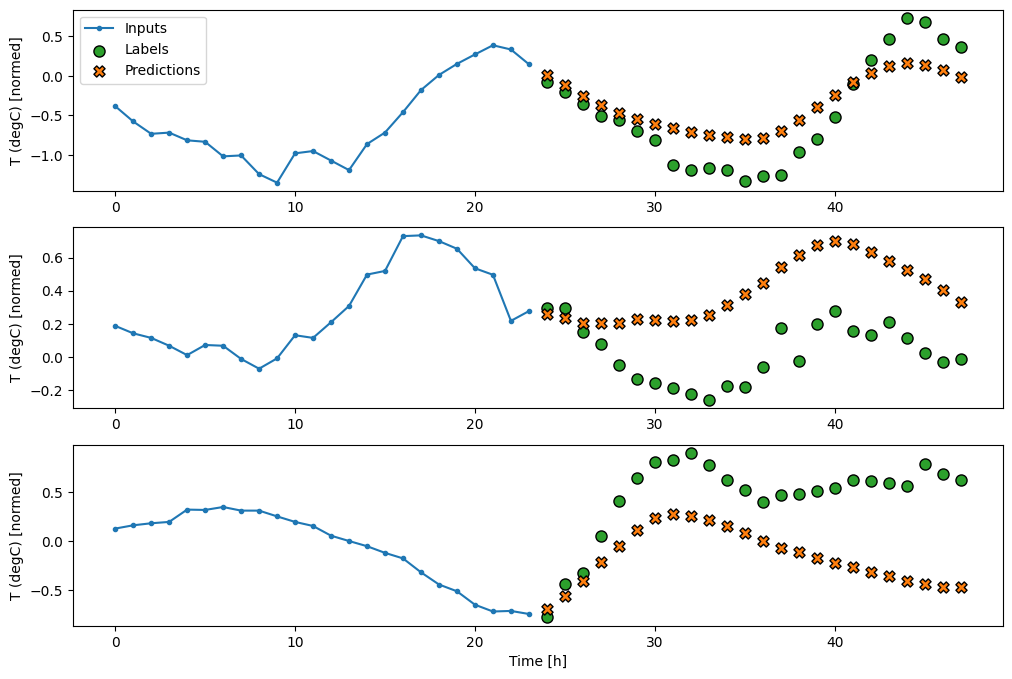
RNN
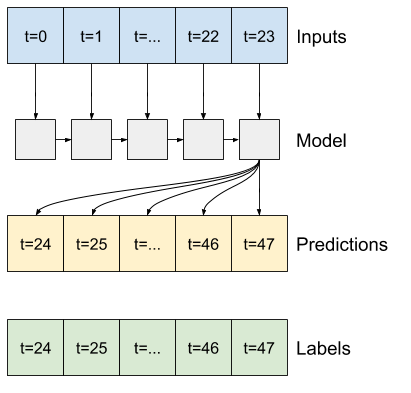
Un modèle récurrent peut apprendre à utiliser un long historique d'entrées, si cela est pertinent pour les prédictions que fait le modèle. Ici, le modèle accumulera l'état interne pendant 24 heures, avant de faire une prédiction unique pour les 24 heures suivantes.
Dans ce format monocoup, le LSTM n'a besoin de produire une sortie qu'au dernier pas de temps, donc définissez return_sequences=False dans tf.keras.layers.LSTM .
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
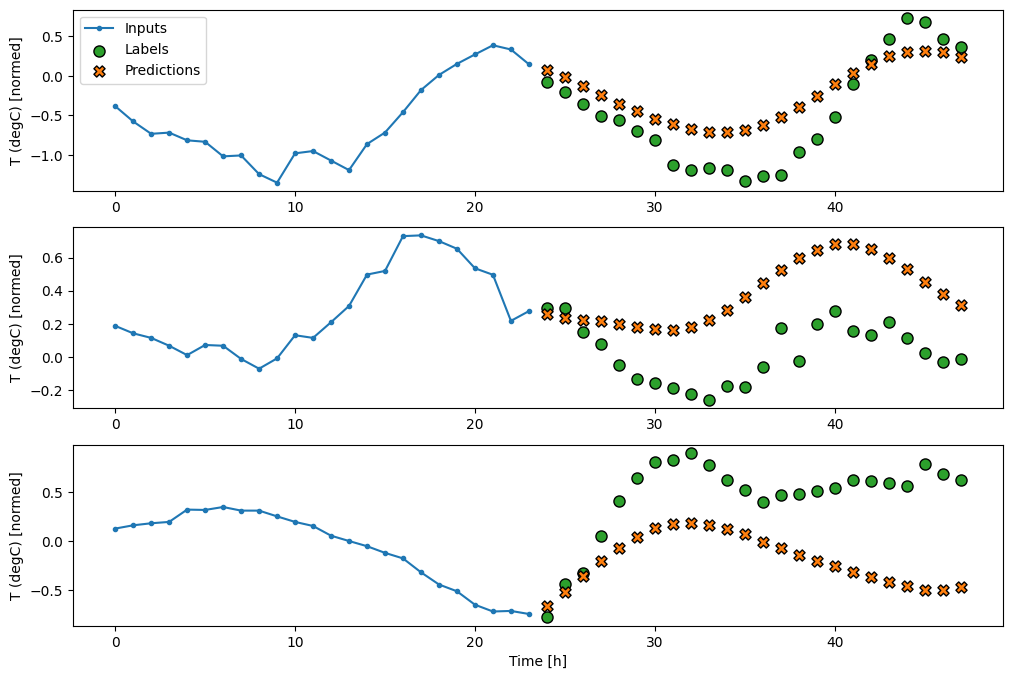
Avancé : modèle autorégressif
Les modèles ci-dessus prédisent tous la séquence de sortie complète en une seule étape.
Dans certains cas, il peut être utile que le modèle décompose cette prédiction en pas de temps individuels. Ensuite, la sortie de chaque modèle peut être réintroduite en elle-même à chaque étape et des prédictions peuvent être faites en fonction de la précédente, comme dans le classique Génération de séquences avec des réseaux de neurones récurrents .
Un avantage évident de ce style de modèle est qu'il peut être configuré pour produire une sortie de longueur variable.
Vous pouvez prendre n'importe lequel des modèles à plusieurs sorties en une seule étape formés dans la première moitié de ce didacticiel et exécuter une boucle de rétroaction autorégressive, mais ici, vous vous concentrerez sur la création d'un modèle qui a été explicitement formé pour le faire.
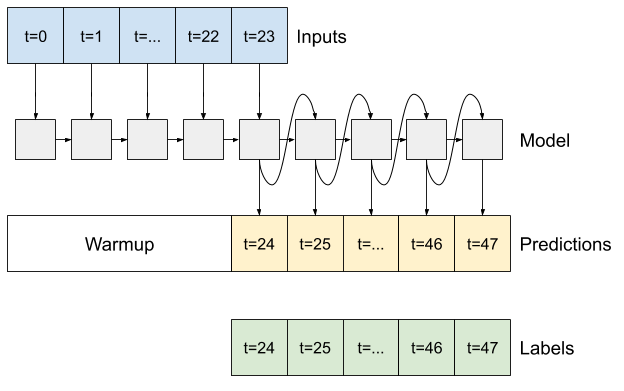
RNN
Ce didacticiel ne construit qu'un modèle RNN autorégressif, mais ce modèle peut être appliqué à tout modèle conçu pour générer un seul pas de temps.
Le modèle aura la même forme de base que les modèles LSTM en une étape précédents : une couche tf.keras.layers.LSTM suivie d'une couche tf.keras.layers.Dense qui convertit les sorties de la couche LSTM en prédictions de modèle.
Un tf.keras.layers.LSTM est un tf.keras.layers.LSTMCell enveloppé dans le niveau supérieur tf.keras.layers.RNN qui gère l'état et les résultats de séquence pour vous (Consultez les réseaux de neurones récurrents (RNN) avec Keras guide pour plus de détails).
Dans ce cas, le modèle doit gérer manuellement les entrées pour chaque étape, il utilise tf.keras.layers.LSTMCell directement pour l'interface de niveau inférieur à pas de temps unique.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
La première méthode dont ce modèle a besoin est une méthode de warmup pour initialiser son état interne en fonction des entrées. Une fois formé, cet état capturera les parties pertinentes de l'historique des entrées. Cela équivaut au modèle LSTM en une seule étape du précédent :
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
Cette méthode renvoie une prédiction à pas de temps unique et l'état interne du LSTM :
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
Avec l'état du RNN et une prédiction initiale, vous pouvez maintenant continuer à itérer le modèle en alimentant les prédictions à chaque étape en arrière comme entrée.
L'approche la plus simple pour collecter les prédictions de sortie consiste à utiliser une liste Python et un tf.stack après la boucle.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Testez ce modèle sur les entrées de l'exemple :
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
Maintenant, entraînez le modèle :
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
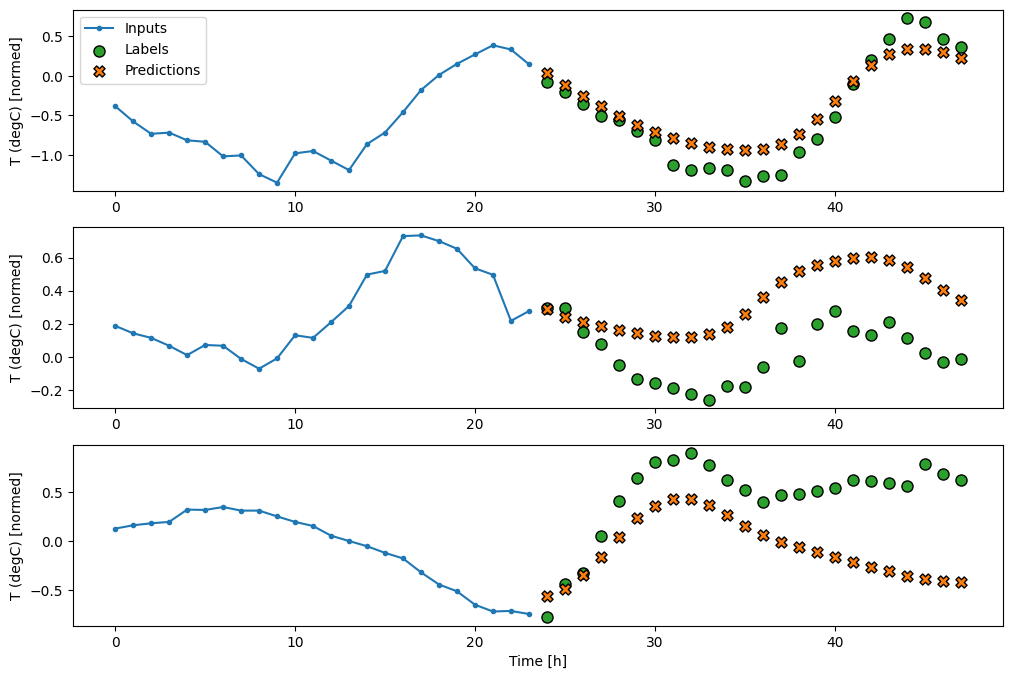
Performance
Il y a clairement des rendements décroissants en fonction de la complexité du modèle sur ce problème :
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
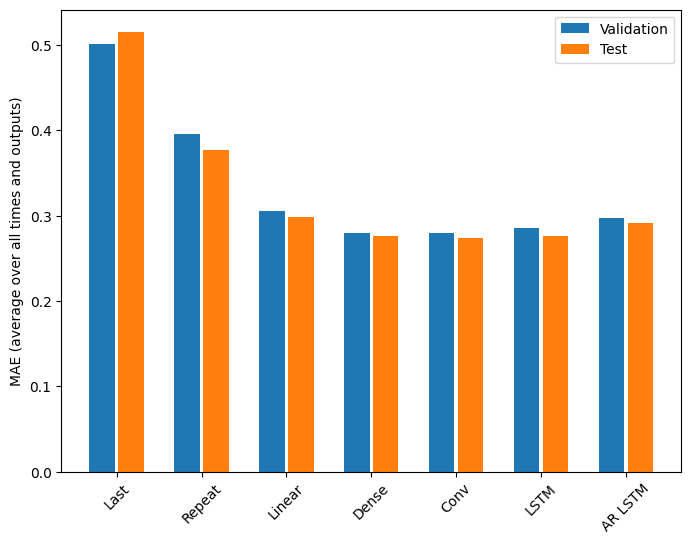
Les métriques pour les modèles à sorties multiples dans la première moitié de ce didacticiel montrent les performances moyennes sur toutes les fonctionnalités de sortie. Ces performances sont similaires mais également moyennées sur les pas de temps de sortie.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
Les gains obtenus en passant d'un modèle dense à des modèles convolutifs et récurrents ne sont que de quelques pour cent (le cas échéant), et le modèle autorégressif a nettement moins bien performé. Donc, ces approches plus complexes ne valent peut-être pas la peine sur ce problème, mais il n'y avait aucun moyen de savoir sans essayer, et ces modèles pourraient être utiles pour votre problème.
Prochaines étapes
Ce didacticiel était une introduction rapide à la prévision de séries temporelles à l'aide de TensorFlow.
Pour en savoir plus, consultez :
- Chapitre 15 de l'apprentissage automatique pratique avec Scikit-Learn, Keras et TensorFlow , 2e édition.
- Chapitre 6 de Deep Learning avec Python .
- Leçon 8 de l'introduction d'Udacity à TensorFlow pour le deep learning , y compris les cahiers d'exercices .
N'oubliez pas non plus que vous pouvez implémenter n'importe quel modèle de série temporelle classique dans TensorFlow. Ce didacticiel se concentre uniquement sur la fonctionnalité intégrée de TensorFlow.
