Aprenda o que há de mais recente em aprendizado de máquina, IA generativa e muito mais no WiML Symposium 2023 Registre-se

Esta página foi traduzida pela API Cloud Translation.

Classificação em dados desbalanceados

Veja no TensorFlow.org

Executar no Google Colab

Ver fonte no GitHub

Baixar caderno

Este tutorial demonstra como classificar um conjunto de dados altamente desequilibrado no qual o número de exemplos em uma classe supera em muito os exemplos em outra. Você trabalhará com o conjunto de dados de detecção de fraude de cartão de crédito hospedado no Kaggle. O objetivo é detectar apenas 492 transações fraudulentas de um total de 284.807 transações. Você usará Keras para definir os pesos do modelo e da classe para ajudar o modelo a aprender com os dados desequilibrados. .

Este tutorial contém código completo para:

Carregue um arquivo CSV usando Pandas.
Crie conjuntos de treinamento, validação e teste.
Defina e treine um modelo usando Keras (incluindo a configuração de pesos de classe).
Avalie o modelo usando várias métricas (incluindo precisão e recall).
Experimente técnicas comuns para lidar com dados desequilibrados, como:
- Ponderação da classe
- Sobreamostragem

Configurar

import tensorflow as tf
from tensorflow import keras

import os
import tempfile

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']

Processamento e exploração de dados

Baixe o conjunto de dados de fraude de cartão de crédito Kaggle

Pandas é uma biblioteca Python com muitos utilitários úteis para carregar e trabalhar com dados estruturados. Ele pode ser usado para baixar CSVs em um Pandas DataFrame .

file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()

raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()

Examine o desequilíbrio do rótulo da classe

Vejamos o desequilíbrio do conjunto de dados:

neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n    Total: {}\n    Positive: {} ({:.2f}% of total)\n'.format(
    total, pos, 100 * pos / total))

Examples:
    Total: 284807
    Positive: 492 (0.17% of total)

Isso mostra a pequena fração de amostras positivas.

Limpe, divida e normalize os dados

Os dados brutos têm alguns problemas. Primeiro, as colunas Time e Amount são muito variáveis para serem usadas diretamente. Elimine a coluna Time (já que não está claro o que isso significa) e pegue o log da coluna Amount para reduzir seu intervalo.

cleaned_df = raw_df.copy()

# You don't want the `Time` column.
cleaned_df.pop('Time')

# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Ammount'] = np.log(cleaned_df.pop('Amount')+eps)

Divida o conjunto de dados em conjuntos de treinamento, validação e teste. O conjunto de validação é usado durante o ajuste do modelo para avaliar a perda e quaisquer métricas, porém o modelo não é ajustado com esses dados. O conjunto de teste é completamente não utilizado durante a fase de treinamento e é usado apenas no final para avaliar quão bem o modelo generaliza para novos dados. Isso é especialmente importante com conjuntos de dados desequilibrados em que o overfitting é uma preocupação significativa devido à falta de dados de treinamento.

# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)

# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))

train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)

Normalize os recursos de entrada usando o sklearn StandardScaler. Isso definirá a média para 0 e o desvio padrão para 1.

scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)

val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)

train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)


print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)

print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)

Training labels shape: (182276,)
Validation labels shape: (45569,)
Test labels shape: (56962,)
Training features shape: (182276, 29)
Validation features shape: (45569, 29)
Test features shape: (56962, 29)

Observe a distribuição de dados

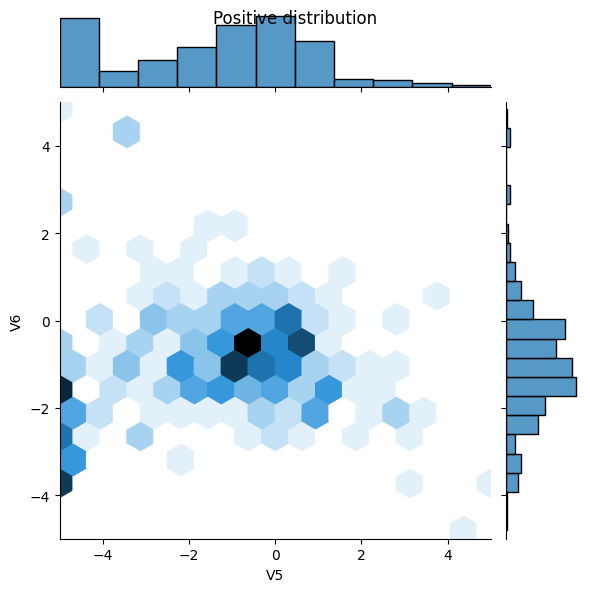
Em seguida, compare as distribuições dos exemplos positivos e negativos sobre algumas características. Boas perguntas para se fazer neste momento são:

Essas distribuições fazem sentido?
- sim. Você normalizou a entrada e estes estão concentrados principalmente na faixa +/- 2 .
Você consegue ver a diferença entre as distribuições?
- Sim, os exemplos positivos contêm uma taxa muito maior de valores extremos.

pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)

sns.jointplot(x=pos_df['V5'], y=pos_df['V6'],
              kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")

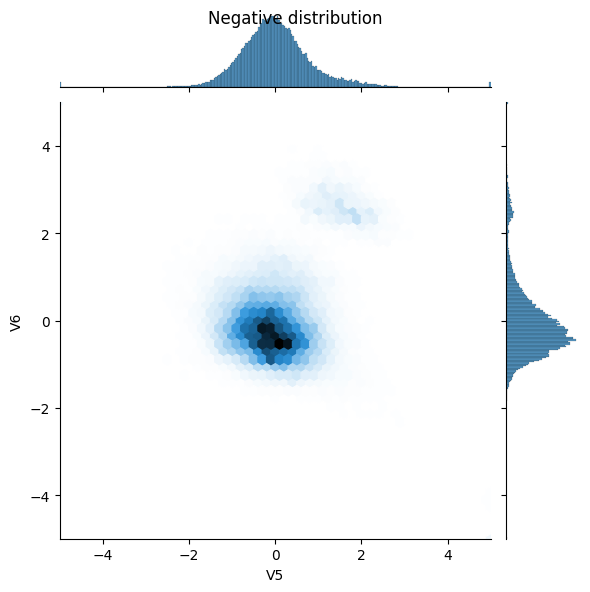
sns.jointplot(x=neg_df['V5'], y=neg_df['V6'],
              kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")

png

Defina o modelo e as métricas

Defina uma função que cria uma rede neural simples com uma camada oculta densamente conectada, uma camada dropout para reduzir o overfitting e uma camada sigmoid de saída que retorna a probabilidade de uma transação ser fraudulenta:

METRICS = [
      keras.metrics.TruePositives(name='tp'),
      keras.metrics.FalsePositives(name='fp'),
      keras.metrics.TrueNegatives(name='tn'),
      keras.metrics.FalseNegatives(name='fn'), 
      keras.metrics.BinaryAccuracy(name='accuracy'),
      keras.metrics.Precision(name='precision'),
      keras.metrics.Recall(name='recall'),
      keras.metrics.AUC(name='auc'),
      keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]

def make_model(metrics=METRICS, output_bias=None):
  if output_bias is not None:
    output_bias = tf.keras.initializers.Constant(output_bias)
  model = keras.Sequential([
      keras.layers.Dense(
          16, activation='relu',
          input_shape=(train_features.shape[-1],)),
      keras.layers.Dropout(0.5),
      keras.layers.Dense(1, activation='sigmoid',
                         bias_initializer=output_bias),
  ])

  model.compile(
      optimizer=keras.optimizers.Adam(learning_rate=1e-3),
      loss=keras.losses.BinaryCrossentropy(),
      metrics=metrics)

  return model

Entendendo métricas úteis

Observe que existem algumas métricas definidas acima que podem ser calculadas pelo modelo que serão úteis ao avaliar o desempenho.

Falsos negativos e falsos positivos são amostras que foram classificadas incorretamente
Verdadeiros negativos e verdadeiros positivos são amostras que foram classificadas corretamente
Precisão é a porcentagem de exemplos classificados corretamente > \(\frac{\text{true samples} }{\text{total samples} }\)
Precisão é a porcentagem de positivos previstos que foram classificados corretamente > \(\frac{\text{true positives} }{\text{true positives + false positives} }\)
Recall é a porcentagem de positivos reais que foram classificados corretamente > \(\frac{\text{true positives} }{\text{true positives + false negatives} }\)
AUC refere-se à área sob a curva de uma curva característica de operação do receptor (ROC-AUC). Essa métrica é igual à probabilidade de um classificador classificar uma amostra aleatória positiva mais alta do que uma amostra aleatória negativa.
AUPRC refere-se à Área Sob a Curva da Curva de Recall de Precisão. Essa métrica calcula pares de precisão-recall para diferentes limites de probabilidade.

Consulte Mais informação:

Modelo de linha de base

Construir o modelo

Agora crie e treine seu modelo usando a função que foi definida anteriormente. Observe que o modelo é ajustado usando um tamanho de lote maior que o padrão de 2048, isso é importante para garantir que cada lote tenha uma chance decente de conter algumas amostras positivas. Se o tamanho do lote fosse muito pequeno, eles provavelmente não teriam transações fraudulentas para aprender.

EPOCHS = 100
BATCH_SIZE = 2048

early_stopping = tf.keras.callbacks.EarlyStopping(
    monitor='val_prc', 
    verbose=1,
    patience=10,
    mode='max',
    restore_best_weights=True)

model = make_model()
model.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 16)                480       
                                                                 
 dropout (Dropout)           (None, 16)                0         
                                                                 
 dense_1 (Dense)             (None, 1)                 17        
                                                                 
=================================================================
Total params: 497
Trainable params: 497
Non-trainable params: 0
_________________________________________________________________

Teste o modelo:

model.predict(train_features[:10])

array([[0.9466284 ],
       [0.7211031 ],
       [0.60527885],
       [0.8335568 ],
       [0.5909625 ],
       [0.6751574 ],
       [0.6623665 ],
       [0.81066036],
       [0.50712407],
       [0.8296292 ]], dtype=float32)

Opcional: Defina a polarização inicial correta.

Essas suposições iniciais não são ótimas. Você sabe que o conjunto de dados está desequilibrado. Defina o viés da camada de saída para refletir isso (consulte: Uma receita para treinar redes neurais: "init well" ). Isso pode ajudar na convergência inicial.

Com a inicialização de viés padrão, a perda deve ser de aproximadamente math.log(2) = 0.69314

results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))

Loss: 1.2781

O viés correto a ser definido pode ser derivado de:

\[ p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) \]

\[ b_0 = -log_e(1/p_0 - 1) \]

\[ b_0 = log_e(pos/neg)\]

initial_bias = np.log([pos/neg])
initial_bias

array([-6.35935934])

Defina isso como o viés inicial e o modelo fornecerá estimativas iniciais muito mais razoáveis.

Deve estar próximo de: pos/total = 0.0018

model = make_model(output_bias=initial_bias)
model.predict(train_features[:10])

array([[2.3598122e-05],
       [1.5476024e-03],
       [6.8338902e-04],
       [9.4873342e-04],
       [1.0742771e-03],
       [7.7475846e-04],
       [1.2199467e-03],
       [5.5399281e-04],
       [1.6213538e-03],
       [3.0470363e-04]], dtype=float32)

Com esta inicialização a perda inicial deve ser aproximadamente:

\[-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317\]

results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))

Loss: 0.0200

Essa perda inicial é cerca de 50 vezes menor do que se fosse com a inicialização ingênua.

Dessa forma, o modelo não precisa passar as primeiras épocas apenas aprendendo que exemplos positivos são improváveis. Isso também facilita a leitura dos gráficos da perda durante o treinamento.

Verifique os pesos iniciais

Para tornar as várias execuções de treinamento mais comparáveis, mantenha os pesos deste modelo inicial em um arquivo de ponto de verificação e carregue-os em cada modelo antes do treinamento:

initial_weights = os.path.join(tempfile.mkdtemp(), 'initial_weights')
model.save_weights(initial_weights)

Confirme se a correção de viés ajuda

Antes de prosseguir, confirme rapidamente se a inicialização cuidadosa do bias realmente ajudou.

Treine o modelo por 20 épocas, com e sem essa inicialização cuidadosa, e compare as perdas:

model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
    train_features,
    train_labels,
    batch_size=BATCH_SIZE,
    epochs=20,
    validation_data=(val_features, val_labels), 
    verbose=0)

model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
    train_features,
    train_labels,
    batch_size=BATCH_SIZE,
    epochs=20,
    validation_data=(val_features, val_labels), 
    verbose=0)

def plot_loss(history, label, n):
  # Use a log scale on y-axis to show the wide range of values.
  plt.semilogy(history.epoch, history.history['loss'],
               color=colors[n], label='Train ' + label)
  plt.semilogy(history.epoch, history.history['val_loss'],
               color=colors[n], label='Val ' + label,
               linestyle="--")
  plt.xlabel('Epoch')
  plt.ylabel('Loss')

plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)

png

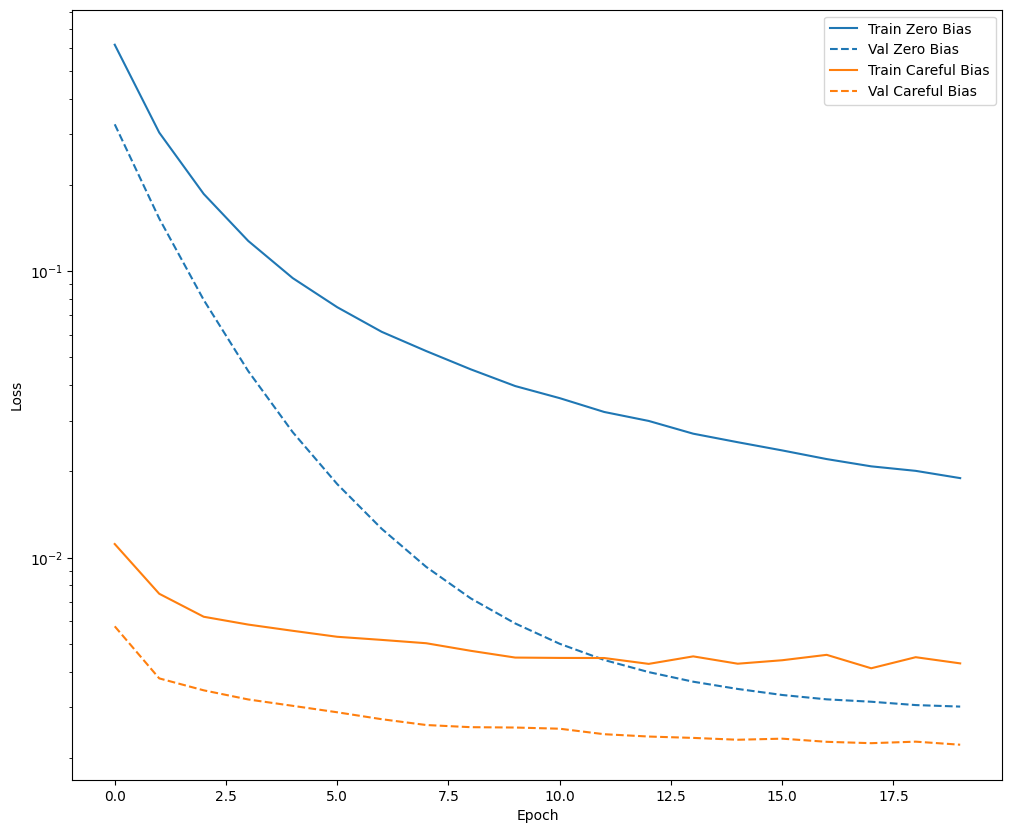
A figura acima deixa claro: Em termos de perda de validação, neste problema, essa inicialização cuidadosa oferece uma clara vantagem.

Treine o modelo

model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
    train_features,
    train_labels,
    batch_size=BATCH_SIZE,
    epochs=EPOCHS,
    callbacks=[early_stopping],
    validation_data=(val_features, val_labels))

Epoch 1/100
90/90 [==============================] - 3s 15ms/step - loss: 0.0161 - tp: 64.0000 - fp: 9.0000 - tn: 227425.0000 - fn: 347.0000 - accuracy: 0.9984 - precision: 0.8767 - recall: 0.1557 - auc: 0.6148 - prc: 0.1692 - val_loss: 0.0115 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7205 - val_prc: 0.2571
Epoch 2/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0087 - tp: 49.0000 - fp: 11.0000 - tn: 181940.0000 - fn: 276.0000 - accuracy: 0.9984 - precision: 0.8167 - recall: 0.1508 - auc: 0.8085 - prc: 0.3735 - val_loss: 0.0054 - val_tp: 35.0000 - val_fp: 6.0000 - val_tn: 45477.0000 - val_fn: 51.0000 - val_accuracy: 0.9987 - val_precision: 0.8537 - val_recall: 0.4070 - val_auc: 0.9065 - val_prc: 0.6598
Epoch 3/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0061 - tp: 126.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 199.0000 - accuracy: 0.9988 - precision: 0.8235 - recall: 0.3877 - auc: 0.8997 - prc: 0.6187 - val_loss: 0.0046 - val_tp: 55.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 31.0000 - val_accuracy: 0.9991 - val_precision: 0.8730 - val_recall: 0.6395 - val_auc: 0.9063 - val_prc: 0.6941
Epoch 4/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 172.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 153.0000 - accuracy: 0.9990 - precision: 0.8473 - recall: 0.5292 - auc: 0.9068 - prc: 0.6448 - val_loss: 0.0044 - val_tp: 58.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 28.0000 - val_accuracy: 0.9992 - val_precision: 0.8788 - val_recall: 0.6744 - val_auc: 0.9064 - val_prc: 0.7114
Epoch 5/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 167.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 158.0000 - accuracy: 0.9990 - precision: 0.8477 - recall: 0.5138 - auc: 0.9134 - prc: 0.6215 - val_loss: 0.0043 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7181
Epoch 6/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 193.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 132.0000 - accuracy: 0.9991 - precision: 0.8733 - recall: 0.5938 - auc: 0.9198 - prc: 0.6760 - val_loss: 0.0042 - val_tp: 59.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 27.0000 - val_accuracy: 0.9992 - val_precision: 0.8806 - val_recall: 0.6860 - val_auc: 0.9064 - val_prc: 0.7370
Epoch 7/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 183.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 142.0000 - accuracy: 0.9991 - precision: 0.8592 - recall: 0.5631 - auc: 0.9202 - prc: 0.6737 - val_loss: 0.0042 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7463
Epoch 8/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 171.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 154.0000 - accuracy: 0.9990 - precision: 0.8465 - recall: 0.5262 - auc: 0.9156 - prc: 0.6574 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7480
Epoch 9/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 196.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8711 - recall: 0.6031 - auc: 0.9218 - prc: 0.6799 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7550
Epoch 10/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 173.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 152.0000 - accuracy: 0.9990 - precision: 0.8650 - recall: 0.5323 - auc: 0.9048 - prc: 0.6520 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9122 - val_prc: 0.7598
Epoch 11/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 190.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8597 - recall: 0.5846 - auc: 0.9172 - prc: 0.6779 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9065 - val_prc: 0.7595
Epoch 12/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 192.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 133.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.5908 - auc: 0.9281 - prc: 0.7312 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9123 - val_prc: 0.7648
Epoch 13/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 185.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 140.0000 - accuracy: 0.9991 - precision: 0.8565 - recall: 0.5692 - auc: 0.9328 - prc: 0.7222 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7615
Epoch 14/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 183.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 142.0000 - accuracy: 0.9990 - precision: 0.8472 - recall: 0.5631 - auc: 0.9295 - prc: 0.6770 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7670
Epoch 15/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 194.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8700 - recall: 0.5969 - auc: 0.9344 - prc: 0.7233 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7672
Epoch 16/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 207.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8697 - recall: 0.6369 - auc: 0.9329 - prc: 0.7194 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7694
Epoch 17/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 190.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8716 - recall: 0.5846 - auc: 0.9345 - prc: 0.7265 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7705
Epoch 18/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8622 - recall: 0.5969 - auc: 0.9344 - prc: 0.7199 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7725
Epoch 19/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 205.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8613 - recall: 0.6308 - auc: 0.9346 - prc: 0.7266 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7739
Epoch 20/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 207.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8809 - recall: 0.6369 - auc: 0.9421 - prc: 0.7634 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7729
Epoch 21/100
90/90 [==============================] - 1s 6ms/step - loss: 0.0040 - tp: 204.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8644 - recall: 0.6277 - auc: 0.9360 - prc: 0.7340 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7756
Epoch 22/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 207.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8884 - recall: 0.6369 - auc: 0.9328 - prc: 0.7277 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7773
Epoch 23/100
90/90 [==============================] - 1s 6ms/step - loss: 0.0041 - tp: 191.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8527 - recall: 0.5877 - auc: 0.9375 - prc: 0.7280 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8857 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7790
Epoch 24/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 196.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6031 - auc: 0.9375 - prc: 0.7466 - val_loss: 0.0038 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7762
Epoch 25/100
90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 204.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8681 - recall: 0.6277 - auc: 0.9467 - prc: 0.7480 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9123 - val_prc: 0.7789
Epoch 26/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8661 - recall: 0.5969 - auc: 0.9360 - prc: 0.7292 - val_loss: 0.0038 - val_tp: 60.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8955 - val_recall: 0.6977 - val_auc: 0.9123 - val_prc: 0.7783
Epoch 27/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8776 - recall: 0.6400 - auc: 0.9376 - prc: 0.7632 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7772
Epoch 28/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 202.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 123.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6215 - auc: 0.9408 - prc: 0.7638 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7808
Epoch 29/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 214.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8807 - recall: 0.6585 - auc: 0.9347 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7806
Epoch 30/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 197.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 128.0000 - accuracy: 0.9991 - precision: 0.8640 - recall: 0.6062 - auc: 0.9346 - prc: 0.7489 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7804
Epoch 31/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 213.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 112.0000 - accuracy: 0.9992 - precision: 0.8659 - recall: 0.6554 - auc: 0.9407 - prc: 0.7615 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7809
Epoch 32/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9407 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7821
Epoch 33/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 210.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 115.0000 - accuracy: 0.9992 - precision: 0.8787 - recall: 0.6462 - auc: 0.9392 - prc: 0.7642 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7826
Epoch 34/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9423 - prc: 0.7759 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7830
Epoch 35/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 35.0000 - tn: 181916.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8566 - recall: 0.6431 - auc: 0.9407 - prc: 0.7381 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836
Epoch 36/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 204.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8831 - recall: 0.6277 - auc: 0.9407 - prc: 0.7587 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840
Epoch 37/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8672 - recall: 0.6431 - auc: 0.9345 - prc: 0.7386 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7849
Epoch 38/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 198.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.6092 - auc: 0.9454 - prc: 0.7488 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7844
Epoch 39/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 209.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8782 - recall: 0.6431 - auc: 0.9407 - prc: 0.7419 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840
Epoch 40/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 198.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8761 - recall: 0.6092 - auc: 0.9546 - prc: 0.7644 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7835
Epoch 41/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8745 - recall: 0.6431 - auc: 0.9377 - prc: 0.7587 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7827
Epoch 42/100
90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 195.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8667 - recall: 0.6000 - auc: 0.9345 - prc: 0.7436 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7834
Epoch 43/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8655 - recall: 0.6338 - auc: 0.9500 - prc: 0.7699 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836
Epoch 44/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8927 - recall: 0.6400 - auc: 0.9438 - prc: 0.7625 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7841
Epoch 45/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 205.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8686 - recall: 0.6308 - auc: 0.9422 - prc: 0.7519 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7847
Epoch 46/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 206.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8766 - recall: 0.6338 - auc: 0.9423 - prc: 0.7529 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7843
Epoch 47/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 219.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8866 - recall: 0.6738 - auc: 0.9377 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7871
Epoch 48/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8729 - recall: 0.6338 - auc: 0.9393 - prc: 0.7676 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7854
Epoch 49/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 215.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 110.0000 - accuracy: 0.9992 - precision: 0.8811 - recall: 0.6615 - auc: 0.9407 - prc: 0.7618 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9125 - val_prc: 0.7855
Epoch 50/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 214.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8699 - recall: 0.6585 - auc: 0.9377 - prc: 0.7727 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7858
Epoch 51/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 219.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8795 - recall: 0.6738 - auc: 0.9393 - prc: 0.7889 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7876
Epoch 52/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 217.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8967 - recall: 0.6677 - auc: 0.9439 - prc: 0.7812 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7887
Epoch 53/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 206.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8803 - recall: 0.6338 - auc: 0.9362 - prc: 0.7734 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7873
Epoch 54/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 223.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 102.0000 - accuracy: 0.9993 - precision: 0.8814 - recall: 0.6862 - auc: 0.9438 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7877
Epoch 55/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 220.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 105.0000 - accuracy: 0.9993 - precision: 0.8943 - recall: 0.6769 - auc: 0.9439 - prc: 0.7866 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886
Epoch 56/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 209.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8970 - recall: 0.6431 - auc: 0.9392 - prc: 0.7613 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886
Epoch 57/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0033 - tp: 221.0000 - fp: 23.0000 - tn: 181928.0000 - fn: 104.0000 - accuracy: 0.9993 - precision: 0.9057 - recall: 0.6800 - auc: 0.9516 - prc: 0.7954 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7873
Epoch 58/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8851 - recall: 0.6400 - auc: 0.9485 - prc: 0.7746 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7875
Epoch 59/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 216.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 109.0000 - accuracy: 0.9992 - precision: 0.8780 - recall: 0.6646 - auc: 0.9531 - prc: 0.7928 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7883
Epoch 60/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 211.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8719 - recall: 0.6492 - auc: 0.9469 - prc: 0.7808 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7882
Epoch 61/100
90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 201.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 124.0000 - accuracy: 0.9992 - precision: 0.8933 - recall: 0.6185 - auc: 0.9424 - prc: 0.7720 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7881
Epoch 62/100
81/90 [==========================>...] - ETA: 0s - loss: 0.0034 - tp: 196.0000 - fp: 21.0000 - tn: 165565.0000 - fn: 106.0000 - accuracy: 0.9992 - precision: 0.9032 - recall: 0.6490 - auc: 0.9413 - prc: 0.7849Restoring model weights from the end of the best epoch: 52.
90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 211.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8941 - recall: 0.6492 - auc: 0.9423 - prc: 0.7828 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7860
Epoch 62: early stopping

Confira o histórico de treinamento

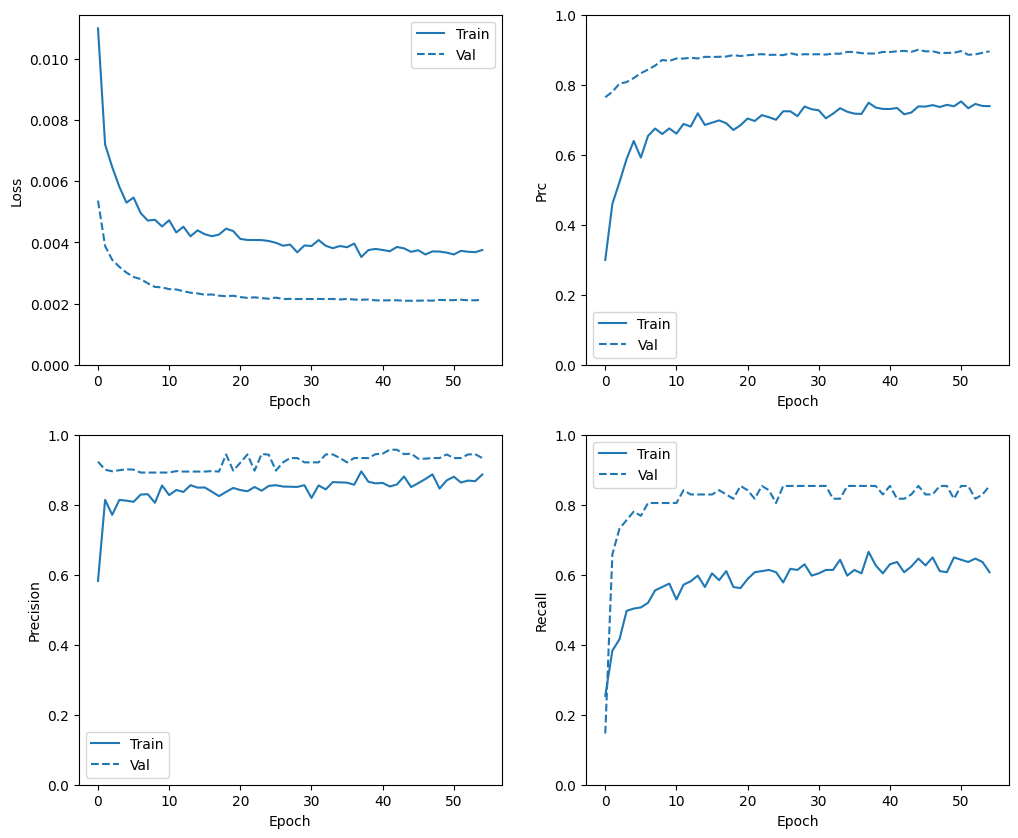
Nesta seção, você produzirá gráficos da precisão e perda do seu modelo no conjunto de treinamento e validação. Eles são úteis para verificar se há overfitting, sobre os quais você pode aprender mais no tutorial Overfit e underfit .

Além disso, você pode produzir esses gráficos para qualquer uma das métricas criadas acima. Os falsos negativos são incluídos como exemplo.

def plot_metrics(history):
  metrics = ['loss', 'prc', 'precision', 'recall']
  for n, metric in enumerate(metrics):
    name = metric.replace("_"," ").capitalize()
    plt.subplot(2,2,n+1)
    plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
    plt.plot(history.epoch, history.history['val_'+metric],
             color=colors[0], linestyle="--", label='Val')
    plt.xlabel('Epoch')
    plt.ylabel(name)
    if metric == 'loss':
      plt.ylim([0, plt.ylim()[1]])
    elif metric == 'auc':
      plt.ylim([0.8,1])
    else:
      plt.ylim([0,1])

    plt.legend();

plot_metrics(baseline_history)

png

Avaliar métricas

Você pode usar uma matriz de confusão para resumir os rótulos reais versus previstos, em que o eixo X é o rótulo previsto e o eixo Y é o rótulo real:

train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)

def plot_cm(labels, predictions, p=0.5):
  cm = confusion_matrix(labels, predictions > p)
  plt.figure(figsize=(5,5))
  sns.heatmap(cm, annot=True, fmt="d")
  plt.title('Confusion matrix @{:.2f}'.format(p))
  plt.ylabel('Actual label')
  plt.xlabel('Predicted label')

  print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
  print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
  print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
  print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
  print('Total Fraudulent Transactions: ', np.sum(cm[1]))

Avalie seu modelo no conjunto de dados de teste e exiba os resultados das métricas que você criou acima:

baseline_results = model.evaluate(test_features, test_labels,
                                  batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
  print(name, ': ', value)
print()

plot_cm(test_labels, test_predictions_baseline)

loss :  0.0024895435199141502
tp :  59.0
fp :  7.0
tn :  56874.0
fn :  22.0
accuracy :  0.9994909167289734
precision :  0.8939393758773804
recall :  0.7283950448036194
auc :  0.9318439960479736
prc :  0.8204483985900879

Legitimate Transactions Detected (True Negatives):  56874
Legitimate Transactions Incorrectly Detected (False Positives):  7
Fraudulent Transactions Missed (False Negatives):  22
Fraudulent Transactions Detected (True Positives):  59
Total Fraudulent Transactions:  81

png

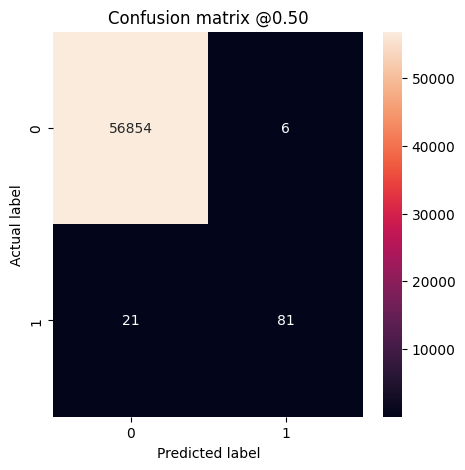
Se o modelo tivesse previsto tudo perfeitamente, esta seria uma matriz diagonal onde os valores fora da diagonal principal, indicando previsões incorretas, seriam zero. Nesse caso, a matriz mostra que você tem relativamente poucos falsos positivos, o que significa que havia relativamente poucas transações legítimas que foram sinalizadas incorretamente. No entanto, você provavelmente gostaria de ter ainda menos falsos negativos, apesar do custo de aumentar o número de falsos positivos. Essa compensação pode ser preferível porque falsos negativos permitiriam transações fraudulentas, enquanto falsos positivos podem fazer com que um e-mail seja enviado a um cliente solicitando que ele verifique a atividade do cartão.

Trace o ROC

Agora trace o ROC . Esse gráfico é útil porque mostra rapidamente a faixa de desempenho que o modelo pode atingir apenas ajustando o limite de saída.

def plot_roc(name, labels, predictions, **kwargs):
  fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)

  plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
  plt.xlabel('False positives [%]')
  plt.ylabel('True positives [%]')
  plt.xlim([-0.5,20])
  plt.ylim([80,100.5])
  plt.grid(True)
  ax = plt.gca()
  ax.set_aspect('equal')

plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');

png

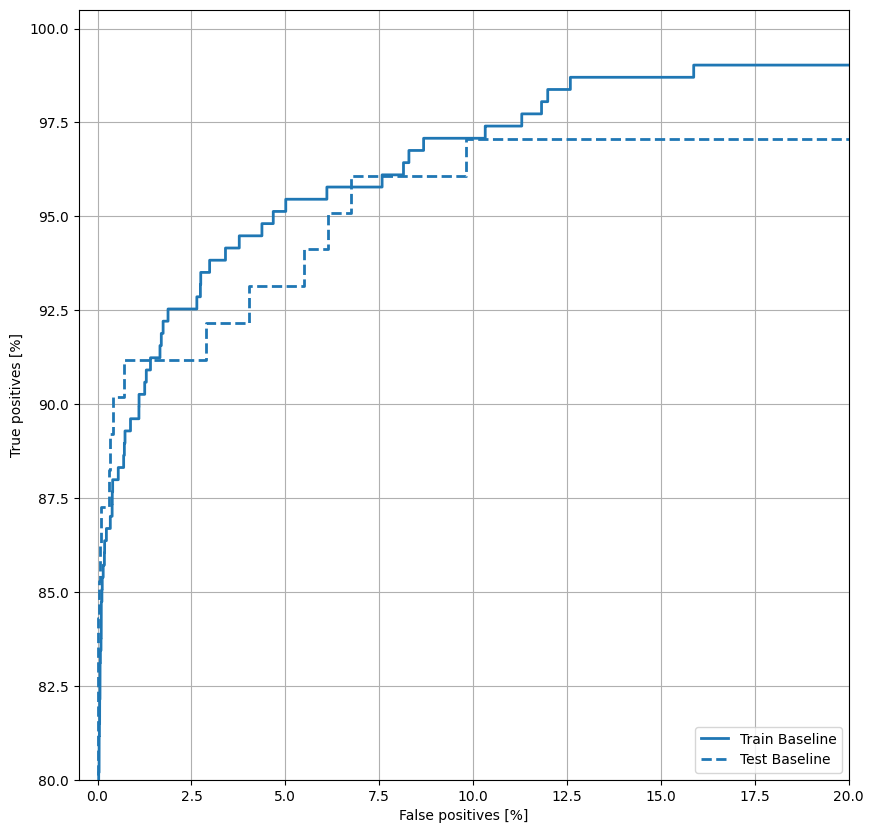
Trace o AUPRC

Agora plote o AUPRC . Área sob a curva de precisão-recordação interpolada, obtida pela plotagem (recall, precisão) de pontos para diferentes valores do limiar de classificação. Dependendo de como é calculado, PR AUC pode ser equivalente à precisão média do modelo.

def plot_prc(name, labels, predictions, **kwargs):
    precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)

    plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
    plt.xlabel('Recall')
    plt.ylabel('Precision')
    plt.grid(True)
    ax = plt.gca()
    ax.set_aspect('equal')

plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');

png

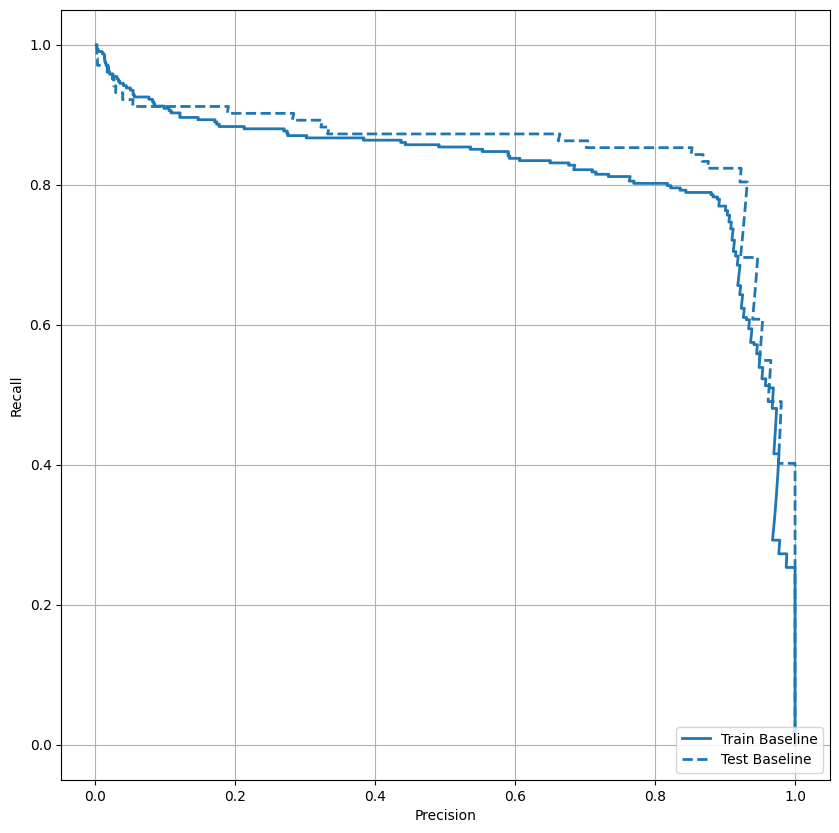
Parece que a precisão é relativamente alta, mas o recall e a área sob a curva ROC (AUC) não são tão altos quanto você gostaria. Os classificadores geralmente enfrentam desafios ao tentar maximizar a precisão e o recall, o que é especialmente verdadeiro ao trabalhar com conjuntos de dados desequilibrados. É importante considerar os custos de diferentes tipos de erros no contexto do problema com o qual você se preocupa. Neste exemplo, um falso negativo (uma transação fraudulenta é perdida) pode ter um custo financeiro, enquanto um falso positivo (uma transação é sinalizada incorretamente como fraudulenta) pode diminuir a satisfação do usuário.

Pesos de classe

Calcular pesos de classe

O objetivo é identificar transações fraudulentas, mas você não tem muitas dessas amostras positivas para trabalhar, então você gostaria que o classificador ponderasse fortemente os poucos exemplos disponíveis. Você pode fazer isso passando os pesos Keras para cada classe por meio de um parâmetro. Isso fará com que o modelo "preste mais atenção" aos exemplos de uma classe sub-representada.

# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)

class_weight = {0: weight_for_0, 1: weight_for_1}

print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))

Weight for class 0: 0.50
Weight for class 1: 289.44

Treine um modelo com pesos de classe

Agora tente treinar novamente e avaliar o modelo com pesos de classe para ver como isso afeta as previsões.

weighted_model = make_model()
weighted_model.load_weights(initial_weights)

weighted_history = weighted_model.fit(
    train_features,
    train_labels,
    batch_size=BATCH_SIZE,
    epochs=EPOCHS,
    callbacks=[early_stopping],
    validation_data=(val_features, val_labels),
    # The class weights go here
    class_weight=class_weight)

Epoch 1/100
90/90 [==============================] - 3s 15ms/step - loss: 4.1298 - tp: 59.0000 - fp: 11.0000 - tn: 238821.0000 - fn: 347.0000 - accuracy: 0.9985 - precision: 0.8429 - recall: 0.1453 - auc: 0.6238 - prc: 0.1649 - val_loss: 0.0119 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7124 - val_prc: 0.0294
Epoch 2/100
90/90 [==============================] - 1s 7ms/step - loss: 1.8711 - tp: 69.0000 - fp: 54.0000 - tn: 181897.0000 - fn: 256.0000 - accuracy: 0.9983 - precision: 0.5610 - recall: 0.2123 - auc: 0.8178 - prc: 0.2117 - val_loss: 0.0060 - val_tp: 56.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 30.0000 - val_accuracy: 0.9991 - val_precision: 0.8485 - val_recall: 0.6512 - val_auc: 0.9427 - val_prc: 0.6870
Epoch 3/100
90/90 [==============================] - 1s 7ms/step - loss: 0.8666 - tp: 187.0000 - fp: 198.0000 - tn: 181753.0000 - fn: 138.0000 - accuracy: 0.9982 - precision: 0.4857 - recall: 0.5754 - auc: 0.9075 - prc: 0.4912 - val_loss: 0.0077 - val_tp: 65.0000 - val_fp: 19.0000 - val_tn: 45464.0000 - val_fn: 21.0000 - val_accuracy: 0.9991 - val_precision: 0.7738 - val_recall: 0.7558 - val_auc: 0.9564 - val_prc: 0.6924
Epoch 4/100
90/90 [==============================] - 1s 7ms/step - loss: 0.6876 - tp: 218.0000 - fp: 530.0000 - tn: 181421.0000 - fn: 107.0000 - accuracy: 0.9965 - precision: 0.2914 - recall: 0.6708 - auc: 0.9152 - prc: 0.5102 - val_loss: 0.0109 - val_tp: 68.0000 - val_fp: 39.0000 - val_tn: 45444.0000 - val_fn: 18.0000 - val_accuracy: 0.9987 - val_precision: 0.6355 - val_recall: 0.7907 - val_auc: 0.9661 - val_prc: 0.6926
Epoch 5/100
90/90 [==============================] - 1s 7ms/step - loss: 0.5229 - tp: 240.0000 - fp: 1102.0000 - tn: 180849.0000 - fn: 85.0000 - accuracy: 0.9935 - precision: 0.1788 - recall: 0.7385 - auc: 0.9395 - prc: 0.5228 - val_loss: 0.0154 - val_tp: 70.0000 - val_fp: 79.0000 - val_tn: 45404.0000 - val_fn: 16.0000 - val_accuracy: 0.9979 - val_precision: 0.4698 - val_recall: 0.8140 - val_auc: 0.9657 - val_prc: 0.7023
Epoch 6/100
90/90 [==============================] - 1s 7ms/step - loss: 0.4753 - tp: 251.0000 - fp: 1839.0000 - tn: 180112.0000 - fn: 74.0000 - accuracy: 0.9895 - precision: 0.1201 - recall: 0.7723 - auc: 0.9336 - prc: 0.4297 - val_loss: 0.0213 - val_tp: 70.0000 - val_fp: 156.0000 - val_tn: 45327.0000 - val_fn: 16.0000 - val_accuracy: 0.9962 - val_precision: 0.3097 - val_recall: 0.8140 - val_auc: 0.9654 - val_prc: 0.6742
Epoch 7/100
90/90 [==============================] - 1s 7ms/step - loss: 0.3870 - tp: 270.0000 - fp: 2554.0000 - tn: 179397.0000 - fn: 55.0000 - accuracy: 0.9857 - precision: 0.0956 - recall: 0.8308 - auc: 0.9463 - prc: 0.3800 - val_loss: 0.0269 - val_tp: 70.0000 - val_fp: 264.0000 - val_tn: 45219.0000 - val_fn: 16.0000 - val_accuracy: 0.9939 - val_precision: 0.2096 - val_recall: 0.8140 - val_auc: 0.9651 - val_prc: 0.6116
Epoch 8/100
90/90 [==============================] - 1s 7ms/step - loss: 0.3942 - tp: 268.0000 - fp: 3219.0000 - tn: 178732.0000 - fn: 57.0000 - accuracy: 0.9820 - precision: 0.0769 - recall: 0.8246 - auc: 0.9434 - prc: 0.3273 - val_loss: 0.0337 - val_tp: 70.0000 - val_fp: 355.0000 - val_tn: 45128.0000 - val_fn: 16.0000 - val_accuracy: 0.9919 - val_precision: 0.1647 - val_recall: 0.8140 - val_auc: 0.9682 - val_prc: 0.5918
Epoch 9/100
90/90 [==============================] - 1s 7ms/step - loss: 0.3886 - tp: 271.0000 - fp: 3845.0000 - tn: 178106.0000 - fn: 54.0000 - accuracy: 0.9786 - precision: 0.0658 - recall: 0.8338 - auc: 0.9397 - prc: 0.2995 - val_loss: 0.0386 - val_tp: 70.0000 - val_fp: 406.0000 - val_tn: 45077.0000 - val_fn: 16.0000 - val_accuracy: 0.9907 - val_precision: 0.1471 - val_recall: 0.8140 - val_auc: 0.9756 - val_prc: 0.5889
Epoch 10/100
90/90 [==============================] - 1s 7ms/step - loss: 0.2951 - tp: 281.0000 - fp: 4348.0000 - tn: 177603.0000 - fn: 44.0000 - accuracy: 0.9759 - precision: 0.0607 - recall: 0.8646 - auc: 0.9623 - prc: 0.2826 - val_loss: 0.0441 - val_tp: 72.0000 - val_fp: 464.0000 - val_tn: 45019.0000 - val_fn: 14.0000 - val_accuracy: 0.9895 - val_precision: 0.1343 - val_recall: 0.8372 - val_auc: 0.9748 - val_prc: 0.5895
Epoch 11/100
90/90 [==============================] - 1s 7ms/step - loss: 0.2703 - tp: 280.0000 - fp: 4697.0000 - tn: 177254.0000 - fn: 45.0000 - accuracy: 0.9740 - precision: 0.0563 - recall: 0.8615 - auc: 0.9660 - prc: 0.2589 - val_loss: 0.0490 - val_tp: 72.0000 - val_fp: 552.0000 - val_tn: 44931.0000 - val_fn: 14.0000 - val_accuracy: 0.9876 - val_precision: 0.1154 - val_recall: 0.8372 - val_auc: 0.9762 - val_prc: 0.5902
Epoch 12/100
90/90 [==============================] - 1s 7ms/step - loss: 0.3358 - tp: 278.0000 - fp: 5262.0000 - tn: 176689.0000 - fn: 47.0000 - accuracy: 0.9709 - precision: 0.0502 - recall: 0.8554 - auc: 0.9468 - prc: 0.2368 - val_loss: 0.0534 - val_tp: 74.0000 - val_fp: 597.0000 - val_tn: 44886.0000 - val_fn: 12.0000 - val_accuracy: 0.9866 - val_precision: 0.1103 - val_recall: 0.8605 - val_auc: 0.9752 - val_prc: 0.5848
Epoch 13/100
90/90 [==============================] - 1s 7ms/step - loss: 0.2833 - tp: 286.0000 - fp: 5502.0000 - tn: 176449.0000 - fn: 39.0000 - accuracy: 0.9696 - precision: 0.0494 - recall: 0.8800 - auc: 0.9582 - prc: 0.2572 - val_loss: 0.0563 - val_tp: 74.0000 - val_fp: 616.0000 - val_tn: 44867.0000 - val_fn: 12.0000 - val_accuracy: 0.9862 - val_precision: 0.1072 - val_recall: 0.8605 - val_auc: 0.9748 - val_prc: 0.5678
Epoch 14/100
90/90 [==============================] - 1s 7ms/step - loss: 0.2969 - tp: 280.0000 - fp: 5630.0000 - tn: 176321.0000 - fn: 45.0000 - accuracy: 0.9689 - precision: 0.0474 - recall: 0.8615 - auc: 0.9594 - prc: 0.2374 - val_loss: 0.0597 - val_tp: 74.0000 - val_fp: 644.0000 - val_tn: 44839.0000 - val_fn: 12.0000 - val_accuracy: 0.9856 - val_precision: 0.1031 - val_recall: 0.8605 - val_auc: 0.9741 - val_prc: 0.5627
Epoch 15/100
90/90 [==============================] - ETA: 0s - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224Restoring model weights from the end of the best epoch: 5.
90/90 [==============================] - 1s 7ms/step - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224 - val_loss: 0.0621 - val_tp: 74.0000 - val_fp: 665.0000 - val_tn: 44818.0000 - val_fn: 12.0000 - val_accuracy: 0.9851 - val_precision: 0.1001 - val_recall: 0.8605 - val_auc: 0.9771 - val_prc: 0.5550
Epoch 15: early stopping

Confira o histórico de treinamento

plot_metrics(weighted_history)

png

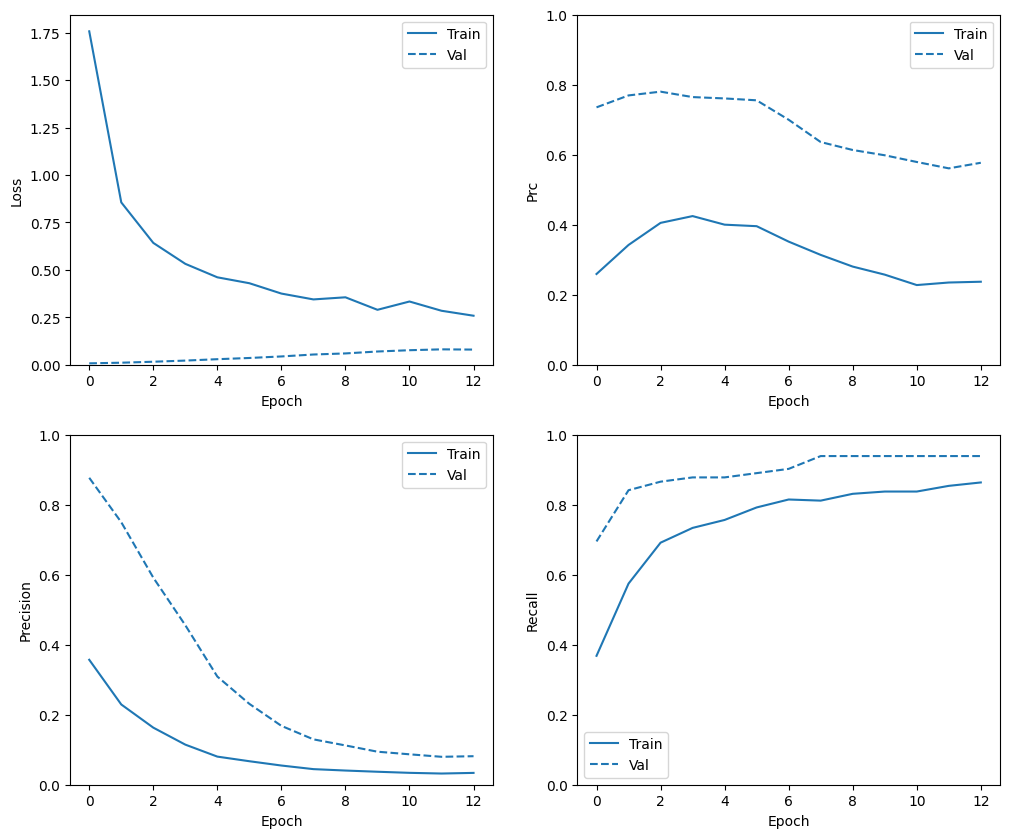
Avaliar métricas

train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)

weighted_results = weighted_model.evaluate(test_features, test_labels,
                                           batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
  print(name, ': ', value)
print()

plot_cm(test_labels, test_predictions_weighted)

loss :  0.014327289536595345
tp :  69.0
fp :  88.0
tn :  56793.0
fn :  12.0
accuracy :  0.9982444643974304
precision :  0.4394904375076294
recall :  0.8518518805503845
auc :  0.9410961866378784
prc :  0.7397712469100952

Legitimate Transactions Detected (True Negatives):  56793
Legitimate Transactions Incorrectly Detected (False Positives):  88
Fraudulent Transactions Missed (False Negatives):  12
Fraudulent Transactions Detected (True Positives):  69
Total Fraudulent Transactions:  81

png

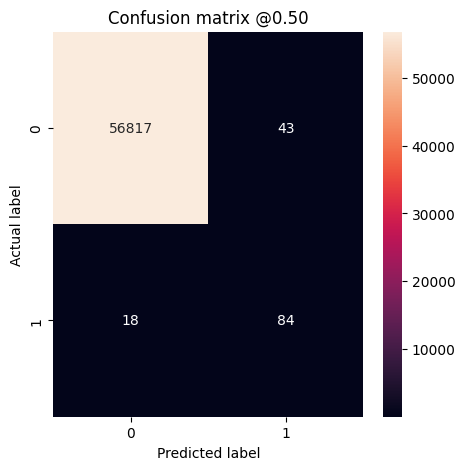
Aqui você pode ver que com pesos de classe a exatidão e precisão são menores porque há mais falsos positivos, mas inversamente o recall e a AUC são maiores porque o modelo também encontrou mais verdadeiros positivos. Apesar de ter menor acurácia, esse modelo tem maior recall (e identifica mais transações fraudulentas). Obviamente, há um custo para ambos os tipos de erro (você também não gostaria de incomodar os usuários sinalizando muitas transações legítimas como fraudulentas). Considere cuidadosamente as compensações entre esses diferentes tipos de erros para seu aplicativo.

Trace o ROC

plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')

plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')


plt.legend(loc='lower right');

png

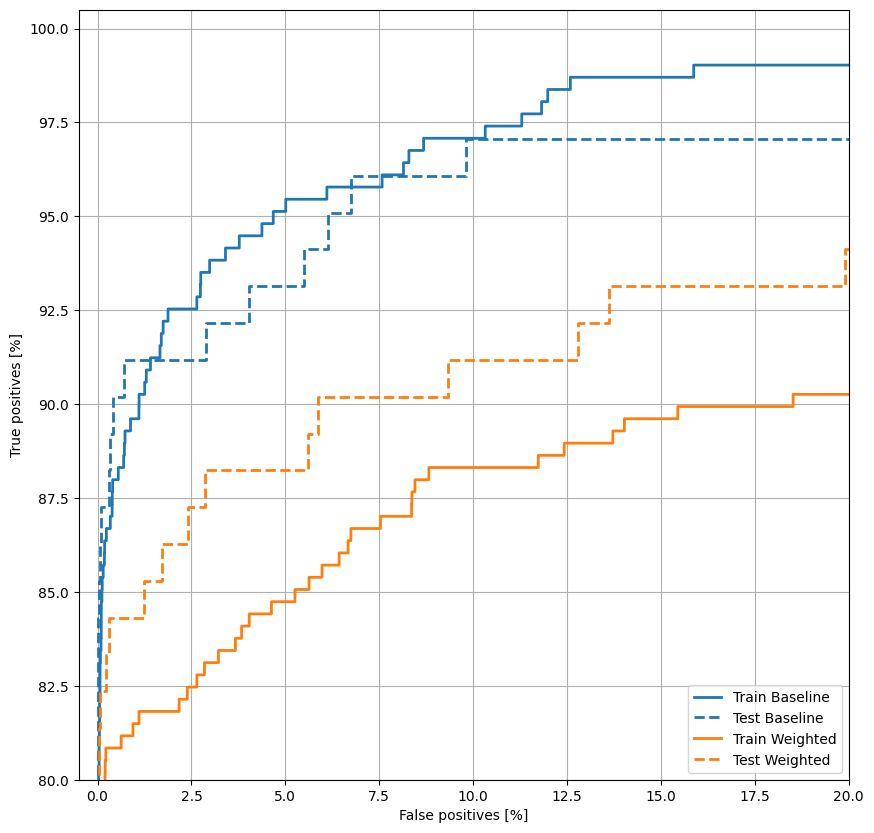
Trace o AUPRC

plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')

plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')


plt.legend(loc='lower right');

png

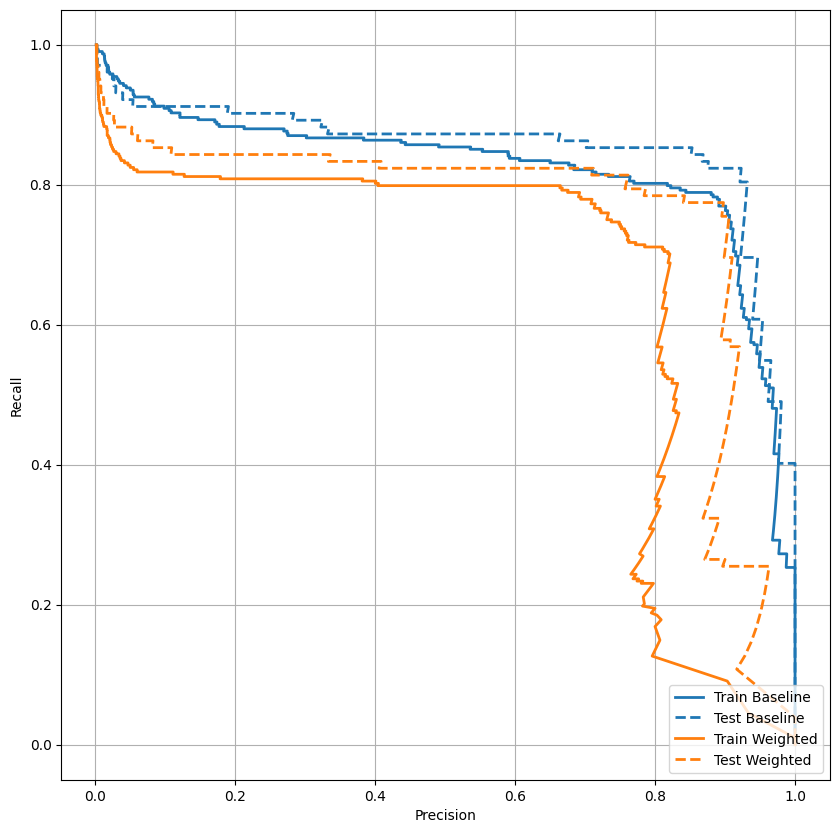
Sobreamostragem

Exagerar na classe minoritária

Uma abordagem relacionada seria reamostrar o conjunto de dados sobreamostrando a classe minoritária.

pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]

pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]

Usando NumPy

Você pode balancear o conjunto de dados manualmente escolhendo o número certo de índices aleatórios dos exemplos positivos:

ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))

res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]

res_pos_features.shape

(181951, 29)

resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)

order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]

resampled_features.shape

(363902, 29)

Usando `tf.data`

Se você estiver usando tf.data , a maneira mais fácil de produzir exemplos equilibrados é começar com um conjunto de dados positive e negative e mesclá-los. Consulte o guia tf.data para obter mais exemplos.

BUFFER_SIZE = 100000

def make_ds(features, labels):
  ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
  ds = ds.shuffle(BUFFER_SIZE).repeat()
  return ds

pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)

Cada conjunto de dados fornece pares (feature, label) :

for features, label in pos_ds.take(1):
  print("Features:\n", features.numpy())
  print()
  print("Label: ", label.numpy())

Features:
 [ 0.56826828  1.24841849 -2.52251105  3.84165891  0.05052604 -0.7621795
 -1.43118352  0.43296139 -1.85102109 -2.50477555  3.20133397 -3.52460861
 -0.95133935 -5.         -1.93144512 -0.7302767  -2.46735228  0.21827555
 -1.45046438  0.21081234  0.39176826 -0.23558789 -0.03611637 -0.62063738
  0.3686766   0.23622961  1.2242418   0.75555829 -1.45589162]

Label:  1

Mescle os dois usando tf.data.Dataset.sample_from_datasets :

resampled_ds = tf.data.Dataset.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)

for features, label in resampled_ds.take(1):
  print(label.numpy().mean())

0.50732421875

Para usar esse conjunto de dados, você precisará do número de etapas por época.

A definição de "época" neste caso é menos clara. Digamos que seja o número de lotes necessários para ver cada exemplo negativo uma vez:

resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch

278.0

Treine com os dados sobreamostrados

Agora tente treinar o modelo com o conjunto de dados reamostrado em vez de usar pesos de classe para ver como esses métodos se comparam.

resampled_model = make_model()
resampled_model.load_weights(initial_weights)

# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1] 
output_layer.bias.assign([0])

val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2) 

resampled_history = resampled_model.fit(
    resampled_ds,
    epochs=EPOCHS,
    steps_per_epoch=resampled_steps_per_epoch,
    callbacks=[early_stopping],
    validation_data=val_ds)

Epoch 1/100
278/278 [==============================] - 10s 32ms/step - loss: 0.5508 - tp: 214194.0000 - fp: 51114.0000 - tn: 290615.0000 - fn: 70383.0000 - accuracy: 0.8060 - precision: 0.8073 - recall: 0.7527 - auc: 0.8600 - prc: 0.8879 - val_loss: 0.2279 - val_tp: 73.0000 - val_fp: 969.0000 - val_tn: 44514.0000 - val_fn: 13.0000 - val_accuracy: 0.9785 - val_precision: 0.0701 - val_recall: 0.8488 - val_auc: 0.9551 - val_prc: 0.7044
Epoch 2/100
278/278 [==============================] - 8s 28ms/step - loss: 0.2235 - tp: 253877.0000 - fp: 15743.0000 - tn: 268530.0000 - fn: 31194.0000 - accuracy: 0.9176 - precision: 0.9416 - recall: 0.8906 - auc: 0.9658 - prc: 0.9746 - val_loss: 0.1367 - val_tp: 73.0000 - val_fp: 777.0000 - val_tn: 44706.0000 - val_fn: 13.0000 - val_accuracy: 0.9827 - val_precision: 0.0859 - val_recall: 0.8488 - val_auc: 0.9596 - val_prc: 0.7072
Epoch 3/100
278/278 [==============================] - 8s 28ms/step - loss: 0.1785 - tp: 258572.0000 - fp: 9840.0000 - tn: 274878.0000 - fn: 26054.0000 - accuracy: 0.9370 - precision: 0.9633 - recall: 0.9085 - auc: 0.9773 - prc: 0.9827 - val_loss: 0.1023 - val_tp: 72.0000 - val_fp: 699.0000 - val_tn: 44784.0000 - val_fn: 14.0000 - val_accuracy: 0.9844 - val_precision: 0.0934 - val_recall: 0.8372 - val_auc: 0.9632 - val_prc: 0.7032
Epoch 4/100
278/278 [==============================] - 8s 29ms/step - loss: 0.1571 - tp: 260447.0000 - fp: 8085.0000 - tn: 276389.0000 - fn: 24423.0000 - accuracy: 0.9429 - precision: 0.9699 - recall: 0.9143 - auc: 0.9826 - prc: 0.9863 - val_loss: 0.0869 - val_tp: 74.0000 - val_fp: 701.0000 - val_tn: 44782.0000 - val_fn: 12.0000 - val_accuracy: 0.9844 - val_precision: 0.0955 - val_recall: 0.8605 - val_auc: 0.9633 - val_prc: 0.6972
Epoch 5/100
278/278 [==============================] - 8s 30ms/step - loss: 0.1440 - tp: 261457.0000 - fp: 7449.0000 - tn: 277093.0000 - fn: 23345.0000 - accuracy: 0.9459 - precision: 0.9723 - recall: 0.9180 - auc: 0.9855 - prc: 0.9883 - val_loss: 0.0774 - val_tp: 73.0000 - val_fp: 679.0000 - val_tn: 44804.0000 - val_fn: 13.0000 - val_accuracy: 0.9848 - val_precision: 0.0971 - val_recall: 0.8488 - val_auc: 0.9645 - val_prc: 0.6971
Epoch 6/100
278/278 [==============================] - 8s 28ms/step - loss: 0.1349 - tp: 262460.0000 - fp: 6942.0000 - tn: 277723.0000 - fn: 22219.0000 - accuracy: 0.9488 - precision: 0.9742 - recall: 0.9220 - auc: 0.9876 - prc: 0.9896 - val_loss: 0.0718 - val_tp: 74.0000 - val_fp: 624.0000 - val_tn: 44859.0000 - val_fn: 12.0000 - val_accuracy: 0.9860 - val_precision: 0.1060 - val_recall: 0.8605 - val_auc: 0.9645 - val_prc: 0.6891
Epoch 7/100
278/278 [==============================] - 8s 28ms/step - loss: 0.1264 - tp: 263166.0000 - fp: 6780.0000 - tn: 278253.0000 - fn: 21145.0000 - accuracy: 0.9510 - precision: 0.9749 - recall: 0.9256 - auc: 0.9895 - prc: 0.9909 - val_loss: 0.0672 - val_tp: 75.0000 - val_fp: 602.0000 - val_tn: 44881.0000 - val_fn: 11.0000 - val_accuracy: 0.9865 - val_precision: 0.1108 - val_recall: 0.8721 - val_auc: 0.9670 - val_prc: 0.6822
Epoch 8/100
278/278 [==============================] - 8s 30ms/step - loss: 0.1190 - tp: 264216.0000 - fp: 6569.0000 - tn: 278270.0000 - fn: 20289.0000 - accuracy: 0.9528 - precision: 0.9757 - recall: 0.9287 - auc: 0.9910 - prc: 0.9920 - val_loss: 0.0628 - val_tp: 74.0000 - val_fp: 570.0000 - val_tn: 44913.0000 - val_fn: 12.0000 - val_accuracy: 0.9872 - val_precision: 0.1149 - val_recall: 0.8605 - val_auc: 0.9671 - val_prc: 0.6830
Epoch 9/100
278/278 [==============================] - 9s 31ms/step - loss: 0.1125 - tp: 264562.0000 - fp: 6339.0000 - tn: 279137.0000 - fn: 19306.0000 - accuracy: 0.9550 - precision: 0.9766 - recall: 0.9320 - auc: 0.9924 - prc: 0.9930 - val_loss: 0.0576 - val_tp: 74.0000 - val_fp: 544.0000 - val_tn: 44939.0000 - val_fn: 12.0000 - val_accuracy: 0.9878 - val_precision: 0.1197 - val_recall: 0.8605 - val_auc: 0.9672 - val_prc: 0.6828
Epoch 10/100
278/278 [==============================] - 8s 30ms/step - loss: 0.1064 - tp: 266549.0000 - fp: 6112.0000 - tn: 278323.0000 - fn: 18360.0000 - accuracy: 0.9570 - precision: 0.9776 - recall: 0.9356 - auc: 0.9934 - prc: 0.9937 - val_loss: 0.0544 - val_tp: 74.0000 - val_fp: 541.0000 - val_tn: 44942.0000 - val_fn: 12.0000 - val_accuracy: 0.9879 - val_precision: 0.1203 - val_recall: 0.8605 - val_auc: 0.9638 - val_prc: 0.6827
Epoch 11/100
278/278 [==============================] - 8s 30ms/step - loss: 0.1005 - tp: 267048.0000 - fp: 6123.0000 - tn: 278896.0000 - fn: 17277.0000 - accuracy: 0.9589 - precision: 0.9776 - recall: 0.9392 - auc: 0.9943 - prc: 0.9944 - val_loss: 0.0493 - val_tp: 74.0000 - val_fp: 500.0000 - val_tn: 44983.0000 - val_fn: 12.0000 - val_accuracy: 0.9888 - val_precision: 0.1289 - val_recall: 0.8605 - val_auc: 0.9578 - val_prc: 0.6761
Epoch 12/100
277/278 [============================>.] - ETA: 0s - loss: 0.0950 - tp: 266855.0000 - fp: 6079.0000 - tn: 277677.0000 - fn: 16685.0000 - accuracy: 0.9599 - precision: 0.9777 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949Restoring model weights from the end of the best epoch: 2.
278/278 [==============================] - 8s 29ms/step - loss: 0.0950 - tp: 267815.0000 - fp: 6094.0000 - tn: 278693.0000 - fn: 16742.0000 - accuracy: 0.9599 - precision: 0.9778 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949 - val_loss: 0.0451 - val_tp: 74.0000 - val_fp: 468.0000 - val_tn: 45015.0000 - val_fn: 12.0000 - val_accuracy: 0.9895 - val_precision: 0.1365 - val_recall: 0.8605 - val_auc: 0.9581 - val_prc: 0.6683
Epoch 12: early stopping

Se o processo de treinamento estivesse considerando todo o conjunto de dados em cada atualização de gradiente, essa sobreamostragem seria basicamente idêntica à ponderação da classe.

Mas ao treinar o modelo em lotes, como você fez aqui, os dados sobreamostrados fornecem um sinal de gradiente mais suave: em vez de cada exemplo positivo ser mostrado em um lote com um peso grande, eles são mostrados em muitos lotes diferentes a cada vez com um peso pequeno.

Esse sinal de gradiente mais suave facilita o treinamento do modelo.

Confira o histórico de treinamento

Observe que as distribuições de métricas serão diferentes aqui, pois os dados de treinamento possuem uma distribuição totalmente diferente dos dados de validação e teste.

plot_metrics(resampled_history)

png

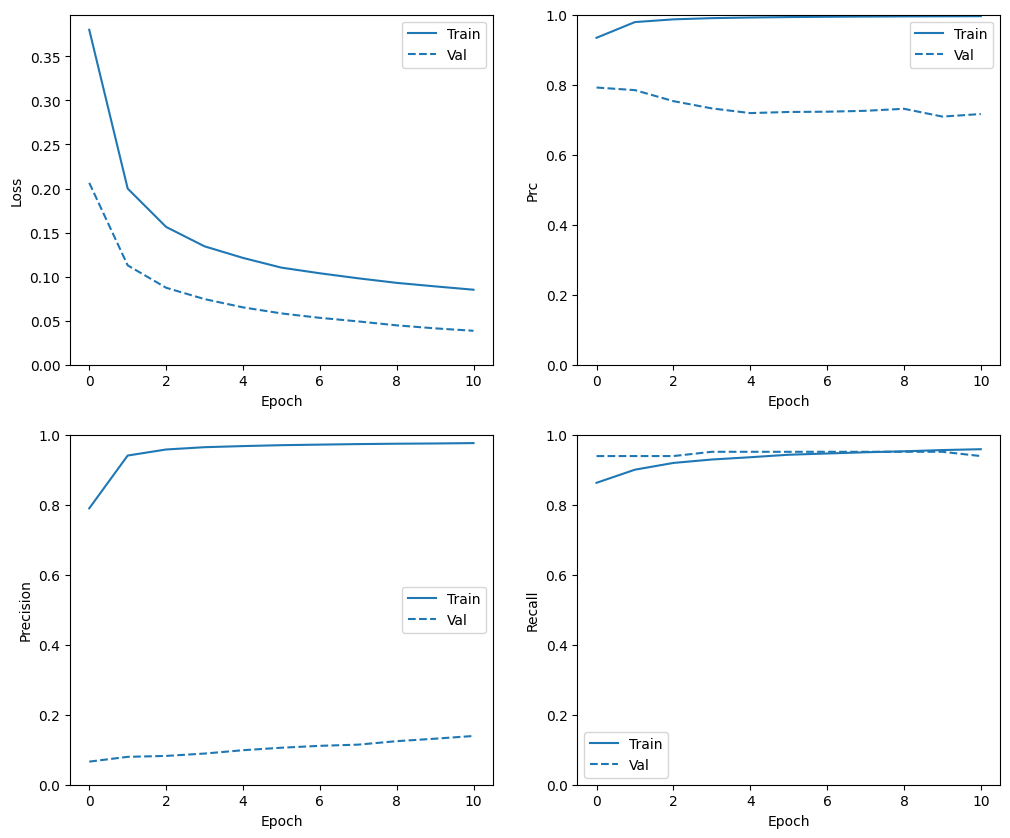
Retreinar

Como o treinamento é mais fácil com os dados balanceados, o procedimento de treinamento acima pode se ajustar rapidamente.

Portanto, divida as épocas para dar ao tf.keras.callbacks.EarlyStopping um controle mais preciso sobre quando parar de treinar.

resampled_model = make_model()
resampled_model.load_weights(initial_weights)

# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1] 
output_layer.bias.assign([0])

resampled_history = resampled_model.fit(
    resampled_ds,
    # These are not real epochs
    steps_per_epoch=20,
    epochs=10*EPOCHS,
    callbacks=[early_stopping],
    validation_data=(val_ds))

Epoch 1/1000
20/20 [==============================] - 3s 73ms/step - loss: 2.0114 - tp: 3382.0000 - fp: 5181.0000 - tn: 60589.0000 - fn: 17377.0000 - accuracy: 0.7393 - precision: 0.3950 - recall: 0.1629 - auc: 0.6308 - prc: 0.3325 - val_loss: 0.4343 - val_tp: 7.0000 - val_fp: 5042.0000 - val_tn: 40441.0000 - val_fn: 79.0000 - val_accuracy: 0.8876 - val_precision: 0.0014 - val_recall: 0.0814 - val_auc: 0.2282 - val_prc: 0.0012
Epoch 2/1000
20/20 [==============================] - 1s 33ms/step - loss: 1.2163 - tp: 7466.0000 - fp: 5137.0000 - tn: 15257.0000 - fn: 13100.0000 - accuracy: 0.5548 - precision: 0.5924 - recall: 0.3630 - auc: 0.4763 - prc: 0.5716 - val_loss: 0.4539 - val_tp: 36.0000 - val_fp: 5893.0000 - val_tn: 39590.0000 - val_fn: 50.0000 - val_accuracy: 0.8696 - val_precision: 0.0061 - val_recall: 0.4186 - val_auc: 0.6494 - val_prc: 0.0054
Epoch 3/1000
20/20 [==============================] - 1s 33ms/step - loss: 0.7406 - tp: 12289.0000 - fp: 5509.0000 - tn: 14872.0000 - fn: 8290.0000 - accuracy: 0.6631 - precision: 0.6905 - recall: 0.5972 - auc: 0.6803 - prc: 0.7580 - val_loss: 0.4611 - val_tp: 75.0000 - val_fp: 6273.0000 - val_tn: 39210.0000 - val_fn: 11.0000 - val_accuracy: 0.8621 - val_precision: 0.0118 - val_recall: 0.8721 - val_auc: 0.9293 - val_prc: 0.4539
Epoch 4/1000
20/20 [==============================] - 1s 33ms/step - loss: 0.5071 - tp: 15891.0000 - fp: 5370.0000 - tn: 15013.0000 - fn: 4686.0000 - accuracy: 0.7545 - precision: 0.7474 - recall: 0.7723 - auc: 0.8298 - prc: 0.8757 - val_loss: 0.4451 - val_tp: 78.0000 - val_fp: 5505.0000 - val_tn: 39978.0000 - val_fn: 8.0000 - val_accuracy: 0.8790 - val_precision: 0.0140 - val_recall: 0.9070 - val_auc: 0.9443 - val_prc: 0.6777
Epoch 5/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.4284 - tp: 17046.0000 - fp: 5072.0000 - tn: 15496.0000 - fn: 3346.0000 - accuracy: 0.7945 - precision: 0.7707 - recall: 0.8359 - auc: 0.8827 - prc: 0.9151 - val_loss: 0.4140 - val_tp: 77.0000 - val_fp: 4338.0000 - val_tn: 41145.0000 - val_fn: 9.0000 - val_accuracy: 0.9046 - val_precision: 0.0174 - val_recall: 0.8953 - val_auc: 0.9463 - val_prc: 0.6903
Epoch 6/1000
20/20 [==============================] - 1s 33ms/step - loss: 0.3836 - tp: 17606.0000 - fp: 4362.0000 - tn: 16113.0000 - fn: 2879.0000 - accuracy: 0.8232 - precision: 0.8014 - recall: 0.8595 - auc: 0.9080 - prc: 0.9336 - val_loss: 0.3824 - val_tp: 77.0000 - val_fp: 3314.0000 - val_tn: 42169.0000 - val_fn: 9.0000 - val_accuracy: 0.9271 - val_precision: 0.0227 - val_recall: 0.8953 - val_auc: 0.9475 - val_prc: 0.6752
Epoch 7/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.3574 - tp: 17856.0000 - fp: 3894.0000 - tn: 16553.0000 - fn: 2657.0000 - accuracy: 0.8401 - precision: 0.8210 - recall: 0.8705 - auc: 0.9208 - prc: 0.9432 - val_loss: 0.3538 - val_tp: 76.0000 - val_fp: 2592.0000 - val_tn: 42891.0000 - val_fn: 10.0000 - val_accuracy: 0.9429 - val_precision: 0.0285 - val_recall: 0.8837 - val_auc: 0.9486 - val_prc: 0.6819
Epoch 8/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.3377 - tp: 17766.0000 - fp: 3483.0000 - tn: 17067.0000 - fn: 2644.0000 - accuracy: 0.8504 - precision: 0.8361 - recall: 0.8705 - auc: 0.9280 - prc: 0.9481 - val_loss: 0.3271 - val_tp: 76.0000 - val_fp: 2047.0000 - val_tn: 43436.0000 - val_fn: 10.0000 - val_accuracy: 0.9549 - val_precision: 0.0358 - val_recall: 0.8837 - val_auc: 0.9497 - val_prc: 0.6910
Epoch 9/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.3188 - tp: 17749.0000 - fp: 2855.0000 - tn: 17547.0000 - fn: 2809.0000 - accuracy: 0.8617 - precision: 0.8614 - recall: 0.8634 - auc: 0.9360 - prc: 0.9539 - val_loss: 0.3051 - val_tp: 74.0000 - val_fp: 1657.0000 - val_tn: 43826.0000 - val_fn: 12.0000 - val_accuracy: 0.9634 - val_precision: 0.0427 - val_recall: 0.8605 - val_auc: 0.9514 - val_prc: 0.7022
Epoch 10/1000
20/20 [==============================] - 1s 33ms/step - loss: 0.3046 - tp: 17772.0000 - fp: 2599.0000 - tn: 17841.0000 - fn: 2748.0000 - accuracy: 0.8695 - precision: 0.8724 - recall: 0.8661 - auc: 0.9402 - prc: 0.9570 - val_loss: 0.2860 - val_tp: 74.0000 - val_fp: 1398.0000 - val_tn: 44085.0000 - val_fn: 12.0000 - val_accuracy: 0.9691 - val_precision: 0.0503 - val_recall: 0.8605 - val_auc: 0.9527 - val_prc: 0.6997
Epoch 11/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.2937 - tp: 17673.0000 - fp: 2352.0000 - tn: 18273.0000 - fn: 2662.0000 - accuracy: 0.8776 - precision: 0.8825 - recall: 0.8691 - auc: 0.9447 - prc: 0.9595 - val_loss: 0.2687 - val_tp: 73.0000 - val_fp: 1235.0000 - val_tn: 44248.0000 - val_fn: 13.0000 - val_accuracy: 0.9726 - val_precision: 0.0558 - val_recall: 0.8488 - val_auc: 0.9534 - val_prc: 0.7066
Epoch 12/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.2813 - tp: 17721.0000 - fp: 2109.0000 - tn: 18523.0000 - fn: 2607.0000 - accuracy: 0.8849 - precision: 0.8936 - recall: 0.8718 - auc: 0.9485 - prc: 0.9621 - val_loss: 0.2524 - val_tp: 73.0000 - val_fp: 1098.0000 - val_tn: 44385.0000 - val_fn: 13.0000 - val_accuracy: 0.9756 - val_precision: 0.0623 - val_recall: 0.8488 - val_auc: 0.9539 - val_prc: 0.7094
Epoch 13/1000
20/20 [==============================] - 1s 36ms/step - loss: 0.2706 - tp: 18031.0000 - fp: 1869.0000 - tn: 18502.0000 - fn: 2558.0000 - accuracy: 0.8919 - precision: 0.9061 - recall: 0.8758 - auc: 0.9520 - prc: 0.9652 - val_loss: 0.2395 - val_tp: 73.0000 - val_fp: 1037.0000 - val_tn: 44446.0000 - val_fn: 13.0000 - val_accuracy: 0.9770 - val_precision: 0.0658 - val_recall: 0.8488 - val_auc: 0.9549 - val_prc: 0.7119
Epoch 14/1000
20/20 [==============================] - 1s 37ms/step - loss: 0.2665 - tp: 18087.0000 - fp: 1748.0000 - tn: 18567.0000 - fn: 2558.0000 - accuracy: 0.8949 - precision: 0.9119 - recall: 0.8761 - auc: 0.9525 - prc: 0.9661 - val_loss: 0.2283 - val_tp: 73.0000 - val_fp: 972.0000 - val_tn: 44511.0000 - val_fn: 13.0000 - val_accuracy: 0.9784 - val_precision: 0.0699 - val_recall: 0.8488 - val_auc: 0.9556 - val_prc: 0.7045
Epoch 15/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.2589 - tp: 18064.0000 - fp: 1630.0000 - tn: 18830.0000 - fn: 2436.0000 - accuracy: 0.9007 - precision: 0.9172 - recall: 0.8812 - auc: 0.9560 - prc: 0.9676 - val_loss: 0.2180 - val_tp: 73.0000 - val_fp: 941.0000 - val_tn: 44542.0000 - val_fn: 13.0000 - val_accuracy: 0.9791 - val_precision: 0.0720 - val_recall: 0.8488 - val_auc: 0.9563 - val_prc: 0.7069
Epoch 16/1000
20/20 [==============================] - 1s 36ms/step - loss: 0.2495 - tp: 18132.0000 - fp: 1481.0000 - tn: 18926.0000 - fn: 2421.0000 - accuracy: 0.9047 - precision: 0.9245 - recall: 0.8822 - auc: 0.9587 - prc: 0.9695 - val_loss: 0.2079 - val_tp: 73.0000 - val_fp: 905.0000 - val_tn: 44578.0000 - val_fn: 13.0000 - val_accuracy: 0.9799 - val_precision: 0.0746 - val_recall: 0.8488 - val_auc: 0.9565 - val_prc: 0.7110
Epoch 17/1000
20/20 [==============================] - 1s 35ms/step - loss: 0.2435 - tp: 18047.0000 - fp: 1378.0000 - tn: 19144.0000 - fn: 2391.0000 - accuracy: 0.9080 - precision: 0.9291 - recall: 0.8830 - auc: 0.9601 - prc: 0.9706 - val_loss: 0.1990 - val_tp: 73.0000 - val_fp: 882.0000 - val_tn: 44601.0000 - val_fn: 13.0000 - val_accuracy: 0.9804 - val_precision: 0.0764 - val_recall: 0.8488 - val_auc: 0.9568 - val_prc: 0.7118
Epoch 18/1000
20/20 [==============================] - 1s 37ms/step - loss: 0.2396 - tp: 18223.0000 - fp: 1289.0000 - tn: 19075.0000 - fn: 2373.0000 - accuracy: 0.9106 - precision: 0.9339 - recall: 0.8848 - auc: 0.9612 - prc: 0.9714 - val_loss: 0.1911 - val_tp: 73.0000 - val_fp: 870.0000 - val_tn: 44613.0000 - val_fn: 13.0000 - val_accuracy: 0.9806 - val_precision: 0.0774 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7148
Epoch 19/1000
20/20 [==============================] - 1s 36ms/step - loss: 0.2324 - tp: 18179.0000 - fp: 1205.0000 - tn: 19254.0000 - fn: 2322.0000 - accuracy: 0.9139 - precision: 0.9378 - recall: 0.8867 - auc: 0.9633 - prc: 0.9728 - val_loss: 0.1839 - val_tp: 73.0000 - val_fp: 857.0000 - val_tn: 44626.0000 - val_fn: 13.0000 - val_accuracy: 0.9809 - val_precision: 0.0785 - val_recall: 0.8488 - val_auc: 0.9576 - val_prc: 0.7165
Epoch 20/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.2318 - tp: 18119.0000 - fp: 1224.0000 - tn: 19279.0000 - fn: 2338.0000 - accuracy: 0.9130 - precision: 0.9367 - recall: 0.8857 - auc: 0.9640 - prc: 0.9728 - val_loss: 0.1758 - val_tp: 73.0000 - val_fp: 823.0000 - val_tn: 44660.0000 - val_fn: 13.0000 - val_accuracy: 0.9817 - val_precision: 0.0815 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7185
Epoch 21/1000
20/20 [==============================] - 1s 35ms/step - loss: 0.2233 - tp: 18041.0000 - fp: 1074.0000 - tn: 19514.0000 - fn: 2331.0000 - accuracy: 0.9169 - precision: 0.9438 - recall: 0.8856 - auc: 0.9660 - prc: 0.9745 - val_loss: 0.1690 - val_tp: 73.0000 - val_fp: 813.0000 - val_tn: 44670.0000 - val_fn: 13.0000 - val_accuracy: 0.9819 - val_precision: 0.0824 - val_recall: 0.8488 - val_auc: 0.9578 - val_prc: 0.7211
Epoch 22/1000
20/20 [==============================] - 1s 35ms/step - loss: 0.2193 - tp: 18258.0000 - fp: 1013.0000 - tn: 19414.0000 - fn: 2275.0000 - accuracy: 0.9197 - precision: 0.9474 - recall: 0.8892 - auc: 0.9666 - prc: 0.9753 - val_loss: 0.1634 - val_tp: 73.0000 - val_fp: 817.0000 - val_tn: 44666.0000 - val_fn: 13.0000 - val_accuracy: 0.9818 - val_precision: 0.0820 - val_recall: 0.8488 - val_auc: 0.9580 - val_prc: 0.7123
Epoch 23/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.2114 - tp: 18439.0000 - fp: 993.0000 - tn: 19417.0000 - fn: 2111.0000 - accuracy: 0.9242 - precision: 0.9489 - recall: 0.8973 - auc: 0.9696 - prc: 0.9774 - val_loss: 0.1577 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9584 - val_prc: 0.7122
Epoch 24/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.2076 - tp: 18459.0000 - fp: 896.0000 - tn: 19582.0000 - fn: 2023.0000 - accuracy: 0.9287 - precision: 0.9537 - recall: 0.9012 - auc: 0.9694 - prc: 0.9776 - val_loss: 0.1528 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9587 - val_prc: 0.7129
Epoch 25/1000
20/20 [==============================] - 1s 35ms/step - loss: 0.2044 - tp: 18340.0000 - fp: 907.0000 - tn: 19664.0000 - fn: 2049.0000 - accuracy: 0.9278 - precision: 0.9529 - recall: 0.8995 - auc: 0.9707 - prc: 0.9783 - val_loss: 0.1483 - val_tp: 73.0000 - val_fp: 800.0000 - val_tn: 44683.0000 - val_fn: 13.0000 - val_accuracy: 0.9822 - val_precision: 0.0836 - val_recall: 0.8488 - val_auc: 0.9591 - val_prc: 0.7054
Epoch 26/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.1997 - tp: 18293.0000 - fp: 918.0000 - tn: 19749.0000 - fn: 2000.0000 - accuracy: 0.9288 - precision: 0.9522 - recall: 0.9014 - auc: 0.9722 - prc: 0.9788 - val_loss: 0.1433 - val_tp: 73.0000 - val_fp: 788.0000 - val_tn: 44695.0000 - val_fn: 13.0000 - val_accuracy: 0.9824 - val_precision: 0.0848 - val_recall: 0.8488 - val_auc: 0.9590 - val_prc: 0.7059
Epoch 27/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.1987 - tp: 18562.0000 - fp: 848.0000 - tn: 19530.0000 - fn: 2020.0000 - accuracy: 0.9300 - precision: 0.9563 - recall: 0.9019 - auc: 0.9720 - prc: 0.9791 - val_loss: 0.1394 - val_tp: 73.0000 - val_fp: 784.0000 - val_tn: 44699.0000 - val_fn: 13.0000 - val_accuracy: 0.9825 - val_precision: 0.0852 - val_recall: 0.8488 - val_auc: 0.9595 - val_prc: 0.7062
Epoch 28/1000
20/20 [==============================] - 1s 34ms/step - loss: 0.1944 - tp: 18320.0000 - fp: 828.0000 - tn: 19823.0000 - fn: 1989.0000 - accuracy: 0.9312 - precision: 0.9568 - recall: 0.9021 - auc: 0.9734 - prc: 0.9798 - val_loss: 0.1351 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9598 - val_prc: 0.7079
Epoch 29/1000
20/20 [==============================] - 1s 35ms/step - loss: 0.1933 - tp: 18455.0000 - fp: 827.0000 - tn: 19704.0000 - fn: 1974.0000 - accuracy: 0.9316 - precision: 0.9571 - recall: 0.9034 - auc: 0.9732 - prc: 0.9797 - val_loss: 0.1313 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9599 - val_prc: 0.7094
Epoch 30/1000
20/20 [==============================] - 1s 35ms/step - loss: 0.1910 - tp: 18417.0000 - fp: 768.0000 - tn: 19858.0000 - fn: 1917.0000 - accuracy: 0.9344 - precision: 0.9600 - recall: 0.9057 - auc: 0.9740 - prc: 0.9802 - val_loss: 0.1282 - val_tp: 73.0000 - val_fp: 759.0000 - val_tn: 44724.0000 - val_fn: 13.0000 - val_accuracy: 0.9831 - val_precision: 0.0877 - val_recall: 0.8488 - val_auc: 0.9602 - val_prc: 0.7094
Epoch 31/1000
20/20 [==============================] - ETA: 0s - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811Restoring model weights from the end of the best epoch: 21.
20/20 [==============================] - 1s 34ms/step - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811 - val_loss: 0.1246 - val_tp: 73.0000 - val_fp: 742.0000 - val_tn: 44741.0000 - val_fn: 13.0000 - val_accuracy: 0.9834 - val_precision: 0.0896 - val_recall: 0.8488 - val_auc: 0.9597 - val_prc: 0.7095
Epoch 31: early stopping

Verifique novamente o histórico de treinamento

plot_metrics(resampled_history)

png

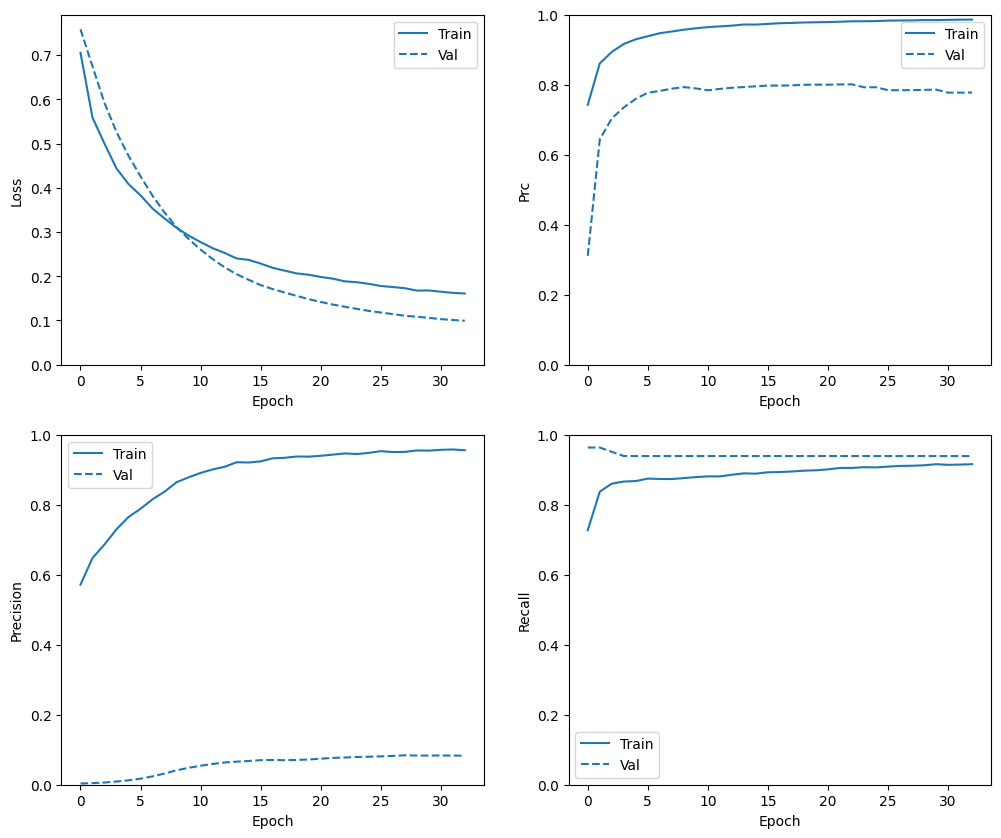
Avaliar métricas

train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)

resampled_results = resampled_model.evaluate(test_features, test_labels,
                                             batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
  print(name, ': ', value)
print()

plot_cm(test_labels, test_predictions_resampled)

loss :  0.16882120072841644
tp :  71.0
fp :  1032.0
tn :  55849.0
fn :  10.0
accuracy :  0.9817070960998535
precision :  0.06436990201473236
recall :  0.8765432238578796
auc :  0.9518552422523499
prc :  0.7423797845840454

Legitimate Transactions Detected (True Negatives):  55849
Legitimate Transactions Incorrectly Detected (False Positives):  1032
Fraudulent Transactions Missed (False Negatives):  10
Fraudulent Transactions Detected (True Positives):  71
Total Fraudulent Transactions:  81

png

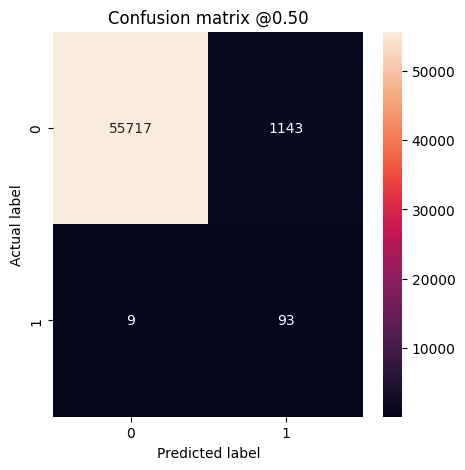
Trace o ROC

plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')

plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')

plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');

png

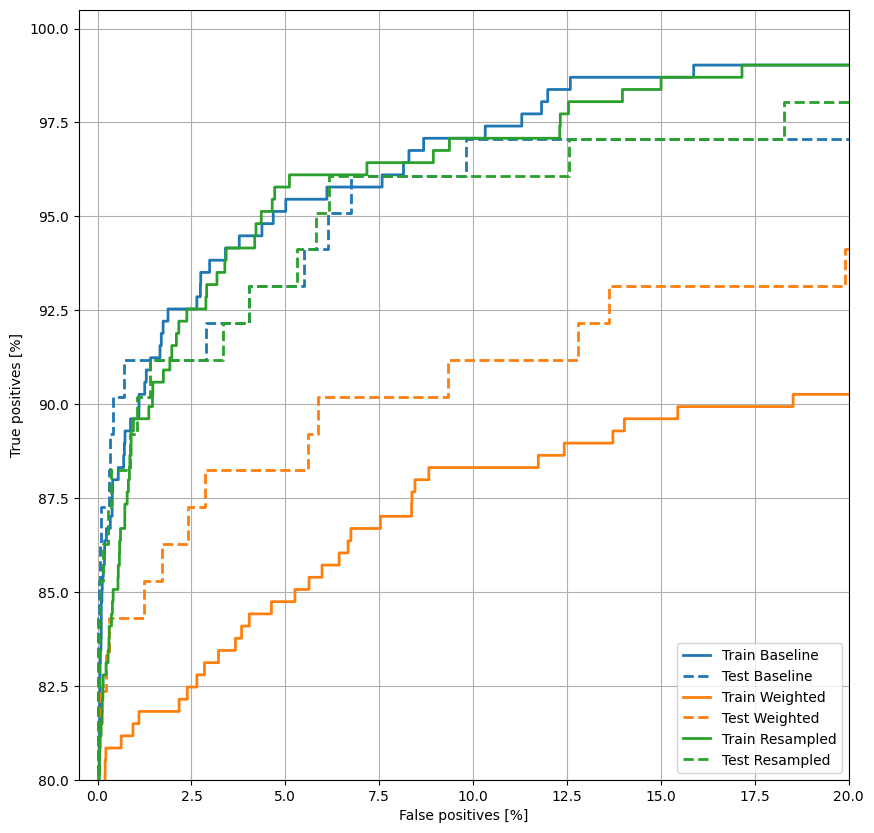
Trace o AUPRC

plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')

plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')

plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');

png

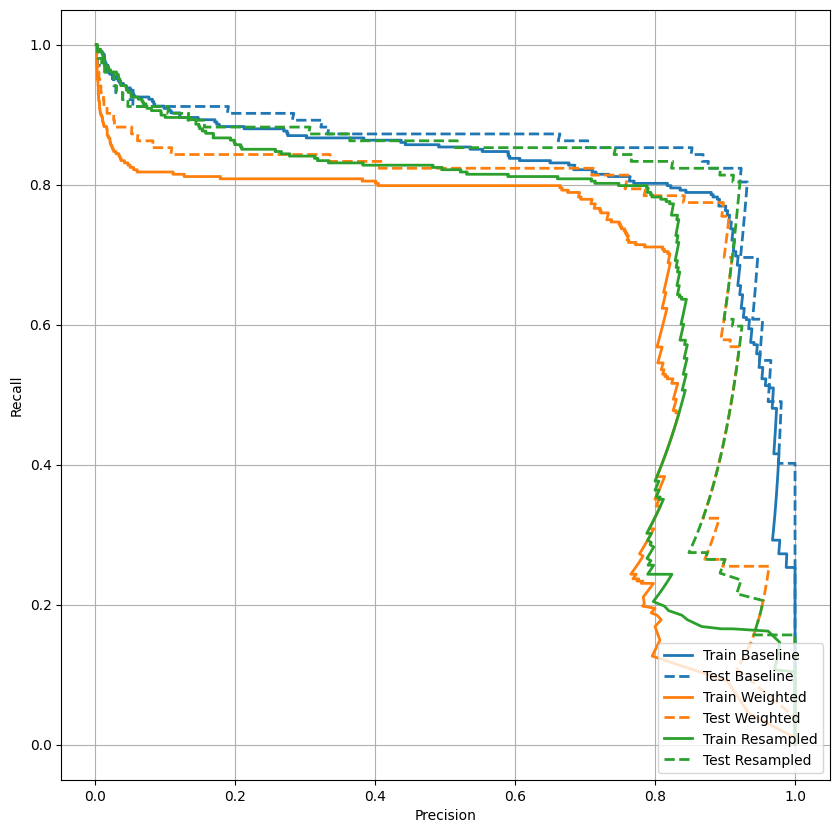
Aplicando este tutorial ao seu problema

A classificação de dados desequilibrada é uma tarefa inerentemente difícil, pois há tão poucas amostras com as quais aprender. Você deve sempre começar com os dados primeiro e fazer o seu melhor para coletar o maior número possível de amostras e pensar substancialmente em quais recursos podem ser relevantes para que o modelo possa tirar o máximo proveito de sua classe minoritária. Em algum momento, seu modelo pode ter dificuldades para melhorar e produzir os resultados desejados, por isso é importante ter em mente o contexto do seu problema e as compensações entre os diferentes tipos de erros.

Classificação em dados desbalanceados

Configurar

Processamento e exploração de dados

Baixe o conjunto de dados de fraude de cartão de crédito Kaggle

Examine o desequilíbrio do rótulo da classe

Limpe, divida e normalize os dados

Observe a distribuição de dados

Defina o modelo e as métricas

Entendendo métricas úteis

Modelo de linha de base

Construir o modelo

Opcional: Defina a polarização inicial correta.

Verifique os pesos iniciais

Confirme se a correção de viés ajuda

Treine o modelo

Confira o histórico de treinamento

Avaliar métricas

Trace o ROC

Trace o AUPRC

Pesos de classe

Calcular pesos de classe

Treine um modelo com pesos de classe

Confira o histórico de treinamento

Avaliar métricas

Trace o ROC

Trace o AUPRC

Sobreamostragem

Exagerar na classe minoritária

Usando NumPy

Usando tf.data

Treine com os dados sobreamostrados

Confira o histórico de treinamento

Retreinar

Verifique novamente o histórico de treinamento

Avaliar métricas

Trace o ROC

Trace o AUPRC

Aplicando este tutorial ao seu problema

Usando `tf.data`