 TensorFlow.org で表示 TensorFlow.org で表示 |
 Google Colab で実行 Google Colab で実行 |
 GitHub でソースを表示 GitHub でソースを表示 |
 ノートブックをダウンロード ノートブックをダウンロード |
このチュートリアルでは、1 つのクラスの例の数が他のクラスの例の数を大幅に上回る、非常に不均衡なデータセットを分類する方法を示します。Kaggle でホストされているクレジットカード不正検出データセットを使用します。目的は、合計 284,807 件のトランザクションからわずか 492 件の不正なトランザクションを検出することです。Keras を使用してモデルを定義し、クラスの重み付けを使用してモデルが不均衡なデータから学習できるようにします。
このチュートリアルには、次の完全なコードが含まれています。
- Pandas を使用して CSV ファイルを読み込む。
- トレーニングセット、検証セット、テストセットを作成する。
- Keras を使用してモデルの定義してトレーニングする(クラスの重みの設定を含む)。
- 様々なメトリクス(適合率や再現率を含む)を使用してモデルを評価する。
- 不均衡データを扱うための一般的なテクニックを試す。
- クラスの重み付け
- オーバーサンプリング
Setup
import tensorflow as tf
from tensorflow import keras
import os
import tempfile
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
2022-12-14 23:05:44.726441: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvinfer.so.7: cannot open shared object file: No such file or directory 2022-12-14 23:05:44.726537: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvinfer_plugin.so.7: cannot open shared object file: No such file or directory 2022-12-14 23:05:44.726547: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
データの処理と調査
Kaggle Credit Card Fraud データセットをダウンロードする
Pandas は、構造化データの読み込みと処理を支援するユーティリティが多数含まれる Python ライブラリです。Pandas を使用し、URL から CSV を Pandas DataFrame にダウンロードします。
注意: このデータセットは、Worldline と ULB (Université Libre de Bruxelles) の機械学習グループによるビッグデータマイニングと不正検出に関する共同研究で収集および分析されたものです。関連トピックに関する現在および過去のプロジェクトの詳細は、こちらと DefeatFraud プロジェクトのページをご覧ください。
file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()
クラスラベルの不均衡を調べる
データセットの不均衡を見てみましょう。
neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n'.format(
total, pos, 100 * pos / total))
Examples:
Total: 284807
Positive: 492 (0.17% of total)
これは、陽性サンプルの割合が少ないことを示しています。
データをクリーニング、分割、正規化する
生データにはいくつかの問題があります。まず、TimeカラムとAmountカラムはむらがあり過ぎてそのままでは使用できません。Timeカラムは意味が明確ではないため削除し、Amountカラムのログを取って範囲を縮小します。
cleaned_df = raw_df.copy()
# You don't want the `Time` column.
cleaned_df.pop('Time')
# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Amount'] = np.log(cleaned_df.pop('Amount')+eps)
データセットをトレーニングセット、検証セット、テストセットに分割します。検証セットはモデルを適合させる間に使用され、損失とメトリクスを評価しますが、モデルはこのデータに適合しません。テストセットはトレーニング段階では全く使用されず、モデルがどの程度新しいデータを一般化したかを評価するために最後にだけ使用されます。これはトレーニングデータ不足による過学習が重大な懸念事項である不均衡データセットでは特に重要です。
# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
sklearn の StandardScaler を使用して入力特徴を正規化します。これで平均は 0、標準偏差は 1 に設定されます。
注意: StandardScalerはtrain_featuresを使用する場合にのみ適合し、モデルが検証セットやテストセットでピークを迎えることがないようにします。
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
Training labels shape: (182276,) Validation labels shape: (45569,) Test labels shape: (56962,) Training features shape: (182276, 29) Validation features shape: (45569, 29) Test features shape: (56962, 29)
警告: モデルをデプロイする場合には、前処理の計算を保存することが非常に重要です。最も簡単なのは、それらをレイヤーとして実装し、エクスポート前にモデルに加える方法です。
データ分散を確認する
次に、いくつかの特徴における陽性の例と陰性の例の分散を比較します。 この時点で自問すべき点は、次のとおりです。
- それらの分散には意味がありますか?
- はい。入力を正規化したので、ほとんどが
+/- 2の範囲内に集中しています。
- はい。入力を正規化したので、ほとんどが
- 分散間の差は見られますか?
- はい。陽性の例には、はるかに高い極値が含まれています。
pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)
sns.jointplot(x=pos_df['V5'], y=pos_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")
sns.jointplot(x=neg_df['V5'], y=neg_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")

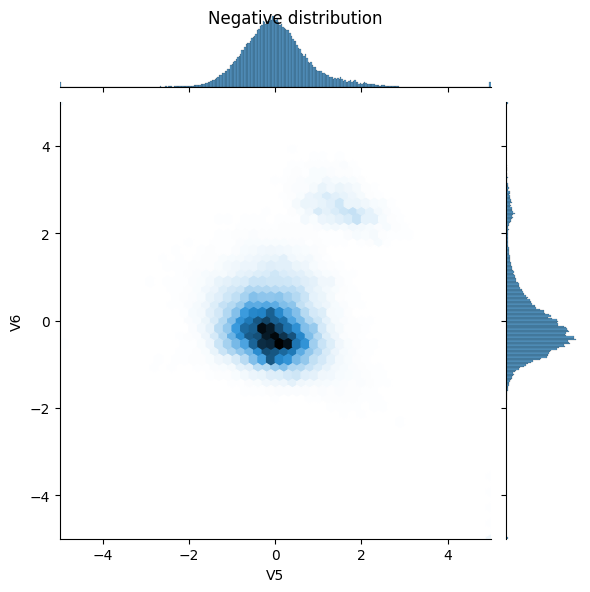
モデルとメトリクスを定義する
密に接続された非表示レイヤー、過学習を防ぐドロップアウトレイヤー、取引が不正である確率を返す出力シグモイドレイヤーを持つ単純なニューラルネットワークを作成する関数を定義します。
METRICS = [
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.BinaryAccuracy(name='accuracy'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc'),
keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]
def make_model(metrics=METRICS, output_bias=None):
if output_bias is not None:
output_bias = tf.keras.initializers.Constant(output_bias)
model = keras.Sequential([
keras.layers.Dense(
16, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid',
bias_initializer=output_bias),
])
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.BinaryCrossentropy(),
metrics=metrics)
return model
有用なメトリクスを理解する
上記で定義したメトリクスのいくつかは、モデルで計算できるため、パフォーマンス評価の際に有用なことに着目してください。
- 偽陰性と偽陽性は誤って分類されたサンプルです。
- 真陰性と真陽性は正しく分類されたサンプルです。
- 正解率は正しく分類された例の割合です。
\(\frac{\text{true samples} }{\text{total samples} }\)
- 適合率は正しく分類された予測陽性の割合です。
\(\frac{\text{true positives} }{\text{true positives + false positives} }\)
- 再現率は正しく分類された実際の陽性の割合です。
\(\frac{\text{true positives} }{\text{true positives + false negatives} }\)
- AUC は受信者動作特性曲線 (ROC-AUC) の曲線下の面積を指します。この指標は、分類器がランダムな正のサンプルをランダムな負のサンプルよりも高くランク付けする確率に等しくなります。
- AUPRC は適合率-再現率曲線の曲線下の面積を指します。この指標は、さまざまな確率しきい値の適合率と再現率のペアを計算します。
注意: 精度は、このタスクに役立つ指標ではありません。常に False を予測することで、このタスクの精度を 99.8% 以上にすることができるからです。
詳細は以下を参照してください。
ベースラインモデル
モデルを構築する
次に、前に定義した関数を使用してモデルを作成し、トレーニングします。モデルはデフォルトよりも大きいバッチサイズ 2048 を使って適合されていることに注目してください。これは、各バッチに必ずいくつかの陽性サンプルが含まれるようにするために重要です。もし、バッチサイズが小さすぎると、学習できる不正取引が全くないという可能性があります。
注意: このモデルはクラスの不均衡をうまく処理できません。後ほどこのチュートリアル内で改善します。
EPOCHS = 100
BATCH_SIZE = 2048
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_prc',
verbose=1,
patience=10,
mode='max',
restore_best_weights=True)
model = make_model()
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 480
dropout (Dropout) (None, 16) 0
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 497
Trainable params: 497
Non-trainable params: 0
_________________________________________________________________
モデルをテスト実行します。
model.predict(train_features[:10])
1/1 [==============================] - 0s 433ms/step
array([[0.32376227],
[0.410775 ],
[0.78519666],
[0.8071737 ],
[0.24630985],
[0.43201268],
[0.14502314],
[0.4868623 ],
[0.392316 ],
[0.38101035]], dtype=float32)
オプション: 正しい初期バイアスを設定する
これら初期の推測はあまり良いとは言えません。データセットは不均衡であることが分かっています。それを反映できるように、出力レイヤーのバイアスを設定します。(参照: ニューラルネットワークのトレーニングのレシピ: 「init well」)これは初期収束に有用です。
デフォルトのバイアス初期化では、損失はmath.log(2) = 0.69314程度になります。
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.5587
設定する正しいバイアスは、以下から導き出すことができます。
\( p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) \) \( b_0 = -log_e(1/p_0 - 1) \) \[ b_0 = log_e(pos/neg)\]
initial_bias = np.log([pos/neg])
initial_bias
array([-6.35935934])
それを初期バイアスとして設定すると、モデルははるかに合理的な初期推測ができるようになります。
これはpos/total = 0.0018に近い値になるはずです。
model = make_model(output_bias=initial_bias)
model.predict(train_features[:10])
1/1 [==============================] - 0s 45ms/step
array([[0.00103091],
[0.00088367],
[0.00175426],
[0.00091999],
[0.00124022],
[0.00087101],
[0.00024934],
[0.00167472],
[0.00049 ],
[0.00128492]], dtype=float32)
この初期化では、初期損失はおおよそ次のようになります。
\[-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317\]
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.0148
この初期の損失は、単純な初期化を行った場合の約 50 分の 1 です。
この方法だと、陽性の例がないことを学習するだけのためにモデルが最初の数エポックを費やす必要がありません。また、これによって、トレーニング中の損失のプロットが読みやすくなります。
初期の重みをチェックポイントする
さまざまなトレーニングの実行を比較しやすくするために、この初期モデルの重みをチェックポイントファイルに保持し、トレーニングの前に各モデルにロードします。
initial_weights = os.path.join(tempfile.mkdtemp(), 'initial_weights')
model.save_weights(initial_weights)
バイアス修正が有効であることを確認する
先に進む前に、慎重なバイアス初期化が実際に役立ったかどうかを素早く確認します。
この慎重な初期化を行った場合と行わなかった場合でモデルを 20 エポックトレーニングしてから損失を比較します。
model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
def plot_loss(history, label, n):
# Use a log scale on y-axis to show the wide range of values.
plt.semilogy(history.epoch, history.history['loss'],
color=colors[n], label='Train ' + label)
plt.semilogy(history.epoch, history.history['val_loss'],
color=colors[n], label='Val ' + label,
linestyle="--")
plt.xlabel('Epoch')
plt.ylabel('Loss')
plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)
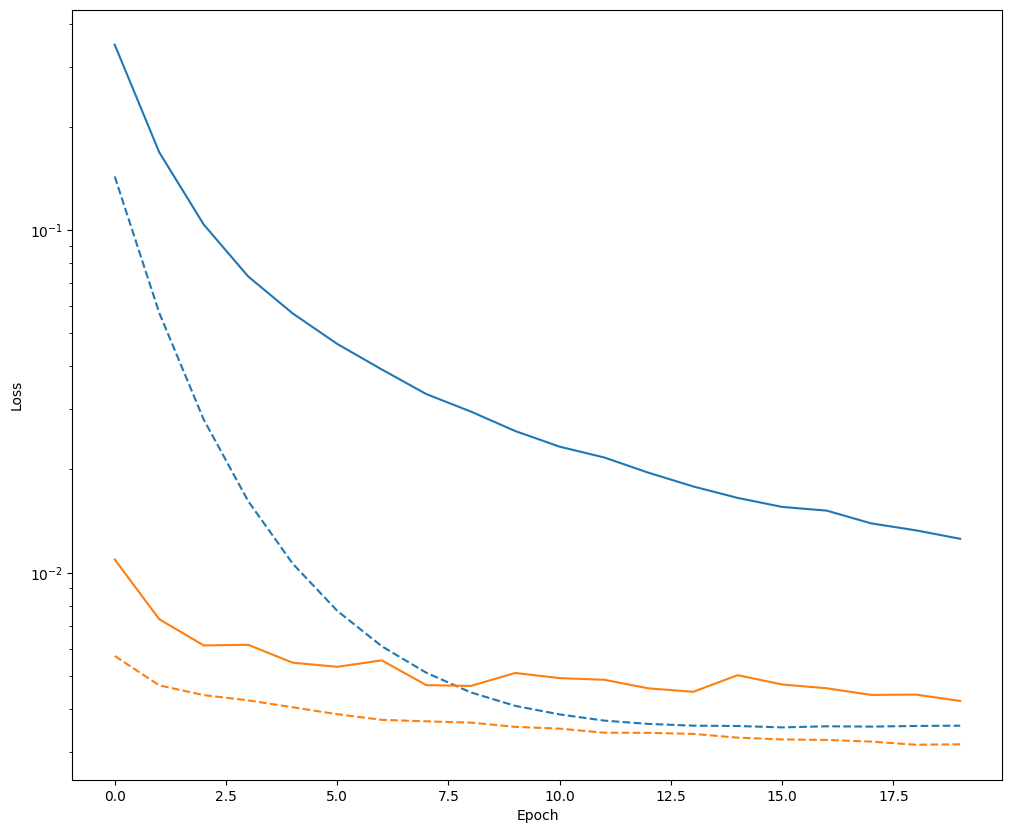
上の図を見れば一目瞭然ですが、検証損失に関しては、この問題ではこのように慎重に初期化することによって、明確なアドバンテージを得ることができます。
モデルをトレーニングする
model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels))
Epoch 1/100 90/90 [==============================] - 2s 11ms/step - loss: 0.0109 - tp: 106.0000 - fp: 56.0000 - tn: 227398.0000 - fn: 285.0000 - accuracy: 0.9985 - precision: 0.6543 - recall: 0.2711 - auc: 0.7874 - prc: 0.3099 - val_loss: 0.0056 - val_tp: 20.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 49.0000 - val_accuracy: 0.9988 - val_precision: 0.8333 - val_recall: 0.2899 - val_auc: 0.8831 - val_prc: 0.6267 Epoch 2/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0073 - tp: 126.0000 - fp: 27.0000 - tn: 181927.0000 - fn: 196.0000 - accuracy: 0.9988 - precision: 0.8235 - recall: 0.3913 - auc: 0.8536 - prc: 0.4774 - val_loss: 0.0048 - val_tp: 29.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 40.0000 - val_accuracy: 0.9989 - val_precision: 0.7838 - val_recall: 0.4203 - val_auc: 0.8837 - val_prc: 0.6447 Epoch 3/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0061 - tp: 163.0000 - fp: 22.0000 - tn: 181932.0000 - fn: 159.0000 - accuracy: 0.9990 - precision: 0.8811 - recall: 0.5062 - auc: 0.8777 - prc: 0.6132 - val_loss: 0.0044 - val_tp: 34.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 35.0000 - val_accuracy: 0.9991 - val_precision: 0.8095 - val_recall: 0.4928 - val_auc: 0.8838 - val_prc: 0.6321 Epoch 4/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0058 - tp: 158.0000 - fp: 33.0000 - tn: 181921.0000 - fn: 164.0000 - accuracy: 0.9989 - precision: 0.8272 - recall: 0.4907 - auc: 0.8958 - prc: 0.6258 - val_loss: 0.0042 - val_tp: 41.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 28.0000 - val_accuracy: 0.9992 - val_precision: 0.8367 - val_recall: 0.5942 - val_auc: 0.8910 - val_prc: 0.6413 Epoch 5/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0055 - tp: 170.0000 - fp: 36.0000 - tn: 181918.0000 - fn: 152.0000 - accuracy: 0.9990 - precision: 0.8252 - recall: 0.5280 - auc: 0.9085 - prc: 0.6395 - val_loss: 0.0040 - val_tp: 42.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 27.0000 - val_accuracy: 0.9992 - val_precision: 0.8400 - val_recall: 0.6087 - val_auc: 0.8983 - val_prc: 0.6740 Epoch 6/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0053 - tp: 172.0000 - fp: 31.0000 - tn: 181923.0000 - fn: 150.0000 - accuracy: 0.9990 - precision: 0.8473 - recall: 0.5342 - auc: 0.9071 - prc: 0.6464 - val_loss: 0.0039 - val_tp: 42.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 27.0000 - val_accuracy: 0.9992 - val_precision: 0.8400 - val_recall: 0.6087 - val_auc: 0.8982 - val_prc: 0.6779 Epoch 7/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0051 - tp: 172.0000 - fp: 31.0000 - tn: 181923.0000 - fn: 150.0000 - accuracy: 0.9990 - precision: 0.8473 - recall: 0.5342 - auc: 0.9135 - prc: 0.6628 - val_loss: 0.0038 - val_tp: 46.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8519 - val_recall: 0.6667 - val_auc: 0.8982 - val_prc: 0.6813 Epoch 8/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0054 - tp: 171.0000 - fp: 28.0000 - tn: 181926.0000 - fn: 151.0000 - accuracy: 0.9990 - precision: 0.8593 - recall: 0.5311 - auc: 0.9073 - prc: 0.6439 - val_loss: 0.0037 - val_tp: 46.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8519 - val_recall: 0.6667 - val_auc: 0.8981 - val_prc: 0.6888 Epoch 9/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0051 - tp: 179.0000 - fp: 33.0000 - tn: 181921.0000 - fn: 143.0000 - accuracy: 0.9990 - precision: 0.8443 - recall: 0.5559 - auc: 0.9167 - prc: 0.6665 - val_loss: 0.0036 - val_tp: 46.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8519 - val_recall: 0.6667 - val_auc: 0.8981 - val_prc: 0.7000 Epoch 10/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0048 - tp: 171.0000 - fp: 28.0000 - tn: 181926.0000 - fn: 151.0000 - accuracy: 0.9990 - precision: 0.8593 - recall: 0.5311 - auc: 0.9151 - prc: 0.6786 - val_loss: 0.0036 - val_tp: 48.0000 - val_fp: 9.0000 - val_tn: 45491.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8421 - val_recall: 0.6957 - val_auc: 0.9053 - val_prc: 0.7026 Epoch 11/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0051 - tp: 178.0000 - fp: 29.0000 - tn: 181925.0000 - fn: 144.0000 - accuracy: 0.9991 - precision: 0.8599 - recall: 0.5528 - auc: 0.9104 - prc: 0.6587 - val_loss: 0.0034 - val_tp: 47.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8545 - val_recall: 0.6812 - val_auc: 0.9053 - val_prc: 0.7099 Epoch 12/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0050 - tp: 179.0000 - fp: 33.0000 - tn: 181921.0000 - fn: 143.0000 - accuracy: 0.9990 - precision: 0.8443 - recall: 0.5559 - auc: 0.9214 - prc: 0.6630 - val_loss: 0.0034 - val_tp: 47.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8545 - val_recall: 0.6812 - val_auc: 0.9053 - val_prc: 0.7207 Epoch 13/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0048 - tp: 177.0000 - fp: 27.0000 - tn: 181927.0000 - fn: 145.0000 - accuracy: 0.9991 - precision: 0.8676 - recall: 0.5497 - auc: 0.9136 - prc: 0.6684 - val_loss: 0.0033 - val_tp: 49.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8596 - val_recall: 0.7101 - val_auc: 0.9126 - val_prc: 0.7302 Epoch 14/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0046 - tp: 183.0000 - fp: 36.0000 - tn: 181918.0000 - fn: 139.0000 - accuracy: 0.9990 - precision: 0.8356 - recall: 0.5683 - auc: 0.9245 - prc: 0.6851 - val_loss: 0.0033 - val_tp: 49.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8596 - val_recall: 0.7101 - val_auc: 0.9126 - val_prc: 0.7323 Epoch 15/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0043 - tp: 192.0000 - fp: 30.0000 - tn: 181924.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8649 - recall: 0.5963 - auc: 0.9324 - prc: 0.7217 - val_loss: 0.0033 - val_tp: 49.0000 - val_fp: 9.0000 - val_tn: 45491.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8448 - val_recall: 0.7101 - val_auc: 0.9125 - val_prc: 0.7339 Epoch 16/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0045 - tp: 190.0000 - fp: 34.0000 - tn: 181920.0000 - fn: 132.0000 - accuracy: 0.9991 - precision: 0.8482 - recall: 0.5901 - auc: 0.9199 - prc: 0.6823 - val_loss: 0.0032 - val_tp: 49.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8750 - val_recall: 0.7101 - val_auc: 0.9126 - val_prc: 0.7428 Epoch 17/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0046 - tp: 185.0000 - fp: 31.0000 - tn: 181923.0000 - fn: 137.0000 - accuracy: 0.9991 - precision: 0.8565 - recall: 0.5745 - auc: 0.9136 - prc: 0.6757 - val_loss: 0.0032 - val_tp: 49.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8909 - val_recall: 0.7101 - val_auc: 0.9126 - val_prc: 0.7463 Epoch 18/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0046 - tp: 186.0000 - fp: 34.0000 - tn: 181920.0000 - fn: 136.0000 - accuracy: 0.9991 - precision: 0.8455 - recall: 0.5776 - auc: 0.9198 - prc: 0.6871 - val_loss: 0.0032 - val_tp: 49.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8909 - val_recall: 0.7101 - val_auc: 0.9126 - val_prc: 0.7495 Epoch 19/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0045 - tp: 179.0000 - fp: 37.0000 - tn: 181917.0000 - fn: 143.0000 - accuracy: 0.9990 - precision: 0.8287 - recall: 0.5559 - auc: 0.9246 - prc: 0.6875 - val_loss: 0.0032 - val_tp: 50.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8621 - val_recall: 0.7246 - val_auc: 0.9198 - val_prc: 0.7475 Epoch 20/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0044 - tp: 188.0000 - fp: 31.0000 - tn: 181923.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8584 - recall: 0.5839 - auc: 0.9231 - prc: 0.6918 - val_loss: 0.0031 - val_tp: 50.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 19.0000 - val_accuracy: 0.9995 - val_precision: 0.8929 - val_recall: 0.7246 - val_auc: 0.9198 - val_prc: 0.7588 Epoch 21/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0042 - tp: 195.0000 - fp: 30.0000 - tn: 181924.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8667 - recall: 0.6056 - auc: 0.9308 - prc: 0.7085 - val_loss: 0.0031 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9199 - val_prc: 0.7603 Epoch 22/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0044 - tp: 185.0000 - fp: 29.0000 - tn: 181925.0000 - fn: 137.0000 - accuracy: 0.9991 - precision: 0.8645 - recall: 0.5745 - auc: 0.9200 - prc: 0.6928 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 18.0000 - val_accuracy: 0.9995 - val_precision: 0.8793 - val_recall: 0.7391 - val_auc: 0.9198 - val_prc: 0.7615 Epoch 23/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0042 - tp: 191.0000 - fp: 34.0000 - tn: 181920.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8489 - recall: 0.5932 - auc: 0.9277 - prc: 0.7225 - val_loss: 0.0031 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9199 - val_prc: 0.7642 Epoch 24/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0041 - tp: 188.0000 - fp: 28.0000 - tn: 181926.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8704 - recall: 0.5839 - auc: 0.9323 - prc: 0.7307 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 18.0000 - val_accuracy: 0.9995 - val_precision: 0.8793 - val_recall: 0.7391 - val_auc: 0.9199 - val_prc: 0.7626 Epoch 25/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0042 - tp: 197.0000 - fp: 36.0000 - tn: 181918.0000 - fn: 125.0000 - accuracy: 0.9991 - precision: 0.8455 - recall: 0.6118 - auc: 0.9246 - prc: 0.7086 - val_loss: 0.0031 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9199 - val_prc: 0.7728 Epoch 26/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0041 - tp: 191.0000 - fp: 31.0000 - tn: 181923.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8604 - recall: 0.5932 - auc: 0.9292 - prc: 0.7152 - val_loss: 0.0031 - val_tp: 49.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8750 - val_recall: 0.7101 - val_auc: 0.9199 - val_prc: 0.7744 Epoch 27/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0041 - tp: 202.0000 - fp: 33.0000 - tn: 181921.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8596 - recall: 0.6273 - auc: 0.9262 - prc: 0.7209 - val_loss: 0.0031 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9198 - val_prc: 0.7687 Epoch 28/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0038 - tp: 213.0000 - fp: 37.0000 - tn: 181917.0000 - fn: 109.0000 - accuracy: 0.9992 - precision: 0.8520 - recall: 0.6615 - auc: 0.9356 - prc: 0.7422 - val_loss: 0.0031 - val_tp: 48.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 21.0000 - val_accuracy: 0.9994 - val_precision: 0.8889 - val_recall: 0.6957 - val_auc: 0.9127 - val_prc: 0.7715 Epoch 29/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0043 - tp: 183.0000 - fp: 30.0000 - tn: 181924.0000 - fn: 139.0000 - accuracy: 0.9991 - precision: 0.8592 - recall: 0.5683 - auc: 0.9214 - prc: 0.7053 - val_loss: 0.0031 - val_tp: 47.0000 - val_fp: 3.0000 - val_tn: 45497.0000 - val_fn: 22.0000 - val_accuracy: 0.9995 - val_precision: 0.9400 - val_recall: 0.6812 - val_auc: 0.9127 - val_prc: 0.7746 Epoch 30/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0044 - tp: 179.0000 - fp: 29.0000 - tn: 181925.0000 - fn: 143.0000 - accuracy: 0.9991 - precision: 0.8606 - recall: 0.5559 - auc: 0.9167 - prc: 0.6924 - val_loss: 0.0031 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9199 - val_prc: 0.7745 Epoch 31/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0039 - tp: 199.0000 - fp: 28.0000 - tn: 181926.0000 - fn: 123.0000 - accuracy: 0.9992 - precision: 0.8767 - recall: 0.6180 - auc: 0.9293 - prc: 0.7386 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8644 - val_recall: 0.7391 - val_auc: 0.9199 - val_prc: 0.7777 Epoch 32/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0044 - tp: 186.0000 - fp: 32.0000 - tn: 181922.0000 - fn: 136.0000 - accuracy: 0.9991 - precision: 0.8532 - recall: 0.5776 - auc: 0.9152 - prc: 0.6856 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8644 - val_recall: 0.7391 - val_auc: 0.9126 - val_prc: 0.7653 Epoch 33/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0041 - tp: 205.0000 - fp: 30.0000 - tn: 181924.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8723 - recall: 0.6366 - auc: 0.9262 - prc: 0.7156 - val_loss: 0.0031 - val_tp: 46.0000 - val_fp: 3.0000 - val_tn: 45497.0000 - val_fn: 23.0000 - val_accuracy: 0.9994 - val_precision: 0.9388 - val_recall: 0.6667 - val_auc: 0.9127 - val_prc: 0.7731 Epoch 34/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0040 - tp: 194.0000 - fp: 27.0000 - tn: 181927.0000 - fn: 128.0000 - accuracy: 0.9991 - precision: 0.8778 - recall: 0.6025 - auc: 0.9308 - prc: 0.7248 - val_loss: 0.0031 - val_tp: 49.0000 - val_fp: 3.0000 - val_tn: 45497.0000 - val_fn: 20.0000 - val_accuracy: 0.9995 - val_precision: 0.9423 - val_recall: 0.7101 - val_auc: 0.9127 - val_prc: 0.7761 Epoch 35/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0042 - tp: 178.0000 - fp: 35.0000 - tn: 181919.0000 - fn: 144.0000 - accuracy: 0.9990 - precision: 0.8357 - recall: 0.5528 - auc: 0.9308 - prc: 0.7084 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8644 - val_recall: 0.7391 - val_auc: 0.9126 - val_prc: 0.7680 Epoch 36/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0041 - tp: 197.0000 - fp: 29.0000 - tn: 181925.0000 - fn: 125.0000 - accuracy: 0.9992 - precision: 0.8717 - recall: 0.6118 - auc: 0.9261 - prc: 0.7202 - val_loss: 0.0031 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9199 - val_prc: 0.7784 Epoch 37/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0041 - tp: 188.0000 - fp: 36.0000 - tn: 181918.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8393 - recall: 0.5839 - auc: 0.9230 - prc: 0.7139 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 9.0000 - val_tn: 45491.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8500 - val_recall: 0.7391 - val_auc: 0.9126 - val_prc: 0.7760 Epoch 38/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0039 - tp: 202.0000 - fp: 29.0000 - tn: 181925.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8745 - recall: 0.6273 - auc: 0.9246 - prc: 0.7336 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 9.0000 - val_tn: 45491.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8500 - val_recall: 0.7391 - val_auc: 0.9126 - val_prc: 0.7762 Epoch 39/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0038 - tp: 204.0000 - fp: 39.0000 - tn: 181915.0000 - fn: 118.0000 - accuracy: 0.9991 - precision: 0.8395 - recall: 0.6335 - auc: 0.9292 - prc: 0.7404 - val_loss: 0.0031 - val_tp: 48.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 21.0000 - val_accuracy: 0.9995 - val_precision: 0.9231 - val_recall: 0.6957 - val_auc: 0.9127 - val_prc: 0.7799 Epoch 40/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0039 - tp: 192.0000 - fp: 29.0000 - tn: 181925.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8688 - recall: 0.5963 - auc: 0.9324 - prc: 0.7400 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 9.0000 - val_tn: 45491.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8500 - val_recall: 0.7391 - val_auc: 0.9127 - val_prc: 0.7764 Epoch 41/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0039 - tp: 198.0000 - fp: 31.0000 - tn: 181923.0000 - fn: 124.0000 - accuracy: 0.9991 - precision: 0.8646 - recall: 0.6149 - auc: 0.9246 - prc: 0.7280 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 9.0000 - val_tn: 45491.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8500 - val_recall: 0.7391 - val_auc: 0.9127 - val_prc: 0.7748 Epoch 42/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0038 - tp: 201.0000 - fp: 31.0000 - tn: 181923.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8664 - recall: 0.6242 - auc: 0.9325 - prc: 0.7437 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 9.0000 - val_tn: 45491.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8500 - val_recall: 0.7391 - val_auc: 0.9127 - val_prc: 0.7726 Epoch 43/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0042 - tp: 182.0000 - fp: 36.0000 - tn: 181918.0000 - fn: 140.0000 - accuracy: 0.9990 - precision: 0.8349 - recall: 0.5652 - auc: 0.9261 - prc: 0.7135 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8644 - val_recall: 0.7391 - val_auc: 0.9127 - val_prc: 0.7750 Epoch 44/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0038 - tp: 199.0000 - fp: 24.0000 - tn: 181930.0000 - fn: 123.0000 - accuracy: 0.9992 - precision: 0.8924 - recall: 0.6180 - auc: 0.9325 - prc: 0.7531 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8644 - val_recall: 0.7391 - val_auc: 0.9127 - val_prc: 0.7713 Epoch 45/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0037 - tp: 200.0000 - fp: 29.0000 - tn: 181925.0000 - fn: 122.0000 - accuracy: 0.9992 - precision: 0.8734 - recall: 0.6211 - auc: 0.9340 - prc: 0.7505 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 18.0000 - val_accuracy: 0.9995 - val_precision: 0.9107 - val_recall: 0.7391 - val_auc: 0.9126 - val_prc: 0.7779 Epoch 46/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0039 - tp: 195.0000 - fp: 25.0000 - tn: 181929.0000 - fn: 127.0000 - accuracy: 0.9992 - precision: 0.8864 - recall: 0.6056 - auc: 0.9416 - prc: 0.7341 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 18.0000 - val_accuracy: 0.9995 - val_precision: 0.9107 - val_recall: 0.7391 - val_auc: 0.9126 - val_prc: 0.7761 Epoch 47/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0040 - tp: 192.0000 - fp: 40.0000 - tn: 181914.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8276 - recall: 0.5963 - auc: 0.9307 - prc: 0.7235 - val_loss: 0.0031 - val_tp: 48.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 21.0000 - val_accuracy: 0.9995 - val_precision: 0.9231 - val_recall: 0.6957 - val_auc: 0.9127 - val_prc: 0.7792 Epoch 48/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0036 - tp: 205.0000 - fp: 30.0000 - tn: 181924.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8723 - recall: 0.6366 - auc: 0.9371 - prc: 0.7668 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 18.0000 - val_accuracy: 0.9995 - val_precision: 0.9107 - val_recall: 0.7391 - val_auc: 0.9127 - val_prc: 0.7772 Epoch 49/100 79/90 [=========================>....] - ETA: 0s - loss: 0.0039 - tp: 170.0000 - fp: 29.0000 - tn: 161480.0000 - fn: 113.0000 - accuracy: 0.9991 - precision: 0.8543 - recall: 0.6007 - auc: 0.9303 - prc: 0.7314Restoring model weights from the end of the best epoch: 39. 90/90 [==============================] - 0s 5ms/step - loss: 0.0038 - tp: 198.0000 - fp: 32.0000 - tn: 181922.0000 - fn: 124.0000 - accuracy: 0.9991 - precision: 0.8609 - recall: 0.6149 - auc: 0.9308 - prc: 0.7420 - val_loss: 0.0031 - val_tp: 51.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 18.0000 - val_accuracy: 0.9995 - val_precision: 0.8793 - val_recall: 0.7391 - val_auc: 0.9127 - val_prc: 0.7790 Epoch 49: early stopping
トレーニング履歴を確認する
このセクションでは、トレーニングと検証のセットでモデルの精度と損失のプロットを作成します。これらは、過適合をチェックするのに役立ちます。詳細については、過適合と学習不足チュートリアルを参照してください。
さらに、上で作成した任意のメトリクスのプロットを作成することができます。 例として、下記には偽陰性が含まれています。
def plot_metrics(history):
metrics = ['loss', 'prc', 'precision', 'recall']
for n, metric in enumerate(metrics):
name = metric.replace("_"," ").capitalize()
plt.subplot(2,2,n+1)
plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
color=colors[0], linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
if metric == 'loss':
plt.ylim([0, plt.ylim()[1]])
elif metric == 'auc':
plt.ylim([0.8,1])
else:
plt.ylim([0,1])
plt.legend()
plot_metrics(baseline_history)
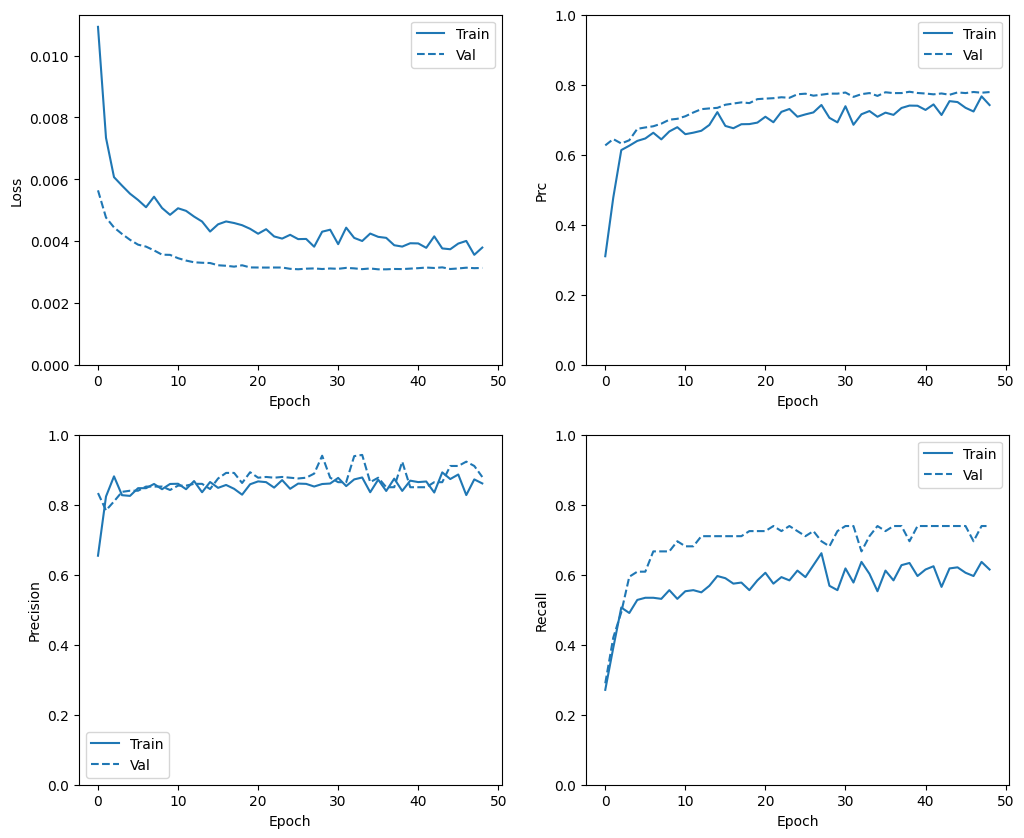
注意: 一般的に、検証曲線はトレーニング曲線よりも優れています。 これは主に、モデルを評価する際にドロップアウトレイヤーがアクティブでないということに起因します。
メトリクスを評価する
混同行列を使用して、実際のラベルと予測されたラベルを要約できます。ここで、X 軸は予測されたラベルであり、Y 軸は実際のラベルです。
train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)
90/90 [==============================] - 0s 1ms/step 28/28 [==============================] - 0s 1ms/step
def plot_cm(labels, predictions, p=0.5):
cm = confusion_matrix(labels, predictions > p)
plt.figure(figsize=(5,5))
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion matrix @{:.2f}'.format(p))
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
テストデータセットでモデルを評価し、上記で作成した行列の結果を表示します。
baseline_results = model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_baseline)
loss : 0.002801472321152687 tp : 71.0 fp : 1.0 tn : 56860.0 fn : 30.0 accuracy : 0.9994557499885559 precision : 0.9861111044883728 recall : 0.7029703259468079 auc : 0.9403578639030457 prc : 0.8531444072723389 Legitimate Transactions Detected (True Negatives): 56860 Legitimate Transactions Incorrectly Detected (False Positives): 1 Fraudulent Transactions Missed (False Negatives): 30 Fraudulent Transactions Detected (True Positives): 71 Total Fraudulent Transactions: 101
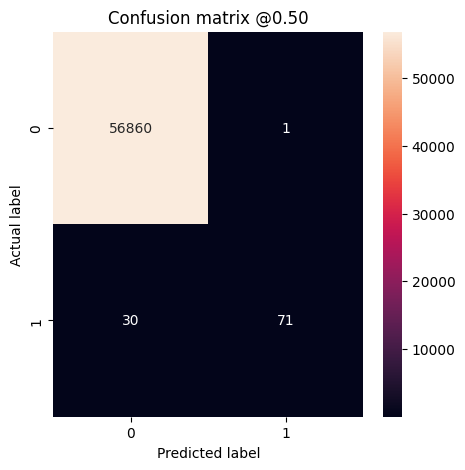
モデルがすべてを完璧に予測した場合は、これは対角行列になり、主な対角線から外れた値が不正確な予測を示してゼロになります。 この場合、行列は偽陽性が比較的少ないことを示し、これは誤ってフラグが立てられた正当な取引が比較的少ないことを意味します。 しかし、偽陽性の数が増えればコストがかかる可能性はありますが、偽陰性の数はさらに少なくした方が良いでしょう。偽陽性は顧客にカード利用履歴の確認を求めるメールを送信する可能性があるのに対し、偽陰性は不正な取引を成立させてしまう可能性があるため、このトレードオフはむしろ望ましいといえます。
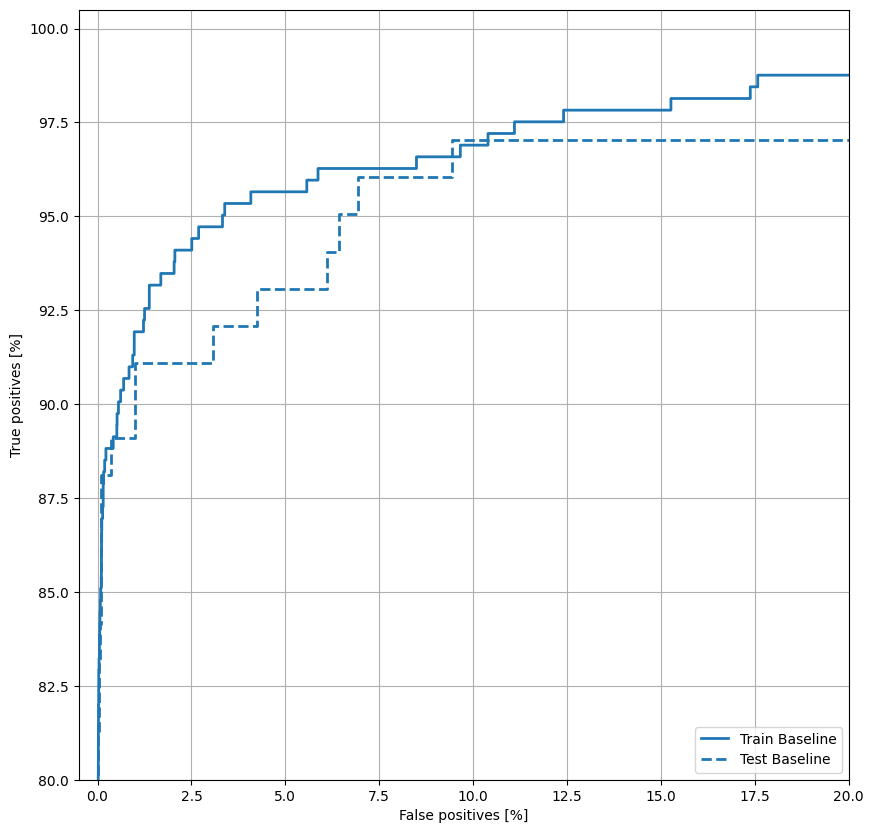
ROC をプロットする
次に、ROC をプロットします。このプロットは、出力しきい値を調整するだけでモデルが到達できるパフォーマンス範囲が一目で分かるので有用です。
def plot_roc(name, labels, predictions, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,20])
plt.ylim([80,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
AUPRC をプロットする
AUPRC をプロットします。補間された適合率-再現率曲線の下の領域は、分類しきい値のさまざまな値に対して(再現率、適合率)点をプロットすることにより取得できます。計算方法によっては、PR AUC はモデルの平均適合率と同等になる場合があります。
def plot_prc(name, labels, predictions, **kwargs):
precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
plt.xlabel('Precision')
plt.ylabel('Recall')
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
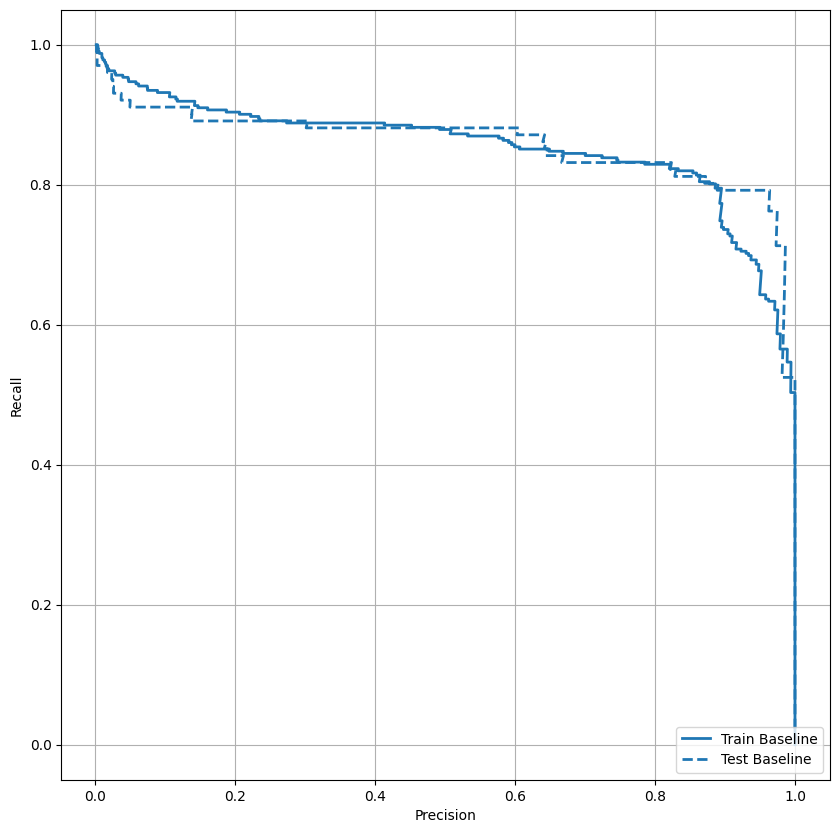
適合率は比較的高いように見えますが、再現率と ROC 曲線の下の曲線下面積 (AUC) は、期待するほど高いものではありません。適合率と再現率の両方を最大化しようとすると、分類器はしばしば課題に直面します。不均衡データセットを扱う場合は特にそうです。大切な問題のコンテキストでは異なるタイプのエラーにかかるコストを考慮することが重要です。 この例では、偽陰性(不正な取引が見逃されている)は金銭的コストを伴う可能性がある一方で、偽陽性(取引が不正であると誤ってフラグが立てられている)はユーザーの幸福度を低下させる可能性があります。
クラスの重み
クラスの重みを計算する
最終目的は不正な取引を特定することですが、処理する陽性サンプルがそれほど多くないので、利用可能な数少ない例の分類器に大きな重み付けをします。 これを行うには、パラメータを介して各クラスの重みを Keras に渡します。 これにより、モデルは十分に表現されていないクラスの例にも「より注意を払う」ようになります。
# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))
Weight for class 0: 0.50 Weight for class 1: 289.44
クラスの重みでモデルをトレーニングする
次に、クラスの重みでモデルを再トレーニングして評価し、それが予測にどのように影響するかを確認します。
注意: class_weights を使用すると、損失の範囲が変更されます。オプティマイザにもよりますが、これはトレーニングの安定性に影響を与える可能性があります。tf.keras.optimizers.SGD のように、ステップサイズが勾配の大きさに依存するオプティマイザは失敗する可能性があります。ここで使用されているオプティマイザ tf.keras.optimizers.Adam は、スケーリングの変更による影響を受けません。また、重み付けのため、総損失は 2 つのモデル間で比較できないことに注意してください。
weighted_model = make_model()
weighted_model.load_weights(initial_weights)
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels),
# The class weights go here
class_weight=class_weight)
Epoch 1/100 90/90 [==============================] - 2s 11ms/step - loss: 2.3129 - tp: 133.0000 - fp: 165.0000 - tn: 238650.0000 - fn: 290.0000 - accuracy: 0.9981 - precision: 0.4463 - recall: 0.3144 - auc: 0.8058 - prc: 0.2802 - val_loss: 0.0063 - val_tp: 27.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 42.0000 - val_accuracy: 0.9989 - val_precision: 0.7714 - val_recall: 0.3913 - val_auc: 0.8841 - val_prc: 0.5301 Epoch 2/100 90/90 [==============================] - 0s 5ms/step - loss: 1.0916 - tp: 180.0000 - fp: 370.0000 - tn: 181584.0000 - fn: 142.0000 - accuracy: 0.9972 - precision: 0.3273 - recall: 0.5590 - auc: 0.8846 - prc: 0.4262 - val_loss: 0.0072 - val_tp: 49.0000 - val_fp: 18.0000 - val_tn: 45482.0000 - val_fn: 20.0000 - val_accuracy: 0.9992 - val_precision: 0.7313 - val_recall: 0.7101 - val_auc: 0.8941 - val_prc: 0.5897 Epoch 3/100 90/90 [==============================] - 0s 5ms/step - loss: 0.7963 - tp: 216.0000 - fp: 544.0000 - tn: 181410.0000 - fn: 106.0000 - accuracy: 0.9964 - precision: 0.2842 - recall: 0.6708 - auc: 0.9169 - prc: 0.4917 - val_loss: 0.0090 - val_tp: 53.0000 - val_fp: 22.0000 - val_tn: 45478.0000 - val_fn: 16.0000 - val_accuracy: 0.9992 - val_precision: 0.7067 - val_recall: 0.7681 - val_auc: 0.9043 - val_prc: 0.6168 Epoch 4/100 90/90 [==============================] - 0s 5ms/step - loss: 0.6105 - tp: 240.0000 - fp: 800.0000 - tn: 181154.0000 - fn: 82.0000 - accuracy: 0.9952 - precision: 0.2308 - recall: 0.7453 - auc: 0.9281 - prc: 0.5541 - val_loss: 0.0114 - val_tp: 53.0000 - val_fp: 34.0000 - val_tn: 45466.0000 - val_fn: 16.0000 - val_accuracy: 0.9989 - val_precision: 0.6092 - val_recall: 0.7681 - val_auc: 0.9200 - val_prc: 0.6427 Epoch 5/100 90/90 [==============================] - 0s 5ms/step - loss: 0.5837 - tp: 240.0000 - fp: 1179.0000 - tn: 180775.0000 - fn: 82.0000 - accuracy: 0.9931 - precision: 0.1691 - recall: 0.7453 - auc: 0.9288 - prc: 0.4826 - val_loss: 0.0152 - val_tp: 54.0000 - val_fp: 72.0000 - val_tn: 45428.0000 - val_fn: 15.0000 - val_accuracy: 0.9981 - val_precision: 0.4286 - val_recall: 0.7826 - val_auc: 0.9307 - val_prc: 0.6217 Epoch 6/100 90/90 [==============================] - 0s 5ms/step - loss: 0.4503 - tp: 259.0000 - fp: 1631.0000 - tn: 180323.0000 - fn: 63.0000 - accuracy: 0.9907 - precision: 0.1370 - recall: 0.8043 - auc: 0.9382 - prc: 0.4635 - val_loss: 0.0195 - val_tp: 54.0000 - val_fp: 121.0000 - val_tn: 45379.0000 - val_fn: 15.0000 - val_accuracy: 0.9970 - val_precision: 0.3086 - val_recall: 0.7826 - val_auc: 0.9420 - val_prc: 0.6180 Epoch 7/100 90/90 [==============================] - 0s 5ms/step - loss: 0.3774 - tp: 265.0000 - fp: 2116.0000 - tn: 179838.0000 - fn: 57.0000 - accuracy: 0.9881 - precision: 0.1113 - recall: 0.8230 - auc: 0.9587 - prc: 0.4556 - val_loss: 0.0247 - val_tp: 54.0000 - val_fp: 180.0000 - val_tn: 45320.0000 - val_fn: 15.0000 - val_accuracy: 0.9957 - val_precision: 0.2308 - val_recall: 0.7826 - val_auc: 0.9448 - val_prc: 0.6166 Epoch 8/100 90/90 [==============================] - 0s 5ms/step - loss: 0.3911 - tp: 267.0000 - fp: 2627.0000 - tn: 179327.0000 - fn: 55.0000 - accuracy: 0.9853 - precision: 0.0923 - recall: 0.8292 - auc: 0.9403 - prc: 0.3966 - val_loss: 0.0300 - val_tp: 56.0000 - val_fp: 271.0000 - val_tn: 45229.0000 - val_fn: 13.0000 - val_accuracy: 0.9938 - val_precision: 0.1713 - val_recall: 0.8116 - val_auc: 0.9574 - val_prc: 0.5708 Epoch 9/100 90/90 [==============================] - 0s 5ms/step - loss: 0.3524 - tp: 269.0000 - fp: 3140.0000 - tn: 178814.0000 - fn: 53.0000 - accuracy: 0.9825 - precision: 0.0789 - recall: 0.8354 - auc: 0.9525 - prc: 0.3345 - val_loss: 0.0372 - val_tp: 56.0000 - val_fp: 399.0000 - val_tn: 45101.0000 - val_fn: 13.0000 - val_accuracy: 0.9910 - val_precision: 0.1231 - val_recall: 0.8116 - val_auc: 0.9583 - val_prc: 0.5338 Epoch 10/100 90/90 [==============================] - 0s 5ms/step - loss: 0.3474 - tp: 270.0000 - fp: 3654.0000 - tn: 178300.0000 - fn: 52.0000 - accuracy: 0.9797 - precision: 0.0688 - recall: 0.8385 - auc: 0.9472 - prc: 0.2990 - val_loss: 0.0435 - val_tp: 56.0000 - val_fp: 492.0000 - val_tn: 45008.0000 - val_fn: 13.0000 - val_accuracy: 0.9889 - val_precision: 0.1022 - val_recall: 0.8116 - val_auc: 0.9581 - val_prc: 0.5103 Epoch 11/100 90/90 [==============================] - 0s 5ms/step - loss: 0.3760 - tp: 274.0000 - fp: 4014.0000 - tn: 177940.0000 - fn: 48.0000 - accuracy: 0.9777 - precision: 0.0639 - recall: 0.8509 - auc: 0.9363 - prc: 0.2969 - val_loss: 0.0488 - val_tp: 57.0000 - val_fp: 552.0000 - val_tn: 44948.0000 - val_fn: 12.0000 - val_accuracy: 0.9876 - val_precision: 0.0936 - val_recall: 0.8261 - val_auc: 0.9582 - val_prc: 0.4941 Epoch 12/100 90/90 [==============================] - 0s 6ms/step - loss: 0.3090 - tp: 276.0000 - fp: 4542.0000 - tn: 177412.0000 - fn: 46.0000 - accuracy: 0.9748 - precision: 0.0573 - recall: 0.8571 - auc: 0.9566 - prc: 0.2807 - val_loss: 0.0552 - val_tp: 58.0000 - val_fp: 625.0000 - val_tn: 44875.0000 - val_fn: 11.0000 - val_accuracy: 0.9860 - val_precision: 0.0849 - val_recall: 0.8406 - val_auc: 0.9611 - val_prc: 0.4743 Epoch 13/100 90/90 [==============================] - 0s 6ms/step - loss: 0.3053 - tp: 277.0000 - fp: 4807.0000 - tn: 177147.0000 - fn: 45.0000 - accuracy: 0.9734 - precision: 0.0545 - recall: 0.8602 - auc: 0.9528 - prc: 0.2449 - val_loss: 0.0600 - val_tp: 58.0000 - val_fp: 670.0000 - val_tn: 44830.0000 - val_fn: 11.0000 - val_accuracy: 0.9851 - val_precision: 0.0797 - val_recall: 0.8406 - val_auc: 0.9603 - val_prc: 0.4704 Epoch 14/100 79/90 [=========================>....] - ETA: 0s - loss: 0.3186 - tp: 260.0000 - fp: 4499.0000 - tn: 156996.0000 - fn: 37.0000 - accuracy: 0.9720 - precision: 0.0546 - recall: 0.8754 - auc: 0.9518 - prc: 0.2507Restoring model weights from the end of the best epoch: 4. 90/90 [==============================] - 0s 5ms/step - loss: 0.3006 - tp: 283.0000 - fp: 5045.0000 - tn: 176909.0000 - fn: 39.0000 - accuracy: 0.9721 - precision: 0.0531 - recall: 0.8789 - auc: 0.9527 - prc: 0.2479 - val_loss: 0.0620 - val_tp: 58.0000 - val_fp: 689.0000 - val_tn: 44811.0000 - val_fn: 11.0000 - val_accuracy: 0.9846 - val_precision: 0.0776 - val_recall: 0.8406 - val_auc: 0.9613 - val_prc: 0.4712 Epoch 14: early stopping
トレーニング履歴を確認する
plot_metrics(weighted_history)
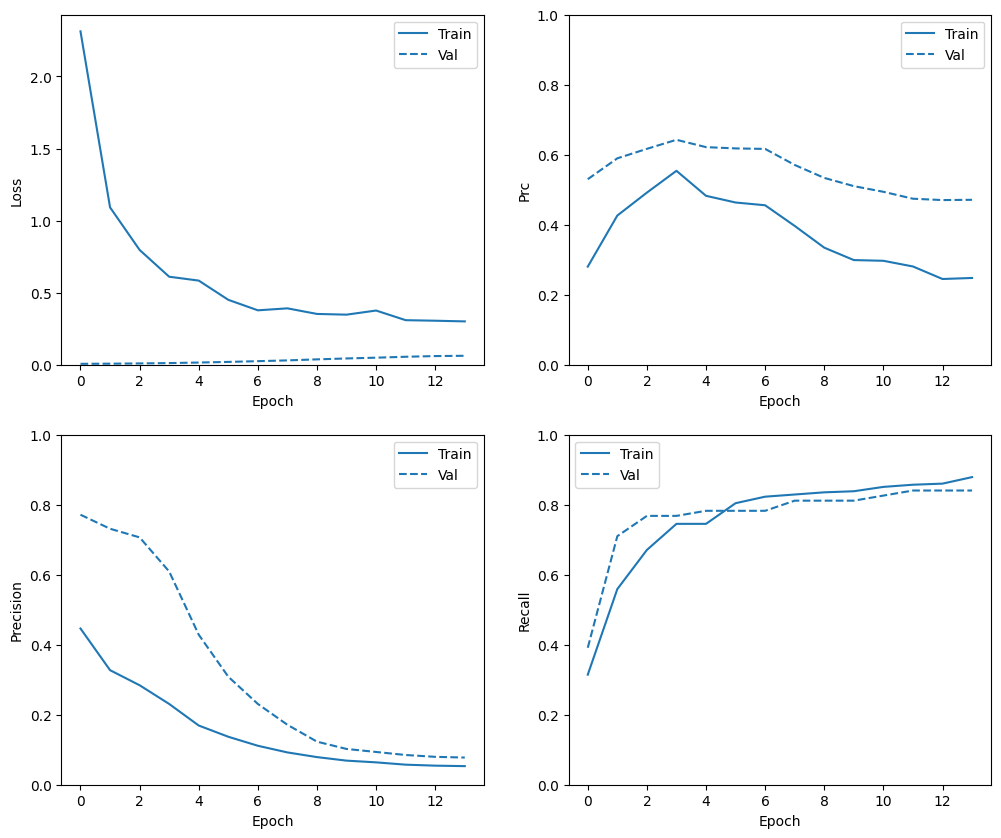
メトリクスを評価する
train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)
90/90 [==============================] - 0s 1ms/step 28/28 [==============================] - 0s 1ms/step
weighted_results = weighted_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_weighted)
loss : 0.00944011565297842 tp : 81.0 fp : 29.0 tn : 56832.0 fn : 20.0 accuracy : 0.9991397857666016 precision : 0.7363636493682861 recall : 0.801980197429657 auc : 0.9742780327796936 prc : 0.7228649854660034 Legitimate Transactions Detected (True Negatives): 56832 Legitimate Transactions Incorrectly Detected (False Positives): 29 Fraudulent Transactions Missed (False Negatives): 20 Fraudulent Transactions Detected (True Positives): 81 Total Fraudulent Transactions: 101
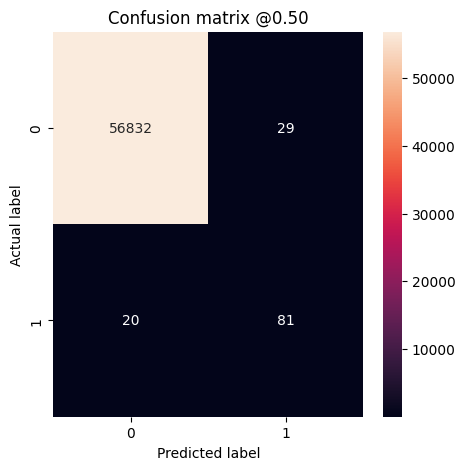
ここでは、クラスの重みを使用すると偽陽性が多くなるため、正解率と適合率が低くなりますが、逆にモデルがより多くの真陽性を検出したため、再現率と AUC が高くなっていることが分かります。このモデルは正解率は低いものの、再現率が高くなるので、より多くの不正取引を特定します。もちろん、両タイプのエラーにはコストがかかります。(あまりにも多くの正当な取引を不正取引としてフラグを立ててユーザーに迷惑をかけたくはないはずです。)アプリケーションのこういった異なるタイプのエラー間のトレードオフは、慎重に検討してください
ROC をプロットする
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
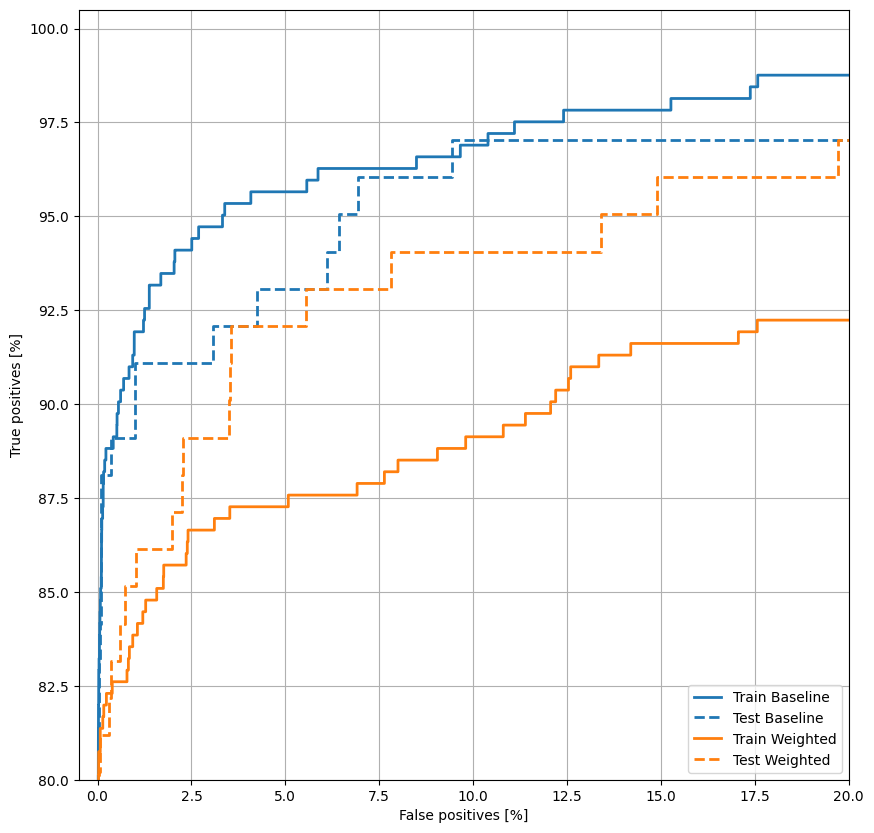
AUPRC をプロットする
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');

オーバーサンプリング
マイノリティクラスをオーバーサンプリングする
関連したアプローチとして、マイノリティクラスをオーバーサンプリングしてデータセットを再サンプルするという方法があります。
pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]
pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]
NumPy を使用する
陽性の例から適切な数のランダムインデックスを選択して、手動でデータセットのバランスをとることができます。
ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))
res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]
res_pos_features.shape
(181954, 29)
resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)
order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]
resampled_features.shape
(363908, 29)
tf.dataを使用する
もしtf.dataを使用している場合、バランスの取れた例を作成する最も簡単な方法は、positiveとnegativeのデータセットから開始し、それらをマージすることです。その他の例については、tf.data ガイドをご覧ください。
BUFFER_SIZE = 100000
def make_ds(features, labels):
ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
ds = ds.shuffle(BUFFER_SIZE).repeat()
return ds
pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)
各データセットは(feature, label)のペアを提供します。
for features, label in pos_ds.take(1):
print("Features:\n", features.numpy())
print()
print("Label: ", label.numpy())
Features: [-2.19541086 1.13428993 -1.53623679 -0.33658631 -0.83969674 -1.57367972 -1.68012623 0.22759802 0.26401501 -3.5197414 2.45072394 -3.59505942 -1.02811684 -5. 1.80441222 -3.70754897 -5. -2.22095608 -0.01134361 -0.93004871 0.75601008 -0.0947461 -1.75493901 0.44294128 -0.03893845 -2.00270316 -2.29191024 0.00709538 0.57125601] Label: 1
tf.data.Dataset.sample_from_datasets を使用し、この 2 つをマージします。
resampled_ds = tf.data.Dataset.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)
for features, label in resampled_ds.take(1):
print(label.numpy().mean())
0.47705078125
このデータセットを使用するには、エポックごとのステップ数が必要です。
この場合の「エポック」の定義はあまり明確ではありません。それぞれの陰性の例を 1 度見るのに必要なバッチ数だとしましょう。
resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch
278.0
オーバーサンプリングデータをトレーニングする
ここで、クラスの重みを使用する代わりに、再サンプルされたデータセットを使用してモデルをトレーニングし、それらの手法がどう比較されるかを確認してみましょう。
注意: 陽性の例を複製することでデータのバランスをとっているため、データセットの総サイズは大きくなり、各エポックではより多くのトレーニングステップが実行されます。
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2)
resampled_history = resampled_model.fit(
resampled_ds,
epochs=EPOCHS,
steps_per_epoch=resampled_steps_per_epoch,
callbacks=[early_stopping],
validation_data=val_ds)
Epoch 1/100 278/278 [==============================] - 8s 22ms/step - loss: 0.4126 - tp: 230239.0000 - fp: 43658.0000 - tn: 297273.0000 - fn: 55136.0000 - accuracy: 0.8423 - precision: 0.8406 - recall: 0.8068 - auc: 0.9048 - prc: 0.9219 - val_loss: 0.1683 - val_tp: 59.0000 - val_fp: 593.0000 - val_tn: 44907.0000 - val_fn: 10.0000 - val_accuracy: 0.9868 - val_precision: 0.0905 - val_recall: 0.8551 - val_auc: 0.9705 - val_prc: 0.6726 Epoch 2/100 278/278 [==============================] - 6s 22ms/step - loss: 0.1984 - tp: 254251.0000 - fp: 12432.0000 - tn: 271931.0000 - fn: 30730.0000 - accuracy: 0.9242 - precision: 0.9534 - recall: 0.8922 - auc: 0.9716 - prc: 0.9779 - val_loss: 0.0992 - val_tp: 59.0000 - val_fp: 605.0000 - val_tn: 44895.0000 - val_fn: 10.0000 - val_accuracy: 0.9865 - val_precision: 0.0889 - val_recall: 0.8551 - val_auc: 0.9667 - val_prc: 0.6655 Epoch 3/100 278/278 [==============================] - 6s 21ms/step - loss: 0.1600 - tp: 258785.0000 - fp: 9416.0000 - tn: 274377.0000 - fn: 26766.0000 - accuracy: 0.9364 - precision: 0.9649 - recall: 0.9063 - auc: 0.9828 - prc: 0.9856 - val_loss: 0.0792 - val_tp: 59.0000 - val_fp: 589.0000 - val_tn: 44911.0000 - val_fn: 10.0000 - val_accuracy: 0.9869 - val_precision: 0.0910 - val_recall: 0.8551 - val_auc: 0.9628 - val_prc: 0.6624 Epoch 4/100 278/278 [==============================] - 6s 21ms/step - loss: 0.1396 - tp: 259655.0000 - fp: 8254.0000 - tn: 277278.0000 - fn: 24157.0000 - accuracy: 0.9431 - precision: 0.9692 - recall: 0.9149 - auc: 0.9877 - prc: 0.9890 - val_loss: 0.0699 - val_tp: 60.0000 - val_fp: 585.0000 - val_tn: 44915.0000 - val_fn: 9.0000 - val_accuracy: 0.9870 - val_precision: 0.0930 - val_recall: 0.8696 - val_auc: 0.9584 - val_prc: 0.6478 Epoch 5/100 278/278 [==============================] - 6s 21ms/step - loss: 0.1261 - tp: 261849.0000 - fp: 7675.0000 - tn: 277421.0000 - fn: 22399.0000 - accuracy: 0.9472 - precision: 0.9715 - recall: 0.9212 - auc: 0.9904 - prc: 0.9911 - val_loss: 0.0607 - val_tp: 60.0000 - val_fp: 527.0000 - val_tn: 44973.0000 - val_fn: 9.0000 - val_accuracy: 0.9882 - val_precision: 0.1022 - val_recall: 0.8696 - val_auc: 0.9550 - val_prc: 0.6405 Epoch 6/100 278/278 [==============================] - 6s 21ms/step - loss: 0.1164 - tp: 262446.0000 - fp: 7264.0000 - tn: 278031.0000 - fn: 21603.0000 - accuracy: 0.9493 - precision: 0.9731 - recall: 0.9239 - auc: 0.9922 - prc: 0.9924 - val_loss: 0.0561 - val_tp: 60.0000 - val_fp: 544.0000 - val_tn: 44956.0000 - val_fn: 9.0000 - val_accuracy: 0.9879 - val_precision: 0.0993 - val_recall: 0.8696 - val_auc: 0.9554 - val_prc: 0.6181 Epoch 7/100 278/278 [==============================] - 6s 22ms/step - loss: 0.1095 - tp: 264558.0000 - fp: 7213.0000 - tn: 277018.0000 - fn: 20555.0000 - accuracy: 0.9512 - precision: 0.9735 - recall: 0.9279 - auc: 0.9932 - prc: 0.9934 - val_loss: 0.0521 - val_tp: 60.0000 - val_fp: 535.0000 - val_tn: 44965.0000 - val_fn: 9.0000 - val_accuracy: 0.9881 - val_precision: 0.1008 - val_recall: 0.8696 - val_auc: 0.9569 - val_prc: 0.6182 Epoch 8/100 278/278 [==============================] - 6s 21ms/step - loss: 0.1028 - tp: 264967.0000 - fp: 7170.0000 - tn: 277903.0000 - fn: 19304.0000 - accuracy: 0.9535 - precision: 0.9737 - recall: 0.9321 - auc: 0.9941 - prc: 0.9940 - val_loss: 0.0468 - val_tp: 59.0000 - val_fp: 489.0000 - val_tn: 45011.0000 - val_fn: 10.0000 - val_accuracy: 0.9890 - val_precision: 0.1077 - val_recall: 0.8551 - val_auc: 0.9583 - val_prc: 0.6195 Epoch 9/100 278/278 [==============================] - 6s 21ms/step - loss: 0.0966 - tp: 266834.0000 - fp: 6861.0000 - tn: 277391.0000 - fn: 18258.0000 - accuracy: 0.9559 - precision: 0.9749 - recall: 0.9360 - auc: 0.9950 - prc: 0.9948 - val_loss: 0.0435 - val_tp: 59.0000 - val_fp: 468.0000 - val_tn: 45032.0000 - val_fn: 10.0000 - val_accuracy: 0.9895 - val_precision: 0.1120 - val_recall: 0.8551 - val_auc: 0.9589 - val_prc: 0.6038 Epoch 10/100 278/278 [==============================] - 6s 21ms/step - loss: 0.0916 - tp: 267421.0000 - fp: 6806.0000 - tn: 278008.0000 - fn: 17109.0000 - accuracy: 0.9580 - precision: 0.9752 - recall: 0.9399 - auc: 0.9955 - prc: 0.9952 - val_loss: 0.0396 - val_tp: 60.0000 - val_fp: 428.0000 - val_tn: 45072.0000 - val_fn: 9.0000 - val_accuracy: 0.9904 - val_precision: 0.1230 - val_recall: 0.8696 - val_auc: 0.9548 - val_prc: 0.6051 Epoch 11/100 277/278 [============================>.] - ETA: 0s - loss: 0.0870 - tp: 268244.0000 - fp: 6786.0000 - tn: 276469.0000 - fn: 15797.0000 - accuracy: 0.9602 - precision: 0.9753 - recall: 0.9444 - auc: 0.9959 - prc: 0.9957Restoring model weights from the end of the best epoch: 1. 278/278 [==============================] - 6s 23ms/step - loss: 0.0870 - tp: 269189.0000 - fp: 6815.0000 - tn: 277494.0000 - fn: 15846.0000 - accuracy: 0.9602 - precision: 0.9753 - recall: 0.9444 - auc: 0.9959 - prc: 0.9957 - val_loss: 0.0365 - val_tp: 60.0000 - val_fp: 401.0000 - val_tn: 45099.0000 - val_fn: 9.0000 - val_accuracy: 0.9910 - val_precision: 0.1302 - val_recall: 0.8696 - val_auc: 0.9509 - val_prc: 0.6138 Epoch 11: early stopping
トレーニングプロセスが勾配の更新ごとにデータセット全体を考慮する場合は、このオーバーサンプリングは基本的にクラスの重み付けと同じになります。
しかし、ここで行ったようにバッチ単位でモデルをトレーニングする場合、オーバーサンプリングされたデータはより滑らかな勾配信号を提供します。それぞれの陽性の例を大きな重みを持つ 1 つのバッチで表示する代わりに、毎回小さな重みを持つ多くの異なるバッチで表示します。
このような滑らかな勾配信号は、モデルのトレーニングを容易にします。
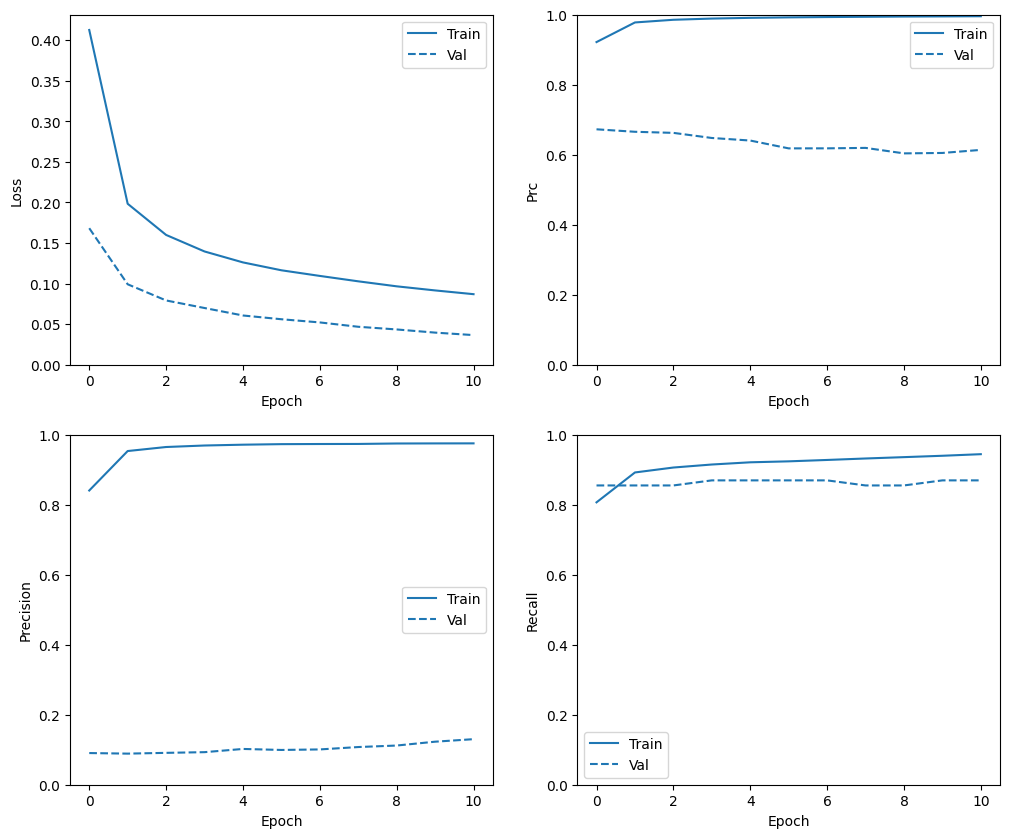
トレーニング履歴を確認する
トレーニングデータは検証データやテストデータとは全く異なる分散を持つため、ここでのメトリクスの分散は異なることに注意してください。
plot_metrics(resampled_history)
再トレーニングする
バランスの取れたデータの方がトレーニングしやすいため、上記のトレーニング方法ではすぐに過学習してしまう可能性があります。
したがって、エポックを分割して、tf.keras.callbacks.EarlyStopping がトレーニングを停止するタイミングをより細かく制御できるようにします。
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
resampled_history = resampled_model.fit(
resampled_ds,
# These are not real epochs
steps_per_epoch=20,
epochs=10*EPOCHS,
callbacks=[early_stopping],
validation_data=(val_ds))
Epoch 1/1000 20/20 [==============================] - 3s 54ms/step - loss: 1.0788 - tp: 9883.0000 - fp: 5709.0000 - tn: 60165.0000 - fn: 10772.0000 - accuracy: 0.8095 - precision: 0.6339 - recall: 0.4785 - auc: 0.8187 - prc: 0.6587 - val_loss: 0.4735 - val_tp: 44.0000 - val_fp: 7517.0000 - val_tn: 37983.0000 - val_fn: 25.0000 - val_accuracy: 0.8345 - val_precision: 0.0058 - val_recall: 0.6377 - val_auc: 0.7719 - val_prc: 0.1136 Epoch 2/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.6680 - tp: 13969.0000 - fp: 5680.0000 - tn: 14619.0000 - fn: 6692.0000 - accuracy: 0.6979 - precision: 0.7109 - recall: 0.6761 - auc: 0.7440 - prc: 0.8238 - val_loss: 0.4738 - val_tp: 57.0000 - val_fp: 7346.0000 - val_tn: 38154.0000 - val_fn: 12.0000 - val_accuracy: 0.8385 - val_precision: 0.0077 - val_recall: 0.8261 - val_auc: 0.8709 - val_prc: 0.3997 Epoch 3/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.5201 - tp: 15755.0000 - fp: 5337.0000 - tn: 15024.0000 - fn: 4844.0000 - accuracy: 0.7514 - precision: 0.7470 - recall: 0.7648 - auc: 0.8243 - prc: 0.8789 - val_loss: 0.4438 - val_tp: 56.0000 - val_fp: 5961.0000 - val_tn: 39539.0000 - val_fn: 13.0000 - val_accuracy: 0.8689 - val_precision: 0.0093 - val_recall: 0.8116 - val_auc: 0.8914 - val_prc: 0.4917 Epoch 4/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.4520 - tp: 16277.0000 - fp: 4793.0000 - tn: 15830.0000 - fn: 4060.0000 - accuracy: 0.7839 - precision: 0.7725 - recall: 0.8004 - auc: 0.8638 - prc: 0.9046 - val_loss: 0.4042 - val_tp: 57.0000 - val_fp: 4418.0000 - val_tn: 41082.0000 - val_fn: 12.0000 - val_accuracy: 0.9028 - val_precision: 0.0127 - val_recall: 0.8261 - val_auc: 0.9071 - val_prc: 0.5734 Epoch 5/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.4011 - tp: 17099.0000 - fp: 3860.0000 - tn: 16322.0000 - fn: 3679.0000 - accuracy: 0.8159 - precision: 0.8158 - recall: 0.8229 - auc: 0.8896 - prc: 0.9251 - val_loss: 0.3656 - val_tp: 57.0000 - val_fp: 3142.0000 - val_tn: 42358.0000 - val_fn: 12.0000 - val_accuracy: 0.9308 - val_precision: 0.0178 - val_recall: 0.8261 - val_auc: 0.9215 - val_prc: 0.5999 Epoch 6/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.3698 - tp: 17030.0000 - fp: 3437.0000 - tn: 17200.0000 - fn: 3293.0000 - accuracy: 0.8357 - precision: 0.8321 - recall: 0.8380 - auc: 0.9073 - prc: 0.9346 - val_loss: 0.3284 - val_tp: 57.0000 - val_fp: 2106.0000 - val_tn: 43394.0000 - val_fn: 12.0000 - val_accuracy: 0.9535 - val_precision: 0.0264 - val_recall: 0.8261 - val_auc: 0.9342 - val_prc: 0.6209 Epoch 7/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.3450 - tp: 17393.0000 - fp: 2816.0000 - tn: 17557.0000 - fn: 3194.0000 - accuracy: 0.8533 - precision: 0.8607 - recall: 0.8449 - auc: 0.9176 - prc: 0.9426 - val_loss: 0.2964 - val_tp: 56.0000 - val_fp: 1409.0000 - val_tn: 44091.0000 - val_fn: 13.0000 - val_accuracy: 0.9688 - val_precision: 0.0382 - val_recall: 0.8116 - val_auc: 0.9453 - val_prc: 0.6271 Epoch 8/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.3227 - tp: 17476.0000 - fp: 2488.0000 - tn: 17993.0000 - fn: 3003.0000 - accuracy: 0.8659 - precision: 0.8754 - recall: 0.8534 - auc: 0.9266 - prc: 0.9487 - val_loss: 0.2685 - val_tp: 57.0000 - val_fp: 1014.0000 - val_tn: 44486.0000 - val_fn: 12.0000 - val_accuracy: 0.9775 - val_precision: 0.0532 - val_recall: 0.8261 - val_auc: 0.9538 - val_prc: 0.6388 Epoch 9/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.3001 - tp: 17545.0000 - fp: 2111.0000 - tn: 18430.0000 - fn: 2874.0000 - accuracy: 0.8783 - precision: 0.8926 - recall: 0.8592 - auc: 0.9358 - prc: 0.9542 - val_loss: 0.2439 - val_tp: 57.0000 - val_fp: 766.0000 - val_tn: 44734.0000 - val_fn: 12.0000 - val_accuracy: 0.9829 - val_precision: 0.0693 - val_recall: 0.8261 - val_auc: 0.9601 - val_prc: 0.6474 Epoch 10/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2841 - tp: 17588.0000 - fp: 1838.0000 - tn: 18720.0000 - fn: 2814.0000 - accuracy: 0.8864 - precision: 0.9054 - recall: 0.8621 - auc: 0.9417 - prc: 0.9580 - val_loss: 0.2229 - val_tp: 57.0000 - val_fp: 672.0000 - val_tn: 44828.0000 - val_fn: 12.0000 - val_accuracy: 0.9850 - val_precision: 0.0782 - val_recall: 0.8261 - val_auc: 0.9649 - val_prc: 0.6646 Epoch 11/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.2695 - tp: 17684.0000 - fp: 1626.0000 - tn: 18962.0000 - fn: 2688.0000 - accuracy: 0.8947 - precision: 0.9158 - recall: 0.8681 - auc: 0.9472 - prc: 0.9616 - val_loss: 0.2051 - val_tp: 57.0000 - val_fp: 631.0000 - val_tn: 44869.0000 - val_fn: 12.0000 - val_accuracy: 0.9859 - val_precision: 0.0828 - val_recall: 0.8261 - val_auc: 0.9677 - val_prc: 0.6582 Epoch 12/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.2608 - tp: 17838.0000 - fp: 1483.0000 - tn: 19004.0000 - fn: 2635.0000 - accuracy: 0.8995 - precision: 0.9232 - recall: 0.8713 - auc: 0.9500 - prc: 0.9639 - val_loss: 0.1904 - val_tp: 57.0000 - val_fp: 619.0000 - val_tn: 44881.0000 - val_fn: 12.0000 - val_accuracy: 0.9862 - val_precision: 0.0843 - val_recall: 0.8261 - val_auc: 0.9692 - val_prc: 0.6674 Epoch 13/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.2480 - tp: 17914.0000 - fp: 1354.0000 - tn: 19123.0000 - fn: 2569.0000 - accuracy: 0.9042 - precision: 0.9297 - recall: 0.8746 - auc: 0.9548 - prc: 0.9670 - val_loss: 0.1775 - val_tp: 58.0000 - val_fp: 600.0000 - val_tn: 44900.0000 - val_fn: 11.0000 - val_accuracy: 0.9866 - val_precision: 0.0881 - val_recall: 0.8406 - val_auc: 0.9696 - val_prc: 0.6689 Epoch 14/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.2393 - tp: 17851.0000 - fp: 1228.0000 - tn: 19433.0000 - fn: 2448.0000 - accuracy: 0.9103 - precision: 0.9356 - recall: 0.8794 - auc: 0.9580 - prc: 0.9687 - val_loss: 0.1656 - val_tp: 59.0000 - val_fp: 579.0000 - val_tn: 44921.0000 - val_fn: 10.0000 - val_accuracy: 0.9871 - val_precision: 0.0925 - val_recall: 0.8551 - val_auc: 0.9706 - val_prc: 0.6725 Epoch 15/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.2296 - tp: 17997.0000 - fp: 1116.0000 - tn: 19406.0000 - fn: 2441.0000 - accuracy: 0.9132 - precision: 0.9416 - recall: 0.8806 - auc: 0.9613 - prc: 0.9710 - val_loss: 0.1556 - val_tp: 58.0000 - val_fp: 587.0000 - val_tn: 44913.0000 - val_fn: 11.0000 - val_accuracy: 0.9869 - val_precision: 0.0899 - val_recall: 0.8406 - val_auc: 0.9713 - val_prc: 0.6760 Epoch 16/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.2228 - tp: 18079.0000 - fp: 1057.0000 - tn: 19426.0000 - fn: 2398.0000 - accuracy: 0.9156 - precision: 0.9448 - recall: 0.8829 - auc: 0.9634 - prc: 0.9726 - val_loss: 0.1474 - val_tp: 58.0000 - val_fp: 592.0000 - val_tn: 44908.0000 - val_fn: 11.0000 - val_accuracy: 0.9868 - val_precision: 0.0892 - val_recall: 0.8406 - val_auc: 0.9711 - val_prc: 0.6768 Epoch 17/1000 20/20 [==============================] - 1s 32ms/step - loss: 0.2160 - tp: 18053.0000 - fp: 1023.0000 - tn: 19497.0000 - fn: 2387.0000 - accuracy: 0.9167 - precision: 0.9464 - recall: 0.8832 - auc: 0.9657 - prc: 0.9740 - val_loss: 0.1401 - val_tp: 59.0000 - val_fp: 591.0000 - val_tn: 44909.0000 - val_fn: 10.0000 - val_accuracy: 0.9868 - val_precision: 0.0908 - val_recall: 0.8551 - val_auc: 0.9711 - val_prc: 0.6801 Epoch 18/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.2113 - tp: 18152.0000 - fp: 986.0000 - tn: 19555.0000 - fn: 2267.0000 - accuracy: 0.9206 - precision: 0.9485 - recall: 0.8890 - auc: 0.9676 - prc: 0.9752 - val_loss: 0.1336 - val_tp: 59.0000 - val_fp: 595.0000 - val_tn: 44905.0000 - val_fn: 10.0000 - val_accuracy: 0.9867 - val_precision: 0.0902 - val_recall: 0.8551 - val_auc: 0.9709 - val_prc: 0.6806 Epoch 19/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.2065 - tp: 18259.0000 - fp: 955.0000 - tn: 19468.0000 - fn: 2278.0000 - accuracy: 0.9211 - precision: 0.9503 - recall: 0.8891 - auc: 0.9690 - prc: 0.9763 - val_loss: 0.1281 - val_tp: 59.0000 - val_fp: 600.0000 - val_tn: 44900.0000 - val_fn: 10.0000 - val_accuracy: 0.9866 - val_precision: 0.0895 - val_recall: 0.8551 - val_auc: 0.9701 - val_prc: 0.6708 Epoch 20/1000 20/20 [==============================] - 1s 26ms/step - loss: 0.2017 - tp: 18234.0000 - fp: 884.0000 - tn: 19611.0000 - fn: 2231.0000 - accuracy: 0.9240 - precision: 0.9538 - recall: 0.8910 - auc: 0.9705 - prc: 0.9770 - val_loss: 0.1235 - val_tp: 59.0000 - val_fp: 610.0000 - val_tn: 44890.0000 - val_fn: 10.0000 - val_accuracy: 0.9864 - val_precision: 0.0882 - val_recall: 0.8551 - val_auc: 0.9696 - val_prc: 0.6711 Epoch 21/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.1950 - tp: 18137.0000 - fp: 831.0000 - tn: 19777.0000 - fn: 2215.0000 - accuracy: 0.9256 - precision: 0.9562 - recall: 0.8912 - auc: 0.9726 - prc: 0.9783 - val_loss: 0.1188 - val_tp: 59.0000 - val_fp: 614.0000 - val_tn: 44886.0000 - val_fn: 10.0000 - val_accuracy: 0.9863 - val_precision: 0.0877 - val_recall: 0.8551 - val_auc: 0.9693 - val_prc: 0.6716 Epoch 22/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.1923 - tp: 18425.0000 - fp: 830.0000 - tn: 19529.0000 - fn: 2176.0000 - accuracy: 0.9266 - precision: 0.9569 - recall: 0.8944 - auc: 0.9733 - prc: 0.9794 - val_loss: 0.1152 - val_tp: 59.0000 - val_fp: 622.0000 - val_tn: 44878.0000 - val_fn: 10.0000 - val_accuracy: 0.9861 - val_precision: 0.0866 - val_recall: 0.8551 - val_auc: 0.9692 - val_prc: 0.6720 Epoch 23/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.1886 - tp: 18374.0000 - fp: 806.0000 - tn: 19662.0000 - fn: 2118.0000 - accuracy: 0.9286 - precision: 0.9580 - recall: 0.8966 - auc: 0.9745 - prc: 0.9799 - val_loss: 0.1117 - val_tp: 59.0000 - val_fp: 609.0000 - val_tn: 44891.0000 - val_fn: 10.0000 - val_accuracy: 0.9864 - val_precision: 0.0883 - val_recall: 0.8551 - val_auc: 0.9687 - val_prc: 0.6724 Epoch 24/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.1844 - tp: 18359.0000 - fp: 784.0000 - tn: 19701.0000 - fn: 2116.0000 - accuracy: 0.9292 - precision: 0.9590 - recall: 0.8967 - auc: 0.9760 - prc: 0.9808 - val_loss: 0.1085 - val_tp: 59.0000 - val_fp: 615.0000 - val_tn: 44885.0000 - val_fn: 10.0000 - val_accuracy: 0.9863 - val_precision: 0.0875 - val_recall: 0.8551 - val_auc: 0.9681 - val_prc: 0.6725 Epoch 25/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.1838 - tp: 18334.0000 - fp: 835.0000 - tn: 19677.0000 - fn: 2114.0000 - accuracy: 0.9280 - precision: 0.9564 - recall: 0.8966 - auc: 0.9760 - prc: 0.9808 - val_loss: 0.1054 - val_tp: 59.0000 - val_fp: 605.0000 - val_tn: 44895.0000 - val_fn: 10.0000 - val_accuracy: 0.9865 - val_precision: 0.0889 - val_recall: 0.8551 - val_auc: 0.9672 - val_prc: 0.6727 Epoch 26/1000 20/20 [==============================] - 1s 27ms/step - loss: 0.1815 - tp: 18355.0000 - fp: 786.0000 - tn: 19667.0000 - fn: 2152.0000 - accuracy: 0.9283 - precision: 0.9589 - recall: 0.8951 - auc: 0.9772 - prc: 0.9816 - val_loss: 0.1022 - val_tp: 59.0000 - val_fp: 594.0000 - val_tn: 44906.0000 - val_fn: 10.0000 - val_accuracy: 0.9867 - val_precision: 0.0904 - val_recall: 0.8551 - val_auc: 0.9676 - val_prc: 0.6633 Epoch 27/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.1777 - tp: 18485.0000 - fp: 719.0000 - tn: 19678.0000 - fn: 2078.0000 - accuracy: 0.9317 - precision: 0.9626 - recall: 0.8989 - auc: 0.9780 - prc: 0.9824 - val_loss: 0.0995 - val_tp: 59.0000 - val_fp: 581.0000 - val_tn: 44919.0000 - val_fn: 10.0000 - val_accuracy: 0.9870 - val_precision: 0.0922 - val_recall: 0.8551 - val_auc: 0.9661 - val_prc: 0.6658 Epoch 28/1000 20/20 [==============================] - ETA: 0s - loss: 0.1745 - tp: 18219.0000 - fp: 729.0000 - tn: 19987.0000 - fn: 2025.0000 - accuracy: 0.9328 - precision: 0.9615 - recall: 0.9000 - auc: 0.9789 - prc: 0.9825Restoring model weights from the end of the best epoch: 18. 20/20 [==============================] - 1s 27ms/step - loss: 0.1745 - tp: 18219.0000 - fp: 729.0000 - tn: 19987.0000 - fn: 2025.0000 - accuracy: 0.9328 - precision: 0.9615 - recall: 0.9000 - auc: 0.9789 - prc: 0.9825 - val_loss: 0.0967 - val_tp: 59.0000 - val_fp: 569.0000 - val_tn: 44931.0000 - val_fn: 10.0000 - val_accuracy: 0.9873 - val_precision: 0.0939 - val_recall: 0.8551 - val_auc: 0.9667 - val_prc: 0.6659 Epoch 28: early stopping
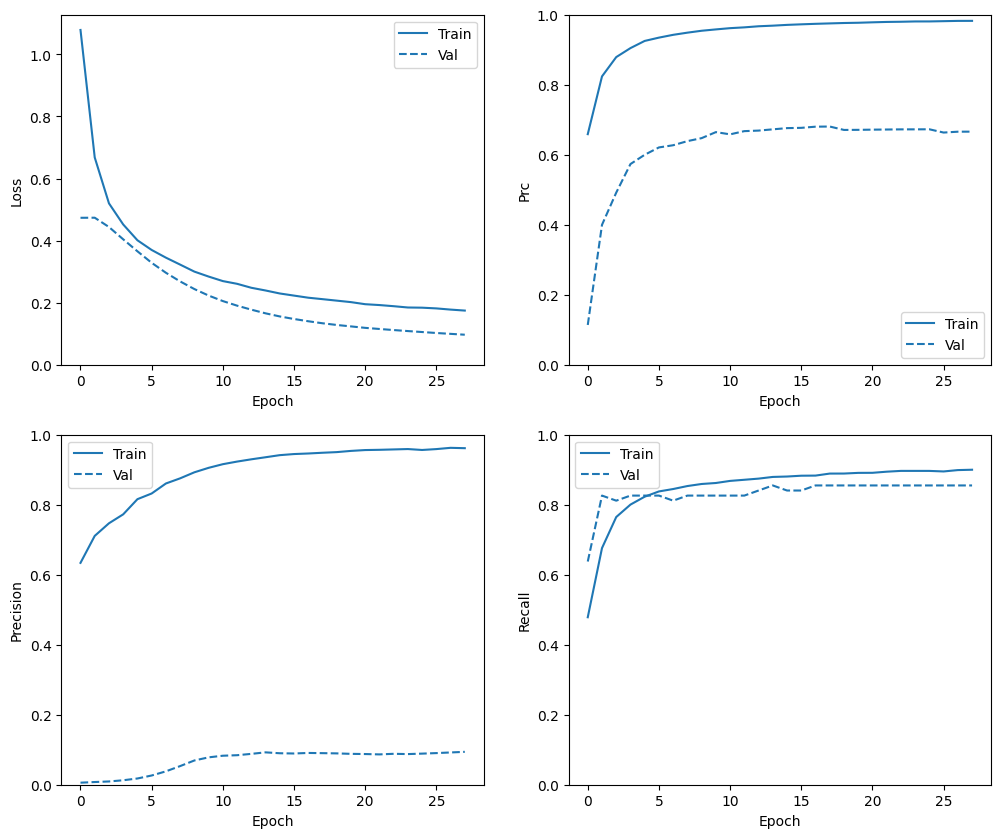
トレーニング履歴を再確認する
plot_metrics(resampled_history)
メトリクスを評価する
train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)
90/90 [==============================] - 0s 1ms/step 28/28 [==============================] - 0s 1ms/step
resampled_results = resampled_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_resampled)
loss : 0.13150924444198608 tp : 91.0 fp : 728.0 tn : 56133.0 fn : 10.0 accuracy : 0.9870439767837524 precision : 0.1111111119389534 recall : 0.9009901285171509 auc : 0.9749700427055359 prc : 0.7914559841156006 Legitimate Transactions Detected (True Negatives): 56133 Legitimate Transactions Incorrectly Detected (False Positives): 728 Fraudulent Transactions Missed (False Negatives): 10 Fraudulent Transactions Detected (True Positives): 91 Total Fraudulent Transactions: 101

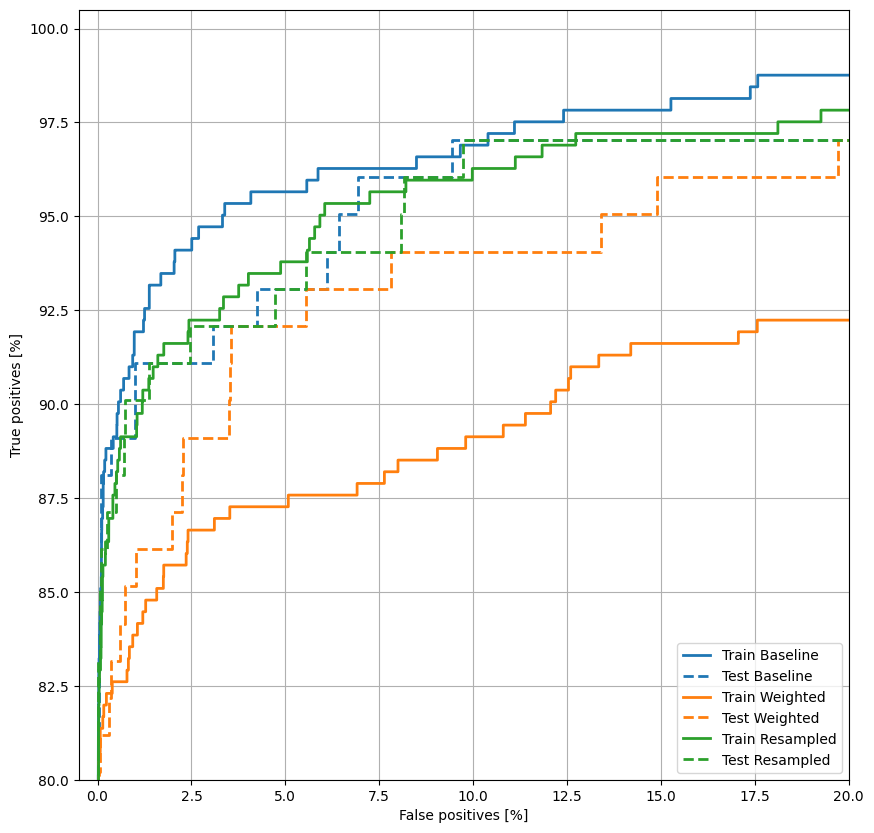
ROC をプロットする
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
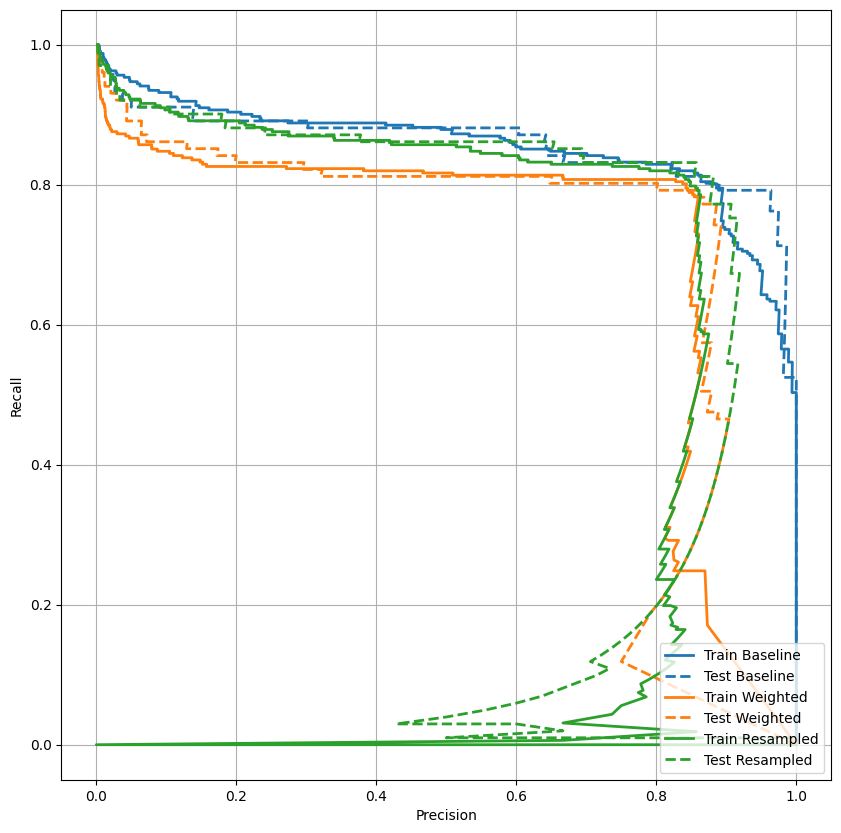
AUPRC をプロットする
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
このチュートリアルを問題に応用する
不均衡データの分類は、学習できるサンプルが非常に少ないため、本質的に難しい作業です。常に最初にデータから始め、できるだけ多くのサンプルを収集するよう最善を尽くし、モデルがマイノリティクラスを最大限に活用するのに適切な特徴はどれかを十分に検討する必要があります。ある時点では、モデルがなかなか改善せず望む結果をうまく生成できないことがあるので、問題のコンテキストおよび異なるタイプのエラー間のトレードオフを考慮することが重要です。
