 TensorFlow.org에서 보기 TensorFlow.org에서 보기
|
 구글 코랩(Colab)에서 실행하기 구글 코랩(Colab)에서 실행하기
|
 깃허브(GitHub) 소스 보기 깃허브(GitHub) 소스 보기
|
 Download notebook Download notebook
|
회귀(regression)는 가격이나 확률 같이 연속된 출력 값을 예측하는 것이 목적입니다. 이와는 달리 분류(classification)는 여러개의 클래스 중 하나의 클래스를 선택하는 것이 목적입니다(예를 들어, 사진에 사과 또는 오렌지가 포함되어 있을 때 어떤 과일인지 인식하는 것).
이 노트북은 Auto MPG 데이터셋을 사용하여 1970년대 후반과 1980년대 초반의 자동차 연비를 예측하는 모델을 만듭니다. 이 기간에 출시된 자동차 정보를 모델에 제공하겠습니다. 이 정보에는 실린더 수, 배기량, 마력(horsepower), 공차 중량 같은 속성이 포함됩니다.
이 예제는 tf.keras API를 사용합니다. 자세한 내용은 케라스 가이드를 참고하세요.
# 산점도 행렬을 그리기 위해 seaborn 패키지를 설치합니다pip install -q seaborn
import pathlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
2.3.0
Auto MPG 데이터셋
이 데이터셋은 UCI 머신 러닝 저장소에서 다운로드할 수 있습니다.
데이터 구하기
먼저 데이터셋을 다운로드합니다.
dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path
Downloading data from http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data 32768/30286 [================================] - 0s 4us/step '/home/kbuilder/.keras/datasets/auto-mpg.data'
판다스를 사용하여 데이터를 읽습니다.
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
데이터 정제하기
이 데이터셋은 일부 데이터가 누락되어 있습니다.
dataset.isna().sum()
MPG 0 Cylinders 0 Displacement 0 Horsepower 6 Weight 0 Acceleration 0 Model Year 0 Origin 0 dtype: int64
문제를 간단하게 만들기 위해서 누락된 행을 삭제하겠습니다.
dataset = dataset.dropna()
"Origin" 열은 수치형이 아니고 범주형이므로 원-핫 인코딩(one-hot encoding)으로 변환하겠습니다:
origin = dataset.pop('Origin')
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()
데이터셋을 훈련 세트와 테스트 세트로 분할하기
이제 데이터를 훈련 세트와 테스트 세트로 분할합니다.
테스트 세트는 모델을 최종적으로 평가할 때 사용합니다.
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)
데이터 조사하기
훈련 세트에서 몇 개의 열을 선택해 산점도 행렬을 만들어 살펴 보겠습니다.
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
<seaborn.axisgrid.PairGrid at 0x7fb7b9461e48>
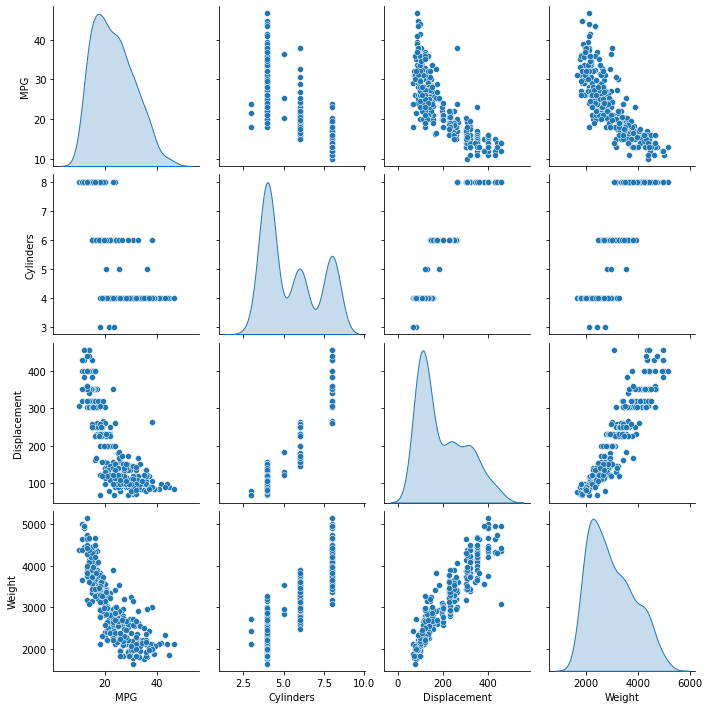
전반적인 통계도 확인해 보죠:
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
특성과 레이블 분리하기
특성에서 타깃 값 또는 "레이블"을 분리합니다. 이 레이블을 예측하기 위해 모델을 훈련시킬 것입니다.
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
데이터 정규화
위 train_stats 통계를 다시 살펴보고 각 특성의 범위가 얼마나 다른지 확인해 보죠.
특성의 스케일과 범위가 다르면 정규화(normalization)하는 것이 권장됩니다. 특성을 정규화하지 않아도 모델이 수렴할 수 있지만, 훈련시키기 어렵고 입력 단위에 의존적인 모델이 만들어집니다.
노트: 의도적으로 훈련 세트만 사용하여 통계치를 생성했습니다. 이 통계는 테스트 세트를 정규화할 때에도 사용됩니다. 이는 테스트 세트를 모델이 훈련에 사용했던 것과 동일한 분포로 투영하기 위해서입니다.
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
정규화된 데이터를 사용하여 모델을 훈련합니다.
주의: 여기에서 입력 데이터를 정규화하기 위해 사용한 통계치(평균과 표준편차)는 원-핫 인코딩과 마찬가지로 모델에 주입되는 모든 데이터에 적용되어야 합니다. 여기에는 테스트 세트는 물론 모델이 실전에 투입되어 얻은 라이브 데이터도 포함됩니다.
모델
모델 만들기
모델을 구성해 보죠. 여기에서는 두 개의 완전 연결(densely connected) 은닉층으로 Sequential 모델을 만들겠습니다. 출력 층은 하나의 연속적인 값을 반환합니다. 나중에 두 번째 모델을 만들기 쉽도록 build_model 함수로 모델 구성 단계를 감싸겠습니다.
def build_model():
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae', 'mse'])
return model
model = build_model()
모델 확인
.summary 메서드를 사용해 모델에 대한 간단한 정보를 출력합니다.
model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 64) 640 _________________________________________________________________ dense_1 (Dense) (None, 64) 4160 _________________________________________________________________ dense_2 (Dense) (None, 1) 65 ================================================================= Total params: 4,865 Trainable params: 4,865 Non-trainable params: 0 _________________________________________________________________
모델을 한번 실행해 보죠. 훈련 세트에서 10 샘플을 하나의 배치로 만들어 model.predict 메서드를 호출해 보겠습니다.
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result
array([[0.6247854 ],
[0.33749408],
[0.20907241],
[0.35342616],
[0.91920185],
[0.19368024],
[1.0528278 ],
[0.8886562 ],
[0.40983236],
[1.1161143 ]], dtype=float32)
제대로 작동하는 것 같네요. 결괏값의 크기와 타입이 기대했던 대로입니다.
모델 훈련
이 모델을 1,000번의 에포크(epoch) 동안 훈련합니다. 훈련 정확도와 검증 정확도는 history 객체에 기록됩니다.
# 에포크가 끝날 때마다 점(.)을 출력해 훈련 진행 과정을 표시합니다
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
EPOCHS = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[PrintDot()])
.................................................................................................... .................................................................................................... .................................................................................................... .................................................................................................... .................................................................................................... .................................................................................................... .................................................................................................... .................................................................................................... .................................................................................................... ....................................................................................................
history 객체에 저장된 통계치를 사용해 모델의 훈련 과정을 시각화해 보죠.
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
import matplotlib.pyplot as plt
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure(figsize=(8,12))
plt.subplot(2,1,1)
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [MPG]')
plt.plot(hist['epoch'], hist['mae'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mae'],
label = 'Val Error')
plt.ylim([0,5])
plt.legend()
plt.subplot(2,1,2)
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mse'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mse'],
label = 'Val Error')
plt.ylim([0,20])
plt.legend()
plt.show()
plot_history(history)
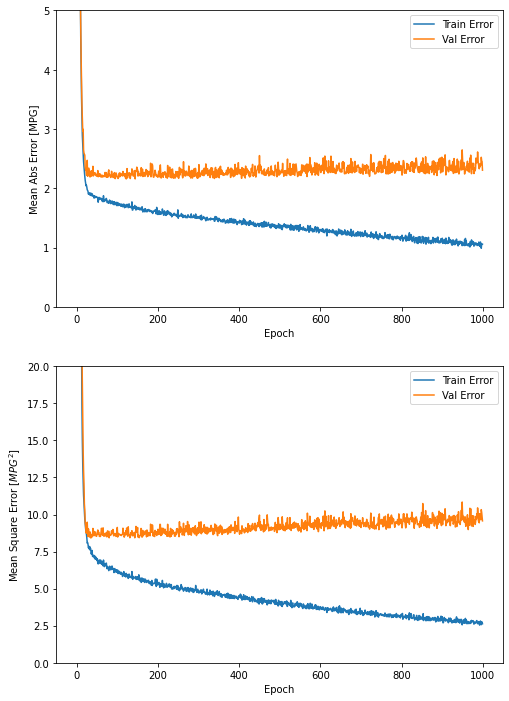
이 그래프를 보면 수 백번 에포크를 진행한 이후에는 모델이 거의 향상되지 않는 것 같습니다. model.fit 메서드를 수정하여 검증 점수가 향상되지 않으면 자동으로 훈련을 멈추도록 만들어 보죠. 에포크마다 훈련 상태를 점검하기 위해 EarlyStopping 콜백(callback)을 사용하겠습니다. 지정된 에포크 횟수 동안 성능 향상이 없으면 자동으로 훈련이 멈춥니다.
이 콜백에 대해 더 자세한 내용은 여기를 참고하세요.
model = build_model()
# patience 매개변수는 성능 향상을 체크할 에포크 횟수입니다
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)
...........................................................
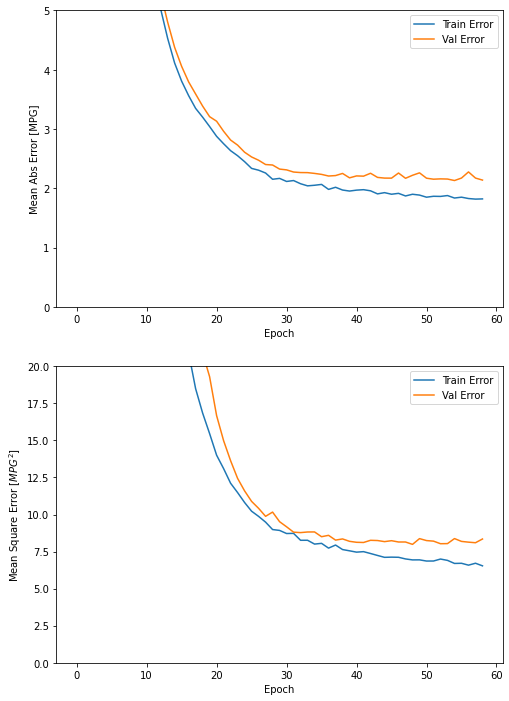
이 그래프를 보면 검증 세트의 평균 오차가 약 +/- 2 MPG입니다. 좋은 결과인가요? 이에 대한 평가는 여러분에게 맡기겠습니다.
모델을 훈련할 때 사용하지 않았던 테스트 세트에서 모델의 성능을 확인해 보죠. 이를 통해 모델이 실전에 투입되었을 때 모델의 성능을 짐작할 수 있습니다:
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=2)
print("테스트 세트의 평균 절대 오차: {:5.2f} MPG".format(mae))
3/3 - 0s - loss: 6.1271 - mae: 1.9506 - mse: 6.1271 테스트 세트의 평균 절대 오차: 1.95 MPG
예측
마지막으로 테스트 세트에 있는 샘플을 사용해 MPG 값을 예측해 보겠습니다:
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
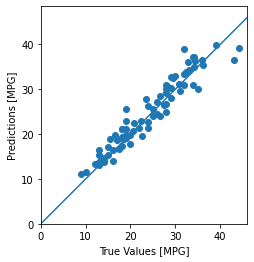
모델이 꽤 잘 예측한 것 같습니다. 오차의 분포를 살펴 보죠.
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
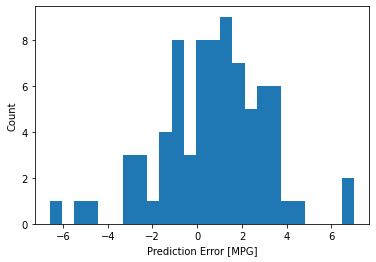
가우시안 분포가 아니지만 아마도 훈련 샘플의 수가 매우 작기 때문일 것입니다.
결론
이 노트북은 회귀 문제를 위한 기법을 소개합니다.
- 평균 제곱 오차(MSE)는 회귀 문제에서 자주 사용하는 손실 함수입니다(분류 문제에서 사용하는 손실 함수와 다릅니다).
- 비슷하게 회귀에서 사용되는 평가 지표도 분류와 다릅니다. 많이 사용하는 회귀 지표는 평균 절댓값 오차(MAE)입니다.
- 수치 입력 데이터의 특성이 여러 가지 범위를 가질 때 동일한 범위가 되도록 각 특성의 스케일을 독립적으로 조정해야 합니다.
- 훈련 데이터가 많지 않다면 과대적합을 피하기 위해 은닉층의 개수가 적은 소규모 네트워크를 선택하는 방법이 좋습니다.
- 조기 종료(Early stopping)은 과대적합을 방지하기 위한 좋은 방법입니다.
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
