 Veja no TensorFlow.org Veja no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Este notebook demonstra como treinar um Variational Autoencoder (VAE) ( 1 , 2 ) no conjunto de dados MNIST. Um VAE é uma tomada probabilística do autoencoder, um modelo que pega dados de entrada de alta dimensão e os comprime em uma representação menor. Ao contrário de um autoencoder tradicional, que mapeia a entrada em um vetor latente, um VAE mapeia os dados de entrada nos parâmetros de uma distribuição de probabilidade, como a média e a variância de uma Gaussiana. Essa abordagem produz um espaço latente contínuo e estruturado, útil para a geração de imagens.

Configurar
pip install tensorflow-probability# to generate gifspip install imageiopip install git+https://github.com/tensorflow/docs
from IPython import display
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import PIL
import tensorflow as tf
import tensorflow_probability as tfp
import time
Carregar o conjunto de dados MNIST
Cada imagem MNIST é originalmente um vetor de 784 inteiros, cada um dos quais está entre 0-255 e representa a intensidade de um pixel. Modele cada pixel com uma distribuição de Bernoulli em nosso modelo e binarize estaticamente o conjunto de dados.
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
def preprocess_images(images):
images = images.reshape((images.shape[0], 28, 28, 1)) / 255.
return np.where(images > .5, 1.0, 0.0).astype('float32')
train_images = preprocess_images(train_images)
test_images = preprocess_images(test_images)
train_size = 60000
batch_size = 32
test_size = 10000
Use tf.data para agrupar e embaralhar os dados
train_dataset = (tf.data.Dataset.from_tensor_slices(train_images)
.shuffle(train_size).batch(batch_size))
test_dataset = (tf.data.Dataset.from_tensor_slices(test_images)
.shuffle(test_size).batch(batch_size))
Defina as redes de codificador e decodificador com tf.keras.Sequential
Neste exemplo de VAE, use dois pequenos ConvNets para as redes do codificador e do decodificador. Na literatura, essas redes também são chamadas de modelos de inferência/reconhecimento e generativos, respectivamente. Use tf.keras.Sequential para simplificar a implementação. Deixe \(x\) e \(z\) denotar a observação e a variável latente, respectivamente, nas descrições a seguir.
Rede do codificador
Isso define a distribuição posterior aproximada \(q(z|x)\), que recebe como entrada uma observação e gera um conjunto de parâmetros para especificar a distribuição condicional da representação latente \(z\). Neste exemplo, simplesmente modele a distribuição como uma gaussiana diagonal e a rede gera os parâmetros de média e variância logarítmica de uma gaussiana fatorada. Saída log-variância em vez da variância diretamente para estabilidade numérica.
Rede do decodificador
Isso define a distribuição condicional da observação \(p(x|z)\), que recebe uma amostra latente \(z\) como entrada e emite os parâmetros para uma distribuição condicional da observação. Modele a distribuição latente antes \(p(z)\) como uma unidade Gaussiana.
Truque de reparametrização
Para gerar uma amostra \(z\) para o decodificador durante o treinamento, você pode amostrar a partir da distribuição latente definida pelos parâmetros emitidos pelo codificador, dada uma observação de entrada \(x\). No entanto, essa operação de amostragem cria um gargalo porque a retropropagação não pode fluir por meio de um nó aleatório.
Para resolver isso, use um truque de reparametrização. Em nosso exemplo, você aproxima \(z\) usando os parâmetros do decodificador e outro parâmetro \(\epsilon\) da seguinte forma:
\[z = \mu + \sigma \odot \epsilon\]
onde \(\mu\) e \(\sigma\) representam a média e o desvio padrão de uma distribuição gaussiana, respectivamente. Eles podem ser derivados da saída do decodificador. O \(\epsilon\) pode ser pensado como um ruído aleatório usado para manter a estocasticidade do \(z\). Gere \(\epsilon\) a partir de uma distribuição normal padrão.
A variável latente \(z\) agora é gerada por uma função de \(\mu\), \(\sigma\) e \(\epsilon\), o que permitiria que o modelo retropropagasse gradientes no codificador através \(\mu\) e \(\sigma\) respectivamente, mantendo a estocasticidade através de \(\epsilon\).
Arquitetura de rede
Para a rede do codificador, use duas camadas convolucionais seguidas por uma camada totalmente conectada. Na rede do decodificador, espelhe essa arquitetura usando uma camada totalmente conectada seguida por três camadas de transposição de convolução (também conhecidas como camadas deconvolucionais em alguns contextos). Observe que é uma prática comum evitar o uso de normalização de lote ao treinar VAEs, pois a estocasticidade adicional devido ao uso de minilotes pode agravar a instabilidade além da estocasticidade da amostragem.
class CVAE(tf.keras.Model):
"""Convolutional variational autoencoder."""
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=2, padding='same',
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=2, padding='same',
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=1, padding='same'),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
Defina a função de perda e o otimizador
Os VAEs treinam maximizando o limite inferior de evidência (ELBO) na probabilidade logarítmica marginal:
\[\log p(x) \ge \text{ELBO} = \mathbb{E}_{q(z|x)}\left[\log \frac{p(x, z)}{q(z|x)}\right].\]
Na prática, otimize a estimativa de Monte Carlo de amostra única dessa expectativa:
\[\log p(x| z) + \log p(z) - \log q(z|x),\]
onde \(z\) é amostrado de \(q(z|x)\).
optimizer = tf.keras.optimizers.Adam(1e-4)
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
def compute_loss(model, x):
mean, logvar = model.encode(x)
z = model.reparameterize(mean, logvar)
x_logit = model.decode(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
@tf.function
def train_step(model, x, optimizer):
"""Executes one training step and returns the loss.
This function computes the loss and gradients, and uses the latter to
update the model's parameters.
"""
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
Treinamento
- Comece iterando sobre o conjunto de dados
- Durante cada iteração, passe a imagem para o codificador para obter um conjunto de parâmetros de média e log-variância do \(q(z|x)\)posterior aproximado29
- em seguida, aplique o truque de reparametrização para amostrar de \(q(z|x)\)
- Finalmente, passe as amostras reparametrizadas para o decodificador para obter os logits da distribuição generativa \(p(x|z)\)
- Nota: Como você usa o conjunto de dados carregado por keras com 60k datapoints no conjunto de treinamento e 10k datapoints no conjunto de teste, nosso ELBO resultante no conjunto de teste é um pouco maior do que os resultados relatados na literatura que usa binarização dinâmica do MNIST de Larochelle.
Gerando imagens
- Após o treinamento, é hora de gerar algumas imagens
- Comece amostrando um conjunto de vetores latentes da distribuição anterior gaussiana unitária \(p(z)\)
- O gerador irá então converter a amostra latente \(z\) em logits da observação, dando uma distribuição \(p(x|z)\)
- Aqui, trace as probabilidades das distribuições de Bernoulli
epochs = 10
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)
def generate_and_save_images(model, epoch, test_sample):
mean, logvar = model.encode(test_sample)
z = model.reparameterize(mean, logvar)
predictions = model.sample(z)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# tight_layout minimizes the overlap between 2 sub-plots
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
test_sample = test_batch[0:num_examples_to_generate, :, :, :]
generate_and_save_images(model, 0, test_sample)
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
train_step(model, train_x, optimizer)
end_time = time.time()
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
display.clear_output(wait=False)
print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
.format(epoch, elbo, end_time - start_time))
generate_and_save_images(model, epoch, test_sample)
Epoch: 10, Test set ELBO: -156.4964141845703, time elapse for current epoch: 4.854437351226807

Exibir uma imagem gerada da última época de treinamento
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
plt.imshow(display_image(epoch))
plt.axis('off') # Display images
(-0.5, 287.5, 287.5, -0.5)
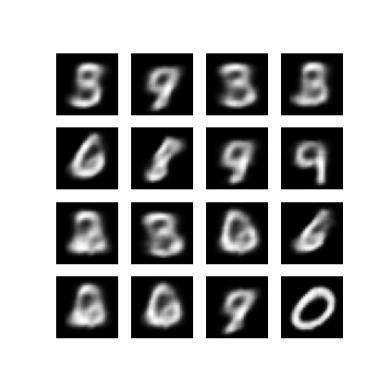
Exiba um GIF animado de todas as imagens salvas
anim_file = 'cvae.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)

Exibir uma variedade 2D de dígitos do espaço latente
A execução do código abaixo mostrará uma distribuição contínua das diferentes classes de dígitos, com cada dígito se transformando em outro no espaço latente 2D. Use a probabilidade do TensorFlow para gerar uma distribuição normal padrão para o espaço latente.
def plot_latent_images(model, n, digit_size=28):
"""Plots n x n digit images decoded from the latent space."""
norm = tfp.distributions.Normal(0, 1)
grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
image_width = digit_size*n
image_height = image_width
image = np.zeros((image_height, image_width))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z = np.array([[xi, yi]])
x_decoded = model.sample(z)
digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
image[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit.numpy()
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='Greys_r')
plt.axis('Off')
plt.show()
plot_latent_images(model, 20)

Próximos passos
Este tutorial demonstrou como implementar um autoencoder variacional convolucional usando o TensorFlow.
Como próxima etapa, você pode tentar melhorar a saída do modelo aumentando o tamanho da rede. Por exemplo, você pode tentar definir os parâmetros de filter para cada uma das camadas Conv2D e Conv2DTranspose para 512. Observe que, para gerar o gráfico de imagem latente 2D final, você precisaria manter latent_dim como 2. Além disso, o tempo de treinamento aumentaria medida que o tamanho da rede aumenta.
Você também pode tentar implementar um VAE usando um conjunto de dados diferente, como CIFAR-10.
Os VAEs podem ser implementados em vários estilos diferentes e de complexidade variável. Você pode encontrar implementações adicionais nas seguintes fontes:
- AutoEncoder Variacional (keras.io)
- Exemplo de VAE do guia "Escrevendo camadas e modelos personalizados" (tensorflow.org)
- Camadas Probabilísticas TFP: Codificador Automático Variacional
Se você quiser saber mais sobre os detalhes dos VAEs, consulte An Introduction to Variational Autoencoders .
