 Veja no TensorFlow.org Veja no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Este tutorial apresenta autoencoders com três exemplos: o básico, remoção de ruído de imagem e detecção de anomalias.
Um autoencoder é um tipo especial de rede neural treinada para copiar sua entrada para sua saída. Por exemplo, dada uma imagem de um dígito manuscrito, um autoencoder primeiro codifica a imagem em uma representação latente de menor dimensão, depois decodifica a representação latente de volta para uma imagem. Um autoencoder aprende a compactar os dados enquanto minimiza o erro de reconstrução.
Para saber mais sobre autoencoders, leia o capítulo 14 do Deep Learning de Ian Goodfellow, Yoshua Bengio e Aaron Courville.
Importar TensorFlow e outras bibliotecas
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
Carregar o conjunto de dados
Para começar, você treinará o autoencoder básico usando o conjunto de dados Fashion MNIST. Cada imagem neste conjunto de dados tem 28 x 28 pixels.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print (x_train.shape)
print (x_test.shape)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz 32768/29515 [=================================] - 0s 0us/step 40960/29515 [=========================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz 26427392/26421880 [==============================] - 0s 0us/step 26435584/26421880 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz 16384/5148 [===============================================================================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz 4423680/4422102 [==============================] - 0s 0us/step 4431872/4422102 [==============================] - 0s 0us/step (60000, 28, 28) (10000, 28, 28)
Primeiro exemplo: codificador automático básico

Defina um autoencoder com duas camadas Dense: um encoder , que comprime as imagens em um vetor latente de 64 dimensões, e um decoder , que reconstrói a imagem original a partir do espaço latente.
Para definir seu modelo, use a API Keras Model Subclassing .
latent_dim = 64
class Autoencoder(Model):
def __init__(self, latent_dim):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential([
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Dense(784, activation='sigmoid'),
layers.Reshape((28, 28))
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Autoencoder(latent_dim)
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
Treine o modelo usando x_train como entrada e destino. O encoder aprenderá a compactar o conjunto de dados de 784 dimensões para o espaço latente e o decoder aprenderá a reconstruir as imagens originais. .
autoencoder.fit(x_train, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test, x_test))
Epoch 1/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0243 - val_loss: 0.0140 Epoch 2/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0116 - val_loss: 0.0106 Epoch 3/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0100 - val_loss: 0.0098 Epoch 4/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0094 - val_loss: 0.0094 Epoch 5/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0092 - val_loss: 0.0092 Epoch 6/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0091 Epoch 7/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0090 Epoch 8/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0089 - val_loss: 0.0090 Epoch 9/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 Epoch 10/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 <keras.callbacks.History at 0x7ff1d35df550>
Agora que o modelo está treinado, vamos testá-lo codificando e decodificando imagens do conjunto de teste.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i])
plt.title("original")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i])
plt.title("reconstructed")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

Segundo exemplo: remoção de ruído de imagem

Um autoencoder também pode ser treinado para remover ruídos de imagens. Na seção a seguir, você criará uma versão com ruído do conjunto de dados Fashion MNIST aplicando ruído aleatório a cada imagem. Você então treinará um autoencoder usando a imagem com ruído como entrada e a imagem original como destino.
Vamos reimportar o conjunto de dados para omitir as modificações feitas anteriormente.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
(60000, 28, 28, 1)
Adicionando ruído aleatório às imagens
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
Plote as imagens barulhentas.
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()

Definir um autoencoder convolucional
Neste exemplo, você treinará um autoencoder convolucional usando camadas Conv2D no encoder e camadas Conv2DTranspose no decoder .
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
Epoch 1/10 1875/1875 [==============================] - 8s 3ms/step - loss: 0.0169 - val_loss: 0.0107 Epoch 2/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0095 - val_loss: 0.0086 Epoch 3/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0082 - val_loss: 0.0080 Epoch 4/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0078 - val_loss: 0.0077 Epoch 5/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0076 - val_loss: 0.0075 Epoch 6/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0074 - val_loss: 0.0074 Epoch 7/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0073 - val_loss: 0.0073 Epoch 8/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0072 - val_loss: 0.0072 Epoch 9/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0071 - val_loss: 0.0071 Epoch 10/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0070 - val_loss: 0.0071 <keras.callbacks.History at 0x7ff1c45a31d0>
Vamos dar uma olhada em um resumo do codificador. Observe como as imagens são reduzidas de 28x28 para 7x7.
autoencoder.encoder.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 14, 14, 16) 160
conv2d_1 (Conv2D) (None, 7, 7, 8) 1160
=================================================================
Total params: 1,320
Trainable params: 1,320
Non-trainable params: 0
_________________________________________________________________
O decodificador faz o upsample das imagens de 7x7 para 28x28.
autoencoder.decoder.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_transpose (Conv2DTra (None, 14, 14, 8) 584
nspose)
conv2d_transpose_1 (Conv2DT (None, 28, 28, 16) 1168
ranspose)
conv2d_2 (Conv2D) (None, 28, 28, 1) 145
=================================================================
Total params: 1,897
Trainable params: 1,897
Non-trainable params: 0
_________________________________________________________________
Plotar as imagens com ruído e as imagens sem ruído produzidas pelo autoencoder.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original + noise
ax = plt.subplot(2, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
bx = plt.subplot(2, n, i + n + 1)
plt.title("reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()

Terceiro exemplo: detecção de anomalias
Visão geral
Neste exemplo, você treinará um autoencoder para detectar anomalias no conjunto de dados ECG5000 . Este conjunto de dados contém 5.000 eletrocardiogramas , cada um com 140 pontos de dados. Você usará uma versão simplificada do conjunto de dados, onde cada exemplo foi rotulado como 0 (correspondente a um ritmo anormal) ou 1 (correspondente a um ritmo normal). Você está interessado em identificar os ritmos anormais.
Como você detectará anomalias usando um autoencoder? Lembre-se de que um autoencoder é treinado para minimizar o erro de reconstrução. Você treinará um autoencoder apenas nos ritmos normais, depois o usará para reconstruir todos os dados. Nossa hipótese é que os ritmos anormais terão maior erro de reconstrução. Você então classificará um ritmo como uma anomalia se o erro de reconstrução ultrapassar um limite fixo.
Carregar dados de ECG
O conjunto de dados que você usará é baseado em um de timeseriesclassification.com .
# Download the dataset
dataframe = pd.read_csv('http://storage.googleapis.com/download.tensorflow.org/data/ecg.csv', header=None)
raw_data = dataframe.values
dataframe.head()
# The last element contains the labels
labels = raw_data[:, -1]
# The other data points are the electrocadriogram data
data = raw_data[:, 0:-1]
train_data, test_data, train_labels, test_labels = train_test_split(
data, labels, test_size=0.2, random_state=21
)
Normalize os dados para [0,1] .
min_val = tf.reduce_min(train_data)
max_val = tf.reduce_max(train_data)
train_data = (train_data - min_val) / (max_val - min_val)
test_data = (test_data - min_val) / (max_val - min_val)
train_data = tf.cast(train_data, tf.float32)
test_data = tf.cast(test_data, tf.float32)
Você treinará o autoencoder usando apenas os ritmos normais, que são rotulados neste conjunto de dados como 1 . Separe os ritmos normais dos ritmos anormais.
train_labels = train_labels.astype(bool)
test_labels = test_labels.astype(bool)
normal_train_data = train_data[train_labels]
normal_test_data = test_data[test_labels]
anomalous_train_data = train_data[~train_labels]
anomalous_test_data = test_data[~test_labels]
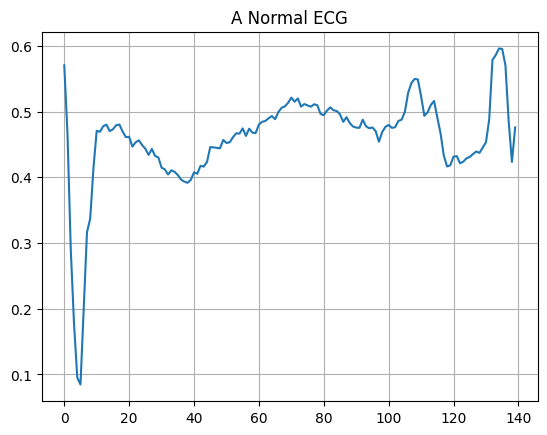
Plote um ECG normal.
plt.grid()
plt.plot(np.arange(140), normal_train_data[0])
plt.title("A Normal ECG")
plt.show()
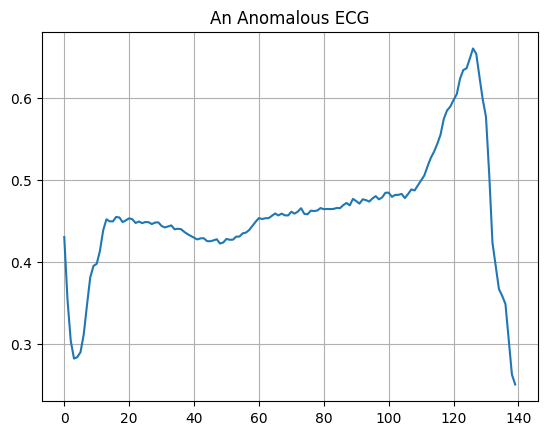
Plote um ECG anômalo.
plt.grid()
plt.plot(np.arange(140), anomalous_train_data[0])
plt.title("An Anomalous ECG")
plt.show()
Construir o modelo
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([
layers.Dense(16, activation="relu"),
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
autoencoder.compile(optimizer='adam', loss='mae')
Observe que o autoencoder é treinado usando apenas os ECGs normais, mas é avaliado usando o conjunto de teste completo.
history = autoencoder.fit(normal_train_data, normal_train_data,
epochs=20,
batch_size=512,
validation_data=(test_data, test_data),
shuffle=True)
Epoch 1/20 5/5 [==============================] - 1s 33ms/step - loss: 0.0576 - val_loss: 0.0531 Epoch 2/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0552 - val_loss: 0.0514 Epoch 3/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0519 - val_loss: 0.0499 Epoch 4/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0483 - val_loss: 0.0475 Epoch 5/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0445 - val_loss: 0.0451 Epoch 6/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0409 - val_loss: 0.0432 Epoch 7/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0377 - val_loss: 0.0415 Epoch 8/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0348 - val_loss: 0.0401 Epoch 9/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0319 - val_loss: 0.0388 Epoch 10/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0293 - val_loss: 0.0378 Epoch 11/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0273 - val_loss: 0.0369 Epoch 12/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0259 - val_loss: 0.0361 Epoch 13/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0249 - val_loss: 0.0354 Epoch 14/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0239 - val_loss: 0.0346 Epoch 15/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0230 - val_loss: 0.0340 Epoch 16/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0222 - val_loss: 0.0335 Epoch 17/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0215 - val_loss: 0.0331 Epoch 18/20 5/5 [==============================] - 0s 9ms/step - loss: 0.0211 - val_loss: 0.0331 Epoch 19/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0208 - val_loss: 0.0329 Epoch 20/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0206 - val_loss: 0.0327
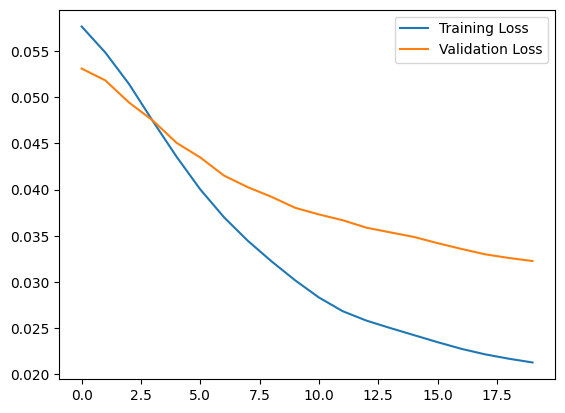
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
<matplotlib.legend.Legend at 0x7ff1d339b790>
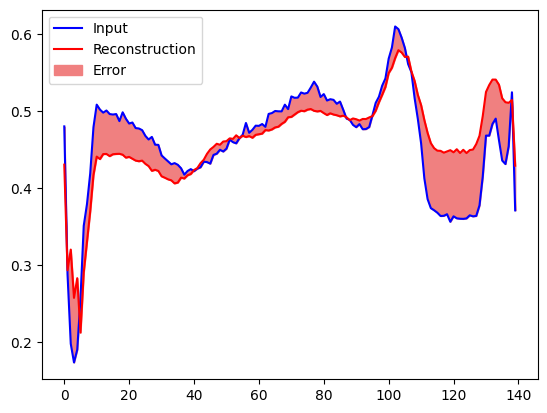
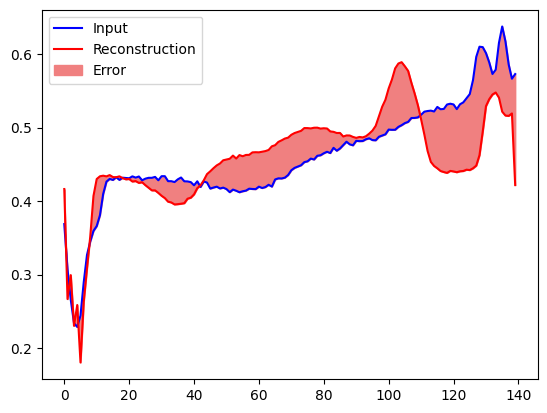
Você logo classificará um ECG como anômalo se o erro de reconstrução for maior que um desvio padrão dos exemplos normais de treinamento. Primeiro, vamos plotar um ECG normal do conjunto de treinamento, a reconstrução depois de codificado e decodificado pelo autoencoder e o erro de reconstrução.
encoded_data = autoencoder.encoder(normal_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(normal_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], normal_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
Crie um gráfico semelhante, desta vez para um exemplo de teste anômalo.
encoded_data = autoencoder.encoder(anomalous_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(anomalous_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], anomalous_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
Detectar anomalias
Detecte anomalias calculando se a perda de reconstrução é maior que um limite fixo. Neste tutorial, você calculará o erro médio médio para exemplos normais do conjunto de treinamento e, em seguida, classificará os exemplos futuros como anômalos se o erro de reconstrução for maior que um desvio padrão do conjunto de treinamento.
Plote o erro de reconstrução em ECGs normais do conjunto de treinamento
reconstructions = autoencoder.predict(normal_train_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_train_data)
plt.hist(train_loss[None,:], bins=50)
plt.xlabel("Train loss")
plt.ylabel("No of examples")
plt.show()

Escolha um valor limite que seja um desvio padrão acima da média.
threshold = np.mean(train_loss) + np.std(train_loss)
print("Threshold: ", threshold)
Threshold: 0.03241627
Se você examinar o erro de reconstrução dos exemplos anômalos no conjunto de teste, notará que a maioria tem um erro de reconstrução maior do que o limite. Variando o limite, você pode ajustar a precisão e a recuperação do seu classificador.
reconstructions = autoencoder.predict(anomalous_test_data)
test_loss = tf.keras.losses.mae(reconstructions, anomalous_test_data)
plt.hist(test_loss[None, :], bins=50)
plt.xlabel("Test loss")
plt.ylabel("No of examples")
plt.show()

Classifique um ECG como uma anomalia se o erro de reconstrução for maior que o limite.
def predict(model, data, threshold):
reconstructions = model(data)
loss = tf.keras.losses.mae(reconstructions, data)
return tf.math.less(loss, threshold)
def print_stats(predictions, labels):
print("Accuracy = {}".format(accuracy_score(labels, predictions)))
print("Precision = {}".format(precision_score(labels, predictions)))
print("Recall = {}".format(recall_score(labels, predictions)))
preds = predict(autoencoder, test_data, threshold)
print_stats(preds, test_labels)
Accuracy = 0.944 Precision = 0.9921875 Recall = 0.9071428571428571
Próximos passos
Para saber mais sobre detecção de anomalias com autoencoders, confira este excelente exemplo interativo criado com TensorFlow.js por Victor Dibia. Para um caso de uso do mundo real, você pode aprender como o Airbus detecta anomalias nos dados de telemetria da ISS usando o TensorFlow. Para saber mais sobre o básico, considere ler esta postagem no blog de François Chollet. Para mais detalhes, confira o capítulo 14 do Deep Learning de Ian Goodfellow, Yoshua Bengio e Aaron Courville.
