 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Yapılan karşılaştırmaların kapalı Bina MNIST öğretici, bu öğretici son çalışmalarını araştırıyor Huang vd. bu, farklı veri kümelerinin performans karşılaştırmalarını nasıl etkilediğini gösterir. Çalışmada yazarlar, klasik makine öğrenme modellerinin nasıl ve ne zaman kuantum modellerinin yanı sıra (veya daha iyi) öğrenebileceğini anlamaya çalışıyorlar. Çalışma ayrıca, özenle hazırlanmış bir veri seti aracılığıyla klasik ve kuantum makine öğrenimi modeli arasında deneysel bir performans ayrımı sergiliyor. Olacaksın:
- Küçültülmüş boyutlu bir Fashion-MNIST veri seti hazırlayın.
- Veri kümesini yeniden etiketlemek ve Öngörülen Kuantum Çekirdeği özelliklerini (PQK) hesaplamak için kuantum devrelerini kullanın.
- Yeniden etiketlenen veri kümesi üzerinde klasik bir sinir ağı eğitin ve performansı, PQK özelliklerine erişimi olan bir modelle karşılaştırın.
Kurmak
pip install tensorflow==2.4.1 tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
1. Veri hazırlama
Bir kuantum bilgisayarda çalıştırmak için fashion-MNIST veri setini hazırlayarak başlayacaksınız.
1.1 Moda-MNIST İndir
İlk adım, geleneksel moda bakanı veri setini elde etmektir. Bu kullanılarak yapılabilir tf.keras.datasets modülü.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Number of original training examples: 60000 Number of original test examples: 10000
Yalnızca tişörtleri/üstleri ve elbiseleri tutmak için veri kümesini filtreleyin, diğer sınıfları kaldırın. Aynı zamanda dönüştürmek etiket, At y , boolean: 0 True ve False 3 için.
def filter_03(x, y):
keep = (y == 0) | (y == 3)
x, y = x[keep], y[keep]
y = y == 0
return x,y
x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12000 Number of filtered test examples: 2000
print(y_train[0])
plt.imshow(x_train[0, :, :])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 Görüntüleri küçültün
Tıpkı MNIST örneğinde olduğu gibi, mevcut kuantum bilgisayarların sınırları içinde olmak için bu görüntüleri küçültmeniz gerekecek. Bu kez ancak boyutlarını yerine azaltmak için PCA dönüşümü kullanacağı tf.image.resize operasyonu.
def truncate_x(x_train, x_test, n_components=10):
"""Perform PCA on image dataset keeping the top `n_components` components."""
n_points_train = tf.gather(tf.shape(x_train), 0)
n_points_test = tf.gather(tf.shape(x_test), 0)
# Flatten to 1D
x_train = tf.reshape(x_train, [n_points_train, -1])
x_test = tf.reshape(x_test, [n_points_test, -1])
# Normalize.
feature_mean = tf.reduce_mean(x_train, axis=0)
x_train_normalized = x_train - feature_mean
x_test_normalized = x_test - feature_mean
# Truncate.
e_values, e_vectors = tf.linalg.eigh(
tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])
DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))
New datapoint dimension: 10
Son adım, veri kümesinin boyutunu yalnızca 1000 eğitim veri noktasına ve 200 test veri noktasına indirgemektir.
N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]
print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))
New number of training examples: 1000 New number of test examples: 200
2. Yeniden etiketleme ve PQK özelliklerini hesaplama
Şimdi, kuantum bileşenlerini dahil ederek ve yukarıda oluşturduğunuz budanmış moda-MNIST veri kümesini yeniden etiketleyerek "biçimli" bir kuantum veri kümesi hazırlayacaksınız. Kuantum ve klasik yöntemler arasında en fazla ayrımı elde etmek için önce PQK özelliklerini hazırlayacak, ardından çıktıları değerlerine göre yeniden etiketleyeceksiniz.
2.1 Kuantum kodlama ve PQK özellikleri
Sen dayalı özelliklerin bir dizi yeni yaratacak x_train , y_train , x_test ve y_test tüm qubits 1-RDM olmak üzere tanımlandığını:
\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)
Burada \(U_\text{1qb}\) tek qubit rotasyonlar ve bir duvar \(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)
İlk olarak, tek kübit dönüşlerin duvarını oluşturabilirsiniz:
def single_qubit_wall(qubits, rotations):
"""Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
wall_circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
wall_circuit.append(gate(qubit) ** rotations[i][j])
return wall_circuit
Devreye bakarak bunun çalıştığını hızlı bir şekilde doğrulayabilirsiniz:
SVGCircuit(single_qubit_wall(
cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))
Eğer hazırlayabilirsiniz Sonraki \(V(\hat{\theta})\) yardımıyla tfq.util.exponential herhangi gidip exponentiate edebilirsiniz cirq.PauliSum nesneleri:
def v_theta(qubits):
"""Prepares a circuit that generates V(\theta)."""
ref_paulis = [
cirq.X(q0) * cirq.X(q1) + \
cirq.Y(q0) * cirq.Y(q1) + \
cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
]
exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols
Bu devre bakarak doğrulamak biraz daha zor olabilir, ancak ne olduğunu görmek için yine de iki kübitlik bir durumu inceleyebilirsiniz:
test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)
Symbols found in circuit:[ref_0]
Artık tam kodlama devrelerinizi bir araya getirmek için ihtiyacınız olan tüm yapı taşlarına sahipsiniz:
def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
"""Prepare the pqk feature circuits around a dataset."""
n_qubits = len(qubits)
n_points = len(classical_source)
# Prepare random single qubit rotation wall.
random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
initial_U = single_qubit_wall(qubits, random_rots)
# Prepare parametrized V
V_circuit, symbols = v_theta(qubits)
exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))
# Convert to `tf.Tensor`
initial_U_tensor = tfq.convert_to_tensor([initial_U])
initial_U_splat = tf.tile(initial_U_tensor, [n_points])
full_circuits = tfq.layers.AddCircuit()(
initial_U_splat, append=exp_circuit)
# Replace placeholders in circuits with values from `classical_source`.
return tfq.resolve_parameters(
full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))
Bazı kübitler seçin ve veri kodlama devrelerini hazırlayın:
qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)
Daha sonra, PQK üzerinde veri kümesi devrelerinin 1-RDM göre özellikleri hesaplamak ve sonuçları depolamak rdm bir tf.Tensor şeklinde [n_points, n_qubits, 3] . Girişler rdm[i][j][k] = \(\langle \psi_i | OP^k_j | \psi_i \rangle\) burada i veri noktası üzerinde endeksler, j qubits üzerinde indeksleri k fazla dizinler \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) .
def get_pqk_features(qubits, data_batch):
"""Get PQK features based on above construction."""
ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
batch_dim = tf.gather(tf.shape(data_batch), 0)
ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
return rdm
x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)
New PQK training dataset has shape: (1000, 11, 3) New PQK testing dataset has shape: (200, 11, 3)
2.2 PQK özelliklerine dayalı yeniden etiketleme
Şimdi bu kuantum oluşturulan özelliklere sahip olduğunu x_train_pqk ve x_test_pqk , bu yeniden etiket veri kümesi zamanıdır. Kuantum ve yapabilecekleriniz klasik performans arasındaki maksimum ayırımı sağlamak için bulunan spektrum bilgilere dayanarak veri kümesi yeniden etiketlemek x_train_pqk ve x_test_pqk .
def compute_kernel_matrix(vecs, gamma):
"""Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
scaled_gamma = gamma / (
tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)
def get_spectrum(datapoints, gamma=1.0):
"""Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
KC_qs = compute_kernel_matrix(datapoints, gamma)
S, V = tf.linalg.eigh(KC_qs)
S = tf.math.abs(S)
return S, V
S_pqk, V_pqk = get_spectrum(
tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))
S_original, V_original = get_spectrum(
tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)
print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)
Eigenvectors of pqk kernel matrix: tf.Tensor( [[-2.09569391e-02 1.05973557e-02 2.16634180e-02 ... 2.80352887e-02 1.55521873e-02 2.82677952e-02] [-2.29303762e-02 4.66355234e-02 7.91163836e-03 ... -6.14174758e-04 -7.07804322e-01 2.85902526e-02] [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02 2.11018627e-03 2.69009806e-02] ... [ 6.05797209e-02 1.32483775e-02 2.69536003e-02 ... -1.38843581e-02 3.05043962e-02 3.85345481e-02] [ 6.33309558e-02 -3.04112374e-03 9.77444276e-03 ... 7.48321265e-02 3.42793856e-03 3.67484428e-02] [ 5.86028099e-02 5.84433973e-03 2.64811981e-03 ... 2.82612257e-02 -3.80136147e-02 3.29943895e-02]], shape=(1200, 1200), dtype=float32) Eigenvectors of original kernel matrix: tf.Tensor( [[ 0.03835681 0.0283473 -0.01169789 ... 0.02343717 0.0211248 0.03206972] [-0.04018159 0.00888097 -0.01388255 ... 0.00582427 0.717551 0.02881948] [-0.0166719 0.01350376 -0.03663862 ... 0.02467175 -0.00415936 0.02195409] ... [-0.03015648 -0.01671632 -0.01603392 ... 0.00100583 -0.00261221 0.02365689] [ 0.0039777 -0.04998879 -0.00528336 ... 0.01560401 -0.04330755 0.02782002] [-0.01665728 -0.00818616 -0.0432341 ... 0.00088256 0.00927396 0.01875088]], shape=(1200, 1200), dtype=float32)
Artık veri setini yeniden etiketlemek için ihtiyacınız olan her şeye sahipsiniz! Artık veri kümesini yeniden etiketlerken performans ayrımını nasıl en üst düzeye çıkaracağınızı daha iyi anlamak için akış şemasına başvurabilirsiniz:
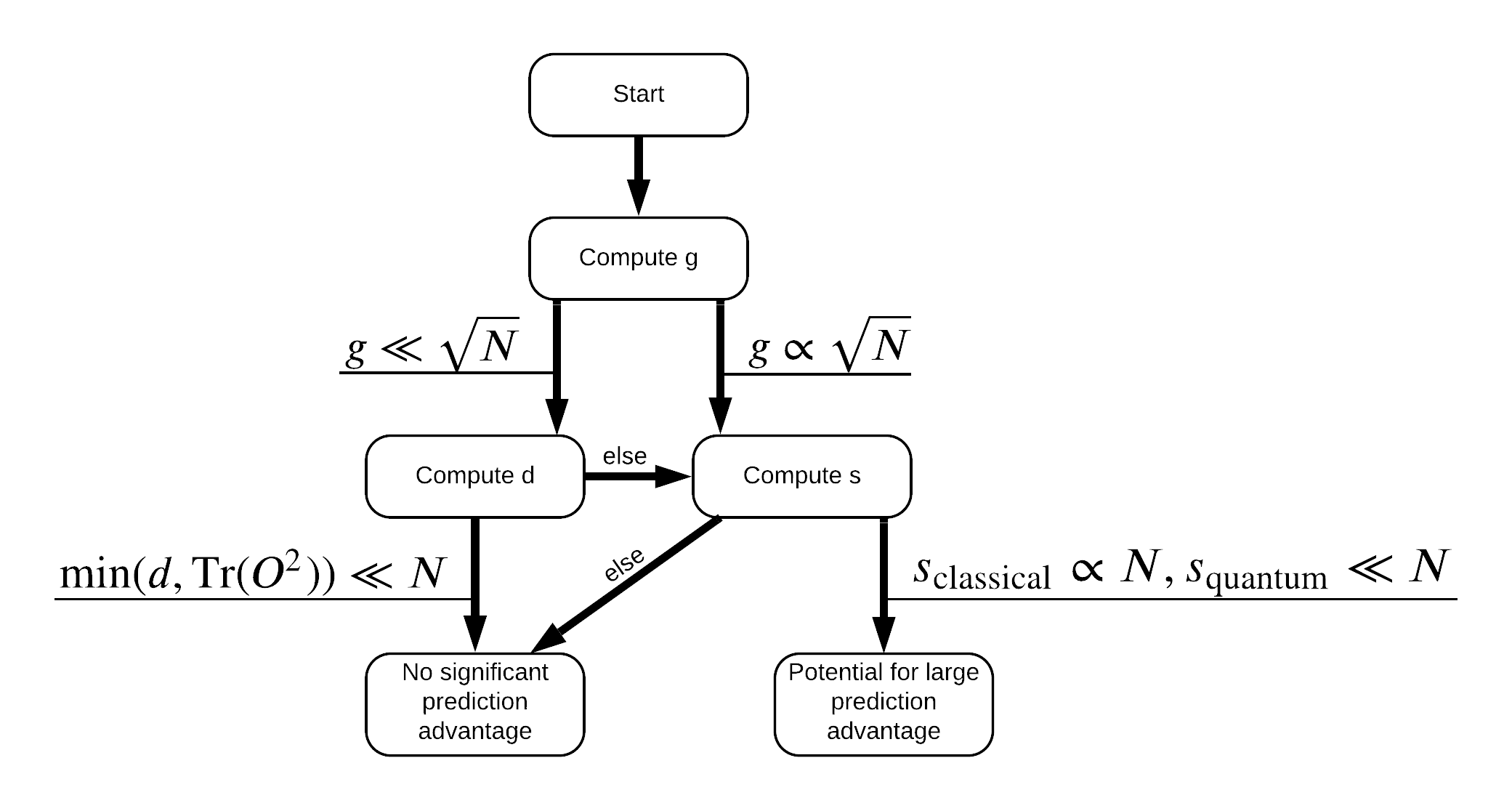
Kuantum ve klasik modeller arasındaki ayrımın üst düzeye çıkarmak için, orijinal veri kümesi arasındaki geometrik farkı maksimize dener ve PQK çekirdeği matrisler özellikleri \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) kullanarak S_pqk, V_pqk ve S_original, V_original . Büyük bir değer \(g\) teminat altın başlangıçta kuantum durumunda bir öngörü avantajı doğru akış şeması aşağı sağa doğru hareket ettiklerini.
def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
"""Prepare new labels that maximize geometric distance between kernels."""
S_diag = tf.linalg.diag(S ** 0.5)
S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
scaling = S_diag @ tf.transpose(V) @ \
V_2 @ S_2_diag @ tf.transpose(V_2) @ \
V @ S_diag
# Generate new lables using the largest eigenvector.
_, vecs = tf.linalg.eig(scaling)
new_labels = tf.math.real(
tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
# Create new labels and add some small amount of noise.
final_y = new_labels > np.median(new_labels)
noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
return noisy_y
y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]
3. Modelleri karşılaştırma
Artık veri kümenizi hazırladığınıza göre, model performansını karşılaştırmanın zamanı geldi. İki küçük ileri beslemeli sinir ağları oluşturmak ve onlar özellikleri de tespit PQK erişimi verildiğinde performansını karşılaştırır x_train_pqk .
3.1 PQK geliştirilmiş modeli oluşturun
Standart kullanarak tf.keras kütüphane artık oluşturabilir özellikleri ve bir tren üzerinde bir modeli x_train_pqk ve y_train_new datapoints:
#docs_infra: no_execute
def create_pqk_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
metrics=['accuracy'])
pqk_model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 32) 1088 _________________________________________________________________ dense_1 (Dense) (None, 16) 528 _________________________________________________________________ dense_2 (Dense) (None, 1) 17 ================================================================= Total params: 1,633 Trainable params: 1,633 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))
3.2 Klasik bir model oluşturun
Yukarıdaki koda benzer şekilde, artık stilize edilmiş veri kümenizdeki PQK özelliklerine erişimi olmayan klasik bir model de oluşturabilirsiniz. Bu model kullanılarak eğitilmiş olabilir x_train ve y_label_new .
#docs_infra: no_execute
def create_fair_classical_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
metrics=['accuracy'])
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 32) 352 _________________________________________________________________ dense_4 (Dense) (None, 16) 528 _________________________________________________________________ dense_5 (Dense) (None, 1) 17 ================================================================= Total params: 897 Trainable params: 897 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
classical_history = model.fit(x_train,
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(x_test, y_test_new))
3.3 Performansı karşılaştırın
Artık iki modeli eğittiğinize göre, ikisi arasındaki doğrulama verilerindeki performans boşluklarını hızla çizebilirsiniz. Tipik olarak her iki model de eğitim verilerinde > 0.9 doğruluk elde edecektir. Ancak doğrulama verilerinde, yalnızca PQK özelliklerinde bulunan bilgilerin, modelin görünmeyen örneklere iyi bir şekilde genellenmesini sağlamak için yeterli olduğu açıkça ortaya çıkıyor.
#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x7f6d846ecee0>
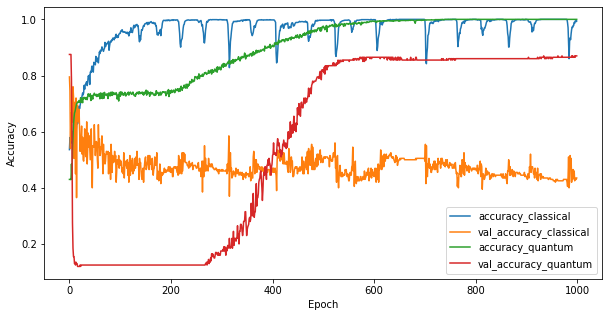
4. Önemli sonuçlar
Bu ve çıkarabileceğimiz birçok önemli sonuç vardır MNIST deneyleri:
Günümüzün kuantum modellerinin klasik veriler üzerinde klasik model performansını geçmesi pek olası değildir. Özellikle günümüzün bir milyondan fazla veri noktasına sahip olabilen klasik veri kümelerinde.
Verilerin klasik olarak simüle edilmesi zor bir kuantum devresinden gelmesi, klasik bir model için verilerin öğrenilmesini zorlaştırmaz.
Model mimarisi veya kullanılan eğitim algoritmalarından bağımsız olarak, kuantum modellerinin öğrenmesi kolay ve klasik modellerin öğrenmesi zor olan veri kümeleri (nihai olarak doğada kuantum) mevcuttur.
