 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
Partendo dei confronti effettuati nel MNIST tutorial, questo tutorial esplora il recente lavoro di Huang et al. che mostra come i diversi set di dati influiscano sui confronti delle prestazioni. Nel lavoro, gli autori cercano di capire come e quando i modelli classici di machine learning possono apprendere così come (o meglio) i modelli quantistici. Il lavoro mostra anche una separazione empirica delle prestazioni tra il modello di machine learning classico e quantistico tramite un set di dati accuratamente realizzato. Desideri:
- Preparare un dataset Fashion-MNIST di dimensioni ridotte.
- Usa circuiti quantistici per rietichettare il set di dati e calcolare le funzionalità Projected Quantum Kernel (PQK).
- Addestra una rete neurale classica sul set di dati rietichettato e confronta le prestazioni con un modello che ha accesso alle funzionalità PQK.
Impostare
pip install tensorflow==2.4.1 tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
1. Preparazione dei dati
Inizierai preparando il set di dati fashion-MNIST per l'esecuzione su un computer quantistico.
1.1 Scarica moda-MNIST
Il primo passo è ottenere il tradizionale set di dati fashion-mnist. Questo può essere fatto utilizzando la tf.keras.datasets modulo.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Number of original training examples: 60000 Number of original test examples: 10000
Filtra il set di dati per mantenere solo le magliette/top e i vestiti, rimuovi le altre classi. Allo stesso tempo, convertito l'etichetta, y , a booleano: true per 0 e false per 3.
def filter_03(x, y):
keep = (y == 0) | (y == 3)
x, y = x[keep], y[keep]
y = y == 0
return x,y
x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12000 Number of filtered test examples: 2000
print(y_train[0])
plt.imshow(x_train[0, :, :])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 Ridimensionare le immagini
Proprio come l'esempio MNIST, dovrai ridimensionare queste immagini per rientrare nei limiti degli attuali computer quantistici. Questa volta però si userà una trasformazione PCA per ridurre le dimensioni invece di un tf.image.resize operazione.
def truncate_x(x_train, x_test, n_components=10):
"""Perform PCA on image dataset keeping the top `n_components` components."""
n_points_train = tf.gather(tf.shape(x_train), 0)
n_points_test = tf.gather(tf.shape(x_test), 0)
# Flatten to 1D
x_train = tf.reshape(x_train, [n_points_train, -1])
x_test = tf.reshape(x_test, [n_points_test, -1])
# Normalize.
feature_mean = tf.reduce_mean(x_train, axis=0)
x_train_normalized = x_train - feature_mean
x_test_normalized = x_test - feature_mean
# Truncate.
e_values, e_vectors = tf.linalg.eigh(
tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])
DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))
New datapoint dimension: 10
L'ultimo passaggio consiste nel ridurre la dimensione del set di dati a soli 1000 punti dati di addestramento e 200 punti dati di test.
N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]
print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))
New number of training examples: 1000 New number of test examples: 200
2. Rietichettatura e calcolo delle funzionalità PQK
Ora preparerai un set di dati quantistico "stimolato" incorporando componenti quantistici e rietichettando il set di dati MNIST di moda troncato che hai creato sopra. Per ottenere la massima separazione tra metodi quantistici e classici, preparerai prima le funzionalità PQK e quindi rietichettarai gli output in base ai loro valori.
2.1 Codifica quantistica e funzionalità PQK
Verrà creato un nuovo set di funzioni, sulla base di x_train , y_train , x_test e y_test che viene definito come il 1-RDM su tutti i qubit di:
\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)
Dove \(U_\text{1qb}\) è una parete di rotazioni qubit singole e \(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)
Innanzitutto, puoi generare il muro di rotazioni di singoli qubit:
def single_qubit_wall(qubits, rotations):
"""Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
wall_circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
wall_circuit.append(gate(qubit) ** rotations[i][j])
return wall_circuit
Puoi verificare rapidamente che funzioni guardando il circuito:
SVGCircuit(single_qubit_wall(
cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))
Poi si può preparare \(V(\hat{\theta})\) con l'aiuto di tfq.util.exponential che può exponentiate ogni pendolarismo cirq.PauliSum oggetti:
def v_theta(qubits):
"""Prepares a circuit that generates V(\theta)."""
ref_paulis = [
cirq.X(q0) * cirq.X(q1) + \
cirq.Y(q0) * cirq.Y(q1) + \
cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
]
exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols
Questo circuito potrebbe essere un po' più difficile da verificare guardandolo, ma puoi comunque esaminare un caso a due qubit per vedere cosa sta succedendo:
test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)
Symbols found in circuit:[ref_0]
Ora hai tutti gli elementi costitutivi necessari per mettere insieme i tuoi circuiti di codifica completi:
def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
"""Prepare the pqk feature circuits around a dataset."""
n_qubits = len(qubits)
n_points = len(classical_source)
# Prepare random single qubit rotation wall.
random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
initial_U = single_qubit_wall(qubits, random_rots)
# Prepare parametrized V
V_circuit, symbols = v_theta(qubits)
exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))
# Convert to `tf.Tensor`
initial_U_tensor = tfq.convert_to_tensor([initial_U])
initial_U_splat = tf.tile(initial_U_tensor, [n_points])
full_circuits = tfq.layers.AddCircuit()(
initial_U_splat, append=exp_circuit)
# Replace placeholders in circuits with values from `classical_source`.
return tfq.resolve_parameters(
full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))
Scegli alcuni qubit e prepara i circuiti di codifica dei dati:
qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)
Successivamente, calcolare la PQK funzioni basate sul 1-RDM dei circuiti set di dati alto e memorizzare i risultati in rdm , un tf.Tensor di forma [n_points, n_qubits, 3] . Le voci in rdm[i][j][k] = \(\langle \psi_i | OP^k_j | \psi_i \rangle\) dove i indici oltre datapoints, j indici oltre qubits e k indici oltre \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) .
def get_pqk_features(qubits, data_batch):
"""Get PQK features based on above construction."""
ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
batch_dim = tf.gather(tf.shape(data_batch), 0)
ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
return rdm
x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)
New PQK training dataset has shape: (1000, 11, 3) New PQK testing dataset has shape: (200, 11, 3)
2.2 Rietichettatura basata sulle caratteristiche PQK
Ora che avete queste caratteristiche quantistiche generato nel x_train_pqk e x_test_pqk , è il momento di ri-label il set di dati. Per ottenere la massima separazione tra il quantum e le prestazioni classica è possibile ri-etichettare il set di dati in base alle informazioni dello spettro si trovano in x_train_pqk e x_test_pqk .
def compute_kernel_matrix(vecs, gamma):
"""Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
scaled_gamma = gamma / (
tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)
def get_spectrum(datapoints, gamma=1.0):
"""Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
KC_qs = compute_kernel_matrix(datapoints, gamma)
S, V = tf.linalg.eigh(KC_qs)
S = tf.math.abs(S)
return S, V
S_pqk, V_pqk = get_spectrum(
tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))
S_original, V_original = get_spectrum(
tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)
print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)
Eigenvectors of pqk kernel matrix: tf.Tensor( [[-2.09569391e-02 1.05973557e-02 2.16634180e-02 ... 2.80352887e-02 1.55521873e-02 2.82677952e-02] [-2.29303762e-02 4.66355234e-02 7.91163836e-03 ... -6.14174758e-04 -7.07804322e-01 2.85902526e-02] [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02 2.11018627e-03 2.69009806e-02] ... [ 6.05797209e-02 1.32483775e-02 2.69536003e-02 ... -1.38843581e-02 3.05043962e-02 3.85345481e-02] [ 6.33309558e-02 -3.04112374e-03 9.77444276e-03 ... 7.48321265e-02 3.42793856e-03 3.67484428e-02] [ 5.86028099e-02 5.84433973e-03 2.64811981e-03 ... 2.82612257e-02 -3.80136147e-02 3.29943895e-02]], shape=(1200, 1200), dtype=float32) Eigenvectors of original kernel matrix: tf.Tensor( [[ 0.03835681 0.0283473 -0.01169789 ... 0.02343717 0.0211248 0.03206972] [-0.04018159 0.00888097 -0.01388255 ... 0.00582427 0.717551 0.02881948] [-0.0166719 0.01350376 -0.03663862 ... 0.02467175 -0.00415936 0.02195409] ... [-0.03015648 -0.01671632 -0.01603392 ... 0.00100583 -0.00261221 0.02365689] [ 0.0039777 -0.04998879 -0.00528336 ... 0.01560401 -0.04330755 0.02782002] [-0.01665728 -0.00818616 -0.0432341 ... 0.00088256 0.00927396 0.01875088]], shape=(1200, 1200), dtype=float32)
Ora hai tutto il necessario per rietichettare il set di dati! Ora puoi consultare il diagramma di flusso per capire meglio come massimizzare la separazione delle prestazioni durante la rietichettatura del set di dati:
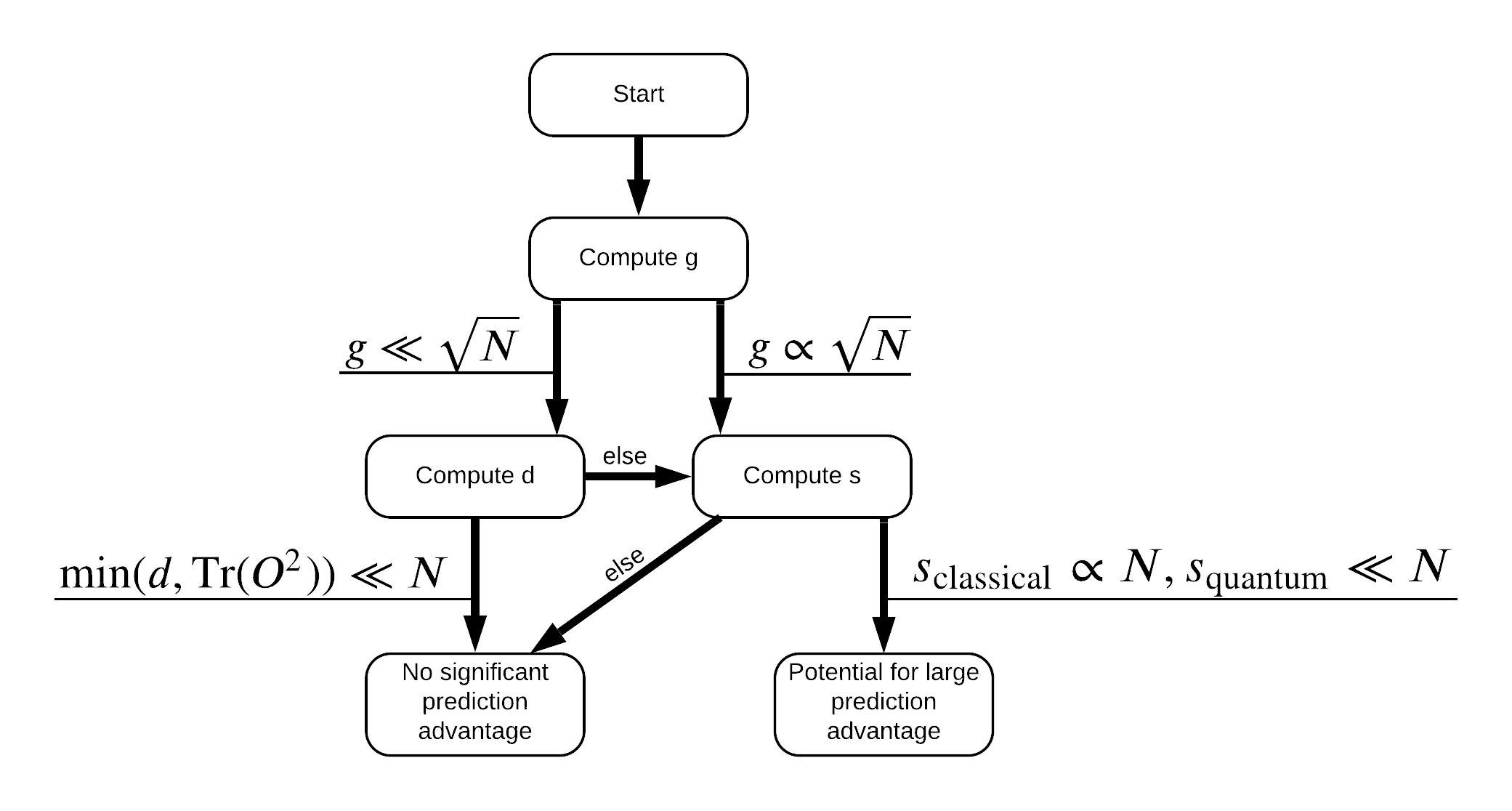
Al fine di massimizzare la separazione tra il quantistica e modelli classici, si cercherà di massimizzare la differenza geometrica tra l'insieme di dati originale e il PQK caratteristiche kernel matrici \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) utilizzando S_pqk, V_pqk e S_original, V_original . Un valore di \(g\) assicura che inizialmente spostarsi verso destra nel diagramma di flusso verso il basso verso un vantaggio predizione nel caso quantistico.
def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
"""Prepare new labels that maximize geometric distance between kernels."""
S_diag = tf.linalg.diag(S ** 0.5)
S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
scaling = S_diag @ tf.transpose(V) @ \
V_2 @ S_2_diag @ tf.transpose(V_2) @ \
V @ S_diag
# Generate new lables using the largest eigenvector.
_, vecs = tf.linalg.eig(scaling)
new_labels = tf.math.real(
tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
# Create new labels and add some small amount of noise.
final_y = new_labels > np.median(new_labels)
noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
return noisy_y
y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]
3. Modelli a confronto
Ora che hai preparato il tuo set di dati, è il momento di confrontare le prestazioni del modello. Potrai creare due reti neurali feedforward piccola e confrontare le prestazioni quando viene somministrato l'accesso al PQK caratteristiche che si trovano in x_train_pqk .
3.1 Creare un modello avanzato PQK
Utilizzando standard di tf.keras funzioni di libreria è ora possibile creare e un treno di un modello sul x_train_pqk e y_train_new datapoints:
#docs_infra: no_execute
def create_pqk_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
metrics=['accuracy'])
pqk_model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 32) 1088 _________________________________________________________________ dense_1 (Dense) (None, 16) 528 _________________________________________________________________ dense_2 (Dense) (None, 1) 17 ================================================================= Total params: 1,633 Trainable params: 1,633 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))
3.2 Creare un modello classico
Simile al codice sopra, ora puoi anche creare un modello classico che non ha accesso alle funzionalità PQK nel tuo set di dati stilted. Questo modello può essere addestrato utilizzando x_train e y_label_new .
#docs_infra: no_execute
def create_fair_classical_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
metrics=['accuracy'])
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 32) 352 _________________________________________________________________ dense_4 (Dense) (None, 16) 528 _________________________________________________________________ dense_5 (Dense) (None, 1) 17 ================================================================= Total params: 897 Trainable params: 897 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
classical_history = model.fit(x_train,
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(x_test, y_test_new))
3.3 Confronta le prestazioni
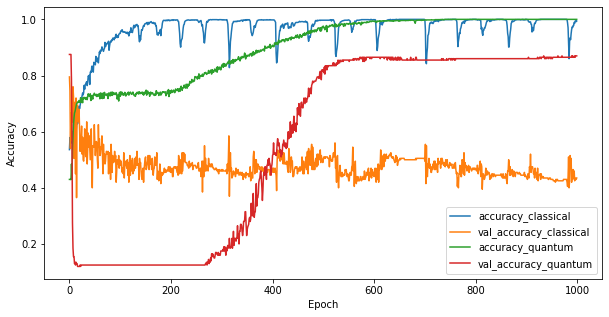
Ora che hai addestrato i due modelli, puoi tracciare rapidamente i divari di prestazioni nei dati di convalida tra i due. In genere entrambi i modelli raggiungono un'accuratezza > 0,9 sui dati di addestramento. Tuttavia, sui dati di convalida diventa chiaro che solo le informazioni trovate nelle funzionalità PQK sono sufficienti per far generalizzare bene il modello a istanze invisibili.
#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x7f6d846ecee0>
4. Conclusioni importanti
Ci sono diverse conclusioni importanti che si possono trarre da questa e le MNIST esperimenti:
È molto improbabile che i modelli quantistici di oggi superino le prestazioni dei modelli classici sui dati classici. Soprattutto sui classici set di dati odierni che possono avere fino a un milione di punti dati.
Solo perché i dati potrebbero provenire da un circuito quantistico difficile da simulare in modo classico, non rende necessariamente i dati difficili da apprendere per un modello classico.
Esistono set di dati (in definitiva di natura quantistica) facili da apprendere per i modelli quantistici e difficili da apprendere per i modelli classici, indipendentemente dall'architettura del modello o dagli algoritmi di addestramento utilizzati.
