 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Membangun off dari perbandingan yang dibuat di MNIST tutorial, tutorial ini mengeksplorasi karya terbaru dari Huang et al. yang menunjukkan bagaimana kumpulan data yang berbeda memengaruhi perbandingan kinerja. Dalam karya tersebut, penulis berusaha memahami bagaimana dan kapan model pembelajaran mesin klasik dapat belajar sebaik (atau lebih baik dari) model kuantum. Karya ini juga menampilkan pemisahan kinerja empiris antara model pembelajaran mesin klasik dan kuantum melalui kumpulan data yang dibuat dengan cermat. Kamu akan:
- Siapkan set data Fashion-MNIST berdimensi lebih kecil.
- Gunakan sirkuit kuantum untuk memberi label ulang pada kumpulan data dan menghitung fitur Projected Quantum Kernel (PQK).
- Latih jaringan saraf klasik pada kumpulan data yang diberi label ulang dan bandingkan kinerjanya dengan model yang memiliki akses ke fitur PQK.
Mempersiapkan
pip install tensorflow==2.4.1 tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
1. Persiapan data
Anda akan mulai dengan menyiapkan dataset fashion-MNIST untuk dijalankan di komputer kuantum.
1.1 Unduh mode-MNIST
Langkah pertama adalah mendapatkan dataset fashion-mnist tradisional. Hal ini dapat dilakukan dengan menggunakan tf.keras.datasets modul.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Number of original training examples: 60000 Number of original test examples: 10000
Filter dataset untuk menyimpan hanya T-shirt/atasan dan gaun, hapus kelas lainnya. Pada saat yang sama convert label, y , ke boolean: Benar untuk 0 dan palsu untuk 3.
def filter_03(x, y):
keep = (y == 0) | (y == 3)
x, y = x[keep], y[keep]
y = y == 0
return x,y
x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12000 Number of filtered test examples: 2000
print(y_train[0])
plt.imshow(x_train[0, :, :])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 Perkecil gambar
Sama seperti contoh MNIST, Anda perlu menurunkan skala gambar-gambar ini agar berada dalam batas-batas komputer kuantum saat ini. Kali ini namun Anda akan menggunakan transformasi PCA untuk mengurangi dimensi bukannya tf.image.resize operasi.
def truncate_x(x_train, x_test, n_components=10):
"""Perform PCA on image dataset keeping the top `n_components` components."""
n_points_train = tf.gather(tf.shape(x_train), 0)
n_points_test = tf.gather(tf.shape(x_test), 0)
# Flatten to 1D
x_train = tf.reshape(x_train, [n_points_train, -1])
x_test = tf.reshape(x_test, [n_points_test, -1])
# Normalize.
feature_mean = tf.reduce_mean(x_train, axis=0)
x_train_normalized = x_train - feature_mean
x_test_normalized = x_test - feature_mean
# Truncate.
e_values, e_vectors = tf.linalg.eigh(
tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])
DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))
New datapoint dimension: 10
Langkah terakhir adalah mengurangi ukuran dataset menjadi hanya 1000 titik data pelatihan dan 200 titik data pengujian.
N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]
print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))
New number of training examples: 1000 New number of test examples: 200
2. Pelabelan ulang dan komputasi fitur PQK
Sekarang Anda akan menyiapkan kumpulan data kuantum "tegak" dengan memasukkan komponen kuantum dan memberi label ulang kumpulan data mode-MNIST terpotong yang telah Anda buat di atas. Untuk mendapatkan pemisahan paling banyak antara metode kuantum dan klasik, pertama-tama Anda akan menyiapkan fitur PQK dan kemudian memberi label ulang output berdasarkan nilainya.
2.1 Pengkodean kuantum dan fitur PQK
Anda akan menciptakan satu set baru fitur, berdasarkan x_train , y_train , x_test dan y_test yang didefinisikan sebagai 1-RDM pada semua qubit dari:
\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)
Dimana \(U_\text{1qb}\) adalah dinding tunggal rotasi qubit dan \(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)
Pertama, Anda dapat membuat dinding rotasi qubit tunggal:
def single_qubit_wall(qubits, rotations):
"""Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
wall_circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
wall_circuit.append(gate(qubit) ** rotations[i][j])
return wall_circuit
Anda dapat dengan cepat memverifikasi ini berfungsi dengan melihat sirkuit:
SVGCircuit(single_qubit_wall(
cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))
Berikutnya Anda dapat mempersiapkan \(V(\hat{\theta})\) dengan bantuan tfq.util.exponential yang dapat exponentiate setiap komuter cirq.PauliSum objek:
def v_theta(qubits):
"""Prepares a circuit that generates V(\theta)."""
ref_paulis = [
cirq.X(q0) * cirq.X(q1) + \
cirq.Y(q0) * cirq.Y(q1) + \
cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
]
exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols
Sirkuit ini mungkin sedikit lebih sulit untuk diverifikasi dengan melihat, tetapi Anda masih dapat memeriksa kasus dua qubit untuk melihat apa yang terjadi:
test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)
Symbols found in circuit:[ref_0]
Sekarang Anda memiliki semua blok bangunan yang Anda butuhkan untuk menyatukan sirkuit pengkodean lengkap Anda:
def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
"""Prepare the pqk feature circuits around a dataset."""
n_qubits = len(qubits)
n_points = len(classical_source)
# Prepare random single qubit rotation wall.
random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
initial_U = single_qubit_wall(qubits, random_rots)
# Prepare parametrized V
V_circuit, symbols = v_theta(qubits)
exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))
# Convert to `tf.Tensor`
initial_U_tensor = tfq.convert_to_tensor([initial_U])
initial_U_splat = tf.tile(initial_U_tensor, [n_points])
full_circuits = tfq.layers.AddCircuit()(
initial_U_splat, append=exp_circuit)
# Replace placeholders in circuits with values from `classical_source`.
return tfq.resolve_parameters(
full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))
Pilih beberapa qubit dan siapkan sirkuit penyandian data:
qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)
Berikutnya, menghitung PQK yang fitur didasarkan pada 1-RDM dari sirkuit dataset di atas dan menyimpan hasil di rdm , sebuah tf.Tensor dengan bentuk [n_points, n_qubits, 3] . Entri dalam rdm[i][j][k] = \(\langle \psi_i | OP^k_j | \psi_i \rangle\) mana i indeks lebih datapoints, j indeks lebih qubit dan k indeks lebih \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) .
def get_pqk_features(qubits, data_batch):
"""Get PQK features based on above construction."""
ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
batch_dim = tf.gather(tf.shape(data_batch), 0)
ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
return rdm
x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)
New PQK training dataset has shape: (1000, 11, 3) New PQK testing dataset has shape: (200, 11, 3)
2.2 Pelabelan ulang berdasarkan fitur PQK
Sekarang bahwa Anda memiliki fitur kuantum yang dihasilkan ini di x_train_pqk dan x_test_pqk , sekarang saatnya untuk kembali label dataset. Untuk mencapai pemisahan maksimum antara kuantum dan kinerja klasik Anda dapat kembali label dataset berdasarkan informasi spektrum ditemukan di x_train_pqk dan x_test_pqk .
def compute_kernel_matrix(vecs, gamma):
"""Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
scaled_gamma = gamma / (
tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)
def get_spectrum(datapoints, gamma=1.0):
"""Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
KC_qs = compute_kernel_matrix(datapoints, gamma)
S, V = tf.linalg.eigh(KC_qs)
S = tf.math.abs(S)
return S, V
S_pqk, V_pqk = get_spectrum(
tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))
S_original, V_original = get_spectrum(
tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)
print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)
Eigenvectors of pqk kernel matrix: tf.Tensor( [[-2.09569391e-02 1.05973557e-02 2.16634180e-02 ... 2.80352887e-02 1.55521873e-02 2.82677952e-02] [-2.29303762e-02 4.66355234e-02 7.91163836e-03 ... -6.14174758e-04 -7.07804322e-01 2.85902526e-02] [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02 2.11018627e-03 2.69009806e-02] ... [ 6.05797209e-02 1.32483775e-02 2.69536003e-02 ... -1.38843581e-02 3.05043962e-02 3.85345481e-02] [ 6.33309558e-02 -3.04112374e-03 9.77444276e-03 ... 7.48321265e-02 3.42793856e-03 3.67484428e-02] [ 5.86028099e-02 5.84433973e-03 2.64811981e-03 ... 2.82612257e-02 -3.80136147e-02 3.29943895e-02]], shape=(1200, 1200), dtype=float32) Eigenvectors of original kernel matrix: tf.Tensor( [[ 0.03835681 0.0283473 -0.01169789 ... 0.02343717 0.0211248 0.03206972] [-0.04018159 0.00888097 -0.01388255 ... 0.00582427 0.717551 0.02881948] [-0.0166719 0.01350376 -0.03663862 ... 0.02467175 -0.00415936 0.02195409] ... [-0.03015648 -0.01671632 -0.01603392 ... 0.00100583 -0.00261221 0.02365689] [ 0.0039777 -0.04998879 -0.00528336 ... 0.01560401 -0.04330755 0.02782002] [-0.01665728 -0.00818616 -0.0432341 ... 0.00088256 0.00927396 0.01875088]], shape=(1200, 1200), dtype=float32)
Sekarang Anda memiliki semua yang Anda butuhkan untuk memberi label ulang pada kumpulan data! Sekarang Anda dapat berkonsultasi dengan diagram alur untuk lebih memahami cara memaksimalkan pemisahan kinerja saat memberi label ulang pada kumpulan data:
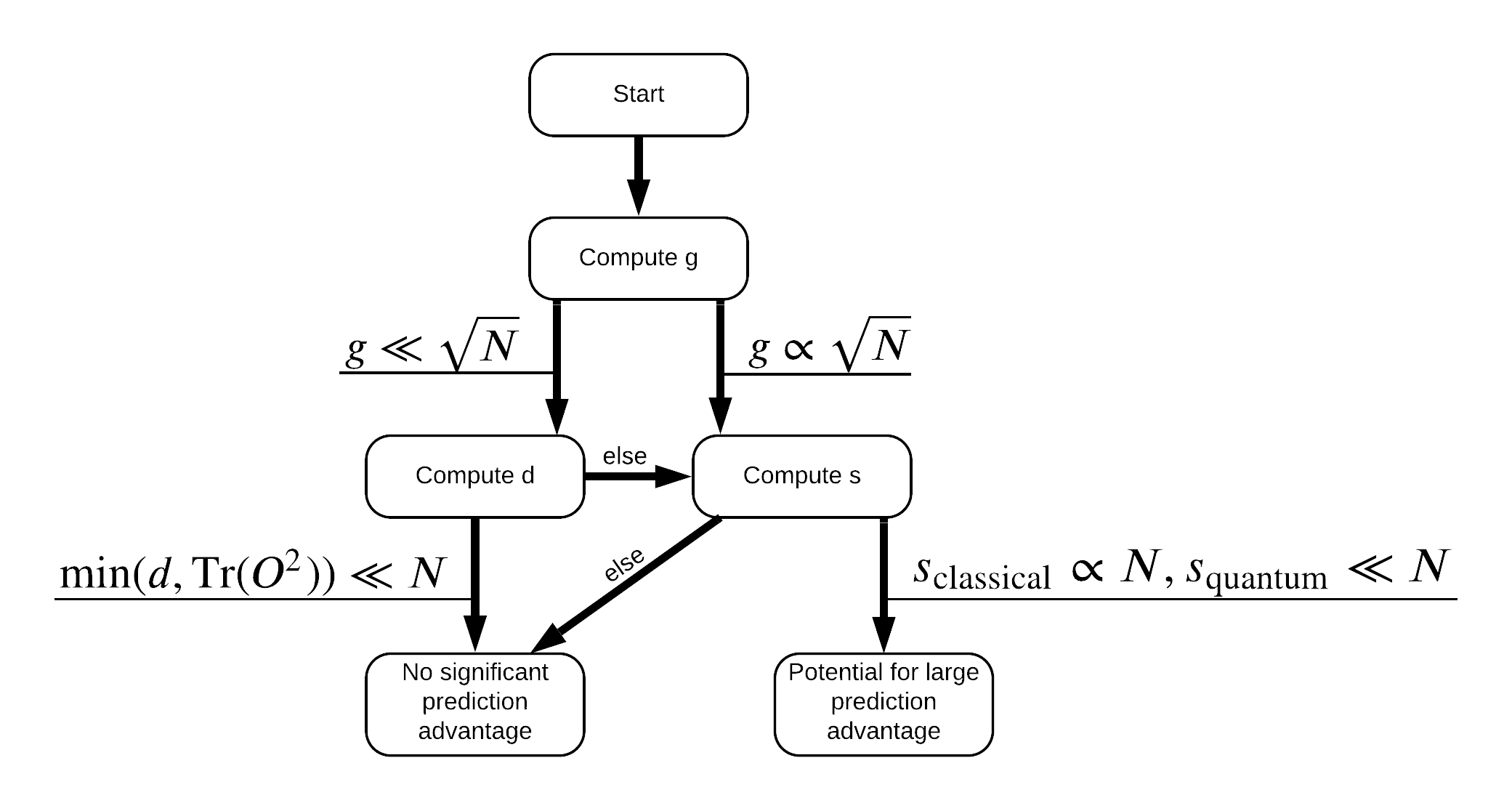
Dalam rangka untuk memaksimalkan pemisahan antara kuantum dan model klasik, Anda akan mencoba untuk memaksimalkan perbedaan geometris antara dataset asli dan PQK fitur kernel matriks \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) menggunakan S_pqk, V_pqk dan S_original, V_original . Nilai besar \(g\) memastikan bahwa Anda awalnya bergerak ke kanan di bawah flowchart menuju keunggulan prediksi dalam kasus kuantum.
def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
"""Prepare new labels that maximize geometric distance between kernels."""
S_diag = tf.linalg.diag(S ** 0.5)
S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
scaling = S_diag @ tf.transpose(V) @ \
V_2 @ S_2_diag @ tf.transpose(V_2) @ \
V @ S_diag
# Generate new lables using the largest eigenvector.
_, vecs = tf.linalg.eig(scaling)
new_labels = tf.math.real(
tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
# Create new labels and add some small amount of noise.
final_y = new_labels > np.median(new_labels)
noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
return noisy_y
y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]
3. Membandingkan model
Sekarang setelah Anda menyiapkan kumpulan data, sekarang saatnya untuk membandingkan kinerja model. Anda akan membuat dua jaringan saraf feedforward kecil dan membandingkan kinerja ketika mereka diberi akses ke PQK yang fitur yang ditemukan di x_train_pqk .
3.1 Buat model yang disempurnakan PQK
Menggunakan standar tf.keras fitur perpustakaan sekarang Anda dapat membuat dan kereta api model di x_train_pqk dan y_train_new datapoints:
#docs_infra: no_execute
def create_pqk_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
metrics=['accuracy'])
pqk_model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 32) 1088 _________________________________________________________________ dense_1 (Dense) (None, 16) 528 _________________________________________________________________ dense_2 (Dense) (None, 1) 17 ================================================================= Total params: 1,633 Trainable params: 1,633 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))
3.2 Membuat model klasik
Mirip dengan kode di atas, kini Anda juga dapat membuat model klasik yang tidak memiliki akses ke fitur PQK di kumpulan data Anda. Model ini dapat dilatih menggunakan x_train dan y_label_new .
#docs_infra: no_execute
def create_fair_classical_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
metrics=['accuracy'])
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 32) 352 _________________________________________________________________ dense_4 (Dense) (None, 16) 528 _________________________________________________________________ dense_5 (Dense) (None, 1) 17 ================================================================= Total params: 897 Trainable params: 897 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
classical_history = model.fit(x_train,
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(x_test, y_test_new))
3.3 Bandingkan kinerja
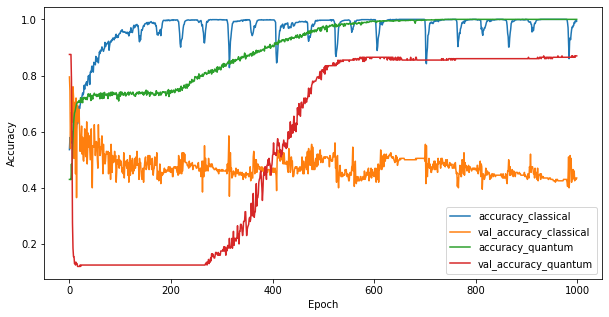
Sekarang setelah Anda melatih kedua model, Anda dapat dengan cepat memplot kesenjangan kinerja dalam data validasi di antara keduanya. Biasanya kedua model akan mencapai akurasi > 0,9 pada data pelatihan. Namun pada data validasi menjadi jelas bahwa hanya informasi yang ditemukan dalam fitur PQK yang cukup untuk membuat model menggeneralisasi dengan baik ke contoh yang tidak terlihat.
#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x7f6d846ecee0>
4. Kesimpulan penting
Ada beberapa kesimpulan penting yang dapat menarik dari ini dan MNIST percobaan:
Sangat tidak mungkin bahwa model kuantum hari ini akan mengalahkan kinerja model klasik pada data klasik. Terutama pada kumpulan data klasik saat ini yang dapat memiliki lebih dari satu juta titik data.
Hanya karena data mungkin berasal dari sirkuit kuantum yang sulit untuk disimulasikan secara klasik, tidak serta merta membuat data sulit dipelajari untuk model klasik.
Kumpulan data (yang pada akhirnya bersifat kuantum) yang mudah dipelajari model kuantum dan sulit dipelajari model klasik memang ada, terlepas dari arsitektur model atau algoritme pelatihan yang digunakan.
