কোয়ান্টাম তথ্য

TensorFlow.org এ দেখুন

Google Colab-এ চালান

GitHub-এ উৎস দেখুন

নোটবুক ডাউনলোড করুন

তৈরি তুলনা বন্ধ নির্মাণের MNIST টিউটোরিয়াল এই টিউটোরিয়ালের সাম্প্রতিক কাজ প্রতিবেদক হুয়াং এট অল। এটি দেখায় কিভাবে বিভিন্ন ডেটাসেট কর্মক্ষমতা তুলনা প্রভাবিত করে। কাজটিতে, লেখকরা কীভাবে এবং কখন ক্লাসিক্যাল মেশিন লার্নিং মডেলগুলি কোয়ান্টাম মডেলের পাশাপাশি (বা এর চেয়ে ভাল) শিখতে পারে তা বোঝার চেষ্টা করেন। কাজটি একটি সাবধানে তৈরি ডেটাসেটের মাধ্যমে ক্লাসিক্যাল এবং কোয়ান্টাম মেশিন লার্নিং মডেলের মধ্যে একটি অভিজ্ঞতামূলক কর্মক্ষমতা বিচ্ছেদও দেখায়। আপনি করবেন:

1. একটি হ্রাস মাত্রা ফ্যাশন-MNIST ডেটাসেট প্রস্তুত করুন৷
2. ডেটাসেট পুনরায় লেবেল করতে কোয়ান্টাম সার্কিট ব্যবহার করুন এবং প্রজেক্টেড কোয়ান্টাম কার্নেল বৈশিষ্ট্য (PQK) গণনা করুন।
3. পুনঃ-লেবেলযুক্ত ডেটাসেটে একটি ক্লাসিক্যাল নিউরাল নেটওয়ার্ককে প্রশিক্ষণ দিন এবং PQK বৈশিষ্ট্যগুলিতে অ্যাক্সেস রয়েছে এমন মডেলের সাথে পারফরম্যান্সের তুলনা করুন।

সেটআপ

pip install tensorflow==2.4.1 tensorflow-quantum

# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)

import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq

# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)

1. ডেটা প্রস্তুতি

আপনি একটি কোয়ান্টাম কম্পিউটারে চালানোর জন্য ফ্যাশন-MNIST ডেটাসেট প্রস্তুত করে শুরু করবেন।

1.1 ফ্যাশন-MNIST ডাউনলোড করুন

প্রথম ধাপ হল ঐতিহ্যবাহী ফ্যাশন-মিনিস্ট ডেটাসেট পাওয়া। এই ব্যবহার করা যেতে পারে tf.keras.datasets মডিউল।

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()

# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0

print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))

Number of original training examples: 60000
Number of original test examples: 10000

শুধু টি-শার্ট/টপস এবং ড্রেস রাখতে ডেটাসেট ফিল্টার করুন, অন্যান্য ক্লাস বাদ দিন। একই সময় ধর্মান্তরিত লেবেল, এ y , বুলিয়ান করতে: 0 জন্য সত্য এবং মিথ্যা 3 জন্য।

def filter_03(x, y):
    keep = (y == 0) | (y == 3)
    x, y = x[keep], y[keep]
    y = y == 0
    return x,y

x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)

print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))

Number of filtered training examples: 12000
Number of filtered test examples: 2000

print(y_train[0])

plt.imshow(x_train[0, :, :])
plt.colorbar()

True
<matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 ইমেজ ডাউনস্কেল

MNIST উদাহরণের মতো, বর্তমান কোয়ান্টাম কম্পিউটারের সীমানার মধ্যে থাকার জন্য আপনাকে এই চিত্রগুলিকে ডাউনস্কেল করতে হবে। এইবার তবে আপনি একটি পিসিএ রূপান্তর ব্যবহার পরিবর্তে মাত্রা একটি কমাতে হবে tf.image.resize অপারেশন।

def truncate_x(x_train, x_test, n_components=10):
  """Perform PCA on image dataset keeping the top `n_components` components."""
  n_points_train = tf.gather(tf.shape(x_train), 0)
  n_points_test = tf.gather(tf.shape(x_test), 0)

  # Flatten to 1D
  x_train = tf.reshape(x_train, [n_points_train, -1])
  x_test = tf.reshape(x_test, [n_points_test, -1])

  # Normalize.
  feature_mean = tf.reduce_mean(x_train, axis=0)
  x_train_normalized = x_train - feature_mean
  x_test_normalized = x_test - feature_mean

  # Truncate.
  e_values, e_vectors = tf.linalg.eigh(
      tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
  return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
    tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])

DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))

New datapoint dimension: 10

শেষ ধাপ হল ডেটাসেটের আকার কমিয়ে মাত্র 1000 প্রশিক্ষণ ডেটাপয়েন্ট এবং 200 টেস্টিং ডেটাপয়েন্টে করা।

N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]

print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))

New number of training examples: 1000
New number of test examples: 200

2. PQK বৈশিষ্ট্যগুলিকে রিলেবেলিং এবং কম্পিউটিং

আপনি এখন কোয়ান্টাম উপাদানগুলিকে অন্তর্ভুক্ত করে এবং আপনার উপরে তৈরি করা ছেঁটে ফেলা ফ্যাশন-MNIST ডেটাসেটটিকে পুনরায় লেবেল করে একটি "স্টিলড" কোয়ান্টাম ডেটাসেট প্রস্তুত করবেন৷ কোয়ান্টাম এবং ক্লাসিক্যাল পদ্ধতির মধ্যে সর্বাধিক বিচ্ছেদ পেতে, আপনি প্রথমে PQK বৈশিষ্ট্যগুলি প্রস্তুত করবেন এবং তারপরে তাদের মানগুলির উপর ভিত্তি করে আউটপুটগুলিকে পুনরায় বেল করবেন।

2.1 কোয়ান্টাম এনকোডিং এবং PQK বৈশিষ্ট্য

আপনি উপর ভিত্তি করে, বৈশিষ্ট্য একটি নতুন সেট তৈরি করবে x_train , y_train , x_test এবং y_test যে সব qubits উপর 1-RDM হতে সংজ্ঞায়িত করা হয়:

\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)

কোথায় \(U_\text{1qb}\) একক qubit ঘুর্ণন এবং একটি প্রাচীর হয় \(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)

প্রথমত, আপনি একক কিউবিট ঘূর্ণনের প্রাচীর তৈরি করতে পারেন:

def single_qubit_wall(qubits, rotations):
  """Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
  wall_circuit = cirq.Circuit()
  for i, qubit in enumerate(qubits):
    for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
      wall_circuit.append(gate(qubit) ** rotations[i][j])

  return wall_circuit

সার্কিটটি দেখে আপনি দ্রুত এই কাজটি যাচাই করতে পারেন:

SVGCircuit(single_qubit_wall(
    cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))

এর পরে আপনি প্রস্তুত করতে পারেন \(V(\hat{\theta})\) সাহায্যে tfq.util.exponential যা কোনো যাতায়াত exponentiate করতে cirq.PauliSum বস্তু:

def v_theta(qubits):
  """Prepares a circuit that generates V(\theta)."""
  ref_paulis = [
      cirq.X(q0) * cirq.X(q1) + \
      cirq.Y(q0) * cirq.Y(q1) + \
      cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
  ]
  exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
  return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols

এই সার্কিটটি দেখে যাচাই করা কিছুটা কঠিন হতে পারে, তবে আপনি এখনও কি ঘটছে তা দেখতে একটি দুটি কিউবিট কেস পরীক্ষা করতে পারেন:

test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)

Symbols found in circuit:[ref_0]

এখন আপনার কাছে সমস্ত বিল্ডিং ব্লক রয়েছে যা আপনাকে আপনার সম্পূর্ণ এনকোডিং সার্কিটগুলিকে একসাথে রাখতে হবে:

def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
  """Prepare the pqk feature circuits around a dataset."""
  n_qubits = len(qubits)
  n_points = len(classical_source)

  # Prepare random single qubit rotation wall.
  random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
  initial_U = single_qubit_wall(qubits, random_rots)

  # Prepare parametrized V
  V_circuit, symbols = v_theta(qubits)
  exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))

  # Convert to `tf.Tensor`
  initial_U_tensor = tfq.convert_to_tensor([initial_U])
  initial_U_splat = tf.tile(initial_U_tensor, [n_points])

  full_circuits = tfq.layers.AddCircuit()(
      initial_U_splat, append=exp_circuit)
  # Replace placeholders in circuits with values from `classical_source`.
  return tfq.resolve_parameters(
      full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
      tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))

কিছু qubits চয়ন করুন এবং ডেটা এনকোডিং সার্কিট প্রস্তুত করুন:

qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)

এর পরে, গনা PQK উপরে ডেটা সেটটি সার্কিট 1-RDM উপর ভিত্তি করে বৈশিষ্ট্য এবং ফলাফলে সংরক্ষণ rdm , একটি tf.Tensor আকৃতি সঙ্গে [n_points, n_qubits, 3] । এন্ট্রিগুলির rdm[i][j][k] = \(\langle \psi_i | OP^k_j | \psi_i \rangle\) যেখানে i datapoints উপর ইনডেক্স, j qubits এবং উপর ইনডেক্স k উপর ইনডেক্স \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) ।

def get_pqk_features(qubits, data_batch):
  """Get PQK features based on above construction."""
  ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
  ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
  batch_dim = tf.gather(tf.shape(data_batch), 0)
  ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
  exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
  rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
  return rdm

x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)

New PQK training dataset has shape: (1000, 11, 3)
New PQK testing dataset has shape: (200, 11, 3)

2.2 PQK বৈশিষ্ট্যের উপর ভিত্তি করে রি-লেবেলিং

এখন আপনি এই কোয়ান্টাম উত্পন্ন বৈশিষ্ট্য আছে x_train_pqk এবং x_test_pqk , এটা পুনরায় লেবেল ডেটা সেটটি করার সময়। কোয়ান্টাম এবং শাস্ত্রীয় কর্মক্ষমতা আপনি পারেন মধ্যে সর্বোচ্চ অনুযায়ী বিবাহবিচ্ছেদ অর্জন বর্ণালী তথ্যের উপর ভিত্তি করে ডেটা সেটটি পুনরায় লেবেল পাওয়া x_train_pqk এবং x_test_pqk ।

def compute_kernel_matrix(vecs, gamma):
  """Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
  scaled_gamma = gamma / (
      tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
  return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)

def get_spectrum(datapoints, gamma=1.0):
  """Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
  KC_qs = compute_kernel_matrix(datapoints, gamma)
  S, V = tf.linalg.eigh(KC_qs)
  S = tf.math.abs(S)
  return S, V

S_pqk, V_pqk = get_spectrum(
    tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))

S_original, V_original = get_spectrum(
    tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)

print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)

Eigenvectors of pqk kernel matrix: tf.Tensor(
[[-2.09569391e-02  1.05973557e-02  2.16634180e-02 ...  2.80352887e-02
   1.55521873e-02  2.82677952e-02]
 [-2.29303762e-02  4.66355234e-02  7.91163836e-03 ... -6.14174758e-04
  -7.07804322e-01  2.85902526e-02]
 [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02
   2.11018627e-03  2.69009806e-02]
 ...
 [ 6.05797209e-02  1.32483775e-02  2.69536003e-02 ... -1.38843581e-02
   3.05043962e-02  3.85345481e-02]
 [ 6.33309558e-02 -3.04112374e-03  9.77444276e-03 ...  7.48321265e-02
   3.42793856e-03  3.67484428e-02]
 [ 5.86028099e-02  5.84433973e-03  2.64811981e-03 ...  2.82612257e-02
  -3.80136147e-02  3.29943895e-02]], shape=(1200, 1200), dtype=float32)
Eigenvectors of original kernel matrix: tf.Tensor(
[[ 0.03835681  0.0283473  -0.01169789 ...  0.02343717  0.0211248
   0.03206972]
 [-0.04018159  0.00888097 -0.01388255 ...  0.00582427  0.717551
   0.02881948]
 [-0.0166719   0.01350376 -0.03663862 ...  0.02467175 -0.00415936
   0.02195409]
 ...
 [-0.03015648 -0.01671632 -0.01603392 ...  0.00100583 -0.00261221
   0.02365689]
 [ 0.0039777  -0.04998879 -0.00528336 ...  0.01560401 -0.04330755
   0.02782002]
 [-0.01665728 -0.00818616 -0.0432341  ...  0.00088256  0.00927396
   0.01875088]], shape=(1200, 1200), dtype=float32)

এখন আপনার কাছে ডেটাসেটটি পুনরায় লেবেল করার জন্য প্রয়োজনীয় সমস্ত কিছু রয়েছে! ডেটাসেটটিকে পুনরায় লেবেল করার সময় কীভাবে পারফরম্যান্স পৃথকীকরণকে সর্বাধিক করা যায় তা আরও ভালভাবে বুঝতে আপনি এখন ফ্লোচার্টের সাথে পরামর্শ করতে পারেন:

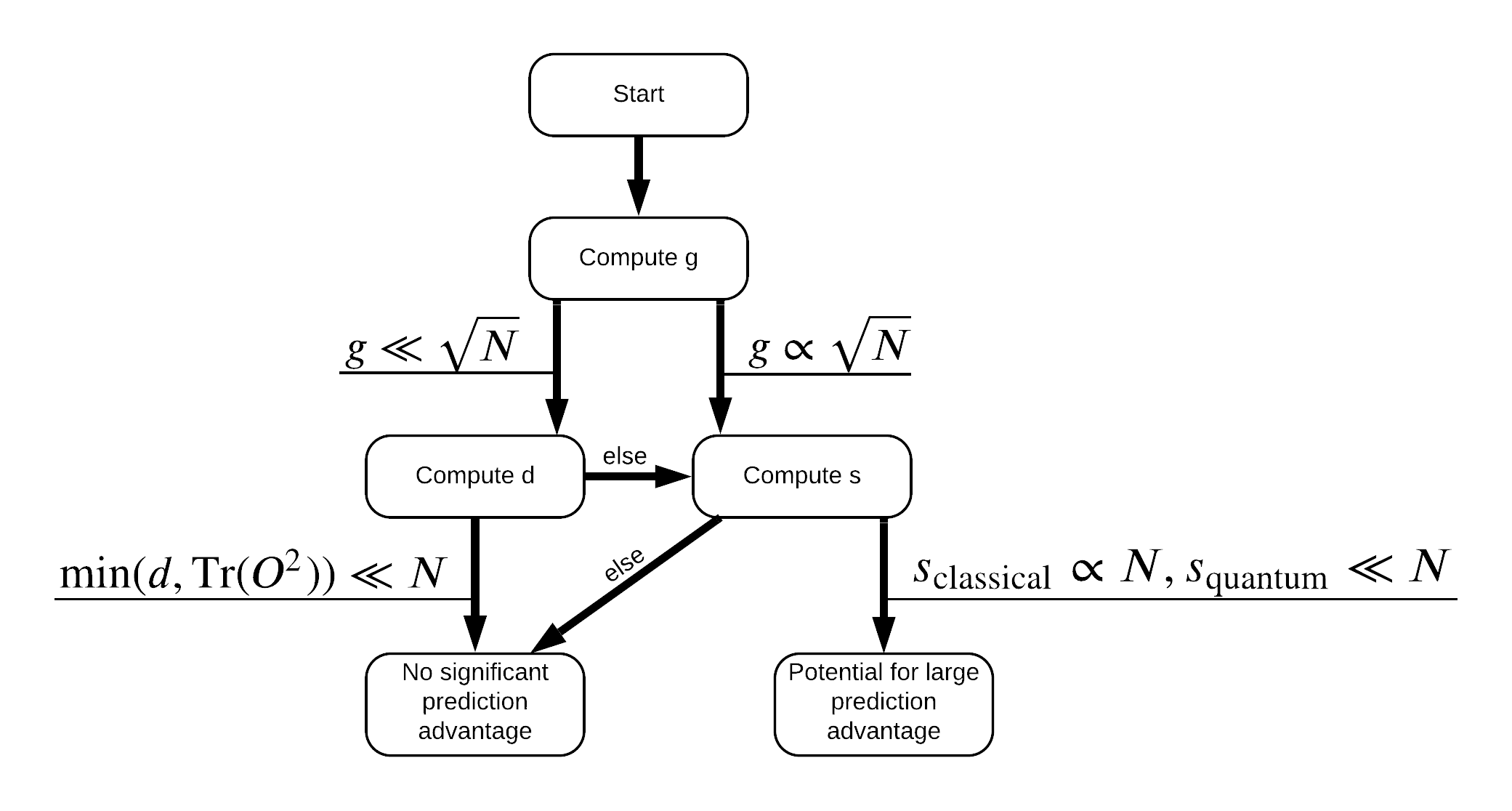
অর্ডার কোয়ান্টাম এবং শাস্ত্রীয় মডেলের মধ্যে অনুযায়ী বিবাহবিচ্ছেদ পূর্ণবিস্তার জন্য, আপনাকে মূল ডেটা সেটটি মধ্যে জ্যামিতিক পার্থক্য পূর্ণবিস্তার করার প্রচেষ্টা করা হবে ও PQK কার্নেল ম্যাট্রিক্স অতিরিক্ত বৈশিষ্ট্যগুলিও উপস্থিত রয়েছে \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) ব্যবহার S_pqk, V_pqk এবং S_original, V_original । এর একটা বড় মূল্য \(g\) নিশ্চিত আপনি প্রাথমিকভাবে কোয়ান্টাম ক্ষেত্রে একটি পূর্বানুমান সুবিধা প্রতি ফ্লোচার্ট নিচে ডানে সরানো হয়।

def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
  """Prepare new labels that maximize geometric distance between kernels."""
  S_diag = tf.linalg.diag(S ** 0.5)
  S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
  scaling = S_diag @ tf.transpose(V) @ \
            V_2 @ S_2_diag @ tf.transpose(V_2) @ \
            V @ S_diag

  # Generate new lables using the largest eigenvector.
  _, vecs = tf.linalg.eig(scaling)
  new_labels = tf.math.real(
      tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
  # Create new labels and add some small amount of noise.
  final_y = new_labels > np.median(new_labels)
  noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
  return noisy_y

y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]

3. মডেল তুলনা

এখন আপনি আপনার ডেটাসেট প্রস্তুত করেছেন এখন মডেলের কর্মক্ষমতা তুলনা করার সময়। আপনি দুটি ছোট feedforward স্নায়ুর নেটওয়ার্ক তৈরি এবং কর্মক্ষমতা তুলনা যখন তারা PQK অ্যাক্সেস দেওয়া হয় পাওয়া বৈশিষ্ট্য হবে x_train_pqk ।

3.1 PQK উন্নত মডেল তৈরি করুন

মান ব্যবহার tf.keras আপনি এখন তৈরি করতে পারেন গ্রন্থাগার বৈশিষ্ট্য এবং একটি ট্রেনে একটি মডেল x_train_pqk এবং y_train_new datapoints:

#docs_infra: no_execute
def create_pqk_model():
    model = tf.keras.Sequential()
    model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
    model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
    model.add(tf.keras.layers.Dense(1))
    return model

pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
              optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
              metrics=['accuracy'])

pqk_model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 32)                1088      
_________________________________________________________________
dense_1 (Dense)              (None, 16)                528       
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 17        
=================================================================
Total params: 1,633
Trainable params: 1,633
Non-trainable params: 0
_________________________________________________________________

#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
          y_train_new,
          batch_size=32,
          epochs=1000,
          verbose=0,
          validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))

3.2 একটি শাস্ত্রীয় মডেল তৈরি করুন

উপরের কোডের অনুরূপ আপনি এখন একটি ক্লাসিক্যাল মডেলও তৈরি করতে পারেন যা আপনার স্টিল করা ডেটাসেটে PQK বৈশিষ্ট্যগুলিতে অ্যাক্সেস নেই। এই মডেল ব্যবহার প্রশিক্ষিত করা যেতে পারে x_train এবং y_label_new ।

#docs_infra: no_execute
def create_fair_classical_model():
    model = tf.keras.Sequential()
    model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
    model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
    model.add(tf.keras.layers.Dense(1))
    return model

model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
              optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
              metrics=['accuracy'])

model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_3 (Dense)              (None, 32)                352       
_________________________________________________________________
dense_4 (Dense)              (None, 16)                528       
_________________________________________________________________
dense_5 (Dense)              (None, 1)                 17        
=================================================================
Total params: 897
Trainable params: 897
Non-trainable params: 0
_________________________________________________________________

#docs_infra: no_execute
classical_history = model.fit(x_train,
          y_train_new,
          batch_size=32,
          epochs=1000,
          verbose=0,
          validation_data=(x_test, y_test_new))

3.3 কর্মক্ষমতা তুলনা করুন

এখন যেহেতু আপনি দুটি মডেলকে প্রশিক্ষিত করেছেন আপনি দ্রুত উভয়ের মধ্যে বৈধতা ডেটাতে কর্মক্ষমতা ফাঁকগুলি প্লট করতে পারেন৷ সাধারণত উভয় মডেলই প্রশিক্ষণ ডেটাতে > 0.9 নির্ভুলতা অর্জন করবে। যাইহোক, যাচাইকরণের ডেটাতে এটি স্পষ্ট হয়ে যায় যে শুধুমাত্র PQK বৈশিষ্ট্যগুলিতে পাওয়া তথ্যগুলি মডেলটিকে অদেখা দৃষ্টান্তগুলিতে ভালভাবে সাধারণীকরণ করার জন্য যথেষ্ট।

#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()

<matplotlib.legend.Legend at 0x7f6d846ecee0>

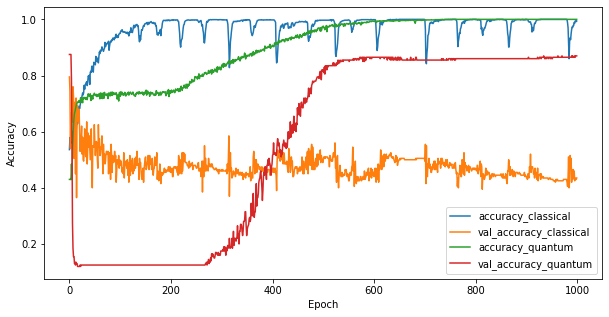
4. গুরুত্বপূর্ণ উপসংহার

সেখানে বেশ কিছু গুরুত্বপূর্ণ সিদ্ধান্তে আপনি এই থেকে আহরণ করতে পারে হয় MNIST পরীক্ষায়:

1. এটা খুবই অসম্ভাব্য যে আজকের কোয়ান্টাম মডেলগুলি ক্লাসিক্যাল ডেটাতে ক্লাসিক্যাল মডেলের পারফরম্যান্সকে পরাজিত করবে। বিশেষ করে আজকের ক্লাসিক্যাল ডেটাসেটগুলিতে যেখানে এক মিলিয়নের বেশি ডেটাপয়েন্ট থাকতে পারে।

2. কোয়ান্টাম সার্কিট ক্লাসিকভাবে অনুকরণ করা কঠিন থেকে ডেটা আসতে পারে বলেই, ক্লাসিক্যাল মডেলের জন্য ডেটা শেখা কঠিন করে তোলে না।

3. ডেটাসেটগুলি (পরিশেষে প্রকৃতিতে কোয়ান্টাম) যেগুলি কোয়ান্টাম মডেলগুলির জন্য সহজ এবং ক্লাসিক্যাল মডেলগুলির শেখার জন্য কঠিন তা বিদ্যমান রয়েছে, মডেল আর্কিটেকচার বা প্রশিক্ষণ অ্যালগরিদম ব্যবহার করা নির্বিশেষে।