Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Tiếng ồn hiện diện trong các máy tính lượng tử ngày nay. Qubit dễ bị nhiễu từ môi trường xung quanh, chế tạo không hoàn hảo, TLS và đôi khi cả tia gamma . Cho đến khi đạt được hiệu chỉnh lỗi quy mô lớn, các thuật toán ngày nay phải có thể duy trì hoạt động khi có nhiễu. Điều này làm cho các thuật toán thử nghiệm dưới nhiễu trở thành một bước quan trọng để xác nhận các thuật toán / mô hình lượng tử sẽ hoạt động trên các máy tính lượng tử ngày nay.
Trong hướng dẫn này, bạn sẽ khám phá những điều cơ bản về mô phỏng mạch nhiễu trong TFQ thông qua API tfq.layers cấp cao.
Thành lập
pip install tensorflow==2.7.0 tensorflow-quantum
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2022-02-04 12:35:30.853880: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Tìm hiểu về tiếng ồn lượng tử
1.1 Tiếng ồn mạch cơ bản
Tiếng ồn trên máy tính lượng tử ảnh hưởng đến các mẫu chuỗi bit mà bạn có thể đo từ nó. Một cách trực quan mà bạn có thể bắt đầu nghĩ về điều này là một máy tính lượng tử ồn ào sẽ "chèn", "xóa" hoặc "thay thế" các cổng ở những nơi ngẫu nhiên như sơ đồ dưới đây:
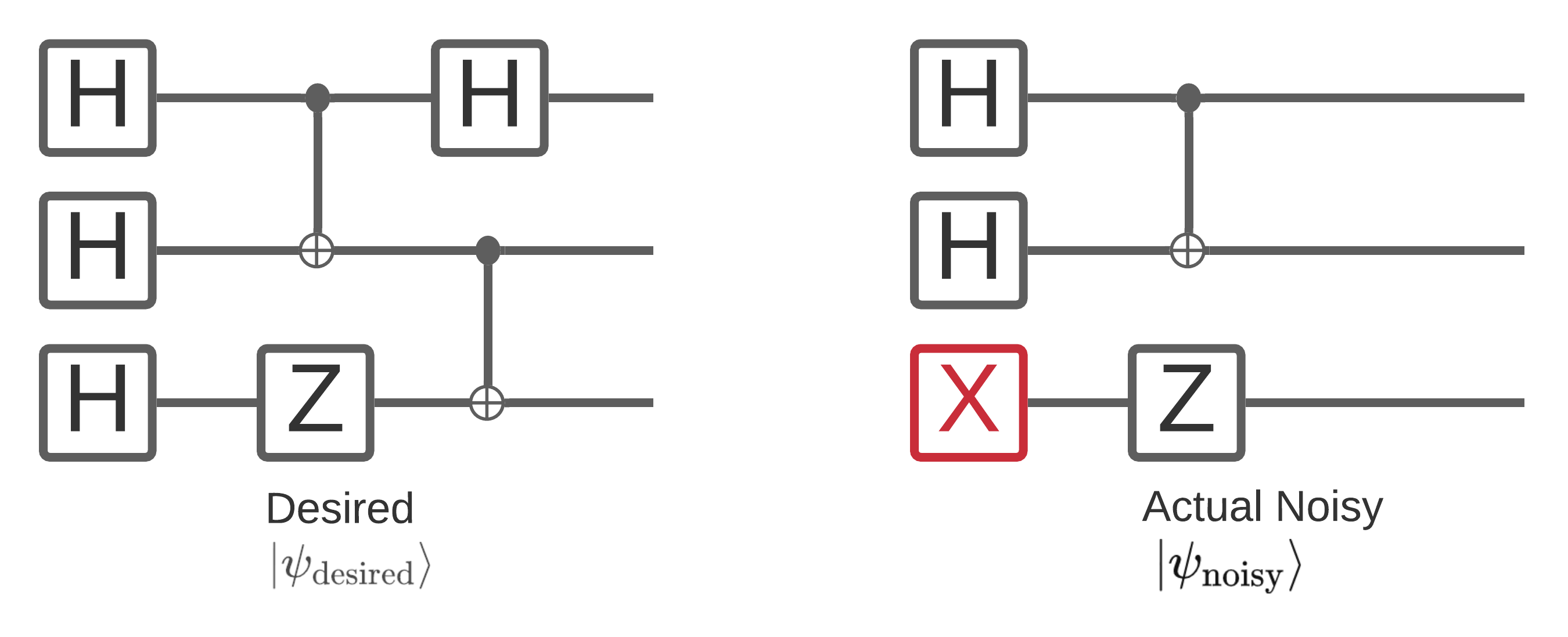
Dựa trên trực giác này, khi xử lý nhiễu, bạn không còn sử dụng một trạng thái thuần túy duy nhất \(|\psi \rangle\) mà thay vào đó xử lý một tập hợp tất cả các hiện thực nhiễu có thể xảy ra đối với mạch mong muốn của bạn: \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) . Trong đó \(p_j\) cho xác suất hệ thống ở trong \(|\psi_j \rangle\) .
Xem lại bức tranh trên, nếu chúng ta biết trước rằng 90% thời gian hệ thống của chúng ta hoạt động hoàn hảo hoặc bị lỗi 10% thời gian chỉ với một chế độ lỗi này, thì tổng thể của chúng ta sẽ là:
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
Nếu có nhiều hơn một cách mà mạch của chúng ta có thể bị lỗi, thì tập hợp \(\rho\) sẽ chứa nhiều hơn chỉ hai thuật ngữ (một thuật ngữ cho mỗi hiện thực nhiễu mới có thể xảy ra). \(\rho\) được gọi là ma trận mật độ mô tả hệ thống ồn ào của bạn.
1.2 Sử dụng các kênh để mô hình hóa nhiễu mạch
Thật không may trong thực tế, gần như không thể biết tất cả các cách mạch của bạn có thể lỗi và xác suất chính xác của chúng. Một giả định đơn giản hóa mà bạn có thể đưa ra là sau mỗi thao tác trong mạch của bạn, có một số loại kênh nắm bắt được một cách đại khái cách hoạt động đó có thể bị lỗi. Bạn có thể nhanh chóng tạo một mạch với một số tiếng ồn:
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
Bạn có thể kiểm tra ma trận mật độ không ồn \(\rho\) với:
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
Và ma trận mật độ nhiễu \(\rho\) với:
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
So sánh hai \( \rho \) khác nhau, bạn có thể thấy rằng tiếng ồn đã ảnh hưởng đến biên độ của trạng thái (và do đó xác suất lấy mẫu). Trong trường hợp không ồn ào, bạn luôn mong đợi lấy mẫu trạng thái \( |11\rangle \) . Nhưng trong trạng thái nhiễu hiện có một xác suất khác không của việc lấy mẫu \( |00\rangle \) hoặc \( |01\rangle \) hoặc \( |10\rangle \) :
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
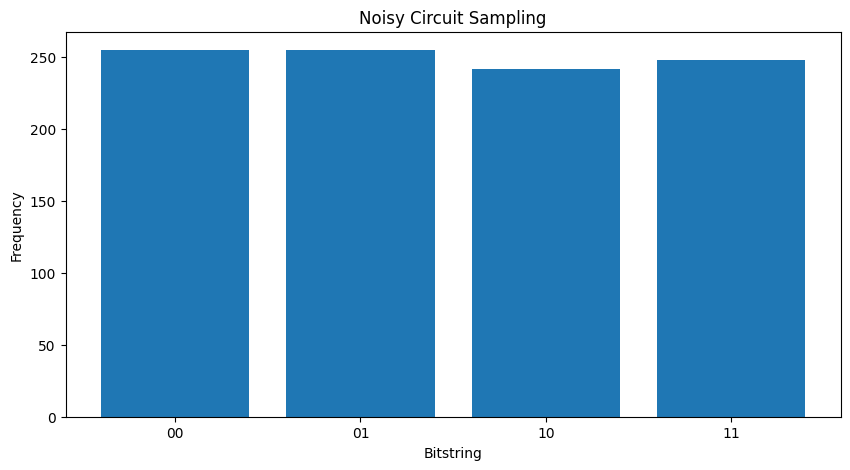
plot_samples(my_noisy_circuit)
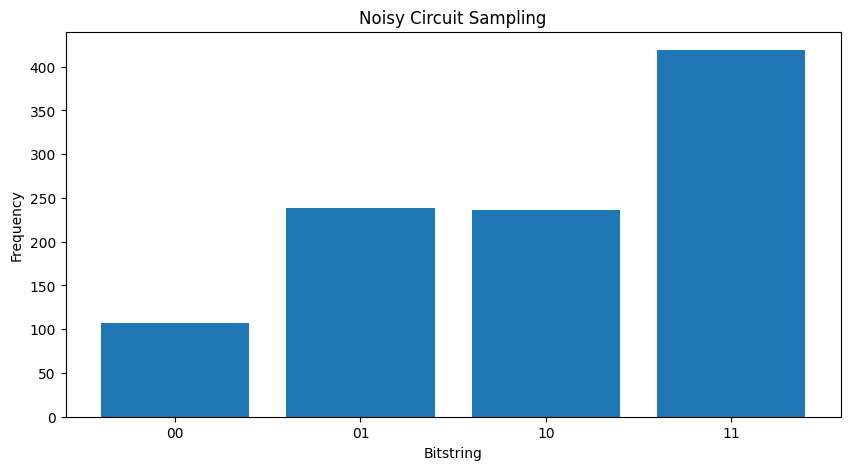
Không có bất kỳ tiếng ồn nào, bạn sẽ luôn nhận được \(|11\rangle\):
"""Sample from my_circuit."""
plot_samples(my_circuit)
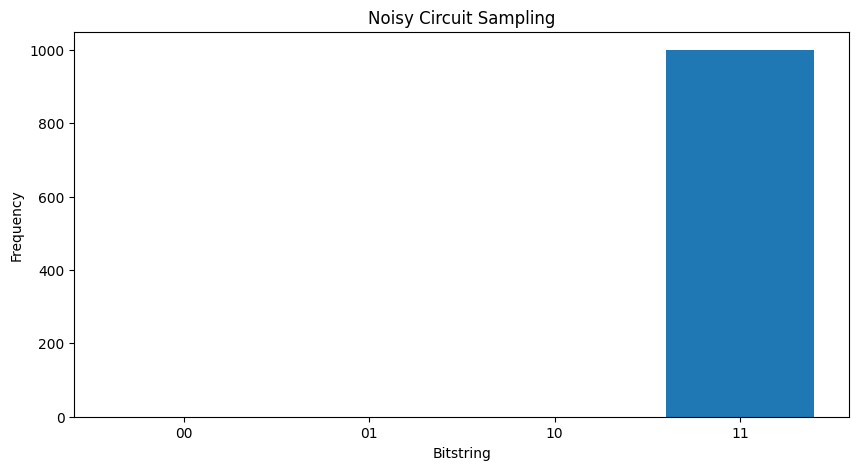
Nếu bạn tăng tiếng ồn thêm một chút, nó sẽ ngày càng khó phân biệt hành vi mong muốn (lấy mẫu \(|11\rangle\) ) với tiếng ồn:
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
2. Tiếng ồn cơ bản trong TFQ
Với sự hiểu biết này về cách tiếng ồn có thể ảnh hưởng đến việc thực thi mạch, bạn có thể khám phá cách tiếng ồn hoạt động trong TFQ. TensorFlow Quantum sử dụng mô phỏng dựa trên monte-carlo / quỹ đạo như một giải pháp thay thế cho mô phỏng ma trận mật độ. Điều này là do độ phức tạp bộ nhớ của mô phỏng ma trận mật độ giới hạn các mô phỏng lớn là <= 20 qubit với các phương pháp mô phỏng ma trận mật độ đầy đủ truyền thống. Monte-carlo / quỹ đạo giao dịch chi phí này trong bộ nhớ để có thêm chi phí theo thời gian. Tùy chọn backend='noisy' có sẵn cho tất cả tfq.layers.Sample , tfq.layers.SampledExpectation và tfq.layers.Expectation (Trong trường hợp Expectation , điều này sẽ thêm một tham số repetitions bắt buộc).
2.1 Lấy mẫu nhiễu trong TFQ
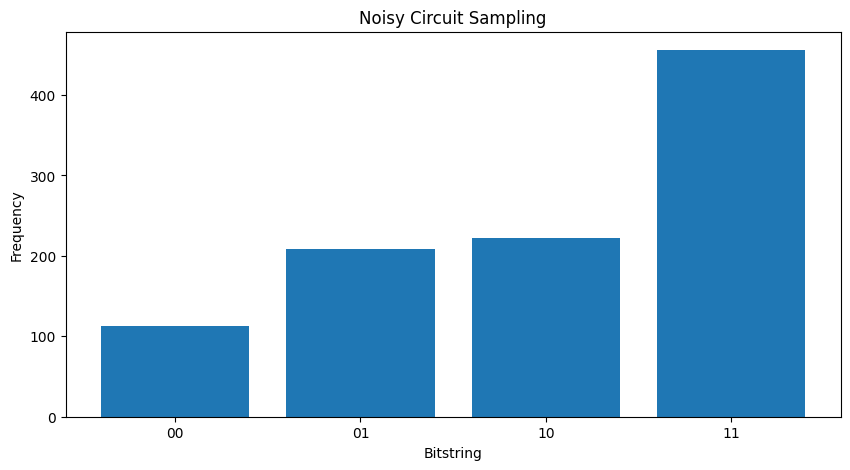
Để tạo lại các biểu đồ trên bằng cách sử dụng TFQ và mô phỏng quỹ đạo, bạn có thể sử dụng tfq.layers.Sample
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
2.2 Kỳ vọng dựa trên mẫu ồn ào
Để thực hiện tính toán kỳ vọng dựa trên mẫu ồn ào, bạn có thể sử dụng tfq.layers.SampleExpectation .
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
Tính toán các ước tính kỳ vọng không ồn ào thông qua lấy mẫu từ mạch:
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[-0.0028, -1. , 1.0264]], dtype=float32)
So sánh chúng với các phiên bản ồn ào:
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
array([[ 0.0242 , -0.33200002, 1.0138001 ],
[ 0.0108 , -0.0012 , 0.9502 ]], dtype=float32)
Bạn có thể thấy rằng tiếng ồn đã ảnh hưởng đặc biệt đến độ chính xác của \(\langle \psi | Z | \psi \rangle\) , với my_really_noisy_circuit tập trung rất nhanh về phía 0.
2.3 Tính toán kỳ vọng phân tích ồn ào
Thực hiện các phép tính kỳ vọng phân tích ồn ào gần giống như trên:
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106850e-15, -3.3359998e-01, 1.0000000e+00],
[ 1.9106857e-15, -3.8000005e-03, 1.0000001e+00]], dtype=float32)
3. Mô hình lai và nhiễu dữ liệu lượng tử
Bây giờ bạn đã thực hiện một số mô phỏng mạch ồn trong TFQ, bạn có thể thử nghiệm xem tiếng ồn ảnh hưởng như thế nào đến các mô hình cổ điển lượng tử và lượng tử lai, bằng cách so sánh và đối chiếu hiệu suất ồn ào và không ồn ào của chúng. Cách kiểm tra đầu tiên tốt để xem liệu một mô hình hoặc thuật toán có mạnh mẽ với nhiễu hay không là kiểm tra dưới mô hình khử cực toàn mạch trông giống như sau:
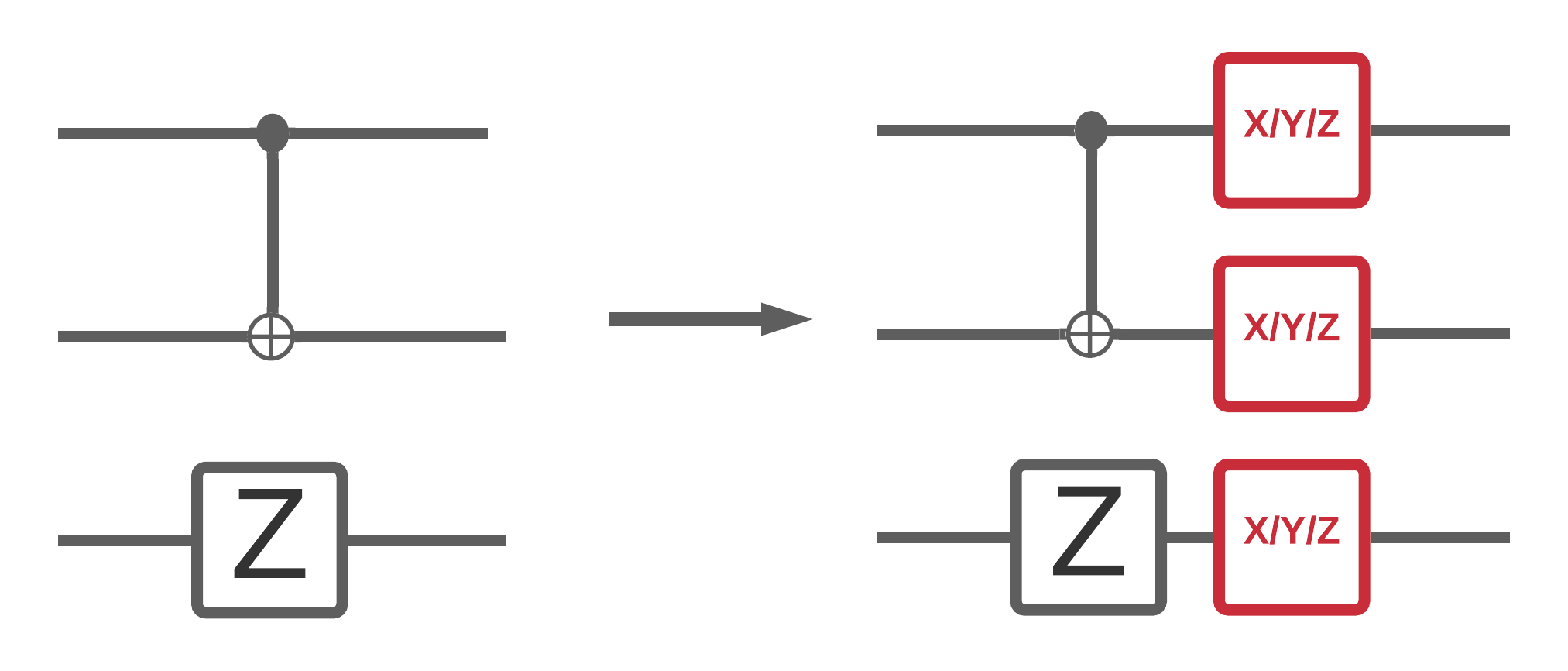
Trong đó mỗi lát thời gian của mạch (đôi khi được gọi là thời điểm) có một kênh khử cực được nối sau mỗi hoạt động của cổng trong lát thời gian đó. Kênh khử cực áp dụng một trong \(\{X, Y, Z \}\) với xác suất \(p\) hoặc không áp dụng gì (giữ nguyên hoạt động ban đầu) với xác suất \(1-p\).
3.1 Dữ liệu
Đối với ví dụ này, bạn có thể sử dụng một số mạch đã chuẩn bị trong mô-đun tfq.datasets làm dữ liệu đào tạo:
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184451072/184449737 [==============================] - 2s 0us/step 184459264/184449737 [==============================] - 2s 0us/step
Viết một hàm trợ giúp nhỏ sẽ giúp tạo dữ liệu cho trường hợp ồn ào và không ồn ào:
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 Xác định một mạch mô hình
Bây giờ bạn có dữ liệu lượng tử ở dạng mạch, bạn sẽ cần một mạch để mô hình hóa dữ liệu này, giống như với dữ liệu, bạn có thể viết một hàm trợ giúp để tạo ra mạch này có chứa nhiễu tùy chọn:
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 Xây dựng và đào tạo mô hình
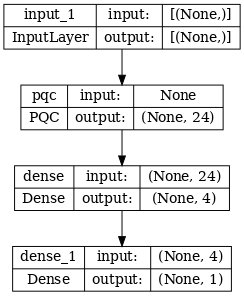
Với dữ liệu và mạch mô hình của bạn đã được xây dựng, chức năng trợ giúp cuối cùng mà bạn sẽ cần là một chức năng có thể lắp ráp cả tf.keras.Model lượng tử hỗn hợp ồn ào hoặc không ồn ào.
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. So sánh hiệu suất
4.1 Đường cơ sở không ồn ào
Với việc tạo dữ liệu và mã xây dựng mô hình, giờ đây bạn có thể so sánh và đối chiếu hiệu suất của mô hình trong cài đặt không ồn ào và ồn ào, trước tiên bạn có thể chạy một khóa đào tạo không ồn ào tham khảo:
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 133ms/step - loss: 0.7212 - accuracy: 0.4688 - val_loss: 0.6834 - val_accuracy: 0.5000 Epoch 2/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6787 - accuracy: 0.4688 - val_loss: 0.6640 - val_accuracy: 0.5000 Epoch 3/50 4/4 [==============================] - 0s 76ms/step - loss: 0.6637 - accuracy: 0.4688 - val_loss: 0.6529 - val_accuracy: 0.5000 Epoch 4/50 4/4 [==============================] - 0s 78ms/step - loss: 0.6505 - accuracy: 0.4688 - val_loss: 0.6423 - val_accuracy: 0.5000 Epoch 5/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6409 - accuracy: 0.4688 - val_loss: 0.6322 - val_accuracy: 0.5000 Epoch 6/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6300 - accuracy: 0.4844 - val_loss: 0.6187 - val_accuracy: 0.5000 Epoch 7/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6171 - accuracy: 0.5781 - val_loss: 0.6007 - val_accuracy: 0.5000 Epoch 8/50 4/4 [==============================] - 0s 79ms/step - loss: 0.6008 - accuracy: 0.6250 - val_loss: 0.5825 - val_accuracy: 0.5833 Epoch 9/50 4/4 [==============================] - 0s 76ms/step - loss: 0.5864 - accuracy: 0.6406 - val_loss: 0.5610 - val_accuracy: 0.6667 Epoch 10/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5670 - accuracy: 0.6719 - val_loss: 0.5406 - val_accuracy: 0.8333 Epoch 11/50 4/4 [==============================] - 0s 79ms/step - loss: 0.5474 - accuracy: 0.6875 - val_loss: 0.5173 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5276 - accuracy: 0.7188 - val_loss: 0.4941 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 0s 75ms/step - loss: 0.5066 - accuracy: 0.7500 - val_loss: 0.4686 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4838 - accuracy: 0.7812 - val_loss: 0.4437 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4618 - accuracy: 0.8281 - val_loss: 0.4182 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4386 - accuracy: 0.8281 - val_loss: 0.3930 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 0s 79ms/step - loss: 0.4158 - accuracy: 0.8438 - val_loss: 0.3673 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 79ms/step - loss: 0.3944 - accuracy: 0.8438 - val_loss: 0.3429 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3735 - accuracy: 0.8594 - val_loss: 0.3203 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3535 - accuracy: 0.8750 - val_loss: 0.2998 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 78ms/step - loss: 0.3345 - accuracy: 0.8906 - val_loss: 0.2815 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3168 - accuracy: 0.8906 - val_loss: 0.2640 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3017 - accuracy: 0.9062 - val_loss: 0.2465 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2840 - accuracy: 0.9219 - val_loss: 0.2328 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2700 - accuracy: 0.9219 - val_loss: 0.2181 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2566 - accuracy: 0.9219 - val_loss: 0.2053 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 77ms/step - loss: 0.2445 - accuracy: 0.9375 - val_loss: 0.1935 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2332 - accuracy: 0.9375 - val_loss: 0.1839 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 78ms/step - loss: 0.2227 - accuracy: 0.9375 - val_loss: 0.1734 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2145 - accuracy: 0.9375 - val_loss: 0.1630 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2047 - accuracy: 0.9375 - val_loss: 0.1564 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1971 - accuracy: 0.9375 - val_loss: 0.1525 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1894 - accuracy: 0.9531 - val_loss: 0.1464 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 74ms/step - loss: 0.1825 - accuracy: 0.9531 - val_loss: 0.1407 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1771 - accuracy: 0.9531 - val_loss: 0.1330 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1704 - accuracy: 0.9531 - val_loss: 0.1288 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1647 - accuracy: 0.9531 - val_loss: 0.1237 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 80ms/step - loss: 0.1603 - accuracy: 0.9531 - val_loss: 0.1221 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1551 - accuracy: 0.9688 - val_loss: 0.1177 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1509 - accuracy: 0.9688 - val_loss: 0.1136 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1466 - accuracy: 0.9688 - val_loss: 0.1110 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1426 - accuracy: 0.9688 - val_loss: 0.1083 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1386 - accuracy: 0.9688 - val_loss: 0.1050 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 83ms/step - loss: 0.1362 - accuracy: 0.9688 - val_loss: 0.0989 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 78ms/step - loss: 0.1324 - accuracy: 0.9688 - val_loss: 0.0978 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1290 - accuracy: 0.9688 - val_loss: 0.0964 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1265 - accuracy: 0.9688 - val_loss: 0.0929 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1234 - accuracy: 0.9688 - val_loss: 0.0923 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1213 - accuracy: 0.9688 - val_loss: 0.0903 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1182 - accuracy: 0.9688 - val_loss: 0.0885 - val_accuracy: 1.0000
Và khám phá kết quả và độ chính xác:
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
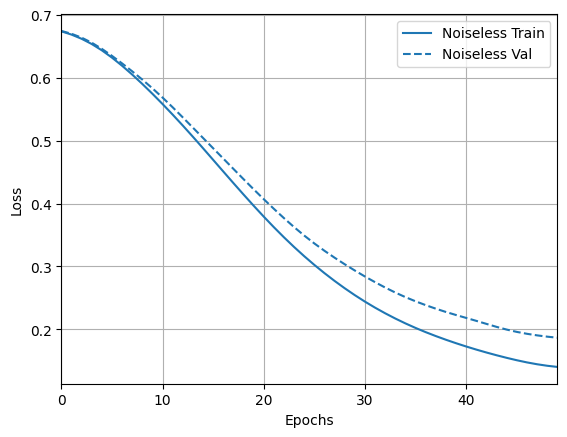
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
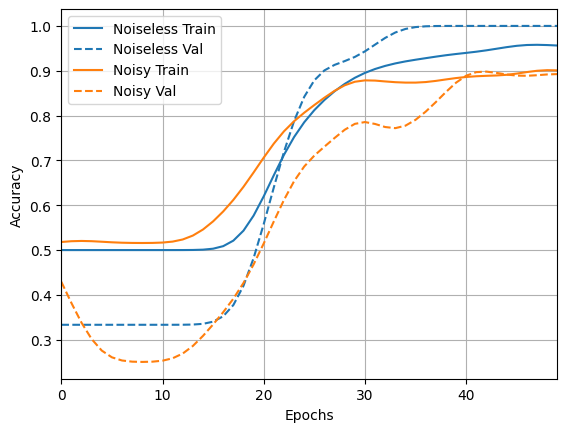
acc_plotter.plot(training_histories)
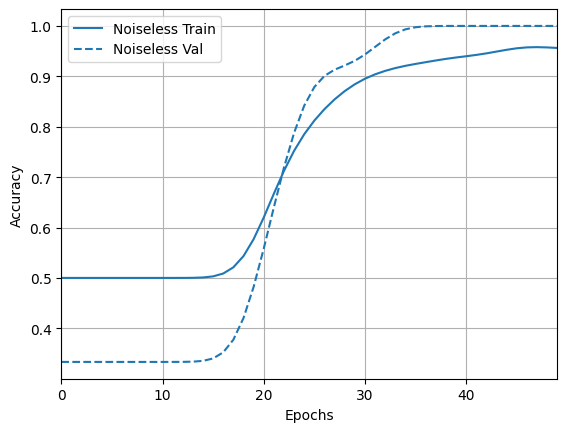
4.2 So sánh ồn ào
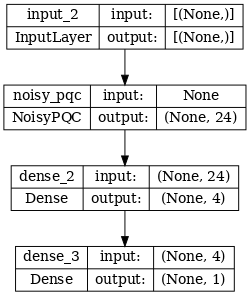
Bây giờ bạn có thể xây dựng một mô hình mới với cấu trúc nhiễu và so sánh với mô hình ở trên, mã gần như giống hệt nhau:
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 8s 2s/step - loss: 0.8265 - accuracy: 0.4844 - val_loss: 0.8369 - val_accuracy: 0.4167 Epoch 2/50 4/4 [==============================] - 7s 2s/step - loss: 0.7613 - accuracy: 0.4844 - val_loss: 0.7695 - val_accuracy: 0.4167 Epoch 3/50 4/4 [==============================] - 7s 2s/step - loss: 0.7151 - accuracy: 0.4844 - val_loss: 0.7290 - val_accuracy: 0.4167 Epoch 4/50 4/4 [==============================] - 7s 2s/step - loss: 0.6915 - accuracy: 0.4844 - val_loss: 0.7014 - val_accuracy: 0.4167 Epoch 5/50 4/4 [==============================] - 7s 2s/step - loss: 0.6837 - accuracy: 0.4844 - val_loss: 0.6811 - val_accuracy: 0.4167 Epoch 6/50 4/4 [==============================] - 7s 2s/step - loss: 0.6717 - accuracy: 0.4844 - val_loss: 0.6801 - val_accuracy: 0.4167 Epoch 7/50 4/4 [==============================] - 7s 2s/step - loss: 0.6739 - accuracy: 0.4844 - val_loss: 0.6726 - val_accuracy: 0.4167 Epoch 8/50 4/4 [==============================] - 7s 2s/step - loss: 0.6713 - accuracy: 0.4844 - val_loss: 0.6661 - val_accuracy: 0.4167 Epoch 9/50 4/4 [==============================] - 7s 2s/step - loss: 0.6710 - accuracy: 0.4844 - val_loss: 0.6667 - val_accuracy: 0.4167 Epoch 10/50 4/4 [==============================] - 7s 2s/step - loss: 0.6669 - accuracy: 0.4844 - val_loss: 0.6627 - val_accuracy: 0.4167 Epoch 11/50 4/4 [==============================] - 7s 2s/step - loss: 0.6637 - accuracy: 0.4844 - val_loss: 0.6550 - val_accuracy: 0.4167 Epoch 12/50 4/4 [==============================] - 7s 2s/step - loss: 0.6616 - accuracy: 0.4844 - val_loss: 0.6593 - val_accuracy: 0.4167 Epoch 13/50 4/4 [==============================] - 7s 2s/step - loss: 0.6536 - accuracy: 0.4844 - val_loss: 0.6514 - val_accuracy: 0.4167 Epoch 14/50 4/4 [==============================] - 7s 2s/step - loss: 0.6489 - accuracy: 0.4844 - val_loss: 0.6481 - val_accuracy: 0.4167 Epoch 15/50 4/4 [==============================] - 7s 2s/step - loss: 0.6491 - accuracy: 0.4844 - val_loss: 0.6484 - val_accuracy: 0.4167 Epoch 16/50 4/4 [==============================] - 7s 2s/step - loss: 0.6389 - accuracy: 0.4844 - val_loss: 0.6396 - val_accuracy: 0.4167 Epoch 17/50 4/4 [==============================] - 7s 2s/step - loss: 0.6307 - accuracy: 0.4844 - val_loss: 0.6337 - val_accuracy: 0.4167 Epoch 18/50 4/4 [==============================] - 7s 2s/step - loss: 0.6296 - accuracy: 0.4844 - val_loss: 0.6260 - val_accuracy: 0.4167 Epoch 19/50 4/4 [==============================] - 7s 2s/step - loss: 0.6194 - accuracy: 0.4844 - val_loss: 0.6282 - val_accuracy: 0.4167 Epoch 20/50 4/4 [==============================] - 7s 2s/step - loss: 0.6095 - accuracy: 0.4844 - val_loss: 0.6138 - val_accuracy: 0.4167 Epoch 21/50 4/4 [==============================] - 7s 2s/step - loss: 0.6075 - accuracy: 0.4844 - val_loss: 0.5874 - val_accuracy: 0.4167 Epoch 22/50 4/4 [==============================] - 7s 2s/step - loss: 0.5981 - accuracy: 0.4844 - val_loss: 0.5981 - val_accuracy: 0.4167 Epoch 23/50 4/4 [==============================] - 7s 2s/step - loss: 0.5823 - accuracy: 0.4844 - val_loss: 0.5818 - val_accuracy: 0.4167 Epoch 24/50 4/4 [==============================] - 7s 2s/step - loss: 0.5768 - accuracy: 0.4844 - val_loss: 0.5617 - val_accuracy: 0.4167 Epoch 25/50 4/4 [==============================] - 7s 2s/step - loss: 0.5651 - accuracy: 0.4844 - val_loss: 0.5638 - val_accuracy: 0.4167 Epoch 26/50 4/4 [==============================] - 7s 2s/step - loss: 0.5496 - accuracy: 0.4844 - val_loss: 0.5532 - val_accuracy: 0.4167 Epoch 27/50 4/4 [==============================] - 7s 2s/step - loss: 0.5340 - accuracy: 0.5000 - val_loss: 0.5345 - val_accuracy: 0.4167 Epoch 28/50 4/4 [==============================] - 7s 2s/step - loss: 0.5297 - accuracy: 0.5156 - val_loss: 0.5308 - val_accuracy: 0.4167 Epoch 29/50 4/4 [==============================] - 7s 2s/step - loss: 0.5120 - accuracy: 0.5312 - val_loss: 0.5224 - val_accuracy: 0.5000 Epoch 30/50 4/4 [==============================] - 7s 2s/step - loss: 0.4992 - accuracy: 0.5781 - val_loss: 0.4921 - val_accuracy: 0.5833 Epoch 31/50 4/4 [==============================] - 7s 2s/step - loss: 0.4823 - accuracy: 0.5938 - val_loss: 0.4975 - val_accuracy: 0.5000 Epoch 32/50 4/4 [==============================] - 7s 2s/step - loss: 0.5025 - accuracy: 0.5781 - val_loss: 0.4814 - val_accuracy: 0.5000 Epoch 33/50 4/4 [==============================] - 7s 2s/step - loss: 0.4655 - accuracy: 0.6562 - val_loss: 0.4391 - val_accuracy: 0.6667 Epoch 34/50 4/4 [==============================] - 7s 2s/step - loss: 0.4552 - accuracy: 0.7031 - val_loss: 0.4528 - val_accuracy: 0.5833 Epoch 35/50 4/4 [==============================] - 7s 2s/step - loss: 0.4516 - accuracy: 0.6719 - val_loss: 0.3993 - val_accuracy: 0.8333 Epoch 36/50 4/4 [==============================] - 7s 2s/step - loss: 0.4320 - accuracy: 0.7656 - val_loss: 0.4225 - val_accuracy: 0.6667 Epoch 37/50 4/4 [==============================] - 7s 2s/step - loss: 0.4060 - accuracy: 0.7656 - val_loss: 0.4001 - val_accuracy: 0.9167 Epoch 38/50 4/4 [==============================] - 7s 2s/step - loss: 0.3858 - accuracy: 0.7812 - val_loss: 0.4152 - val_accuracy: 0.8333 Epoch 39/50 4/4 [==============================] - 7s 2s/step - loss: 0.3964 - accuracy: 0.7656 - val_loss: 0.3899 - val_accuracy: 0.7500 Epoch 40/50 4/4 [==============================] - 7s 2s/step - loss: 0.3640 - accuracy: 0.8125 - val_loss: 0.3689 - val_accuracy: 0.7500 Epoch 41/50 4/4 [==============================] - 7s 2s/step - loss: 0.3676 - accuracy: 0.7812 - val_loss: 0.3786 - val_accuracy: 0.7500 Epoch 42/50 4/4 [==============================] - 7s 2s/step - loss: 0.3466 - accuracy: 0.8281 - val_loss: 0.3313 - val_accuracy: 0.8333 Epoch 43/50 4/4 [==============================] - 7s 2s/step - loss: 0.3520 - accuracy: 0.8594 - val_loss: 0.3398 - val_accuracy: 0.8333 Epoch 44/50 4/4 [==============================] - 7s 2s/step - loss: 0.3402 - accuracy: 0.8438 - val_loss: 0.3135 - val_accuracy: 0.9167 Epoch 45/50 4/4 [==============================] - 7s 2s/step - loss: 0.3253 - accuracy: 0.8281 - val_loss: 0.3469 - val_accuracy: 0.8333 Epoch 46/50 4/4 [==============================] - 7s 2s/step - loss: 0.3239 - accuracy: 0.8281 - val_loss: 0.3038 - val_accuracy: 0.9167 Epoch 47/50 4/4 [==============================] - 7s 2s/step - loss: 0.2948 - accuracy: 0.8594 - val_loss: 0.3056 - val_accuracy: 0.9167 Epoch 48/50 4/4 [==============================] - 7s 2s/step - loss: 0.2972 - accuracy: 0.9219 - val_loss: 0.2699 - val_accuracy: 0.9167 Epoch 49/50 4/4 [==============================] - 7s 2s/step - loss: 0.3041 - accuracy: 0.8281 - val_loss: 0.2754 - val_accuracy: 0.9167 Epoch 50/50 4/4 [==============================] - 7s 2s/step - loss: 0.2944 - accuracy: 0.8750 - val_loss: 0.2988 - val_accuracy: 0.9167
loss_plotter.plot(training_histories)
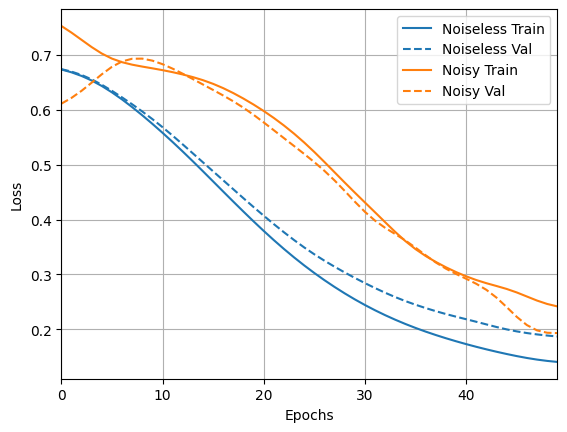
acc_plotter.plot(training_histories)