TensorFlow.org에서 보기 TensorFlow.org에서 보기 |  Google Colab에서 실행 Google Colab에서 실행 |  GitHub에서 소스 보기 GitHub에서 소스 보기 |  노트북 다운로드 노트북 다운로드 |
노이즈는 현대 양자 컴퓨터에 존재합니다. 큐 비트는 주변 환경으로부터의 간섭, 불완전한 제조, TLS 때로는되기 쉽다 감마선 . 대규모 오류 수정에 도달할 때까지 오늘날의 알고리즘은 노이즈가 있는 상태에서 기능을 유지해야 합니다. 이것은 노이즈 하에서 알고리즘을 테스트하는 것을 양자 알고리즘/모델이 오늘날의 양자 컴퓨터에서 작동할 것인지 검증하기 위한 중요한 단계로 만듭니다.
이 튜토리얼에서 당신은 높은 수준의를 통해 TFQ 시끄러운 회로 시뮬레이션의 기초를 모색 할 것입니다 tfq.layers API.
설정
pip install tensorflow==2.4.1 tensorflow-quantum
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2021-10-12 11:23:10.079578: E tensorflow/stream_executor/cuda/cuda_driver.cc:328] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. 양자 잡음의 이해
1.1 기본 회로 노이즈
양자 컴퓨터의 노이즈는 측정할 수 있는 비트열 샘플에 영향을 줍니다. 이에 대해 생각할 수 있는 한 가지 직관적인 방법은 노이즈가 많은 양자 컴퓨터가 아래 다이어그램과 같은 임의의 위치에 게이트를 "삽입", "삭제" 또는 "교체"한다는 것입니다.
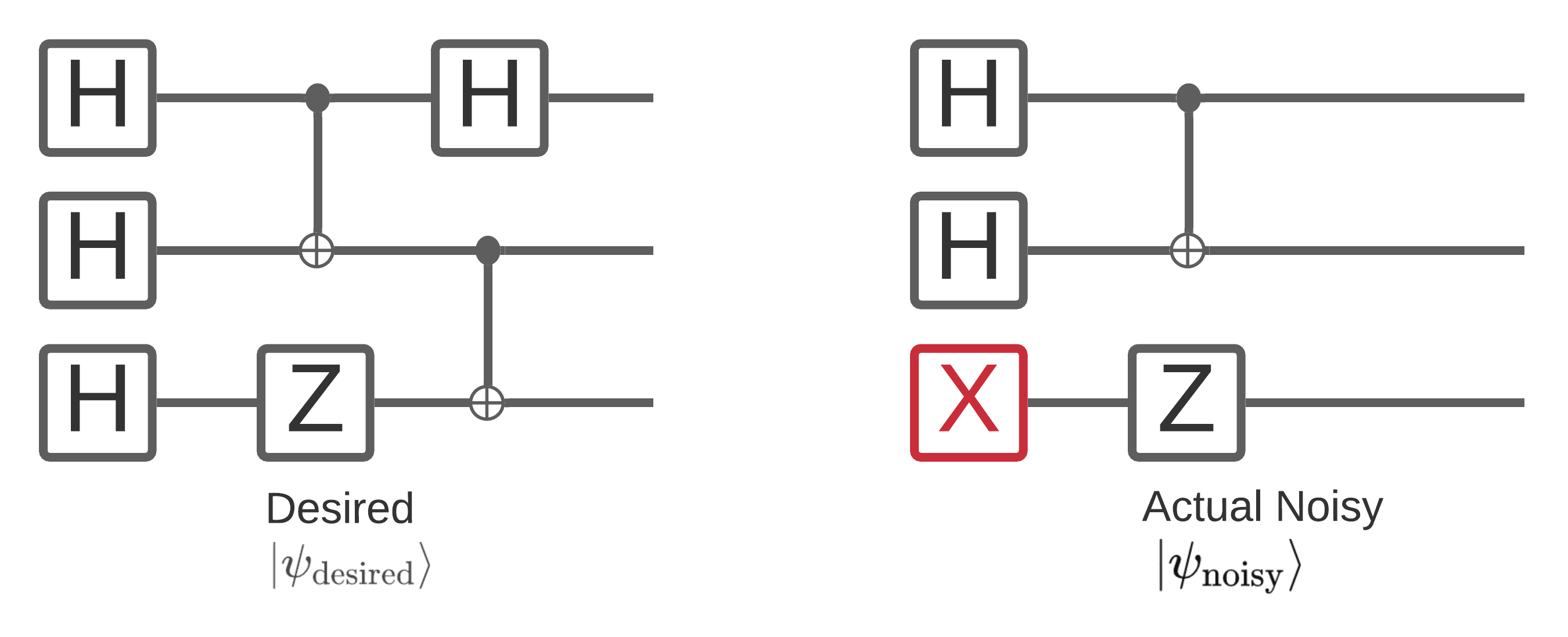
노이즈를 처리 할 때이 직관의 해제 구축, 당신은 더 이상 하나의 순수한 상태 사용되지 않습니다 \(|\psi \rangle\) 대신하여 원하는 회로의 모든 가능한 소음 실현의 앙상블을 다루는 : \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) . 어디 \(p_j\) 가능성을 제공하는 시스템에 있음을 \(|\psi_j \rangle\) .
위의 그림을 다시 방문하여 시스템이 완벽하게 실행되는 시간의 90% 또는 이 한 가지 모드의 오류로 오류가 발생한 시간의 10%를 미리 알았다면 앙상블은 다음과 같습니다.
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
더 우리의 회로 오류 수 있다는 하나의 방법보다 더 있었다면, 다음 앙상블 \(\rho\) 더 두 용어 (일어날 수있는 각각의 새로운 시끄러운 실현을위한 하나) 이상 포함됩니다. \(\rho\) 라고 밀도 행렬 하여 노이즈 시스템을 설명.
1.2 채널을 사용하여 회로 노이즈 모델링
불행히도 실제로 회로에서 오류가 발생할 수 있는 모든 방법과 정확한 확률을 아는 것은 거의 불가능합니다. 당신이 할 수있는 단순화 가정은 회로의 각 작업 후에 어떤 종류가 있다는 것입니다 채널 대략 캡처 그 작업이 오류 수있는 방법을 것이다. 약간의 노이즈가 있는 회로를 빠르게 만들 수 있습니다.
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
당신은 노이즈 밀도 행렬 검사 할 수 있습니다 \(\rho\) 과를 :
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
그리고 잡음 밀도 행렬 \(\rho\) 과 :
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
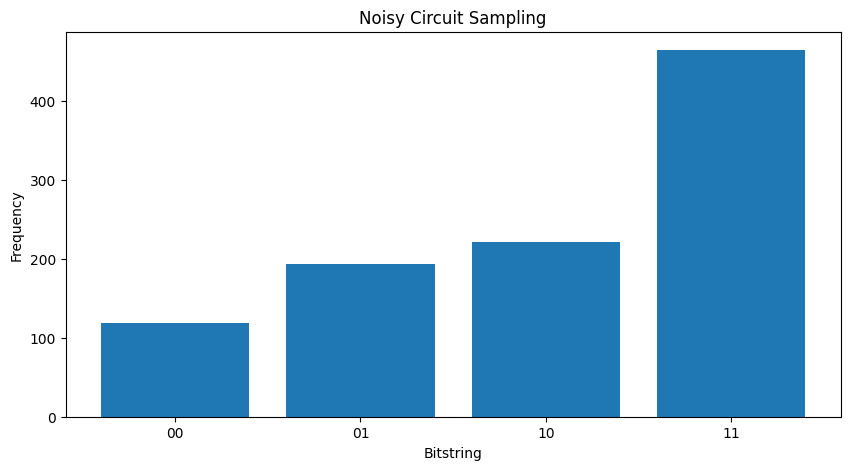
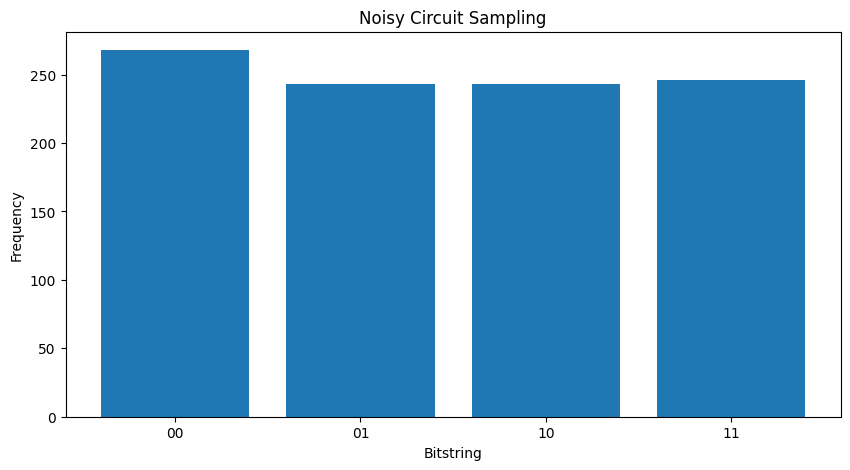
두 개의 다른 비교 \( \rho \) '당신이 잡음이 국가의 진폭 (결과적으로 샘플링 확률을) 영향 것을 볼 수 있습니다이야. 무소음 경우 당신은 항상 샘플 기대 \( |11\rangle \) 상태를. 그러나 시끄러운 상태로 현재 샘플의 제로가 아닌 확률이 \( |00\rangle \) 또는 \( |01\rangle \) 또는 \( |10\rangle \) 뿐만 아니라 :
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
plot_samples(my_noisy_circuit)
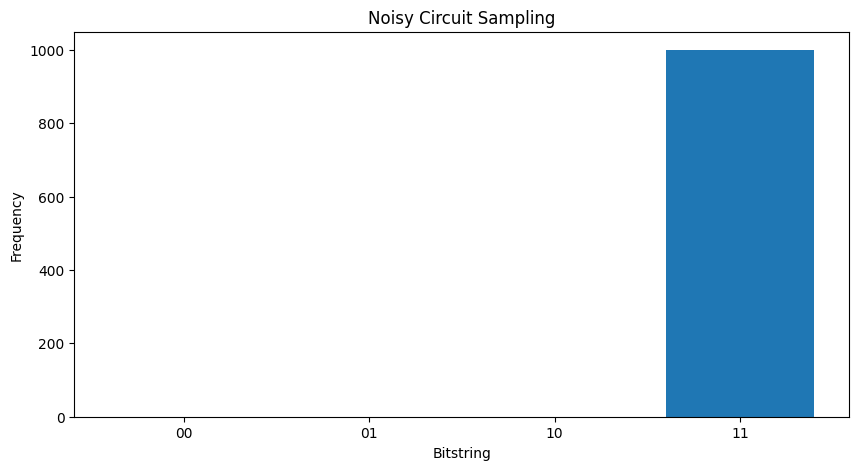
소음없이 당신은 항상 얻을 것이다 \(|11\rangle\):
"""Sample from my_circuit."""
plot_samples(my_circuit)
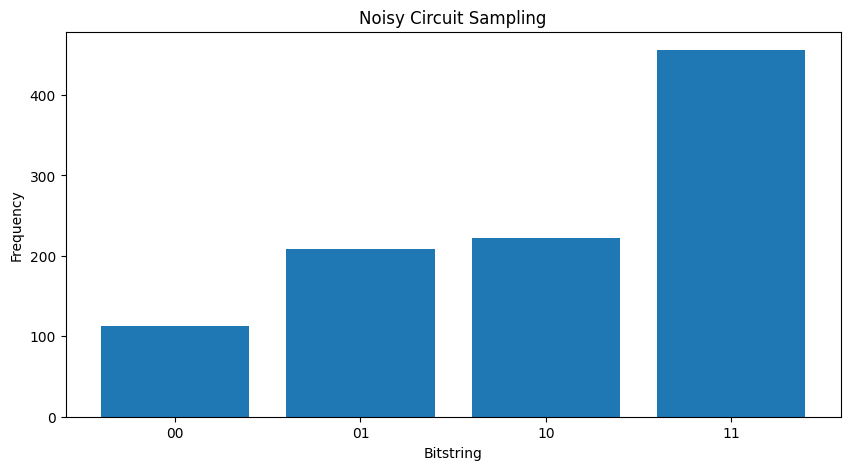
당신은 노이즈가 증가하면 조금 더가 (샘플링 원하는 동작을 구분하기 힘들어 될 것 \(|11\rangle\) 잡음에서) :
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
2. TFQ의 기본 노이즈
노이즈가 회로 실행에 어떤 영향을 미칠 수 있는지에 대한 이러한 이해를 통해 TFQ에서 노이즈가 작동하는 방식을 탐색할 수 있습니다. TensorFlow Quantum은 밀도 매트릭스 시뮬레이션의 대안으로 몬테카를로/궤적 기반 시뮬레이션을 사용합니다. 이는 밀도 매트릭스 시뮬레이션의 메모리 복잡성으로 인해 기존의 전체 밀도 매트릭스 시뮬레이션 방법으로 대규모 시뮬레이션을 <= 20큐비트로 제한하기 때문입니다. 몬테카를로/궤적은 이 비용을 시간에 따른 추가 비용과 교환합니다. backend='noisy' 모든 가능한 옵션 tfq.layers.Sample , tfq.layers.SampledExpectation 및 tfq.layers.Expectation (의 경우 Expectation 이것은 필요한 추가 않습니다 repetitions 매개 변수).
2.1 TFQ의 노이즈 샘플링
당신이 사용할 수있는 TFQ 및 궤도 시뮬레이션을 사용하여 위의 플롯을 다시 만들려면 tfq.layers.Sample
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
2.2 노이즈가 많은 샘플 기반 기대
당신이 사용할 수있는 노이즈 샘플을 기반으로 기대 계산을 수행하려면 tfq.layers.SampleExpectation :
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
회로에서 샘플링을 통해 무소음 기대 추정치를 계산합니다.
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[ 0.0076, -1. , 0.9796]], dtype=float32)
노이즈가 있는 버전과 비교:
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
array([[ 0.0208 , -0.32099998, 1.0731999 ],
[-0.0126 , 0.0062 , 1.012 ]], dtype=float32)
당신은 소음이 특히 영향을 것을 볼 수 있습니다 \(\langle \psi | Z | \psi \rangle\) 와 정확도를 my_really_noisy_circuit 0으로 매우 빠르게 집중.
2.3 잡음이 있는 분석 기대값 계산
잡음이 있는 분석적 기대 계산을 수행하는 것은 위와 거의 동일합니다.
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106853e-15, -3.2819998e-01, 1.0000000e+00],
[ 1.9106855e-15, 1.3200002e-02, 1.0000000e+00]], dtype=float32)
3. 하이브리드 모델과 양자 데이터 노이즈
이제 TFQ에서 일부 잡음이 있는 회로 시뮬레이션을 구현했으므로 잡음이 없는 성능과 잡음이 없는 성능을 비교하고 대조하여 잡음이 양자 및 하이브리드 양자 클래식 모델에 미치는 영향을 실험할 수 있습니다. 모델이나 알고리즘이 노이즈에 강한지 확인하기 위한 좋은 첫 번째 확인은 다음과 같은 회로 전체 탈분극 모델에서 테스트하는 것입니다.
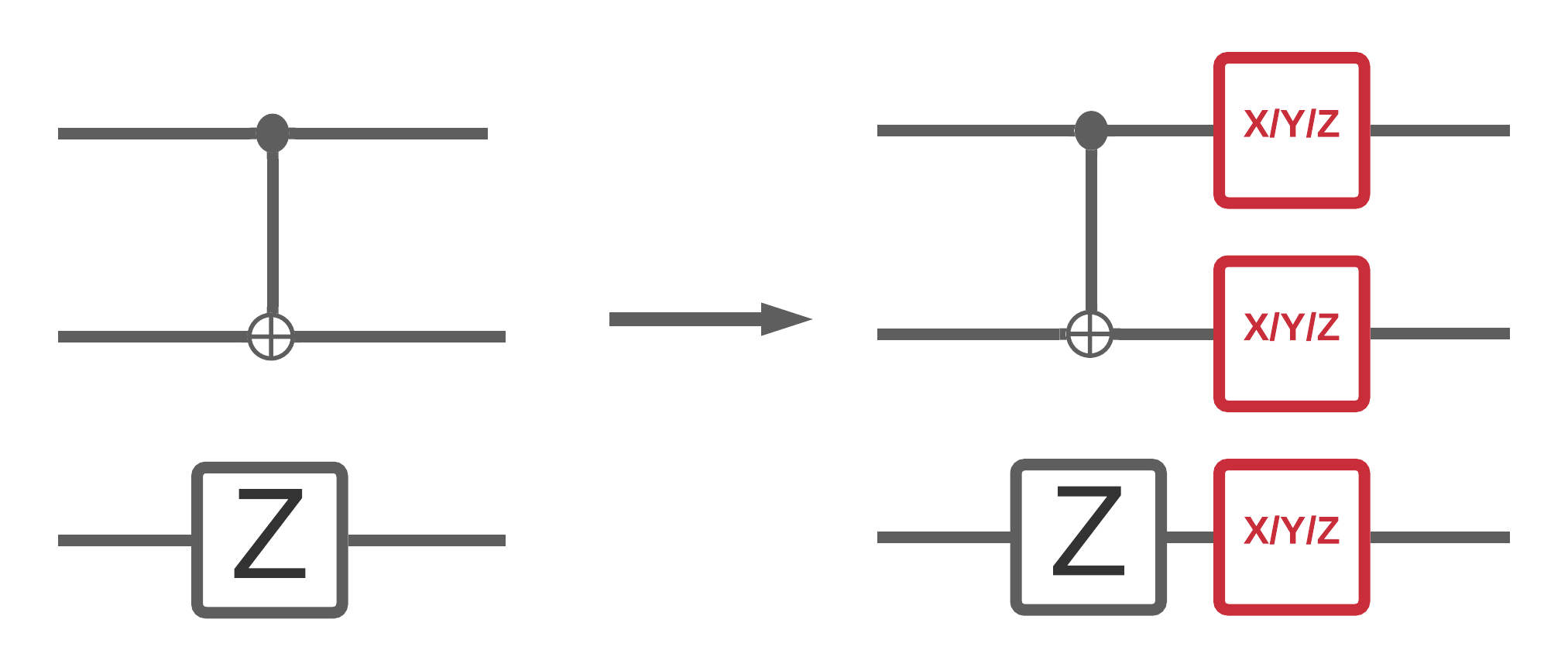
회로의 각 타임 슬라이스(모멘트라고도 함)에는 해당 타임 슬라이스의 각 게이트 작업 후에 추가된 탈분극 채널이 있습니다. 탈분극 갖는 채널 중 하나에 적용 \(\{X, Y, Z \}\) 확률로 \(p\) 또는 확률과 아무것도 (일본어 동작을 유지) 가하지 \(1-p\).
3.1 데이터
이 예를 들어, 당신은 몇 가지 준비 회로 사용할 수 있습니다 tfq.datasets 훈련 데이터로 모듈 :
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184451072/184449737 [==============================] - 1s 0us/step
작은 도우미 함수를 작성하면 노이즈 대 노이즈 없는 경우에 대한 데이터를 생성하는 데 도움이 됩니다.
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 모델 회로 정의
이제 회로 형태의 양자 데이터가 있으므로 이 데이터를 모델링하는 회로가 필요합니다. 데이터와 마찬가지로 선택적으로 노이즈를 포함하는 이 회로를 생성하는 도우미 함수를 작성할 수 있습니다.
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 모델 구축 및 교육
데이터 및 모델 회로가 내장되어, 당신이 필요합니다 최종 도우미 기능은 잡음이나 노이즈 하이브리드 양자 모두 조합 할 수 있습니다 하나입니다 tf.keras.Model :
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. 성능 비교
4.1 무소음 베이스라인
데이터 생성 및 모델 구축 코드를 사용하여 이제 무소음 및 시끄러운 설정에서 모델 성능을 비교하고 대조할 수 있습니다. 먼저 참조 무소음 교육을 실행할 수 있습니다.
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
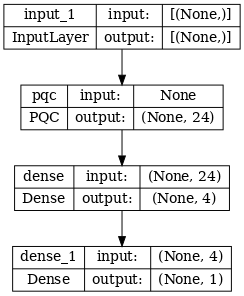
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 218ms/step - loss: 0.7061 - accuracy: 0.5354 - val_loss: 0.6503 - val_accuracy: 0.6667 Epoch 2/50 4/4 [==============================] - 0s 86ms/step - loss: 0.6802 - accuracy: 0.5396 - val_loss: 0.6689 - val_accuracy: 0.6667 Epoch 3/50 4/4 [==============================] - 0s 83ms/step - loss: 0.6861 - accuracy: 0.4500 - val_loss: 0.6975 - val_accuracy: 0.6667 Epoch 4/50 4/4 [==============================] - 0s 82ms/step - loss: 0.6710 - accuracy: 0.4417 - val_loss: 0.7223 - val_accuracy: 0.6667 Epoch 5/50 4/4 [==============================] - 0s 82ms/step - loss: 0.6695 - accuracy: 0.4729 - val_loss: 0.7348 - val_accuracy: 0.6667 Epoch 6/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6526 - accuracy: 0.6146 - val_loss: 0.7379 - val_accuracy: 0.9167 Epoch 7/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6480 - accuracy: 0.7875 - val_loss: 0.7291 - val_accuracy: 1.0000 Epoch 8/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6365 - accuracy: 0.7771 - val_loss: 0.7116 - val_accuracy: 1.0000 Epoch 9/50 4/4 [==============================] - 0s 78ms/step - loss: 0.6311 - accuracy: 0.7521 - val_loss: 0.6915 - val_accuracy: 0.9167 Epoch 10/50 4/4 [==============================] - 0s 79ms/step - loss: 0.6081 - accuracy: 0.7000 - val_loss: 0.6706 - val_accuracy: 0.9167 Epoch 11/50 4/4 [==============================] - 0s 86ms/step - loss: 0.6163 - accuracy: 0.6771 - val_loss: 0.6395 - val_accuracy: 0.8333 Epoch 12/50 4/4 [==============================] - 0s 83ms/step - loss: 0.5897 - accuracy: 0.6500 - val_loss: 0.6194 - val_accuracy: 0.8333 Epoch 13/50 4/4 [==============================] - 1s 148ms/step - loss: 0.5791 - accuracy: 0.6708 - val_loss: 0.6012 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 83ms/step - loss: 0.5650 - accuracy: 0.6396 - val_loss: 0.5838 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 87ms/step - loss: 0.5702 - accuracy: 0.7167 - val_loss: 0.5576 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 89ms/step - loss: 0.5475 - accuracy: 0.6750 - val_loss: 0.5391 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 0s 84ms/step - loss: 0.5346 - accuracy: 0.7146 - val_loss: 0.5167 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 92ms/step - loss: 0.5329 - accuracy: 0.7812 - val_loss: 0.4905 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 90ms/step - loss: 0.4863 - accuracy: 0.7708 - val_loss: 0.4731 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 88ms/step - loss: 0.4724 - accuracy: 0.7875 - val_loss: 0.4549 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 94ms/step - loss: 0.4780 - accuracy: 0.8396 - val_loss: 0.4301 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 85ms/step - loss: 0.4446 - accuracy: 0.8375 - val_loss: 0.4101 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 92ms/step - loss: 0.4458 - accuracy: 0.8396 - val_loss: 0.3863 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 93ms/step - loss: 0.4097 - accuracy: 0.8750 - val_loss: 0.3616 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 89ms/step - loss: 0.3907 - accuracy: 0.8750 - val_loss: 0.3410 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 91ms/step - loss: 0.3842 - accuracy: 0.8646 - val_loss: 0.3180 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 90ms/step - loss: 0.3509 - accuracy: 0.9062 - val_loss: 0.2951 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 91ms/step - loss: 0.3495 - accuracy: 0.8688 - val_loss: 0.2813 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 94ms/step - loss: 0.3393 - accuracy: 0.8917 - val_loss: 0.2606 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 92ms/step - loss: 0.3277 - accuracy: 0.8750 - val_loss: 0.2449 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 90ms/step - loss: 0.2935 - accuracy: 0.9292 - val_loss: 0.2331 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 91ms/step - loss: 0.2875 - accuracy: 0.9229 - val_loss: 0.2188 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 94ms/step - loss: 0.2820 - accuracy: 0.9354 - val_loss: 0.2049 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 93ms/step - loss: 0.2705 - accuracy: 0.8958 - val_loss: 0.1957 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 91ms/step - loss: 0.2499 - accuracy: 0.9500 - val_loss: 0.1832 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 92ms/step - loss: 0.2445 - accuracy: 0.9354 - val_loss: 0.1705 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 90ms/step - loss: 0.2533 - accuracy: 0.9437 - val_loss: 0.1623 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 96ms/step - loss: 0.2253 - accuracy: 0.9542 - val_loss: 0.1525 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 89ms/step - loss: 0.2189 - accuracy: 0.9646 - val_loss: 0.1425 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 95ms/step - loss: 0.2273 - accuracy: 0.9417 - val_loss: 0.1372 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 85ms/step - loss: 0.2346 - accuracy: 0.9437 - val_loss: 0.1325 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 96ms/step - loss: 0.2227 - accuracy: 0.9479 - val_loss: 0.1235 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 1s 149ms/step - loss: 0.2134 - accuracy: 0.9437 - val_loss: 0.1192 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 85ms/step - loss: 0.2066 - accuracy: 0.9250 - val_loss: 0.1149 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 83ms/step - loss: 0.2168 - accuracy: 0.9375 - val_loss: 0.1095 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 84ms/step - loss: 0.1759 - accuracy: 0.9604 - val_loss: 0.1053 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 81ms/step - loss: 0.1850 - accuracy: 0.9833 - val_loss: 0.0980 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 81ms/step - loss: 0.1910 - accuracy: 0.9479 - val_loss: 0.0913 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 80ms/step - loss: 0.1698 - accuracy: 0.9250 - val_loss: 0.0911 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 83ms/step - loss: 0.1698 - accuracy: 0.9542 - val_loss: 0.0855 - val_accuracy: 1.0000
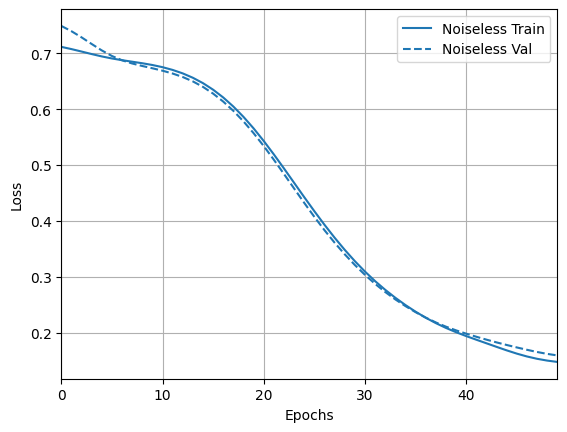
그리고 결과와 정확성을 살펴보십시오.
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
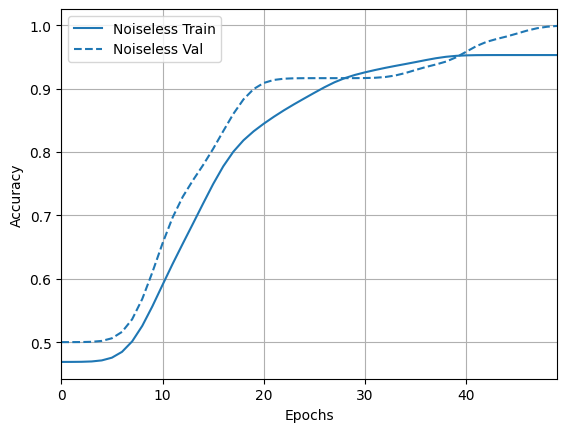
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
acc_plotter.plot(training_histories)
4.2 시끄러운 비교
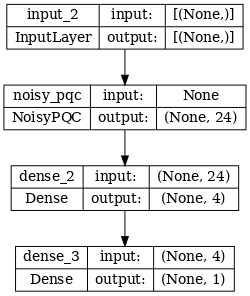
이제 노이즈 구조로 새 모델을 빌드하고 위와 비교하면 코드가 거의 동일합니다.
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 8s 2s/step - loss: 0.6710 - accuracy: 0.3771 - val_loss: 0.8007 - val_accuracy: 0.7500 Epoch 2/50 4/4 [==============================] - 7s 2s/step - loss: 0.6745 - accuracy: 0.4271 - val_loss: 0.7787 - val_accuracy: 0.7500 Epoch 3/50 4/4 [==============================] - 7s 2s/step - loss: 0.6698 - accuracy: 0.4354 - val_loss: 0.7603 - val_accuracy: 0.7500 Epoch 4/50 4/4 [==============================] - 7s 2s/step - loss: 0.6528 - accuracy: 0.4083 - val_loss: 0.7550 - val_accuracy: 0.7500 Epoch 5/50 4/4 [==============================] - 7s 2s/step - loss: 0.6535 - accuracy: 0.4313 - val_loss: 0.7370 - val_accuracy: 0.8333 Epoch 6/50 4/4 [==============================] - 7s 2s/step - loss: 0.6445 - accuracy: 0.4979 - val_loss: 0.7201 - val_accuracy: 0.8333 Epoch 7/50 4/4 [==============================] - 7s 2s/step - loss: 0.6333 - accuracy: 0.4917 - val_loss: 0.7185 - val_accuracy: 0.8333 Epoch 8/50 4/4 [==============================] - 7s 2s/step - loss: 0.6152 - accuracy: 0.5854 - val_loss: 0.6988 - val_accuracy: 0.9167 Epoch 9/50 4/4 [==============================] - 7s 2s/step - loss: 0.5806 - accuracy: 0.6562 - val_loss: 0.6805 - val_accuracy: 0.9167 Epoch 10/50 4/4 [==============================] - 7s 2s/step - loss: 0.5872 - accuracy: 0.6854 - val_loss: 0.6599 - val_accuracy: 0.9167 Epoch 11/50 4/4 [==============================] - 7s 2s/step - loss: 0.5753 - accuracy: 0.7875 - val_loss: 0.6401 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 7s 2s/step - loss: 0.5682 - accuracy: 0.8354 - val_loss: 0.6097 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 7s 2s/step - loss: 0.5380 - accuracy: 0.8396 - val_loss: 0.5732 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 7s 2s/step - loss: 0.5061 - accuracy: 0.7708 - val_loss: 0.5657 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 7s 2s/step - loss: 0.5043 - accuracy: 0.8604 - val_loss: 0.5254 - val_accuracy: 1.0000 Epoch 16/50 4/4 [==============================] - 7s 2s/step - loss: 0.4795 - accuracy: 0.8708 - val_loss: 0.4805 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 7s 2s/step - loss: 0.4456 - accuracy: 0.8000 - val_loss: 0.4539 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 7s 2s/step - loss: 0.4512 - accuracy: 0.9021 - val_loss: 0.4331 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 7s 2s/step - loss: 0.4210 - accuracy: 0.8688 - val_loss: 0.4411 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 7s 2s/step - loss: 0.4167 - accuracy: 0.8646 - val_loss: 0.3781 - val_accuracy: 0.9167 Epoch 21/50 4/4 [==============================] - 7s 2s/step - loss: 0.3550 - accuracy: 0.9375 - val_loss: 0.3492 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 7s 2s/step - loss: 0.3720 - accuracy: 0.9000 - val_loss: 0.3550 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 7s 2s/step - loss: 0.3251 - accuracy: 0.9292 - val_loss: 0.3234 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 7s 2s/step - loss: 0.3264 - accuracy: 0.9333 - val_loss: 0.2942 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 7s 2s/step - loss: 0.2937 - accuracy: 0.9125 - val_loss: 0.3439 - val_accuracy: 0.9167 Epoch 26/50 4/4 [==============================] - 7s 2s/step - loss: 0.2798 - accuracy: 0.9250 - val_loss: 0.2842 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 7s 2s/step - loss: 0.2835 - accuracy: 0.9479 - val_loss: 0.2385 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 7s 2s/step - loss: 0.2610 - accuracy: 0.9417 - val_loss: 0.2352 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 7s 2s/step - loss: 0.2916 - accuracy: 0.8875 - val_loss: 0.2221 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 7s 2s/step - loss: 0.2620 - accuracy: 0.9417 - val_loss: 0.2054 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 7s 2s/step - loss: 0.2015 - accuracy: 0.9417 - val_loss: 0.2074 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 7s 2s/step - loss: 0.2462 - accuracy: 0.9292 - val_loss: 0.1961 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 7s 2s/step - loss: 0.2042 - accuracy: 0.9938 - val_loss: 0.1820 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 7s 2s/step - loss: 0.1951 - accuracy: 0.9667 - val_loss: 0.1748 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 7s 2s/step - loss: 0.2175 - accuracy: 0.9271 - val_loss: 0.1628 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 7s 2s/step - loss: 0.1792 - accuracy: 0.9563 - val_loss: 0.1569 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 7s 2s/step - loss: 0.1809 - accuracy: 0.9229 - val_loss: 0.1613 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 7s 2s/step - loss: 0.1747 - accuracy: 0.9313 - val_loss: 0.1622 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 7s 2s/step - loss: 0.1588 - accuracy: 1.0000 - val_loss: 0.1483 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 7s 2s/step - loss: 0.1709 - accuracy: 0.9437 - val_loss: 0.1428 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 7s 2s/step - loss: 0.1743 - accuracy: 0.9563 - val_loss: 0.1420 - val_accuracy: 0.9167 Epoch 42/50 4/4 [==============================] - 7s 2s/step - loss: 0.2167 - accuracy: 0.9021 - val_loss: 0.1526 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 7s 2s/step - loss: 0.1694 - accuracy: 0.9271 - val_loss: 0.1315 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 7s 2s/step - loss: 0.1597 - accuracy: 0.9646 - val_loss: 0.1601 - val_accuracy: 0.9167 Epoch 45/50 4/4 [==============================] - 7s 2s/step - loss: 0.1764 - accuracy: 0.9437 - val_loss: 0.1094 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 7s 2s/step - loss: 0.1582 - accuracy: 0.9542 - val_loss: 0.1403 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 7s 2s/step - loss: 0.1879 - accuracy: 0.9542 - val_loss: 0.0674 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 7s 2s/step - loss: 0.1812 - accuracy: 0.9708 - val_loss: 0.0751 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 7s 2s/step - loss: 0.1231 - accuracy: 0.9875 - val_loss: 0.1512 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 7s 2s/step - loss: 0.1537 - accuracy: 0.9292 - val_loss: 0.0958 - val_accuracy: 1.0000
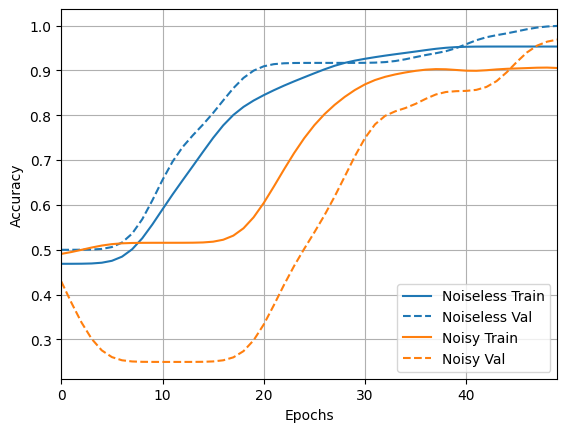
loss_plotter.plot(training_histories)
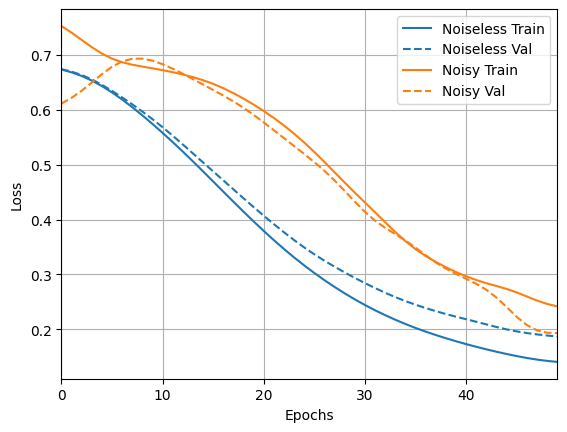
acc_plotter.plot(training_histories)