TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
आधुनिक समय के क्वांटम कंप्यूटरों में शोर मौजूद है। Qubits आसपास के वातावरण से हस्तक्षेप, अपूर्ण निर्माण, टीएलएस और कभी कभी भी लिए अतिसंवेदनशील होते हैं गामा किरणों । जब तक बड़े पैमाने पर त्रुटि सुधार नहीं हो जाता, तब तक आज के एल्गोरिदम को शोर की उपस्थिति में कार्यात्मक बने रहने में सक्षम होना चाहिए। यह शोर के तहत परीक्षण एल्गोरिदम को क्वांटम एल्गोरिदम/मॉडल को मान्य करने के लिए एक महत्वपूर्ण कदम बनाता है जो आज के क्वांटम कंप्यूटरों पर कार्य करेगा।
इस ट्यूटोरियल में आप उच्च स्तर के माध्यम से TFQ में शोर सर्किट अनुकरण की मूल बातें पता लगाने जाएगा tfq.layers एपीआई।
सेट अप
pip install tensorflow==2.4.1 tensorflow-quantum
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2021-10-12 11:23:10.079578: E tensorflow/stream_executor/cuda/cuda_driver.cc:328] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. क्वांटम शोर को समझना
1.1 बुनियादी सर्किट शोर
क्वांटम कंप्यूटर पर शोर उन बिटस्ट्रिंग नमूनों को प्रभावित करता है जिन्हें आप इससे मापने में सक्षम हैं। इसके बारे में सोचने का एक सहज तरीका यह है कि एक शोर क्वांटम कंप्यूटर नीचे दिए गए आरेख जैसे यादृच्छिक स्थानों में "सम्मिलित", "हटाएं" या "प्रतिस्थापित" करेगा:
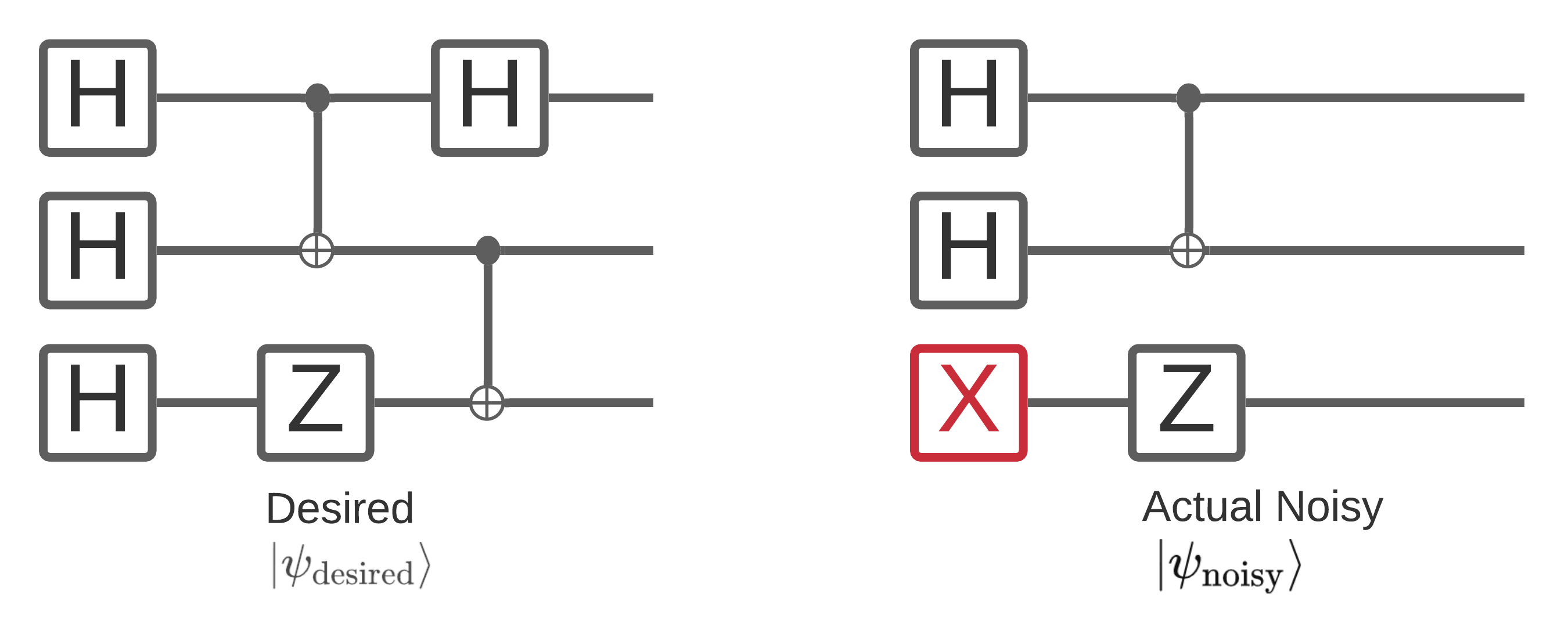
इस अंतर्ज्ञान के बंद का निर्माण, जब शोर के साथ काम, आप अब एक भी शुद्ध राज्य का उपयोग कर रहे \(|\psi \rangle\) लेकिन इसके बजाय अपने वांछित सर्किट के सभी संभव शोर प्रतीति का सम्मिश्रण के साथ काम: \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) । कहाँ \(p_j\) संभावना देता है प्रणाली में है कि \(|\psi_j \rangle\) ।
उपरोक्त तस्वीर पर दोबारा गौर करते हुए, अगर हमें पहले से पता था कि हमारे सिस्टम ने 90% समय पूरी तरह से निष्पादित किया है, या विफलता के इस एक मोड के साथ 10% समय त्रुटिपूर्ण है, तो हमारा पहनावा होगा:
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
अगर वहाँ सिर्फ एक ही रास्ता है कि हमारे सर्किट त्रुटि सकता है की तुलना में अधिक था, तो कलाकारों की टुकड़ी \(\rho\) सिर्फ दो शब्दों (प्रत्येक नए शोर प्रतीति है कि हो सकता है के लिए एक) की तुलना में अधिक होते हैं। \(\rho\) रूप में निर्दिष्ट है घनत्व मैट्रिक्स अपने शोर प्रणाली का वर्णन।
1.2 सर्किट शोर को मॉडल करने के लिए चैनलों का उपयोग करना
दुर्भाग्य से व्यवहार में यह जानना लगभग असंभव है कि आपके सर्किट में त्रुटि कैसे हो सकती है और उनकी सटीक संभावनाएं। एक सरल बनाने धारणा आप कर सकते हैं वहाँ किसी तरह का है कि आपके सर्किट में प्रत्येक ऑपरेशन के बाद है चैनल कि मोटे तौर पर कैप्चर कैसे है कि आपरेशन त्रुटि हो सकती है। आप कुछ शोर के साथ जल्दी से एक सर्किट बना सकते हैं:
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
आप शान्त घनत्व मैट्रिक्स जांच कर सकते हैं \(\rho\) साथ:
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
और शोर घनत्व मैट्रिक्स \(\rho\) साथ:
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
दो अलग-अलग मुकाबले \( \rho \) 's आप देख सकते हैं कि शोर राज्य के आयाम (और फलस्वरूप नमूना संभावनाओं) को प्रभावित किया है। शान्त मामले में आप हमेशा के नमूने के लिए उम्मीद करेंगे \( |11\rangle \) राज्य। लेकिन शोर राज्य में अब नमूने के एक अशून्य संभावना है \( |00\rangle \) या \( |01\rangle \) या \( |10\rangle \) साथ ही:
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
plot_samples(my_noisy_circuit)
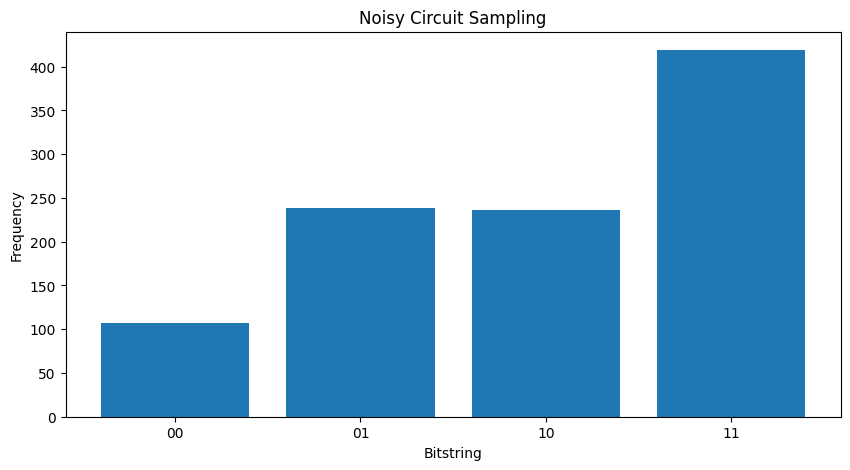
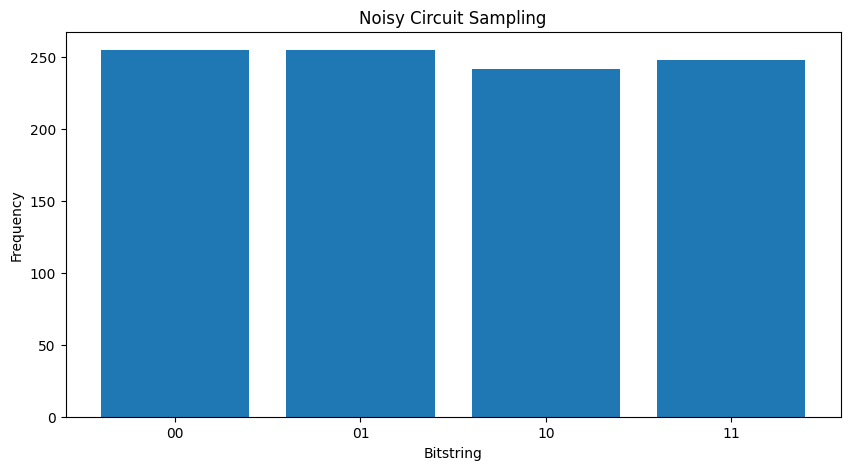
किसी भी शोर के बिना तुम हमेशा मिल जाएगा \(|11\rangle\):
"""Sample from my_circuit."""
plot_samples(my_circuit)
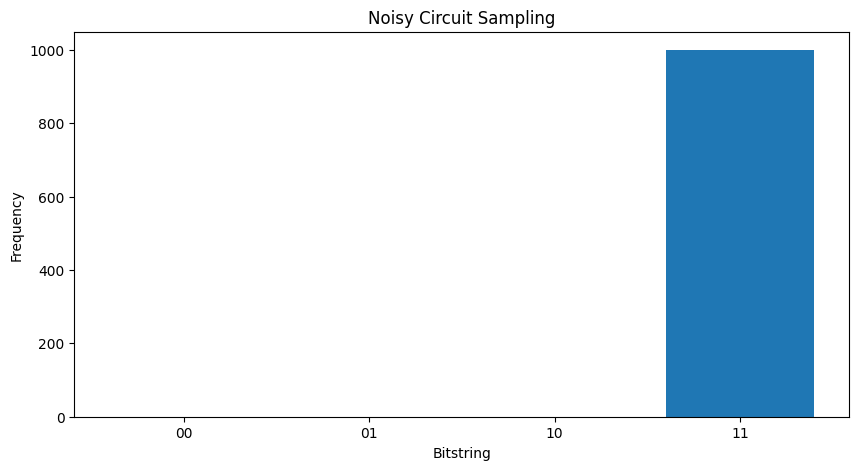
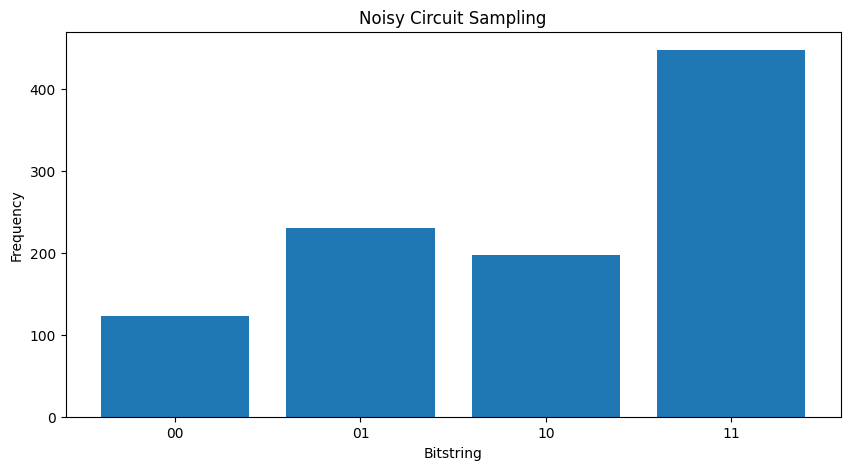
आप शोर को बढ़ाते हैं थोड़ा और आगे यह वांछित व्यवहार भेद करने के लिए (नमूना कठिन है और कठिन हो जाएगा \(|11\rangle\) शोर से):
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
2. टीएफक्यू में मूल शोर
शोर सर्किट निष्पादन को कैसे प्रभावित कर सकता है, इस समझ के साथ, आप यह पता लगा सकते हैं कि टीएफक्यू में शोर कैसे काम करता है। TensorFlow क्वांटम घनत्व मैट्रिक्स सिमुलेशन के विकल्प के रूप में मोंटे-कार्लो / प्रक्षेपवक्र आधारित सिमुलेशन का उपयोग करता है। ऐसा इसलिए है क्योंकि घनत्व मैट्रिक्स सिमुलेशन की मेमोरी जटिलता बड़े सिमुलेशन को पारंपरिक पूर्ण घनत्व मैट्रिक्स सिमुलेशन विधियों के साथ <= 20 qubits तक सीमित करती है। मोंटे-कार्लो / प्रक्षेपवक्र इस लागत को समय पर अतिरिक्त लागत के लिए स्मृति में ट्रेड करता है। backend='noisy' विकल्प सभी के लिए उपलब्ध tfq.layers.Sample , tfq.layers.SampledExpectation और tfq.layers.Expectation (के मामले में Expectation यह एक आवश्यक जोड़ता है repetitions पैरामीटर)।
2.1 टीएफक्यू में शोर नमूनाकरण
TFQ और प्रक्षेपवक्र सिमुलेशन का उपयोग कर आप उपयोग कर सकते हैं इसके बाद के संस्करण भूखंडों से बनाने के लिए tfq.layers.Sample
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
2.2 शोर नमूना आधारित अपेक्षा
शोर नमूना आधारित उम्मीद गणना आप उपयोग कर सकते हैं ऐसा करने के लिए tfq.layers.SampleExpectation :
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
सर्किट से नमूने के माध्यम से नीरव अपेक्षा अनुमानों की गणना करें:
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[ 0.0076, -1. , 0.9796]], dtype=float32)
शोर संस्करणों वाले लोगों की तुलना करें:
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
array([[ 0.0208 , -0.32099998, 1.0731999 ],
[-0.0126 , 0.0062 , 1.012 ]], dtype=float32)
आप देख सकते हैं कि शोर विशेष रूप से प्रभावित किया है \(\langle \psi | Z | \psi \rangle\) साथ सटीकता, my_really_noisy_circuit 0 की ओर बहुत तेजी से ध्यान केंद्रित।
2.3 शोर विश्लेषणात्मक अपेक्षा गणना
शोर विश्लेषणात्मक अपेक्षा गणना करना लगभग ऊपर के समान है:
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106853e-15, -3.2819998e-01, 1.0000000e+00],
[ 1.9106855e-15, 1.3200002e-02, 1.0000000e+00]], dtype=float32)
3. हाइब्रिड मॉडल और क्वांटम डेटा शोर
अब जब आपने TFQ में कुछ शोर सर्किट सिमुलेशन लागू कर दिए हैं, तो आप उनके शोर बनाम नीरव प्रदर्शन की तुलना और इसके विपरीत, क्वांटम और हाइब्रिड क्वांटम शास्त्रीय मॉडल पर शोर को कैसे प्रभावित करते हैं, इसका प्रयोग कर सकते हैं। यह देखने के लिए एक अच्छी पहली जांच है कि कोई मॉडल या एल्गोरिदम शोर के लिए मजबूत है या नहीं, सर्किट वाइड डीपोलराइजिंग मॉडल के तहत परीक्षण करना है जो कुछ इस तरह दिखता है:
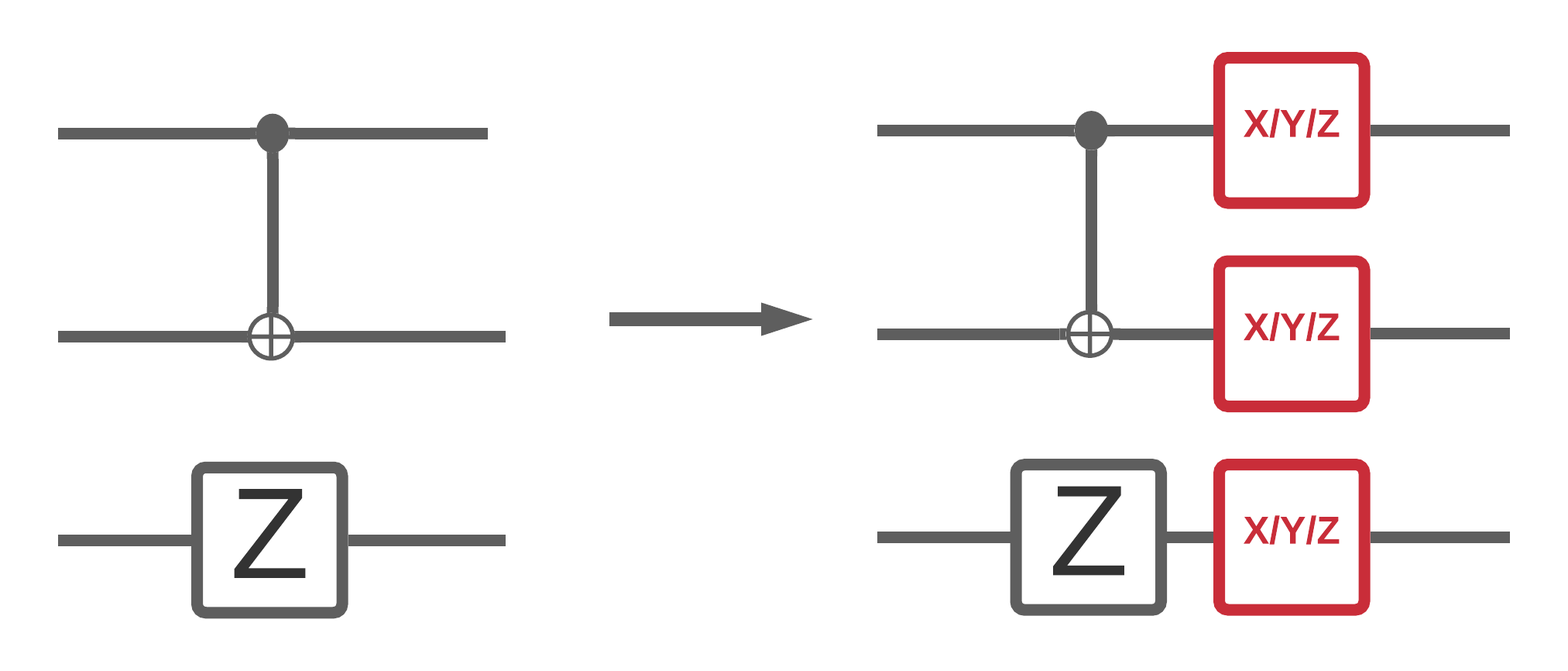
जहां हर बार सर्किट के स्लाइस (कभी-कभी पल के रूप में संदर्भित) में उस समय स्लाइस में प्रत्येक गेट ऑपरेशन के बाद एक विध्रुवण चैनल जोड़ा जाता है। साथ depolarizing चैनल में से एक लागू \(\{X, Y, Z \}\) संभावना के साथ \(p\) या कुछ भी नहीं (मूल आपरेशन रखने के लिए) संभावना के साथ लागू \(1-p\)।
3.1 डेटा
इस उदाहरण के लिए आप में कुछ तैयार सर्किट का उपयोग कर सकते tfq.datasets प्रशिक्षण डेटा के रूप में मॉड्यूल:
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184451072/184449737 [==============================] - 1s 0us/step
एक छोटा सहायक कार्य लिखने से शोर बनाम नीरव मामले के लिए डेटा उत्पन्न करने में मदद मिलेगी:
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 एक मॉडल सर्किट को परिभाषित करें
अब जब आपके पास सर्किट के रूप में क्वांटम डेटा है, तो आपको इस डेटा को मॉडल करने के लिए एक सर्किट की आवश्यकता होगी, जैसे डेटा के साथ आप वैकल्पिक रूप से शोर वाले इस सर्किट को उत्पन्न करने के लिए एक सहायक फ़ंक्शन लिख सकते हैं:
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 मॉडल निर्माण और प्रशिक्षण
अपने डेटा और मॉडल सर्किट बनाया के साथ, अंतिम सहायक समारोह आप की आवश्यकता होगी एक है कि दोनों एक शोर या एक शान्त संकर क्वांटम इकट्ठा कर सकते हैं tf.keras.Model :
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. प्रदर्शन की तुलना करें
4.1 नीरव आधार रेखा
अपने डेटा जनरेशन और मॉडल बिल्डिंग कोड के साथ, अब आप नीरव और शोर सेटिंग्स में मॉडल के प्रदर्शन की तुलना और इसके विपरीत कर सकते हैं, पहले आप एक संदर्भ नीरव प्रशिक्षण चला सकते हैं:
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 218ms/step - loss: 0.7061 - accuracy: 0.5354 - val_loss: 0.6503 - val_accuracy: 0.6667 Epoch 2/50 4/4 [==============================] - 0s 86ms/step - loss: 0.6802 - accuracy: 0.5396 - val_loss: 0.6689 - val_accuracy: 0.6667 Epoch 3/50 4/4 [==============================] - 0s 83ms/step - loss: 0.6861 - accuracy: 0.4500 - val_loss: 0.6975 - val_accuracy: 0.6667 Epoch 4/50 4/4 [==============================] - 0s 82ms/step - loss: 0.6710 - accuracy: 0.4417 - val_loss: 0.7223 - val_accuracy: 0.6667 Epoch 5/50 4/4 [==============================] - 0s 82ms/step - loss: 0.6695 - accuracy: 0.4729 - val_loss: 0.7348 - val_accuracy: 0.6667 Epoch 6/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6526 - accuracy: 0.6146 - val_loss: 0.7379 - val_accuracy: 0.9167 Epoch 7/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6480 - accuracy: 0.7875 - val_loss: 0.7291 - val_accuracy: 1.0000 Epoch 8/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6365 - accuracy: 0.7771 - val_loss: 0.7116 - val_accuracy: 1.0000 Epoch 9/50 4/4 [==============================] - 0s 78ms/step - loss: 0.6311 - accuracy: 0.7521 - val_loss: 0.6915 - val_accuracy: 0.9167 Epoch 10/50 4/4 [==============================] - 0s 79ms/step - loss: 0.6081 - accuracy: 0.7000 - val_loss: 0.6706 - val_accuracy: 0.9167 Epoch 11/50 4/4 [==============================] - 0s 86ms/step - loss: 0.6163 - accuracy: 0.6771 - val_loss: 0.6395 - val_accuracy: 0.8333 Epoch 12/50 4/4 [==============================] - 0s 83ms/step - loss: 0.5897 - accuracy: 0.6500 - val_loss: 0.6194 - val_accuracy: 0.8333 Epoch 13/50 4/4 [==============================] - 1s 148ms/step - loss: 0.5791 - accuracy: 0.6708 - val_loss: 0.6012 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 83ms/step - loss: 0.5650 - accuracy: 0.6396 - val_loss: 0.5838 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 87ms/step - loss: 0.5702 - accuracy: 0.7167 - val_loss: 0.5576 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 89ms/step - loss: 0.5475 - accuracy: 0.6750 - val_loss: 0.5391 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 0s 84ms/step - loss: 0.5346 - accuracy: 0.7146 - val_loss: 0.5167 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 92ms/step - loss: 0.5329 - accuracy: 0.7812 - val_loss: 0.4905 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 90ms/step - loss: 0.4863 - accuracy: 0.7708 - val_loss: 0.4731 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 88ms/step - loss: 0.4724 - accuracy: 0.7875 - val_loss: 0.4549 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 94ms/step - loss: 0.4780 - accuracy: 0.8396 - val_loss: 0.4301 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 85ms/step - loss: 0.4446 - accuracy: 0.8375 - val_loss: 0.4101 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 92ms/step - loss: 0.4458 - accuracy: 0.8396 - val_loss: 0.3863 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 93ms/step - loss: 0.4097 - accuracy: 0.8750 - val_loss: 0.3616 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 89ms/step - loss: 0.3907 - accuracy: 0.8750 - val_loss: 0.3410 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 91ms/step - loss: 0.3842 - accuracy: 0.8646 - val_loss: 0.3180 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 90ms/step - loss: 0.3509 - accuracy: 0.9062 - val_loss: 0.2951 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 91ms/step - loss: 0.3495 - accuracy: 0.8688 - val_loss: 0.2813 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 94ms/step - loss: 0.3393 - accuracy: 0.8917 - val_loss: 0.2606 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 92ms/step - loss: 0.3277 - accuracy: 0.8750 - val_loss: 0.2449 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 90ms/step - loss: 0.2935 - accuracy: 0.9292 - val_loss: 0.2331 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 91ms/step - loss: 0.2875 - accuracy: 0.9229 - val_loss: 0.2188 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 94ms/step - loss: 0.2820 - accuracy: 0.9354 - val_loss: 0.2049 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 93ms/step - loss: 0.2705 - accuracy: 0.8958 - val_loss: 0.1957 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 91ms/step - loss: 0.2499 - accuracy: 0.9500 - val_loss: 0.1832 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 92ms/step - loss: 0.2445 - accuracy: 0.9354 - val_loss: 0.1705 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 90ms/step - loss: 0.2533 - accuracy: 0.9437 - val_loss: 0.1623 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 96ms/step - loss: 0.2253 - accuracy: 0.9542 - val_loss: 0.1525 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 89ms/step - loss: 0.2189 - accuracy: 0.9646 - val_loss: 0.1425 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 95ms/step - loss: 0.2273 - accuracy: 0.9417 - val_loss: 0.1372 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 85ms/step - loss: 0.2346 - accuracy: 0.9437 - val_loss: 0.1325 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 96ms/step - loss: 0.2227 - accuracy: 0.9479 - val_loss: 0.1235 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 1s 149ms/step - loss: 0.2134 - accuracy: 0.9437 - val_loss: 0.1192 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 85ms/step - loss: 0.2066 - accuracy: 0.9250 - val_loss: 0.1149 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 83ms/step - loss: 0.2168 - accuracy: 0.9375 - val_loss: 0.1095 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 84ms/step - loss: 0.1759 - accuracy: 0.9604 - val_loss: 0.1053 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 81ms/step - loss: 0.1850 - accuracy: 0.9833 - val_loss: 0.0980 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 81ms/step - loss: 0.1910 - accuracy: 0.9479 - val_loss: 0.0913 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 80ms/step - loss: 0.1698 - accuracy: 0.9250 - val_loss: 0.0911 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 83ms/step - loss: 0.1698 - accuracy: 0.9542 - val_loss: 0.0855 - val_accuracy: 1.0000
और परिणाम और सटीकता का अन्वेषण करें:
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
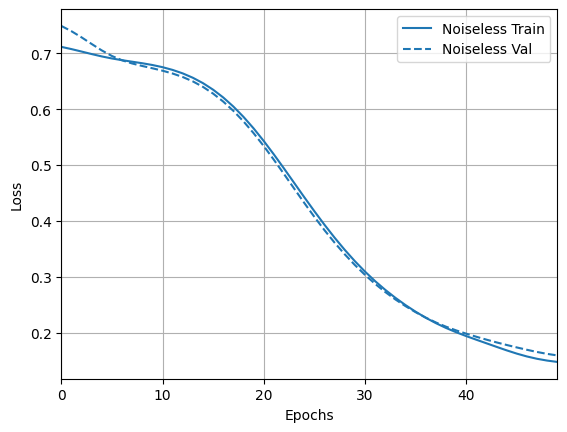
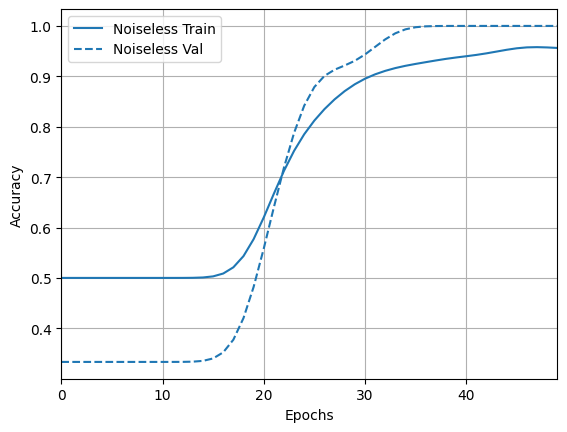
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
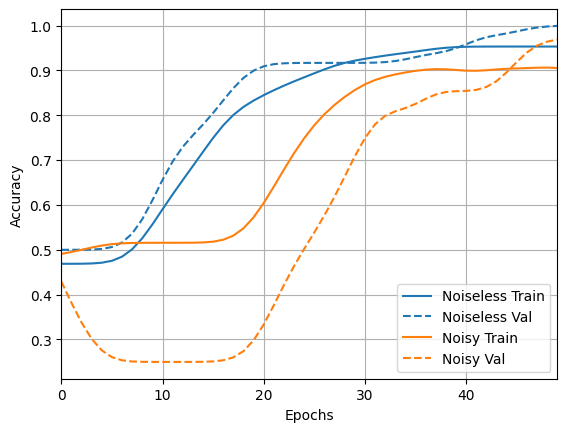
acc_plotter.plot(training_histories)
4.2 शोर तुलना
अब आप शोर संरचना के साथ एक नया मॉडल बना सकते हैं और उपरोक्त की तुलना में, कोड लगभग समान है:
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
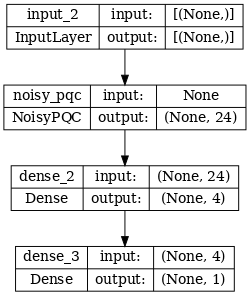
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 8s 2s/step - loss: 0.6710 - accuracy: 0.3771 - val_loss: 0.8007 - val_accuracy: 0.7500 Epoch 2/50 4/4 [==============================] - 7s 2s/step - loss: 0.6745 - accuracy: 0.4271 - val_loss: 0.7787 - val_accuracy: 0.7500 Epoch 3/50 4/4 [==============================] - 7s 2s/step - loss: 0.6698 - accuracy: 0.4354 - val_loss: 0.7603 - val_accuracy: 0.7500 Epoch 4/50 4/4 [==============================] - 7s 2s/step - loss: 0.6528 - accuracy: 0.4083 - val_loss: 0.7550 - val_accuracy: 0.7500 Epoch 5/50 4/4 [==============================] - 7s 2s/step - loss: 0.6535 - accuracy: 0.4313 - val_loss: 0.7370 - val_accuracy: 0.8333 Epoch 6/50 4/4 [==============================] - 7s 2s/step - loss: 0.6445 - accuracy: 0.4979 - val_loss: 0.7201 - val_accuracy: 0.8333 Epoch 7/50 4/4 [==============================] - 7s 2s/step - loss: 0.6333 - accuracy: 0.4917 - val_loss: 0.7185 - val_accuracy: 0.8333 Epoch 8/50 4/4 [==============================] - 7s 2s/step - loss: 0.6152 - accuracy: 0.5854 - val_loss: 0.6988 - val_accuracy: 0.9167 Epoch 9/50 4/4 [==============================] - 7s 2s/step - loss: 0.5806 - accuracy: 0.6562 - val_loss: 0.6805 - val_accuracy: 0.9167 Epoch 10/50 4/4 [==============================] - 7s 2s/step - loss: 0.5872 - accuracy: 0.6854 - val_loss: 0.6599 - val_accuracy: 0.9167 Epoch 11/50 4/4 [==============================] - 7s 2s/step - loss: 0.5753 - accuracy: 0.7875 - val_loss: 0.6401 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 7s 2s/step - loss: 0.5682 - accuracy: 0.8354 - val_loss: 0.6097 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 7s 2s/step - loss: 0.5380 - accuracy: 0.8396 - val_loss: 0.5732 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 7s 2s/step - loss: 0.5061 - accuracy: 0.7708 - val_loss: 0.5657 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 7s 2s/step - loss: 0.5043 - accuracy: 0.8604 - val_loss: 0.5254 - val_accuracy: 1.0000 Epoch 16/50 4/4 [==============================] - 7s 2s/step - loss: 0.4795 - accuracy: 0.8708 - val_loss: 0.4805 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 7s 2s/step - loss: 0.4456 - accuracy: 0.8000 - val_loss: 0.4539 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 7s 2s/step - loss: 0.4512 - accuracy: 0.9021 - val_loss: 0.4331 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 7s 2s/step - loss: 0.4210 - accuracy: 0.8688 - val_loss: 0.4411 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 7s 2s/step - loss: 0.4167 - accuracy: 0.8646 - val_loss: 0.3781 - val_accuracy: 0.9167 Epoch 21/50 4/4 [==============================] - 7s 2s/step - loss: 0.3550 - accuracy: 0.9375 - val_loss: 0.3492 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 7s 2s/step - loss: 0.3720 - accuracy: 0.9000 - val_loss: 0.3550 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 7s 2s/step - loss: 0.3251 - accuracy: 0.9292 - val_loss: 0.3234 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 7s 2s/step - loss: 0.3264 - accuracy: 0.9333 - val_loss: 0.2942 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 7s 2s/step - loss: 0.2937 - accuracy: 0.9125 - val_loss: 0.3439 - val_accuracy: 0.9167 Epoch 26/50 4/4 [==============================] - 7s 2s/step - loss: 0.2798 - accuracy: 0.9250 - val_loss: 0.2842 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 7s 2s/step - loss: 0.2835 - accuracy: 0.9479 - val_loss: 0.2385 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 7s 2s/step - loss: 0.2610 - accuracy: 0.9417 - val_loss: 0.2352 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 7s 2s/step - loss: 0.2916 - accuracy: 0.8875 - val_loss: 0.2221 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 7s 2s/step - loss: 0.2620 - accuracy: 0.9417 - val_loss: 0.2054 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 7s 2s/step - loss: 0.2015 - accuracy: 0.9417 - val_loss: 0.2074 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 7s 2s/step - loss: 0.2462 - accuracy: 0.9292 - val_loss: 0.1961 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 7s 2s/step - loss: 0.2042 - accuracy: 0.9938 - val_loss: 0.1820 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 7s 2s/step - loss: 0.1951 - accuracy: 0.9667 - val_loss: 0.1748 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 7s 2s/step - loss: 0.2175 - accuracy: 0.9271 - val_loss: 0.1628 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 7s 2s/step - loss: 0.1792 - accuracy: 0.9563 - val_loss: 0.1569 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 7s 2s/step - loss: 0.1809 - accuracy: 0.9229 - val_loss: 0.1613 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 7s 2s/step - loss: 0.1747 - accuracy: 0.9313 - val_loss: 0.1622 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 7s 2s/step - loss: 0.1588 - accuracy: 1.0000 - val_loss: 0.1483 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 7s 2s/step - loss: 0.1709 - accuracy: 0.9437 - val_loss: 0.1428 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 7s 2s/step - loss: 0.1743 - accuracy: 0.9563 - val_loss: 0.1420 - val_accuracy: 0.9167 Epoch 42/50 4/4 [==============================] - 7s 2s/step - loss: 0.2167 - accuracy: 0.9021 - val_loss: 0.1526 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 7s 2s/step - loss: 0.1694 - accuracy: 0.9271 - val_loss: 0.1315 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 7s 2s/step - loss: 0.1597 - accuracy: 0.9646 - val_loss: 0.1601 - val_accuracy: 0.9167 Epoch 45/50 4/4 [==============================] - 7s 2s/step - loss: 0.1764 - accuracy: 0.9437 - val_loss: 0.1094 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 7s 2s/step - loss: 0.1582 - accuracy: 0.9542 - val_loss: 0.1403 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 7s 2s/step - loss: 0.1879 - accuracy: 0.9542 - val_loss: 0.0674 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 7s 2s/step - loss: 0.1812 - accuracy: 0.9708 - val_loss: 0.0751 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 7s 2s/step - loss: 0.1231 - accuracy: 0.9875 - val_loss: 0.1512 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 7s 2s/step - loss: 0.1537 - accuracy: 0.9292 - val_loss: 0.0958 - val_accuracy: 1.0000
loss_plotter.plot(training_histories)
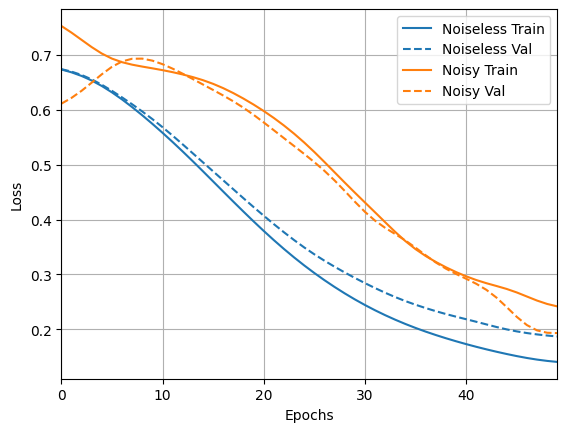
acc_plotter.plot(training_histories)