רַעַשׁ

הצג באתר TensorFlow.org

הפעל בגוגל קולאב

צפה במקור ב-GitHub

הורד מחברת

רעש קיים במחשבים קוונטיים של ימינו. קוויביטים רגישים להפרעות מהסביבה שמסביב, ייצור לא מושלם, TLS ולפעמים אפילו קרני גמא . עד שמגיעים לתיקון שגיאות בקנה מידה גדול, האלגוריתמים של היום חייבים להיות מסוגלים להישאר פונקציונליים בנוכחות רעש. זה הופך את בדיקת אלגוריתמים תחת רעש לשלב חשוב לאימות אלגוריתמים קוונטיים / מודלים שיתפקדו במחשבים הקוונטיים של היום.

במדריך זה תחקור את היסודות של הדמיית מעגלים רועשים ב-TFQ באמצעות ה-API ברמה גבוהה של tfq.layers .

להכין

pip install tensorflow==2.7.0 tensorflow-quantum

pip install -q git+https://github.com/tensorflow/docs

# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)

<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>

import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots

2022-02-04 12:35:30.853880: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected

1. הבנת רעש קוונטי

1.1 רעש מעגל בסיסי

רעש במחשב קוונטי משפיע על דגימות מיתרי הסיביות שאתה מסוגל למדוד ממנו. דרך אינטואיטיבית אחת שאתה יכול להתחיל לחשוב על זה היא שמחשב קוונטי רועש "יכניס", "ימחק" או "יחליף" שערים במקומות אקראיים כמו הדיאגרמה שלהלן:

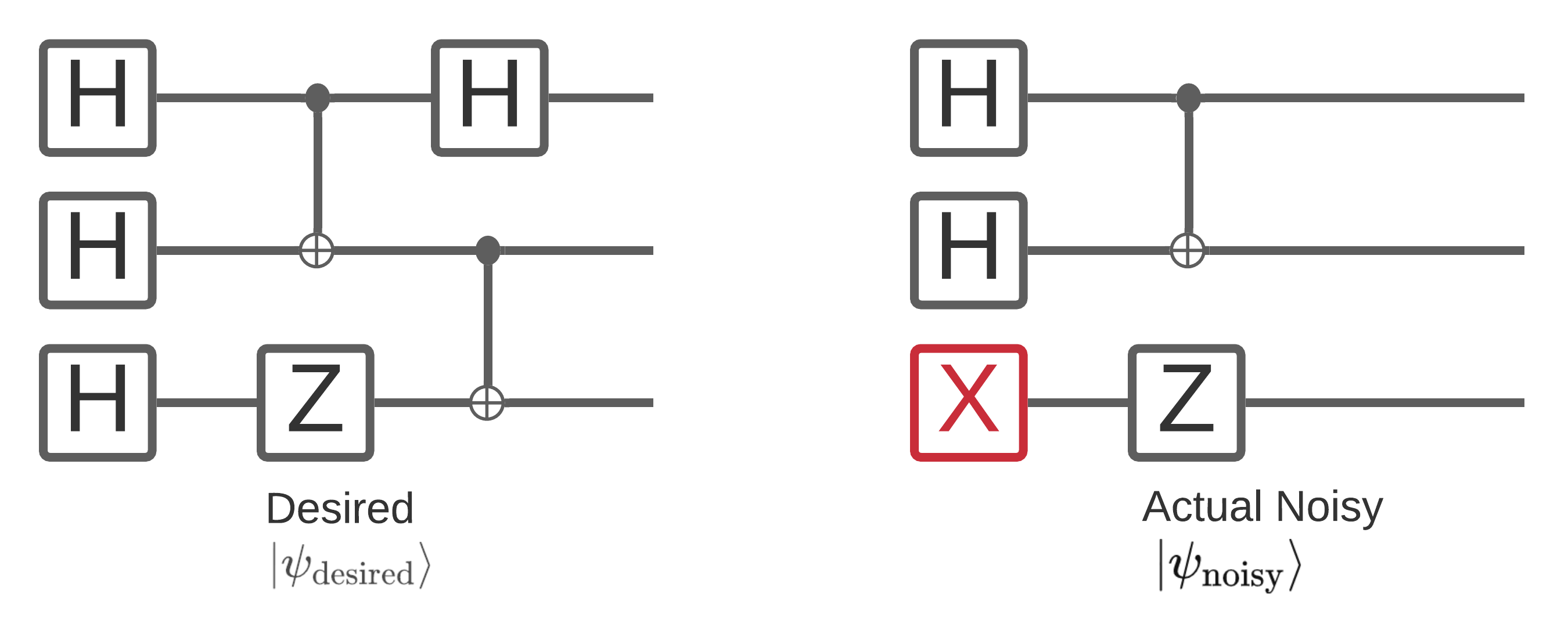
בהתבסס על האינטואיציה הזו, כשאתה מתמודד עם רעש, אתה כבר לא משתמש במצב טהור אחד \(|\psi \rangle\) אלא מתמודד עם מכלול של כל המימושים הרועשים האפשריים של המעגל הרצוי שלך: \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) . כאשר \(p_j\) נותן את ההסתברות שהמערכת נמצאת ב- \(|\psi_j \rangle\) .

אם נבקר מחדש בתמונה שלמעלה, אם היינו יודעים מראש ש-90% מהמקרים המערכת שלנו בוצעה בצורה מושלמת, או שגה ב-10% מהפעמים רק במצב הכשל האחד הזה, אז האנסמבל שלנו יהיה:

\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)

אם הייתה יותר מדרך אחת שבה המעגל שלנו יכול לשגות, אז האנסמבל \(\rho\) היה מכיל יותר משני מונחים בלבד (אחד עבור כל מימוש רועש חדש שיכול לקרות). \(\rho\) מכונה מטריצת הצפיפות המתארת ​​את המערכת הרועשת שלך.

1.2 שימוש בערוצים לדגם רעשי מעגל

למרבה הצער בפועל זה כמעט בלתי אפשרי לדעת את כל הדרכים שבהן המעגל שלך עלול לשגות ואת ההסתברויות המדויקות שלהן. הנחה מפשטת שאתה יכול לעשות היא שאחרי כל פעולה במעגל שלך יש איזשהו ערוץ שלוכד בערך איך הפעולה הזו עלולה לשגות. אתה יכול ליצור במהירות מעגל עם קצת רעש:

def x_circuit(qubits):
  """Produces an X wall circuit on `qubits`."""
  return cirq.Circuit(cirq.X.on_each(*qubits))

def make_noisy(circuit, p):
  """Add a depolarization channel to all qubits in `circuit` before measurement."""
  return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))

my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit

my_noisy_circuit

אתה יכול לבחון את מטריצת הצפיפות \(\rho\) עם:

rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)

array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
       [0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
       [0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
       [0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)

ומטריצת הצפיפות הרועשת \(\rho\) עם:

rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)

array([[0.111+0.j, 0.   +0.j, 0.   +0.j, 0.   +0.j],
       [0.   +0.j, 0.222+0.j, 0.   +0.j, 0.   +0.j],
       [0.   +0.j, 0.   +0.j, 0.222+0.j, 0.   +0.j],
       [0.   +0.j, 0.   +0.j, 0.   +0.j, 0.444+0.j]], dtype=complex64)

בהשוואה בין שני ה- \( \rho \) השונים ניתן לראות שהרעש השפיע על אמפליטודות המצב (וכתוצאה מכך על הסתברויות הדגימה). במקרה חסר רעש תמיד היית מצפה לדגום את מצב \( |11\rangle \) . אבל במצב הרועש יש כעת הסתברות שאינה אפס לדגימה של \( |00\rangle \) או \( |01\rangle \) או \( |10\rangle \) גם כן:

"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
  samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
  freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
  plt.figure(figsize=(10,5))
  plt.title('Noisy Circuit Sampling')
  plt.xlabel('Bitstring')
  plt.ylabel('Frequency')
  plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])

plot_samples(my_noisy_circuit)

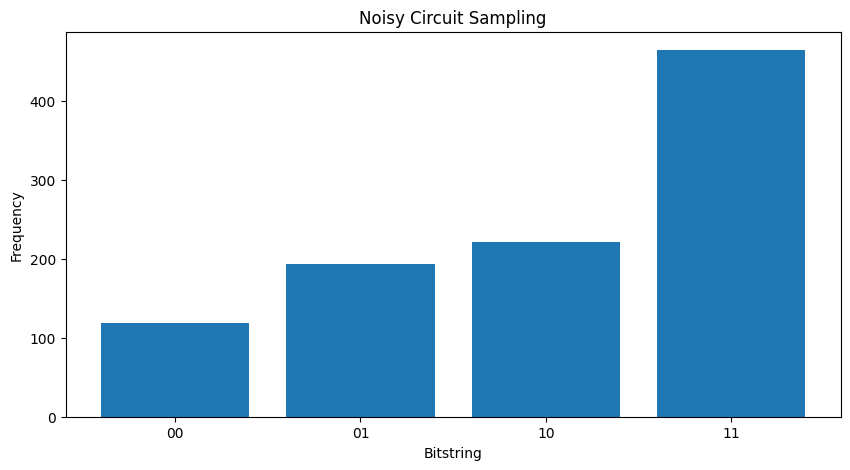
בלי שום רעש תקבל תמיד \(|11\rangle\):

"""Sample from my_circuit."""
plot_samples(my_circuit)

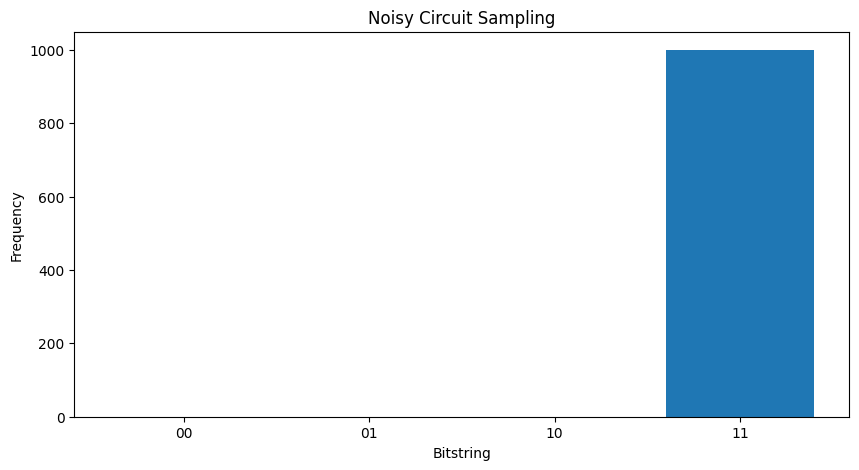
אם תגדיל את הרעש עוד קצת, יהיה קשה יותר ויותר להבחין בין ההתנהגות הרצויה (דגימת \(|11\rangle\) ) לבין הרעש:

my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)

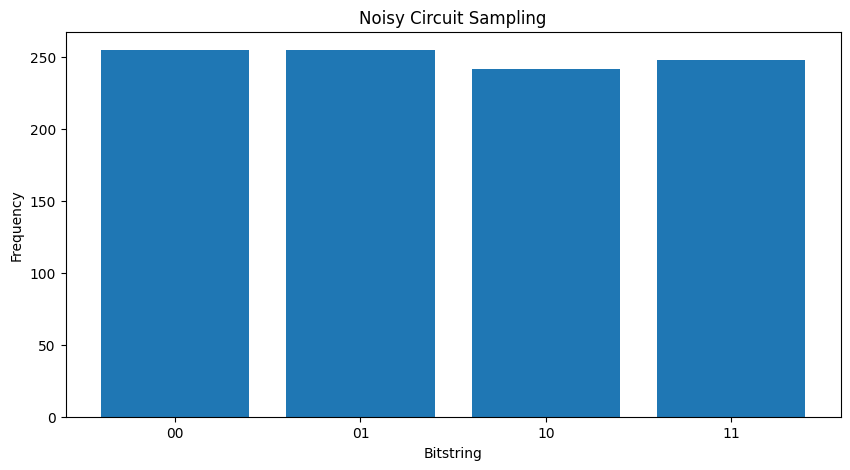
2. רעש בסיסי ב-TFQ

עם ההבנה הזו של האופן שבו רעש יכול להשפיע על ביצוע מעגלים, אתה יכול לחקור כיצד פועל רעש ב-TFQ. TensorFlow Quantum משתמש בסימולציה מבוססת מונטה-קרלו/מסלול כחלופה להדמיית מטריצת צפיפות. הסיבה לכך היא שמורכבות הזיכרון של הדמיית מטריצות צפיפות מגבילה סימולציות גדולות להיות <= 20 קיוביטים עם שיטות הדמיית מטריצות צפיפות מלאה מסורתיות. מונטה-קרלו / מסלול מחליף עלות זו בזיכרון תמורת עלות נוספת בזמן. האפשרות backend='noisy' זמינה לכל tfq.layers.Sample , tfq.layers.SampledExpectation ו- tfq.layers.Expectation (במקרה של Expectation זה כן מוסיף פרמטר repetitions נדרש).

2.1 דגימה רועשת ב-TFQ

כדי ליצור מחדש את העלילות לעיל באמצעות TFQ וסימולציית מסלול אתה יכול להשתמש ב- tfq.layers.Sample

"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)

numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])

<BarContainer object of 4 artists>

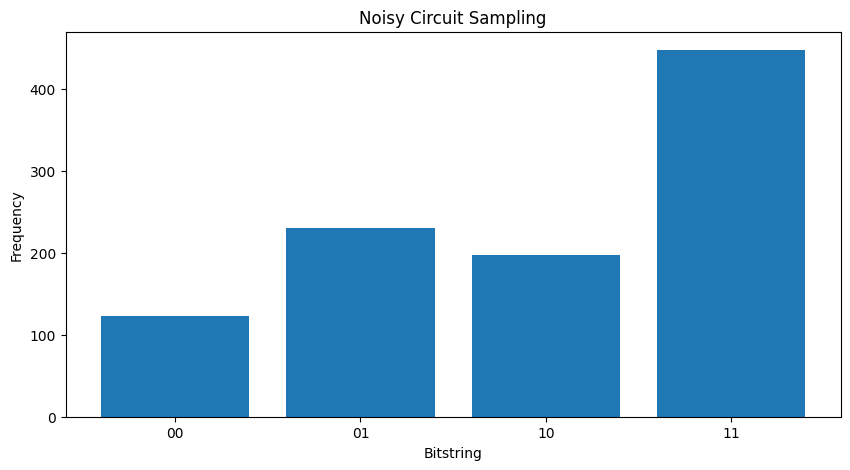
2.2 ציפייה מבוססת מדגם רועשת

כדי לבצע חישוב ציפיות מבוסס מדגם רועש, אתה יכול להשתמש ב- tfq.layers.SampleExpectation :

some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables

[cirq.X(cirq.GridQubit(0, 0)),
 cirq.Z(cirq.GridQubit(0, 0)),
 cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]

חשב את הערכות הציפיות חסרות הרעש באמצעות דגימה מהמעגל:

noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
    my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()

array([[-0.0028, -1.    ,  1.0264]], dtype=float32)

השווה את אלה עם הגרסאות הרועשות:

noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
    [my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()

array([[ 0.0242    , -0.33200002,  1.0138001 ],
       [ 0.0108    , -0.0012    ,  0.9502    ]], dtype=float32)

אתה יכול לראות שהרעש השפיע במיוחד על דיוק ה- \(\langle \psi | Z | \psi \rangle\) , כאשר my_really_noisy_circuit מתרכז מהר מאוד לכיוון 0.

2.3 חישוב ציפיות אנליטי רועש

ביצוע חישובי ציפיות אנליטיים רועשים זהה כמעט לאלו שלמעלה:

noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
    my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()

array([[ 1.9106853e-15, -1.0000000e+00,  1.0000002e+00]], dtype=float32)

noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
    [my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()

array([[ 1.9106850e-15, -3.3359998e-01,  1.0000000e+00],
       [ 1.9106857e-15, -3.8000005e-03,  1.0000001e+00]], dtype=float32)

3. מודלים היברידיים ורעש נתונים קוונטיים

כעת, לאחר שיישמת כמה סימולציות של מעגלים רועשים ב-TFQ, אתה יכול להתנסות כיצד רעש משפיע על מודלים קוונטיים קלאסיים קוונטיים והיברידיים, על ידי השוואה וניגודיות של הביצועים הרועשים לעומת חסרי הרעש שלהם. בדיקה ראשונה טובה כדי לראות אם דגם או אלגוריתם עמידים בפני רעש היא לבדוק תחת מודל דה-פולריזציה רחב מעגל שנראה בערך כך:

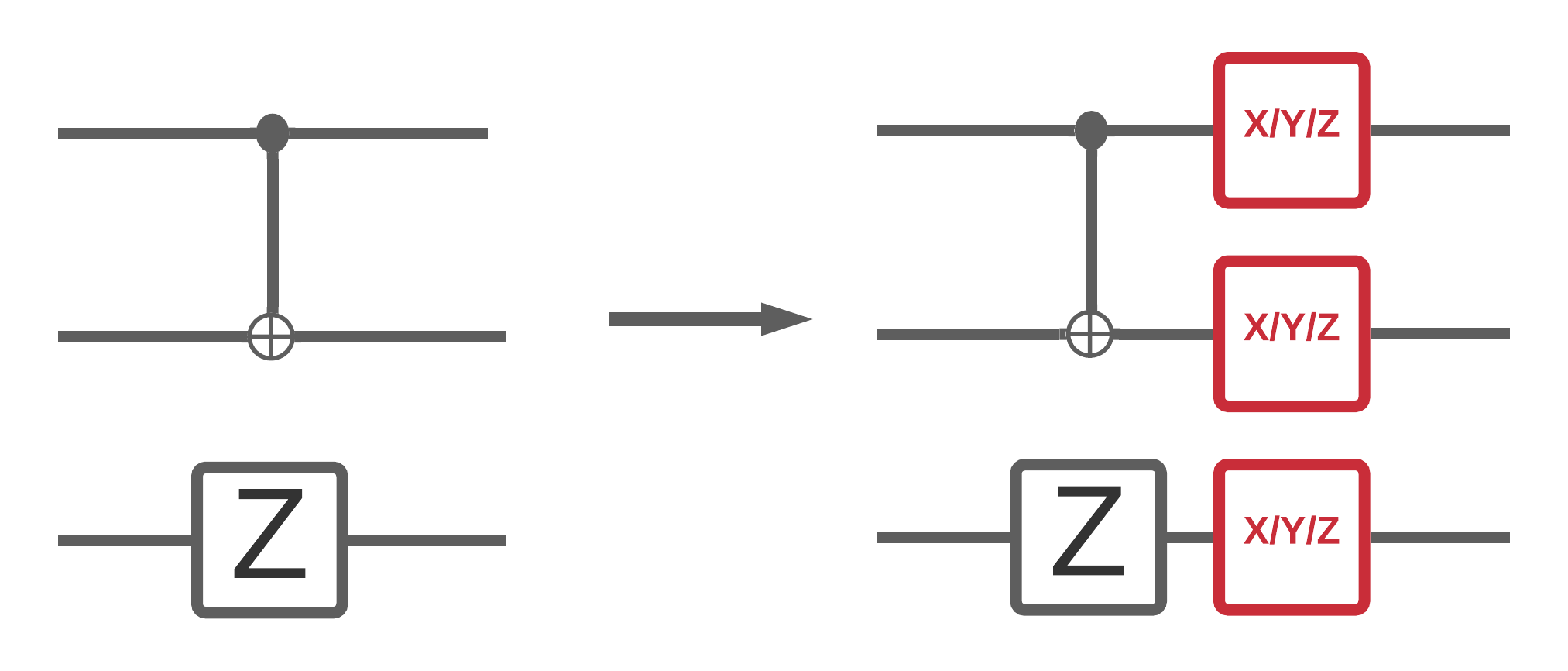
כאשר לכל פרוסת זמן של המעגל (המכונה לפעמים רגע) יש תעלת דה-פולריזציה שצורפה לאחר כל פעולת שער באותה פרוסת זמן. ערוץ הדפולריזציה עם החל אחד של \(\{X, Y, Z \}\) עם הסתברות \(p\) או החל כלום (שמור על הפעולה המקורית) עם הסתברות \(1-p\).

3.1 נתונים

עבור דוגמה זו אתה יכול להשתמש בכמה מעגלים מוכנים במודול tfq.datasets אימון:

qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]

Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 
184451072/184449737 [==============================] - 2s 0us/step
184459264/184449737 [==============================] - 2s 0us/step

כתיבת פונקציית עוזר קטנה תעזור ליצור את הנתונים עבור המקרה הרועש לעומת חסר הרעש:

def get_data(qubits, depolarize_p=0.):
  """Return quantum data circuits and labels in `tf.Tensor` form."""
  circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
  if depolarize_p >= 1e-5:
    circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
  tmp = list(zip(circuits, labels))
  random.shuffle(tmp)
  circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
  labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])

  return circuits_tensor, labels_tensor

3.2 הגדר מעגל דגם

כעת, כשיש לך נתונים קוונטיים בצורה של מעגלים, תזדקק למעגל כדי לדגמן את הנתונים האלה, כמו בנתונים אתה יכול לכתוב פונקציית עוזר ליצור מעגל זה שמכיל רעש באופן אופציונלי:

def modelling_circuit(qubits, depth, depolarize_p=0.):
  """A simple classifier circuit."""
  dim = len(qubits)
  ret = cirq.Circuit(cirq.H.on_each(*qubits))

  for i in range(depth):
    # Entangle layer.
    ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
    ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
    # Learnable rotation layer.
    # i_params = sympy.symbols(f'layer-{i}-0:{dim}')
    param = sympy.Symbol(f'layer-{i}')
    single_qb = cirq.X
    if i % 2 == 1:
      single_qb = cirq.Y
    ret += cirq.Circuit(single_qb(q) ** param for q in qubits)

  if depolarize_p >= 1e-5:
    ret = ret.with_noise(cirq.depolarize(depolarize_p))

  return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]

modelling_circuit(qubits, 3)[0]

3.3 בניית מודל והדרכה

עם מעגל הנתונים והדגם שלך בנוי, פונקציית העזר הסופית שתזדקק לה היא כזו שיכולה להרכיב tf.keras.Model היברידי קוונטי רועש או חסר רעש:

def build_keras_model(qubits, depolarize_p=0.):
  """Prepare a noisy hybrid quantum classical Keras model."""
  spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)

  circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
  if depolarize_p >= 1e-5:
    quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
  else:
    quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)

  intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
  post_process = tf.keras.layers.Dense(1)(intermediate)

  return tf.keras.Model(inputs=[spin_input], outputs=[post_process])

4. השוו ביצועים

4.1 קו בסיס נטול רעש

עם יצירת הנתונים וקוד בניית המודל שלך, כעת תוכל להשוות ולהשוות את ביצועי המודל בהגדרות חסרות הרעש והרעש, ראשית תוכל להפעיל אימון ללא רעש ייחוס:

training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)

phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
                   loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
                   metrics=['accuracy'])


# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)

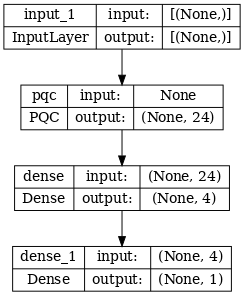
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
                         y=noiseless_labels,
                         batch_size=16,
                         epochs=n_epochs,
                         validation_split=0.15,
                         verbose=1)

Epoch 1/50
4/4 [==============================] - 1s 133ms/step - loss: 0.7212 - accuracy: 0.4688 - val_loss: 0.6834 - val_accuracy: 0.5000
Epoch 2/50
4/4 [==============================] - 0s 80ms/step - loss: 0.6787 - accuracy: 0.4688 - val_loss: 0.6640 - val_accuracy: 0.5000
Epoch 3/50
4/4 [==============================] - 0s 76ms/step - loss: 0.6637 - accuracy: 0.4688 - val_loss: 0.6529 - val_accuracy: 0.5000
Epoch 4/50
4/4 [==============================] - 0s 78ms/step - loss: 0.6505 - accuracy: 0.4688 - val_loss: 0.6423 - val_accuracy: 0.5000
Epoch 5/50
4/4 [==============================] - 0s 77ms/step - loss: 0.6409 - accuracy: 0.4688 - val_loss: 0.6322 - val_accuracy: 0.5000
Epoch 6/50
4/4 [==============================] - 0s 77ms/step - loss: 0.6300 - accuracy: 0.4844 - val_loss: 0.6187 - val_accuracy: 0.5000
Epoch 7/50
4/4 [==============================] - 0s 77ms/step - loss: 0.6171 - accuracy: 0.5781 - val_loss: 0.6007 - val_accuracy: 0.5000
Epoch 8/50
4/4 [==============================] - 0s 79ms/step - loss: 0.6008 - accuracy: 0.6250 - val_loss: 0.5825 - val_accuracy: 0.5833
Epoch 9/50
4/4 [==============================] - 0s 76ms/step - loss: 0.5864 - accuracy: 0.6406 - val_loss: 0.5610 - val_accuracy: 0.6667
Epoch 10/50
4/4 [==============================] - 0s 77ms/step - loss: 0.5670 - accuracy: 0.6719 - val_loss: 0.5406 - val_accuracy: 0.8333
Epoch 11/50
4/4 [==============================] - 0s 79ms/step - loss: 0.5474 - accuracy: 0.6875 - val_loss: 0.5173 - val_accuracy: 0.9167
Epoch 12/50
4/4 [==============================] - 0s 77ms/step - loss: 0.5276 - accuracy: 0.7188 - val_loss: 0.4941 - val_accuracy: 0.9167
Epoch 13/50
4/4 [==============================] - 0s 75ms/step - loss: 0.5066 - accuracy: 0.7500 - val_loss: 0.4686 - val_accuracy: 0.9167
Epoch 14/50
4/4 [==============================] - 0s 76ms/step - loss: 0.4838 - accuracy: 0.7812 - val_loss: 0.4437 - val_accuracy: 0.9167
Epoch 15/50
4/4 [==============================] - 0s 76ms/step - loss: 0.4618 - accuracy: 0.8281 - val_loss: 0.4182 - val_accuracy: 0.9167
Epoch 16/50
4/4 [==============================] - 0s 76ms/step - loss: 0.4386 - accuracy: 0.8281 - val_loss: 0.3930 - val_accuracy: 1.0000
Epoch 17/50
4/4 [==============================] - 0s 79ms/step - loss: 0.4158 - accuracy: 0.8438 - val_loss: 0.3673 - val_accuracy: 1.0000
Epoch 18/50
4/4 [==============================] - 0s 79ms/step - loss: 0.3944 - accuracy: 0.8438 - val_loss: 0.3429 - val_accuracy: 1.0000
Epoch 19/50
4/4 [==============================] - 0s 77ms/step - loss: 0.3735 - accuracy: 0.8594 - val_loss: 0.3203 - val_accuracy: 1.0000
Epoch 20/50
4/4 [==============================] - 0s 77ms/step - loss: 0.3535 - accuracy: 0.8750 - val_loss: 0.2998 - val_accuracy: 1.0000
Epoch 21/50
4/4 [==============================] - 0s 78ms/step - loss: 0.3345 - accuracy: 0.8906 - val_loss: 0.2815 - val_accuracy: 1.0000
Epoch 22/50
4/4 [==============================] - 0s 76ms/step - loss: 0.3168 - accuracy: 0.8906 - val_loss: 0.2640 - val_accuracy: 1.0000
Epoch 23/50
4/4 [==============================] - 0s 76ms/step - loss: 0.3017 - accuracy: 0.9062 - val_loss: 0.2465 - val_accuracy: 1.0000
Epoch 24/50
4/4 [==============================] - 0s 76ms/step - loss: 0.2840 - accuracy: 0.9219 - val_loss: 0.2328 - val_accuracy: 1.0000
Epoch 25/50
4/4 [==============================] - 0s 76ms/step - loss: 0.2700 - accuracy: 0.9219 - val_loss: 0.2181 - val_accuracy: 1.0000
Epoch 26/50
4/4 [==============================] - 0s 76ms/step - loss: 0.2566 - accuracy: 0.9219 - val_loss: 0.2053 - val_accuracy: 1.0000
Epoch 27/50
4/4 [==============================] - 0s 77ms/step - loss: 0.2445 - accuracy: 0.9375 - val_loss: 0.1935 - val_accuracy: 1.0000
Epoch 28/50
4/4 [==============================] - 0s 76ms/step - loss: 0.2332 - accuracy: 0.9375 - val_loss: 0.1839 - val_accuracy: 1.0000
Epoch 29/50
4/4 [==============================] - 0s 78ms/step - loss: 0.2227 - accuracy: 0.9375 - val_loss: 0.1734 - val_accuracy: 1.0000
Epoch 30/50
4/4 [==============================] - 0s 76ms/step - loss: 0.2145 - accuracy: 0.9375 - val_loss: 0.1630 - val_accuracy: 1.0000
Epoch 31/50
4/4 [==============================] - 0s 76ms/step - loss: 0.2047 - accuracy: 0.9375 - val_loss: 0.1564 - val_accuracy: 1.0000
Epoch 32/50
4/4 [==============================] - 0s 76ms/step - loss: 0.1971 - accuracy: 0.9375 - val_loss: 0.1525 - val_accuracy: 1.0000
Epoch 33/50
4/4 [==============================] - 0s 75ms/step - loss: 0.1894 - accuracy: 0.9531 - val_loss: 0.1464 - val_accuracy: 1.0000
Epoch 34/50
4/4 [==============================] - 0s 74ms/step - loss: 0.1825 - accuracy: 0.9531 - val_loss: 0.1407 - val_accuracy: 1.0000
Epoch 35/50
4/4 [==============================] - 0s 77ms/step - loss: 0.1771 - accuracy: 0.9531 - val_loss: 0.1330 - val_accuracy: 1.0000
Epoch 36/50
4/4 [==============================] - 0s 75ms/step - loss: 0.1704 - accuracy: 0.9531 - val_loss: 0.1288 - val_accuracy: 1.0000
Epoch 37/50
4/4 [==============================] - 0s 76ms/step - loss: 0.1647 - accuracy: 0.9531 - val_loss: 0.1237 - val_accuracy: 1.0000
Epoch 38/50
4/4 [==============================] - 0s 80ms/step - loss: 0.1603 - accuracy: 0.9531 - val_loss: 0.1221 - val_accuracy: 1.0000
Epoch 39/50
4/4 [==============================] - 0s 76ms/step - loss: 0.1551 - accuracy: 0.9688 - val_loss: 0.1177 - val_accuracy: 1.0000
Epoch 40/50
4/4 [==============================] - 0s 75ms/step - loss: 0.1509 - accuracy: 0.9688 - val_loss: 0.1136 - val_accuracy: 1.0000
Epoch 41/50
4/4 [==============================] - 0s 76ms/step - loss: 0.1466 - accuracy: 0.9688 - val_loss: 0.1110 - val_accuracy: 1.0000
Epoch 42/50
4/4 [==============================] - 0s 76ms/step - loss: 0.1426 - accuracy: 0.9688 - val_loss: 0.1083 - val_accuracy: 1.0000
Epoch 43/50
4/4 [==============================] - 0s 75ms/step - loss: 0.1386 - accuracy: 0.9688 - val_loss: 0.1050 - val_accuracy: 1.0000
Epoch 44/50
4/4 [==============================] - 0s 83ms/step - loss: 0.1362 - accuracy: 0.9688 - val_loss: 0.0989 - val_accuracy: 1.0000
Epoch 45/50
4/4 [==============================] - 0s 78ms/step - loss: 0.1324 - accuracy: 0.9688 - val_loss: 0.0978 - val_accuracy: 1.0000
Epoch 46/50
4/4 [==============================] - 0s 77ms/step - loss: 0.1290 - accuracy: 0.9688 - val_loss: 0.0964 - val_accuracy: 1.0000
Epoch 47/50
4/4 [==============================] - 0s 75ms/step - loss: 0.1265 - accuracy: 0.9688 - val_loss: 0.0929 - val_accuracy: 1.0000
Epoch 48/50
4/4 [==============================] - 0s 77ms/step - loss: 0.1234 - accuracy: 0.9688 - val_loss: 0.0923 - val_accuracy: 1.0000
Epoch 49/50
4/4 [==============================] - 0s 77ms/step - loss: 0.1213 - accuracy: 0.9688 - val_loss: 0.0903 - val_accuracy: 1.0000
Epoch 50/50
4/4 [==============================] - 0s 77ms/step - loss: 0.1182 - accuracy: 0.9688 - val_loss: 0.0885 - val_accuracy: 1.0000

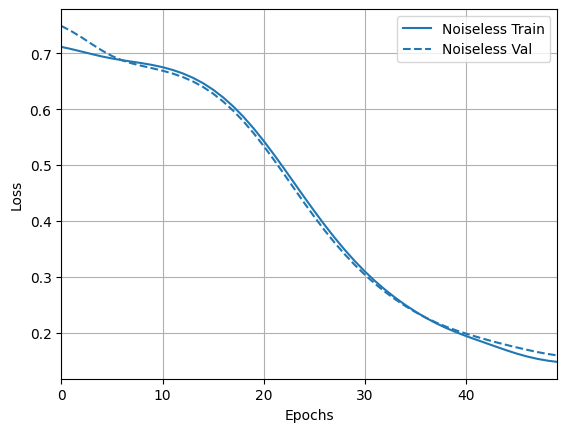
וחקור את התוצאות והדיוק:

loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)

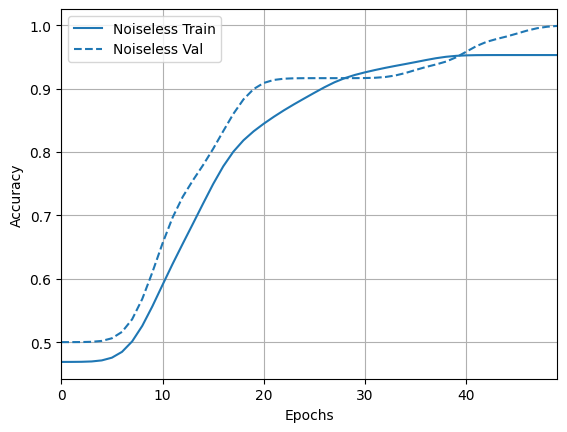
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
acc_plotter.plot(training_histories)

4.2 השוואה רועשת

עכשיו אתה יכול לבנות דגם חדש עם מבנה רועש ולהשוות לאמור לעיל, הקוד כמעט זהה:

depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)

noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
                   loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
                   metrics=['accuracy'])


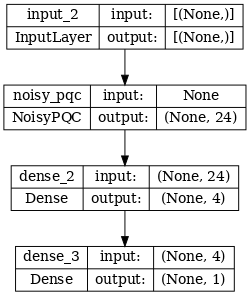
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)

noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
                         y=noisy_labels,
                         batch_size=16,
                         epochs=n_epochs,
                         validation_split=0.15,
                         verbose=1)

Epoch 1/50
4/4 [==============================] - 8s 2s/step - loss: 0.8265 - accuracy: 0.4844 - val_loss: 0.8369 - val_accuracy: 0.4167
Epoch 2/50
4/4 [==============================] - 7s 2s/step - loss: 0.7613 - accuracy: 0.4844 - val_loss: 0.7695 - val_accuracy: 0.4167
Epoch 3/50
4/4 [==============================] - 7s 2s/step - loss: 0.7151 - accuracy: 0.4844 - val_loss: 0.7290 - val_accuracy: 0.4167
Epoch 4/50
4/4 [==============================] - 7s 2s/step - loss: 0.6915 - accuracy: 0.4844 - val_loss: 0.7014 - val_accuracy: 0.4167
Epoch 5/50
4/4 [==============================] - 7s 2s/step - loss: 0.6837 - accuracy: 0.4844 - val_loss: 0.6811 - val_accuracy: 0.4167
Epoch 6/50
4/4 [==============================] - 7s 2s/step - loss: 0.6717 - accuracy: 0.4844 - val_loss: 0.6801 - val_accuracy: 0.4167
Epoch 7/50
4/4 [==============================] - 7s 2s/step - loss: 0.6739 - accuracy: 0.4844 - val_loss: 0.6726 - val_accuracy: 0.4167
Epoch 8/50
4/4 [==============================] - 7s 2s/step - loss: 0.6713 - accuracy: 0.4844 - val_loss: 0.6661 - val_accuracy: 0.4167
Epoch 9/50
4/4 [==============================] - 7s 2s/step - loss: 0.6710 - accuracy: 0.4844 - val_loss: 0.6667 - val_accuracy: 0.4167
Epoch 10/50
4/4 [==============================] - 7s 2s/step - loss: 0.6669 - accuracy: 0.4844 - val_loss: 0.6627 - val_accuracy: 0.4167
Epoch 11/50
4/4 [==============================] - 7s 2s/step - loss: 0.6637 - accuracy: 0.4844 - val_loss: 0.6550 - val_accuracy: 0.4167
Epoch 12/50
4/4 [==============================] - 7s 2s/step - loss: 0.6616 - accuracy: 0.4844 - val_loss: 0.6593 - val_accuracy: 0.4167
Epoch 13/50
4/4 [==============================] - 7s 2s/step - loss: 0.6536 - accuracy: 0.4844 - val_loss: 0.6514 - val_accuracy: 0.4167
Epoch 14/50
4/4 [==============================] - 7s 2s/step - loss: 0.6489 - accuracy: 0.4844 - val_loss: 0.6481 - val_accuracy: 0.4167
Epoch 15/50
4/4 [==============================] - 7s 2s/step - loss: 0.6491 - accuracy: 0.4844 - val_loss: 0.6484 - val_accuracy: 0.4167
Epoch 16/50
4/4 [==============================] - 7s 2s/step - loss: 0.6389 - accuracy: 0.4844 - val_loss: 0.6396 - val_accuracy: 0.4167
Epoch 17/50
4/4 [==============================] - 7s 2s/step - loss: 0.6307 - accuracy: 0.4844 - val_loss: 0.6337 - val_accuracy: 0.4167
Epoch 18/50
4/4 [==============================] - 7s 2s/step - loss: 0.6296 - accuracy: 0.4844 - val_loss: 0.6260 - val_accuracy: 0.4167
Epoch 19/50
4/4 [==============================] - 7s 2s/step - loss: 0.6194 - accuracy: 0.4844 - val_loss: 0.6282 - val_accuracy: 0.4167
Epoch 20/50
4/4 [==============================] - 7s 2s/step - loss: 0.6095 - accuracy: 0.4844 - val_loss: 0.6138 - val_accuracy: 0.4167
Epoch 21/50
4/4 [==============================] - 7s 2s/step - loss: 0.6075 - accuracy: 0.4844 - val_loss: 0.5874 - val_accuracy: 0.4167
Epoch 22/50
4/4 [==============================] - 7s 2s/step - loss: 0.5981 - accuracy: 0.4844 - val_loss: 0.5981 - val_accuracy: 0.4167
Epoch 23/50
4/4 [==============================] - 7s 2s/step - loss: 0.5823 - accuracy: 0.4844 - val_loss: 0.5818 - val_accuracy: 0.4167
Epoch 24/50
4/4 [==============================] - 7s 2s/step - loss: 0.5768 - accuracy: 0.4844 - val_loss: 0.5617 - val_accuracy: 0.4167
Epoch 25/50
4/4 [==============================] - 7s 2s/step - loss: 0.5651 - accuracy: 0.4844 - val_loss: 0.5638 - val_accuracy: 0.4167
Epoch 26/50
4/4 [==============================] - 7s 2s/step - loss: 0.5496 - accuracy: 0.4844 - val_loss: 0.5532 - val_accuracy: 0.4167
Epoch 27/50
4/4 [==============================] - 7s 2s/step - loss: 0.5340 - accuracy: 0.5000 - val_loss: 0.5345 - val_accuracy: 0.4167
Epoch 28/50
4/4 [==============================] - 7s 2s/step - loss: 0.5297 - accuracy: 0.5156 - val_loss: 0.5308 - val_accuracy: 0.4167
Epoch 29/50
4/4 [==============================] - 7s 2s/step - loss: 0.5120 - accuracy: 0.5312 - val_loss: 0.5224 - val_accuracy: 0.5000
Epoch 30/50
4/4 [==============================] - 7s 2s/step - loss: 0.4992 - accuracy: 0.5781 - val_loss: 0.4921 - val_accuracy: 0.5833
Epoch 31/50
4/4 [==============================] - 7s 2s/step - loss: 0.4823 - accuracy: 0.5938 - val_loss: 0.4975 - val_accuracy: 0.5000
Epoch 32/50
4/4 [==============================] - 7s 2s/step - loss: 0.5025 - accuracy: 0.5781 - val_loss: 0.4814 - val_accuracy: 0.5000
Epoch 33/50
4/4 [==============================] - 7s 2s/step - loss: 0.4655 - accuracy: 0.6562 - val_loss: 0.4391 - val_accuracy: 0.6667
Epoch 34/50
4/4 [==============================] - 7s 2s/step - loss: 0.4552 - accuracy: 0.7031 - val_loss: 0.4528 - val_accuracy: 0.5833
Epoch 35/50
4/4 [==============================] - 7s 2s/step - loss: 0.4516 - accuracy: 0.6719 - val_loss: 0.3993 - val_accuracy: 0.8333
Epoch 36/50
4/4 [==============================] - 7s 2s/step - loss: 0.4320 - accuracy: 0.7656 - val_loss: 0.4225 - val_accuracy: 0.6667
Epoch 37/50
4/4 [==============================] - 7s 2s/step - loss: 0.4060 - accuracy: 0.7656 - val_loss: 0.4001 - val_accuracy: 0.9167
Epoch 38/50
4/4 [==============================] - 7s 2s/step - loss: 0.3858 - accuracy: 0.7812 - val_loss: 0.4152 - val_accuracy: 0.8333
Epoch 39/50
4/4 [==============================] - 7s 2s/step - loss: 0.3964 - accuracy: 0.7656 - val_loss: 0.3899 - val_accuracy: 0.7500
Epoch 40/50
4/4 [==============================] - 7s 2s/step - loss: 0.3640 - accuracy: 0.8125 - val_loss: 0.3689 - val_accuracy: 0.7500
Epoch 41/50
4/4 [==============================] - 7s 2s/step - loss: 0.3676 - accuracy: 0.7812 - val_loss: 0.3786 - val_accuracy: 0.7500
Epoch 42/50
4/4 [==============================] - 7s 2s/step - loss: 0.3466 - accuracy: 0.8281 - val_loss: 0.3313 - val_accuracy: 0.8333
Epoch 43/50
4/4 [==============================] - 7s 2s/step - loss: 0.3520 - accuracy: 0.8594 - val_loss: 0.3398 - val_accuracy: 0.8333
Epoch 44/50
4/4 [==============================] - 7s 2s/step - loss: 0.3402 - accuracy: 0.8438 - val_loss: 0.3135 - val_accuracy: 0.9167
Epoch 45/50
4/4 [==============================] - 7s 2s/step - loss: 0.3253 - accuracy: 0.8281 - val_loss: 0.3469 - val_accuracy: 0.8333
Epoch 46/50
4/4 [==============================] - 7s 2s/step - loss: 0.3239 - accuracy: 0.8281 - val_loss: 0.3038 - val_accuracy: 0.9167
Epoch 47/50
4/4 [==============================] - 7s 2s/step - loss: 0.2948 - accuracy: 0.8594 - val_loss: 0.3056 - val_accuracy: 0.9167
Epoch 48/50
4/4 [==============================] - 7s 2s/step - loss: 0.2972 - accuracy: 0.9219 - val_loss: 0.2699 - val_accuracy: 0.9167
Epoch 49/50
4/4 [==============================] - 7s 2s/step - loss: 0.3041 - accuracy: 0.8281 - val_loss: 0.2754 - val_accuracy: 0.9167
Epoch 50/50
4/4 [==============================] - 7s 2s/step - loss: 0.2944 - accuracy: 0.8750 - val_loss: 0.2988 - val_accuracy: 0.9167

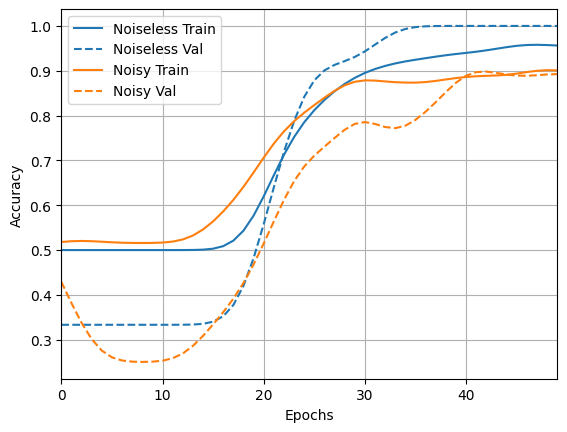
loss_plotter.plot(training_histories)

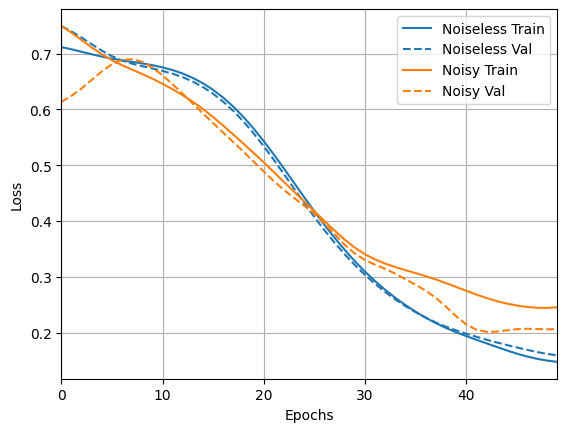
acc_plotter.plot(training_histories)