TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
আধুনিক দিনের কোয়ান্টাম কম্পিউটারে শব্দ বিদ্যমান। কিউবিট আশেপাশের পরিবেশ, অসম্পূর্ণ বানোয়াট, TLS এবং কখনও কখনও গামা রশ্মি থেকে হস্তক্ষেপের জন্য সংবেদনশীল। যতক্ষণ না বড় আকারের ত্রুটি সংশোধন করা হয়, আজকের অ্যালগরিদমগুলি অবশ্যই গোলমালের উপস্থিতিতে কার্যকরী থাকতে সক্ষম হবে। এটি কোয়ান্টাম অ্যালগরিদম / মডেলগুলি আজকের কোয়ান্টাম কম্পিউটারগুলিতে কাজ করবে যাচাই করার জন্য গোলমালের অধীনে অ্যালগরিদম পরীক্ষা করাকে একটি গুরুত্বপূর্ণ পদক্ষেপ করে তোলে।
এই টিউটোরিয়ালে আপনি উচ্চ স্তরের tfq.layers API-এর মাধ্যমে TFQ-তে নয়েজ সার্কিট সিমুলেশনের মূল বিষয়গুলি অন্বেষণ করবেন।
সেটআপ
pip install tensorflow==2.7.0 tensorflow-quantum
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2022-02-04 12:35:30.853880: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. কোয়ান্টাম শব্দ বোঝা
1.1 মৌলিক সার্কিট শব্দ
একটি কোয়ান্টাম কম্পিউটারে গোলমাল বিটস্ট্রিং নমুনাগুলিকে প্রভাবিত করে যা আপনি এটি থেকে পরিমাপ করতে পারবেন। একটি স্বজ্ঞাত উপায় যা আপনি এটি সম্পর্কে ভাবতে শুরু করতে পারেন তা হল যে একটি কোলাহলপূর্ণ কোয়ান্টাম কম্পিউটার নীচের চিত্রের মতো এলোমেলো জায়গায় গেটগুলি "ঢোকাবে", "মুছে ফেলবে" বা "প্রতিস্থাপন করবে":
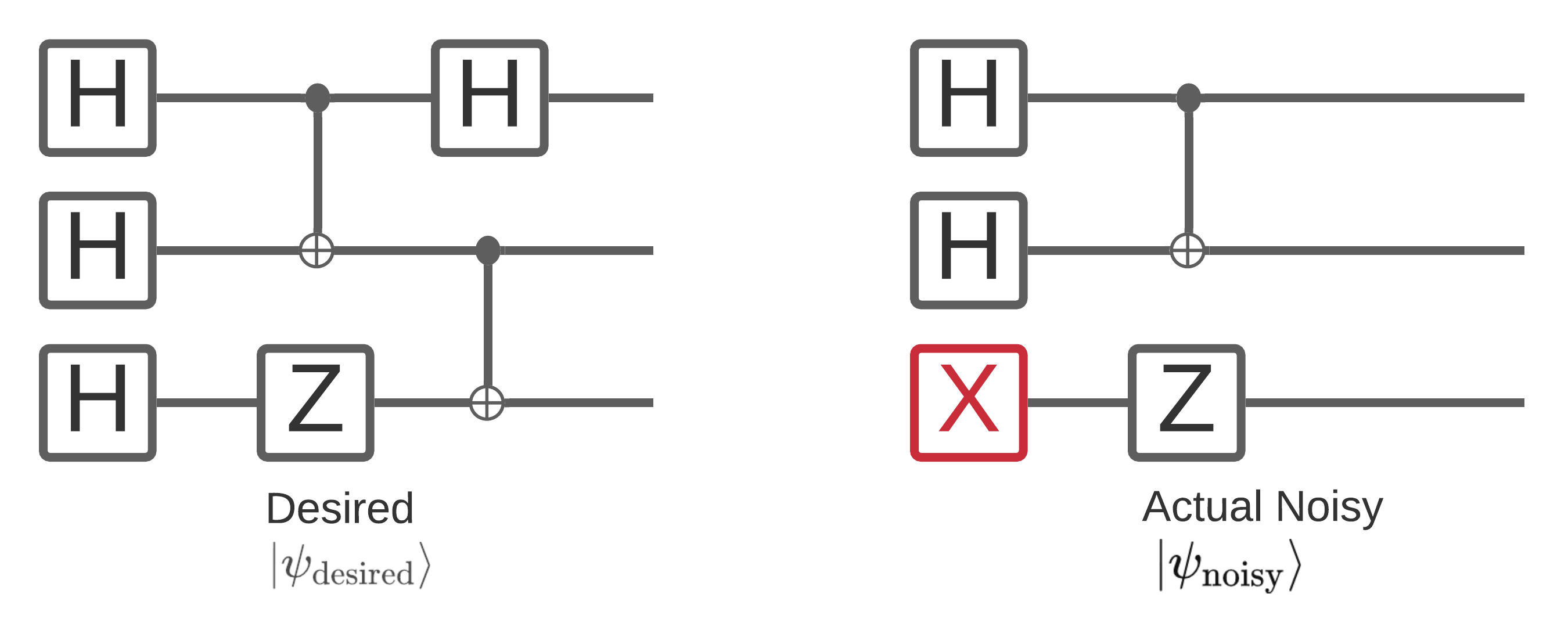
এই অন্তর্দৃষ্টি তৈরি করে, শব্দের সাথে কাজ করার সময়, আপনি আর একটি একক বিশুদ্ধ অবস্থা \(|\psi \rangle\) ব্যবহার করছেন না বরং আপনার পছন্দসই সার্কিটের সমস্ত সম্ভাব্য গোলমাল উপলব্ধির একটি সংকলন নিয়ে কাজ করছেন: \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) । যেখানে \(p_j\) সম্ভাব্যতা দেয় যে সিস্টেমটি \(|\psi_j \rangle\) এ রয়েছে।
উপরের চিত্রটি পুনরালোচনা করে, যদি আমরা আগে থেকে জানতাম যে আমাদের সিস্টেমের 90% সময় নিখুঁতভাবে কার্যকর হয়েছে, বা 10% সময়ের ব্যর্থতার এই একটি মোডের সাথে ত্রুটি হয়েছে, তাহলে আমাদের সংযোজন হবে:
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
যদি আমাদের সার্কিটটি ত্রুটি করতে পারে এমন একটির চেয়ে বেশি উপায় থাকে, তাহলে এনসেম্বল \(\rho\) এ দুটির বেশি পদ থাকবে (প্রতিটি নতুন শোরগোল উপলব্ধির জন্য একটি যা ঘটতে পারে)। \(\rho\) কে ঘনত্ব ম্যাট্রিক্স হিসাবে উল্লেখ করা হয় যা আপনার নয়েজ সিস্টেমের বর্ণনা দেয়।
1.2 সার্কিট শব্দ মডেল করতে চ্যানেল ব্যবহার করে
দুর্ভাগ্যবশত অনুশীলনে আপনার সার্কিটের ত্রুটি এবং তাদের সঠিক সম্ভাবনার সমস্ত উপায় জানা প্রায় অসম্ভব। একটি সরলীকরণ অনুমান আপনি করতে পারেন যে আপনার সার্কিটে প্রতিটি অপারেশনের পরে এমন কিছু চ্যানেল রয়েছে যা মোটামুটিভাবে ক্যাপচার করে যে সেই অপারেশনটি কীভাবে ত্রুটি হতে পারে। আপনি কিছু শব্দের সাথে দ্রুত একটি সার্কিট তৈরি করতে পারেন:
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
আপনি শব্দহীন ঘনত্ব ম্যাট্রিক্স \(\rho\) এর সাথে পরীক্ষা করতে পারেন:
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
এবং কোলাহলপূর্ণ ঘনত্ব ম্যাট্রিক্স \(\rho\) এর সাথে:
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
দুটি ভিন্ন \( \rho \) এর সাথে তুলনা করলে আপনি দেখতে পাচ্ছেন যে শব্দটি রাজ্যের প্রশস্ততাকে প্রভাবিত করেছে (এবং এর ফলে সম্ভাব্যতার নমুনা)। শব্দহীন ক্ষেত্রে আপনি সর্বদা \( |11\rangle \) অবস্থার নমুনা আশা করবেন। কিন্তু কোলাহলপূর্ণ অবস্থায় এখন \( |00\rangle \) বা \( |01\rangle \) বা \( |10\rangle \) -placeholder14 নমুনা নেওয়ার একটি অশূন্য সম্ভাবনা রয়েছে:
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
plot_samples(my_noisy_circuit)
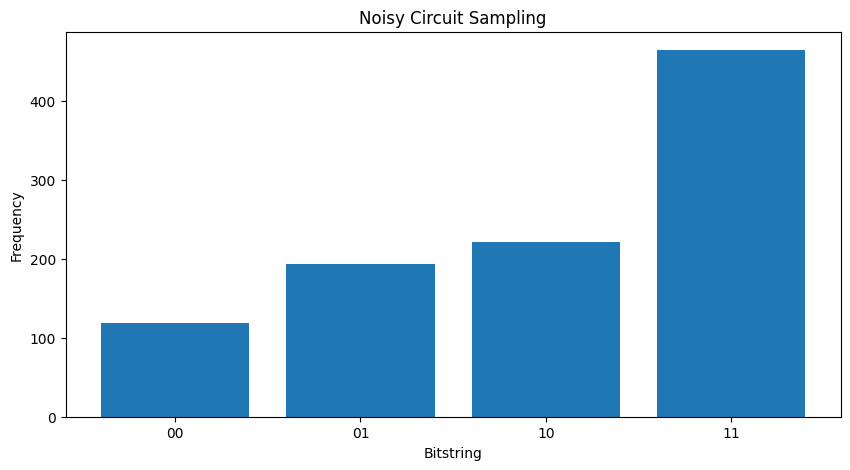
কোন শব্দ ছাড়াই আপনি সর্বদা \(|11\rangle\)পাবেন:
"""Sample from my_circuit."""
plot_samples(my_circuit)
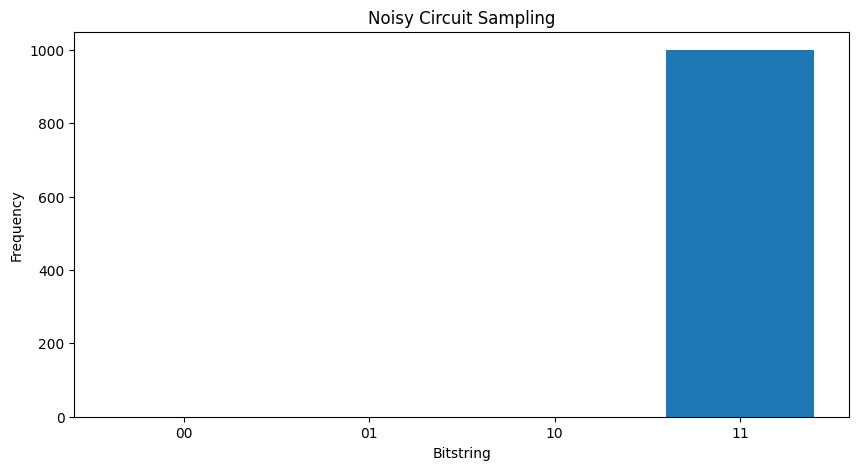
আপনি যদি আওয়াজ আরও খানিকটা বাড়িয়ে দেন তবে আওয়াজ থেকে কাঙ্খিত আচরণ (স্যাম্পলিং \(|11\rangle\) ) আলাদা করা কঠিন থেকে কঠিন হবে:
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
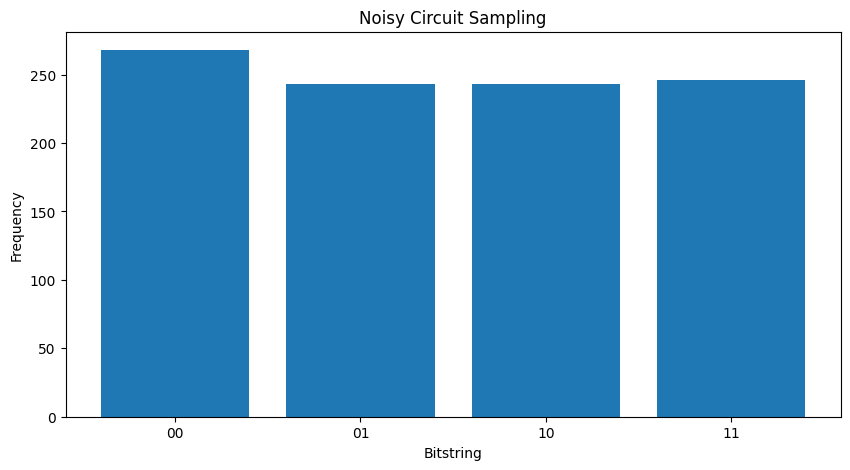
2. TFQ-এ মৌলিক শব্দ
গোলমাল কীভাবে সার্কিট সম্পাদনকে প্রভাবিত করতে পারে এই বোঝার সাথে, আপনি TFQ-এ শব্দ কীভাবে কাজ করে তা অন্বেষণ করতে পারেন। টেনসরফ্লো কোয়ান্টাম ঘনত্ব ম্যাট্রিক্স সিমুলেশনের বিকল্প হিসাবে মন্টে-কার্লো / ট্র্যাজেক্টরি ভিত্তিক সিমুলেশন ব্যবহার করে। এর কারণ হল ঘনত্ব ম্যাট্রিক্স সিমুলেশনের মেমরি জটিলতা প্রথাগত পূর্ণ ঘনত্ব ম্যাট্রিক্স সিমুলেশন পদ্ধতির সাথে বড় সিমুলেশনকে <= 20 কিউবিট সীমাবদ্ধ করে। মন্টে-কার্লো / ট্র্যাজেক্টরি সময়ের অতিরিক্ত খরচের জন্য এই খরচ মেমরিতে ট্রেড করে। backend backend='noisy' বিকল্পটি সমস্ত tfq.layers.Sample , tfq.layers.SampledExpectation এবং tfq.layers.Expectation এর জন্য উপলব্ধ ( Expectation ক্ষেত্রে এটি একটি প্রয়োজনীয় repetitions পরামিতি যোগ করে)।
2.1 TFQ-এ শোরগোল স্যাম্পলিং
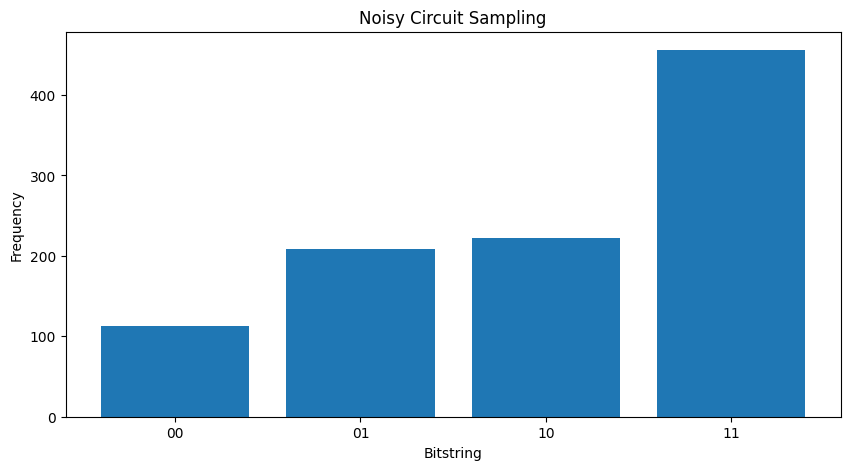
TFQ এবং ট্র্যাজেক্টরি সিমুলেশন ব্যবহার করে উপরের প্লটগুলি পুনরায় তৈরি করতে আপনি tfq.layers.Sample ব্যবহার করতে পারেন
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
2.2 কোলাহলপূর্ণ নমুনা ভিত্তিক প্রত্যাশা
কোলাহলপূর্ণ নমুনা ভিত্তিক প্রত্যাশা গণনা করতে আপনি tfq.layers.SampleExpectation ব্যবহার করতে পারেন:
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
সার্কিট থেকে নমুনা নেওয়ার মাধ্যমে শব্দহীন প্রত্যাশা অনুমান গণনা করুন:
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[-0.0028, -1. , 1.0264]], dtype=float32)
কোলাহলপূর্ণ সংস্করণগুলির সাথে তাদের তুলনা করুন:
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
array([[ 0.0242 , -0.33200002, 1.0138001 ],
[ 0.0108 , -0.0012 , 0.9502 ]], dtype=float32)
আপনি দেখতে পাচ্ছেন যে গোলমাল \(\langle \psi | Z | \psi \rangle\) নির্ভুলতাকে বিশেষভাবে প্রভাবিত করেছে, my_really_noisy_circuit খুব দ্রুত 0 এর দিকে ঘনীভূত হচ্ছে।
2.3 শোরগোল বিশ্লেষণাত্মক প্রত্যাশা গণনা
কোলাহলপূর্ণ বিশ্লেষণাত্মক প্রত্যাশার গণনা করা উপরেরটির প্রায় অনুরূপ:
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106850e-15, -3.3359998e-01, 1.0000000e+00],
[ 1.9106857e-15, -3.8000005e-03, 1.0000001e+00]], dtype=float32)
3. হাইব্রিড মডেল এবং কোয়ান্টাম ডেটা গোলমাল
এখন যেহেতু আপনি TFQ-তে কিছু গোলমাল সার্কিট সিমুলেশন প্রয়োগ করেছেন, আপনি কোলাহলপূর্ণ বনাম শব্দহীন কর্মক্ষমতা তুলনা করে এবং বৈসাদৃশ্য করে কোয়ান্টাম এবং হাইব্রিড কোয়ান্টাম ক্লাসিক্যাল মডেলগুলিকে কীভাবে শব্দ প্রভাবিত করে তা নিয়ে পরীক্ষা করতে পারেন। একটি মডেল বা অ্যালগরিদম গোলমালের জন্য শক্তিশালী কিনা তা দেখার জন্য একটি ভাল প্রথম পরীক্ষা হল সার্কিট ওয়াইড ডিপোলারাইজিং মডেলের অধীনে পরীক্ষা করা যা দেখতে এরকম কিছু:
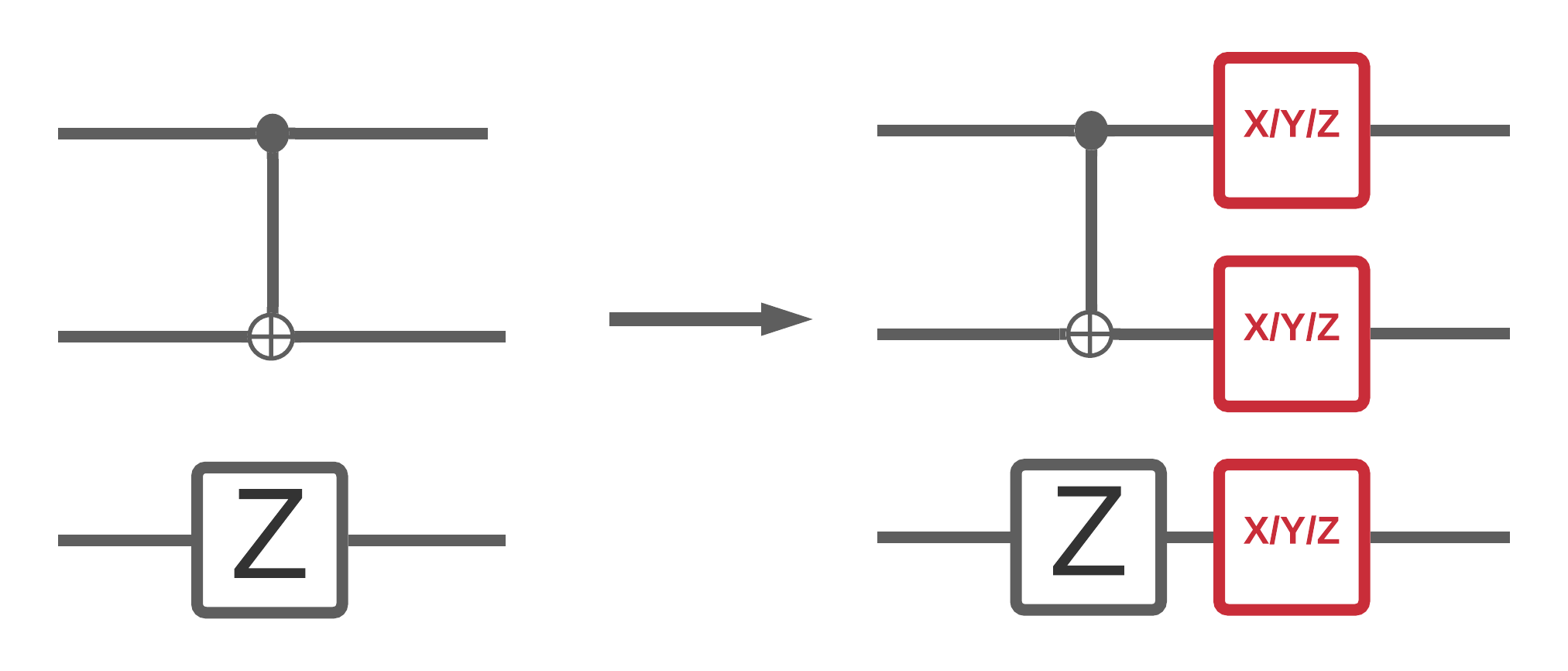
যেখানে সার্কিটের প্রতিটি স্লাইস (কখনও কখনও মোমেন্ট হিসাবে উল্লেখ করা হয়) সেই সময়ের স্লাইসে প্রতিটি গেট অপারেশনের পরে একটি ডিপোলারাইজিং চ্যানেল যুক্ত থাকে। সম্ভাব্যতা l10n-placeholder19-এর সাথে l10n-placeholder18-এর একটি প্রয়োগ করে অথবা সম্ভাব্যতা \(p\) \(1-p\) \(\{X, Y, Z \}\) কিছুই প্রয়োগ না করে (মূল ক্রিয়াকলাপটি রাখুন) সহ ডিপোলারাইজিং চ্যানেল।
3.1 ডেটা
এই উদাহরণের জন্য আপনি প্রশিক্ষণ ডেটা হিসাবে tfq.datasets মডিউলে কিছু প্রস্তুত সার্কিট ব্যবহার করতে পারেন:
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184451072/184449737 [==============================] - 2s 0us/step 184459264/184449737 [==============================] - 2s 0us/step
একটি ছোট সহায়ক ফাংশন লেখা গোলমাল বনাম শব্দহীন ক্ষেত্রে ডেটা তৈরি করতে সহায়তা করবে:
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 একটি মডেল সার্কিট সংজ্ঞায়িত করুন
এখন যেহেতু আপনার কাছে সার্কিট আকারে কোয়ান্টাম ডেটা রয়েছে, এই ডেটা মডেল করার জন্য আপনার একটি সার্কিটের প্রয়োজন হবে, যেমন ডেটার সাথে আপনি একটি সহায়ক ফাংশন লিখতে পারেন যাতে এই সার্কিটটি ঐচ্ছিকভাবে নয়েজ ধারণ করে:
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 মডেল বিল্ডিং এবং প্রশিক্ষণ
আপনার ডেটা এবং মডেল সার্কিট তৈরি করে, আপনার চূড়ান্ত সহায়ক ফাংশনটি প্রয়োজন হবে যা একটি কোলাহলপূর্ণ বা শব্দহীন হাইব্রিড কোয়ান্টাম tf.keras.Model উভয়কেই একত্র করতে পারে:
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. কর্মক্ষমতা তুলনা করুন
4.1 শব্দহীন বেসলাইন
আপনার ডেটা জেনারেশন এবং মডেল বিল্ডিং কোডের সাহায্যে, আপনি এখন শব্দহীন এবং কোলাহলপূর্ণ সেটিংসে মডেলের কর্মক্ষমতা তুলনা করতে এবং বৈসাদৃশ্য করতে পারেন, প্রথমে আপনি একটি রেফারেন্স নীরবহীন প্রশিক্ষণ চালাতে পারেন:
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
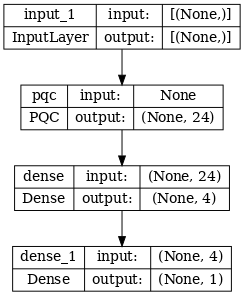
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 133ms/step - loss: 0.7212 - accuracy: 0.4688 - val_loss: 0.6834 - val_accuracy: 0.5000 Epoch 2/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6787 - accuracy: 0.4688 - val_loss: 0.6640 - val_accuracy: 0.5000 Epoch 3/50 4/4 [==============================] - 0s 76ms/step - loss: 0.6637 - accuracy: 0.4688 - val_loss: 0.6529 - val_accuracy: 0.5000 Epoch 4/50 4/4 [==============================] - 0s 78ms/step - loss: 0.6505 - accuracy: 0.4688 - val_loss: 0.6423 - val_accuracy: 0.5000 Epoch 5/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6409 - accuracy: 0.4688 - val_loss: 0.6322 - val_accuracy: 0.5000 Epoch 6/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6300 - accuracy: 0.4844 - val_loss: 0.6187 - val_accuracy: 0.5000 Epoch 7/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6171 - accuracy: 0.5781 - val_loss: 0.6007 - val_accuracy: 0.5000 Epoch 8/50 4/4 [==============================] - 0s 79ms/step - loss: 0.6008 - accuracy: 0.6250 - val_loss: 0.5825 - val_accuracy: 0.5833 Epoch 9/50 4/4 [==============================] - 0s 76ms/step - loss: 0.5864 - accuracy: 0.6406 - val_loss: 0.5610 - val_accuracy: 0.6667 Epoch 10/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5670 - accuracy: 0.6719 - val_loss: 0.5406 - val_accuracy: 0.8333 Epoch 11/50 4/4 [==============================] - 0s 79ms/step - loss: 0.5474 - accuracy: 0.6875 - val_loss: 0.5173 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5276 - accuracy: 0.7188 - val_loss: 0.4941 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 0s 75ms/step - loss: 0.5066 - accuracy: 0.7500 - val_loss: 0.4686 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4838 - accuracy: 0.7812 - val_loss: 0.4437 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4618 - accuracy: 0.8281 - val_loss: 0.4182 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4386 - accuracy: 0.8281 - val_loss: 0.3930 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 0s 79ms/step - loss: 0.4158 - accuracy: 0.8438 - val_loss: 0.3673 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 79ms/step - loss: 0.3944 - accuracy: 0.8438 - val_loss: 0.3429 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3735 - accuracy: 0.8594 - val_loss: 0.3203 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3535 - accuracy: 0.8750 - val_loss: 0.2998 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 78ms/step - loss: 0.3345 - accuracy: 0.8906 - val_loss: 0.2815 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3168 - accuracy: 0.8906 - val_loss: 0.2640 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3017 - accuracy: 0.9062 - val_loss: 0.2465 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2840 - accuracy: 0.9219 - val_loss: 0.2328 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2700 - accuracy: 0.9219 - val_loss: 0.2181 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2566 - accuracy: 0.9219 - val_loss: 0.2053 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 77ms/step - loss: 0.2445 - accuracy: 0.9375 - val_loss: 0.1935 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2332 - accuracy: 0.9375 - val_loss: 0.1839 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 78ms/step - loss: 0.2227 - accuracy: 0.9375 - val_loss: 0.1734 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2145 - accuracy: 0.9375 - val_loss: 0.1630 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2047 - accuracy: 0.9375 - val_loss: 0.1564 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1971 - accuracy: 0.9375 - val_loss: 0.1525 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1894 - accuracy: 0.9531 - val_loss: 0.1464 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 74ms/step - loss: 0.1825 - accuracy: 0.9531 - val_loss: 0.1407 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1771 - accuracy: 0.9531 - val_loss: 0.1330 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1704 - accuracy: 0.9531 - val_loss: 0.1288 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1647 - accuracy: 0.9531 - val_loss: 0.1237 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 80ms/step - loss: 0.1603 - accuracy: 0.9531 - val_loss: 0.1221 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1551 - accuracy: 0.9688 - val_loss: 0.1177 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1509 - accuracy: 0.9688 - val_loss: 0.1136 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1466 - accuracy: 0.9688 - val_loss: 0.1110 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1426 - accuracy: 0.9688 - val_loss: 0.1083 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1386 - accuracy: 0.9688 - val_loss: 0.1050 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 83ms/step - loss: 0.1362 - accuracy: 0.9688 - val_loss: 0.0989 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 78ms/step - loss: 0.1324 - accuracy: 0.9688 - val_loss: 0.0978 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1290 - accuracy: 0.9688 - val_loss: 0.0964 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1265 - accuracy: 0.9688 - val_loss: 0.0929 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1234 - accuracy: 0.9688 - val_loss: 0.0923 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1213 - accuracy: 0.9688 - val_loss: 0.0903 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1182 - accuracy: 0.9688 - val_loss: 0.0885 - val_accuracy: 1.0000
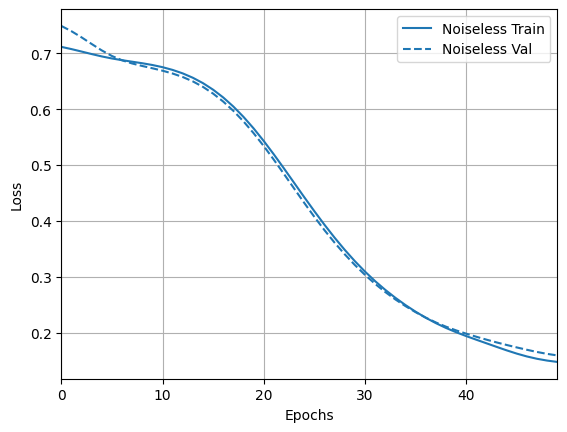
এবং ফলাফল এবং নির্ভুলতা অন্বেষণ করুন:
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
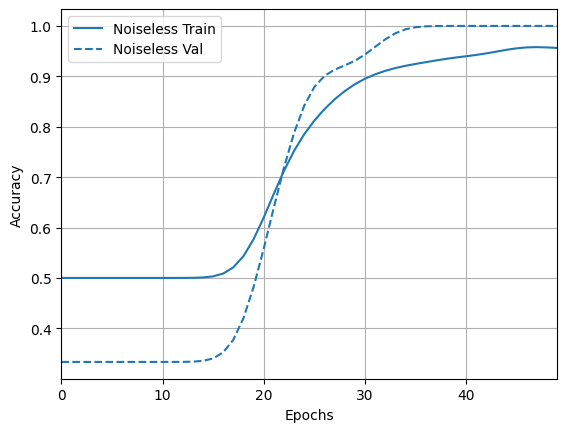
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
acc_plotter.plot(training_histories)
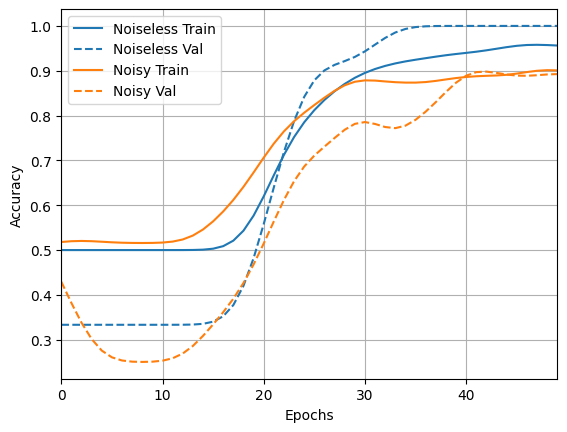
4.2 গোলমাল তুলনা
এখন আপনি কোলাহলপূর্ণ কাঠামোর সাথে একটি নতুন মডেল তৈরি করতে পারেন এবং উপরের সাথে তুলনা করতে পারেন, কোডটি প্রায় অভিন্ন:
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
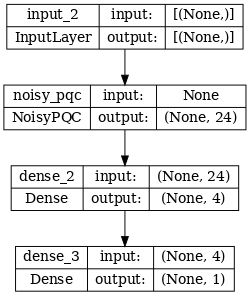
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 8s 2s/step - loss: 0.8265 - accuracy: 0.4844 - val_loss: 0.8369 - val_accuracy: 0.4167 Epoch 2/50 4/4 [==============================] - 7s 2s/step - loss: 0.7613 - accuracy: 0.4844 - val_loss: 0.7695 - val_accuracy: 0.4167 Epoch 3/50 4/4 [==============================] - 7s 2s/step - loss: 0.7151 - accuracy: 0.4844 - val_loss: 0.7290 - val_accuracy: 0.4167 Epoch 4/50 4/4 [==============================] - 7s 2s/step - loss: 0.6915 - accuracy: 0.4844 - val_loss: 0.7014 - val_accuracy: 0.4167 Epoch 5/50 4/4 [==============================] - 7s 2s/step - loss: 0.6837 - accuracy: 0.4844 - val_loss: 0.6811 - val_accuracy: 0.4167 Epoch 6/50 4/4 [==============================] - 7s 2s/step - loss: 0.6717 - accuracy: 0.4844 - val_loss: 0.6801 - val_accuracy: 0.4167 Epoch 7/50 4/4 [==============================] - 7s 2s/step - loss: 0.6739 - accuracy: 0.4844 - val_loss: 0.6726 - val_accuracy: 0.4167 Epoch 8/50 4/4 [==============================] - 7s 2s/step - loss: 0.6713 - accuracy: 0.4844 - val_loss: 0.6661 - val_accuracy: 0.4167 Epoch 9/50 4/4 [==============================] - 7s 2s/step - loss: 0.6710 - accuracy: 0.4844 - val_loss: 0.6667 - val_accuracy: 0.4167 Epoch 10/50 4/4 [==============================] - 7s 2s/step - loss: 0.6669 - accuracy: 0.4844 - val_loss: 0.6627 - val_accuracy: 0.4167 Epoch 11/50 4/4 [==============================] - 7s 2s/step - loss: 0.6637 - accuracy: 0.4844 - val_loss: 0.6550 - val_accuracy: 0.4167 Epoch 12/50 4/4 [==============================] - 7s 2s/step - loss: 0.6616 - accuracy: 0.4844 - val_loss: 0.6593 - val_accuracy: 0.4167 Epoch 13/50 4/4 [==============================] - 7s 2s/step - loss: 0.6536 - accuracy: 0.4844 - val_loss: 0.6514 - val_accuracy: 0.4167 Epoch 14/50 4/4 [==============================] - 7s 2s/step - loss: 0.6489 - accuracy: 0.4844 - val_loss: 0.6481 - val_accuracy: 0.4167 Epoch 15/50 4/4 [==============================] - 7s 2s/step - loss: 0.6491 - accuracy: 0.4844 - val_loss: 0.6484 - val_accuracy: 0.4167 Epoch 16/50 4/4 [==============================] - 7s 2s/step - loss: 0.6389 - accuracy: 0.4844 - val_loss: 0.6396 - val_accuracy: 0.4167 Epoch 17/50 4/4 [==============================] - 7s 2s/step - loss: 0.6307 - accuracy: 0.4844 - val_loss: 0.6337 - val_accuracy: 0.4167 Epoch 18/50 4/4 [==============================] - 7s 2s/step - loss: 0.6296 - accuracy: 0.4844 - val_loss: 0.6260 - val_accuracy: 0.4167 Epoch 19/50 4/4 [==============================] - 7s 2s/step - loss: 0.6194 - accuracy: 0.4844 - val_loss: 0.6282 - val_accuracy: 0.4167 Epoch 20/50 4/4 [==============================] - 7s 2s/step - loss: 0.6095 - accuracy: 0.4844 - val_loss: 0.6138 - val_accuracy: 0.4167 Epoch 21/50 4/4 [==============================] - 7s 2s/step - loss: 0.6075 - accuracy: 0.4844 - val_loss: 0.5874 - val_accuracy: 0.4167 Epoch 22/50 4/4 [==============================] - 7s 2s/step - loss: 0.5981 - accuracy: 0.4844 - val_loss: 0.5981 - val_accuracy: 0.4167 Epoch 23/50 4/4 [==============================] - 7s 2s/step - loss: 0.5823 - accuracy: 0.4844 - val_loss: 0.5818 - val_accuracy: 0.4167 Epoch 24/50 4/4 [==============================] - 7s 2s/step - loss: 0.5768 - accuracy: 0.4844 - val_loss: 0.5617 - val_accuracy: 0.4167 Epoch 25/50 4/4 [==============================] - 7s 2s/step - loss: 0.5651 - accuracy: 0.4844 - val_loss: 0.5638 - val_accuracy: 0.4167 Epoch 26/50 4/4 [==============================] - 7s 2s/step - loss: 0.5496 - accuracy: 0.4844 - val_loss: 0.5532 - val_accuracy: 0.4167 Epoch 27/50 4/4 [==============================] - 7s 2s/step - loss: 0.5340 - accuracy: 0.5000 - val_loss: 0.5345 - val_accuracy: 0.4167 Epoch 28/50 4/4 [==============================] - 7s 2s/step - loss: 0.5297 - accuracy: 0.5156 - val_loss: 0.5308 - val_accuracy: 0.4167 Epoch 29/50 4/4 [==============================] - 7s 2s/step - loss: 0.5120 - accuracy: 0.5312 - val_loss: 0.5224 - val_accuracy: 0.5000 Epoch 30/50 4/4 [==============================] - 7s 2s/step - loss: 0.4992 - accuracy: 0.5781 - val_loss: 0.4921 - val_accuracy: 0.5833 Epoch 31/50 4/4 [==============================] - 7s 2s/step - loss: 0.4823 - accuracy: 0.5938 - val_loss: 0.4975 - val_accuracy: 0.5000 Epoch 32/50 4/4 [==============================] - 7s 2s/step - loss: 0.5025 - accuracy: 0.5781 - val_loss: 0.4814 - val_accuracy: 0.5000 Epoch 33/50 4/4 [==============================] - 7s 2s/step - loss: 0.4655 - accuracy: 0.6562 - val_loss: 0.4391 - val_accuracy: 0.6667 Epoch 34/50 4/4 [==============================] - 7s 2s/step - loss: 0.4552 - accuracy: 0.7031 - val_loss: 0.4528 - val_accuracy: 0.5833 Epoch 35/50 4/4 [==============================] - 7s 2s/step - loss: 0.4516 - accuracy: 0.6719 - val_loss: 0.3993 - val_accuracy: 0.8333 Epoch 36/50 4/4 [==============================] - 7s 2s/step - loss: 0.4320 - accuracy: 0.7656 - val_loss: 0.4225 - val_accuracy: 0.6667 Epoch 37/50 4/4 [==============================] - 7s 2s/step - loss: 0.4060 - accuracy: 0.7656 - val_loss: 0.4001 - val_accuracy: 0.9167 Epoch 38/50 4/4 [==============================] - 7s 2s/step - loss: 0.3858 - accuracy: 0.7812 - val_loss: 0.4152 - val_accuracy: 0.8333 Epoch 39/50 4/4 [==============================] - 7s 2s/step - loss: 0.3964 - accuracy: 0.7656 - val_loss: 0.3899 - val_accuracy: 0.7500 Epoch 40/50 4/4 [==============================] - 7s 2s/step - loss: 0.3640 - accuracy: 0.8125 - val_loss: 0.3689 - val_accuracy: 0.7500 Epoch 41/50 4/4 [==============================] - 7s 2s/step - loss: 0.3676 - accuracy: 0.7812 - val_loss: 0.3786 - val_accuracy: 0.7500 Epoch 42/50 4/4 [==============================] - 7s 2s/step - loss: 0.3466 - accuracy: 0.8281 - val_loss: 0.3313 - val_accuracy: 0.8333 Epoch 43/50 4/4 [==============================] - 7s 2s/step - loss: 0.3520 - accuracy: 0.8594 - val_loss: 0.3398 - val_accuracy: 0.8333 Epoch 44/50 4/4 [==============================] - 7s 2s/step - loss: 0.3402 - accuracy: 0.8438 - val_loss: 0.3135 - val_accuracy: 0.9167 Epoch 45/50 4/4 [==============================] - 7s 2s/step - loss: 0.3253 - accuracy: 0.8281 - val_loss: 0.3469 - val_accuracy: 0.8333 Epoch 46/50 4/4 [==============================] - 7s 2s/step - loss: 0.3239 - accuracy: 0.8281 - val_loss: 0.3038 - val_accuracy: 0.9167 Epoch 47/50 4/4 [==============================] - 7s 2s/step - loss: 0.2948 - accuracy: 0.8594 - val_loss: 0.3056 - val_accuracy: 0.9167 Epoch 48/50 4/4 [==============================] - 7s 2s/step - loss: 0.2972 - accuracy: 0.9219 - val_loss: 0.2699 - val_accuracy: 0.9167 Epoch 49/50 4/4 [==============================] - 7s 2s/step - loss: 0.3041 - accuracy: 0.8281 - val_loss: 0.2754 - val_accuracy: 0.9167 Epoch 50/50 4/4 [==============================] - 7s 2s/step - loss: 0.2944 - accuracy: 0.8750 - val_loss: 0.2988 - val_accuracy: 0.9167
loss_plotter.plot(training_histories)
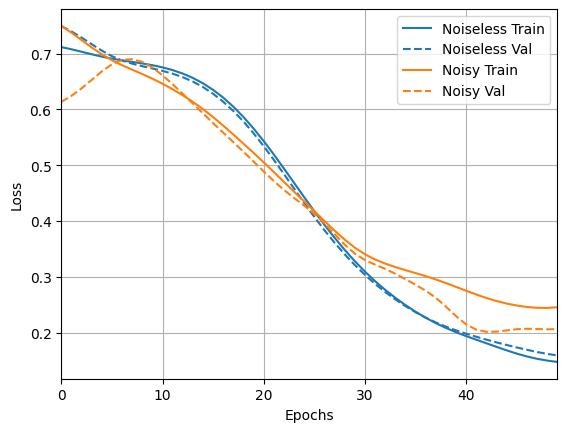
acc_plotter.plot(training_histories)