 ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูแหล่งที่มาบน GitHub ดูแหล่งที่มาบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
บทช่วยสอนนี้สร้างเครือข่ายนิวรัลควอนตัม (QNN) เพื่อจำแนก MNIST เวอร์ชันที่เรียบง่าย ซึ่งคล้ายกับแนวทางที่ใช้ใน Farhi et al ประสิทธิภาพของโครงข่ายประสาทควอนตัมในปัญหาข้อมูลแบบคลาสสิกนี้ เปรียบเทียบกับโครงข่ายประสาทเทียมแบบคลาสสิก
ติดตั้ง
pip install tensorflow==2.7.0
ติดตั้ง TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
ตอนนี้นำเข้า TensorFlow และการพึ่งพาโมดูล:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
import seaborn as sns
import collections
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:29:39.759643: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. โหลดข้อมูล
ในบทช่วยสอนนี้ คุณจะสร้างตัวแยกประเภทไบนารีเพื่อแยกความแตกต่างระหว่างตัวเลข 3 และ 6 ตาม Farhi et al ส่วนนี้ครอบคลุมถึงการจัดการข้อมูลที่:
- โหลดข้อมูลดิบจาก Keras
- กรองชุดข้อมูลให้เหลือเพียง 3s และ 6s
- ลดขนาดรูปภาพเพื่อให้พอดีกับคอมพิวเตอร์ควอนตัม
- ลบตัวอย่างที่ขัดแย้ง
- แปลงภาพไบนารีเป็นวงจร Cirq
- แปลงวงจร Cirq เป็นวงจรควอนตัม TensorFlow
1.1 โหลดข้อมูลดิบ
โหลดชุดข้อมูล MNIST ที่แจกจ่ายด้วย Keras
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train[..., np.newaxis]/255.0, x_test[..., np.newaxis]/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step Number of original training examples: 60000 Number of original test examples: 10000
กรองชุดข้อมูลเพื่อเก็บเฉพาะ 3s และ 6s ลบคลาสอื่น ในเวลาเดียวกันให้แปลงป้ายกำกับ y เป็นบูลีน: True สำหรับ 3 และ False สำหรับ 6
def filter_36(x, y):
keep = (y == 3) | (y == 6)
x, y = x[keep], y[keep]
y = y == 3
return x,y
x_train, y_train = filter_36(x_train, y_train)
x_test, y_test = filter_36(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12049 Number of filtered test examples: 1968
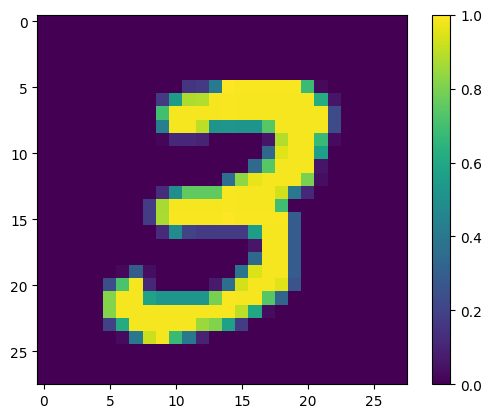
แสดงตัวอย่างแรก:
print(y_train[0])
plt.imshow(x_train[0, :, :, 0])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7fac6ad4bd90>
1.2 ลดขนาดภาพ
ขนาดรูปภาพ 28x28 ใหญ่เกินไปสำหรับคอมพิวเตอร์ควอนตัมปัจจุบัน ปรับขนาดภาพลงเป็น 4x4:
x_train_small = tf.image.resize(x_train, (4,4)).numpy()
x_test_small = tf.image.resize(x_test, (4,4)).numpy()
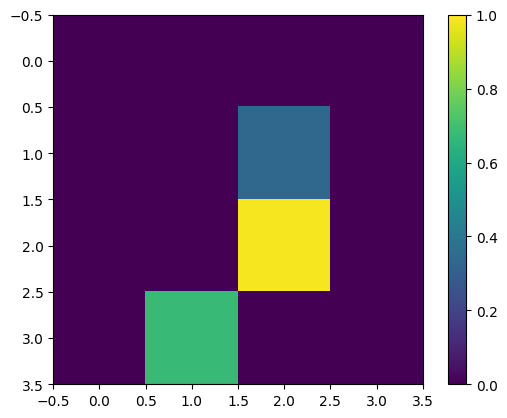
อีกครั้ง แสดงตัวอย่างการฝึกครั้งแรก—หลังจากปรับขนาด:
print(y_train[0])
plt.imshow(x_train_small[0,:,:,0], vmin=0, vmax=1)
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7fabf807fe10>
1.3 ลบตัวอย่างที่ขัดแย้ง
จากส่วนที่ 3.3 การเรียนรู้เพื่อแยกแยะตัวเลข ของ Farhi et al. ให้กรองชุดข้อมูลเพื่อลบภาพที่ระบุว่าเป็นของทั้งสองคลาส
นี่ไม่ใช่ขั้นตอนการเรียนรู้ด้วยเครื่องมาตรฐาน แต่รวมอยู่ในความสนใจในการติดตามบทความนี้
def remove_contradicting(xs, ys):
mapping = collections.defaultdict(set)
orig_x = {}
# Determine the set of labels for each unique image:
for x,y in zip(xs,ys):
orig_x[tuple(x.flatten())] = x
mapping[tuple(x.flatten())].add(y)
new_x = []
new_y = []
for flatten_x in mapping:
x = orig_x[flatten_x]
labels = mapping[flatten_x]
if len(labels) == 1:
new_x.append(x)
new_y.append(next(iter(labels)))
else:
# Throw out images that match more than one label.
pass
num_uniq_3 = sum(1 for value in mapping.values() if len(value) == 1 and True in value)
num_uniq_6 = sum(1 for value in mapping.values() if len(value) == 1 and False in value)
num_uniq_both = sum(1 for value in mapping.values() if len(value) == 2)
print("Number of unique images:", len(mapping.values()))
print("Number of unique 3s: ", num_uniq_3)
print("Number of unique 6s: ", num_uniq_6)
print("Number of unique contradicting labels (both 3 and 6): ", num_uniq_both)
print()
print("Initial number of images: ", len(xs))
print("Remaining non-contradicting unique images: ", len(new_x))
return np.array(new_x), np.array(new_y)
จำนวนผลลัพธ์ไม่ตรงกับค่าที่รายงานอย่างใกล้ชิด แต่ไม่ได้ระบุขั้นตอนที่แน่นอน
นอกจากนี้ ยังควรสังเกตด้วยว่าการใช้ตัวอย่างการกรองที่ขัดแย้ง ณ จุดนี้ไม่ได้ป้องกันโมเดลจากการรับตัวอย่างการฝึกที่ขัดแย้งโดยสิ้นเชิง: ขั้นตอนต่อไปจะเป็นการรวมข้อมูลสองส่วนซึ่งจะทำให้เกิดการชนกันมากขึ้น
x_train_nocon, y_train_nocon = remove_contradicting(x_train_small, y_train)
Number of unique images: 10387 Number of unique 3s: 4912 Number of unique 6s: 5426 Number of unique contradicting labels (both 3 and 6): 49 Initial number of images: 12049 Remaining non-contradicting unique images: 10338
1.4 เข้ารหัสข้อมูลเป็นวงจรควอนตัม
ในการประมวลผลภาพโดยใช้คอมพิวเตอร์ควอนตัม Farhi et al. เสนอให้แสดงแต่ละพิกเซลด้วย qubit โดยมีสถานะขึ้นอยู่กับค่าของพิกเซล ขั้นตอนแรกคือการแปลงเป็นการเข้ารหัสไบนารี
THRESHOLD = 0.5
x_train_bin = np.array(x_train_nocon > THRESHOLD, dtype=np.float32)
x_test_bin = np.array(x_test_small > THRESHOLD, dtype=np.float32)
หากคุณต้องลบภาพที่ขัดแย้ง ณ จุดนี้ คุณจะเหลือเพียง 193 ซึ่งไม่น่าจะเพียงพอสำหรับการฝึกอบรมที่มีประสิทธิภาพ
_ = remove_contradicting(x_train_bin, y_train_nocon)
Number of unique images: 193 Number of unique 3s: 80 Number of unique 6s: 69 Number of unique contradicting labels (both 3 and 6): 44 Initial number of images: 10338 Remaining non-contradicting unique images: 149ตัวยึดตำแหน่ง23
qubits ที่ดัชนีพิกเซลที่มีค่าที่เกินขีดจำกัด จะถูกหมุนผ่านเกท \(X\)
def convert_to_circuit(image):
"""Encode truncated classical image into quantum datapoint."""
values = np.ndarray.flatten(image)
qubits = cirq.GridQubit.rect(4, 4)
circuit = cirq.Circuit()
for i, value in enumerate(values):
if value:
circuit.append(cirq.X(qubits[i]))
return circuit
x_train_circ = [convert_to_circuit(x) for x in x_train_bin]
x_test_circ = [convert_to_circuit(x) for x in x_test_bin]
นี่คือวงจรที่สร้างขึ้นสำหรับตัวอย่างแรก (แผนภาพวงจรไม่แสดง qubits ที่มีประตูเป็นศูนย์):
SVGCircuit(x_train_circ[0])
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
เปรียบเทียบวงจรนี้กับดัชนีที่ค่าภาพเกินเกณฑ์:
bin_img = x_train_bin[0,:,:,0]
indices = np.array(np.where(bin_img)).T
indices
array([[2, 2],
[3, 1]])
แปลงวงจร Cirq เหล่านี้เป็นเทนเซอร์สำหรับ tfq :
x_train_tfcirc = tfq.convert_to_tensor(x_train_circ)
x_test_tfcirc = tfq.convert_to_tensor(x_test_circ)
2. โครงข่ายประสาทควอนตัม
มีคำแนะนำเพียงเล็กน้อยสำหรับโครงสร้างวงจรควอนตัมที่จำแนกภาพ เนื่องจากการจัดประเภทขึ้นอยู่กับความคาดหวังของการอ่าน qubit Farhi et al เสนอให้ใช้สองประตู qubit โดยที่การอ่าน qubit จะดำเนินการเสมอ สิ่งนี้คล้ายกันในบางวิธีในการเรียกใช้ Unitary RNN ขนาดเล็กข้ามพิกเซล
2.1 สร้างวงจรโมเดล
ตัวอย่างต่อไปนี้แสดงวิธีการแบบแบ่งชั้น แต่ละเลเยอร์ใช้ n อินสแตนซ์ของเกตเดียวกัน โดยที่ qubit ข้อมูลแต่ละอันทำงานบน qubit ที่อ่านข้อมูล
เริ่มต้นด้วยคลาสง่าย ๆ ที่จะเพิ่มเลเยอร์ของเกตเหล่านี้ลงในวงจร:
class CircuitLayerBuilder():
def __init__(self, data_qubits, readout):
self.data_qubits = data_qubits
self.readout = readout
def add_layer(self, circuit, gate, prefix):
for i, qubit in enumerate(self.data_qubits):
symbol = sympy.Symbol(prefix + '-' + str(i))
circuit.append(gate(qubit, self.readout)**symbol)
สร้างเลเยอร์วงจรตัวอย่างเพื่อดูว่ามีลักษณะอย่างไร:
demo_builder = CircuitLayerBuilder(data_qubits = cirq.GridQubit.rect(4,1),
readout=cirq.GridQubit(-1,-1))
circuit = cirq.Circuit()
demo_builder.add_layer(circuit, gate = cirq.XX, prefix='xx')
SVGCircuit(circuit)
ตอนนี้สร้างแบบจำลองสองชั้น จับคู่ขนาดวงจรข้อมูล และรวมการดำเนินการเตรียมการและการอ่านข้อมูล
def create_quantum_model():
"""Create a QNN model circuit and readout operation to go along with it."""
data_qubits = cirq.GridQubit.rect(4, 4) # a 4x4 grid.
readout = cirq.GridQubit(-1, -1) # a single qubit at [-1,-1]
circuit = cirq.Circuit()
# Prepare the readout qubit.
circuit.append(cirq.X(readout))
circuit.append(cirq.H(readout))
builder = CircuitLayerBuilder(
data_qubits = data_qubits,
readout=readout)
# Then add layers (experiment by adding more).
builder.add_layer(circuit, cirq.XX, "xx1")
builder.add_layer(circuit, cirq.ZZ, "zz1")
# Finally, prepare the readout qubit.
circuit.append(cirq.H(readout))
return circuit, cirq.Z(readout)
model_circuit, model_readout = create_quantum_model()
2.2 ห่อโมเดลวงจรในโมเดล tfq-keras
สร้างแบบจำลอง Keras ด้วยส่วนประกอบควอนตัม โมเดลนี้ป้อน "ข้อมูลควอนตัม" จาก x_train_circ ที่เข้ารหัสข้อมูลคลาสสิก มันใช้เลเยอร์ Parametrized Quantum Circuit , tfq.layers.PQC เพื่อฝึกวงจรแบบจำลองบนข้อมูลควอนตัม
เพื่อจำแนกภาพเหล่านี้ Farhi et al. เสนอให้คาดหวังการอ่าน qubit ในวงจรพารามิเตอร์ ความคาดหวังจะส่งกลับค่าระหว่าง 1 ถึง -1
# Build the Keras model.
model = tf.keras.Sequential([
# The input is the data-circuit, encoded as a tf.string
tf.keras.layers.Input(shape=(), dtype=tf.string),
# The PQC layer returns the expected value of the readout gate, range [-1,1].
tfq.layers.PQC(model_circuit, model_readout),
])
ถัดไป อธิบายขั้นตอนการฝึกอบรมให้กับโมเดลโดยใช้วิธีการ compile
เนื่องจากการอ่านค่าที่คาดไว้อยู่ในช่วง [-1,1] การเพิ่มประสิทธิภาพการสูญเสียบานพับจึงค่อนข้างจะพอดี
หากต้องการใช้บานพับที่สูญเสียที่นี่ คุณต้องทำการปรับเล็กน้อยสองครั้ง ขั้นแรกให้แปลงป้ายกำกับ y_train_nocon จากบูลีนเป็น [-1,1] ตามที่คาดไว้โดยการสูญเสียบานพับ
y_train_hinge = 2.0*y_train_nocon-1.0
y_test_hinge = 2.0*y_test-1.0
ประการที่สอง ใช้ตัวชี้วัด hinge_accuracy ที่จัดการ [-1, 1] อย่างถูกต้องเป็นอาร์กิวเมนต์ y_true labels tf.losses.BinaryAccuracy(threshold=0.0) คาดว่า y_true จะเป็นบูลีน ดังนั้นจึงไม่สามารถใช้กับความสูญเสียของบานพับได้)
def hinge_accuracy(y_true, y_pred):
y_true = tf.squeeze(y_true) > 0.0
y_pred = tf.squeeze(y_pred) > 0.0
result = tf.cast(y_true == y_pred, tf.float32)
return tf.reduce_mean(result)
model.compile(
loss=tf.keras.losses.Hinge(),
optimizer=tf.keras.optimizers.Adam(),
metrics=[hinge_accuracy])
print(model.summary())
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
pqc (PQC) (None, 1) 32
=================================================================
Total params: 32
Trainable params: 32
Non-trainable params: 0
_________________________________________________________________
None
ฝึกโมเดลควอนตัม
ตอนนี้ฝึกแบบจำลอง—ซึ่งใช้เวลาประมาณ 45 นาที หากคุณไม่ต้องการรอนานขนาดนั้น ให้ใช้ชุดย่อยของข้อมูล (ชุด NUM_EXAMPLES=500 ด้านล่าง) สิ่งนี้ไม่ส่งผลต่อความคืบหน้าของโมเดลระหว่างการฝึกจริงๆ (มีเพียง 32 พารามิเตอร์ และไม่ต้องการข้อมูลมากเพื่อจำกัดสิ่งเหล่านี้) การใช้ตัวอย่างน้อยลงจะทำให้การฝึกสิ้นสุดลงเร็วขึ้น (5 นาที) แต่ดำเนินการนานพอที่จะแสดงว่ามีความคืบหน้าในบันทึกการตรวจสอบ
EPOCHS = 3
BATCH_SIZE = 32
NUM_EXAMPLES = len(x_train_tfcirc)
x_train_tfcirc_sub = x_train_tfcirc[:NUM_EXAMPLES]
y_train_hinge_sub = y_train_hinge[:NUM_EXAMPLES]
การฝึกโมเดลนี้เพื่อการลู่เข้าควรมีความแม่นยำ >85% ในชุดทดสอบ
qnn_history = model.fit(
x_train_tfcirc_sub, y_train_hinge_sub,
batch_size=32,
epochs=EPOCHS,
verbose=1,
validation_data=(x_test_tfcirc, y_test_hinge))
qnn_results = model.evaluate(x_test_tfcirc, y_test)
Epoch 1/3 324/324 [==============================] - 68s 207ms/step - loss: 0.6745 - hinge_accuracy: 0.7719 - val_loss: 0.3959 - val_hinge_accuracy: 0.8004 Epoch 2/3 324/324 [==============================] - 68s 209ms/step - loss: 0.3964 - hinge_accuracy: 0.8291 - val_loss: 0.3498 - val_hinge_accuracy: 0.8997 Epoch 3/3 324/324 [==============================] - 66s 204ms/step - loss: 0.3599 - hinge_accuracy: 0.8854 - val_loss: 0.3395 - val_hinge_accuracy: 0.9042 62/62 [==============================] - 3s 41ms/step - loss: 0.3395 - hinge_accuracy: 0.9042ตัวยึดตำแหน่ง43
3. โครงข่ายประสาทเทียมแบบคลาสสิก
แม้ว่าโครงข่ายประสาทควอนตัมจะใช้ได้กับปัญหา MNIST แบบง่ายนี้ แต่โครงข่ายประสาทเทียมแบบคลาสสิกแบบพื้นฐานสามารถทำงานได้ดีกว่า QNN ในงานนี้ หลังจากยุคเดียว โครงข่ายประสาทเทียมแบบคลาสสิกสามารถบรรลุความแม่นยำ > 98% ในชุดพักสาย
ในตัวอย่างต่อไปนี้ โครงข่ายประสาทเทียมแบบคลาสสิกใช้สำหรับปัญหาการจำแนกประเภท 3-6 โดยใช้รูปภาพขนาด 28x28 ทั้งหมดแทนการสุ่มตัวอย่างย่อยของรูปภาพ สิ่งนี้มาบรรจบกันอย่างง่ายดายเพื่อความแม่นยำเกือบ 100% ของชุดทดสอบ
def create_classical_model():
# A simple model based off LeNet from https://keras.io/examples/mnist_cnn/
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(32, [3, 3], activation='relu', input_shape=(28,28,1)))
model.add(tf.keras.layers.Conv2D(64, [3, 3], activation='relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(tf.keras.layers.Dropout(0.25))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(128, activation='relu'))
model.add(tf.keras.layers.Dropout(0.5))
model.add(tf.keras.layers.Dense(1))
return model
model = create_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
model.summary()
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 26, 26, 32) 320
conv2d_1 (Conv2D) (None, 24, 24, 64) 18496
max_pooling2d (MaxPooling2D (None, 12, 12, 64) 0
)
dropout (Dropout) (None, 12, 12, 64) 0
flatten (Flatten) (None, 9216) 0
dense (Dense) (None, 128) 1179776
dropout_1 (Dropout) (None, 128) 0
dense_1 (Dense) (None, 1) 129
=================================================================
Total params: 1,198,721
Trainable params: 1,198,721
Non-trainable params: 0
_________________________________________________________________
model.fit(x_train,
y_train,
batch_size=128,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
cnn_results = model.evaluate(x_test, y_test)
95/95 [==============================] - 3s 31ms/step - loss: 0.0400 - accuracy: 0.9842 - val_loss: 0.0057 - val_accuracy: 0.9970 62/62 [==============================] - 0s 3ms/step - loss: 0.0057 - accuracy: 0.9970
รุ่นข้างต้นมีพารามิเตอร์เกือบ 1.2M เพื่อการเปรียบเทียบที่ยุติธรรมยิ่งขึ้น ให้ลองใช้แบบจำลอง 37 พารามิเตอร์ ในภาพตัวอย่างย่อย:
def create_fair_classical_model():
# A simple model based off LeNet from https://keras.io/examples/mnist_cnn/
model = tf.keras.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=(4,4,1)))
model.add(tf.keras.layers.Dense(2, activation='relu'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_1 (Flatten) (None, 16) 0
dense_2 (Dense) (None, 2) 34
dense_3 (Dense) (None, 1) 3
=================================================================
Total params: 37
Trainable params: 37
Non-trainable params: 0
_________________________________________________________________
model.fit(x_train_bin,
y_train_nocon,
batch_size=128,
epochs=20,
verbose=2,
validation_data=(x_test_bin, y_test))
fair_nn_results = model.evaluate(x_test_bin, y_test)
Epoch 1/20 81/81 - 1s - loss: 0.6678 - accuracy: 0.6546 - val_loss: 0.6326 - val_accuracy: 0.7358 - 503ms/epoch - 6ms/step Epoch 2/20 81/81 - 0s - loss: 0.6186 - accuracy: 0.7654 - val_loss: 0.5787 - val_accuracy: 0.7515 - 98ms/epoch - 1ms/step Epoch 3/20 81/81 - 0s - loss: 0.5629 - accuracy: 0.7861 - val_loss: 0.5247 - val_accuracy: 0.7764 - 104ms/epoch - 1ms/step Epoch 4/20 81/81 - 0s - loss: 0.5150 - accuracy: 0.8301 - val_loss: 0.4825 - val_accuracy: 0.8196 - 103ms/epoch - 1ms/step Epoch 5/20 81/81 - 0s - loss: 0.4762 - accuracy: 0.8493 - val_loss: 0.4490 - val_accuracy: 0.8293 - 97ms/epoch - 1ms/step Epoch 6/20 81/81 - 0s - loss: 0.4438 - accuracy: 0.8527 - val_loss: 0.4216 - val_accuracy: 0.8298 - 99ms/epoch - 1ms/step Epoch 7/20 81/81 - 0s - loss: 0.4169 - accuracy: 0.8555 - val_loss: 0.3986 - val_accuracy: 0.8313 - 98ms/epoch - 1ms/step Epoch 8/20 81/81 - 0s - loss: 0.3951 - accuracy: 0.8595 - val_loss: 0.3794 - val_accuracy: 0.8313 - 105ms/epoch - 1ms/step Epoch 9/20 81/81 - 0s - loss: 0.3773 - accuracy: 0.8596 - val_loss: 0.3635 - val_accuracy: 0.8328 - 98ms/epoch - 1ms/step Epoch 10/20 81/81 - 0s - loss: 0.3620 - accuracy: 0.8611 - val_loss: 0.3499 - val_accuracy: 0.8333 - 97ms/epoch - 1ms/step Epoch 11/20 81/81 - 0s - loss: 0.3488 - accuracy: 0.8714 - val_loss: 0.3382 - val_accuracy: 0.8720 - 98ms/epoch - 1ms/step Epoch 12/20 81/81 - 0s - loss: 0.3372 - accuracy: 0.8831 - val_loss: 0.3279 - val_accuracy: 0.8720 - 95ms/epoch - 1ms/step Epoch 13/20 81/81 - 0s - loss: 0.3271 - accuracy: 0.8831 - val_loss: 0.3187 - val_accuracy: 0.8725 - 97ms/epoch - 1ms/step Epoch 14/20 81/81 - 0s - loss: 0.3181 - accuracy: 0.8832 - val_loss: 0.3107 - val_accuracy: 0.8725 - 96ms/epoch - 1ms/step Epoch 15/20 81/81 - 0s - loss: 0.3101 - accuracy: 0.8833 - val_loss: 0.3035 - val_accuracy: 0.8725 - 96ms/epoch - 1ms/step Epoch 16/20 81/81 - 0s - loss: 0.3030 - accuracy: 0.8833 - val_loss: 0.2972 - val_accuracy: 0.8725 - 105ms/epoch - 1ms/step Epoch 17/20 81/81 - 0s - loss: 0.2966 - accuracy: 0.8833 - val_loss: 0.2913 - val_accuracy: 0.8725 - 104ms/epoch - 1ms/step Epoch 18/20 81/81 - 0s - loss: 0.2908 - accuracy: 0.8928 - val_loss: 0.2861 - val_accuracy: 0.8725 - 104ms/epoch - 1ms/step Epoch 19/20 81/81 - 0s - loss: 0.2856 - accuracy: 0.8955 - val_loss: 0.2816 - val_accuracy: 0.8725 - 99ms/epoch - 1ms/step Epoch 20/20 81/81 - 0s - loss: 0.2809 - accuracy: 0.8952 - val_loss: 0.2773 - val_accuracy: 0.8725 - 101ms/epoch - 1ms/step 62/62 [==============================] - 0s 895us/step - loss: 0.2773 - accuracy: 0.8725
4. การเปรียบเทียบ
อินพุตความละเอียดสูงและโมเดลที่ทรงพลังยิ่งขึ้นทำให้ CNN แก้ปัญหานี้ได้ง่าย ในขณะที่แบบจำลองคลาสสิกของกำลังที่คล้ายกัน (~32 พารามิเตอร์) จะฝึกให้มีความแม่นยำใกล้เคียงกันในเวลาเพียงเสี้ยววินาที ไม่ทางใดก็ทางหนึ่ง โครงข่ายประสาทเทียมแบบคลาสสิกมีประสิทธิภาพเหนือกว่าโครงข่ายประสาทควอนตัมอย่างง่ายดาย สำหรับข้อมูลแบบคลาสสิก เป็นเรื่องยากที่จะเอาชนะโครงข่ายประสาทแบบคลาสสิก
qnn_accuracy = qnn_results[1]
cnn_accuracy = cnn_results[1]
fair_nn_accuracy = fair_nn_results[1]
sns.barplot(["Quantum", "Classical, full", "Classical, fair"],
[qnn_accuracy, cnn_accuracy, fair_nn_accuracy])
/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation. FutureWarning <AxesSubplot:>ตัวยึดตำแหน่ง53

