 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
يبني هذا البرنامج التعليمي شبكة عصبية كمومية (QNN) لتصنيف نسخة مبسطة من MNIST ، على غرار الطريقة المستخدمة في Farhi et al . تتم مقارنة أداء الشبكة العصبية الكمومية في مشكلة البيانات الكلاسيكية هذه مع الشبكة العصبية الكلاسيكية.
يثبت
pip install tensorflow==2.7.0
تثبيت TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
الآن قم باستيراد TensorFlow وتبعيات الوحدة النمطية:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
import seaborn as sns
import collections
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:29:39.759643: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. تحميل البيانات
في هذا البرنامج التعليمي سوف تقوم ببناء مصنف ثنائي للتمييز بين الرقمين 3 و 6 ، باتباع Farhi et al. يغطي هذا القسم معالجة البيانات التي:
- يقوم بتحميل البيانات الأولية من Keras.
- لتصفية مجموعة البيانات إلى 3 ثوانٍ و 6 ثوانٍ فقط.
- يعمل على تصغير حجم الصور بحيث يمكن وضعها في جهاز كمبيوتر كمي.
- يزيل أي أمثلة متناقضة.
- يحول الصور الثنائية إلى دوائر Cirq.
- يحول دوائر Cirq إلى دوائر الكم TensorFlow.
1.1 تحميل البيانات الأولية
قم بتحميل مجموعة بيانات MNIST الموزعة مع Keras.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train[..., np.newaxis]/255.0, x_test[..., np.newaxis]/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step Number of original training examples: 60000 Number of original test examples: 10000
قم بتصفية مجموعة البيانات للاحتفاظ بـ 3s و 6s فقط ، وإزالة الفئات الأخرى. في نفس الوقت ، قم بتحويل التسمية ، y ، إلى قيمة منطقية: True لـ 3 و False لـ 6.
def filter_36(x, y):
keep = (y == 3) | (y == 6)
x, y = x[keep], y[keep]
y = y == 3
return x,y
x_train, y_train = filter_36(x_train, y_train)
x_test, y_test = filter_36(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12049 Number of filtered test examples: 1968
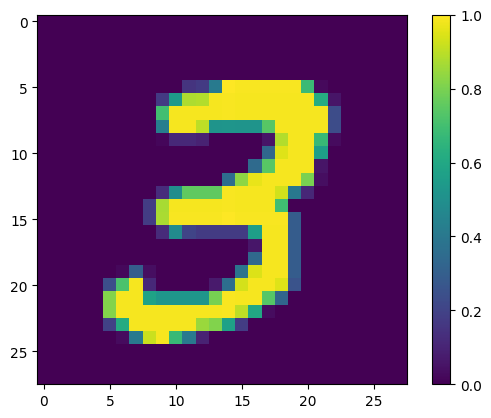
اعرض المثال الأول:
print(y_train[0])
plt.imshow(x_train[0, :, :, 0])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7fac6ad4bd90>
1.2 تصغير الصور
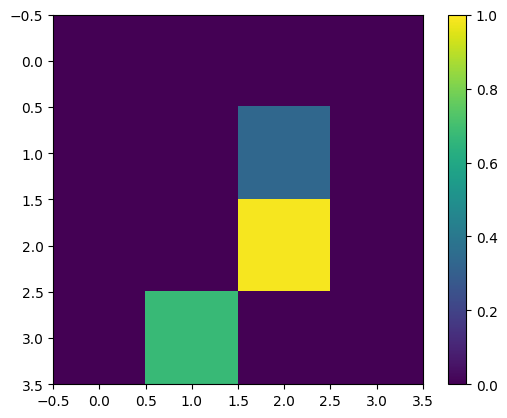
حجم الصورة 28 × 28 كبير جدًا بالنسبة لأجهزة الكمبيوتر الكمومية الحالية. تغيير حجم الصورة إلى 4x4:
x_train_small = tf.image.resize(x_train, (4,4)).numpy()
x_test_small = tf.image.resize(x_test, (4,4)).numpy()
مرة أخرى ، اعرض مثال التدريب الأول - بعد تغيير الحجم:
print(y_train[0])
plt.imshow(x_train_small[0,:,:,0], vmin=0, vmax=1)
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7fabf807fe10>
1.3 إزالة الأمثلة المتناقضة
من القسم 3.3 تعلم التمييز بين أرقام فارحي وآخرون. ، قم بتصفية مجموعة البيانات لإزالة الصور المصنفة على أنها تنتمي إلى كلا الفئتين.
هذا ليس إجراءً قياسيًا للتعلم الآلي ، ولكنه مدرج في مصلحة متابعة البحث.
def remove_contradicting(xs, ys):
mapping = collections.defaultdict(set)
orig_x = {}
# Determine the set of labels for each unique image:
for x,y in zip(xs,ys):
orig_x[tuple(x.flatten())] = x
mapping[tuple(x.flatten())].add(y)
new_x = []
new_y = []
for flatten_x in mapping:
x = orig_x[flatten_x]
labels = mapping[flatten_x]
if len(labels) == 1:
new_x.append(x)
new_y.append(next(iter(labels)))
else:
# Throw out images that match more than one label.
pass
num_uniq_3 = sum(1 for value in mapping.values() if len(value) == 1 and True in value)
num_uniq_6 = sum(1 for value in mapping.values() if len(value) == 1 and False in value)
num_uniq_both = sum(1 for value in mapping.values() if len(value) == 2)
print("Number of unique images:", len(mapping.values()))
print("Number of unique 3s: ", num_uniq_3)
print("Number of unique 6s: ", num_uniq_6)
print("Number of unique contradicting labels (both 3 and 6): ", num_uniq_both)
print()
print("Initial number of images: ", len(xs))
print("Remaining non-contradicting unique images: ", len(new_x))
return np.array(new_x), np.array(new_y)
الأعداد الناتجة لا تتطابق بشكل وثيق مع القيم المبلغ عنها ، ولكن لم يتم تحديد الإجراء الدقيق.
من الجدير بالذكر هنا أيضًا أن تطبيق أمثلة متناقضة للتصفية في هذه المرحلة لا يمنع تمامًا النموذج من تلقي أمثلة تدريبية متناقضة: الخطوة التالية تقوم بترتيب البيانات الثنائية التي ستؤدي إلى مزيد من التصادمات.
x_train_nocon, y_train_nocon = remove_contradicting(x_train_small, y_train)
Number of unique images: 10387 Number of unique 3s: 4912 Number of unique 6s: 5426 Number of unique contradicting labels (both 3 and 6): 49 Initial number of images: 12049 Remaining non-contradicting unique images: 10338
1.4 تشفير البيانات كدوائر كمومية
لمعالجة الصور باستخدام الكمبيوتر الكمومي ، فارهي وآخرون. اقترح تمثيل كل بكسل مع كيوبت ، مع اعتماد الحالة على قيمة البكسل. الخطوة الأولى هي التحويل إلى تشفير ثنائي.
THRESHOLD = 0.5
x_train_bin = np.array(x_train_nocon > THRESHOLD, dtype=np.float32)
x_test_bin = np.array(x_test_small > THRESHOLD, dtype=np.float32)
إذا قمت بإزالة الصور المتناقضة في هذه المرحلة ، فلن يتبقى لك سوى 193 صورة ، على الأرجح لن تكون كافية للتدريب الفعال.
_ = remove_contradicting(x_train_bin, y_train_nocon)
Number of unique images: 193 Number of unique 3s: 80 Number of unique 6s: 69 Number of unique contradicting labels (both 3 and 6): 44 Initial number of images: 10338 Remaining non-contradicting unique images: 149
يتم تدوير الكيوبتات في مؤشرات البكسل ذات القيم التي تتجاوز العتبة من خلال بوابة \(X\) .
def convert_to_circuit(image):
"""Encode truncated classical image into quantum datapoint."""
values = np.ndarray.flatten(image)
qubits = cirq.GridQubit.rect(4, 4)
circuit = cirq.Circuit()
for i, value in enumerate(values):
if value:
circuit.append(cirq.X(qubits[i]))
return circuit
x_train_circ = [convert_to_circuit(x) for x in x_train_bin]
x_test_circ = [convert_to_circuit(x) for x in x_test_bin]
هذه هي الدائرة التي تم إنشاؤها للمثال الأول (لا تظهر الرسوم البيانية للدائرة كيوبتات بدون بوابات):
SVGCircuit(x_train_circ[0])
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
قارن هذه الدائرة بالمؤشرات حيث تتجاوز قيمة الصورة العتبة:
bin_img = x_train_bin[0,:,:,0]
indices = np.array(np.where(bin_img)).T
indices
array([[2, 2],
[3, 1]])
قم بتحويل دوائر Cirq هذه إلى موترات لـ tfq :
x_train_tfcirc = tfq.convert_to_tensor(x_train_circ)
x_test_tfcirc = tfq.convert_to_tensor(x_test_circ)
2. الشبكة العصبية الكمومية
هناك القليل من الإرشادات المتعلقة بهيكل الدائرة الكمومية الذي يصنف الصور. نظرًا لأن التصنيف يعتمد على توقع قراءة qubit ، Farhi et al. اقترح استخدام بوابتين كيوبت ، مع العمل دائمًا على قراءة كيوبت. هذا مشابه في بعض النواحي لتشغيل RNN صغير عبر وحدات البكسل.
2.1 بناء نموذج الدائرة
يوضح هذا المثال التالي هذا النهج متعدد الطبقات. تستخدم كل طبقة عدد n من مثيلات البوابة نفسها ، حيث تعمل كل وحدة من وحدات البيانات qubit على قراءة qubit.
ابدأ بفصل بسيط يضيف طبقة من هذه البوابات إلى الدائرة:
class CircuitLayerBuilder():
def __init__(self, data_qubits, readout):
self.data_qubits = data_qubits
self.readout = readout
def add_layer(self, circuit, gate, prefix):
for i, qubit in enumerate(self.data_qubits):
symbol = sympy.Symbol(prefix + '-' + str(i))
circuit.append(gate(qubit, self.readout)**symbol)
قم ببناء مثال لطبقة الدائرة لترى كيف تبدو:
demo_builder = CircuitLayerBuilder(data_qubits = cirq.GridQubit.rect(4,1),
readout=cirq.GridQubit(-1,-1))
circuit = cirq.Circuit()
demo_builder.add_layer(circuit, gate = cirq.XX, prefix='xx')
SVGCircuit(circuit)
الآن قم ببناء نموذج من طبقتين ، يطابق حجم دائرة البيانات ، ويتضمن عمليات التحضير والقراءة.
def create_quantum_model():
"""Create a QNN model circuit and readout operation to go along with it."""
data_qubits = cirq.GridQubit.rect(4, 4) # a 4x4 grid.
readout = cirq.GridQubit(-1, -1) # a single qubit at [-1,-1]
circuit = cirq.Circuit()
# Prepare the readout qubit.
circuit.append(cirq.X(readout))
circuit.append(cirq.H(readout))
builder = CircuitLayerBuilder(
data_qubits = data_qubits,
readout=readout)
# Then add layers (experiment by adding more).
builder.add_layer(circuit, cirq.XX, "xx1")
builder.add_layer(circuit, cirq.ZZ, "zz1")
# Finally, prepare the readout qubit.
circuit.append(cirq.H(readout))
return circuit, cirq.Z(readout)
model_circuit, model_readout = create_quantum_model()
2.2 لف دائرة النموذج في نموذج tfq-keras
بناء نموذج Keras مع المكونات الكمومية. يتم تغذية هذا النموذج بـ "البيانات الكمومية" ، من x_train_circ ، والتي تشفر البيانات الكلاسيكية. يستخدم طبقة دائرة كمومية باراميتريزيد ، tfq.layers.PQC ، لتدريب دائرة النموذج ، على البيانات الكمومية.
لتصنيف هذه الصور ، فارحي وآخرون. اقترح أخذ توقع قراءة كيوبت في دائرة ذات معلمات. يُرجع التوقع قيمة بين 1 و -1.
# Build the Keras model.
model = tf.keras.Sequential([
# The input is the data-circuit, encoded as a tf.string
tf.keras.layers.Input(shape=(), dtype=tf.string),
# The PQC layer returns the expected value of the readout gate, range [-1,1].
tfq.layers.PQC(model_circuit, model_readout),
])
بعد ذلك ، قم بوصف إجراء التدريب للنموذج باستخدام طريقة compile .
نظرًا لأن القراءة المتوقعة تقع في النطاق [-1,1] ، فإن تحسين خسارة المفصلة يعد مناسبًا طبيعيًا إلى حد ما.
لاستخدام فقدان المفصلة هنا ، تحتاج إلى إجراء تعديلين صغيرين. قم أولاً بتحويل الملصقات ، y_train_nocon ، من منطقية إلى [-1,1] ، كما هو متوقع من خلال خسارة المفصلة.
y_train_hinge = 2.0*y_train_nocon-1.0
y_test_hinge = 2.0*y_test-1.0
ثانيًا ، استخدم مقياس hinge_accuracy الذي يتعامل بشكل صحيح مع [-1, 1] y_true labels. tf.losses.BinaryAccuracy(threshold=0.0) تتوقع أن تكون y_true قيمة منطقية ، وبالتالي لا يمكن استخدامها مع فقد المفصلة).
def hinge_accuracy(y_true, y_pred):
y_true = tf.squeeze(y_true) > 0.0
y_pred = tf.squeeze(y_pred) > 0.0
result = tf.cast(y_true == y_pred, tf.float32)
return tf.reduce_mean(result)
model.compile(
loss=tf.keras.losses.Hinge(),
optimizer=tf.keras.optimizers.Adam(),
metrics=[hinge_accuracy])
print(model.summary())
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
pqc (PQC) (None, 1) 32
=================================================================
Total params: 32
Trainable params: 32
Non-trainable params: 0
_________________________________________________________________
None
تدريب النموذج الكمي
الآن قم بتدريب النموذج - يستغرق هذا حوالي 45 دقيقة. إذا كنت لا تريد الانتظار كل هذا الوقت ، فاستخدم مجموعة فرعية صغيرة من البيانات (قم بتعيين NUM_EXAMPLES=500 ، أدناه). هذا لا يؤثر حقًا على تقدم النموذج أثناء التدريب (يحتوي فقط على 32 معلمة ، ولا يحتاج إلى الكثير من البيانات لتقييدها). يؤدي استخدام عدد أقل من الأمثلة إلى إنهاء التدريب في وقت مبكر (5 دقائق) ، ولكنه يمتد لفترة كافية لإظهار أنه يحرز تقدمًا في سجلات التحقق من الصحة.
EPOCHS = 3
BATCH_SIZE = 32
NUM_EXAMPLES = len(x_train_tfcirc)
x_train_tfcirc_sub = x_train_tfcirc[:NUM_EXAMPLES]
y_train_hinge_sub = y_train_hinge[:NUM_EXAMPLES]
يجب أن يحقق تدريب هذا النموذج على التقارب دقة> 85٪ على مجموعة الاختبار.
qnn_history = model.fit(
x_train_tfcirc_sub, y_train_hinge_sub,
batch_size=32,
epochs=EPOCHS,
verbose=1,
validation_data=(x_test_tfcirc, y_test_hinge))
qnn_results = model.evaluate(x_test_tfcirc, y_test)
Epoch 1/3 324/324 [==============================] - 68s 207ms/step - loss: 0.6745 - hinge_accuracy: 0.7719 - val_loss: 0.3959 - val_hinge_accuracy: 0.8004 Epoch 2/3 324/324 [==============================] - 68s 209ms/step - loss: 0.3964 - hinge_accuracy: 0.8291 - val_loss: 0.3498 - val_hinge_accuracy: 0.8997 Epoch 3/3 324/324 [==============================] - 66s 204ms/step - loss: 0.3599 - hinge_accuracy: 0.8854 - val_loss: 0.3395 - val_hinge_accuracy: 0.9042 62/62 [==============================] - 3s 41ms/step - loss: 0.3395 - hinge_accuracy: 0.9042
3. الشبكة العصبية الكلاسيكية
بينما تعمل الشبكة العصبية الكمومية لحل مشكلة MNIST المبسطة ، يمكن للشبكة العصبية الكلاسيكية الأساسية أن تتفوق بسهولة على QNN في هذه المهمة. بعد حقبة واحدة ، يمكن للشبكة العصبية الكلاسيكية تحقيق> 98 ٪ من الدقة في مجموعة الانتظار.
في المثال التالي ، يتم استخدام الشبكة العصبية الكلاسيكية لمشكلة التصنيف 3-6 باستخدام صورة 28 × 28 بأكملها بدلاً من أخذ عينات فرعية للصورة. يتقارب هذا بسهولة إلى ما يقرب من 100٪ من دقة مجموعة الاختبار.
def create_classical_model():
# A simple model based off LeNet from https://keras.io/examples/mnist_cnn/
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(32, [3, 3], activation='relu', input_shape=(28,28,1)))
model.add(tf.keras.layers.Conv2D(64, [3, 3], activation='relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(tf.keras.layers.Dropout(0.25))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(128, activation='relu'))
model.add(tf.keras.layers.Dropout(0.5))
model.add(tf.keras.layers.Dense(1))
return model
model = create_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
model.summary()
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 26, 26, 32) 320
conv2d_1 (Conv2D) (None, 24, 24, 64) 18496
max_pooling2d (MaxPooling2D (None, 12, 12, 64) 0
)
dropout (Dropout) (None, 12, 12, 64) 0
flatten (Flatten) (None, 9216) 0
dense (Dense) (None, 128) 1179776
dropout_1 (Dropout) (None, 128) 0
dense_1 (Dense) (None, 1) 129
=================================================================
Total params: 1,198,721
Trainable params: 1,198,721
Non-trainable params: 0
_________________________________________________________________
model.fit(x_train,
y_train,
batch_size=128,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
cnn_results = model.evaluate(x_test, y_test)
95/95 [==============================] - 3s 31ms/step - loss: 0.0400 - accuracy: 0.9842 - val_loss: 0.0057 - val_accuracy: 0.9970 62/62 [==============================] - 0s 3ms/step - loss: 0.0057 - accuracy: 0.9970
النموذج أعلاه لديه ما يقرب من 1.2M معلمات. للحصول على مقارنة أكثر إنصافًا ، جرب نموذجًا مكونًا من 37 معلمة على الصور المجمعة:
def create_fair_classical_model():
# A simple model based off LeNet from https://keras.io/examples/mnist_cnn/
model = tf.keras.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=(4,4,1)))
model.add(tf.keras.layers.Dense(2, activation='relu'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_1 (Flatten) (None, 16) 0
dense_2 (Dense) (None, 2) 34
dense_3 (Dense) (None, 1) 3
=================================================================
Total params: 37
Trainable params: 37
Non-trainable params: 0
_________________________________________________________________
model.fit(x_train_bin,
y_train_nocon,
batch_size=128,
epochs=20,
verbose=2,
validation_data=(x_test_bin, y_test))
fair_nn_results = model.evaluate(x_test_bin, y_test)
Epoch 1/20 81/81 - 1s - loss: 0.6678 - accuracy: 0.6546 - val_loss: 0.6326 - val_accuracy: 0.7358 - 503ms/epoch - 6ms/step Epoch 2/20 81/81 - 0s - loss: 0.6186 - accuracy: 0.7654 - val_loss: 0.5787 - val_accuracy: 0.7515 - 98ms/epoch - 1ms/step Epoch 3/20 81/81 - 0s - loss: 0.5629 - accuracy: 0.7861 - val_loss: 0.5247 - val_accuracy: 0.7764 - 104ms/epoch - 1ms/step Epoch 4/20 81/81 - 0s - loss: 0.5150 - accuracy: 0.8301 - val_loss: 0.4825 - val_accuracy: 0.8196 - 103ms/epoch - 1ms/step Epoch 5/20 81/81 - 0s - loss: 0.4762 - accuracy: 0.8493 - val_loss: 0.4490 - val_accuracy: 0.8293 - 97ms/epoch - 1ms/step Epoch 6/20 81/81 - 0s - loss: 0.4438 - accuracy: 0.8527 - val_loss: 0.4216 - val_accuracy: 0.8298 - 99ms/epoch - 1ms/step Epoch 7/20 81/81 - 0s - loss: 0.4169 - accuracy: 0.8555 - val_loss: 0.3986 - val_accuracy: 0.8313 - 98ms/epoch - 1ms/step Epoch 8/20 81/81 - 0s - loss: 0.3951 - accuracy: 0.8595 - val_loss: 0.3794 - val_accuracy: 0.8313 - 105ms/epoch - 1ms/step Epoch 9/20 81/81 - 0s - loss: 0.3773 - accuracy: 0.8596 - val_loss: 0.3635 - val_accuracy: 0.8328 - 98ms/epoch - 1ms/step Epoch 10/20 81/81 - 0s - loss: 0.3620 - accuracy: 0.8611 - val_loss: 0.3499 - val_accuracy: 0.8333 - 97ms/epoch - 1ms/step Epoch 11/20 81/81 - 0s - loss: 0.3488 - accuracy: 0.8714 - val_loss: 0.3382 - val_accuracy: 0.8720 - 98ms/epoch - 1ms/step Epoch 12/20 81/81 - 0s - loss: 0.3372 - accuracy: 0.8831 - val_loss: 0.3279 - val_accuracy: 0.8720 - 95ms/epoch - 1ms/step Epoch 13/20 81/81 - 0s - loss: 0.3271 - accuracy: 0.8831 - val_loss: 0.3187 - val_accuracy: 0.8725 - 97ms/epoch - 1ms/step Epoch 14/20 81/81 - 0s - loss: 0.3181 - accuracy: 0.8832 - val_loss: 0.3107 - val_accuracy: 0.8725 - 96ms/epoch - 1ms/step Epoch 15/20 81/81 - 0s - loss: 0.3101 - accuracy: 0.8833 - val_loss: 0.3035 - val_accuracy: 0.8725 - 96ms/epoch - 1ms/step Epoch 16/20 81/81 - 0s - loss: 0.3030 - accuracy: 0.8833 - val_loss: 0.2972 - val_accuracy: 0.8725 - 105ms/epoch - 1ms/step Epoch 17/20 81/81 - 0s - loss: 0.2966 - accuracy: 0.8833 - val_loss: 0.2913 - val_accuracy: 0.8725 - 104ms/epoch - 1ms/step Epoch 18/20 81/81 - 0s - loss: 0.2908 - accuracy: 0.8928 - val_loss: 0.2861 - val_accuracy: 0.8725 - 104ms/epoch - 1ms/step Epoch 19/20 81/81 - 0s - loss: 0.2856 - accuracy: 0.8955 - val_loss: 0.2816 - val_accuracy: 0.8725 - 99ms/epoch - 1ms/step Epoch 20/20 81/81 - 0s - loss: 0.2809 - accuracy: 0.8952 - val_loss: 0.2773 - val_accuracy: 0.8725 - 101ms/epoch - 1ms/step 62/62 [==============================] - 0s 895us/step - loss: 0.2773 - accuracy: 0.8725
4. المقارنة
تجعل المدخلات عالية الدقة والنموذج الأكثر قوة هذه المشكلة سهلة لشبكة CNN. بينما يتدرب النموذج الكلاسيكي لقوة مماثلة (~ 32 معلمة) إلى دقة مماثلة في جزء صغير من الوقت. بطريقة أو بأخرى ، تتفوق الشبكة العصبية الكلاسيكية بسهولة على الشبكة العصبية الكمومية. بالنسبة للبيانات الكلاسيكية ، من الصعب التغلب على الشبكة العصبية الكلاسيكية.
qnn_accuracy = qnn_results[1]
cnn_accuracy = cnn_results[1]
fair_nn_accuracy = fair_nn_results[1]
sns.barplot(["Quantum", "Classical, full", "Classical, fair"],
[qnn_accuracy, cnn_accuracy, fair_nn_accuracy])
/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation. FutureWarning <AxesSubplot:>

