 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Hướng dẫn này cho thấy cách mạng nơ-ron cổ điển có thể học cách sửa lỗi hiệu chuẩn qubit. Nó giới thiệu Cirq , một khuôn khổ Python để tạo, chỉnh sửa và gọi các mạch Lượng tử quy mô trung gian Noisy (NISQ) và trình bày cách Cirq giao tiếp với TensorFlow Quantum.
Thành lập
pip install tensorflow==2.7.0
Cài đặt TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Bây giờ nhập TensorFlow và các phụ thuộc mô-đun:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Khái niệm cơ bản
1.1 Mạch lượng tử tuần hoàn và tham số hóa
Trước khi khám phá TensorFlow Quantum (TFQ), chúng ta hãy xem xét một số khái niệm cơ bản về Cirq . Cirq là một thư viện Python cho tính toán lượng tử của Google. Bạn sử dụng nó để xác định các mạch, bao gồm cả cổng tĩnh và cổng được tham số hóa.
Cirq sử dụng các ký hiệu SymPy để biểu diễn các tham số tự do.
a, b = sympy.symbols('a b')
Đoạn mã sau tạo một mạch hai qubit bằng cách sử dụng các tham số của bạn:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Để đánh giá mạch, bạn có thể sử dụng giao diện cirq.Simulator . Bạn thay thế các tham số miễn phí trong một mạch bằng các số cụ thể bằng cách truyền vào một đối tượng cirq.ParamResolver . Đoạn mã sau đây tính toán đầu ra vectơ trạng thái thô của mạch được tham số hóa của bạn:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Các vectơ trạng thái không thể truy cập trực tiếp bên ngoài mô phỏng (lưu ý các số phức trong đầu ra ở trên). Để thực tế về mặt vật lý, bạn phải chỉ định một phép đo, phép đo này chuyển đổi một vectơ trạng thái thành một số thực mà máy tính cổ điển có thể hiểu được. Cirq chỉ định các phép đo bằng cách sử dụng kết hợp các toán tử Pauli \(\hat{X}\), \(\hat{Y}\)và \(\hat{Z}\). Như minh họa, đoạn mã sau đo lường \(\hat{Z}_0\) và \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) trên vector trạng thái mà bạn vừa mô phỏng:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 Mạch lượng tử làm tenxơ
TensorFlow Quantum (TFQ) cung cấp tfq.convert_to_tensor , một chức năng chuyển đổi các đối tượng Cirq thành tensor. Điều này cho phép bạn gửi các đối tượng Cirq đến các lớp lượng tử và các hoạt động lượng tử của chúng tôi. Hàm có thể được gọi trên danh sách hoặc mảng của Cirq Circuits và Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Điều này mã hóa các đối tượng Cirq dưới dạng các tensors tf.string mà các hoạt động tfq giải mã khi cần thiết.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Mô phỏng mạch theo lô
TFQ cung cấp các phương pháp tính toán giá trị kỳ vọng, mẫu và vectơ trạng thái. Hiện tại, hãy tập trung vào các giá trị kỳ vọng .
Giao diện cấp cao nhất để tính toán các giá trị kỳ vọng là lớp tfq.layers.Expectation , là tf.keras.Layer . Ở dạng đơn giản nhất, lớp này tương đương với việc mô phỏng một mạch được tham số hóa trên nhiều cirq.ParamResolvers ; tuy nhiên, TFQ cho phép phân phối theo ngữ nghĩa TensorFlow và các mạch được mô phỏng bằng cách sử dụng mã C ++ hiệu quả.
Tạo một loạt các giá trị để thay thế cho các tham số a và b của chúng tôi:
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
Thực thi mạch theo lô trên các giá trị tham số trong Cirq yêu cầu một vòng lặp:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
Thao tác tương tự được đơn giản hóa trong TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Tối ưu hóa lượng tử-cổ điển lai
Bây giờ bạn đã thấy những điều cơ bản, hãy sử dụng TensorFlow Quantum để xây dựng một mạng nơ-ron cổ điển-lượng tử lai . Bạn sẽ huấn luyện một mạng nơ-ron cổ điển để kiểm soát một qubit. Điều khiển sẽ được tối ưu hóa để chuẩn bị chính xác qubit ở trạng thái 0 hoặc 1 , khắc phục lỗi hiệu chuẩn hệ thống mô phỏng. Hình này cho thấy kiến trúc:
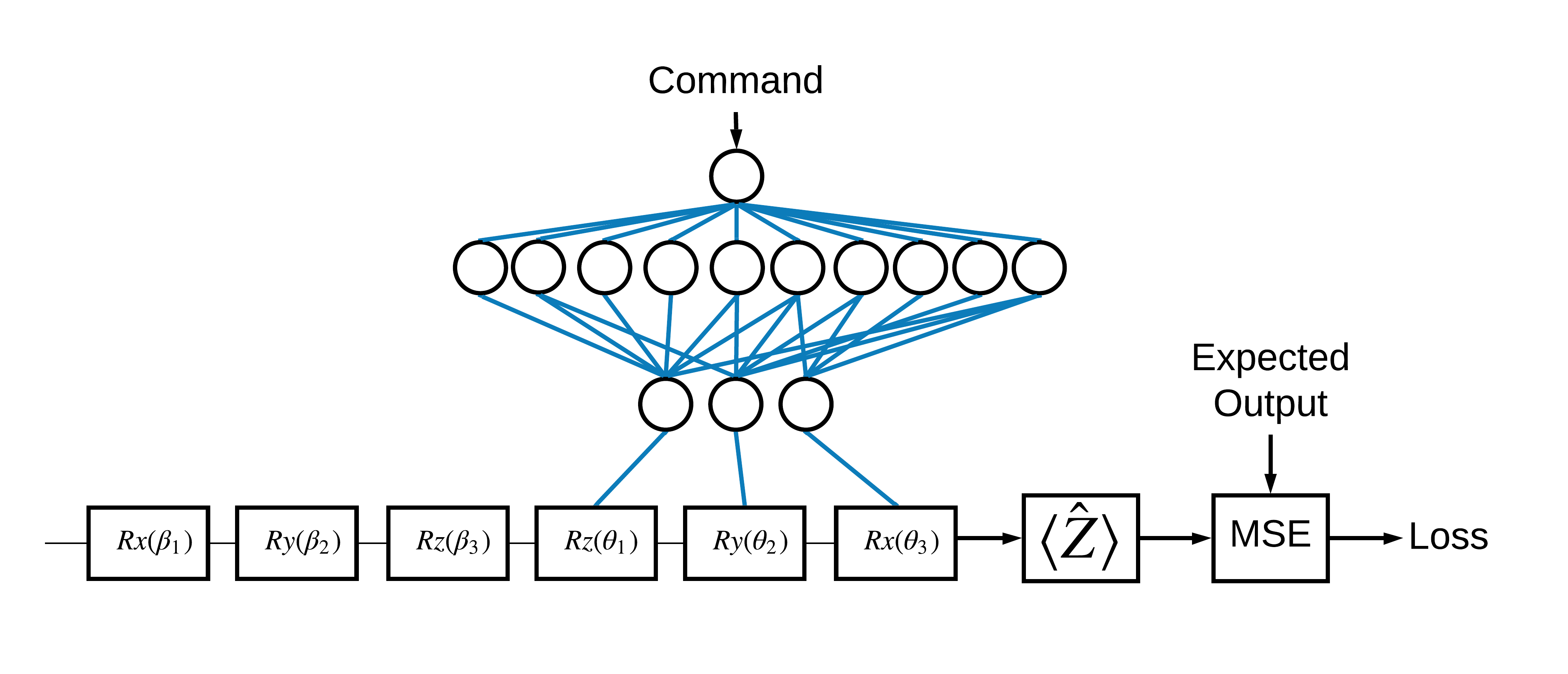
Ngay cả khi không có mạng nơron, đây là một vấn đề đơn giản cần giải quyết, nhưng chủ đề này tương tự như các vấn đề điều khiển lượng tử thực mà bạn có thể giải quyết bằng cách sử dụng TFQ. Nó thể hiện một ví dụ end-to-end của phép tính lượng tử-cổ điển bằng cách sử dụng lớp tfq.layers.ControlledPQC (Parametrated Quantum Circuit) bên trong tf.keras.Model .
Để thực hiện hướng dẫn này, kiến trúc này được chia thành 3 phần:
- Mạch đầu vào hoặc mạch điểm dữ liệu: Ba cổng \(R\) đầu tiên.
- Mạch điều khiển : Ba cổng \(R\) khác.
- Bộ điều khiển : Mạng thần kinh cổ điển cài đặt các thông số của mạch được điều khiển.
2.1 Định nghĩa mạch điều khiển
Xác định một phép quay bit đơn có thể học được, như được chỉ ra trong hình trên. Điều này sẽ tương ứng với mạch được điều khiển của chúng tôi.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 Bộ điều khiển
Bây giờ xác định mạng bộ điều khiển:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Đưa ra một loạt lệnh, bộ điều khiển xuất ra một loạt các tín hiệu điều khiển cho mạch được điều khiển.
Bộ điều khiển được khởi tạo ngẫu nhiên nên các kết quả đầu ra này vẫn chưa hữu ích.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Kết nối bộ điều khiển với mạch
Sử dụng tfq để kết nối bộ điều khiển với mạch được điều khiển, như một keras.Model duy nhất.
Xem hướng dẫn API chức năng Keras để biết thêm về kiểu định nghĩa mô hình này.
Đầu tiên xác định các đầu vào cho mô hình:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Tiếp theo, áp dụng các phép toán cho các đầu vào đó, để xác định tính toán.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Bây giờ đóng gói tính toán này dưới dạng tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
Kiến trúc mạng được biểu thị bằng biểu đồ của mô hình bên dưới. So sánh âm mưu mô hình này với sơ đồ kiến trúc để xác minh tính đúng đắn.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
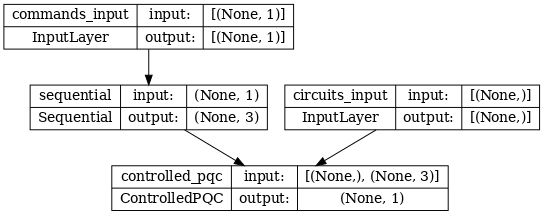
Mô hình này có hai đầu vào: Các lệnh cho bộ điều khiển và mạch đầu vào có đầu ra mà bộ điều khiển đang cố gắng sửa.
2.4 Tập dữ liệu
Mô hình cố gắng xuất ra giá trị đo chính xác chính xác của \(\hat{Z}\) cho mỗi lệnh. Các lệnh và giá trị đúng được xác định bên dưới.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Đây không phải là toàn bộ tập dữ liệu đào tạo cho nhiệm vụ này. Mỗi điểm dữ liệu trong bộ dữ liệu cũng cần một mạch đầu vào.
2.4 Định nghĩa mạch đầu vào
Mạch đầu vào bên dưới xác định hiệu chuẩn sai ngẫu nhiên mà mô hình sẽ tìm hiểu để sửa.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Có hai bản sao của mạch, một bản cho mỗi điểm dữ liệu.
datapoint_circuits.shape
TensorShape([2])
2.5 Đào tạo
Với các đầu vào được xác định, bạn có thể chạy thử mô hình tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Bây giờ, hãy chạy một quy trình đào tạo tiêu chuẩn để điều chỉnh các giá trị này theo expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
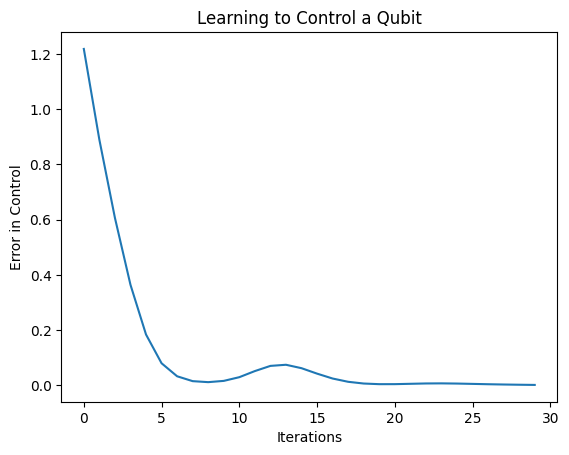
Từ biểu đồ này, bạn có thể thấy rằng mạng nơ-ron đã học được cách khắc phục sự hiệu chuẩn sai hệ thống.
2.6 Xác minh kết quả đầu ra
Bây giờ hãy sử dụng mô hình được đào tạo để sửa lỗi hiệu chuẩn qubit. Với Cirq:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
Giá trị của hàm mất mát trong quá trình đào tạo cung cấp một ý tưởng sơ bộ về mức độ học tập của mô hình. Sự mất mát càng thấp, các giá trị kỳ vọng trong ô trên càng gần với giá trị desired_values muốn. Nếu bạn không quan tâm đến các giá trị tham số, bạn luôn có thể kiểm tra kết quả đầu ra từ phía trên bằng cách sử dụng tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Học cách chuẩn bị eigenstates của các toán tử khác nhau
Lựa chọn của các eigenstates \(\pm \hat{Z}\) tương ứng với 1 và 0 là tùy ý. Bạn có thể dễ dàng muốn 1 tương ứng với \(+ \hat{Z}\) eigenstate và 0 để tương ứng với eigenstate \(-\hat{X}\) . Một cách để thực hiện điều này là chỉ định một toán tử đo lường khác nhau cho mỗi lệnh, như được chỉ ra trong hình bên dưới:
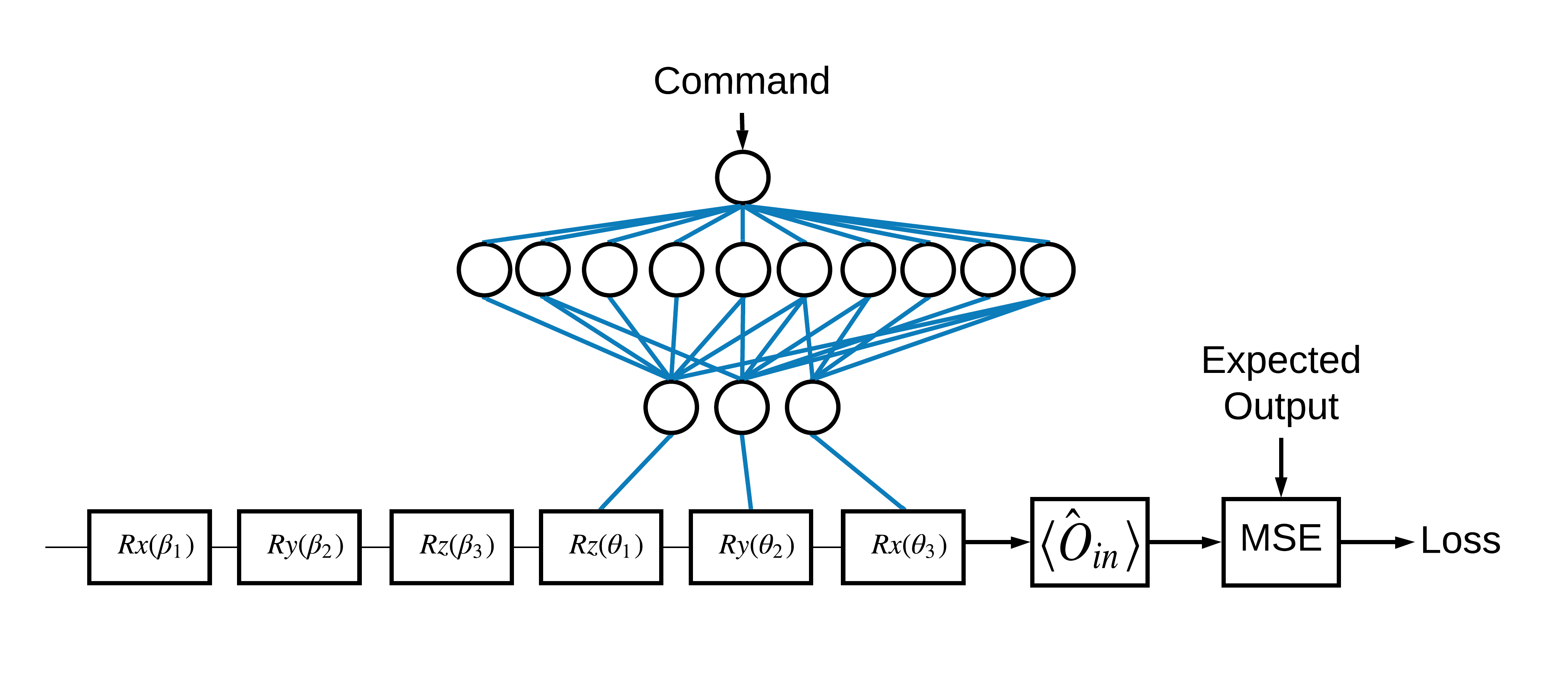
Điều này yêu cầu sử dụng tfq.layers.Expectation . Bây giờ đầu vào của bạn đã phát triển bao gồm ba đối tượng: mạch, lệnh và toán tử. Đầu ra vẫn là giá trị kỳ vọng.
3.1 Định nghĩa mô hình mới
Chúng ta hãy xem qua mô hình để thực hiện nhiệm vụ này:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Đây là mạng bộ điều khiển:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Kết hợp mạch và bộ điều khiển thành một keras.Model duy nhất. Mô hình sử dụng tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 Tập dữ liệu
Bây giờ bạn cũng sẽ bao gồm các toán tử mà bạn muốn đo lường cho mỗi điểm dữ liệu mà bạn cung cấp cho model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Đào tạo
Bây giờ bạn đã có đầu vào và đầu ra mới, bạn có thể đào tạo lại một lần nữa bằng cách sử dụng keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
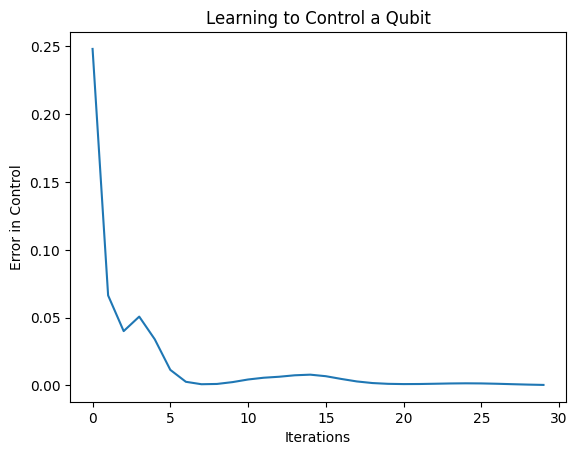
Hàm mất mát đã giảm xuống 0.
Bộ controller có sẵn dưới dạng mô hình độc lập. Gọi cho bộ điều khiển và kiểm tra phản ứng của nó đối với từng tín hiệu lệnh. Sẽ mất một số công việc để so sánh chính xác các kết quả đầu ra này với nội dung của random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
