 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запустить в Google Colab Запустить в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
В этом руководстве показано, как классическая нейронная сеть может научиться исправлять ошибки калибровки кубитов. Он представляет Cirq , платформу Python для создания, редактирования и вызова схем Noisy Intermediate Scale Quantum (NISQ), и демонстрирует, как Cirq взаимодействует с TensorFlow Quantum.
Настраивать
pip install tensorflow==2.7.0
Установите TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Теперь импортируйте TensorFlow и зависимости модуля:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Основы
1.1 Cirq и параметризованные квантовые схемы
Прежде чем приступить к изучению TensorFlow Quantum (TFQ), давайте рассмотрим некоторые основы Cirq . Cirq — это библиотека Python для квантовых вычислений от Google. Вы используете его для определения цепей, включая статические и параметризованные вентили.
Cirq использует символы SymPy для представления свободных параметров.
a, b = sympy.symbols('a b')
Следующий код создает схему из двух кубитов, используя ваши параметры:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Для оценки цепей можно использовать интерфейс cirq.Simulator . Вы заменяете свободные параметры в цепи определенными номерами, передавая объект cirq.ParamResolver . Следующий код вычисляет исходный вектор состояния вашей параметризованной схемы:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Векторы состояния не доступны напрямую вне симуляции (обратите внимание на комплексные числа в выходных данных выше). Чтобы быть физически реалистичным, вы должны указать измерение, которое преобразует вектор состояния в действительное число, понятное классическим компьютерам. Cirq задает измерения, используя комбинации операторов Паули \(\hat{X}\), \(\hat{Y}\)и \(\hat{Z}\). В качестве иллюстрации следующий код измеряет \(\hat{Z}_0\) и \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) в только что смоделированном векторе состояния:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2. Квантовые схемы как тензоры
TensorFlow Quantum (TFQ) предоставляет tfq.convert_to_tensor функцию, которая преобразует объекты Cirq в тензоры. Это позволяет отправлять объекты Cirq в наши квантовые слои и квантовые операции . Функцию можно вызывать для списков или массивов Cirq Circuits и Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Это кодирует объекты Cirq как тензоры tf.string , которые операции tfq декодируют по мере необходимости.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Моделирование схемы дозирования
TFQ предоставляет методы для вычисления значений ожидания, выборок и векторов состояния. А пока давайте сосредоточимся на ожидаемых значениях .
Интерфейс самого высокого уровня для вычисления ожидаемых значений — слой tfq.layers.Expectation , который представляет собой tf.keras.Layer . В своей простейшей форме этот уровень эквивалентен моделированию параметризованной схемы с множеством cirq.ParamResolvers ; однако TFQ позволяет выполнять пакетную обработку в соответствии с семантикой TensorFlow, а схемы моделируются с использованием эффективного кода C++.
Создайте пакет значений для замены наших параметров a и b :
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
Пакетное выполнение схемы по значениям параметров в Cirq требует цикла:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
Эта же операция упрощена в TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Гибридная квантово-классическая оптимизация
Теперь, когда вы ознакомились с основами, давайте воспользуемся TensorFlow Quantum для построения гибридной квантово-классической нейронной сети . Вы будете обучать классическую нейронную сеть управлять одним кубитом. Управление будет оптимизировано для правильной подготовки кубита в состоянии 0 или 1 , преодолевая смоделированную систематическую ошибку калибровки. На этом рисунке показана архитектура:
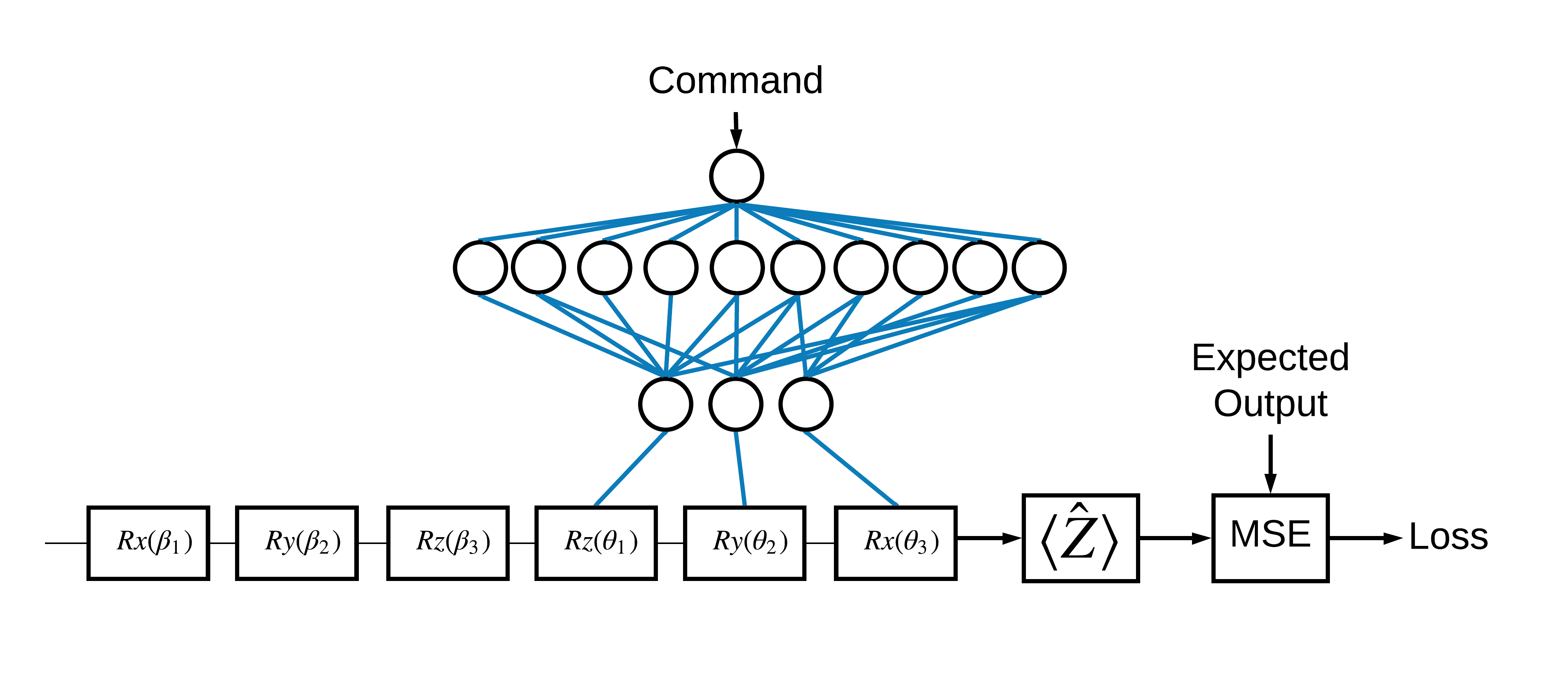
Даже без нейронной сети решить эту задачу несложно, но тема похожа на реальные проблемы квантового управления, которые вы можете решить с помощью TFQ. Он демонстрирует сквозной пример квантово-классического вычисления с использованием tfq.layers.ControlledPQC (параметризованная квантовая схема) внутри tf.keras.Model .
Для реализации этого руководства эта архитектура разделена на 3 части:
- Входная схема или схема точки данных: первые три \(R\) .
- Управляемая схема : остальные три \(R\) .
- Контроллер : классическая нейросеть, задающая параметры управляемой цепи.
2.1 Определение управляемой цепи
Определите обучаемое вращение одного бита, как показано на рисунке выше. Это будет соответствовать нашей управляемой схеме.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 Контроллер
Теперь определите сеть контроллера:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Получив пакет команд, контроллер выдает пакет управляющих сигналов для управляемой схемы.
Контроллер инициализируется случайным образом, поэтому эти выходы пока бесполезны.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Подключите контроллер к цепи
Используйте tfq для подключения контроллера к управляемой схеме, как одиночный keras.Model .
Дополнительные сведения об этом стиле определения модели см. в руководстве по функциональному API Keras .
Сначала определите входные данные для модели:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Затем примените операции к этим входам, чтобы определить вычисление.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Теперь упакуйте это вычисление как tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
Архитектура сети указана на графике модели ниже. Сравните этот график модели с архитектурной диаграммой, чтобы проверить правильность.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
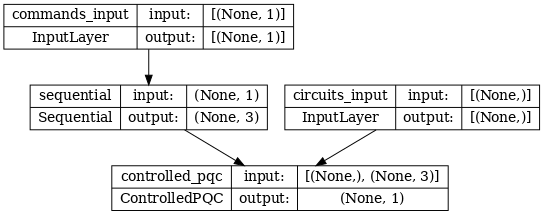
Эта модель принимает два входа: команды для контроллера и входную схему, выход которой контроллер пытается исправить.
2.4 Набор данных
Модель пытается вывести правильное значение измерения \(\hat{Z}\) для каждой команды. Команды и правильные значения определены ниже.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Это не весь обучающий набор данных для этой задачи. Каждая точка данных в наборе данных также нуждается во входной цепи.
2.4 Определение входной цепи
Входная схема ниже определяет случайную неточность, которую модель научится исправлять.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Есть две копии схемы, по одной для каждой точки данных.
datapoint_circuits.shape
TensorShape([2])
2.5 Обучение
Определив входные данные, вы можете протестировать модель tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Теперь запустите стандартный процесс обучения, чтобы настроить эти значения в соответствии с expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
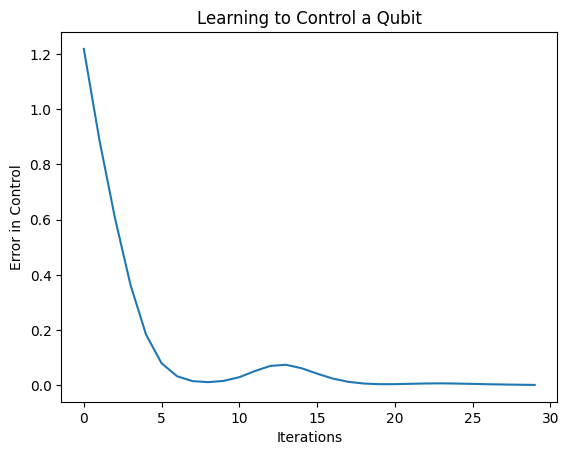
Из этого графика видно, что нейронная сеть научилась преодолевать систематическую раскалибровку.
2.6 Проверка выходных данных
Теперь используйте обученную модель, чтобы исправить ошибки калибровки кубита. С Цирком:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
Значение функции потерь во время обучения дает приблизительное представление о том, насколько хорошо обучается модель. Чем ниже потери, тем ближе ожидаемые значения в приведенной выше ячейке к desired_values . Если вас не интересуют значения параметров, вы всегда можете проверить выходные данные сверху, используя tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Учимся готовить собственные состояния разных операторов
Выбор собственных состояний \(\pm \hat{Z}\) , соответствующих 1 и 0, был произвольным. С тем же успехом вы могли бы захотеть, чтобы 1 соответствовало собственному состоянию \(+ \hat{Z}\) а 0 — собственному состоянию \(-\hat{X}\) . Один из способов добиться этого — указать разные операторы измерения для каждой команды, как показано на рисунке ниже:
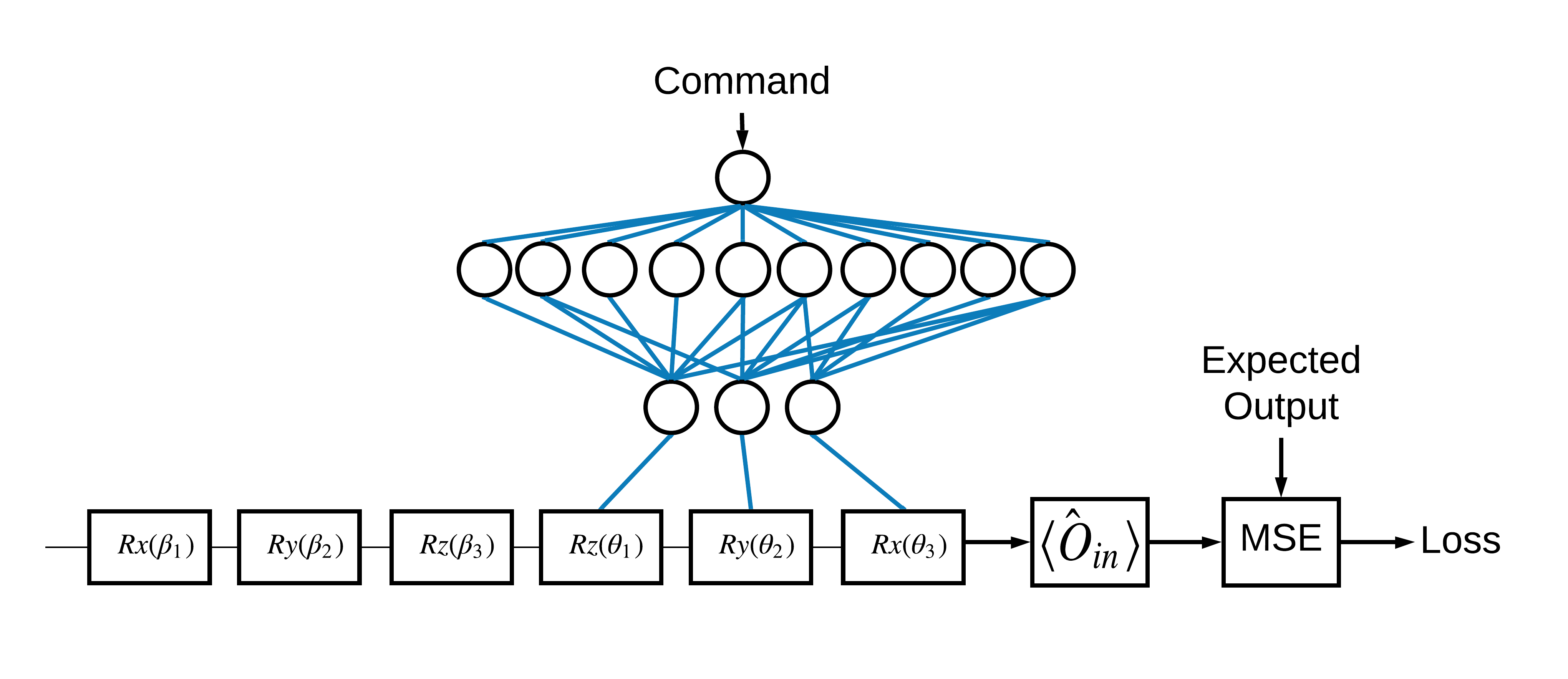
Для этого необходимо использовать tfq.layers.Expectation . Теперь ваш ввод расширился до трех объектов: схема, команда и оператор. Результат по-прежнему является ожидаемым значением.
3.1 Новое определение модели
Давайте посмотрим на модель для выполнения этой задачи:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Вот сеть контроллера:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Объедините схему и контроллер в один keras.Model с помощью tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 Набор данных
Теперь вы также включите операторы, которые вы хотите измерить для каждой точки данных, которую вы предоставляете для model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Обучение
Теперь, когда у вас есть новые входные и выходные данные, вы можете снова тренироваться с помощью keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
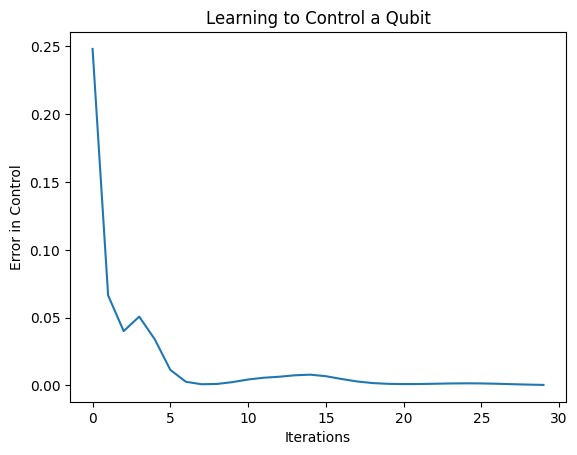
Функция потерь упала до нуля.
controller доступен как автономная модель. Вызовите контроллер и проверьте его реакцию на каждый командный сигнал. Потребуется некоторая работа, чтобы правильно сравнить эти выходные данные с содержимым random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
