 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar libreta Descargar libreta |
Este tutorial muestra cómo una red neuronal clásica puede aprender a corregir errores de calibración de qubit. Presenta Cirq , un marco de Python para crear, editar e invocar circuitos Noisy Intermediate Scale Quantum (NISQ), y demuestra cómo Cirq interactúa con TensorFlow Quantum.
Configuración
pip install tensorflow==2.7.0
Instale TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Ahora importa TensorFlow y las dependencias del módulo:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Los fundamentos
1.1 Cirq y circuitos cuánticos parametrizados
Antes de explorar TensorFlow Quantum (TFQ), veamos algunos conceptos básicos de Cirq . Cirq es una biblioteca de Python para computación cuántica de Google. Lo usa para definir circuitos, incluidas puertas estáticas y parametrizadas.
Cirq usa símbolos SymPy para representar parámetros libres.
a, b = sympy.symbols('a b')
El siguiente código crea un circuito de dos qubits usando sus parámetros:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Para evaluar circuitos, puede utilizar la interfaz cirq.Simulator . Reemplaza los parámetros libres en un circuito con números específicos pasando un objeto cirq.ParamResolver . El siguiente código calcula la salida del vector de estado sin procesar de su circuito parametrizado:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Los vectores de estado no son directamente accesibles fuera de la simulación (observe los números complejos en el resultado anterior). Para ser físicamente realista, debe especificar una medida que convierta un vector de estado en un número real que las computadoras clásicas puedan entender. Cirq especifica medidas mediante combinaciones de los operadores de Pauli \(\hat{X}\), \(\hat{Y}\)y \(\hat{Z}\). Como ilustración, el siguiente código mide \(\hat{Z}_0\) y \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) en el vector de estado que acaba de simular:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 Circuitos cuánticos como tensores
TensorFlow Quantum (TFQ) proporciona tfq.convert_to_tensor , una función que convierte objetos Cirq en tensores. Esto le permite enviar objetos Cirq a nuestras capas cuánticas y operaciones cuánticas . La función se puede llamar en listas o matrices de Cirq Circuits y Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Esto codifica los objetos Cirq como tensores tf.string que las operaciones tfq decodifican según sea necesario.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Simulación del circuito de dosificación
TFQ proporciona métodos para calcular valores esperados, muestras y vectores de estado. Por ahora, concentrémonos en los valores esperados .
La interfaz de más alto nivel para calcular los valores esperados es la capa tfq.layers.Expectation , que es una tf.keras.Layer . En su forma más simple, esta capa es equivalente a simular un circuito parametrizado sobre muchos cirq.ParamResolvers ; sin embargo, TFQ permite el procesamiento por lotes siguiendo la semántica de TensorFlow, y los circuitos se simulan utilizando código C++ eficiente.
Cree un lote de valores para sustituir nuestros parámetros a y b :
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
La ejecución del circuito de procesamiento por lotes sobre valores de parámetros en Cirq requiere un bucle:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
La misma operación se simplifica en TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Optimización híbrida cuántica-clásica
Ahora que ha visto los conceptos básicos, usemos TensorFlow Quantum para construir una red neuronal clásica cuántica híbrida . Entrenarás una red neuronal clásica para controlar un solo qubit. El control se optimizará para preparar correctamente el qubit en el estado 0 o 1 , superando un error de calibración sistemático simulado. Esta figura muestra la arquitectura:

Incluso sin una red neuronal, este es un problema sencillo de resolver, pero el tema es similar a los problemas reales de control cuántico que podría resolver usando TFQ. Demuestra un ejemplo de extremo a extremo de un cálculo clásico cuántico utilizando la tfq.layers.ControlledPQC (Parametrized Quantum Circuit) dentro de un tf.keras.Model .
Para la implementación de este tutorial, esta arquitectura se divide en 3 partes:
- El circuito de entrada o circuito de punto de datos: Las primeras tres puertas \(R\) .
- El circuito controlado : Las otras tres puertas \(R\) .
- El controlador : La clásica red neuronal que establece los parámetros del circuito controlado.
2.1 La definición de circuito controlado
Defina una rotación de un solo bit aprendible, como se indica en la figura anterior. Esto corresponderá a nuestro circuito controlado.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 El controlador
Ahora defina la red del controlador:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Dado un lote de comandos, el controlador emite un lote de señales de control para el circuito controlado.
El controlador se inicializa aleatoriamente, por lo que estas salidas aún no son útiles.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Conectar el controlador al circuito
Use tfq para conectar el controlador al circuito controlado, como un solo keras.Model .
Consulte la guía de la API funcional de Keras para obtener más información sobre este estilo de definición de modelo.
Primero defina las entradas al modelo:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
A continuación, aplique operaciones a esas entradas para definir el cálculo.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Ahora empaquete este cálculo como tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
La arquitectura de la red se indica mediante el gráfico del modelo siguiente. Compare este gráfico modelo con el diagrama de arquitectura para verificar que sea correcto.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
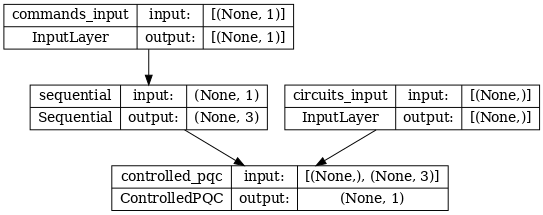
Este modelo toma dos entradas: los comandos para el controlador y el circuito de entrada cuya salida el controlador intenta corregir.
2.4 El conjunto de datos
El modelo intenta generar el valor de medición correcto correcto de \(\hat{Z}\) para cada comando. Los comandos y valores correctos se definen a continuación.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Este no es el conjunto de datos de entrenamiento completo para esta tarea. Cada punto de datos en el conjunto de datos también necesita un circuito de entrada.
2.4 Definición del circuito de entrada
El circuito de entrada a continuación define la mala calibración aleatoria que el modelo aprenderá a corregir.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Hay dos copias del circuito, una para cada punto de datos.
datapoint_circuits.shape
TensorShape([2])
2.5 Formación
Con las entradas definidas, puede probar el modelo tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Ahora ejecute un proceso de entrenamiento estándar para ajustar estos valores hacia los expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
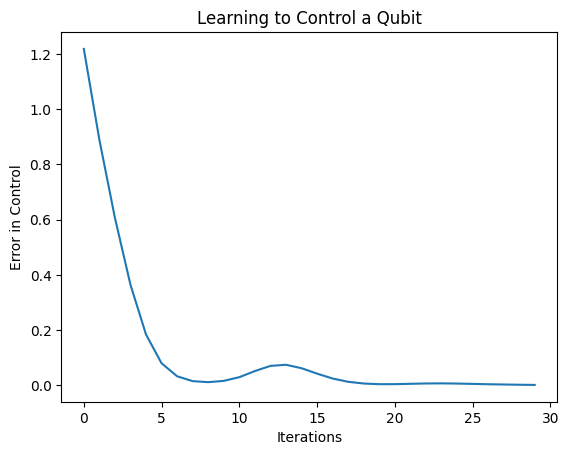
A partir de este gráfico, puede ver que la red neuronal ha aprendido a superar la mala calibración sistemática.
2.6 Verificar salidas
Ahora use el modelo entrenado para corregir los errores de calibración de qubit. Con cirq:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
El valor de la función de pérdida durante el entrenamiento proporciona una idea aproximada de qué tan bien está aprendiendo el modelo. Cuanto menor sea la pérdida, más cerca estarán los valores esperados en la celda anterior de los desired_values . Si no está tan preocupado por los valores de los parámetros, siempre puede verificar las salidas desde arriba usando tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Aprender a preparar estados propios de diferentes operadores
La elección de los autoestados \(\pm \hat{Z}\) correspondientes a 1 y 0 fue arbitraria. Podrías haber querido fácilmente que 1 correspondiera al estado \(+ \hat{Z}\) y 0 para corresponder al estado \(-\hat{X}\) . Una forma de lograr esto es especificando un operador de medición diferente para cada comando, como se indica en la siguiente figura:

Esto requiere el uso de tfq.layers.Expectation . Ahora su entrada ha crecido para incluir tres objetos: circuito, comando y operador. La salida sigue siendo el valor esperado.
3.1 Definición del nuevo modelo
Echemos un vistazo al modelo para realizar esta tarea:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Aquí está la red del controlador:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Combine el circuito y el controlador en un solo keras. tfq keras.Model
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 El conjunto de datos
Ahora también incluirá los operadores que desea medir para cada punto de datos que proporcione para model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Formación
Ahora que tiene sus nuevas entradas y salidas, puede entrenar una vez más usando keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()

La función de pérdida se ha reducido a cero.
El controller está disponible como modelo independiente. Llame al controlador y verifique su respuesta a cada señal de comando. Tomaría algo de trabajo comparar correctamente estas salidas con el contenido de random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
