 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu öğretici, klasik bir sinir ağının qubit kalibrasyon hatalarını düzeltmeyi nasıl öğrenebileceğini gösterir. Gürültülü Orta Ölçekli Kuantum (NISQ) devrelerini oluşturmak, düzenlemek ve çağırmak için bir Python çerçevesi olan Cirq'i tanıtır ve Cirq'in TensorFlow Quantum ile nasıl arayüz oluşturduğunu gösterir.
Kurmak
pip install tensorflow==2.7.0
TensorFlow Quantum'u yükleyin:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Şimdi TensorFlow ve modül bağımlılıklarını içe aktarın:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Temel Bilgiler
1.1 Cirq ve parametreli kuantum devreleri
TensorFlow Quantum'u (TFQ) keşfetmeden önce, bazı Cirq temellerine bakalım. Cirq, Google'dan kuantum hesaplama için bir Python kitaplığıdır. Statik ve parametreli kapılar dahil devreleri tanımlamak için kullanırsınız.
Cirq, ücretsiz parametreleri temsil etmek için SymPy sembollerini kullanır.
a, b = sympy.symbols('a b')
Aşağıdaki kod, parametrelerinizi kullanarak iki kübitlik bir devre oluşturur:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Devreleri değerlendirmek için cirq.Simulator arayüzünü kullanabilirsiniz. Bir cirq.ParamResolver nesnesini ileterek, bir devredeki serbest parametreleri belirli sayılarla değiştirirsiniz. Aşağıdaki kod, parametreli devrenizin ham durum vektörü çıktısını hesaplar:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Durum vektörlerine simülasyon dışında doğrudan erişilemez (yukarıdaki çıktıdaki karmaşık sayılara dikkat edin). Fiziksel olarak gerçekçi olmak için, bir durum vektörünü klasik bilgisayarların anlayabileceği gerçek bir sayıya dönüştüren bir ölçüm belirtmelisiniz. Cirq, Pauli operatörlerinin \(\hat{X}\), \(\hat{Y}\)ve \(\hat{Z}\)kombinasyonlarını kullanarak ölçümleri belirtir. Örnek olarak, aşağıdaki kod, simüle ettiğiniz durum vektöründe \(\hat{Z}_0\) ve \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) ölçer:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281yer tutucu24 l10n-yer
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 Tensör olarak kuantum devreleri
TensorFlow Quantum (TFQ), Cirq nesnelerini tensörlere dönüştüren bir işlev olan tfq.convert_to_tensor sağlar. Bu, Cirq nesnelerini kuantum katmanlarımıza ve kuantum operasyonlarımıza göndermenizi sağlar. İşlev, Cirq Circuits ve Cirq Paulis listelerinde veya dizilerinde çağrılabilir:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Bu, Cirq nesnelerini, tfq işlemlerinin gerektiği gibi tf.string tensörleri olarak kodlar.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Dozajlama devresi simülasyonu
TFQ, beklenti değerlerinin, örneklerin ve durum vektörlerinin hesaplanması için yöntemler sağlar. Şimdilik, beklenti değerlerine odaklanalım.
Beklenti değerlerini hesaplamak için en üst düzey arabirim, bir tf.keras.Layer olan tfq.layers.Expectation katmanıdır. En basit biçiminde, bu katman, birçok cirq.ParamResolvers üzerinde parametreli bir devreyi simüle etmeye eşdeğerdir; bununla birlikte, TFQ, TensorFlow semantiğini izleyen toplu işlemeye izin verir ve devreler verimli C++ kodu kullanılarak simüle edilir.
a ve b parametrelerimizin yerine geçecek bir grup değer oluşturun:
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
Cirq'de parametre değerleri üzerinden toplu devre yürütme bir döngü gerektirir:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
Aynı işlem TFQ'da basitleştirilmiştir:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Hibrit kuantum-klasik optimizasyon
Artık temel bilgileri öğrendiğinize göre, hibrit bir kuantum-klasik sinir ağı oluşturmak için TensorFlow Quantum'u kullanalım. Tek bir kübiti kontrol etmek için klasik bir sinir ağını eğiteceksiniz. Kontrol, simüle edilmiş bir sistematik kalibrasyon hatasının üstesinden gelerek kübiti 0 veya 1 durumunda doğru şekilde hazırlamak için optimize edilecektir. Bu şekil mimariyi gösterir:
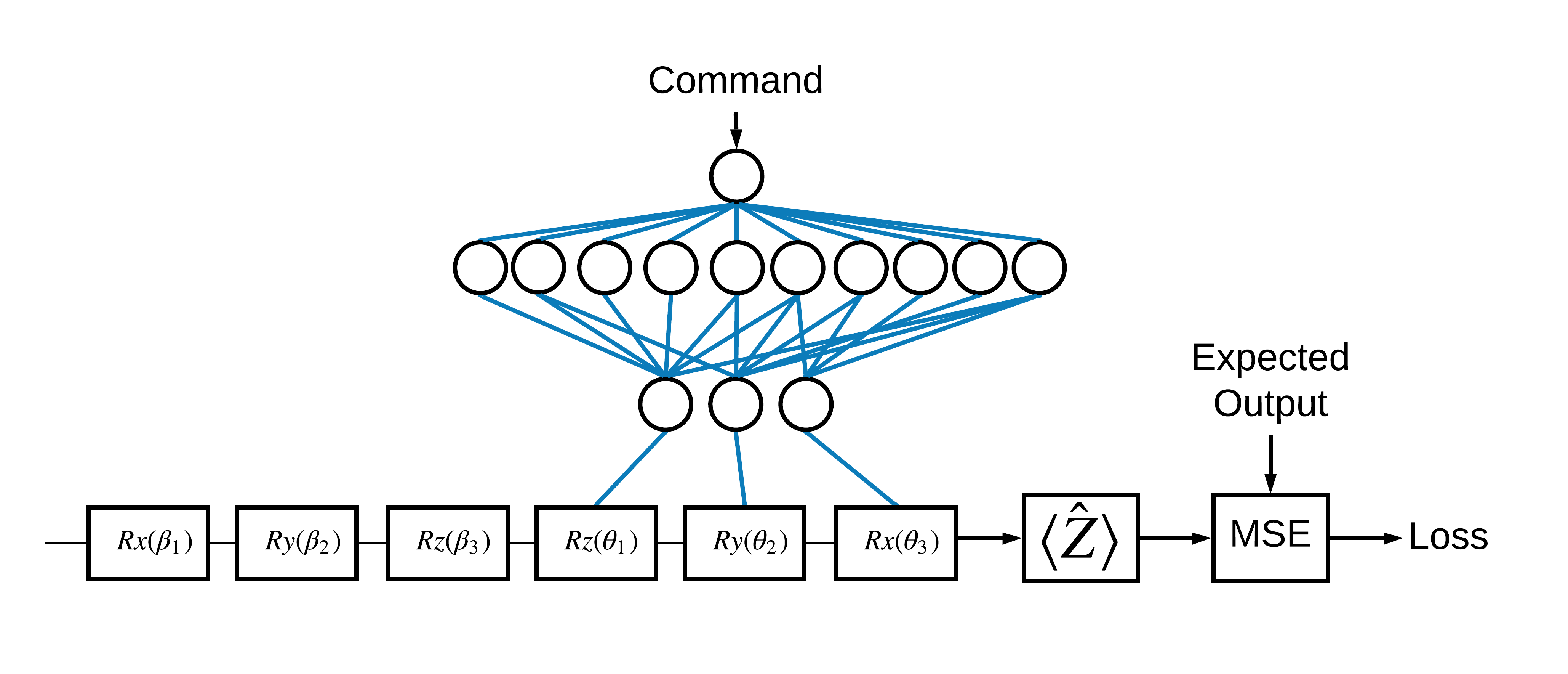
Bir sinir ağı olmadan bile, bu çözülmesi kolay bir problemdir, ancak tema, TFQ kullanarak çözebileceğiniz gerçek kuantum kontrol problemlerine benzer. Bir tf.keras.Model içindeki tfq.layers.ControlledPQC (Parametreli Kuantum Devresi) katmanını kullanan bir kuantum-klasik hesaplamanın uçtan uca bir örneğini gösterir.
Bu öğreticinin uygulanması için bu mimari 3 bölüme ayrılmıştır:
- Giriş devresi veya veri noktası devresi : İlk üç \(R\) kapısı.
- Kontrollü devre : Diğer üç \(R\) kapısı.
- Kontrolör : Kontrol edilen devrenin parametrelerini ayarlayan klasik sinir ağı.
2.1 Kontrollü devre tanımı
Yukarıdaki şekilde gösterildiği gibi, öğrenilebilir bir tek bit dönüşü tanımlayın. Bu bizim kontrollü devremize karşılık gelecektir.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 Kontrolör
Şimdi denetleyici ağını tanımlayın:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Bir grup komut verildiğinde, kontrolör, kontrol edilen devre için bir grup kontrol sinyali verir.
Denetleyici rastgele başlatılır, bu nedenle bu çıkışlar henüz kullanışlı değildir.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Kontrolörü devreye bağlayın
Denetleyiciyi kontrollü devreye tek bir keras.Model olarak bağlamak için tfq kullanın.
Bu model tanımı stili hakkında daha fazla bilgi için Keras İşlevsel API kılavuzuna bakın.
İlk önce modele girdileri tanımlayın:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Ardından, hesaplamayı tanımlamak için işlemleri bu girdilere uygulayın.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Şimdi bu hesaplamayı bir tf.keras.Model olarak paketleyin:
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
Ağ mimarisi, aşağıdaki modelin çizimi ile belirtilmiştir. Doğruluğu doğrulamak için bu model grafiğini mimari diyagramla karşılaştırın.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
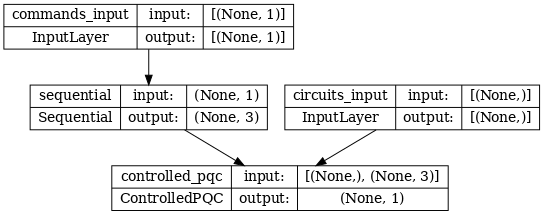
Bu model iki girdi alır: Denetleyici için komutlar ve denetleyicinin çıkışını düzeltmeye çalıştığı giriş devresi.
2.4 Veri seti
Model, her komut için \(\hat{Z}\) doğru ölçüm değerini çıkarmaya çalışır. Komutlar ve doğru değerler aşağıda tanımlanmıştır.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Bu, bu görev için tüm eğitim veri kümesi değildir. Veri kümesindeki her veri noktasının ayrıca bir giriş devresine ihtiyacı vardır.
2.4 Giriş devresi tanımı
Aşağıdaki giriş devresi, modelin düzeltmeyi öğreneceği rastgele yanlış kalibrasyonu tanımlar.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Her veri noktası için bir tane olmak üzere devrenin iki kopyası vardır.
datapoint_circuits.shape
TensorShape([2])
2.5 Eğitim
Tanımlanan girişlerle tfq modelini test edebilirsiniz.
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Şimdi bu değerleri expected_outputs göre ayarlamak için standart bir eğitim süreci çalıştırın.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
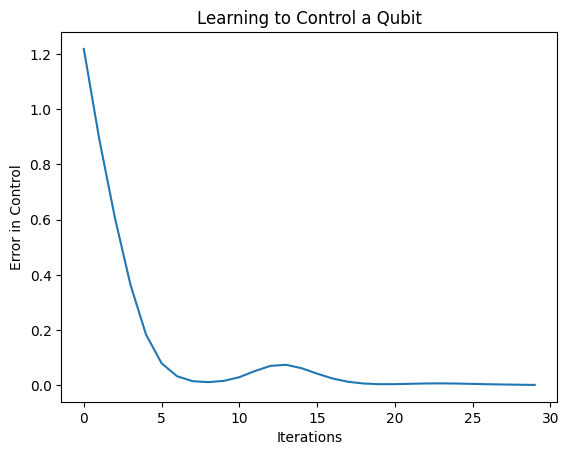
Bu çizimden, sinir ağının sistematik yanlış kalibrasyonun üstesinden gelmeyi öğrendiğini görebilirsiniz.
2.6 Çıkışları doğrulama
Şimdi, qubit kalibrasyon hatalarını düzeltmek için eğitilmiş modeli kullanın. Cirq ile:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
Eğitim sırasında kayıp fonksiyonunun değeri, modelin ne kadar iyi öğrendiği hakkında kabaca bir fikir sağlar. Kayıp ne kadar düşükse, yukarıdaki hücredeki beklenti değerleri desired_values o kadar yakındır. Parametre değerleriyle ilgilenmiyorsanız, çıktıları her zaman tfq kullanarak yukarıdan kontrol edebilirsiniz:
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Farklı operatörlerin öz durumlarını hazırlamayı öğrenme
1 ve 0'a karşılık gelen \(\pm \hat{Z}\) tutucu9 özdurumlarının seçimi keyfiydi. 1'in \(+ \hat{Z}\) \(-\hat{X}\) özdurumuna karşılık gelmesini aynı kolaylıkla isteyebilirsiniz. Bunu başarmanın bir yolu, aşağıdaki şekilde gösterildiği gibi her komut için farklı bir ölçüm operatörü belirlemektir:
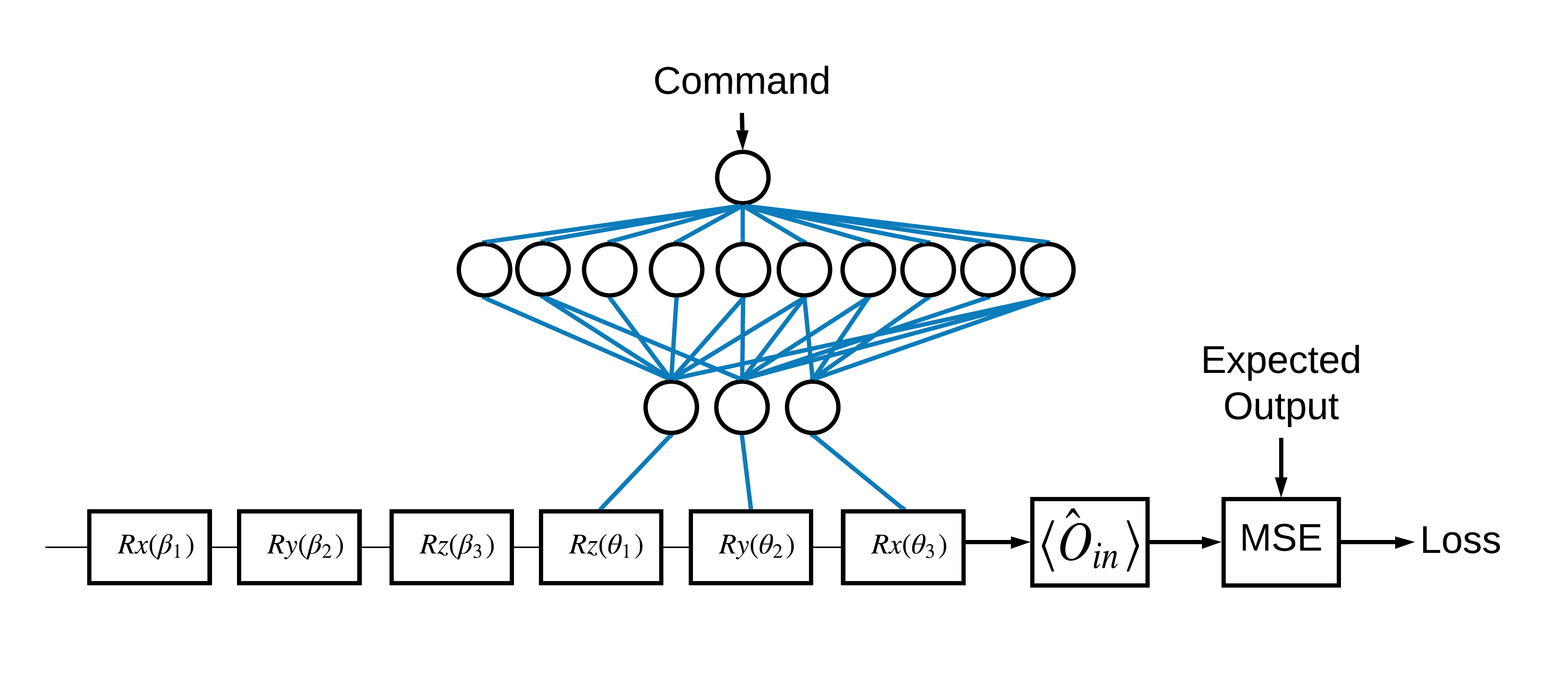
Bu, tfq.layers.Expectation kullanımını gerektirir. Artık girdiniz üç nesne içerecek şekilde büyüdü: devre, komut ve operatör. Çıktı hala beklenti değeridir.
3.1 Yeni model tanımı
Bu görevi gerçekleştirmek için modele bir göz atalım:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
İşte denetleyici ağı:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Devreyi ve denetleyiciyi tek bir keras.Model kullanarak tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 Veri seti
Şimdi model_circuit için sağladığınız her veri noktası için ölçmek istediğiniz operatörleri de dahil edeceksiniz:
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Eğitim
Artık yeni girdilerinize ve çıktılarınıza sahip olduğunuza göre, keraları kullanarak bir kez daha antrenman yapabilirsiniz.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024-yer tutucu61 l10n-yer
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
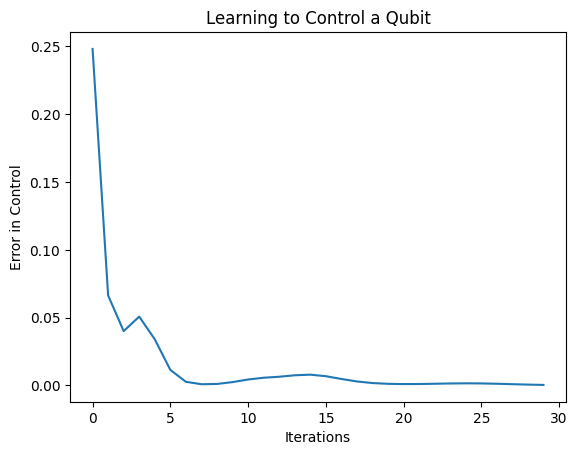
Kayıp fonksiyonu sıfıra düştü.
controller bağımsız bir model olarak mevcuttur. Kontrol cihazını arayın ve her bir komut sinyaline verdiği yanıtı kontrol edin. Bu çıktıları random_rotations içeriğiyle doğru bir şekilde karşılaştırmak biraz çalışma gerektirecektir.
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
