 Veja no TensorFlow.org Veja no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Este tutorial mostra como uma rede neural clássica pode aprender a corrigir erros de calibração de qubit. Ele apresenta o Cirq , uma estrutura Python para criar, editar e invocar circuitos Noisy Intermediate Scale Quantum (NISQ) e demonstra como o Cirq faz interface com o TensorFlow Quantum.
Configurar
pip install tensorflow==2.7.0
Instale o TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Agora importe o TensorFlow e as dependências do módulo:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. O básico
1.1 Cirq e circuitos quânticos parametrizados
Antes de explorar o TensorFlow Quantum (TFQ), vejamos alguns conceitos básicos do Cirq . Cirq é uma biblioteca Python para computação quântica do Google. Você o usa para definir circuitos, incluindo portas estáticas e parametrizadas.
O Cirq usa símbolos SymPy para representar parâmetros livres.
a, b = sympy.symbols('a b')
O código a seguir cria um circuito de dois qubits usando seus parâmetros:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Para avaliar circuitos, você pode usar a interface cirq.Simulator . Você substitui parâmetros livres em um circuito por números específicos passando um objeto cirq.ParamResolver . O código a seguir calcula a saída do vetor de estado bruto do seu circuito parametrizado:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Os vetores de estado não são diretamente acessíveis fora da simulação (observe os números complexos na saída acima). Para ser fisicamente realista, você deve especificar uma medida, que converte um vetor de estado em um número real que os computadores clássicos possam entender. Cirq especifica medições usando combinações dos operadores de Pauli \(\hat{X}\), \(\hat{Y}\)e \(\hat{Z}\). Como ilustração, o código a seguir mede \(\hat{Z}_0\) e \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) no vetor de estado que você acabou de simular:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 Circuitos quânticos como tensores
O TensorFlow Quantum (TFQ) fornece tfq.convert_to_tensor , uma função que converte objetos Cirq em tensores. Isso permite que você envie objetos Cirq para nossas camadas quânticas e operações quânticas . A função pode ser chamada em listas ou arrays de Cirq Circuits e Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Isso codifica os objetos Cirq como tensores tf.string que as operações tfq decodificam conforme necessário.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Simulação de circuito de batelada
O TFQ fornece métodos para calcular valores esperados, amostras e vetores de estado. Por enquanto, vamos nos concentrar nos valores esperados .
A interface de nível mais alto para calcular os valores esperados é a camada tfq.layers.Expectation , que é uma tf.keras.Layer . Na sua forma mais simples, esta camada é equivalente a simular um circuito parametrizado sobre muitos cirq.ParamResolvers ; no entanto, o TFQ permite lotes seguindo a semântica do TensorFlow e os circuitos são simulados usando código C++ eficiente.
Crie um lote de valores para substituir nossos parâmetros a e b :
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
A execução do circuito em lote sobre valores de parâmetro no Cirq requer um loop:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
A mesma operação é simplificada no TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Otimização clássica quântica híbrida
Agora que você viu o básico, vamos usar o TensorFlow Quantum para construir uma rede neural quântica clássica híbrida . Você treinará uma rede neural clássica para controlar um único qubit. O controle será otimizado para preparar corretamente o qubit no estado 0 ou 1 , superando um erro sistemático de calibração simulado. Esta figura mostra a arquitetura:
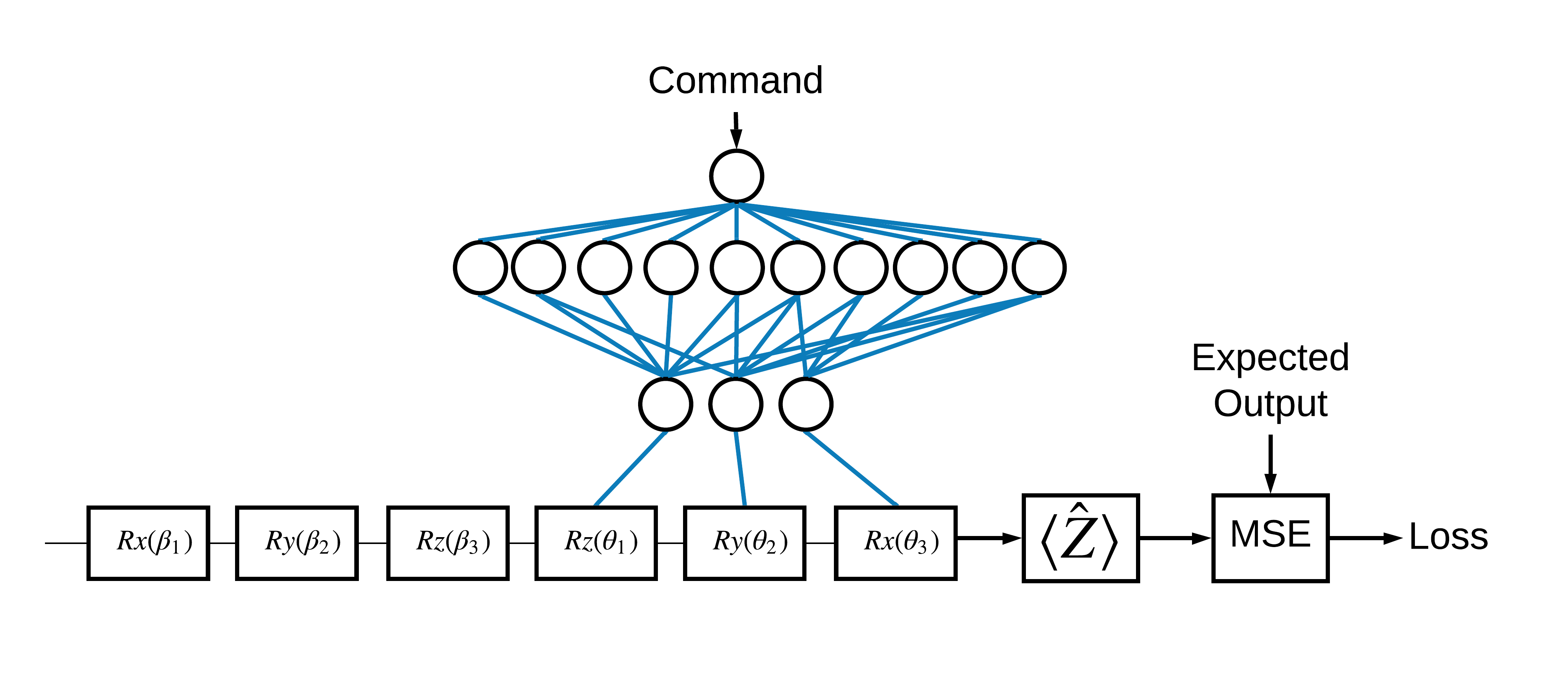
Mesmo sem uma rede neural, esse é um problema simples de resolver, mas o tema é semelhante aos problemas reais de controle quântico que você pode resolver usando o TFQ. Ele demonstra um exemplo de ponta a ponta de uma computação quântica clássica usando a tfq.layers.ControlledPQC (Parametrized Quantum Circuit) dentro de um tf.keras.Model .
Para a implementação deste tutorial, esta arquitetura é dividida em 3 partes:
- O circuito de entrada ou circuito de ponto de dados: As três primeiras portas \(R\) .
- O circuito controlado : As outras três portas \(R\) .
- O controlador : A rede neural clássica que define os parâmetros do circuito controlado.
2.1 A definição do circuito controlado
Defina uma rotação de bit único que pode ser aprendida, conforme indicado na figura acima. Isso corresponderá ao nosso circuito controlado.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 O controlador
Agora defina a rede do controlador:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Dado um lote de comandos, o controlador emite um lote de sinais de controle para o circuito controlado.
O controlador é inicializado aleatoriamente, portanto, essas saídas ainda não são úteis.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Conecte o controlador ao circuito
Use tfq para conectar o controlador ao circuito controlado, como um único keras.Model .
Consulte o guia Keras Functional API para saber mais sobre esse estilo de definição de modelo.
Primeiro defina as entradas para o modelo:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Em seguida, aplique as operações a essas entradas para definir a computação.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Agora empacote este cálculo como um tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
A arquitetura da rede é indicada pelo gráfico do modelo abaixo. Compare este gráfico de modelo com o diagrama de arquitetura para verificar a exatidão.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
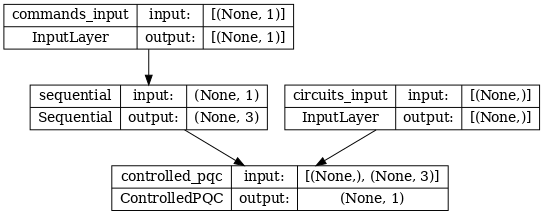
Este modelo recebe duas entradas: os comandos para o controlador e o circuito de entrada cuja saída o controlador está tentando corrigir.
2.4 O conjunto de dados
O modelo tenta gerar o valor de medição correto correto de \(\hat{Z}\) para cada comando. Os comandos e valores corretos são definidos abaixo.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Este não é todo o conjunto de dados de treinamento para esta tarefa. Cada ponto de dados no conjunto de dados também precisa de um circuito de entrada.
2.4 Definição do circuito de entrada
O circuito de entrada abaixo define o erro de calibração aleatório que o modelo aprenderá a corrigir.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Existem duas cópias do circuito, uma para cada ponto de dados.
datapoint_circuits.shape
TensorShape([2])
2.5 Treinamento
Com as entradas definidas, você pode testar o modelo tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Agora execute um processo de treinamento padrão para ajustar esses valores para as expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
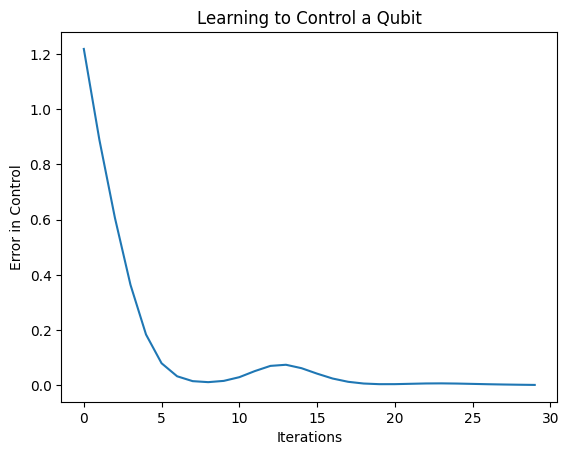
A partir desse gráfico, você pode ver que a rede neural aprendeu a superar o erro de calibração sistemático.
2.6 Verifique as saídas
Agora use o modelo treinado, para corrigir os erros de calibração do qubit. Com Cirq:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
O valor da função de perda durante o treinamento fornece uma ideia aproximada de quão bem o modelo está aprendendo. Quanto menor a perda, mais próximos os valores esperados na célula acima estarão dos desired_values . Se você não estiver tão preocupado com os valores dos parâmetros, sempre poderá verificar as saídas acima usando tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Aprendendo a preparar autoestados de diferentes operadores
A escolha dos \(\pm \hat{Z}\) correspondentes a 1 e 0 foi arbitrária. Você poderia facilmente querer que 1 correspondesse ao \(+ \hat{Z}\) e 0 correspondesse ao \(-\hat{X}\) . Uma maneira de fazer isso é especificando um operador de medição diferente para cada comando, conforme indicado na figura abaixo:
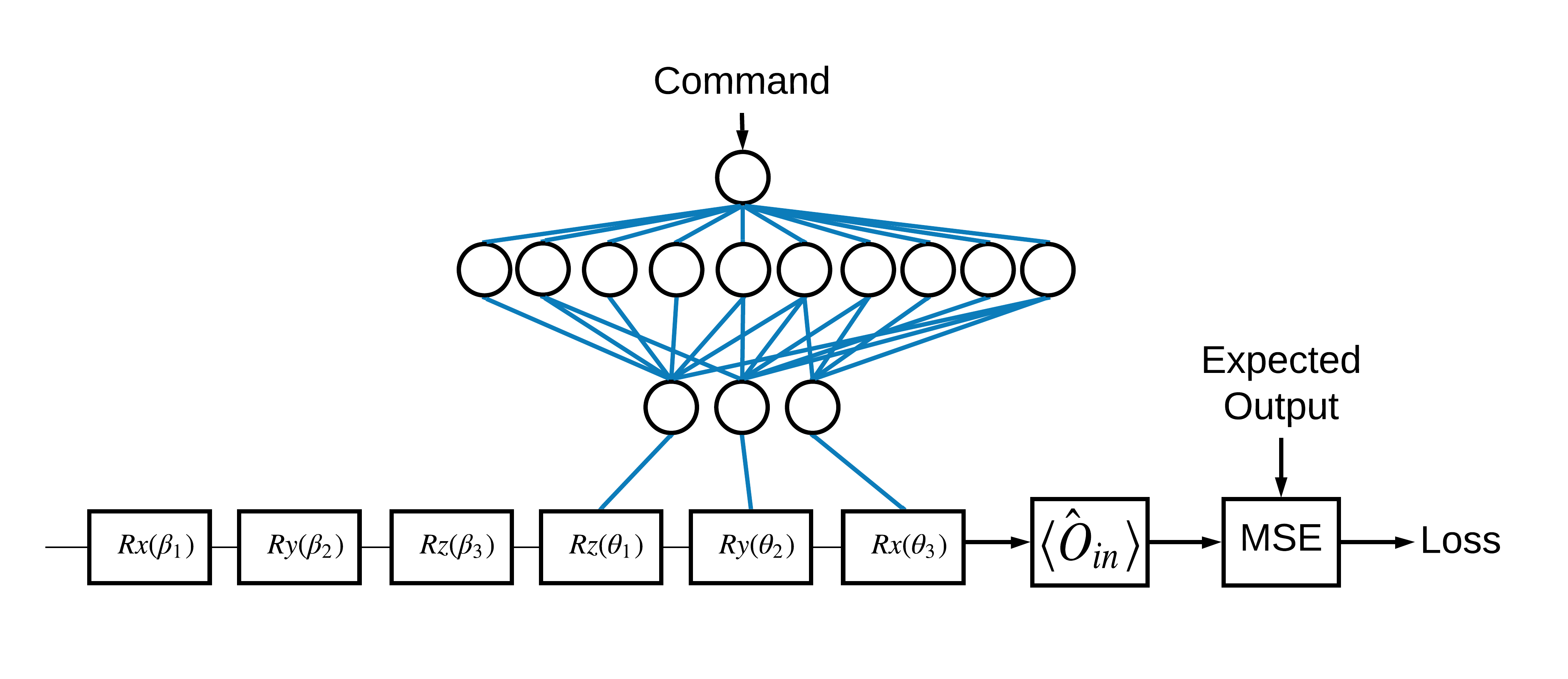
Isso requer o uso de tfq.layers.Expectation . Agora sua entrada cresceu para incluir três objetos: circuito, comando e operador. A saída ainda é o valor esperado.
3.1 Nova definição de modelo
Vamos dar uma olhada no modelo para realizar esta tarefa:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Aqui está a rede do controlador:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Combine o circuito e o controlador em um único keras.Model usando tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 O conjunto de dados
Agora você também incluirá os operadores que deseja medir para cada ponto de dados fornecido para model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Treinamento
Agora que você tem suas novas entradas e saídas, você pode treinar novamente usando keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
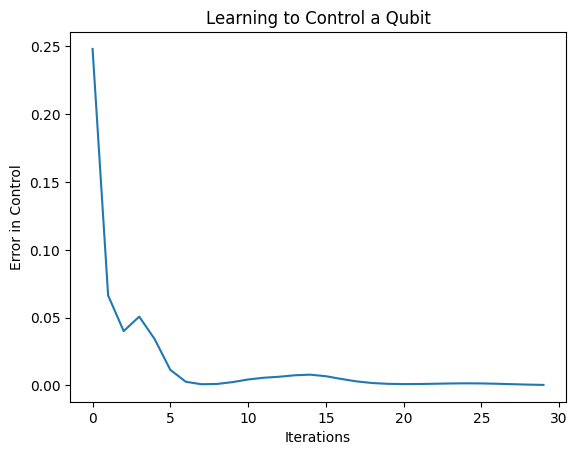
A função de perda caiu para zero.
O controller está disponível como um modelo autônomo. Chame o controlador e verifique sua resposta a cada sinal de comando. Levaria algum trabalho para comparar corretamente essas saídas com o conteúdo de random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
