 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Ce tutoriel montre comment un réseau de neurones classique peut apprendre à corriger les erreurs d'étalonnage des qubits. Il présente Cirq , un framework Python pour créer, modifier et invoquer des circuits Noisy Intermediate Scale Quantum (NISQ), et montre comment Cirq s'interface avec TensorFlow Quantum.
Installer
pip install tensorflow==2.7.0
Installez TensorFlow Quantum :
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Importez maintenant TensorFlow et les dépendances du module :
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Les bases
1.1 Cirq et circuits quantiques paramétrés
Avant d'explorer TensorFlow Quantum (TFQ), examinons quelques principes de base de Cirq . Cirq est une bibliothèque Python pour l'informatique quantique de Google. Vous l'utilisez pour définir des circuits, y compris des portes statiques et paramétrées.
Cirq utilise les symboles SymPy pour représenter les paramètres libres.
a, b = sympy.symbols('a b')
Le code suivant crée un circuit à deux qubits à l'aide de vos paramètres :
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Pour évaluer les circuits, vous pouvez utiliser l'interface cirq.Simulator . Vous remplacez les paramètres libres dans un circuit par des nombres spécifiques en transmettant un objet cirq.ParamResolver . Le code suivant calcule la sortie du vecteur d'état brut de votre circuit paramétré :
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Les vecteurs d'état ne sont pas directement accessibles en dehors de la simulation (notez les nombres complexes dans la sortie ci-dessus). Pour être physiquement réaliste, vous devez spécifier une mesure, qui convertit un vecteur d'état en un nombre réel que les ordinateurs classiques peuvent comprendre. Cirq spécifie les mesures en utilisant des combinaisons des opérateurs Pauli \(\hat{X}\), \(\hat{Y}\)et \(\hat{Z}\). A titre d'illustration, le code suivant mesure \(\hat{Z}_0\) et \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) sur le vecteur d'état que vous venez de simuler :
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 Circuits quantiques comme tenseurs
TensorFlow Quantum (TFQ) fournit tfq.convert_to_tensor , une fonction qui convertit les objets Cirq en tenseurs. Cela vous permet d'envoyer des objets Cirq à nos couches quantiques et opérations quantiques . La fonction peut être appelée sur des listes ou tableaux de Cirq Circuits et Cirq Paulis :
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Cela encode les objets Cirq en tant que tenseurs tf.string que les opérations tfq décodent selon les besoins.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Simulation du circuit de dosage
TFQ fournit des méthodes pour calculer les valeurs d'attente, les échantillons et les vecteurs d'état. Pour l'instant, concentrons-nous sur les valeurs d'attente .
L'interface de plus haut niveau pour le calcul des valeurs d'attente est la couche tfq.layers.Expectation , qui est un tf.keras.Layer . Dans sa forme la plus simple, cette couche équivaut à simuler un circuit paramétré sur plusieurs cirq.ParamResolvers ; cependant, TFQ permet le traitement par lots suivant la sémantique TensorFlow, et les circuits sont simulés à l'aide d'un code C++ efficace.
Créez un lot de valeurs pour remplacer nos paramètres a et b :
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
L'exécution du circuit par lots sur les valeurs des paramètres dans Cirq nécessite une boucle :
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
La même opération est simplifiée dans TFQ :
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Optimisation hybride quantique-classique
Maintenant que vous avez vu les bases, utilisons TensorFlow Quantum pour construire un réseau neuronal hybride quantique-classique . Vous entraînerez un réseau de neurones classique pour contrôler un seul qubit. Le contrôle sera optimisé pour préparer correctement le qubit à l'état 0 ou 1 , en surmontant une erreur d'étalonnage systématique simulée. Cette figure montre l'architecture :
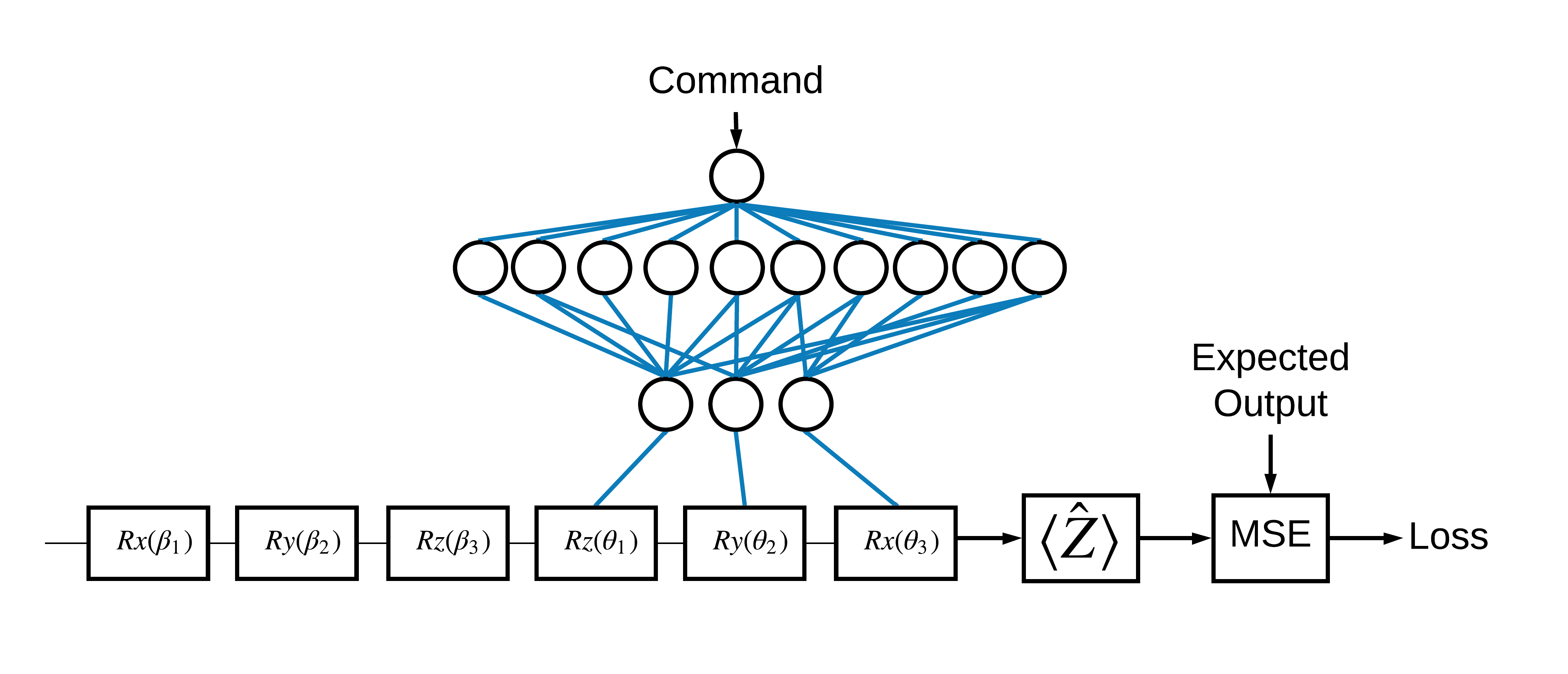
Même sans réseau de neurones, il s'agit d'un problème simple à résoudre, mais le thème est similaire aux vrais problèmes de contrôle quantique que vous pourriez résoudre à l'aide de TFQ. Il illustre un exemple de bout en bout d'un calcul classique quantique utilisant la tfq.layers.ControlledPQC (Circuit Quantique Paramétré) à l'intérieur d'un tf.keras.Model .
Pour la mise en place de ce tutoriel, cette architecture est découpée en 3 parties :
- Le circuit d'entrée ou circuit de point de données : Les trois premières portes \(R\) .
- Le circuit contrôlé : Les trois autres portes \(R\) .
- Le contrôleur : Le réseau de neurones classique définissant les paramètres du circuit contrôlé.
2.1 La définition du circuit commandé
Définissez une rotation de bit unique apprenable, comme indiqué dans la figure ci-dessus. Cela correspondra à notre circuit contrôlé.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 Le contrôleur
Définissez maintenant le réseau du contrôleur :
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Étant donné un lot de commandes, le contrôleur délivre un lot de signaux de commande pour le circuit commandé.
Le contrôleur est initialisé de manière aléatoire, de sorte que ces sorties ne sont pas encore utiles.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Connecter le contrôleur au circuit
Utilisez tfq pour connecter le contrôleur au circuit contrôlé, comme un seul keras.Model .
Consultez le guide de l'API fonctionnelle Keras pour en savoir plus sur ce style de définition de modèle.
Définissez d'abord les entrées du modèle :
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Appliquez ensuite des opérations à ces entrées pour définir le calcul.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Maintenant, empaquetez ce calcul en tant que tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
L'architecture du réseau est indiquée par le tracé du modèle ci-dessous. Comparez ce tracé de modèle au diagramme d'architecture pour vérifier l'exactitude.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
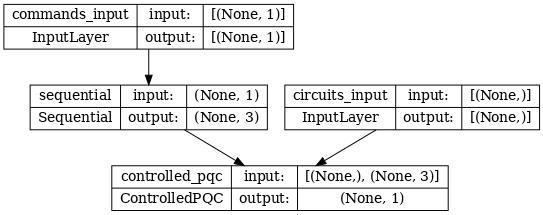
Ce modèle prend deux entrées : les commandes pour le contrôleur et le circuit d'entrée dont la sortie le contrôleur tente de corriger.
2.4 Le jeu de données
Le modèle tente de générer la valeur de mesure correcte correcte de \(\hat{Z}\) pour chaque commande. Les commandes et les valeurs correctes sont définies ci-dessous.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Il ne s'agit pas de l'intégralité de l'ensemble de données d'entraînement pour cette tâche. Chaque point de données du jeu de données nécessite également un circuit d'entrée.
2.4 Définition du circuit d'entrée
Le circuit d'entrée ci-dessous définit le défaut d'étalonnage aléatoire que le modèle apprendra à corriger.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Il existe deux copies du circuit, une pour chaque point de données.
datapoint_circuits.shape
TensorShape([2])
2.5 Formation
Avec les entrées définies, vous pouvez tester le modèle tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Exécutez maintenant un processus de formation standard pour ajuster ces valeurs vers les expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
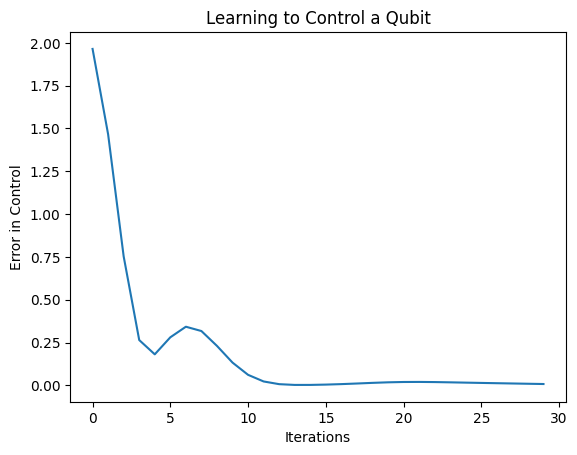
À partir de ce graphique, vous pouvez voir que le réseau de neurones a appris à surmonter le mauvais calibrage systématique.
2.6 Vérifier les sorties
Utilisez maintenant le modèle entraîné pour corriger les erreurs d'étalonnage du qubit. Avec Cirq :
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
La valeur de la fonction de perte pendant la formation donne une idée approximative de la qualité de l'apprentissage du modèle. Plus la perte est faible, plus les valeurs attendues dans la cellule ci-dessus sont proches des desired_values . Si vous n'êtes pas aussi concerné par les valeurs des paramètres, vous pouvez toujours vérifier les sorties ci-dessus en utilisant tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Apprendre à préparer les états propres de différents opérateurs
Le choix des états propres \(\pm \hat{Z}\) correspondant à 1 et 0 était arbitraire. Vous auriez tout aussi bien pu vouloir que 1 corresponde à l'état propre \(+ \hat{Z}\) et 0 corresponde à l'état propre \(-\hat{X}\) . Une façon d'y parvenir consiste à spécifier un opérateur de mesure différent pour chaque commande, comme indiqué dans la figure ci-dessous :
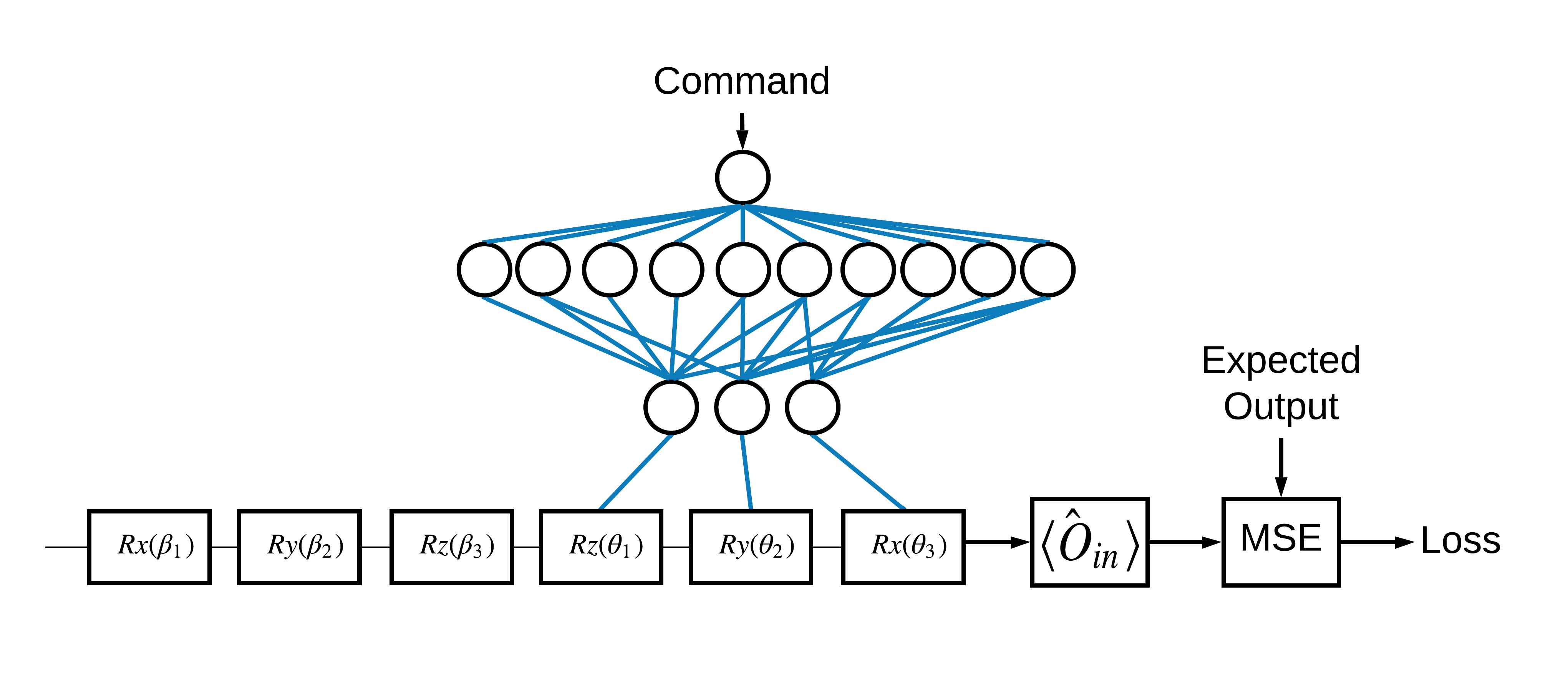
Cela nécessite l'utilisation de tfq.layers.Expectation . Maintenant, votre entrée s'est développée pour inclure trois objets : circuit, commande et opérateur. La sortie est toujours la valeur attendue.
3.1 Nouvelle définition de modèle
Jetons un coup d'œil au modèle pour accomplir cette tâche :
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Voici le réseau du contrôleur :
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Combinez le circuit et le contrôleur en un seul keras.Model utilisant tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 Le jeu de données
Maintenant, vous allez également inclure les opérateurs que vous souhaitez mesurer pour chaque point de données que vous fournissez pour model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Formation
Maintenant que vous avez vos nouvelles entrées et sorties, vous pouvez à nouveau vous entraîner à l'aide de keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
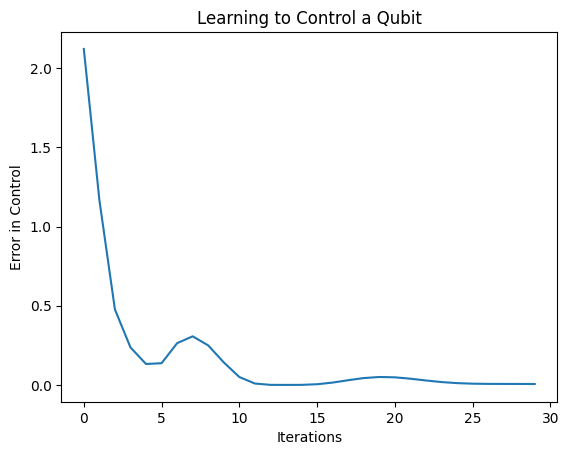
La fonction de perte est tombée à zéro.
Le controller est disponible en tant que modèle autonome. Appelez le contrôleur et vérifiez sa réponse à chaque signal de commande. Il faudrait du travail pour comparer correctement ces sorties au contenu de random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
