 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Ten samouczek pokazuje, jak klasyczna sieć neuronowa może nauczyć się poprawiać błędy kalibracji kubitów. Wprowadza Cirq , framework Pythona do tworzenia, edytowania i wywoływania obwodów Noisy Intermediate Scale Quantum (NISQ) i demonstruje, jak Cirq współpracuje z TensorFlow Quantum.
Ustawiać
pip install tensorflow==2.7.0
Zainstaluj TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Teraz zaimportuj TensorFlow i zależności modułu:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Podstawy
1.1 Cirq i sparametryzowane obwody kwantowe
Przed zapoznaniem się z TensorFlow Quantum (TFQ), przyjrzyjmy się podstawom Cirq . Cirq to biblioteka Pythona do obliczeń kwantowych od Google. Używasz go do definiowania obwodów, w tym bramek statycznych i sparametryzowanych.
Cirq używa symboli SymPy do reprezentowania wolnych parametrów.
a, b = sympy.symbols('a b')
Poniższy kod tworzy obwód z dwoma kubitami przy użyciu twoich parametrów:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Do oceny obwodów możesz użyć interfejsu cirq.Simulator . Wolne parametry w obwodzie można zastąpić określonymi liczbami, przekazując obiekt cirq.ParamResolver . Poniższy kod oblicza wyjściowy wektor stanu surowego twojego sparametryzowanego obwodu:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Wektory stanu nie są bezpośrednio dostępne poza symulacją (zwróć uwagę na liczby zespolone w powyższym wyniku). Aby być fizycznie realistycznym, musisz określić pomiar, który konwertuje wektor stanu na liczbę rzeczywistą, zrozumiałą dla klasycznych komputerów. Cirq określa pomiary przy użyciu kombinacji operatorów Pauliego \(\hat{X}\), \(\hat{Y}\)i \(\hat{Z}\). Na przykład poniższy kod mierzy \(\hat{Z}_0\) i \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) na wektorze stanu, który właśnie symulowałeś:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 Obwody kwantowe jako tensory
TensorFlow Quantum (TFQ) udostępnia tfq.convert_to_tensor , funkcję, która konwertuje obiekty Cirq na tensory. Pozwala to na wysyłanie obiektów Cirq do naszych warstw kwantowych i operacji kwantowych . Funkcję można wywołać na listach lub tablicach Cirq Circuits i Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
To koduje obiekty Cirq jako tensory tf.string , które w razie potrzeby dekodują operacje tfq .
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Symulacja obwodu dozowania
TFQ zapewnia metody obliczania wartości oczekiwanych, próbek i wektorów stanu. Na razie skupmy się na wartościach oczekiwanych .
Interfejsem najwyższego poziomu do obliczania wartości oczekiwanych jest warstwa tfq.layers.Expectation , która jest tf.keras.Layer . W najprostszej postaci ta warstwa jest równoważna symulacji sparametryzowanego obwodu przez wiele cirq.ParamResolvers ; jednak TFQ umożliwia grupowanie zgodnie z semantyką TensorFlow, a obwody są symulowane przy użyciu wydajnego kodu C++.
Utwórz grupę wartości, które zastąpią nasze parametry a i b :
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
Wsadowe wykonanie obwodu powyżej wartości parametrów w Cirq wymaga pętli:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
Ta sama operacja jest uproszczona w TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Hybrydowa optymalizacja kwantowo-klasyczna
Teraz, gdy znasz już podstawy, użyjmy TensorFlow Quantum do skonstruowania hybrydowej kwantowo-klasycznej sieci neuronowej . Wytrenujesz klasyczną sieć neuronową do sterowania pojedynczym kubitem. Kontrolka zostanie zoptymalizowana, aby poprawnie przygotować kubit w stanie 0 lub 1 , pokonując symulowany systematyczny błąd kalibracji. Ten rysunek przedstawia architekturę:
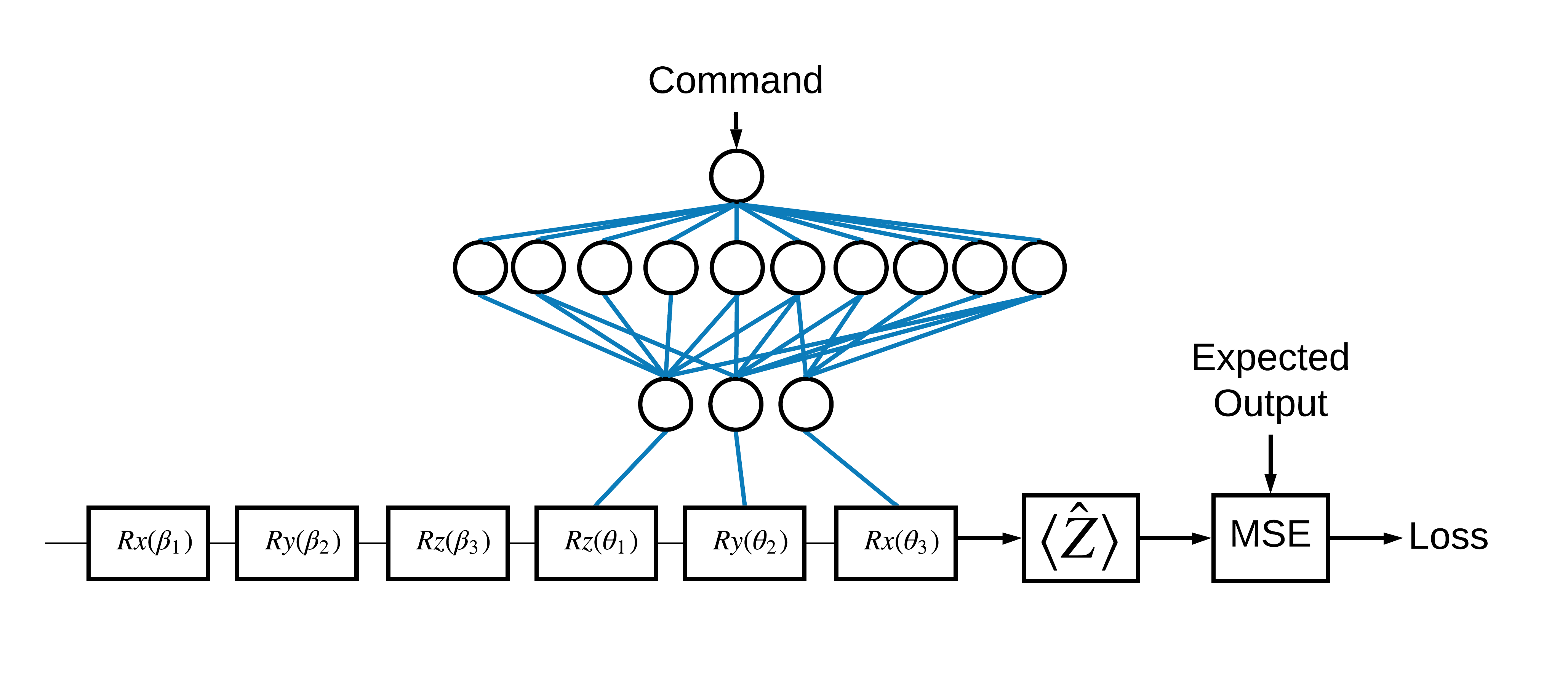
Nawet bez sieci neuronowej jest to prosty problem do rozwiązania, ale temat jest podobny do rzeczywistych problemów z kontrolą kwantową, które można rozwiązać za pomocą TFQ. Pokazuje kompleksowy przykład kwantowo-klasycznych obliczeń przy użyciu tfq.layers.ControlledPQC (Parametrized Quantum Circuit) wewnątrz tf.keras.Model .
W celu wdrożenia tego samouczka ta architektura jest podzielona na 3 części:
- Obwód wejściowy lub obwód punktu danych : Pierwsze trzy bramki \(R\) .
- Obwód kontrolowany : Pozostałe trzy bramki \(R\) .
- Sterownik : Klasyczna sieć neuronowa ustawiająca parametry sterowanego obwodu.
2.1 Definicja obwodu kontrolowanego
Zdefiniuj możliwą do nauki rotację pojedynczego bitu, jak pokazano na powyższym rysunku. To będzie odpowiadało naszemu sterowanemu obwodowi.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 Kontroler
Teraz zdefiniuj sieć kontrolera:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Po otrzymaniu partii poleceń sterownik wyprowadza partię sygnałów sterujących dla sterowanego obwodu.
Kontroler jest inicjowany losowo, więc te wyjścia nie są jeszcze przydatne.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Podłącz sterownik do obwodu
Za pomocą tfq podłączyć sterownik do sterowanego obwodu, jako pojedynczy keras.Model .
Więcej informacji na temat tego stylu definicji modelu można znaleźć w przewodniku Keras Functional API .
Najpierw zdefiniuj dane wejściowe do modelu:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Następnie zastosuj operacje do tych danych wejściowych, aby zdefiniować obliczenia.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Teraz spakuj to obliczenie jako tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
Architekturę sieci wskazuje poniższy wykres modelu. Porównaj ten wykres modelu z diagramem architektury, aby zweryfikować poprawność.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
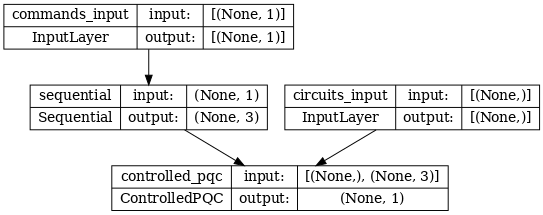
Ten model przyjmuje dwa wejścia: polecenia dla kontrolera i obwód wejściowy, którego wyjście kontroler próbuje skorygować.
2.4 Zbiór danych
Model próbuje wyprowadzić poprawną poprawną wartość pomiaru \(\hat{Z}\) dla każdego polecenia. Polecenia i prawidłowe wartości są zdefiniowane poniżej.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
To nie jest cały zestaw danych treningowych dla tego zadania. Każdy punkt danych w zestawie danych wymaga również obwodu wejściowego.
2.4 Definicja obwodu wejściowego
Poniższy obwód wejściowy definiuje losową błędną kalibrację, którą model nauczy się poprawiać.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Istnieją dwie kopie obwodu, po jednej dla każdego punktu danych.
datapoint_circuits.shape
TensorShape([2])
2.5 Trening
Po zdefiniowaniu danych wejściowych można przetestować model tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Teraz uruchom standardowy proces uczenia, aby dostosować te wartości do wartości expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
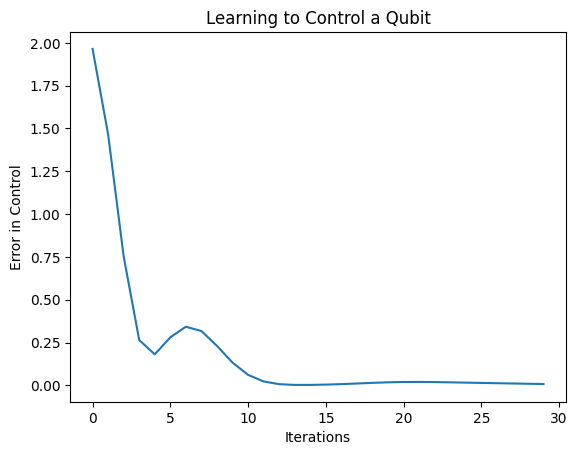
Z tego wykresu widać, że sieć neuronowa nauczyła się przezwyciężać systematyczną błędną kalibrację.
2.6 Weryfikacja wyjść
Teraz użyj wytrenowanego modelu, aby poprawić błędy kalibracji kubitów. Z Cirq:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
Wartość funkcji straty podczas uczenia daje ogólne pojęcie o tym, jak dobrze model się uczy. Im mniejsza strata, tym wartości oczekiwane w powyższej komórce są desired_values . Jeśli nie przejmujesz się wartościami parametrów, zawsze możesz sprawdzić dane wyjściowe z góry za pomocą tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Nauka przygotowywania stanów własnych różnych operatorów
Wybór stanów własnych \(\pm \hat{Z}\) odpowiadający 1 i 0 był arbitralny. Równie dobrze mógłbyś chcieć, aby 1 odpowiadało stanowi własnemu \(+ \hat{Z}\) a 0 odpowiadało stanowi własnemu \(-\hat{X}\) . Jednym ze sposobów osiągnięcia tego jest określenie innego operatora pomiaru dla każdego polecenia, jak pokazano na poniższym rysunku:
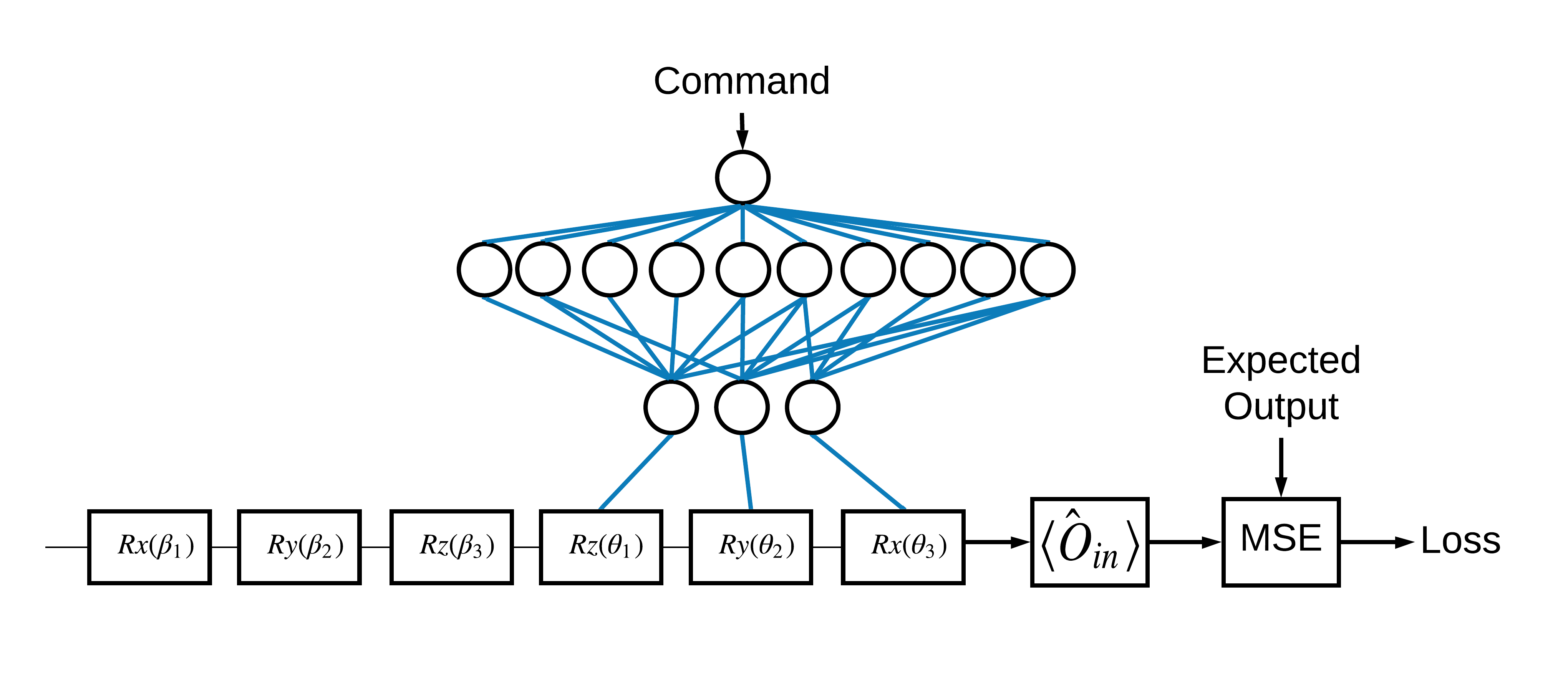
Wymaga to użycia tfq.layers.Expectation . Teraz twoje dane wejściowe urosły do trzech obiektów: obwodu, polecenia i operatora. Wynikiem jest nadal wartość oczekiwana.
3.1 Nowa definicja modelu
Rzućmy okiem na model, aby wykonać to zadanie:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Oto sieć kontrolera:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Połącz obwód i kontroler w jeden keras.Model za pomocą tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 Zbiór danych
Teraz uwzględnisz również operatory, które chcesz mierzyć dla każdego punktu danych, który dostarczasz dla model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Szkolenie
Teraz, gdy masz nowe wejścia i wyjścia, możesz ponownie trenować przy użyciu keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
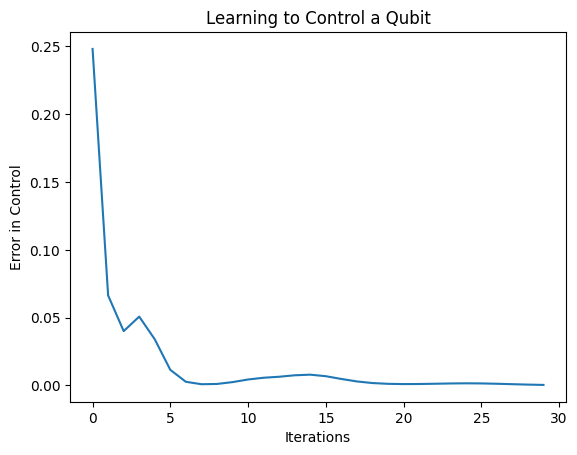
Funkcja straty spadła do zera.
controller jest dostępny jako samodzielny model. Zadzwoń do kontrolera i sprawdź jego odpowiedź na każdy sygnał polecenia. Prawidłowe porównanie tych wyników z zawartością random_rotations zajęłoby trochę pracy.
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
