 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
Questo tutorial mostra come una rete neurale classica può imparare a correggere gli errori di calibrazione dei qubit. Introduce Cirq , un framework Python per creare, modificare e invocare circuiti Noisy Intermediate Scale Quantum (NISQ) e dimostra come Cirq si interfaccia con TensorFlow Quantum.
Impostare
pip install tensorflow==2.7.0
Installa TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Ora importa TensorFlow e le dipendenze del modulo:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Le basi
1.1 Circ e circuiti quantistici parametrizzati
Prima di esplorare TensorFlow Quantum (TFQ), diamo un'occhiata ad alcune nozioni di base su Cirq . Circq è una libreria Python per l'informatica quantistica di Google. Lo usi per definire i circuiti, comprese le porte statiche e parametrizzate.
Cirq utilizza i simboli SymPy per rappresentare parametri liberi.
a, b = sympy.symbols('a b')
Il codice seguente crea un circuito a due qubit usando i tuoi parametri:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Per valutare i circuiti, è possibile utilizzare l'interfaccia cirq.Simulator . Sostituisci i parametri liberi in un circuito con numeri specifici passando un oggetto cirq.ParamResolver . Il codice seguente calcola l'uscita del vettore di stato grezzo del circuito parametrizzato:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
I vettori di stato non sono direttamente accessibili al di fuori della simulazione (notare i numeri complessi nell'output sopra). Per essere fisicamente realistici, è necessario specificare una misura, che converta un vettore di stato in un numero reale che i computer classici possono comprendere. Cirq specifica le misurazioni utilizzando le combinazioni degli operatori Pauli \(\hat{X}\), \(\hat{Y}\)e \(\hat{Z}\). A titolo illustrativo, il codice seguente misura \(\hat{Z}_0\) e \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) sul vettore di stato appena simulato:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 I circuiti quantistici come tensori
TensorFlow Quantum (TFQ) fornisce tfq.convert_to_tensor , una funzione che converte gli oggetti Cirq in tensori. Ciò ti consente di inviare oggetti Cirq ai nostri livelli quantistici e operazioni quantistiche . La funzione può essere chiamata su elenchi o array di Cirq Circuits e Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Questo codifica gli oggetti Cirq come tensori tf.string che le operazioni tfq decodificano secondo necessità.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Simulazione del circuito di dosaggio
TFQ fornisce metodi per calcolare valori di aspettativa, campioni e vettori di stato. Per ora, concentriamoci sui valori delle aspettative .
L'interfaccia di livello più alto per il calcolo dei valori di aspettativa è il livello tfq.layers.Expectation , che è un tf.keras.Layer . Nella sua forma più semplice, questo livello equivale a simulare un circuito parametrizzato su molti cirq.ParamResolvers ; tuttavia, TFQ consente il batch seguendo la semantica TensorFlow e i circuiti vengono simulati utilizzando codice C++ efficiente.
Crea un batch di valori da sostituire ai nostri a b :
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
L'esecuzione del circuito in batch sui valori dei parametri in Cirq richiede un ciclo:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
La stessa operazione è semplificata in TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Ottimizzazione ibrida quantistica-classica
Ora che hai visto le basi, usiamo TensorFlow Quantum per costruire una rete neurale ibrida quantistica-classica . Addestrerai una rete neurale classica per controllare un singolo qubit. Il controllo sarà ottimizzato per preparare correttamente il qubit nello stato 0 o 1 , superando un errore di calibrazione sistematico simulato. Questa figura mostra l'architettura:
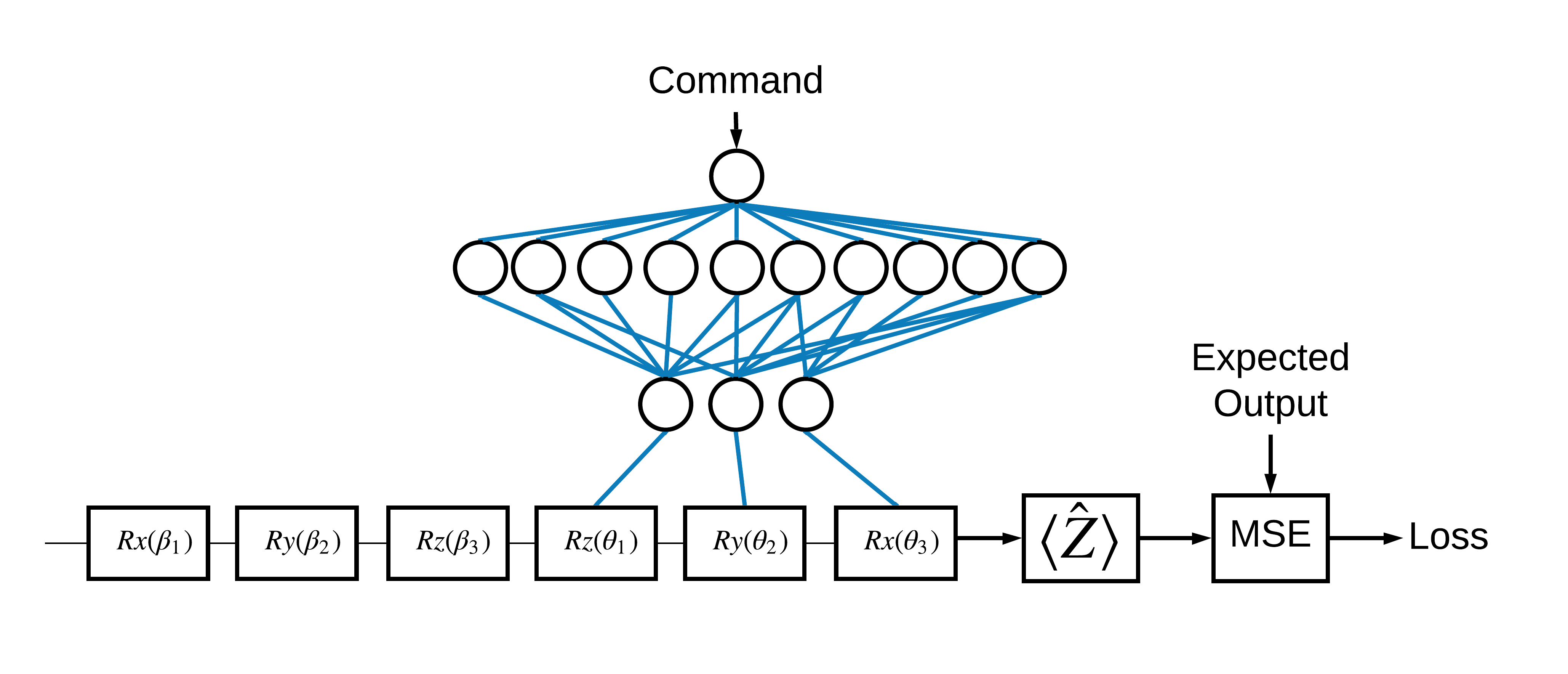
Anche senza una rete neurale questo è un problema semplice da risolvere, ma il tema è simile ai veri problemi di controllo quantistico che potresti risolvere usando TFQ. Dimostra un esempio end-to-end di un calcolo quantistico classico utilizzando il tfq.layers.ControlledPQC (Parametrized Quantum Circuit) all'interno di un tf.keras.Model .
Per l'implementazione di questo tutorial, questa architettura è divisa in 3 parti:
- Il circuito di ingresso o il circuito del punto dati: le prime tre porte \(R\) .
- Il circuito controllato : le altre tre porte \(R\) .
- Il controller : la classica rete neurale che imposta i parametri del circuito controllato.
2.1 La definizione del circuito controllato
Definire una rotazione a bit singolo apprendibile, come indicato nella figura sopra. Questo corrisponderà al nostro circuito controllato.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 Il controllore
Ora definisci la rete del controller:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Dato un batch di comandi, il controller emette un batch di segnali di controllo per il circuito controllato.
Il controller viene inizializzato in modo casuale, quindi queste uscite non sono ancora utili.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Collegare il controller al circuito
Utilizzare tfq per collegare il controller al circuito controllato, come un unico keras.Model .
Consulta la guida dell'API funzionale Keras per ulteriori informazioni su questo stile di definizione del modello.
Per prima cosa definisci gli input per il modello:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Quindi applica le operazioni a quegli input, per definire il calcolo.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Ora impacchetta questo calcolo come tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
L'architettura di rete è indicata dal grafico del modello sottostante. Confronta questo grafico modello con il diagramma dell'architettura per verificarne la correttezza.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
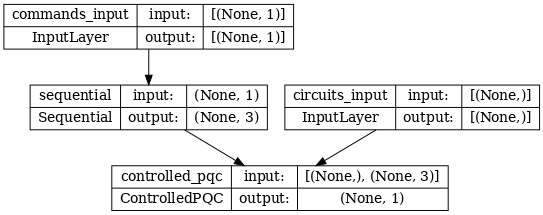
Questo modello accetta due input: i comandi per il controller e il circuito di input la cui uscita il controller sta tentando di correggere.
2.4 Il set di dati
Il modello tenta di emettere il valore di misurazione corretto corretto di \(\hat{Z}\) per ogni comando. I comandi ei valori corretti sono definiti di seguito.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Questo non è l'intero set di dati di addestramento per questa attività. Ogni punto dati nel set di dati necessita anche di un circuito di ingresso.
2.4 Definizione del circuito di ingresso
Il circuito di ingresso di seguito definisce l'errata calibrazione casuale che il modello imparerà a correggere.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Ci sono due copie del circuito, una per ogni datapoint.
datapoint_circuits.shape
TensorShape([2])
2.5 Formazione
Con gli input definiti è possibile eseguire il test del modello tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Ora esegui un processo di addestramento standard per regolare questi valori verso gli expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
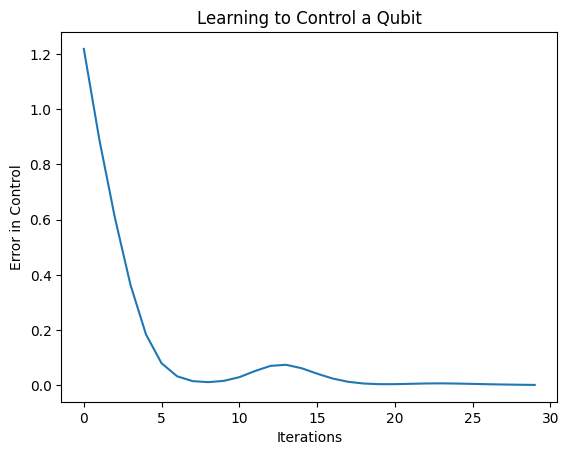
Da questa trama si può vedere che la rete neurale ha imparato a superare la sistematica errata calibrazione.
2.6 Verificare le uscite
Ora usa il modello addestrato, per correggere gli errori di calibrazione dei qubit. Con Circo:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
Il valore della funzione di perdita durante l'allenamento fornisce un'idea approssimativa di quanto bene stia imparando il modello. Minore è la perdita, più vicini sono i valori di aspettativa nella cella sopra a desired_values . Se non sei così interessato ai valori dei parametri, puoi sempre controllare gli output dall'alto usando tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Imparare a preparare autostati di diversi operatori
La scelta degli autostati \(\pm \hat{Z}\) corrispondenti a 1 e 0 era arbitraria. Avresti potuto facilmente desiderare che 1 corrispondesse all'autostato \(+ \hat{Z}\) e 0 all'autostato \(-\hat{X}\) . Un modo per ottenere ciò è specificare un operatore di misurazione diverso per ciascun comando, come indicato nella figura seguente:
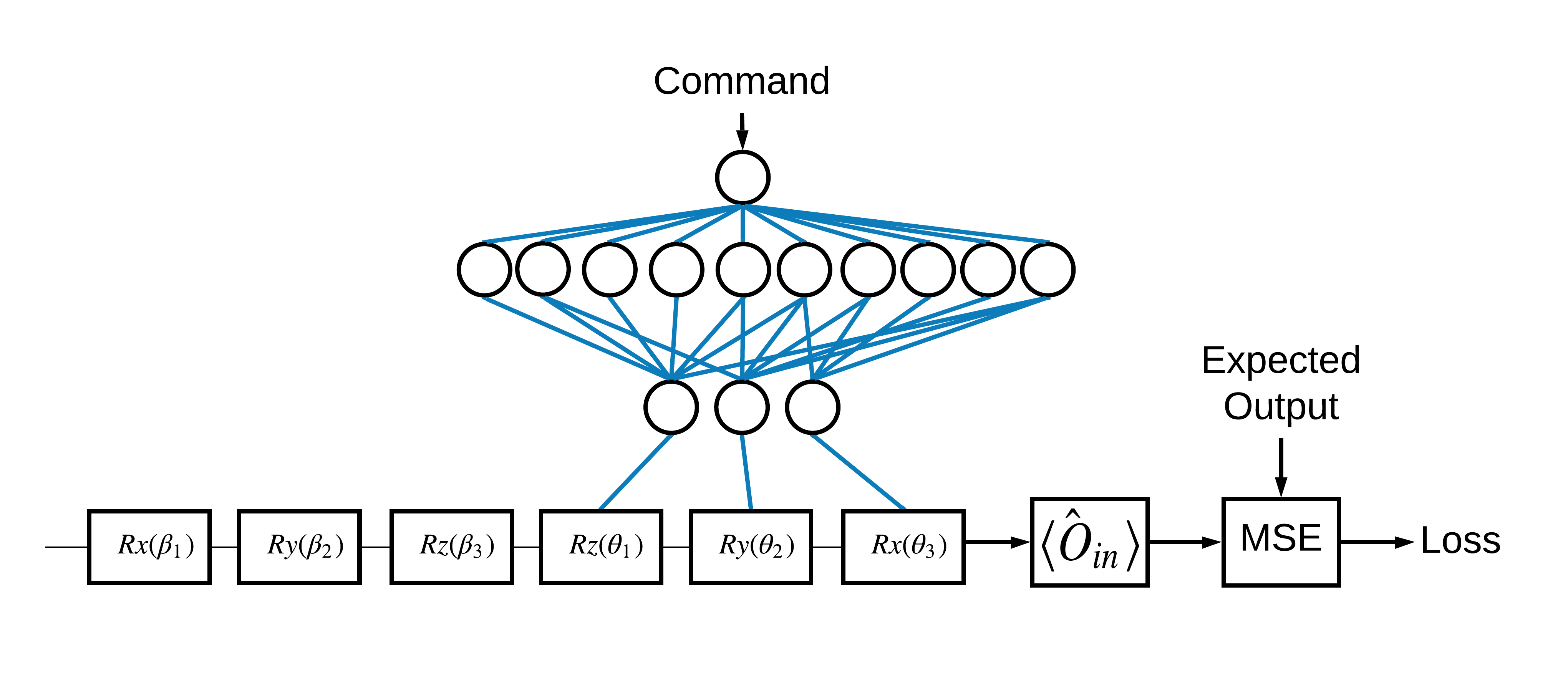
Ciò richiede l'uso di tfq.layers.Expectation . Ora il tuo input è cresciuto fino a includere tre oggetti: circuito, comando e operatore. L'output è ancora il valore atteso.
3.1 Nuova definizione del modello
Diamo un'occhiata al modello per svolgere questo compito:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Ecco la rete del controller:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Combina il circuito e il controller in un unico keras.Model usando tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 Il set di dati
Ora includerai anche gli operatori che desideri misurare per ogni punto dati fornito per model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Formazione
Ora che hai i tuoi nuovi input e output puoi allenarti ancora una volta usando keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
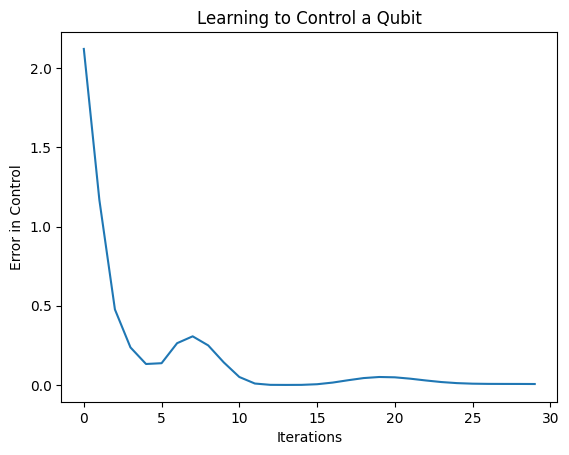
La funzione di perdita è scesa a zero.
Il controller è disponibile come modello autonomo. Chiamare il controller e verificarne la risposta a ciascun segnale di comando. Ci vorrebbe del lavoro per confrontare correttamente questi output con il contenuto di random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
