 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
يوضح هذا البرنامج التعليمي كيف يمكن للشبكة العصبية الكلاسيكية أن تتعلم كيفية تصحيح أخطاء معايرة الكيوبت. يقدم Cirq ، إطار عمل Python لإنشاء ، وتحرير ، واستدعاء دوائر Noisy Intermediate Scale Quantum (NISQ) ، ويوضح كيفية تفاعل Cirq مع TensorFlow Quantum.
يثبت
pip install tensorflow==2.7.0
تثبيت TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
الآن قم باستيراد TensorFlow وتبعيات الوحدة النمطية:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. الأساسيات
1.1 Cirq والدوائر الكمومية ذات المعلمات
قبل استكشاف TensorFlow Quantum (TFQ) ، دعنا نلقي نظرة على بعض أساسيات Cirq . Cirq هي مكتبة Python للحوسبة الكمية من Google. يمكنك استخدامه لتحديد الدوائر ، بما في ذلك البوابات الثابتة والمعاملات.
يستخدم Cirq رموز SymPy لتمثيل المعلمات المجانية.
a, b = sympy.symbols('a b')
يُنشئ الكود التالي دارة ثنائية الكيوبت باستخدام معلماتك:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
لتقييم الدوائر ، يمكنك استخدام واجهة cirq.Simulator . يمكنك استبدال المعلمات المجانية في دائرة بأرقام محددة عن طريق تمرير كائن cirq.ParamResolver . تحسب الكود التالي خرج متجه الحالة الخام لدائرتك ذات المعلمات:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
لا يمكن الوصول إلى نواقل الحالة بشكل مباشر خارج نطاق المحاكاة (لاحظ الأرقام المركبة في المخرجات أعلاه). لكي تكون واقعيًا ماديًا ، يجب عليك تحديد قياس يحول متجه الحالة إلى رقم حقيقي يمكن أن تفهمه أجهزة الكمبيوتر الكلاسيكية. تحدد Cirq القياسات باستخدام مجموعات عوامل Pauli \(\hat{X}\)و \(\hat{Y}\)و \(\hat{Z}\). كتوضيح ، يقيس الكود التالي \(\hat{Z}_0\) و \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) في متجه الحالة الذي قمت بمحاكاته للتو:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 الدوائر الكمومية كموترات
يوفر TensorFlow Quantum (TFQ) tfq.convert_to_tensor ، وهي وظيفة تحول كائنات Cirq إلى موترات. يتيح لك هذا إرسال كائنات Cirq إلى طبقاتنا الكمومية وعملياتنا الكمومية . يمكن استدعاء الوظيفة في قوائم أو مصفوفات دوائر Cirq و Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
يؤدي هذا إلى ترميز كائنات Cirq على أنها tf.string التي تقوم عمليات tfq بفك تشفيرها حسب الحاجة.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 محاكاة دارة الخلط
يوفر TFQ طرقًا لحساب قيم التوقع والعينات ومتجهات الحالة. في الوقت الحالي ، دعنا نركز على قيم التوقع .
أعلى واجهة مستوى لحساب قيم التوقعات هي tfq.layers.Expectation layer ، وهي طبقة tf.keras.Layer . في أبسط أشكالها ، هذه الطبقة تعادل محاكاة دارة ذات معلمات عبر العديد من cirq.ParamResolvers . ومع ذلك ، يسمح TFQ بتجميع دلالات TensorFlow التالية ، وتتم محاكاة الدوائر باستخدام كود C ++ الفعال.
أنشئ مجموعة من القيم لاستبدال المعلمات a و b الخاصة بنا:
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
يتطلب تنفيذ دارة التجميع على قيم المعلمات في Cirq حلقة:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
تم تبسيط العملية نفسها في TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. التحسين الكمي الكلاسيكي الهجين
الآن بعد أن رأيت الأساسيات ، دعنا نستخدم TensorFlow Quantum لبناء شبكة عصبية هجينة كلاسيكية الكم . سوف تقوم بتدريب شبكة عصبية كلاسيكية للتحكم في كيوبت واحد. سيتم تحسين التحكم لإعداد الكيوبت بشكل صحيح في الحالة 0 أو 1 ، للتغلب على خطأ معايرة منهجي محاكى. يوضح هذا الشكل العمارة:
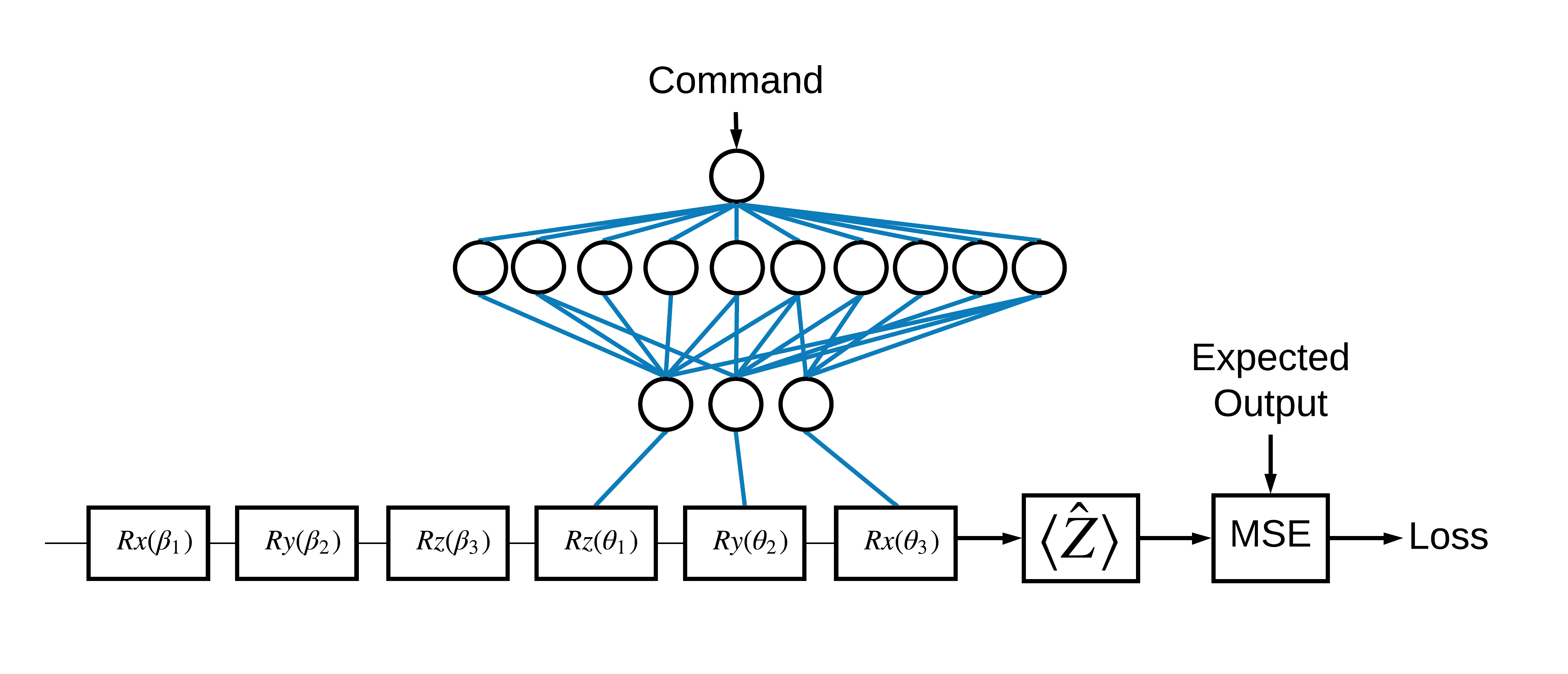
حتى بدون وجود شبكة عصبية ، فهذه مشكلة مباشرة يجب حلها ، لكن الموضوع مشابه لمشاكل التحكم الكمي الحقيقية التي قد تحلها باستخدام TFQ. يوضح مثالاً شاملاً للحساب الكلاسيكي الكمي باستخدام tfq.layers.ControlledPQC (الدائرة الكمية المعلمة) داخل نموذج tf.keras.Model .
لتنفيذ هذا البرنامج التعليمي ، يتم تقسيم هذه البنية إلى 3 أجزاء:
- دارة الإدخال أو دارة نقطة البيانات : البوابات الثلاثة الأولى \(R\) .
- الدائرة المتحكم بها: البوابات الثلاثة الأخرى \(R\) .
- المتحكم : الشبكة العصبية الكلاسيكية التي تحدد معلمات الدائرة المتحكم فيها.
2.1 تعريف الدائرة المتحكم بها
حدد دوران بت واحد قابل للتعلم ، كما هو موضح في الشكل أعلاه. هذا سوف يتوافق مع دائرتنا الخاضعة للرقابة.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 وحدة التحكم
حدد الآن شبكة التحكم:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
بالنظر إلى مجموعة من الأوامر ، تقوم وحدة التحكم بإخراج مجموعة من إشارات التحكم للدائرة المتحكم فيها.
تتم تهيئة وحدة التحكم بشكل عشوائي بحيث لا تكون هذه المخرجات مفيدة حتى الآن.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 قم بتوصيل وحدة التحكم بالدائرة
استخدم tfq لتوصيل وحدة التحكم بالدائرة المتحكم بها ، كنموذج keras.Model واحد.
راجع دليل Keras Functional API لمزيد من المعلومات حول هذا النمط من تعريف النموذج.
حدد أولاً مدخلات النموذج:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
بعد ذلك ، قم بتطبيق العمليات على تلك المدخلات ، لتحديد الحساب.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
الآن قم بتجميع هذه العملية الحسابية كنموذج tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
تتم الإشارة إلى بنية الشبكة بواسطة مخطط النموذج أدناه. قارن مخطط النموذج هذا بمخطط العمارة للتحقق من صحته.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
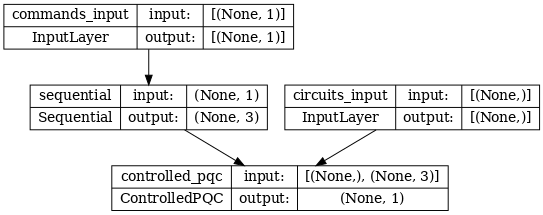
يأخذ هذا النموذج مدخلين: أوامر وحدة التحكم ، ودائرة الإدخال التي تحاول وحدة التحكم تصحيح إخراجها.
2.4 مجموعة البيانات
يحاول النموذج إخراج قيمة القياس الصحيحة الصحيحة لـ \(\hat{Z}\) لكل أمر. الأوامر والقيم الصحيحة معرّفة أدناه.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
هذه ليست مجموعة بيانات التدريب الكاملة لهذه المهمة. تحتاج كل نقطة بيانات في مجموعة البيانات أيضًا إلى دائرة إدخال.
2.4 تعريف دارة الإدخال
تحدد دائرة الإدخال أدناه المعايرة العشوائية الخاطئة التي سيتعلم النموذج تصحيحها.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
هناك نسختان من الدائرة ، واحدة لكل نقطة بيانات.
datapoint_circuits.shape
TensorShape([2])
2.5 التدريب
باستخدام المدخلات المحددة ، يمكنك اختبار نموذج tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
قم الآن بتشغيل عملية تدريب قياسية لضبط هذه القيم نحو المخرجات expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
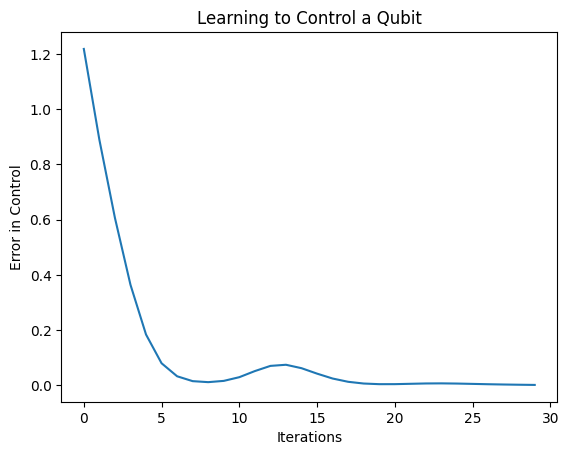
من هذه المؤامرة ، يمكنك أن ترى أن الشبكة العصبية قد تعلمت التغلب على سوء التقدير المنهجي.
2.6 التحقق من النواتج
الآن استخدم النموذج المدرب لتصحيح أخطاء معايرة الكيوبت. مع سيرك:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
توفر قيمة دالة الخسارة أثناء التدريب فكرة تقريبية عن مدى جودة تعلم النموذج. كلما انخفضت الخسارة ، كلما اقتربت قيم التوقع في الخلية أعلاه من القيم desired_values . إذا لم تكن مهتمًا بقيم المعلمات ، فيمكنك دائمًا التحقق من المخرجات أعلاه باستخدام tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 تعلم إعداد eigenstates لمشغلين مختلفين
كان اختيار \(\pm \hat{Z}\) المقابل لـ 1 و 0 تعسفياً. كان من الممكن أن تريد بسهولة أن تتوافق 1 مع \(+ \hat{Z}\) eigenstate و 0 لتتوافق مع \(-\hat{X}\) eigenstate. تتمثل إحدى طرق تحقيق ذلك في تحديد عامل قياس مختلف لكل أمر ، كما هو موضح في الشكل أدناه:
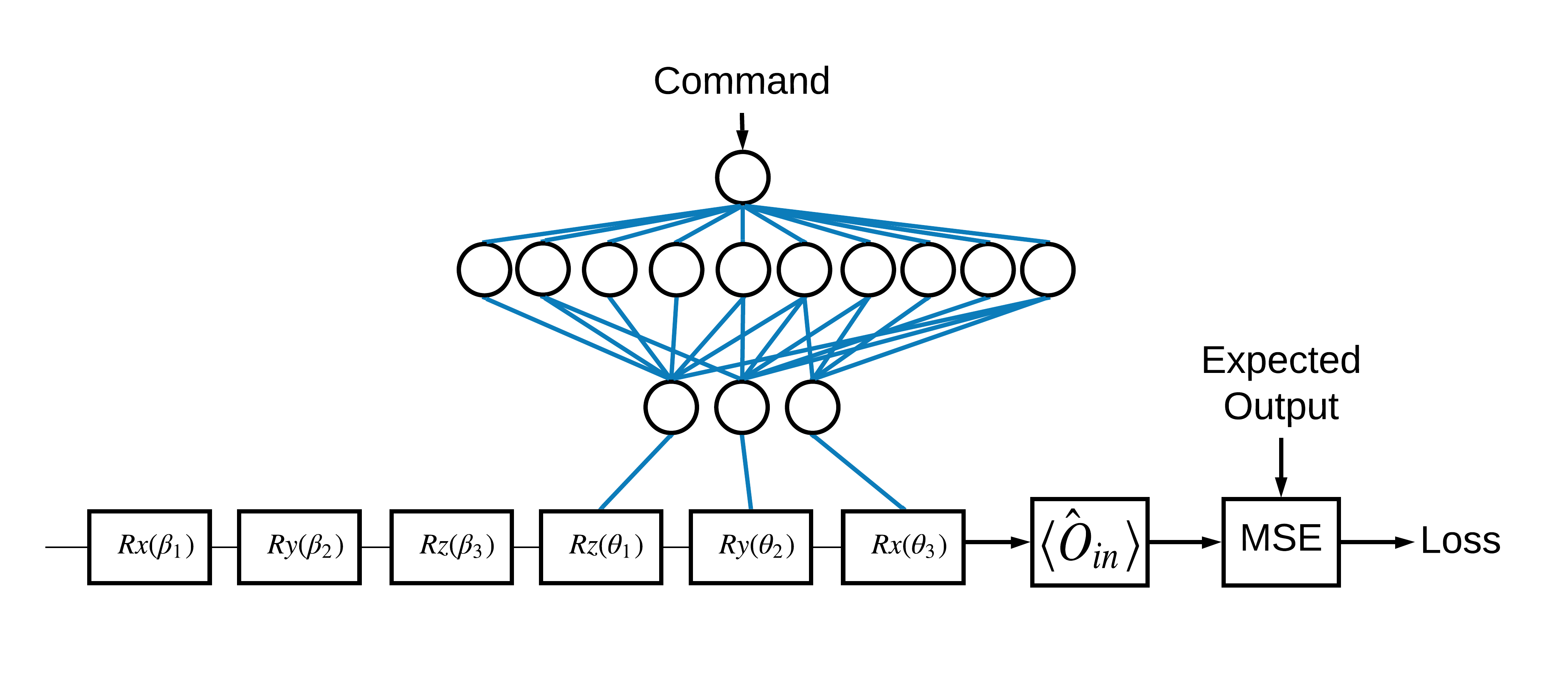
هذا يتطلب استخدام tfq.layers.Expectation . نمت الآن مدخلاتك لتشمل ثلاثة كائنات: الدائرة ، والأمر ، والمشغل. الناتج لا يزال هو قيمة التوقع.
3.1 تعريف نموذج جديد
دعنا نلقي نظرة على النموذج لإنجاز هذه المهمة:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
ها هي شبكة التحكم:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
اجمع بين الدائرة ووحدة التحكم في وحدة keras.Model واحدة tfq
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 مجموعة البيانات
ستقوم الآن أيضًا بتضمين المشغلين الذين ترغب في قياسهم لكل نقطة بيانات توفرها لـ model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 التدريب
الآن بعد أن أصبح لديك مدخلات ومخرجات جديدة ، يمكنك التدريب مرة أخرى باستخدام keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
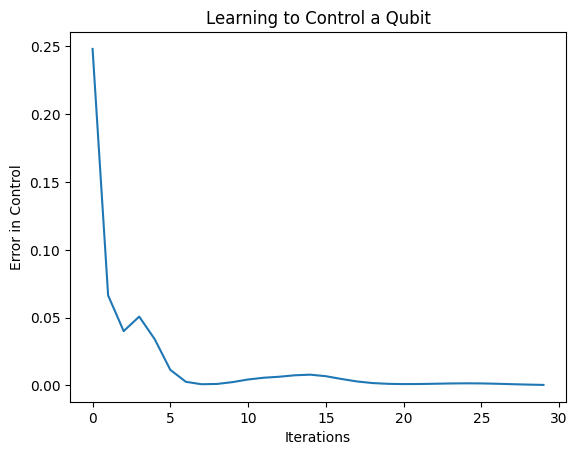
انخفضت وظيفة الخسارة إلى الصفر.
controller متاح كنموذج قائم بذاته. اتصل بوحدة التحكم وتحقق من استجابتها لكل إشارة أمر. قد يستغرق الأمر بعض العمل لمقارنة هذه المخرجات بشكل صحيح بمحتويات random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
