 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu öğretici, kuantum devrelerinin beklenti değerleri için gradyan hesaplama algoritmalarını araştırır.
Bir kuantum devresinde belirli bir gözlemlenebilirin beklenen değerinin gradyanını hesaplamak ilgili bir süreçtir. Gözlemlenebilirlerin beklenti değerleri, yazılması kolay analitik gradyan formüllerine sahip matris çarpımı veya vektör toplama gibi geleneksel makine öğrenimi dönüşümlerinin aksine, her zaman kolay yazılabilen analitik gradyan formüllerine sahip olma lüksüne sahip değildir. Sonuç olarak, farklı senaryolar için kullanışlı olan farklı kuantum gradyan hesaplama yöntemleri vardır. Bu öğretici, iki farklı farklılaşma şemasını karşılaştırır ve karşılaştırır.
Kurmak
pip install tensorflow==2.7.0
TensorFlow Quantum'u yükleyin:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Şimdi TensorFlow ve modül bağımlılıklarını içe aktarın:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Ön
Kuantum devreleri için gradyan hesaplama kavramını biraz daha somutlaştıralım. Bunun gibi parametreli bir devreniz olduğunu varsayalım:
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Bir gözlemlenebilir ile birlikte:
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
Bu operatöre baktığınızda, \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
ve \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) tanımlarsanız, o zaman \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\). Bunu kontrol edelim:
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. Farklılaştırıcıya duyulan ihtiyaç
Daha büyük devrelerde, belirli bir kuantum devresinin gradyanlarını kesin olarak hesaplayan bir formüle sahip olduğunuz için her zaman çok şanslı olmayacaksınız. Gradyanı hesaplamak için basit bir formülün yeterli olmaması durumunda, tfq.differentiators.Differentiator . Differentiators.Differentiator sınıfı, devrelerinizin gradyanlarını hesaplamak için algoritmalar tanımlamanıza izin verir. Örneğin, yukarıdaki örneği TensorFlow Quantum'da (TFQ) şu şekilde yeniden oluşturabilirsiniz:
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
Ancak, örneklemeye dayalı tahmin beklentisine geçerseniz (gerçek bir cihazda ne olur) değerler biraz değişebilir. Bu, artık kusurlu bir tahmininiz olduğu anlamına gelir:
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
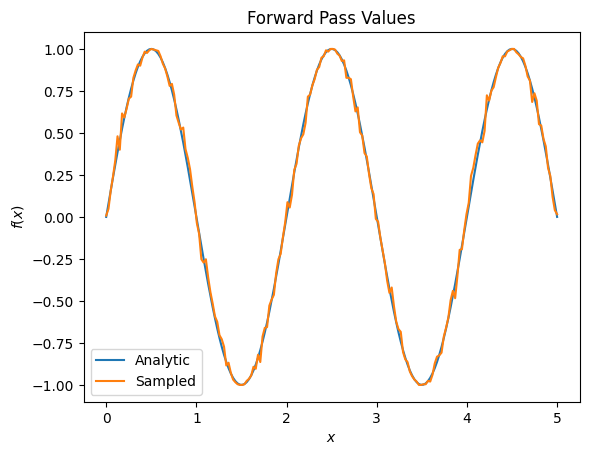
Bu, gradyanlar söz konusu olduğunda hızla ciddi bir doğruluk sorununa dönüşebilir:
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
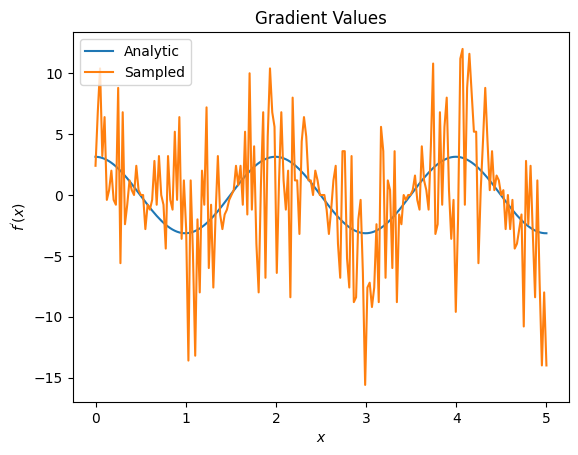
Burada, sonlu fark formülünün analitik durumda gradyanları hesaplamak için hızlı olmasına rağmen, örnekleme tabanlı yöntemlere geldiğinde çok gürültülü olduğunu görebilirsiniz. İyi bir eğimin hesaplanabilmesi için daha dikkatli teknikler kullanılmalıdır. Daha sonra, analitik beklenti gradyan hesaplamaları için pek uygun olmayan, ancak gerçek dünyadaki örnek tabanlı durumda çok daha iyi performans gösteren çok daha yavaş bir tekniğe bakacaksınız:
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
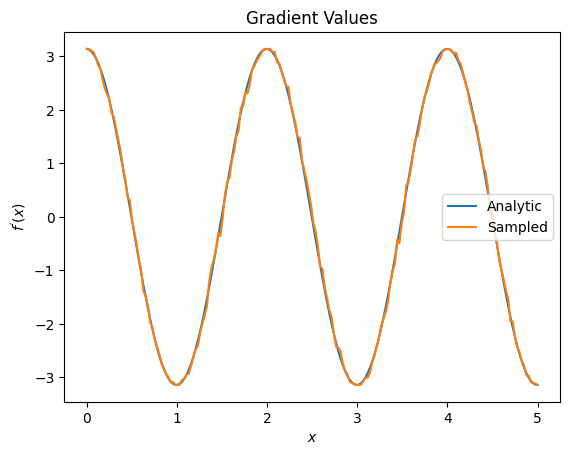
Yukarıdan, belirli farklılaştırıcıların belirli araştırma senaryoları için en iyi şekilde kullanıldığını görebilirsiniz. Genel olarak, cihaz gürültüsüne vb. karşı dayanıklı olan daha yavaş örnek tabanlı yöntemler, daha "gerçek dünya" ortamında algoritmaları test ederken veya uygularken büyük fark yaratır. Sonlu fark gibi daha hızlı yöntemler, analitik hesaplamalar için harikadır ve daha yüksek verim istiyorsunuz, ancak henüz algoritmanızın cihaz uygulanabilirliği ile ilgilenmiyorsunuz.
3. Çoklu gözlemlenebilirler
İkinci bir gözlemlenebiliri tanıtalım ve TensorFlow Quantum'un tek bir devre için birden çok gözlemlenebiliri nasıl desteklediğini görelim.
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
Bu gözlemlenebilir öncekiyle aynı devre ile kullanılıyorsa, o zaman \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) ve \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\)'a sahip olursunuz. Hızlı bir kontrol yapın:
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
Bu bir eşleşme (yeterince yakın).
Şimdi \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) tanımlarsanız, o zaman \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\). Bir devre ile birlikte kullanmak üzere TensorFlow Quantum'da birden fazla gözlemlenebilir tanımlamak, \(g\)öğesine daha fazla terim eklemekle eşdeğerdir.
Bu, bir devredeki belirli bir sembolün gradyanının, o devreye uygulanan o sembol için gözlemlenebilir her birine göre gradyanların toplamına eşit olduğu anlamına gelir. Bu, TensorFlow gradyan alma ve geri yayılımla uyumludur (burada tüm gözlemlenebilirler üzerindeki gradyanların toplamını belirli bir sembol için gradyan olarak verirsiniz).
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
Burada ilk girdinin Pauli X'e göre beklenti olduğunu ve ikincisinin Pauli Z'ye göre beklenti olduğunu görüyorsunuz. Şimdi gradyanı aldığınızda:
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
Burada her gözlemlenebilir için gradyanların toplamının gerçekten de \(\alpha\)gradyanı olduğunu doğruladınız. Bu davranış, tüm TensorFlow Quantum farklılaştırıcıları tarafından desteklenir ve TensorFlow'un geri kalanıyla uyumlulukta çok önemli bir rol oynar.
4. Gelişmiş kullanım
TensorFlow Quantum alt sınıfı tfq.differentiators.Differentiator . Differentiators.Differentiator içinde bulunan tüm farklılaştırıcılar. Bir farklılaştırıcı uygulamak için, kullanıcının iki arabirimden birini uygulaması gerekir. Standart, degradenin bir tahminini elde etmek için hangi devrelerin ölçüleceğini temel sınıfa söyleyen get_gradient_circuits uygulamaktır. Alternatif olarak, differentiate_analytic ve differentiate_sampled öğelerini aşırı yükleyebilirsiniz; tfq.differentiators.Adjoint . Differentiators.Adjoint sınıfı bu yolu kullanır.
Aşağıdaki, bir devrenin gradyanını uygulamak için TensorFlow Quantum'u kullanır. Küçük bir parametre kaydırma örneği kullanacaksınız.
Yukarıda tanımladığınız devreyi hatırlayın, \(|\alpha⟩ = Y^{\alpha}|0⟩\). Daha önce olduğu gibi, bu devrenin \(X\) tutucu11 gözlenebilir, \(f(\alpha) = ⟨\alpha|X|\alpha⟩\)tutucu12'ye karşı beklenen değeri olarak bir fonksiyon tanımlayabilirsiniz. Parametre kaydırma kurallarını kullanarak, bu devre için türevin olduğunu bulabilirsiniz.
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
get_gradient_circuits işlevi, bu türevin bileşenlerini döndürür.
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
Differentiator temel sınıfı, yukarıda gördüğünüz parametre kaydırma formülünde olduğu gibi türevi hesaplamak için get_gradient_circuits döndürülen bileşenleri kullanır. Bu yeni farklılaştırıcı artık mevcut tfq.layer nesneleri ile kullanılabilir:
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
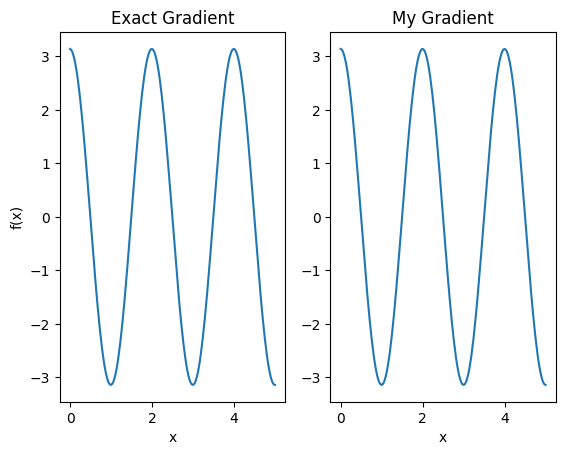
Bu yeni farklılaştırıcı artık farklılaştırılabilir operasyonlar oluşturmak için kullanılabilir.
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
