 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
W tym samouczku omówiono algorytmy obliczania gradientu dla wartości oczekiwanych obwodów kwantowych.
Obliczanie gradientu wartości oczekiwanej pewnej obserwowalnej w obwodzie kwantowym jest procesem złożonym. Wartości oczekiwane obserwabli nie mają luksusu posiadania analitycznych formuł gradientów, które zawsze są łatwe do zapisania — w przeciwieństwie do tradycyjnych przekształceń uczenia maszynowego, takich jak mnożenie macierzy lub dodawanie wektorów, które mają analityczne formuły gradientów, które są łatwe do zapisania. W rezultacie istnieją różne metody obliczania gradientów kwantowych, które przydają się w różnych scenariuszach. Ten samouczek porównuje i kontrastuje dwa różne schematy różnicowania.
Ustawiać
pip install tensorflow==2.7.0
Zainstaluj TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Teraz zaimportuj TensorFlow i zależności modułu:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Wstępne
Stwórzmy bardziej konkretne pojęcie obliczania gradientu dla obwodów kwantowych. Załóżmy, że masz sparametryzowany obwód taki jak ten:
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Wraz z obserwowalnym:
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
Patrząc na ten operator wiesz, że \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
a jeśli zdefiniujesz \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) to \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\). Sprawdźmy to:
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. Potrzeba wyróżnika
W przypadku większych obwodów nie zawsze będziesz miał szczęście mieć wzór, który precyzyjnie oblicza gradienty danego obwodu kwantowego. W przypadku, gdy prosta formuła nie wystarczy do obliczenia gradientu, klasa tfq.differentiators.Differentiator umożliwia zdefiniowanie algorytmów obliczania gradientów Twoich obwodów. Na przykład możesz odtworzyć powyższy przykład w TensorFlow Quantum (TFQ) za pomocą:
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
Jeśli jednak przełączysz się na szacowanie oczekiwań na podstawie próbkowania (co miałoby miejsce na prawdziwym urządzeniu), wartości mogą się nieco zmienić. Oznacza to, że masz teraz niedoskonałe oszacowanie:
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
Może to szybko spowodować poważny problem z dokładnością, jeśli chodzi o gradienty:
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
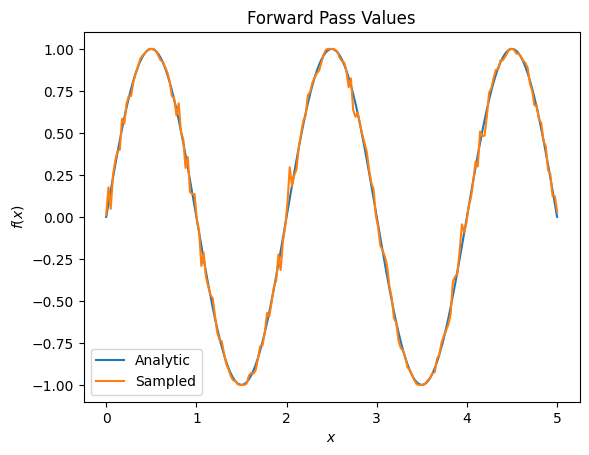
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
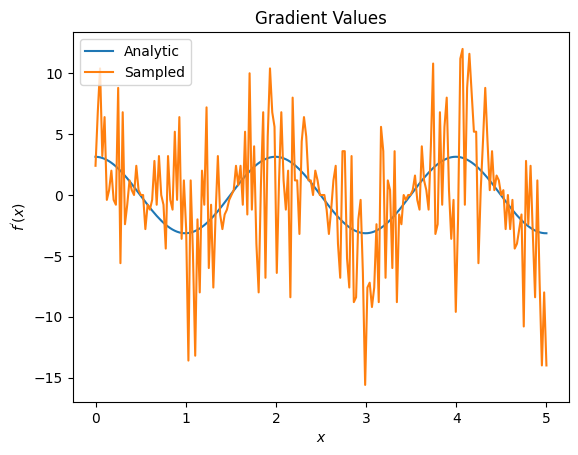
Tutaj widać, że chociaż formuła różnic skończonych pozwala szybko obliczyć same gradienty w przypadku analitycznym, to w przypadku metod opartych na próbkowaniu było zbyt głośno. Należy zastosować bardziej ostrożne techniki, aby zapewnić, że można obliczyć dobre nachylenie. Następnie przyjrzymy się znacznie wolniejszej technice, która nie byłaby tak dobrze dopasowana do analitycznych obliczeń gradientu oczekiwań, ale działa znacznie lepiej w przypadku rzeczywistych próbek:
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
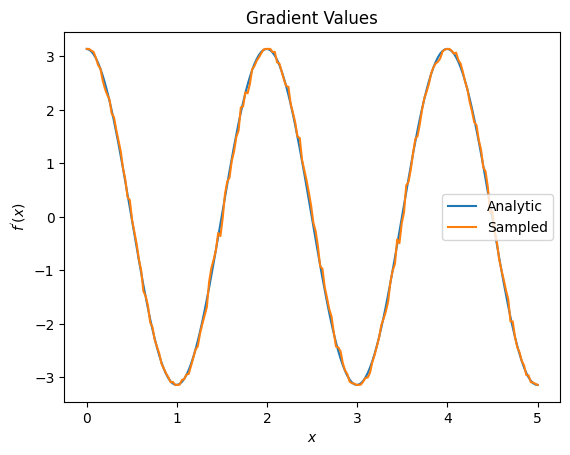
Z powyższego widać, że pewne wyróżniki najlepiej wykorzystać do konkretnych scenariuszy badawczych. Ogólnie rzecz biorąc, wolniejsze metody oparte na próbkach, które są odporne na szum urządzenia itp., są świetnymi wyróżnikami podczas testowania lub implementowania algorytmów w bardziej „rzeczywistym” otoczeniu. Szybsze metody, takie jak różnica skończona, świetnie nadają się do obliczeń analitycznych i chcesz uzyskać wyższą przepustowość, ale nie martwisz się jeszcze o rentowność swojego algorytmu.
3. Wiele obserwowalnych
Przedstawmy drugi obserwowalny i zobaczmy, jak TensorFlow Quantum obsługuje wiele obserwowalnych dla jednego obwodu.
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
Jeśli ten obserwowalny jest używany z tym samym obwodem co poprzednio, masz \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) i \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\). Wykonaj szybkie sprawdzenie:
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
To pasuje (wystarczająco blisko).
Teraz, jeśli zdefiniujesz \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) to \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\). Zdefiniowanie więcej niż jednego obserwowalnego w TensorFlow Quantum do użycia wraz z obwodem jest równoznaczne z dodaniem większej liczby warunków do \(g\).
Oznacza to, że gradient określonego symbolu w obwodzie jest równy sumie gradientów w odniesieniu do każdego obserwowalnego dla tego symbolu zastosowanego do tego obwodu. Jest to zgodne z pobieraniem gradientów i propagacją wsteczną TensorFlow (gdzie podajesz sumę gradientów na wszystkich obserwowalnych jako gradient dla konkretnego symbolu).
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
Tutaj widzisz, że pierwszy wpis to oczekiwanie na Pauli X, a drugi to oczekiwanie na Pauli Z. Teraz, gdy weźmiesz gradient:
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
Tutaj sprawdziłeś, że suma gradientów dla każdego obserwowalnego jest rzeczywiście gradientem \(\alpha\). To zachowanie jest obsługiwane przez wszystkie wyróżniki TensorFlow Quantum i odgrywa kluczową rolę w kompatybilności z resztą TensorFlow.
4. Zaawansowane użycie
Wszystkie wyróżniki, które istnieją w podklasie TensorFlow Quantum tfq.differentiators.Differentiator . Aby zaimplementować wyróżnik, użytkownik musi zaimplementować jeden z dwóch interfejsów. Standardem jest implementacja get_gradient_circuits , która informuje klasę bazową, które obwody należy zmierzyć, aby uzyskać oszacowanie gradientu. Alternatywnie można przeciążyć differentiate_analytic i differentiate_sampled ; klasa tfq.differentiators.Adjoint podąża tą drogą.
Poniższe używa TensorFlow Quantum do zaimplementowania gradientu obwodu. Użyjesz małego przykładu przesuwania parametrów.
Przypomnij sobie obwód, który zdefiniowałeś powyżej, \(|\alpha⟩ = Y^{\alpha}|0⟩\). Tak jak poprzednio, możesz zdefiniować funkcję jako wartość oczekiwaną tego obwodu względem obserwowalnego \(X\) , \(f(\alpha) = ⟨\alpha|X|\alpha⟩\). Używając reguł przesuwania parametrów , dla tego obwodu, możesz znaleźć pochodną
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
Funkcja get_gradient_circuits zwraca składniki tej pochodnej.
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
Klasa bazowa Differentiator wykorzystuje komponenty zwrócone z get_gradient_circuits do obliczenia pochodnej, tak jak we wzorze przesunięcia parametrów, który widzieliśmy powyżej. Ten nowy wyróżnik może być teraz używany z istniejącymi obiektami tfq.layer :
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
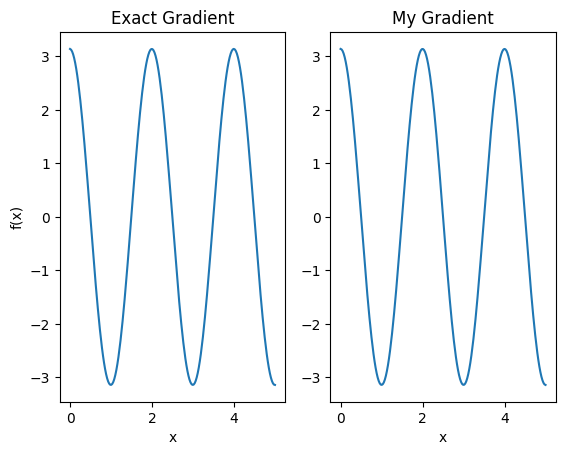
Ten nowy wyróżnik może być teraz używany do generowania różnicowalnych operacji.
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
